Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets
Abstract
:1. Introduction
2. Simplified Neutrosophic Sets
- (1)
- The sufficient and necessary condition of B ⊆ C for SvNSs is TB(ai) ≤ TC(ai), UB(ai) ≥ UC(ai), and FB(ai) ≥ FC(ai), while that for IvNSs is , , , , , and ;
- (2)
- The sufficient and necessary condition of B = C is B ⊆ C and C ⊆ B;
- (3)
- The complement of a SvNS B is , and then that of an IvNS B is ;
- (4)
- If B and C are SvNSs, then:
3. Simplified Neutrosophic Generalized Distance-based Entropy and Dimension Root Entropy
3.1. Simplified Neutrosophic Generalized Distance-Based Entropy
3.2. Simplified Neutrosophic Dimension Root Entropy
4. Comparative Analysis of Entropy Measures for IvNSs
5. Decision-Making Example Using Simplified Neutrosophic Entropy in IvNS Setting
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Probability measure of fuzzy events. J. Math. Anal. Appl. 1968, 23, 421–427. [Google Scholar] [CrossRef]
- De Luca, A.S.; Termini, S. A definition of nonprobabilistic entropy in the setting of fuzzy set theory. Inf. Control. 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. Object background segmentation using new definitions of entropy. IEEE Proc. 1989, 366, 284–295. [Google Scholar] [CrossRef]
- Yager, R.R. On the measures of fuzziness and negation Part I: Membership in the unit interval. Int. J. Gen. Syst. 2008, 5, 221–229. [Google Scholar] [CrossRef]
- Parkash, O.; Sharma, P.K.; Mahajan, R. New measures of weighted fuzzy entropy and their applications for the study of maximum weighted fuzzy entropy principle. Inf. Sci. 2008, 178, 2389–2395. [Google Scholar] [CrossRef]
- Verma, R.; Sharma, B.D. On generalized exponential fuzzy entropy. Int. J. Math. Comput. Sci. 2011, 5, 1895–1898. [Google Scholar]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy on intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Valchos, I.K.; Sergiadis, G.D. Intuitionistic fuzzy information—A pattern recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Jiang, S.Y. A note on information entropy measure for vague sets. Inf. Sci. 2008, 178, 4184–4191. [Google Scholar] [CrossRef]
- Ye, J. Two effective measures of intuitionistic fuzzy entropy. Computing 2010, 87, 55–62. [Google Scholar] [CrossRef]
- Verma, R.; Sharma, B.D. Exponential entropy on intuitionistic fuzzy sets. Kybernetika 2013, 49, 114–127. [Google Scholar]
- Verma, R.; Sharma, B.D. On intuitionistic fuzzy entropy of order-alpha. Adv. Fuzzy Syst. 2014, 14, 1–8. [Google Scholar] [CrossRef]
- Verma, R.; Sharma, B.D. R-norm entropy on intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2015, 28, 327–335. [Google Scholar]
- Ye, J. Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets. Appl. Math. Model. 2010, 34, 3864–3870. [Google Scholar] [CrossRef]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, similarity measure of interval valued intuitionistic sets and their applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Xing, H.Y.; Liu, F.C.; Ye, J.; Tang, P. Some new entropy measures for interval-valued intuitionistic fuzzy sets based on distances and their relationships with similarity and inclusion measures. Inf. Sci. 2014, 283, 55–69. [Google Scholar] [CrossRef]
- Tian, H.; Li, J.; Zhang, F.; Xu, Y.; Cui, C.; Deng, Y.; Xiao, S. Entropy analysis on intuitionistic fuzzy sets and interval-valued intuitionistic fuzzy sets and its applications in mode assessment on open communities. J. Adv. Comput. Intell. Intell. Inform. 2018, 22, 147–155. [Google Scholar] [CrossRef]
- Majumder, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar] [CrossRef]
- Aydoğdu, A. On entropy and similarity measure of interval valued neutrosophic sets. Neutrosophic Sets Syst. 2015, 9, 47–49. [Google Scholar]
- Ye, J.; Du, S.G. Some distances, similarity and entropy measures for interval-valued neutrosophic sets and their relationship. Int. J. Mach. Learn. Cybern. 2017, 1–9. [Google Scholar] [CrossRef]
- Ye, J.; Cui, W.H. Exponential Entropy for Simplified Neutrosophic Sets and Its Application in Decision Making. Entropy 2018, 20, 357. [Google Scholar] [CrossRef]
- Cui, W.H.; Ye, J. Improved Symmetry Measures of Simplified Neutrosophic Sets and Their Decision-Making Method Based on a Sine Entropy Weight Model. Symmetry 2018, 10, 225. [Google Scholar] [CrossRef]
- Ye, J. Fault Diagnoses of Hydraulic Turbine Using the Dimension Root Similarity Measure of Single-valued Neutrosophic Sets. Intell. Autom. Soft Comput. 2017, 1–8. [Google Scholar] [CrossRef]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar] [CrossRef]
- Peng, J.-J.; Wang, J.-Q.; Wang, J.; Zhang, H.; Chen, X. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
| Hn | a1 = 1 | a2 = 2 | a3 = 3 | a4 = 4 | a5 = 5 |
|---|---|---|---|---|---|
| H | <1,[0.2, 0.3], [0.6, 0.6], [0.7, 0.8]> | <2,[0.3, 0.3], [0.5, 0.6], [0.5, 0.6]> | <3,[0.4, 0.5], [0.5, 0.5], [0, 0.1]> | <4,[1, 1], [0.4, 0.4], [0, 0.1]> | <5,[0.7, 0.8], [0.5, 0.5], [0, 0]> |
| H2 | <1,[0.04, 0.09], [0.84, 0.84], [0.91, 0.96]> | <2,[0.09, 0.09], [0.75, 0.84], [0.75, 0.84]> | <3,[0.16, 0.25], [0.75, 0.75], [0, 0.19]> | <4,[1, 1], [0.64, 0.64], [0, 0.19]> | <5,[0.49, 0.64], [0.75, 0.75], [0, 0]> |
| H3 | <1,[0.008, 0.027], [0.936, 0.936], [0.973, 0.992] | <2,[0.027, 0.027], [0.875, 0.936], [0.875, 0.936]> | <3,[0.064, 0.125], [0.875, 0.875], [0, 0.271]> | <4,[1, 1], [0.784, 0.784], [0, 0.271]> | <5,[0.343, 0.512], [0.875, 0.875], [0, 0]> |
| H4 | <1,[0.0016, 0.0081], [0.9744, 0.9744], [0.9919, 0.9984]> | <2,[0.0081, 0.0081], [0.9375, 0.9744], [0.9375, 0.9744]> | <3,[0.0256, 0.0625], [0.9375, 0.9375], [0, 0.3439]> | <4,[1, 1], [0.8704, 0.8704], [0, 0.3439]> | <5,[0.2401, 0.4096], [0.9375, 0.9375], [0, 0]> |
| Entropy Value | H | H2 | H3 | H4 | Ranking Order |
|---|---|---|---|---|---|
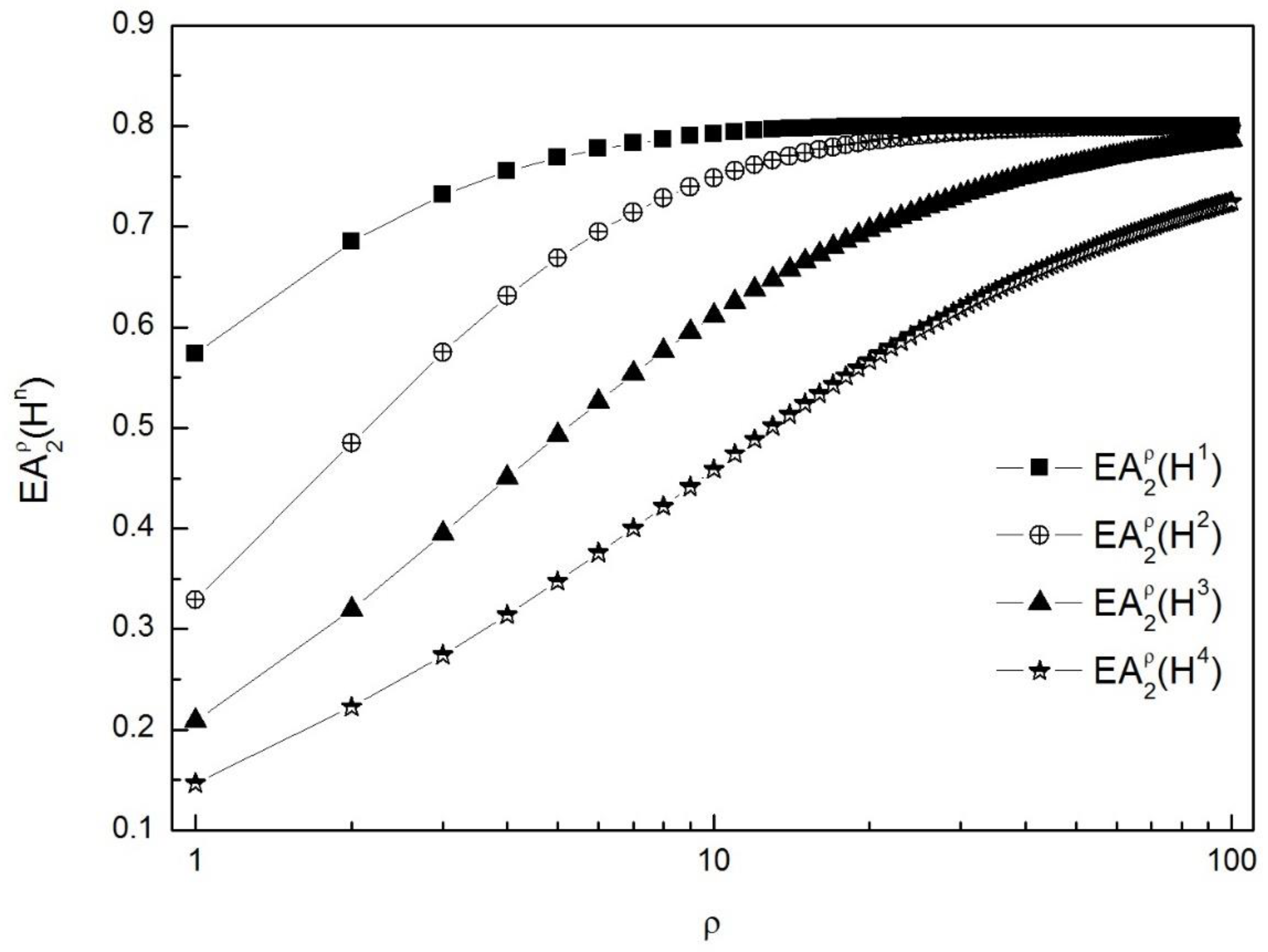
| 0.5733 | 0.3293 | 0.2083 | 0.1465 | > > > | |
| 0.6853 | 0.485 | 0.3193 | 0.2228 | > > > | |
| 0.7317 | 0.5749 | 0.395 | 0.2743 | > > > | |
| 0.7551 | 0.6313 | 0.4503 | 0.3143 | > > > | |
| 0.7686 | 0.6688 | 0.4927 | 0.3473 | > > > | |
| 0.7922 | 0.7484 | 0.611 | 0.4589 | > > > | |
| 0.7992 | 0.7848 | 0.6963 | 0.5667 | > > > | |
| 0.7999 | 0.7942 | 0.7309 | 0.6191 | > > > | |
| 0.8 | 0.7976 | 0.7499 | 0.6505 | > > > | |
| 0.8 | 0.799 | 0.7618 | 0.6719 | > > > | |
| 0.8 | 0.8 | 0.7862 | 0.7247 | = > > | |
| EB2(Hn) | 0.3534 | 0.2013 | 0.1231 | 0.0829 | EB2(H) > EB2(H2) > EB2(H3) > EB2(H4) |
| R1(Hn) [21] | 0.5733 | 0.3293 | 0.2083 | 0.1465 | R1(H) > R1(H2) > R1(H3) > R1(H4) |
| R2(Hn) [21] | 0.439 | 0.2824 | 0.175 | 0.1184 | R2(H) > R2(H2) > R2(H3) > R2(H4) |
| R3(Hn) [21] | 0.52 | 0.2707 | 0.1477 | 0.0811 | R3(H) > R3(H2) > R3(H3) > R3(H4) |
| R4(Hn) [21] | 0.24 | 0.1 | 0.0556 | 0.0228 | R4(H) > R4(H2) > R4(H3) > R4(H4) |
| R5(Hn) [19,21] | 0.9 | 0.6109 | 0.4464 | 0.366 | R5(H) > R5(H2) > R5(H3) > R5(H4) |
| R6(Hn) [20] | 0.2938 | 0.2684 | 0.2698 | 0.2719 | R6(H) > R6(H4) > R6(H3) > R6(H2) |
| R7(Hn) [22] | 0.6886 | 0.4919 | 0.3255 | 0.2272 | R7(H) > R7(H2) > R7(H3) > R7(H4) |
| R8(Hn) [23] | 0.6695 | 0.4521 | 0.2902 | 0.2027 | R8(H) > R8(H2) > R8(H3) > R8(H4) |
| g1 | g2 | g3 | g4 | Ranking Order | |
|---|---|---|---|---|---|
| 0.6333 | 0.5333 | 0.6556 | 0.4444 | g3 > g1 > g2 > g4 | |
| 0.8111 | 0.7333 | 0.8378 | 0.6356 | g3 > g1 > g2 > g4 | |
| 0.8867 | 0.832 | 0.9116 | 0.7351 | g3 > g1 > g2 > g4 | |
| 0.9252 | 0.8869 | 0.9466 | 0.7945 | g3 > g1 > g2 > g4 | |
| 0.9477 | 0.9203 | 0.9653 | 0.8332 | g3 > g1 > g2 > g4 | |
| 0.987 | 0.9804 | 0.993 | 0.9132 | g3 > g1 > g2 > g4 | |
| 0.9987 | 0.9981 | 0.9994 | 0.9412 | g3 > g1 > g2 > g4 | |
| 0.9999 | 0.9998 | 0.9999 | 0.9441 | g3 = g1 > g2 > g4 | |
| 1 | 1 | 1 | 0.9444 | g3 = g1 = g2 > g4 | |
| 1 | 1 | 1 | 0.9444 | g3 = g1 = g2 > g4 | |
| 1 | 1 | 1 | 0.9444 | g3 = g1 = g2 > g4 | |
| EB2(gi) | 0.4302 | 0.3572 | 0.4571 | 0.2945 | g3 > g1 > g2 > g4 |
| R1(gi) [21] | 0.6333 | 0.5333 | 0.6556 | 0.4444 | g3 > g1 > g2 > g4 |
| R2(gi) [21] | 0.5654 | 0.4836 | 0.5972 | 0.3963 | g3 > g1 > g2 > g4 |
| R3(gi) [21] | 0.5111 | 0.4222 | 0.5333 | 0.3333 | g3 > g1 > g2 > g4 |
| R4(gi) [21] | 0.4333 | 0.3 | 0.4667 | 0.2333 | g3 > g1 > g2 > g4 |
| R5(gi) [19,21] | 0.52 | 0.5133 | 0.57 | 0.3933 | g3 > g1 > g2 > g4 |
| R6(gi) [20] | 0.5687 | 0.364 | 0.5728 | 0.3818 | g3 > g1 > g4 > g2 |
| R7(gi) [22] | 0.8165 | 0.7406 | 0.8429 | 0.6431 | g3 > g1 > g2 > g4 |
| R8(gi) [23] | 0.7852 | 0.6985 | 0.8129 | 0.5997 | g3 > g1 > g2 > g4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.-H.; Ye, J. Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets. Entropy 2018, 20, 844. https://doi.org/10.3390/e20110844
Cui W-H, Ye J. Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets. Entropy. 2018; 20(11):844. https://doi.org/10.3390/e20110844
Chicago/Turabian StyleCui, Wen-Hua, and Jun Ye. 2018. "Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets" Entropy 20, no. 11: 844. https://doi.org/10.3390/e20110844
APA StyleCui, W.-H., & Ye, J. (2018). Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets. Entropy, 20(11), 844. https://doi.org/10.3390/e20110844





