Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids
Abstract
:1. Introduction
2. Analysis of the ORC System
3. Modeling
3.1. Entropy Modeling
3.2. Entransy Modeling
4. Global Model
4.1. Working Fluid Selection
4.2. Assumptions
- (a)
- The system is in a steady state.
- (b)
- Heat and friction losses, as well as the potential and kinetic energy, are neglected.
- (c)
- There are no pressure drops in the heat exchangers, condensers and pipes.
- (d)
- The ambient condition is set to 0.1 MPa.
- (e)
- The temperature of cooling water is set to 283.15 K.
- (f)
- The isentropic efficiencies of the expander and the pump are both set to be 0.8.
5. Results and Discussion
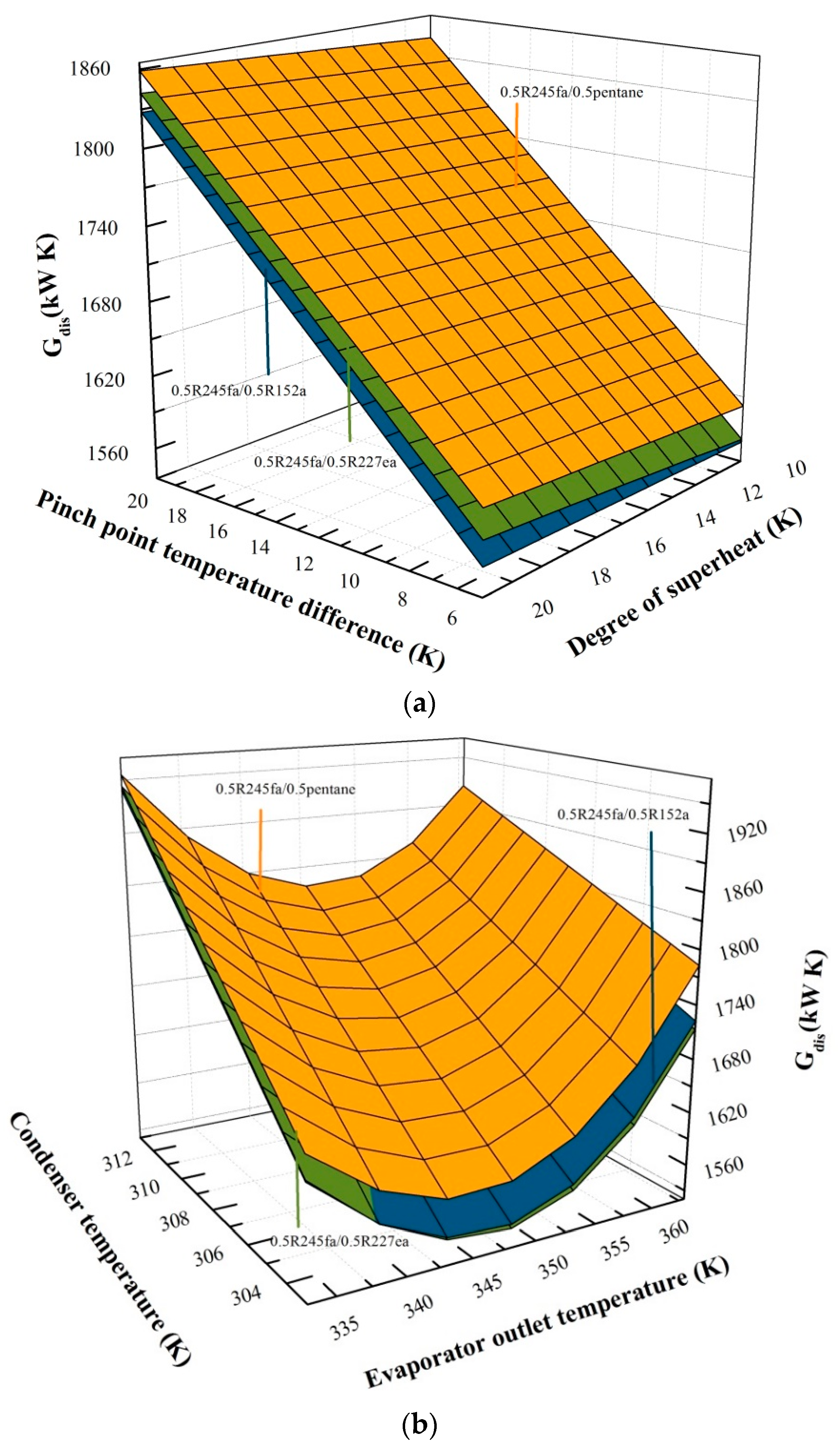
5.1. Effects of Operation Parameters on Entransy Dissipation
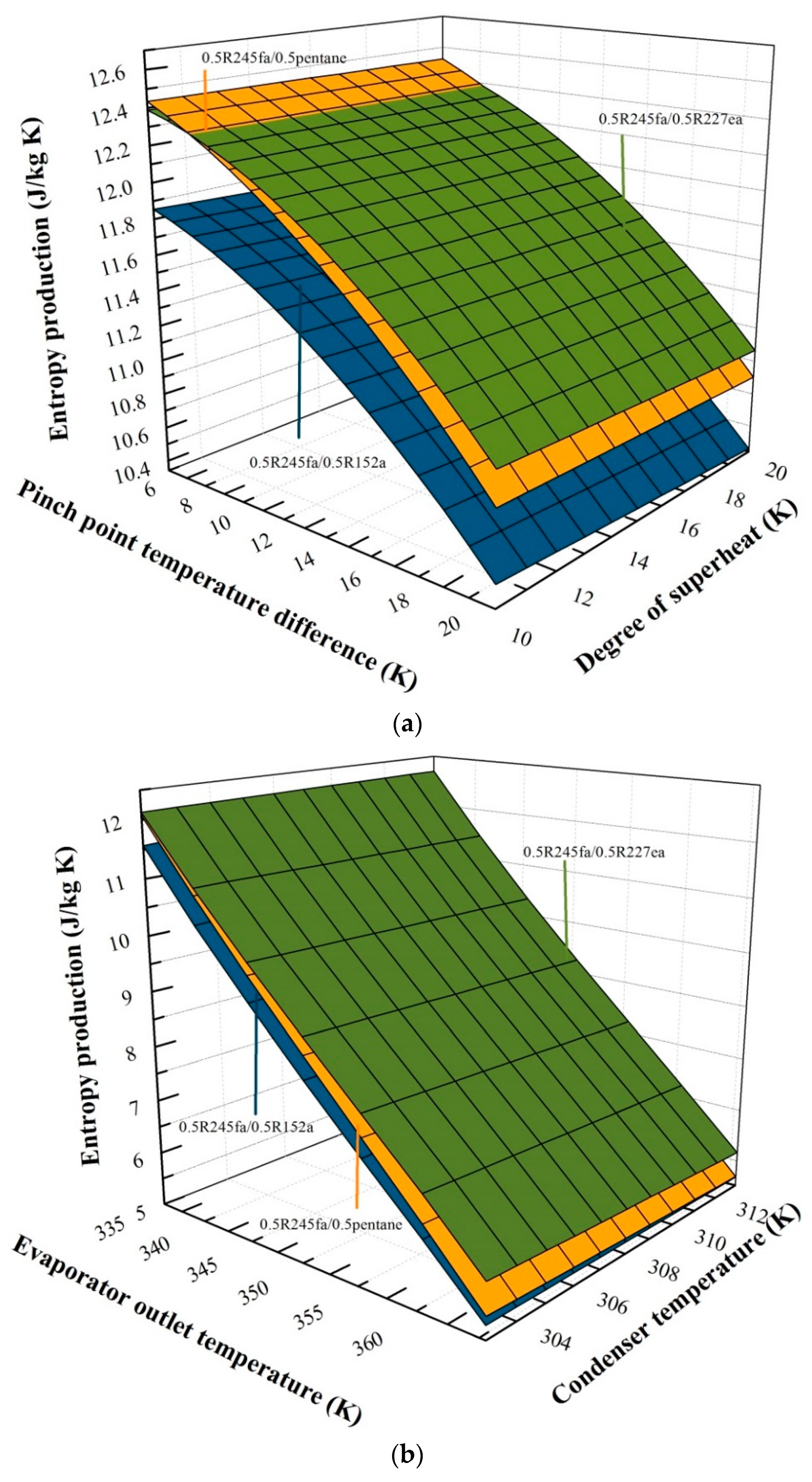
5.2. Effects of Operation Parameters for Entropy Generation
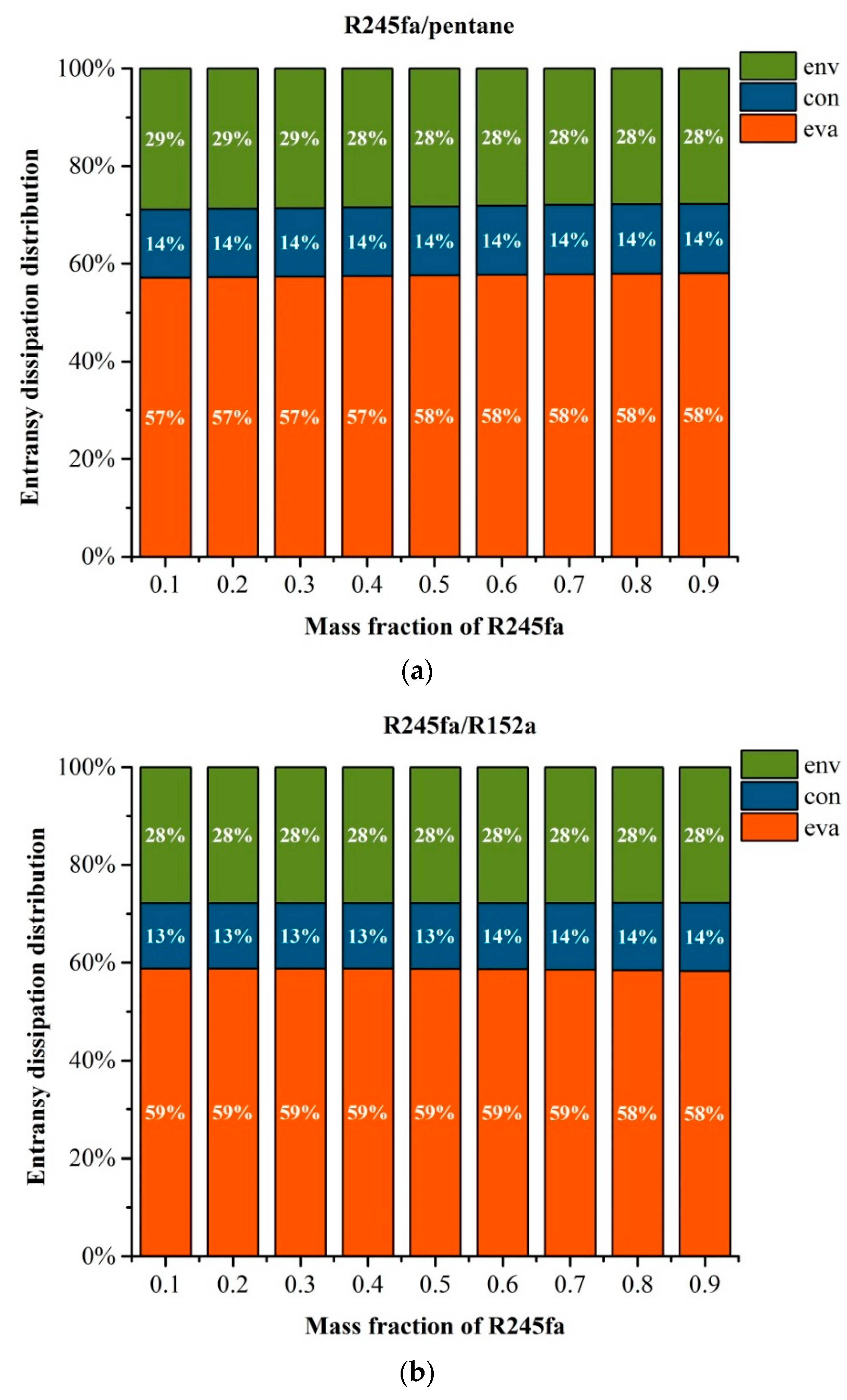
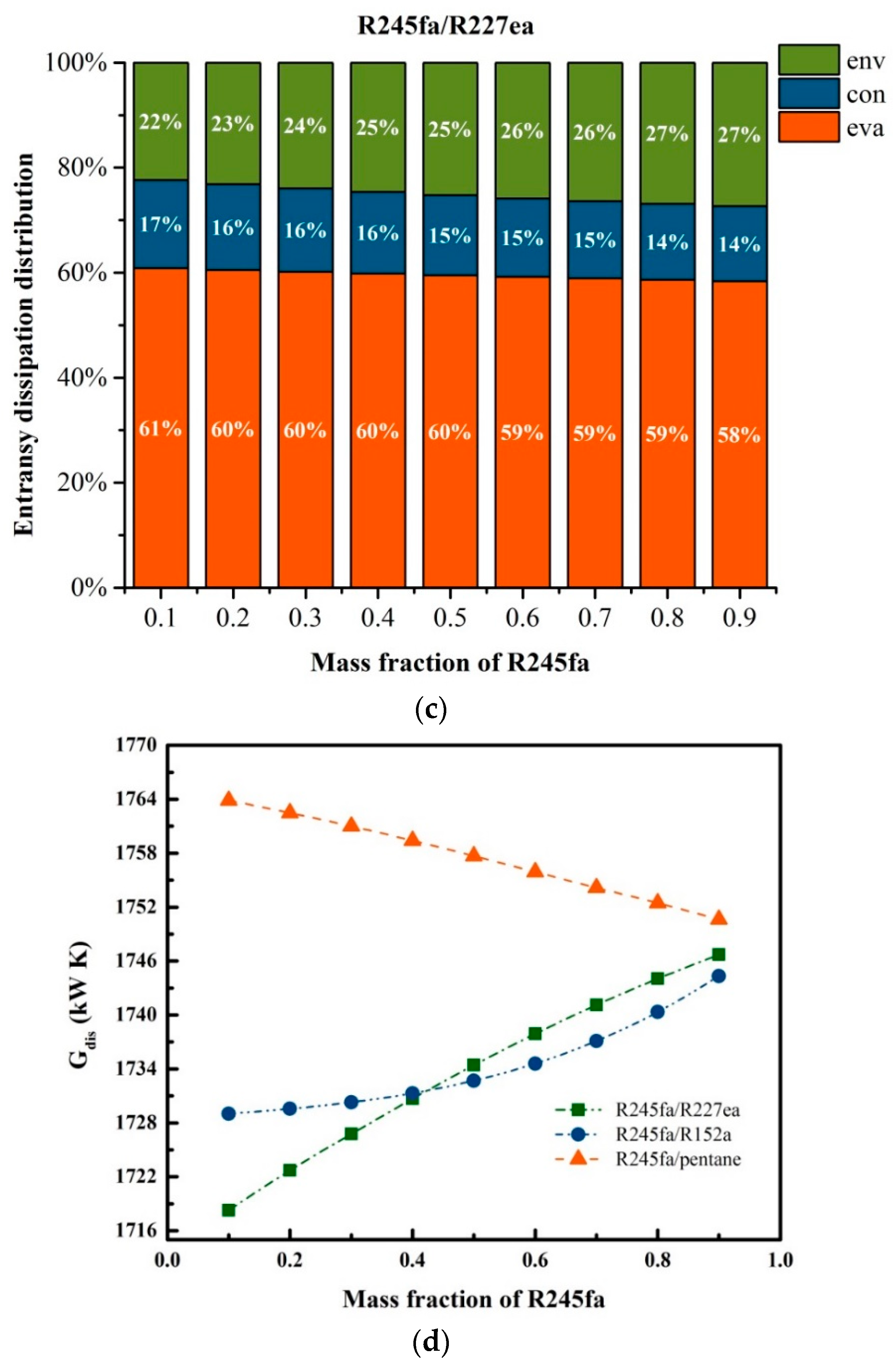
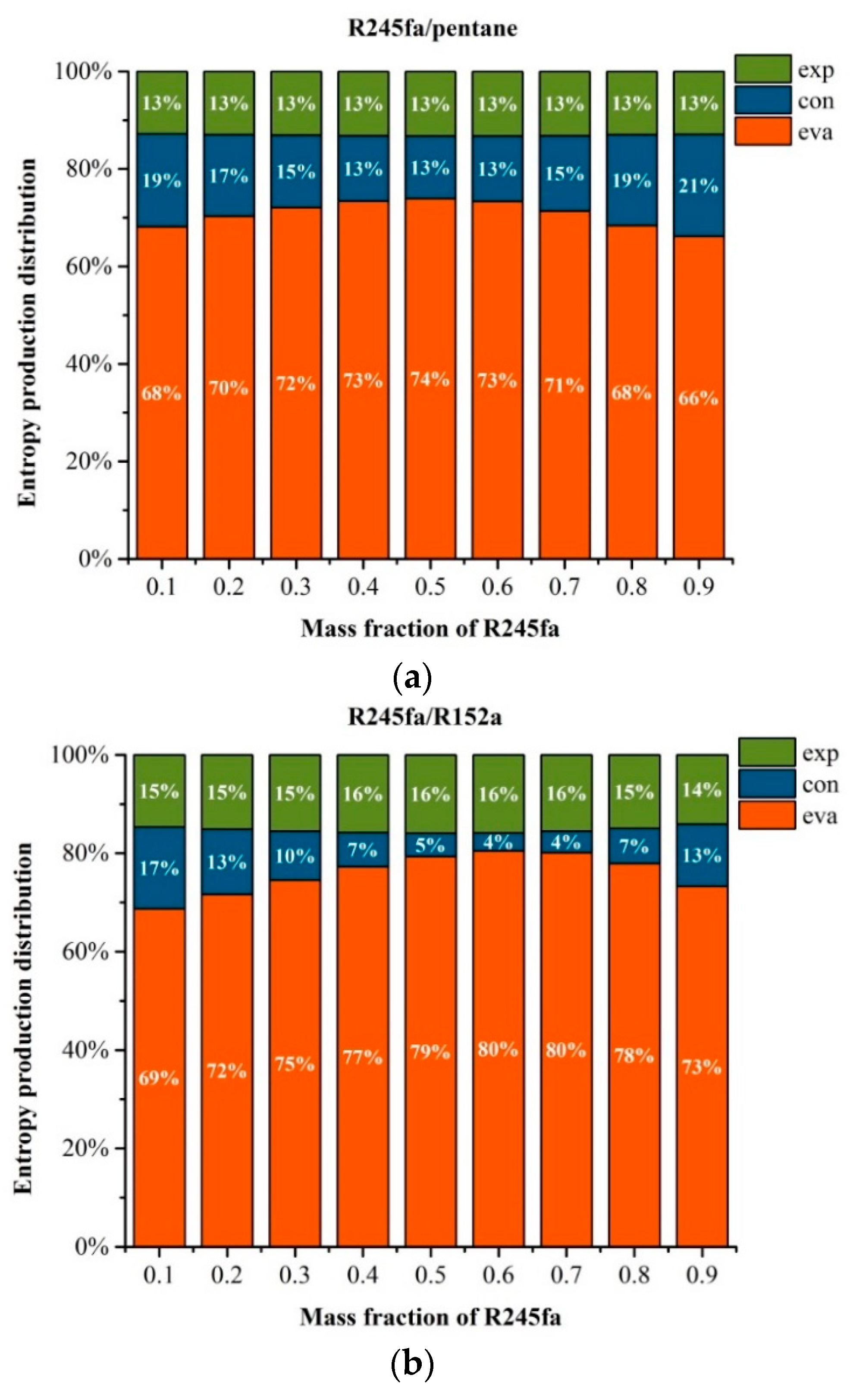
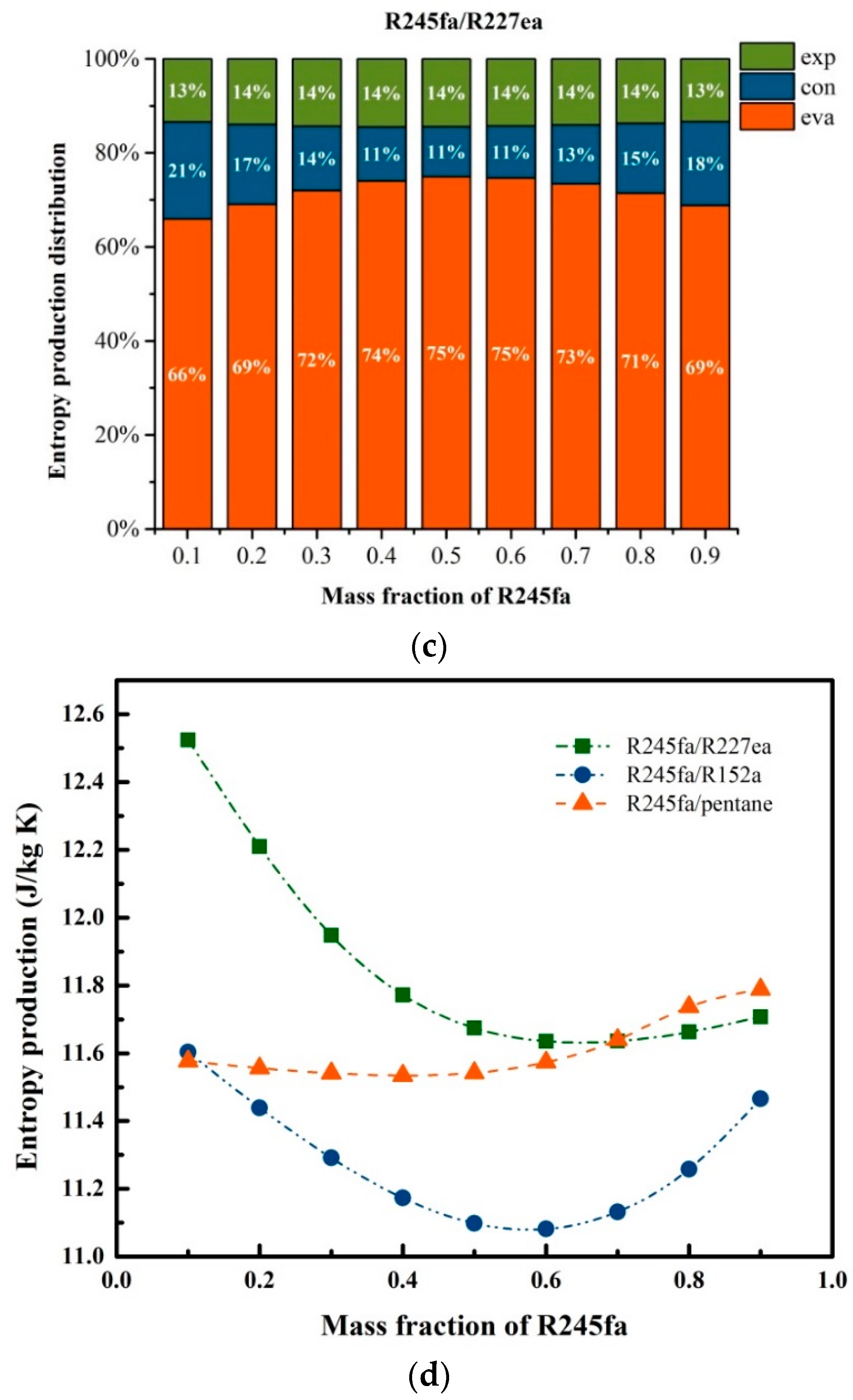
5.3. Effects of Mass Fraction on Entransy Dissipation and Entropy Generation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ORC | organic Rankine cycle |
| h | specific enthalpy, kJ/kg |
| m | mass flow rate, kg/s |
| Q | heat exchange power, kW; ratio of vapor moles to total moles |
| s | specific entropy, J/(kg·K) |
| T | temperature, K |
| W | power, kW |
| efficiency | |
| i | state points |
| glide | glide temperature |
| cr | critical point |
| in | inlet |
| l | liquid |
| out | outlet |
| sup | degree of superheat |
| wf | working fluid |
| con | condenser |
| eva | evaporator |
| col | cooling water |
| exp | expander |
| sys | system |
| env | environment |
| h | heat source |
| p | pump |
| PPTD | pinch point temperature difference |
References
- Roy, J.P.; Mishra, M.K.; Misra, A. Performance analysis of an Organic Rankine Cycle with superheating under different heat source temperature conditions. Appl. Energy 2011, 88, 2995–3004. [Google Scholar] [CrossRef]
- Rayegan, R.; Tao, Y.X. A procedure to select working fluids for solar organic Rankine cycles (ORCs). Renew. Energy 2011, 36, 659–670. [Google Scholar] [CrossRef]
- Guo, T.; Wang, H.X.; Zhang, S.J. Fluids and parameters optimization for a novel cogeneration system driven by low-temperature geothermal sources. Energy 2011, 36, 2639–2649. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Hamdullahpur, F.; Dincer, I. Greenhouse gas emission and exergy assessments of an integrated organic Rankine cycle with a biomass combustor for combined cooling, heating and power production. Appl. Therm. Eng. 2011, 31, 439–446. [Google Scholar] [CrossRef]
- Sun, F.; Ikegami, Y.; Jia, B.; Arima, H. Optimization design and exergy analysis of organic Rankine cycle in ocean thermal energy conversion. Appl. Ocean Res. 2012, 35, 38–46. [Google Scholar] [CrossRef]
- Macchi, E.; Astolfi, M. Organic Rankine Cycle (ORC) Power Systems: Technologies and Applications; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Song, J.; Gu, C.W. Parametric analysis of a dual loop Organic Rankine Cycle (ORC) system for engine waste heat recovery. Energy Convers. Manag. 2015, 105, 995–1005. [Google Scholar] [CrossRef]
- Wang, D.X.; Ling, X.; Peng, H. Performance analysis of double organic Rankine cycle for discontinuous low temperature waste heat recovery. Appl. Therm. Eng. 2012, 48, 63–71. [Google Scholar] [CrossRef]
- Yang, S.C.; Hung, T.C.; Feng, Y.Q.; Wu, C.J.; Wong, K.W.; Huang, K.C. Experimental investigation on a 3 kW organic Rankine cycle for low-grade waste heat under different operation parameters. Appl. Therm. Eng. 2016, 113, 756–764. [Google Scholar] [CrossRef]
- Shu, G.; Yu, G.; Tian, H.; Wei, H.; Liang, X.; Huang, Z. Multi-approach evaluations of a cascade-Organic Rankine Cycle (C-ORC) system driven by diesel engine waste heat: Part A—Thermodynamic evaluations. Energy Convers. Manag. 2016, 108, 579–595. [Google Scholar] [CrossRef]
- Yu, G.; Shu, G.; Tian, H.; Wei, H.; Liang, X. Multi-approach evaluations of a cascade-Organic Rankine Cycle (C-ORC) system driven by diesel engine waste heat: Part B-techno-economic evaluations. Energy Convers. Manag. 2016, 108, 596–608. [Google Scholar] [CrossRef]
- Feng, Y.Q.; Hung, T.C.; He, Y.L.; Wang, Q.; Wang, S.; Li, B.X.; Lin, J.R.; Zhang, W. Operation characteristic and performance comparison of organic Rankine cycle (ORC) for low-grade waste heat using R245fa, R123 and their mixtures. Energy Convers. Manag. 2017, 144, 153–163. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Exergy, exergoeconomic and environmental analyses and evolutionary algorithm based multi-objective optimization of combined cycle power plants. Energy 2011, 36, 5886–5898. [Google Scholar] [CrossRef]
- Groniewsky, A.; Imre, A. Prediction of the ORC Working Fluid’s Temperature-Entropy Saturation Boundary Using Redlich-Kwong Equation of State. Entropy 2018, 20, 93. [Google Scholar] [CrossRef]
- Li, M.; Zhao, B. Analytical thermal efficiency of medium-low temperature organic Rankine cycles derived from entropy-generation analysis. Energy 2016, 106, 121–130. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, Z.; Zhou, Y.; Jiang, L.; Yu, L. Applicability of entropy, entransy and exergy analyses to the optimization of the Organic Rankine Cycle. Energy Convers. Manag. 2014, 88, 267–276. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in Organic Rankine Cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Yang, K.; Yang, F.; Wang, Z.; Zhao, G.; Liu, H.; Wang, E.; Yao, B. Performance analysis of regenerative organic Rankine cycle (RORC) using the pure working fluid and the zeotropic mixture over the whole operating range of a diesel engine. Energy Convers. Manag. 2014, 84, 282–294. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Performance comparison of low-grade ORCs (organic Rankine cycles) using R245fa, pentane and their mixtures based on the thermoeconomic multi-objective optimization and decision makings. Energy 2015, 93, 2018–2029. [Google Scholar] [CrossRef]
- Dong, B.; Xu, G.; Cai, Y.; Li, H. Analysis of zeotropic mixtures used in high temperature Organic Rankine cycle. Energy Convers. Manag. 2014, 84, 253–260. [Google Scholar] [CrossRef]
- Xiao, L.; Wu, S.Y.; Yi, T.T.; Liu, C.; Li, Y.R. Multi-objective optimization of evaporation and condensation temperatures for subcritical organic Rankine cycle. Energy 2015, 83, 723–733. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.; Greg, K.; Zhang, Y.; Li, B.; Yang, J. Thermoeconomic comparison between pure and mixture working fluids of organic Rankine cycles (ORCs) for low temperature waste heat recovery. Energy Convers. Manag. 2015, 106, 859–872. [Google Scholar] [CrossRef]
- Lecompte, S.; Ameel, B.; Ziviani, D.; van den Broek, M.; De Paepe, M. Exergy analysis of zeotropic mixtures as working fluids in Organic Rankine Cycles. Energy Convers. Manag. 2014, 85, 727–739. [Google Scholar] [CrossRef]
- Chys, M.; van den Broek, M.; Vanslambrouck, B.; De Paepe, M. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Angelino, G.; Paliano, P.C.D. Multicomponent Working Fluids For Organic Rankine Cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Shu, G.Q.; Gao, Y.U.; Tian, H.; Wei, H.Q.; Liang, X.Y. Study of mixtures based on hydrocarbons used in ORC (Organic Rankine Cycle) for engine waste heat recovery. Energy 2014, 74, 428–438. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C.N. On the use of SAFT-VR Mie for assessing large-glide fluorocarbon working-fluid mixtures in organic Rankine cycles. Appl. Energy 2016, 163, 263–282. [Google Scholar] [CrossRef]
- Liu, Q.; Duan, Y.; Yang, Z. Effect of condensation temperature glide on the performance of organic Rankine cycles with zeotropic mixture working fluids. Appl. Energy 2014, 115, 394–404. [Google Scholar] [CrossRef]
- Garg, P.; Kumar, P.; Srinivasan, K.; Dutta, P. Evaluation of isopentane, R-245fa and their mixtures as working fluids for organic Rankine cycles. Appl. Therm. Eng. 2013, 51, 292–300. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Markides, C.N. Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System. Energies 2016, 9, 448. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, H.G.; Wang, Z.; Zhang, J.; Yang, F.B.; Wang, E.H.; Yao, B. Study of zeotropic mixtures of ORC (organic Rankine cycle) under engine various operating conditions. Energy 2013, 58, 494–510. [Google Scholar] [CrossRef]
- Cheng, X.T.; Liang, X.G. Discussion on the entransy expressions of the thermodynamic laws and their applications. Energy 2013, 56, 46–51. [Google Scholar] [CrossRef]
- Li, T.L.; Fu, W.C.; Zhu, J.L. An integrated optimization for organic Rankine cycle based on entransy theory and thermodynamics. Energy 2014, 72, 561–573. [Google Scholar] [CrossRef]
- Li, T.; Yuan, Z.; Xu, P.; Zhu, J. Entransy dissipation/loss-based optimization of two-stage organic Rankine cycle(TSORC) with R245fa for geothermal power generation. Sci. China Technol. Sci. 2016, 59, 1524. [Google Scholar] [CrossRef]
- Györke, G.; Deiters, U.K.; Groniewsky, A.; Lassu, I.; Imre, A.R. Novel classification of pure working fluids for Organic Rankine Cycle. Energy 2018, 145, 288–300. [Google Scholar] [CrossRef]
- Cheng, X.T.; Liang, X.G. Entransy loss in thermodynamic processes and its application. Energy 2012, 44, 964–972. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhao, L. Analysis of zeotropic mixtures used in low-temperature solar Rankine cycles for power generation. Sol. Energy 2009, 83, 605–613. [Google Scholar] [CrossRef]
- Salcedo, R.; Antipova, E.; Boer, D.; Jiménez, L.; Guillén-Gosálbez, G. Multi-objective optimization of solar Rankine cycles coupled with reverse osmosis desalination considering economic and life cycle environmental concerns. Desalination 2012, 286, 358–371. [Google Scholar] [CrossRef]
- Feidt, M.; Kheiri, A.; Pelloux-Prayer, S. Performance optimization of low-temperature power generation by supercritical ORCs (organic Rankine cycles) using low GWP (global warming potential) working fluids. Energy 2014, 67, 513–526. [Google Scholar]
- Imre, A.R.; Quiñones-Cisneros, S.E.; Deiters, U.K. Adiabatic Processes in the Vapor−Liquid Two-Phase Region. 2. Binary Mixtures 2015, 54, 6559–6568. [Google Scholar]
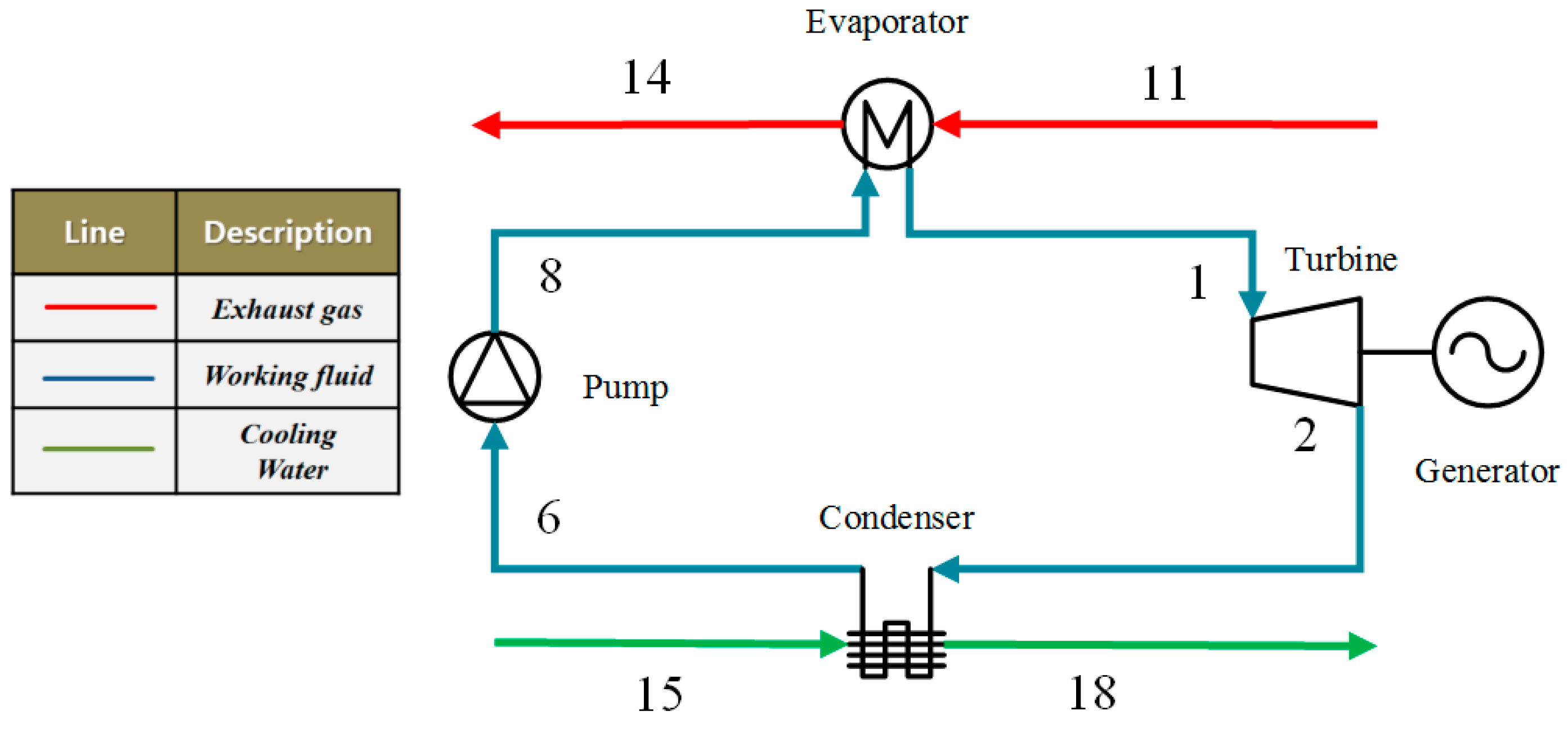
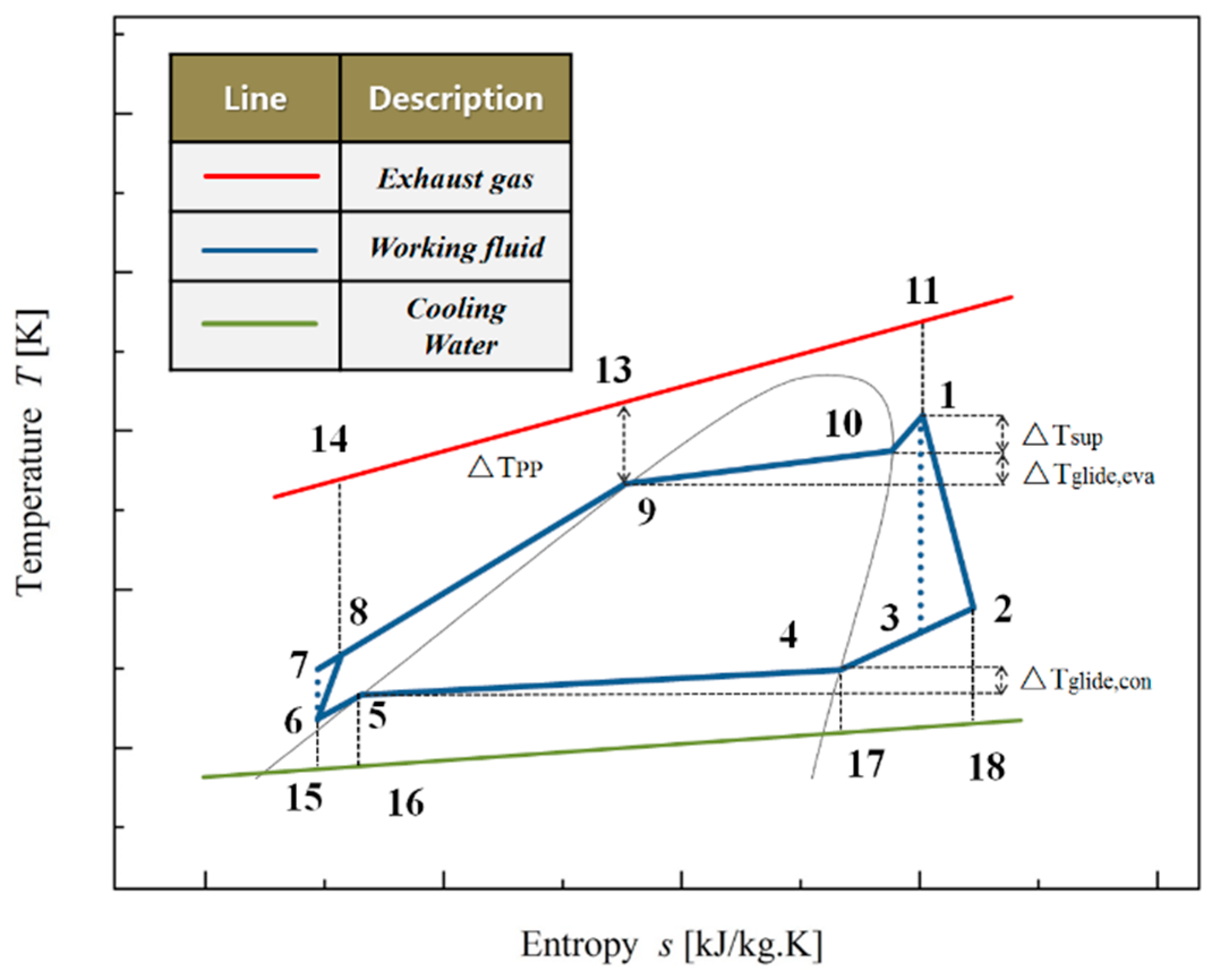
| NO. | Working Fluids | M (kg·kmol−1) | Tcr(K) | Pcr(MPa) | Tboiling(K) |
|---|---|---|---|---|---|
| 1 | R245fa | 134.05 | 427.05 | 3.65 | 288.29 |
| 2 | R227ea | 170.03 | 374.90 | 2.93 | 256.81 |
| 3 | R152a | 66.051 | 386.41 | 4.51 | 249.13 |
| 4 | Pentane | 86.175 | 507.82 | 3.03 | 341.86 |
| Item | Unit | Value |
|---|---|---|
| Heat sources temperature | °C | 120 |
| Expander isentropic efficiency | % | 80 |
| Pump isentropic efficiency | % | 80 |
| Mass flow of heat sources | kg·s−1 | 0.5 |
| Cooling water temperature | °C | 10 |
| Evaporator outlet temperature | °C | 60 |
| Degree of superheat | °C | 10 |
| PPDT in evaporator | °C | 15 |
| Condenser temperature | °C | 20 |
| Environmental temperature | °C | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.-q.; Luo, Q.-h.; Wang, Q.; Wang, S.; He, Z.-x.; Zhang, W.; Wang, X.; An, Q.-s. Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids. Entropy 2018, 20, 818. https://doi.org/10.3390/e20110818
Feng Y-q, Luo Q-h, Wang Q, Wang S, He Z-x, Zhang W, Wang X, An Q-s. Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids. Entropy. 2018; 20(11):818. https://doi.org/10.3390/e20110818
Chicago/Turabian StyleFeng, Yong-qiang, Qian-hao Luo, Qian Wang, Shuang Wang, Zhi-xia He, Wei Zhang, Xin Wang, and Qing-song An. 2018. "Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids" Entropy 20, no. 11: 818. https://doi.org/10.3390/e20110818
APA StyleFeng, Y.-q., Luo, Q.-h., Wang, Q., Wang, S., He, Z.-x., Zhang, W., Wang, X., & An, Q.-s. (2018). Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids. Entropy, 20(11), 818. https://doi.org/10.3390/e20110818





