Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation
Abstract
1. Introduction
2. Data
3. Reconstruction of the Liability Network
- Interbank network , connecting banks with banks.
- Bank-firm network , containing information about deposits firms have at financial institutions.
- Firm-bank network , containing information about liabilities firms have towards financial institutions (bank loans).
- Firm-firm network with inter-firm liabilities, which are omitted in this work; thus, for all .
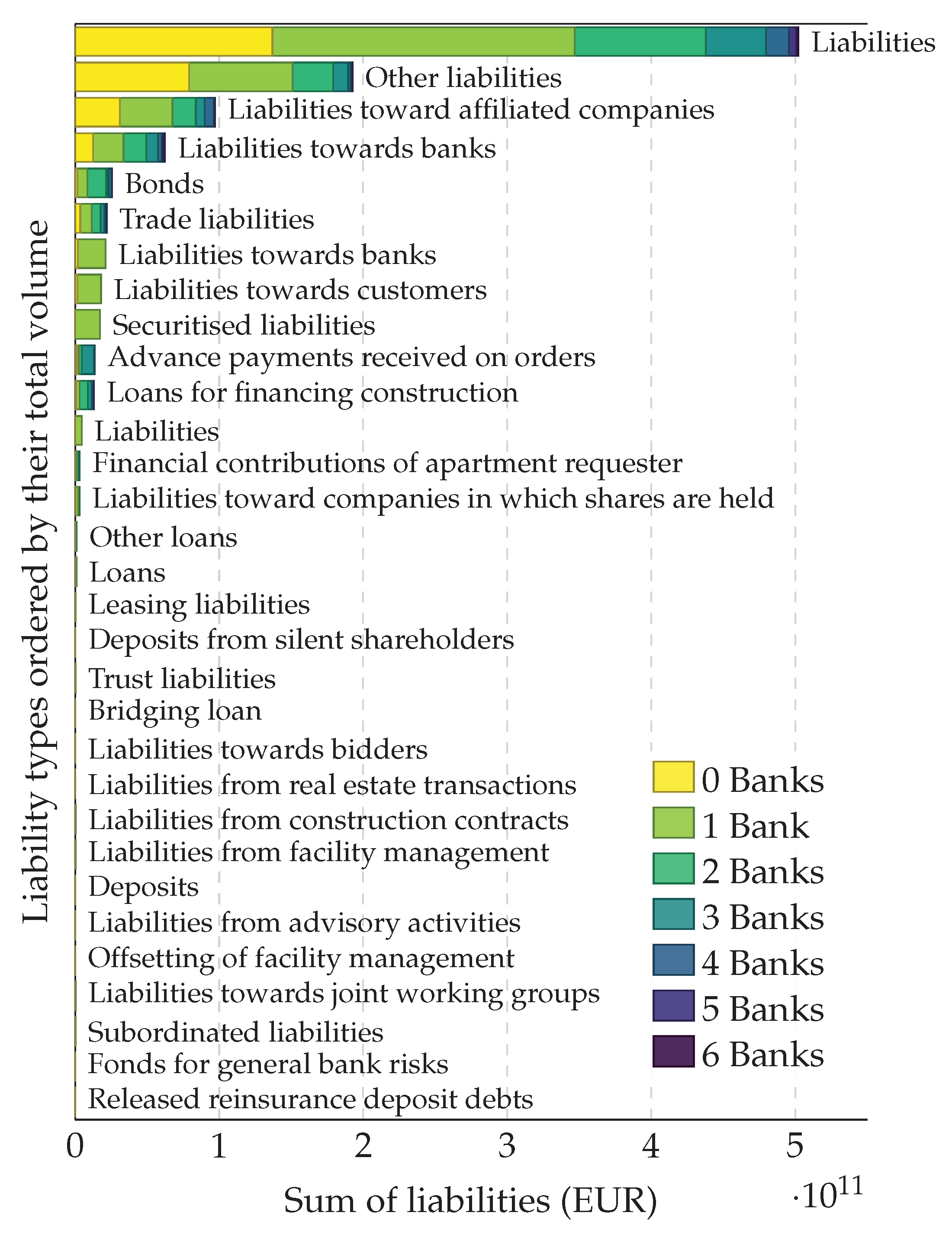
- For every firm c, take the aggregated liabilities the firm has toward banks from the balance sheet.
- Then, take the set of aggregated loans (referred to as assets, or , where i is the index of a bank/firm) of all banks from their balance sheets, and assign them to the entries of the vector ℓ in the following way:
- Normalize the resulting vector,
- Partition the aggregated liabilities with the distribution to obtain the entries for the firm-bank network, , where we use vector notation and : means column.
4. The Liability Network of Austria
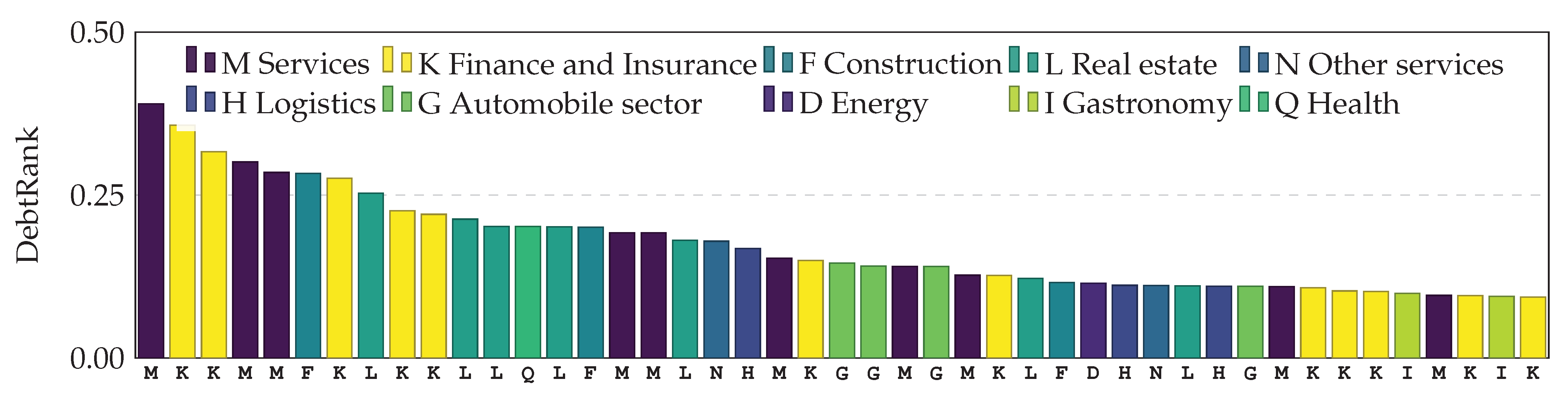
5. Systemically Important Firms and Banks in Austria
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. DebtRank
| Interpretation | |
| U | Node i is undistressed at time t |
| D | Node i is in distress at time t |
| I | Node i is inactive at time t |
References
- Bank for International Settlements. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems; Bank for International Settlements: Basel, Switzerland, 2010. [Google Scholar]
- Battiston, S.; Puliga, M.; Kaushik, R.; Tasca, P.; Caldarelli, G. DebtRank: Too Central to Fail? Financial Networks, the FED and Systemic Risk. Sci. Rep. 2012, 2, 541. [Google Scholar] [CrossRef] [PubMed]
- Markose, S.; Giansante, S.; Shaghaghi, A.R. Too interconnected to fail financial network of US CDS market: Topological fragility and systemic risk. J. Econ. Behav. Organ. 2012, 83, 627–646. [Google Scholar] [CrossRef]
- Billio, M.; Getmansky, M.; Lo, A.W.; Pelizzon, L. Econometric measures of connectedness and systemic risk in the finance and insurance sectors. J. Financ. Econ. 2012, 104, 535–559. [Google Scholar] [CrossRef]
- Thurner, S.; Poledna, S. DebtRank-transparency: Controlling systemic risk in financial networks. Sci. Rep. 2013, 3, 1888. [Google Scholar] [CrossRef] [PubMed]
- Poledna, S.; Thurner, S. Elimination of systemic risk in financial networks by means of a systemic risk transaction tax. Quant. Financ. 2016, 16, 1599–1613. [Google Scholar] [CrossRef]
- Leduc, M.V.; Poledna, S.; Thurner, S. Systemic Risk Management in Financial Networks with Credit Default Swaps. J. Netw. Theory Financ. 2017, 3, 1–21. [Google Scholar] [CrossRef]
- Poledna, S.; Bochmann, O.; Thurner, S. Basel III capital surcharges for G-SIBs are far less effective in managing systemic risk in comparison to network-based, systemic risk-dependent financial transaction taxes. J. Econ. Dyn. Control 2017, 77, 230–246. [Google Scholar] [CrossRef]
- Adrian, T.; Brunnermeier, M. CoVaR; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2011.
- Acharya, V.; Pedersen, L.; Philippon, T.; Richardson, M. Measuring Systemic Risk; Technical Report; CEPR: Washington, DC, USA, 2012; Available online: http://ssrn.com/abstract=1573171 (accessed on 27 July 2018).
- Brownlees, C.T.; Engle, R.F. Volatility, Correlation and Tails for Systemic Risk Measurement. Available at SSRN 1611229. Available online: https://ssrn.com/abstract=1611229 (accessed on 27 July 2018).
- Huang, X.; Zhou, H.; Zhu, H. Systemic risk contributions. J. Financ. Serv. Res. 2012, 42, 55–83. [Google Scholar] [CrossRef]
- Saracco, F.; Di Clemente, R.; Gabrielli, A.; Squartini, T. Detecting early signs of the 2007–2008 crisis in the world trade. Sci. Rep. 2016, 6, 30286. [Google Scholar] [CrossRef] [PubMed]
- Upper, C.; Worms, A. Estimating Bilateral Exposures in the German Interbank Market: Is There a Danger of Contagion? Technical Report 9; Deutsche Bundesbank, Research Centre: Frankfurt am Main, Germany, 2002. [Google Scholar]
- Boss, M.; Summer, M.; Thurner, S. Contagion flow through banking networks. Lect. Notes Comput. Sci. 2004, 3038, 1070–1077. [Google Scholar]
- Boss, M.; Elsinger, H.; Summer, M.; Thurner, S. The network topology of the interbank market. Quant. Financ. 2005, 4, 677–684. [Google Scholar] [CrossRef]
- Soramäki, K.; Bech, M.L.; Arnold, J.; Glass, R.J.; Beyeler, W.E. The topology of interbank payment flows. Phys. A Stat. Mech. Appl. 2007, 379, 317–333. [Google Scholar] [CrossRef]
- Iori, G.; De Masi, G.; Precup, O.V.; Gabbi, G.; Caldarelli, G. A network analysis of the Italian overnight money market. J. Econ. Dyn. Control 2008, 32, 259–278. [Google Scholar] [CrossRef]
- Cajueiro, D.O.; Tabak, B.M.; Andrade, R.F. Fluctuations in interbank network dynamics. Phys. Rev. E 2009, 79, 037101. [Google Scholar] [CrossRef] [PubMed]
- Bech, M.L.; Atalay, E. The topology of the federal funds market. Phys. A Stat. Mech. Appl. 2010, 389, 5223–5246. [Google Scholar] [CrossRef]
- Fricke, D.; Lux, T. Core–periphery structure in the overnight money market: Evidence from the e-mid trading platform. Comput. Econ. 2014, 45, 359–395. [Google Scholar] [CrossRef]
- Iori, G.; Mantegna, R.N.; Marotta, L.; Micciche, S.; Porter, J.; Tumminello, M. Networked relationships in the e-MID Interbank market: A trading model with memory. J. Econ. Dyn. Control 2015, 50, 98–116. [Google Scholar] [CrossRef]
- Markose, S. Systemic Risk from Global Financial Derivatives: A Network Analysis of Contagion and its Mitigation with Super-Spreader Tax; IMF Working Paper WP/12/282; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- Poledna, S.; Molina-Borboa, J.L.; Martínez-Jaramillo, S.; van der Leij, M.; Thurner, S. The multi-layer network nature of systemic risk and its implications for the costs of financial crises. J. Financ. Stab. 2015, 20, 70–81. [Google Scholar] [CrossRef]
- León, C.; Berndsen, R.; Renneboog, L. Financial Stability and Interacting Networks of Financial Institutions and Market Infrastructures; European Banking Center Discussion Paper Series; SSRN: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Fujiwara, Y.; Aoyama, H.; Ikeda, Y.; Iyetomi, H.; Souma, W. Structure and temporal change of the credit network between banks and large firms in Japan. Economics 2009, 3, 1–18. [Google Scholar]
- De Masi, G.; Gallegati, M. Bank–firms topology in Italy. Empir. Econ. 2012, 43, 851–866. [Google Scholar] [CrossRef]
- Aoyama, H. Systemic risk in Japanese credit network. In Econophysics of Agent-Based Models; Springer: Berlin, Germany, 2014; pp. 219–228. [Google Scholar]
- Marotta, L.; Micciche, S.; Fujiwara, Y.; Iyetomi, H.; Aoyama, H.; Gallegati, M.; Mantegna, R.N. Bank-firm credit network in Japan: An analysis of a bipartite network. PLoS ONE 2015, 10, e0123079. [Google Scholar] [CrossRef] [PubMed]
- De Masi, G.; Fujiwara, Y.; Gallegati, M.; Greenwald, B.; Stiglitz, J.E. An analysis of the Japanese credit network. Evol. Inst. Econ. Rev. 2011, 7, 209–232. [Google Scholar] [CrossRef]
- Miranda, R.; Tabak, B. Contagion Risk within Firm-Bank Bivariate Networks; Technical Report; Central Bank of Brazil, Research Department: Brasilia, Brazil, 2013. [Google Scholar]
- Lux, T. A model of the topology of the bank—Firm credit network and its role as channel of contagion. J. Econ. Dyn. Control 2016, 66, 36–53. [Google Scholar] [CrossRef]
- Wirtschaftskammer Österreich. ÖNACE—Klassifikation der Wirtschaftstätigkeiten. 2008. Available online: http://wko.at/statistik/oenace/oenace2008.pdf (accessed on 27 July 2018).
- Hu, Y. Efficient, high-quality force-directed graph drawing. Math. J. 2006, 10, 37–71. [Google Scholar]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. Icwsm 2009, 8, 361–362. [Google Scholar]
- Anand, K.; van Lelyveld, I.; Banai, Á.; Friedrich, S.; Garratt, R.; Hałaj, G.; Fique, J.; Hansen, I.; Jaramillo, S.M.; Lee, H.; et al. The missing links: A global study on uncovering financial network structures from partial data. J. Financ. Stab. 2018, 35, 107–119. [Google Scholar] [CrossRef]
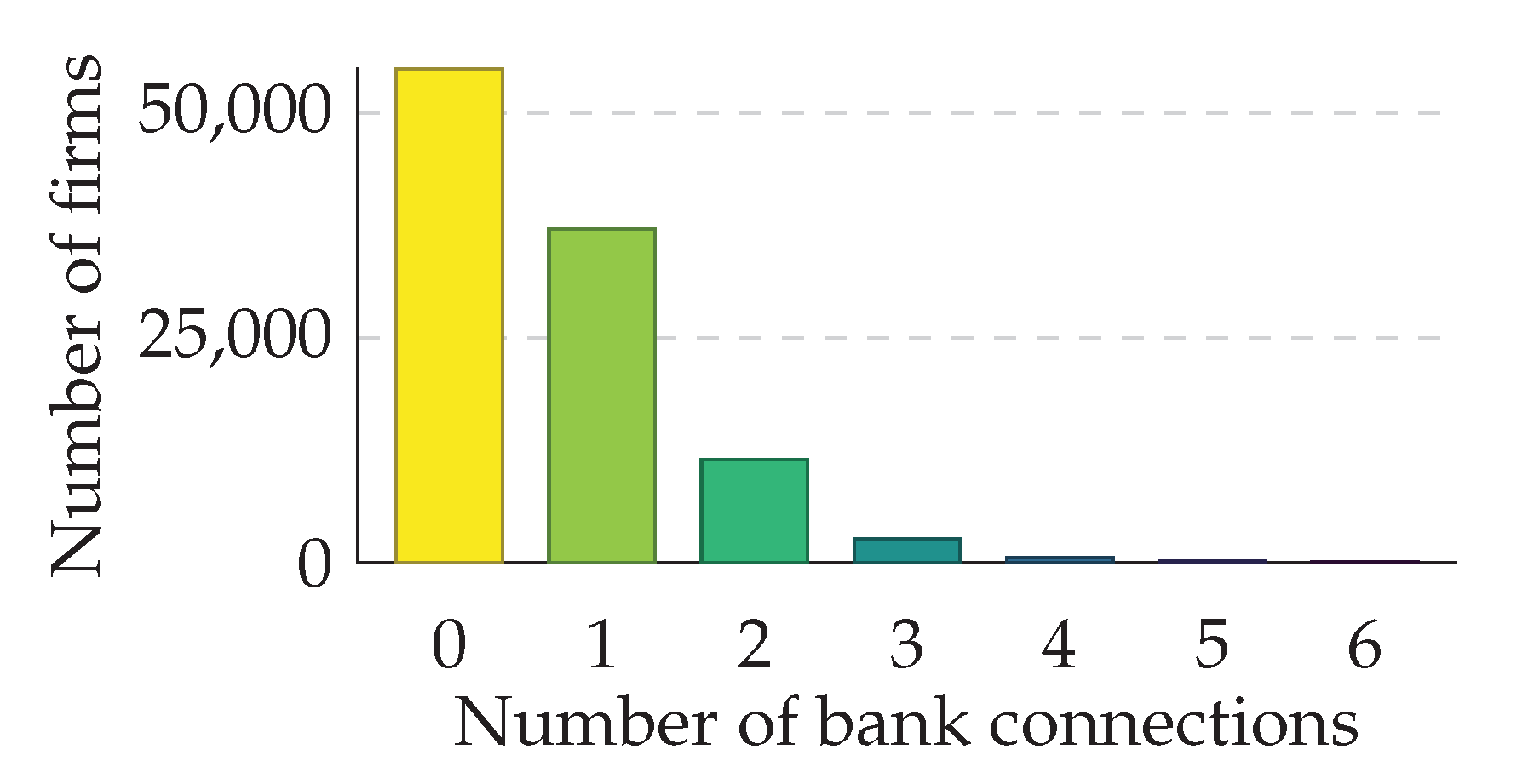
 and firms
and firms  . Connections are either loans or
. Connections are either loans or  deposits
deposits  . Banks are connected to firms and to each other, whereas firms only interact with banks.
. Banks are connected to firms and to each other, whereas firms only interact with banks.
 and firms
and firms  . Connections are either loans or
. Connections are either loans or  deposits
deposits  . Banks are connected to firms and to each other, whereas firms only interact with banks.
. Banks are connected to firms and to each other, whereas firms only interact with banks.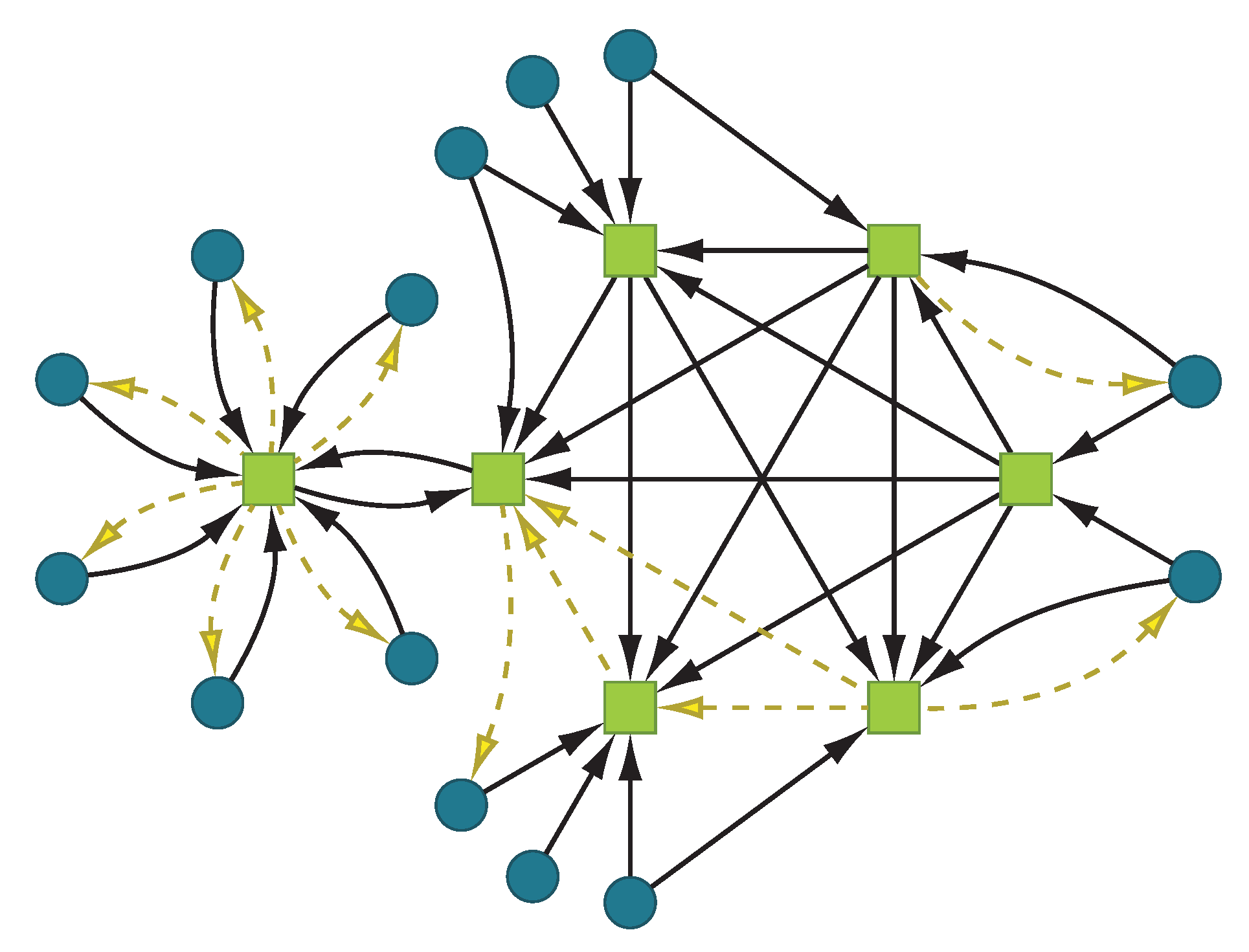
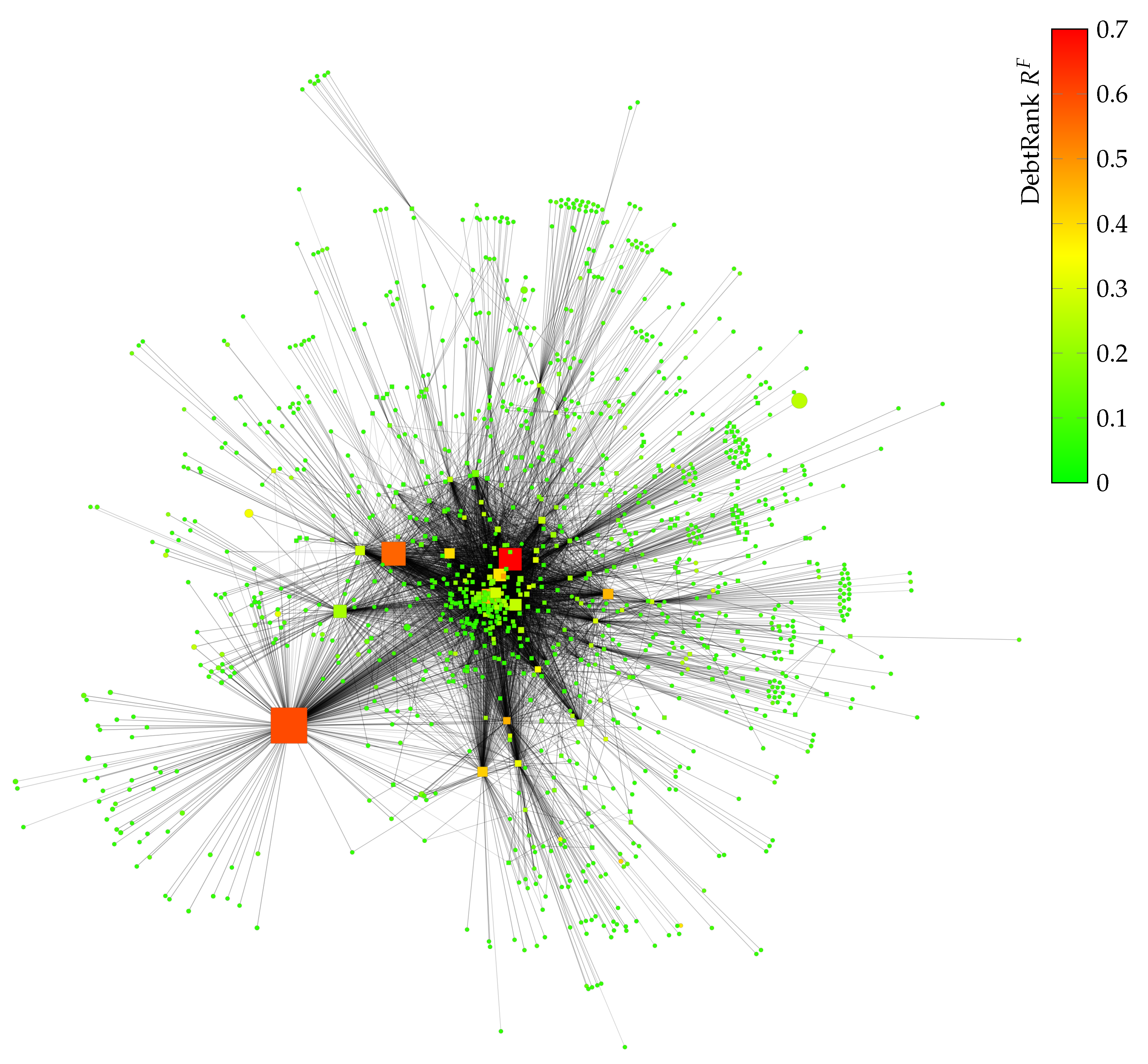
 and 49,363 firm nodes
and 49,363 firm nodes  in 2008. The network represents approximately 80.2% of total liabilities towards banks of firms and all interbank liabilities. The node size corresponds to the total assets held by each node.
in 2008. The network represents approximately 80.2% of total liabilities towards banks of firms and all interbank liabilities. The node size corresponds to the total assets held by each node.
 and 49,363 firm nodes
and 49,363 firm nodes  in 2008. The network represents approximately 80.2% of total liabilities towards banks of firms and all interbank liabilities. The node size corresponds to the total assets held by each node.
in 2008. The network represents approximately 80.2% of total liabilities towards banks of firms and all interbank liabilities. The node size corresponds to the total assets held by each node.
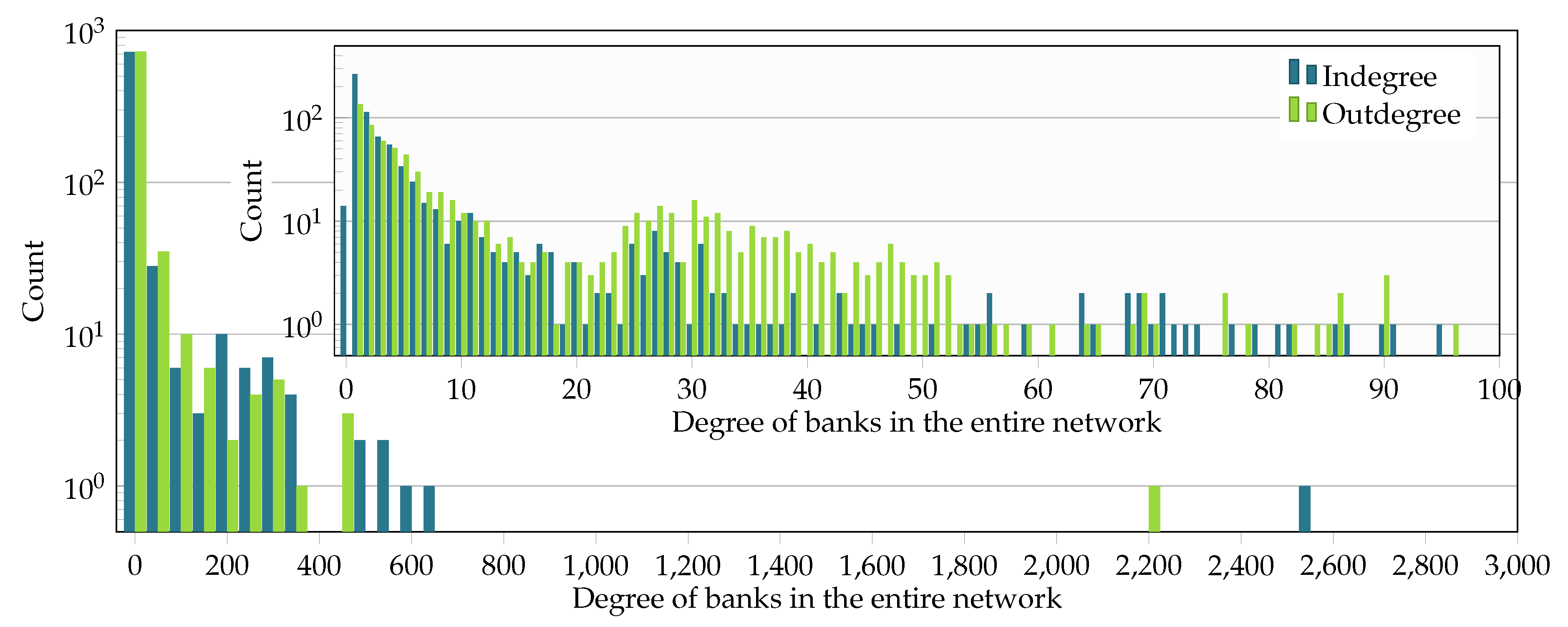
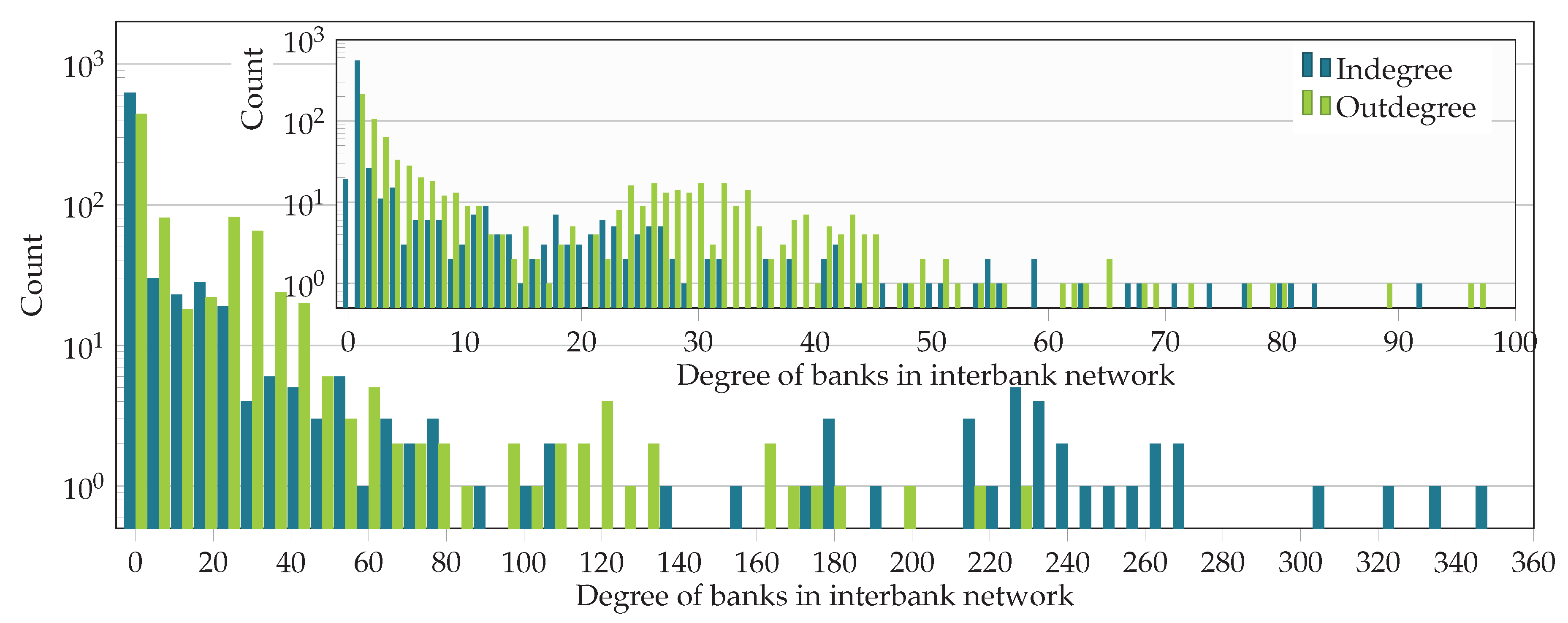
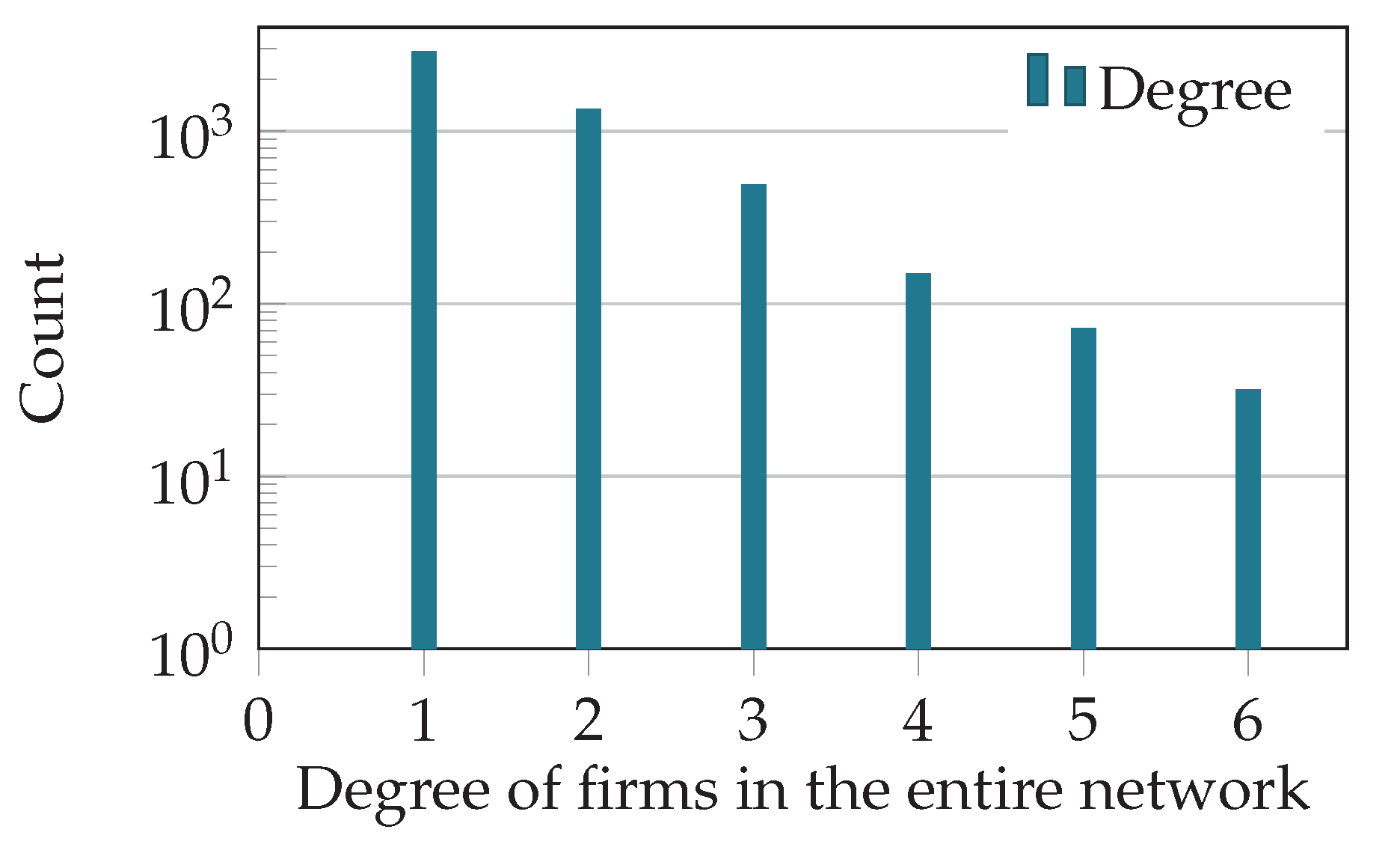
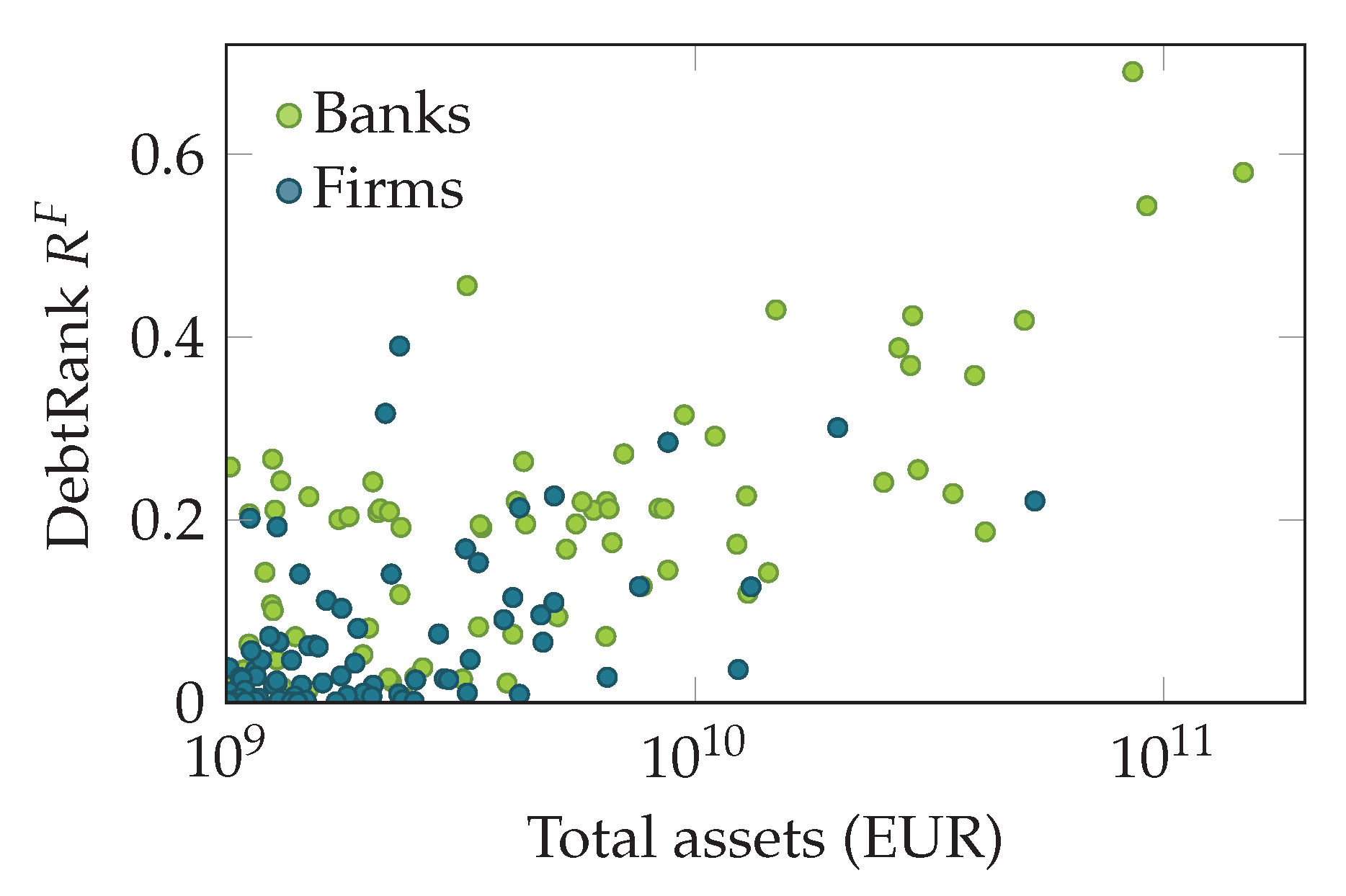

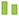 ] and firms [
] and firms [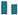 ]. Banks and firms have a qualitatively similar DebtRank distribution. The highest DebtRank of a firm is 0.39.
]. Banks and firms have a qualitatively similar DebtRank distribution. The highest DebtRank of a firm is 0.39.
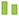 ] and firms [
] and firms [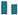 ]. Banks and firms have a qualitatively similar DebtRank distribution. The highest DebtRank of a firm is 0.39.
]. Banks and firms have a qualitatively similar DebtRank distribution. The highest DebtRank of a firm is 0.39.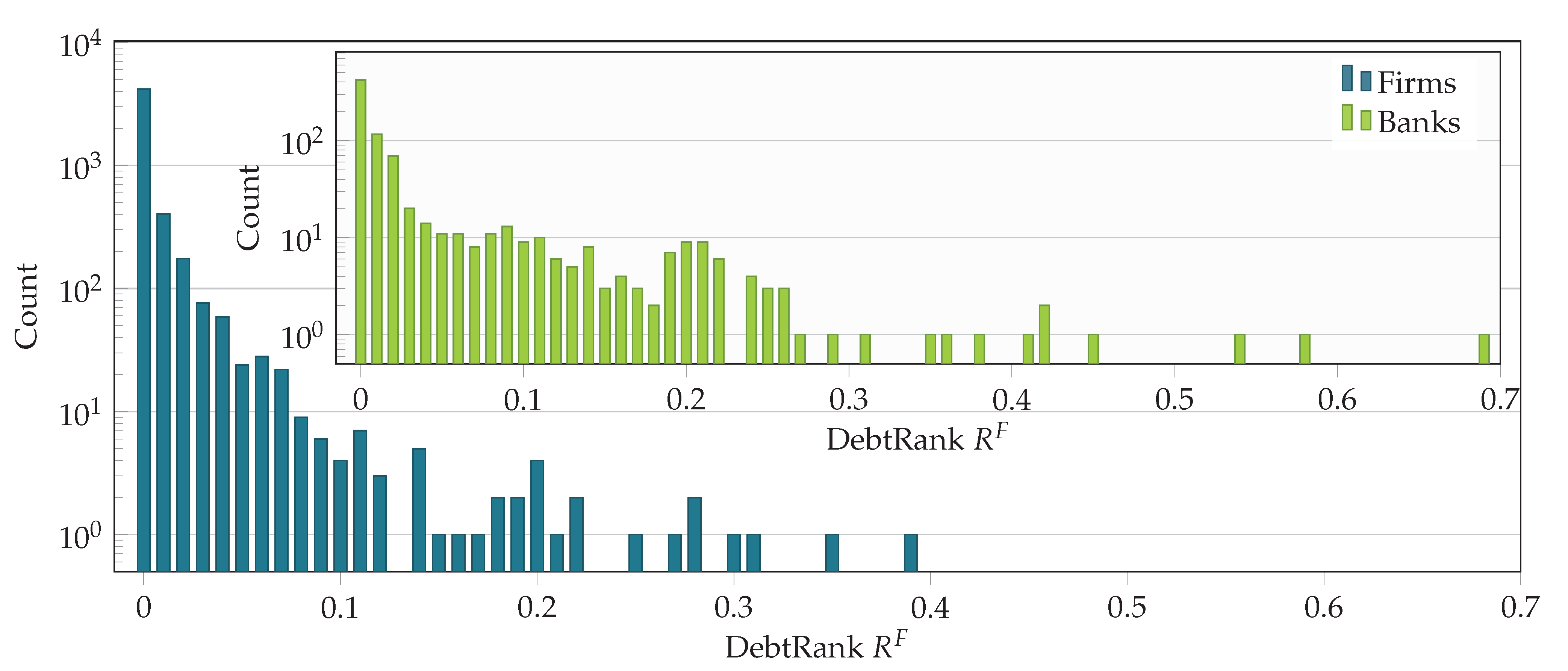
| Network | Nodes | Links | ||
|---|---|---|---|---|
| Entire network F | 50,159 | 140,528 | 0.126 | 0.001 |
| Interbank network B | 796 | 12,783 | 0.337 | 0.005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poledna, S.; Hinteregger, A.; Thurner, S. Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation. Entropy 2018, 20, 792. https://doi.org/10.3390/e20100792
Poledna S, Hinteregger A, Thurner S. Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation. Entropy. 2018; 20(10):792. https://doi.org/10.3390/e20100792
Chicago/Turabian StylePoledna, Sebastian, Abraham Hinteregger, and Stefan Thurner. 2018. "Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation" Entropy 20, no. 10: 792. https://doi.org/10.3390/e20100792
APA StylePoledna, S., Hinteregger, A., & Thurner, S. (2018). Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation. Entropy, 20(10), 792. https://doi.org/10.3390/e20100792





