A QUBO Formulation of the Stereo Matching Problem for D-Wave Quantum Annealers
Abstract
1. Introduction
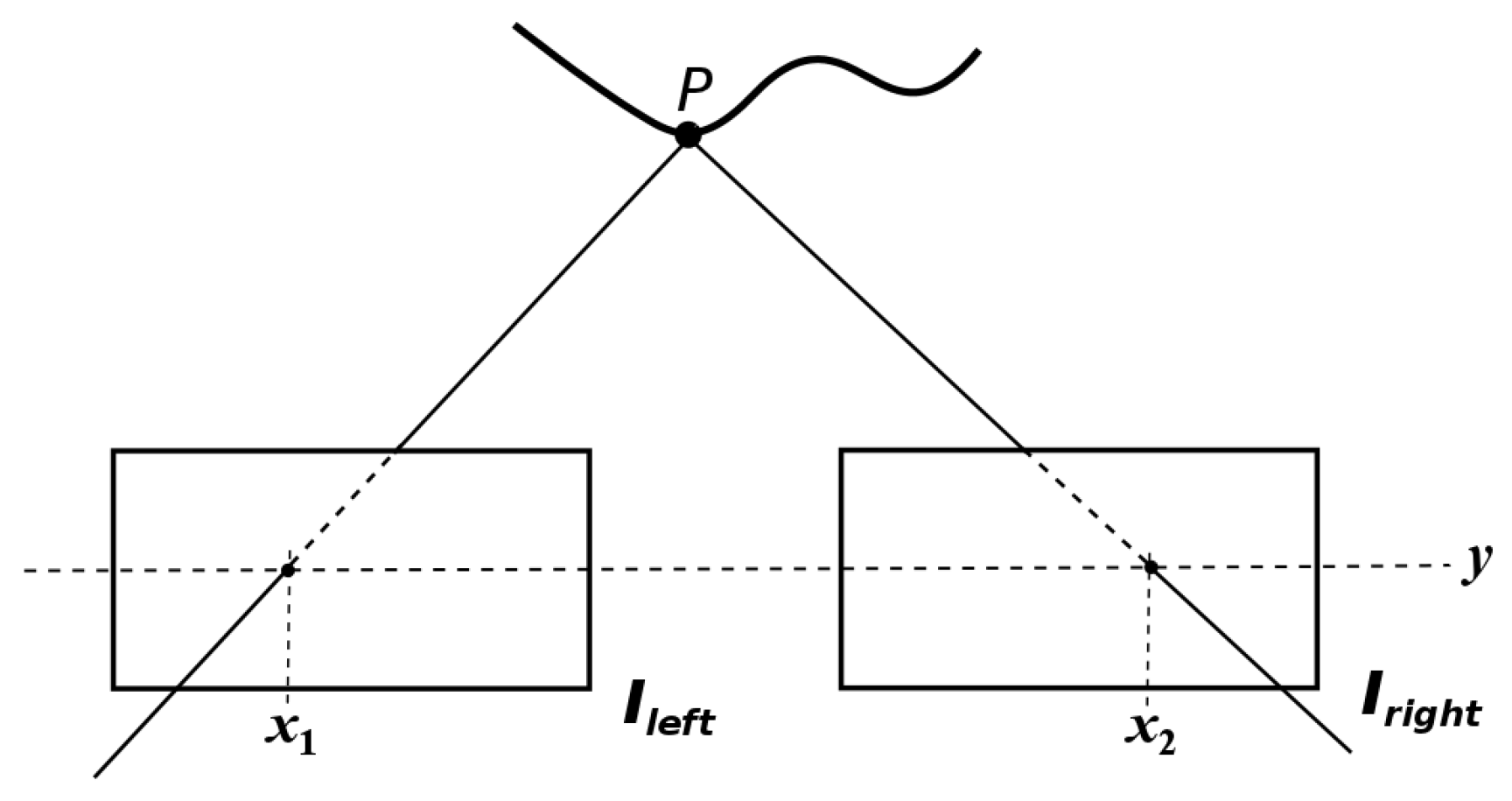
- The stereo matching problem [4]: Which parts of the left and right images are projections of the same scene element?
- The reconstruction problem, which is stated as follows: given a number of corresponding parts of the left and right images, what can we say about the 3-D locations and structures of the observed objects?
2. Results
2.1. Quantum Annealing
2.1.1. QUBO Formulation Approach to the Stereo Matching Problem
2.1.2. Energy Function
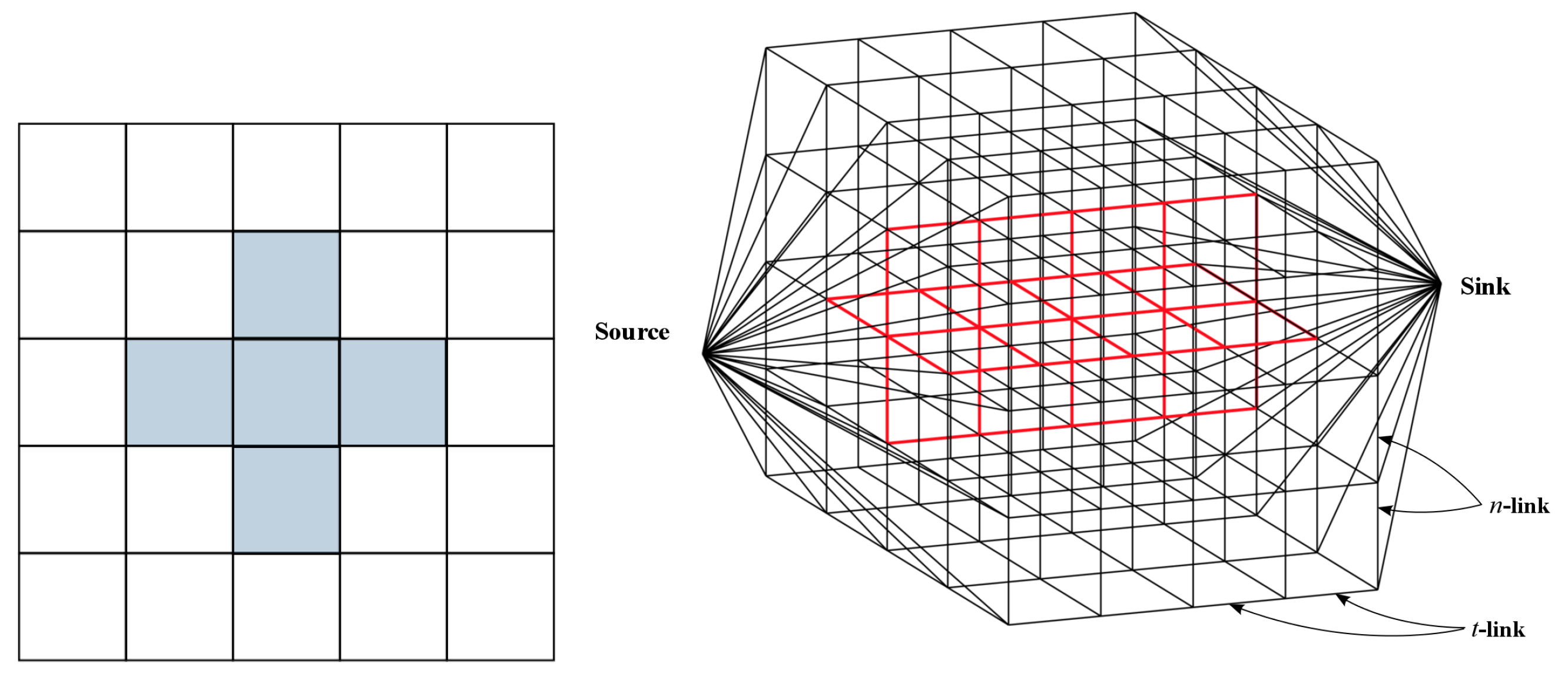
2.1.3. Graph Construction
- To each pixel p in the image, we associate a chain composed of vertices, say . These vertices are connected by edges called t-links, , where . For a disparity range from 0 to L values, and for each pixel p, we will have vertices in the chain and t-links between these vertices; each edge defines a labeling with one specific value. Additionally, there are two t-links that connect the first vertex with the source and the last vertex with the sink. Hence, there exist such edges in the graph for each pixel p. The weights of those edges directly depend on the function , which specifies the cost of applying a specific label to a pixel.
- To each pair of neighbor pixels, p and q, there will be links that connect the corresponding chains with edges called n-links. For instance, let and be the chain vertices for two neighbor pixels p and q; the n-links between chains are . Usually a 4-neighborhood is assumed for every pixel. The weights of these edges should reflect the penalty when assigning different labels to neighboring pixels.
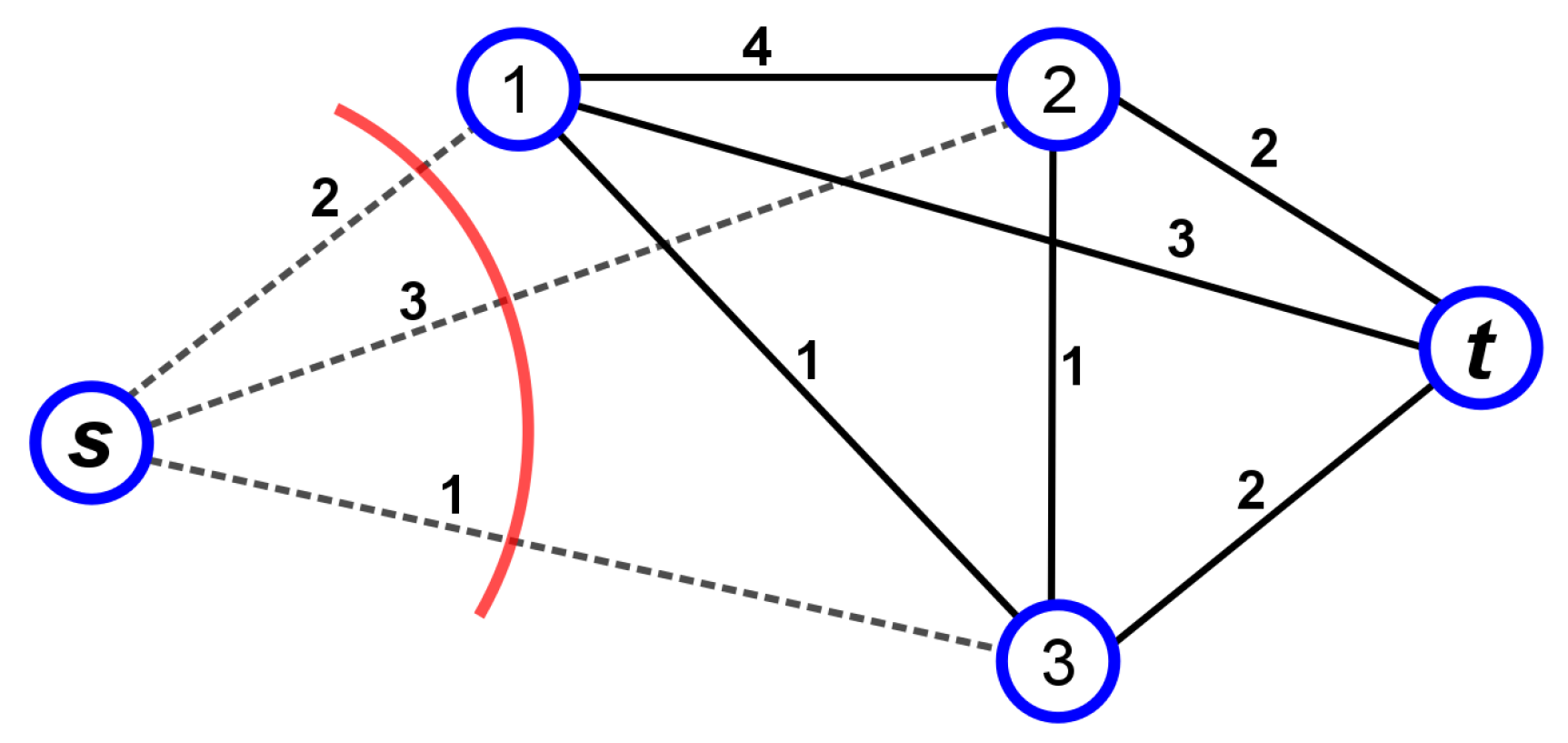
2.1.4. QUBO Formulation of the Stereo Matching Problem via the Minimum Multicut Problem
3. Experiments and Discussion
- (i)
- Construct the weighted graph described in Section 2.1.3 for the given stereo pair of images.
- (ii)
- Formulate the stereo matching problem as the minimum multi-cut problem for the pair using the weighted graph from the previous step.
- (iii)
- Construct the QUBO expression given in Equation (20) from the weighted graph in step (ii) for a single pair.
- (iv)
- Embed into the Chimera graph topology of the D-Wave computer.
- (v)
- Find the minimum energy solution to the QUBO/Ising problem by quantum annealing.
- Each vertex is mapped to a connected subtree in .
- Each edge must be mapped to at least one edge in .
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klette, R. Concise Computer Vision: An Introduction into Theory and Algorithms; Springer Publishing Company: London, UK, 2014. [Google Scholar]
- Stockman, G.; Shapiro, L.G. Computer Vision, 1st ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications, 1st ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Brown, M.Z.; Burschka, D.; Hager, G.D. Advances in Computational Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 993–1008. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Proceedings of the International Workshop on Vision Algorithms: Theory and Practice, Corfu, Greece, 21–22 September 2000; Springer: London, UK, 2000; pp. 298–372. [Google Scholar]
- Darrell, T.; Gordon, G.; Harville, M.; Woodfill, J. Integrated Person Tracking Using Stereo, Color, and Pattern Detection. Int. J. Comput. Vis. 2000, 37, 175–185. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; IEEE Computer Society: Washington, DC, USA, 2006; Volume 1, pp. 519–528. [Google Scholar] [CrossRef]
- Uyttendaele, M.; Criminisi, A.; Kang, S.B.; Winder, S.; Szeliski, R.; Hartley, R. Image-Based Interactive Exploration of Real-World Environments. IEEE Comput. Graph. Appl. 2004, 24, 52–63. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, M.; Konolige, K.; Bolles, R.C. Localization and Mapping for Autonomous Navigation in Outdoor Terrains: A Stereo Vision Approach. In Proceedings of the 2007 IEEE Workshop on Applications of Computer Vision (WACV ’07), Austin, TX, USA, 21–22 February 2007; p. 7. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2014, 56, 172–185. [Google Scholar] [CrossRef]
- Biamonte, J.D.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum principal component analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef] [PubMed]
- Adachi, S.H.; Henderson, M.P. Application of Quantum Annealing to Training of Deep Neural Networks. arXiv, 2015; arXiv:1510.06356. [Google Scholar]
- Kulchytskyy, B.; Andriyash, E.; Amin, M.; Melko, R. Quantum Boltzmann Machine. arXiv, 2016; arXiv:1601.02036. [Google Scholar]
- Benedetti, M.; Realpe-Gómez, J.; Biswa, R.; Perdomo-Ortiz, A. Estimation of effective temperatures in quantum annealers for sampling applications: A case study with possible applications in deep learning. Phys. Rev. A 2016, 94, 022308. [Google Scholar] [CrossRef]
- Benedetti, M.; Realpe-Gómez, J.; Biswa, R.; Perdomo-Ortiz, A. Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models. Phys. Rev. X 2017, 7, 130503. [Google Scholar] [CrossRef]
- IBM Quantum Experience. Available online: http://research.ibm.com/ibm-q/ (accessed on 7 January 2018).
- D-Wave systems. Available online: http://www.dwavesys.com/ (accessed on 7 January 2018).
- Perdomo-Ortiz, A.; Dickson, N.; Drew-Brook, M.; Rose, G.; Aspuru-Guzik, A. Finding low-energy conformations of lattice protein models by quantum annealing. Sci. Rep. 2012, 2, 571. [Google Scholar] [CrossRef] [PubMed]
- Perdomo-Ortiz, A.; Fluegemann, J.; Narasimhan, S.; Biswas, R.; Smelyanskiy, V. A quantum annealing approach for fault detection and diagnosis of graph-based systems. Eur. Phys. J. Spec. Top. 2015, 224, 131–148. [Google Scholar] [CrossRef]
- King, J.; Yarkoni, S.; Nevisi, M.M.; Hilton, J.P.; McGeoch, C.C. Benchmarking a quantum annealing processor with the time-to-target metric. arXiv, 2015; arXiv:quant-ph/1508.05087. [Google Scholar]
- Bian, Z.; Chudak, F.; Israel, R.B.; Lackey, B.; Macready, W.G.; Roy, A. Mapping Constrained Optimization Problems to Quantum Annealing with Application to Fault Diagnosis. Front. ICT 2016, 3, 14. [Google Scholar] [CrossRef]
- Tsukamoto, S.; Takatsu, M.; Matsubara, S.; Tamura, H. An Accelerator Architecture for Combinatorial Optimization Problems. Fujitsu Sci. Tech. J. 2017, 53, 8–13. [Google Scholar]
- Yamaoka, M.; Yoshimura, C.; Hayashi, M.; Okuyama, T.; Aoki, H.; Mizuno, H. Ising Computer. Hitachi Rev. 2016, 65, 78–82. [Google Scholar]
- Venegas-Andraca, S.; Cruz-Santos, W.; McGeoch, C.; Lanzagorta, M. A cross-disciplinary introduction to quantum annealing-based algorithms. Contemp. Phys. 2018, 5982, 174–196. [Google Scholar] [CrossRef]
- Apolloni, B.; Cesa-Bianchi, N.; de Falco, D. A numerical implementation of Quantum Annealing. In Proceedings of the Stochastic Processes, Physics and Geometry, Ascona, Switzerland, 4–9 July 1988; pp. 97–111. [Google Scholar]
- Apolloni, B.; Carvalho, C.; de Falco, D. Quantum stochastic optimization. Stoch. Process. Appl. 1989, 33, 233–244. [Google Scholar] [CrossRef]
- Somorjai, R. Novel approach for computing the global minimum of proteins. 1. General concepts, methods, and approximations. J. Phys. Chem. 1991, 95, 4141–4146. [Google Scholar] [CrossRef]
- Amara, P.; Hsu, D.; Straub, J.E. Global energy minimum searches using an approximate solution of the imaginary time Schroedinger equation. J. Phys. Chem. 1993, 97, 6715–6721. [Google Scholar] [CrossRef]
- Finnila, A.; Gomez, M.; Sebenik, C.; Stenson, C.; Doll, J. Quantum annealing: A new method for minimizing multidimensional functions. Chem. Phys. Lett. 1994, 219, 343–348. [Google Scholar] [CrossRef]
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355–5363. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Santoro, G.E.; Tosatti, E. Optimization using quantum mechanics: quantum annealing through adiabatic evolution. J. Phys. A Math. Gen. 2006, 39, R393–R431. [Google Scholar] [CrossRef]
- Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. A Math. Gen. 1982, 15, 3241. [Google Scholar] [CrossRef]
- Boros, E.; Hammer, P.L. Pseudo-boolean Optimization. Discret. Appl. Math. 2002, 123, 155–225. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Lundgren, A.; Preda, D. A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem. Science 2001, 292, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Jansen, S.; Ruskai, M.B.; Seiler, R. Bounds for the adiabatic approximation with applications to quantum computation. J. Math. Phys 2007, 48, 102111. [Google Scholar] [CrossRef]
- Forsyth, D.A.; Ponce, J. Computer Vision: A Modern Approach; Pearson: New York, NY, USA, 2002. [Google Scholar]
- Ohta, Y.; Kanade, T. Stereo by Intra- and Inter-Scanline Search Using Dynamic Programming. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 139–154. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, N.N.; Shum, H.Y. Stereo matching using belief propagation. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 787–800. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast Approximate Energy Minimization via Graph Cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Boykov, Y.; Kolmogorov, V. An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [PubMed]
- Veksler, O. Reducing Search Space for Stereo Correspondence with Graph Cuts. In Proceedings of the British Machine Vision Conference 2006, Edinburgh, UK, 4–7 September 2006; pp. 709–718. [Google Scholar]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1982. [Google Scholar]
- Dahlhaus, E.; Johnson, D.S.; Papadimitriou, C.H.; Seymour, P.D.; Yannakakis, M. The Complexity of Multiterminal Cuts. SIAM J. Comput. 1994, 23, 864–894. [Google Scholar] [CrossRef]
- Garg, N.; Vazirani, V.; Yannakakis, M. Primal-dual approximation algorithms for integral flow and multicut in trees. Algorithmica 1997, 18, 3–20. [Google Scholar] [CrossRef]
- Boros, E.; Gruber, A. On Quadratization of Pseudo-Boolean Functions. arXiv, 2014; arXiv:1404.6538. [Google Scholar]
- Anthony, M.; Boros, E.; Crama, Y.; Gruber, A. Quadratization of symmetric pseudo-Boolean functions. Discret. Appl. Math. 2016, 203, 1–12. [Google Scholar] [CrossRef]
- Freedman, D.; Drineas, P. Energy Minimization via Graph Cuts: Settling What is Possible. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–26 June 2005; pp. 939–946. [Google Scholar] [CrossRef]
- Ishikawa, H. Transformation of General Binary MRF Minimization to the First-Order Case. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1234–1249. [Google Scholar] [CrossRef] [PubMed]
- Tanburn, R.; Dattani, N.S. Quadratization in Pseudo-Boolean Optimization and Adiabatic Quantum Computing. Available online: https://github.com/ndattani/quadratizationReview (accessed on 17 September 2018).
- Zureiki, A.; Devy, M.; Chatila, R. Stereo Matching using Reduced-Graph Cuts. In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; Volume 1, pp. 237–240. [Google Scholar] [CrossRef]
- Zhang, Y.; Hartley, R.I.; Wang, L. Fast Multi-labelling for Stereo Matching. In Proceedings of the 11th European Conference on Computer Vision (ECCV 2010), Heraklion, Crete, Greece, 5–11 September 2010; pp. 524–537. [Google Scholar]
- Choi, V. Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process. 2008, 7, 193–209. [Google Scholar] [CrossRef]
- Choi, V. Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Inf. Process. 2011, 10, 343–353. [Google Scholar] [CrossRef]
- Booth, M.; Reinhardt, S.P.; Roy, A. Partitioning Optimization Problems for Hybrid Classical/Quantum Execution; Technical Report; D-Wave the Quantum Computing Company: Burnaby, CA, USA, 9 January 2017. [Google Scholar]
- IBM ILOG CPLEX Optimizer. Available online: http://www-01.ibm.com/software/integration/optimization/cplex-optimizer (accessed on 14 September 2018).
- METSlib An Open Source Tabu Search Metaheuristic framework in modern C++. Available online: http://projects.coin-or.org/metslib (accessed on 14 September 2018).
- Rosenberg, G.; Vazifeh, M.; Woods, B.; Haber, E. Building an iterative heuristic solver for a quantum annealer. Comput. Optim. Appl. 2016, 65, 845–869. [Google Scholar] [CrossRef]
- Qbsolv Software, Version 2000Q. D-Wave Systems: Burnaby, CA, USA, 2000. Available online: https://www.dwavesys.com/software (accessed on 14 September 2018).
- D-Wave sOurce Code and Documentation. Available online: https://github.com/dwavesystems/qbsolv (accessed on 14 September 2018).

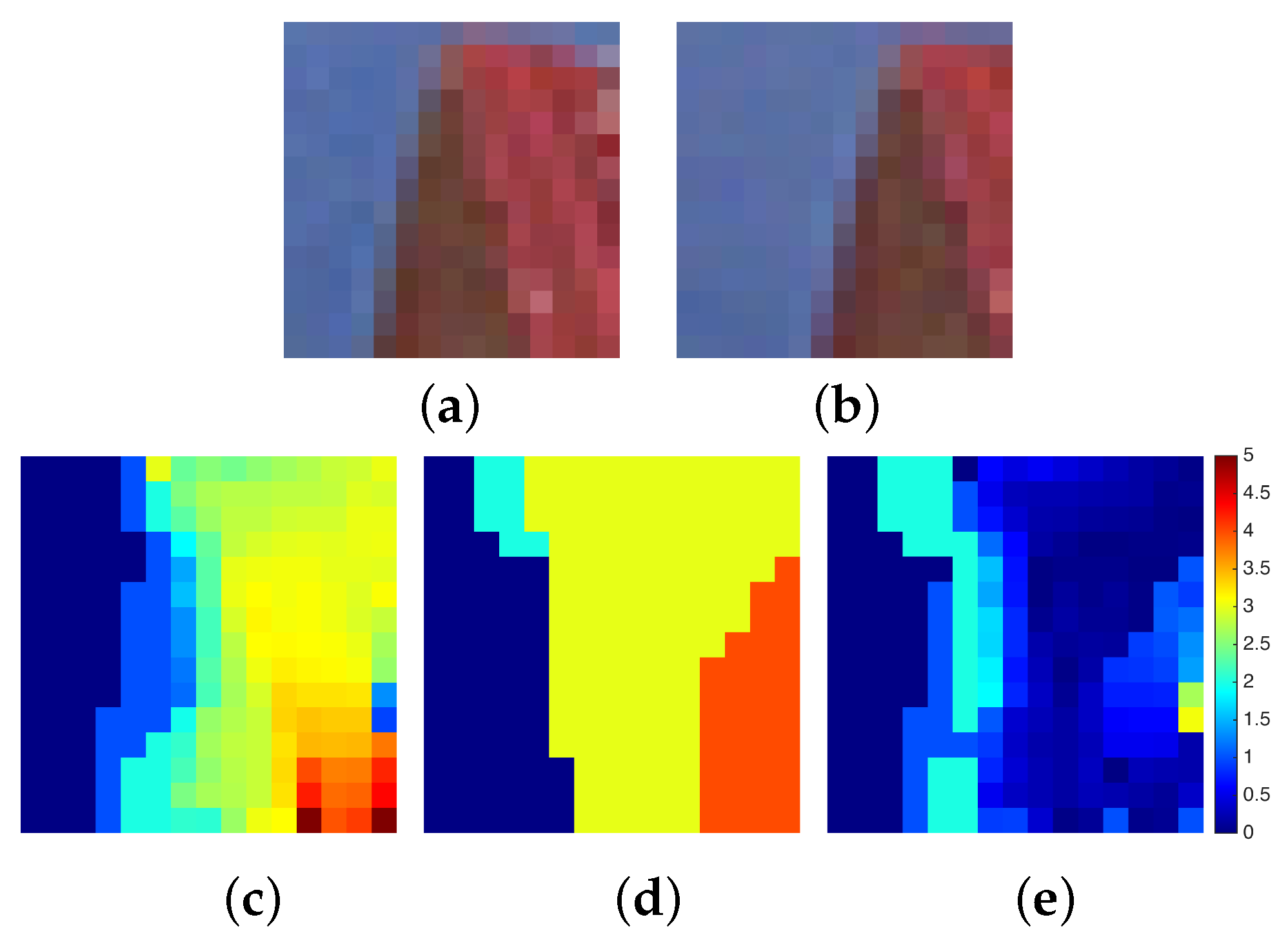
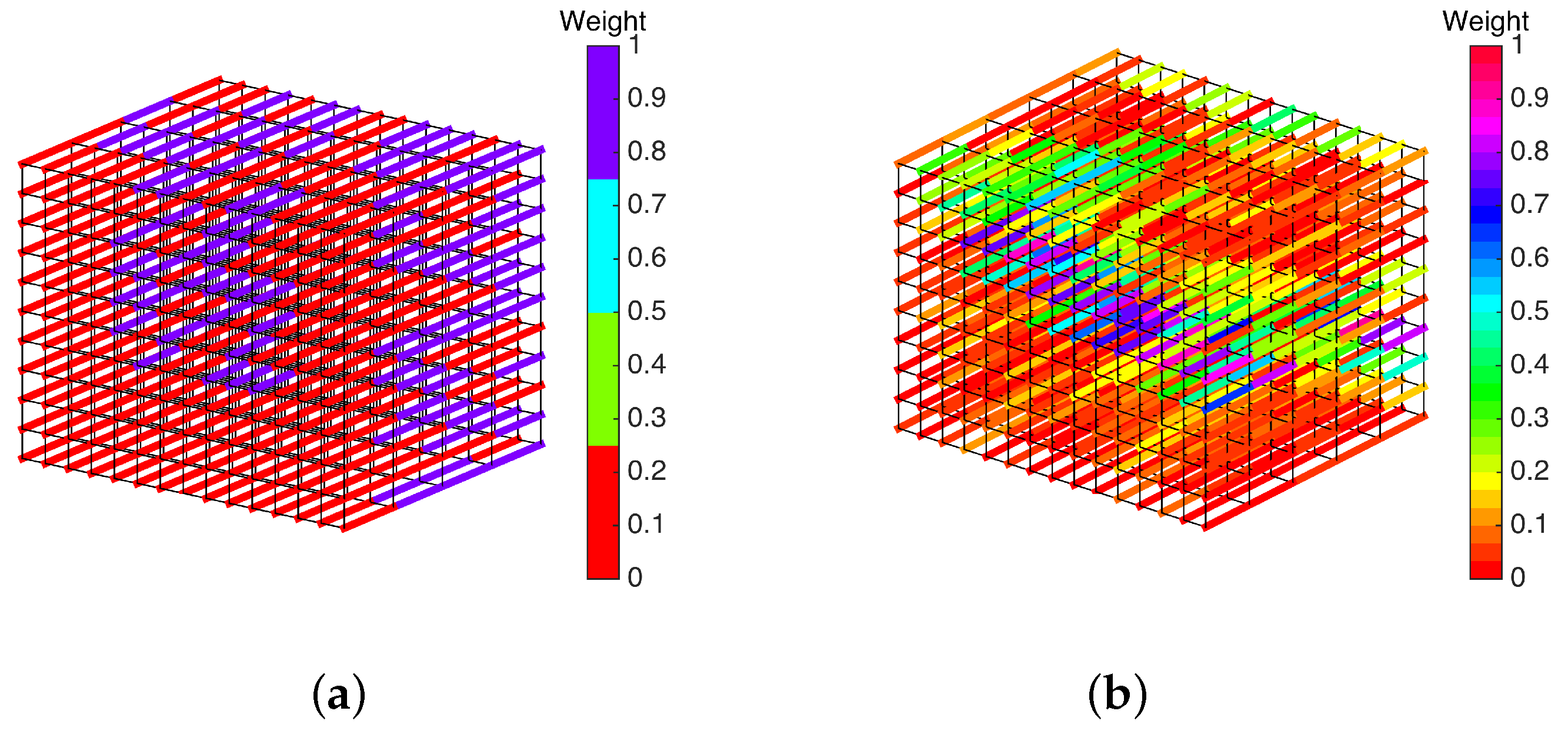
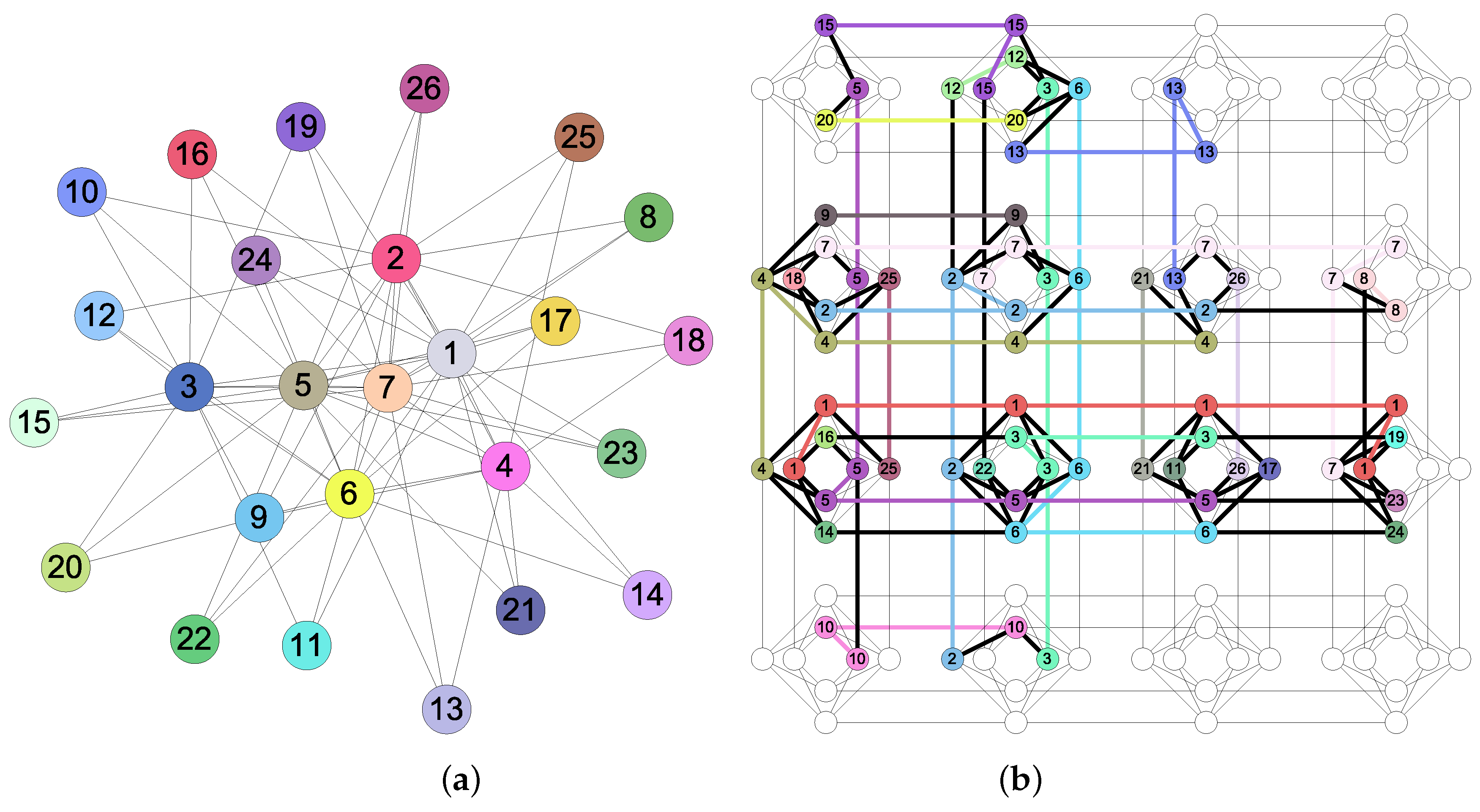
| Case | ROI | L | |||
|---|---|---|---|---|---|
| (a) | 3 | 902 | 2745 | 6392 | |
| (b) | 5 | 1052 | 3125 | 7302 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Santos, W.; Venegas-Andraca, S.E.; Lanzagorta, M. A QUBO Formulation of the Stereo Matching Problem for D-Wave Quantum Annealers. Entropy 2018, 20, 786. https://doi.org/10.3390/e20100786
Cruz-Santos W, Venegas-Andraca SE, Lanzagorta M. A QUBO Formulation of the Stereo Matching Problem for D-Wave Quantum Annealers. Entropy. 2018; 20(10):786. https://doi.org/10.3390/e20100786
Chicago/Turabian StyleCruz-Santos, William, Salvador E. Venegas-Andraca, and Marco Lanzagorta. 2018. "A QUBO Formulation of the Stereo Matching Problem for D-Wave Quantum Annealers" Entropy 20, no. 10: 786. https://doi.org/10.3390/e20100786
APA StyleCruz-Santos, W., Venegas-Andraca, S. E., & Lanzagorta, M. (2018). A QUBO Formulation of the Stereo Matching Problem for D-Wave Quantum Annealers. Entropy, 20(10), 786. https://doi.org/10.3390/e20100786






