Estimating Mixture Entropy with Pairwise Distances
Abstract
:1. Introduction
2. Background and Definitions
3. Estimators Based on Pairwise-Distances
3.1. Overview
3.2. Lower Bound
3.3. Upper Bound
3.4. Exact Estimation in the “Clustered” Case
4. Gaussian Mixtures
5. Estimating Mutual Information
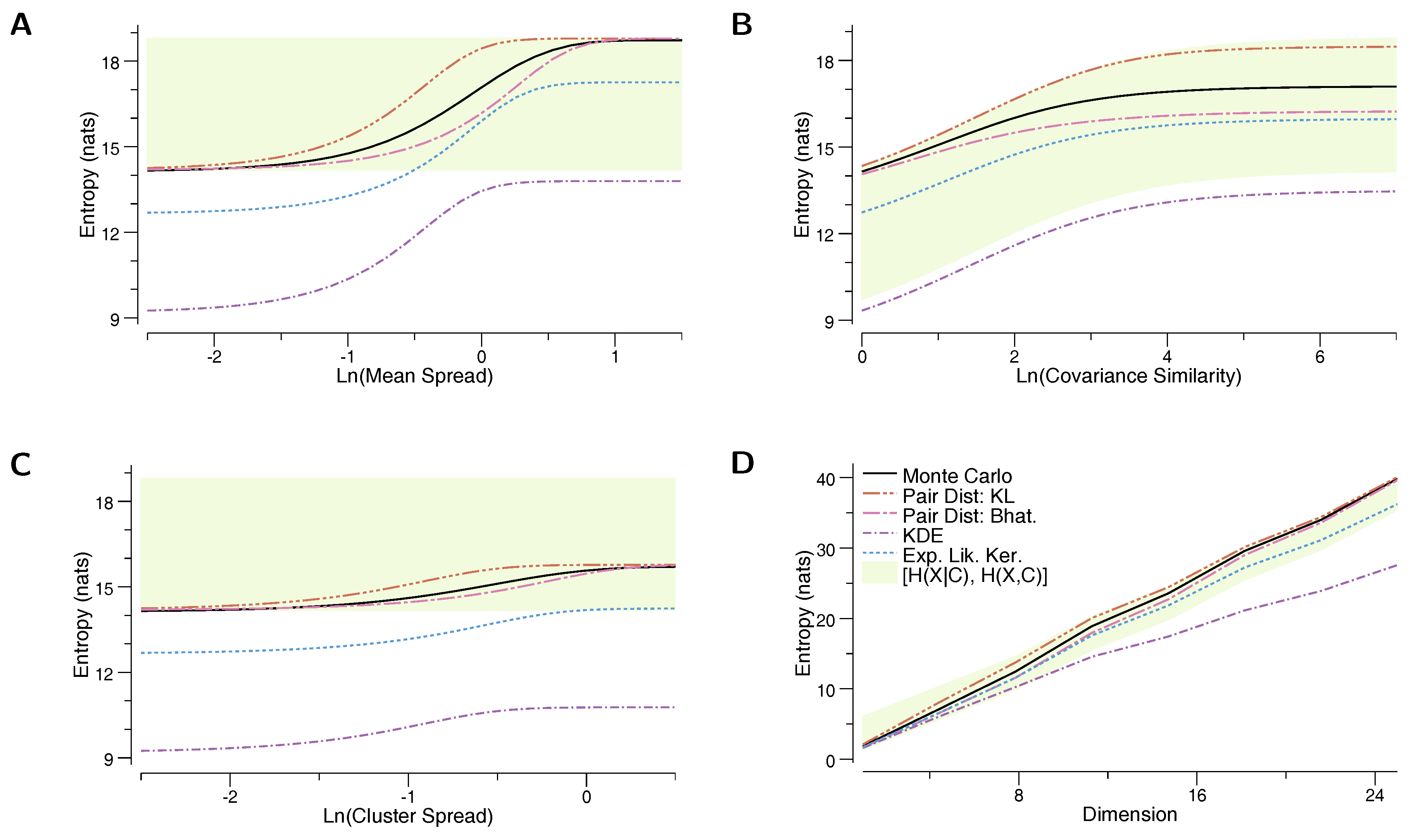
6. Numerical Results
- The true entropy, , as estimated by a Monte Carlo sampling of the mixture model. Two thousand samples were used for each MC estimate for the mixtures of Gaussians, and 5000 samples were used for the mixtures of uniform distributions.
- Our proposed upper-bound, based on the KL divergence, (Equation (12))
- Our proposed lower-bound, based on the Bhattacharyya distance, (Equation (11))
- The kernel density estimate based on the component means, (Equation (3))
- The lower bound based on the “Expected Likelihood Kernel”, (Equation (4))
- The lower bound based on the conditional entropy, (Equation (1))
- The upper bound based on the joint entropy, (Equation (2)).
6.1. Mixture of Gaussians
6.2. Mixture of Uniforms
7. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Chernoff α-Divergence Is Not a Distance Function for α ∉ [0, 1]
Appendix B. For Clustered Mixtures, ĤBD ≥ ĤELK
References
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Goldberger, J.; Gordon, S.; Greenspan, H. An Efficient Image Similarity Measure Based on Approximations of KL-Divergence Between Two Gaussian Mixtures. In Proceedings of the 9th International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 3, pp. 487–493. [Google Scholar]
- Viola, P.; Schraudolph, N.N.; Sejnowski, T.J. Empirical Entropy Manipulation for Real-World Problems. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 1996; pp. 851–857. [Google Scholar]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; Volume 4, pp. 317–320. [Google Scholar]
- Chen, J.Y.; Hershey, J.R.; Olsen, P.A.; Yashchin, E. Accelerated monte carlo for kullback-leibler divergence between gaussian mixture models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 4553–4556. [Google Scholar]
- Capristan, F.M.; Alonso, J.J. Range Safety Assessment Tool (RSAT): An analysis environment for safety assessment of launch and reentry vehicles. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 304. [Google Scholar]
- Schraudolph, N.N. Optimization of Entropy with Neural Networks. Ph.D. Thesis, University of California, San Diego, CA, USA, 1995. [Google Scholar]
- Schraudolph, N.N. Gradient-based manipulation of nonparametric entropy estimates. IEEE Trans. Neural Netw. 2004, 15, 828–837. [Google Scholar] [CrossRef] [PubMed]
- Shwartz, S.; Zibulevsky, M.; Schechner, Y.Y. Fast kernel entropy estimation and optimization. Signal Process. 2005, 85, 1045–1058. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D.; Wolpert, D.H. Nonlinear Information Bottleneck. arXiv, 2017; arXiv:1705.02436. [Google Scholar]
- Contreras-Reyes, J.E.; Cortés, D.D. Bounds on Rényi and Shannon Entropies for Finite Mixtures of Multivariate Skew-Normal Distributions: Application to Swordfish (Xiphias gladius Linnaeus). Entropy 2016, 18, 382. [Google Scholar] [CrossRef]
- Carreira-Perpinan, M.A. Mode-finding for mixtures of Gaussian distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1318–1323. [Google Scholar] [CrossRef]
- Zobay, O. Variational Bayesian inference with Gaussian-mixture approximations. Electron. J. Stat. 2014, 8, 355–389. [Google Scholar] [CrossRef]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stat. Sci. 1997, 6, 17–39. [Google Scholar]
- Joe, H. Estimation of entropy and other functionals of a multivariate density. Ann. Inst. Stat. Math. 1989, 41, 683–697. [Google Scholar] [CrossRef]
- Nair, C.; Prabhakar, B.; Shah, D. On entropy for mixtures of discrete and continuous variables. arXiv, 2006; arXiv:cs/0607075. [Google Scholar]
- Huber, M.F.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U.D. On entropy approximation for Gaussian mixture random vectors. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Korea, 20–22 August 2008; pp. 181–188. [Google Scholar]
- Hall, P.; Morton, S.C. On the estimation of entropy. Ann. Inst. Stat. Math. 1993, 45, 69–88. [Google Scholar] [CrossRef]
- Principe, J.C.; Xu, D.; Fisher, J. Information theoretic learning. Unsuperv. Adapt. Filter 2000, 1, 265–319. [Google Scholar]
- Xu, J.W.; Paiva, A.R.; Park, I.; Principe, J.C. A reproducing kernel Hilbert space framework for information-theoretic learning. IEEE Trans. Signal Process. 2008, 56, 5891–5902. [Google Scholar]
- Jebara, T.; Kondor, R. Bhattacharyya and expected likelihood kernels. In Learning Theory and Kernel Machines; Springer: Berlin, Germany, 2003; pp. 57–71. [Google Scholar]
- Jebara, T.; Kondor, R.; Howard, A. Probability product kernels. J. Mach. Learn. Res. 2004, 5, 819–844. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S.I. Similarity Measures and Generalized Divergences. In Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-Way Data Analysis and Blind Source Separation; JohnWiley & Sons: Hoboken, NJ, USA, 2009; pp. 81–129. [Google Scholar]
- Cichocki, A.; Amari, S.I. Families of alpha-beta-and gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Gil, M.; Alajaji, F.; Linder, T. Rényi divergence measures for commonly used univariate continuous distributions. Inf. Sci. 2013, 249, 124–131. [Google Scholar] [CrossRef]
- Crooks, G.E. On Measures of Entropy and Information. Available online: http://threeplusone.com/on_information.pdf (accessed on 12 July 2017).
- Nielsen, F. Chernoff information of exponential families. arXiv, 2011; arXiv:1102.2684. [Google Scholar]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Haussler, D.; Opper, M. Mutual information, metric entropy and cumulative relative entropy risk. Ann. Stat. 1997, 25, 2451–2492. [Google Scholar] [CrossRef]
- Fukunaga, K. Introduction to Statistical Pattern Recognition, 2nd ed.; Academic Press: Boston, MA, USA, 1990. [Google Scholar]
- Paisley, J. Two Useful Bounds for Variational Inference; Princeton University: Princeton, NJ, USA, 2010. [Google Scholar]
- Sason, I.; Verdú, S. f-Divergence Inequalities. IEEE Trans. Inf. Theory 2016, 62, 5973–6006. [Google Scholar] [CrossRef]
- Hero, A.O.; Ma, B.; Michel, O.; Gorman, J. Alpha-Divergence for Classification, Indexing and Retrieval. Available online: https://pdfs.semanticscholar.org/6d51/fbf90c59c2bb8cbf0cb609a224f53d1b68fb.pdf (accessed on 14 July 2017).
- Dowson, D.; Landau, B. The Fréchet distance between multivariate normal distributions. J. Multivar. Anal. 1982, 12, 450–455. [Google Scholar] [CrossRef]
- Olkin, I.; Pukelsheim, F. The distance between two random vectors with given dispersion matrices. Linear Algebra Appl. 1982, 48, 257–263. [Google Scholar] [CrossRef]
- Pardo, L. Statistical Inference Based on Divergence Measures; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Hobza, T.; Morales, D.; Pardo, L. Rényi statistics for testing equality of autocorrelation coefficients. Stat. Methodol. 2009, 6, 424–436. [Google Scholar]
- Nielsen, F. Generalized Bhattacharyya and Chernoff upper bounds on Bayes error using quasi-arithmetic means. Pattern Recognit. Lett. 2014, 42, 25–34. [Google Scholar] [CrossRef]
- GitHub. Available online: https://www.github.com/btracey/mixent (accessed on 14 July 2017).
- Gonum Numeric Library. Available online: https://www.gonum.org (accessed on 14 July 2017).
- Tishby, N.; Pereira, F.; Bialek, W. The information bottleneck method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 22–24 September 1999. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. Entropy 2017, 19, 361. https://doi.org/10.3390/e19070361
Kolchinsky A, Tracey BD. Estimating Mixture Entropy with Pairwise Distances. Entropy. 2017; 19(7):361. https://doi.org/10.3390/e19070361
Chicago/Turabian StyleKolchinsky, Artemy, and Brendan D. Tracey. 2017. "Estimating Mixture Entropy with Pairwise Distances" Entropy 19, no. 7: 361. https://doi.org/10.3390/e19070361
APA StyleKolchinsky, A., & Tracey, B. D. (2017). Estimating Mixture Entropy with Pairwise Distances. Entropy, 19(7), 361. https://doi.org/10.3390/e19070361



