1. Introduction
Critical behavior, where long-range correlations decay as a power law with distance, has many important physics applications ranging from phase transitions in condensed matter experiments to turbulence and inflationary fluctuations in our early Universe. It has important applications beyond the traditional purview of physics, as well [
1,
2,
3,
4,
5], including applications to music [
4,
6], genomics [
7,
8] and human languages [
9,
10,
11,
12].
In
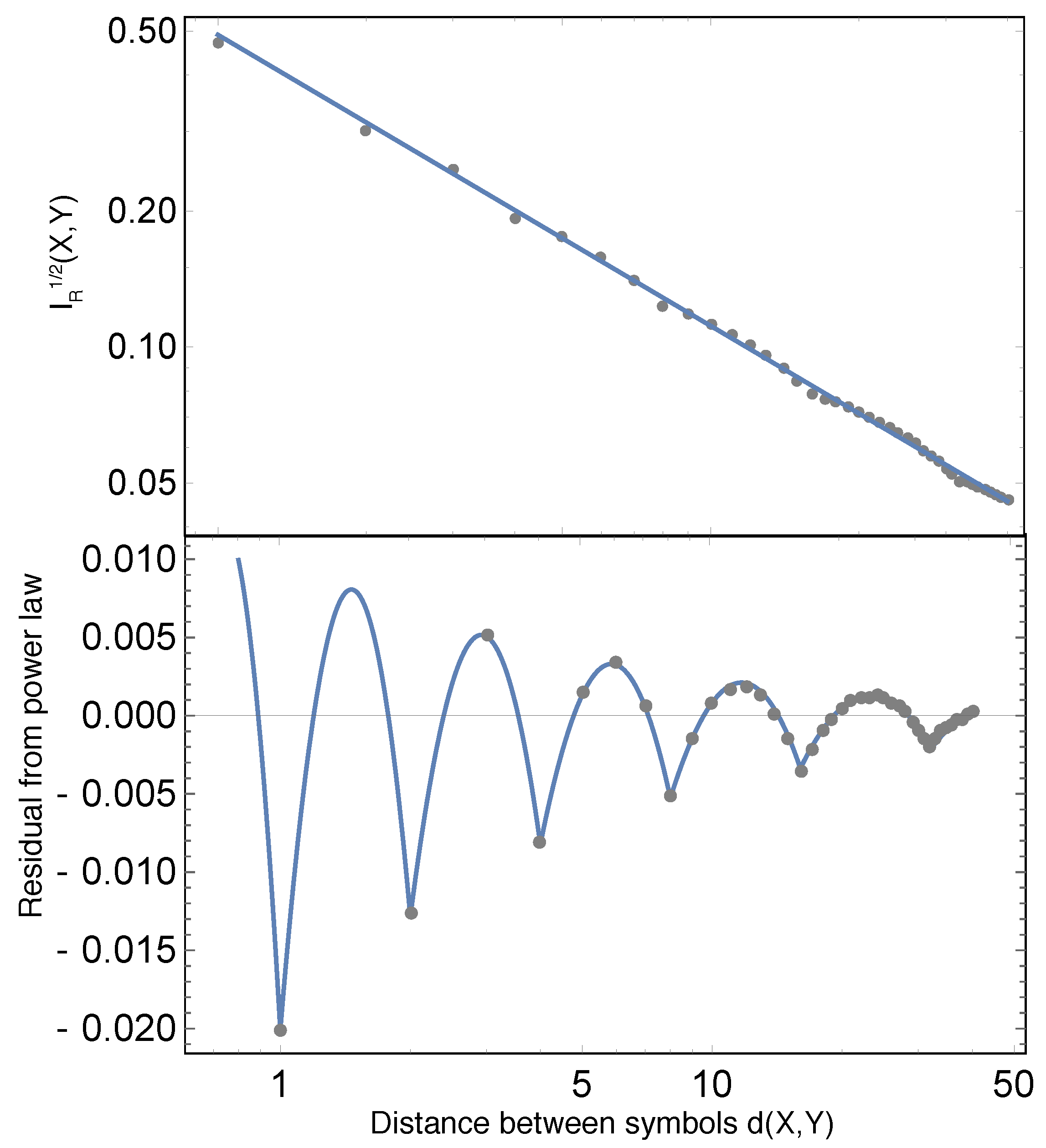
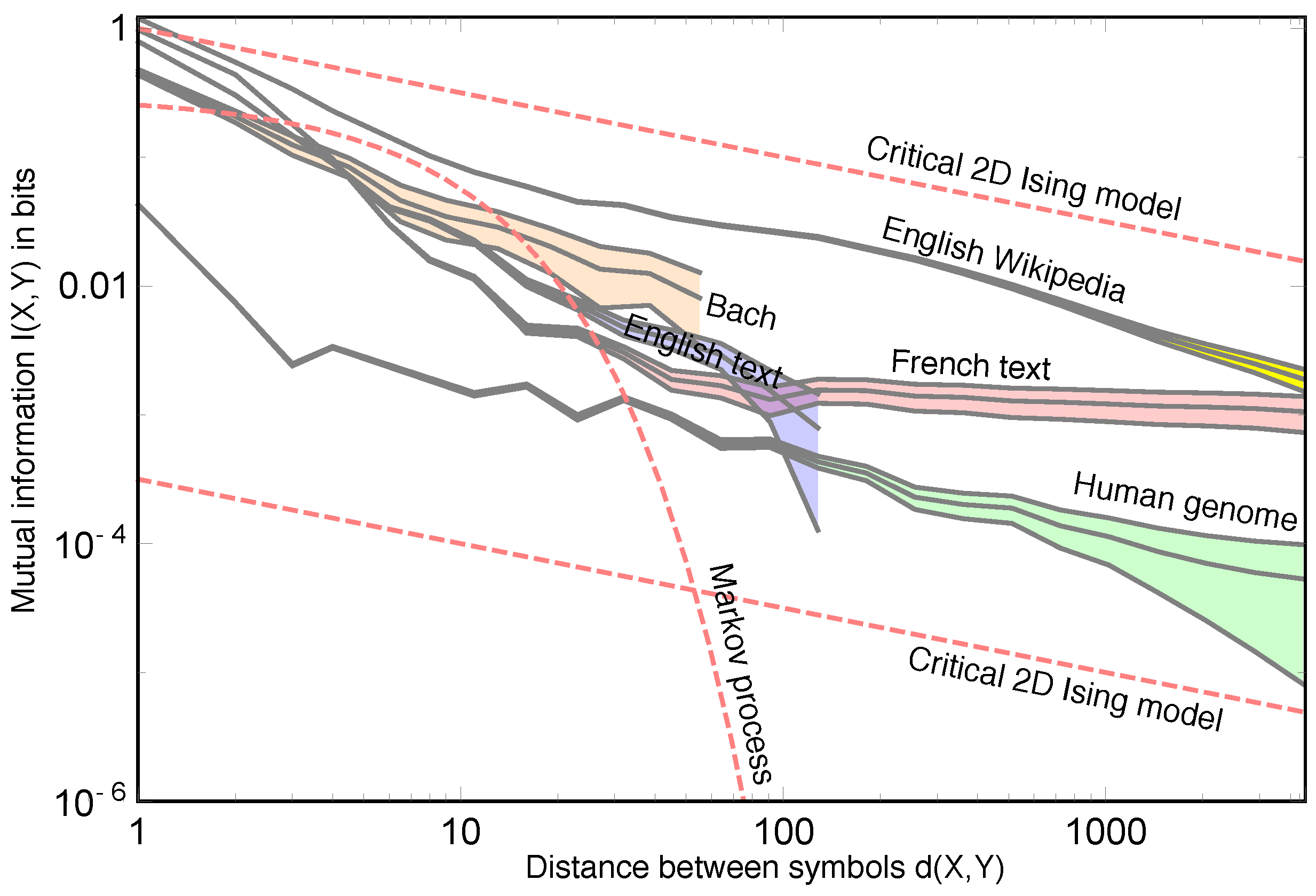
Figure 1, we plot a statistic that can be applied to all of the above examples: the mutual information between two symbols as a function of the number of symbols in between the two symbols [
9]. As discussed in previous works [
9,
11,
13], the plot shows that the number of bits of information provided by a symbol about another drops roughly as a power law (The power law discussed here should not be confused with another famous power law that occurs in natural languages: Zipf’s law [
14]. Zipf’s law implies power law behavior in one-point statistics (in the histogram of word frequencies), whereas we are interested in two-point statistics. In the former case, the power law is in the frequency of words; in the latter case, the power law is in the separation between characters. One can easily cook up sequences that obey Zipf’s law, but are not critical and do not exhibit a power law in the mutual information. However, there are models of certain physical systems where Zipf’s law follows from criticality [
15,
16].) with distance in sequences (defined as the number of symbols between the two symbols of interest) as diverse as the human genome, music by Bach and text in English and French. Why is this, when so many other correlations in nature instead drop exponentially [
17]?
Better understanding the statistical properties of natural languages is interesting not only for geneticists, musicologists and linguists, but also for the machine learning community. Any tasks that involve natural language processing (e.g., data compression, speech-to-text conversion, auto-correction) exploit statistical properties of language and can all be further improved if we can better understand these properties, even in the context of a toy model of these data sequences. Indeed, the difficulty of automatic natural language processing has been known at least as far back as Turing, whose eponymous test [
22] relies on this fact. A tempting explanation is that natural language is something uniquely human. However, this is far from a satisfactory one, especially given the recent successes of machines at performing tasks as complex and as “human” as playing Jeopardy! [
23], chess [
24], Atari games [
25] and Go [
26]. We will show that computer descriptions of language suffer from a much simpler problem that has involved no talk about meaning or being non-human: they tend to get the basic statistical properties wrong.
To illustrate this point, consider Markov models of natural language. From a linguistics point of view, it has been known for decades that such models are fundamentally unsuitable for modeling human language [
27]. However, linguistic arguments typically do not produce an observable that can be used to quantitatively falsify any Markovian model of language. Instead, these arguments rely on highly specific knowledge about the data, in this case, an understanding of the language’s grammar. This knowledge is non-trivial for a human speaker to acquire, much less an artificial neural network. In contrast, the mutual information is comparatively trivial to observe, requiring no specific knowledge about the data, and it immediately indicates that natural languages would be poorly approximated by a Markov/hidden Markov model, as we will demonstrate.
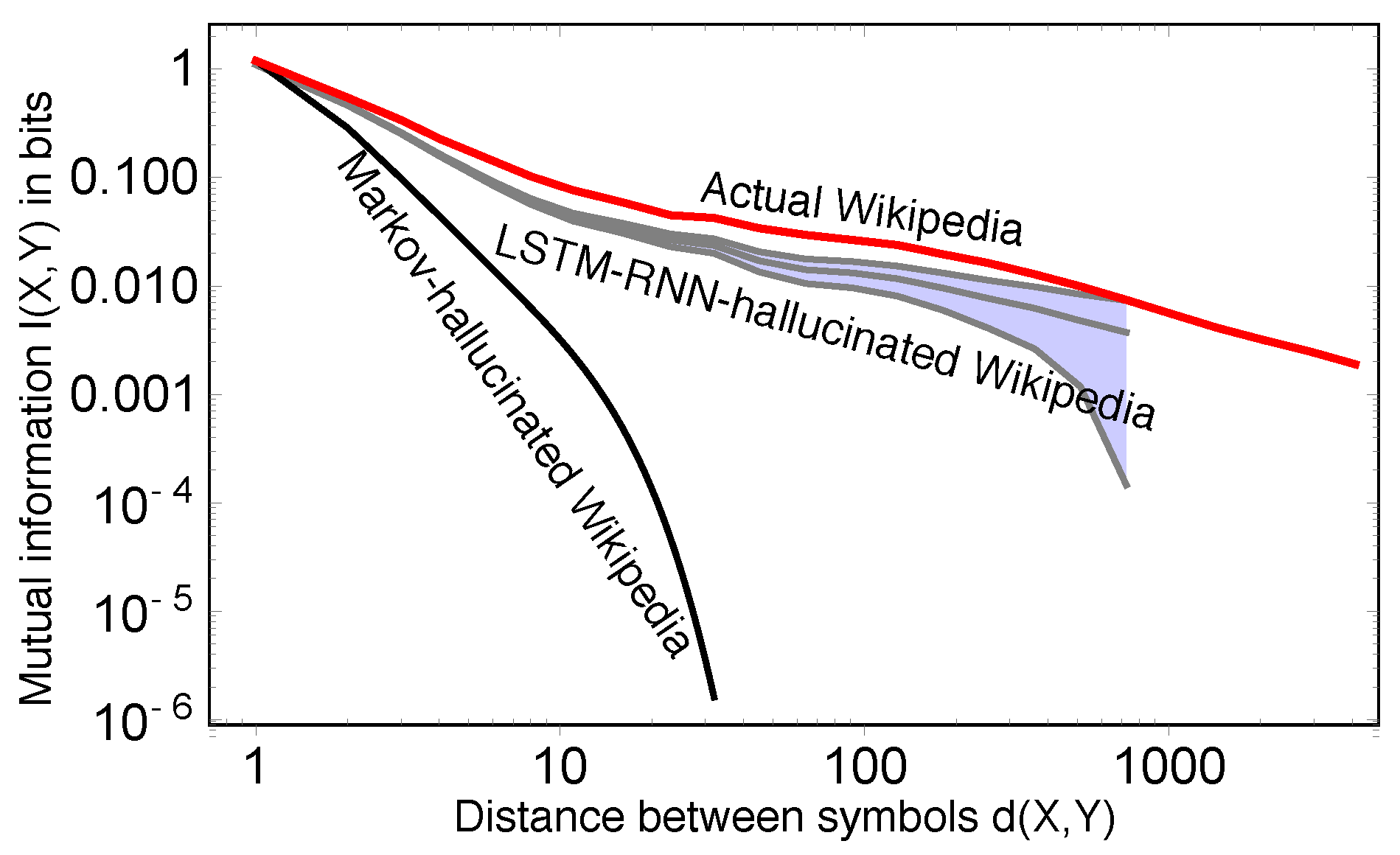
Furthermore, the mutual information decay may offer a partial explanation of the impressive progress that has been made by using deep neural networks for natural language processing (see, e.g., [
28,
29,
30,
31,
32]) (for recent reviews of deep neural networks, see [
33,
34]), We will see that a key reason that currently popular recurrent neural networks with long-short-term memory (LSTM) [
35] do much better is that they can replicate critical behavior, but that even they can be further improved, since they can under-predict long-range mutual information.
While motivated by questions about natural languages and other data sequences, we will explore the information-theoretic properties of formal languages. For simplicity, we focus on probabilistic regular grammars and probabilistic context-free grammars (PCFGs). Of course, real-world data sources like English are likely more complex than a context-free grammar [
36], just as a real-world magnet is more complex than the Ising model. However, these formal languages serve as toy models that capture some aspects of the real data source, and the theoretical techniques we develop for studying these toy models might be adapted to more complex formal languages. Of course, independent of their connection to natural languages, formal languages are also theoretically interesting in their own right and have connections to, e.g., group theory [
37].
This paper is organized as follows. In
Section 2, we show how Markov processes exhibit exponential decay in mutual information with scale; we give a rigorous proof of this and other results in a series of Appendices. To enable such proofs, we introduce a convenient quantity that we term rational mutual information, which bounds the mutual information and converges to it in the near-independence limit. In
Section 3, we define a subclass of generative grammars and show that they exhibit critical behavior with power law decays. We then generalize our discussion using Bayesian nets and relate our findings to theorems in statistical physics. In
Section 4, we discuss our results and explain how LSTM RNNs can reproduce critical behavior by emulating our generative grammar model.
2. Markov Implies Exponential Decay
For two discrete random variables
X and
Y, the following definitions of mutual information are all equivalent:
where
is the Shannon entropy [
38] and
is the Kullback–Leibler divergence [
39] between the joint probability distribution and the product of the individual marginals. If the base of the logarithm is taken to be
, then
is measured in bits. The mutual information can be interpreted as how much one variable knows about the other:
is the reduction in the number of bits needed to specify for
X once
Y is specified. Equivalently, it is the number of encoding bits saved by using the true joint probability
instead of approximating
X and
Y as independent. It is thus a measure of statistical dependencies between
X and
Y. Although it is more conventional to measure quantities such as the correlation coefficient
in statistics and statistical physics, the mutual information is more suitable for generic data, since it does not require that the variables
X and
Y are numbers or have any algebraic structure, whereas
requires that we are able to multiply
and average. Whereas it makes sense to multiply numbers, it is meaningless to multiply or average two characters such as “!” and “?”.
The rest of this paper is largely a study of the mutual information between two random variables that are realizations of a discrete stochastic process, with some separation in time. More concretely, we can think of sequences of random variables, where each one might take values from some finite alphabet. For example, if we model English as a discrete stochastic process and take , X could represent the first character (“F”) in this sentence, whereas Y could represent the third character (“r”) in this sentence.
In particular, we start by studying the mutual information function of a Markov process, which is analytically tractable. Let us briefly recapitulate some basic facts about Markov processes (see, e.g., [
40] for a pedagogical review). A Markov process is defined by a matrix
of conditional probabilities
. Such Markov matrices (also known as stochastic matrices) thus have the properties
and
. They fully specify the dynamics of the model:
where
is a vector with components
that specifies the probability distribution at time
t. Let
denote the eigenvalues of
, sorted by decreasing magnitude:
All Markov matrices have
, which is why blowup is avoided when Equation (
2) is iterated, and
, with the corresponding eigenvector giving a stationary probability distribution
satisfying
.
In addition, two mild conditions are usually imposed on Markov matrices: is irreducible, meaning that every state is accessible from every other state (otherwise, we could decompose the Markov process into separate Markov processes). Second, to avoid processes like that will never converge, we take the Markov process to be aperiodic. It is easy to show using the Perron–Frobenius theorem that being irreducible and aperiodic implies and, therefore, that is unique.
This section is devoted to the intuition behind the following theorem, whose full proof is given in
Appendix A and
Appendix B. The theorem states roughly that for a Markov process, the mutual information between two points in time
and
decays exponentially for large separation
:
Theorem 1. Let be a Markov matrix that generates a Markov process. If is irreducible and aperiodic, then the asymptotic behavior of the mutual information is exponential decay toward zero for with decay timescale where is the second largest eigenvalue of . If is reducible or periodic, I can instead decay to a constant; no Markov process whatsoever can produce power law decay. Suppose is irreducible and aperiodic so that as , as mentioned above. This convergence of one-point statistics, e.g., , has been well-studied [40]. However, one can also study higher order statistics such as the joint probability distribution for two points in time. For succinctness, let us write , where , and . We are interested in the asymptotic situation where the Markov process has converged to its steady state, so the marginal distribution , independently of time. If the joint probability distribution approximately factorizes as
for sufficiently large and well-separated times
and
(as we will soon prove), the mutual information will be small. We can therefore Taylor expand the logarithm from Equation (
1) around the point
, giving:
where we have defined the rational mutual information:
For comparing the rational mutual information with the usual mutual information, it will be convenient to take
e as the base
B of the logarithm. We derive useful properties of the rational mutual information in
Appendix A. To mention just one, we note that the rational mutual information is not just asymptotically equal to the mutual information in the limit of near-independence, but it also provides a strict upper bound on it:
.
Let us without loss of generality take
. Then, iterating Equation (
2)
times gives
. Since
, we obtain:
We will continue the proof by considering the typical case where the eigenvalues of
are all distinct (non-degenerate), and the Markov matrix is irreducible and aperiodic; we will generalize to the other cases (which form a set of measure zero) in
Appendix B. Since the eigenvalues are distinct, we can diagonalize
by writing:
for some invertible matrix
and some a diagonal matrix
, whose diagonal elements are the eigenvalues:
. Raising Equation (
5) to the power
gives
, i.e.,
Since
is non-degenerate, irreducible and aperiodic,
, so all terms except the first in the sum of Equation (
6) decay exponentially with
, at a decay rate that grows with
c. Defining
, we have:
where we have made use of the fact that an irreducible and aperiodic Markov process must converge to its stationary distribution for large
, and we have defined
as the expression in square brackets above, satisfying
. Note that
in order for
to be properly normalized.
Substituting Equation (
7) into Equation (
8) and using the facts that
and
, we obtain:
where the term in the last parentheses is of the form
.
In summary, we have shown that an irreducible and aperiodic Markov process with non-degenerate eigenvalues cannot produce critical behavior, because the mutual information decays exponentially. In fact, no Markov processes can, as we show in
Appendix B.
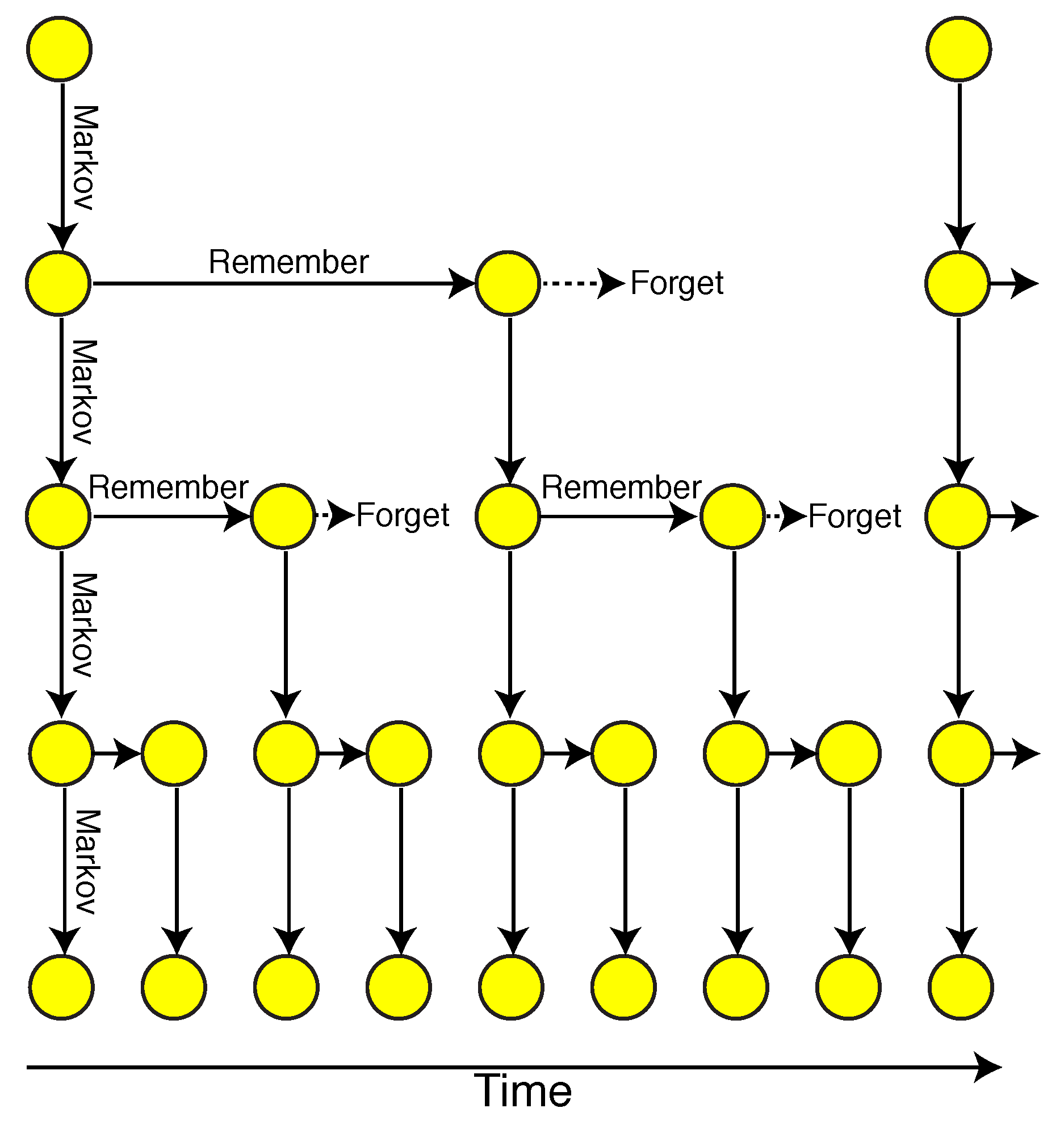
To hammer the final nail into the coffin of Markov processes as models of critical behavior, we need to close a final loophole. Their fundamental problem is the lack of long-term memory, which can be superficially overcome by redefining the state space to include symbols from the past. For example, if the current state is one of
n, and we wish the process to depend on the the last
symbols, we can define an expanded state space consisting of the
possible sequences of length
and a corresponding
Markov matrix (or an
table of conditional probabilities for the next symbol given the last
symbols). Although such a model could fit the curves in
Figure 1 in theory, it cannot in practice, because
requires way more parameters than there are atoms in our observable Universe (
): even for as few as
symbols and
, the Markov process involves over
parameters. Scale-invariance aside, we can also see how Markov processes fail simply by considering the structure of text. To model English well,
would need to correctly close parentheses even if they were opened more than
characters ago, requiring an
-matrix with more than
parameters, where
is the number of characters used.
We can significantly generalize Theorem 1 into a theorem about hidden Markov models (HMM). In an HMM, the observed sequence
is only part of the picture: there are hidden variables
that themselves form a Markov chain. We can think of an HMM as follows: imagine a machine with an internal state space
Y that updates itself according to some Markovian dynamics. The internal dynamics are never observed, but at each time-step, it also produces some output
that forms the sequence that we can observe. These models are quite general and are used to model a wealth of empirical data (see, e.g., [
41]).
Theorem 2. Let be a Markov matrix that generates the transitions between hidden states in an HMM. If is irreducible and aperiodic, then the asymptotic behavior of the mutual information is exponential decay toward zero for with decay timescale where is the second largest eigenvalue of . This theorem is a strict generalization of Theorem 1, since given any Markov process with corresponding matrix , we can construct an HMM that reproduces the exact statistics of by using as the transition matrix between the Y’s and generating from by simply setting with probability one.
The proof is very similar in spirit to the proof of Theorem 1, so we will just present a sketch here, leaving a full proof to
Appendix B. Let
be the Markov matrix that governs
. To compute the joint probability between two random variables
and
, we simply compute the joint probability distribution between
and
, which again involves a factor of
, and then, we use two factors of
to convert the joint probability on
to a joint probability on
. These additional two factors of
will not change the fact that there is an exponential decay given by
.
A simple, intuitive bound from information theory (namely the data processing inequality [
40]) gives
. However, Theorem 1 implies that
decays exponentially. Hence,
must also decay at least as fast as exponentially.
There is a well-known correspondence between so-called probabilistic regular grammars [
42] (sometimes referred to as stochastic regular grammars) and HMMs. Given a probabilistic regular grammar, one can generate an HMM that reproduces all statistics and vice versa. Hence, we can also state Theorem 2 as follows:
Corollary 1. No probabilistic regular grammar exhibits criticality.
In the next section, we will show that this statement is not true for context-free grammars.
3. Power Laws from Generative Grammar
If computationally-feasible Markov processes cannot produce critical behavior, then how do such sequences arise? In this section, we construct a toy model where sequences exhibit criticality. In the parlance of theoretical linguistics, our language is generated by a stochastic or probabilistic context-free grammar (PCFG) [
43,
44,
45,
46]. We will discuss the relationship between our model and a generic PCFG in
Section 3.3.
3.1. A Simple Recursive Grammar Model
We can formalize the above considerations by giving production rules for a toy language
L over an alphabet
A. The language is defined by how a native speaker of
L produces sentences: first, she/he draws one of the
characters from some probability distribution
on
A. She/he then takes this character
and replaces it with
q new symbols, drawn from a probability distribution
, where
is the first symbol and
is any of the second symbols. This is repeated over and over. After
u steps, she/he has a sentence of length
(This exponential blowup is reminiscent of de Sitter space in cosmic inflation. There is actually a much deeper mathematical analogy involving conformal symmetry and
p-adic numbers that has been discussed [
47]).
One can ask for the character statistics of the sentence at production step
u given the statistics of the sentence at production step
. The character distribution is simply:
Of course this equation does not imply that the process is a Markov process when the sentences are read left to right. To characterize the statistics as read from left to right, we really want to compute the statistical dependencies within a given sequence, e.g., at fixed u.
To see that the mutual information decays like a power law rather than exponentially with separation, consider two random variables
X and
Y separated by
. One can ask how many generations took place between
X and the nearest ancestor of
X and
Y. Typically, this will be about
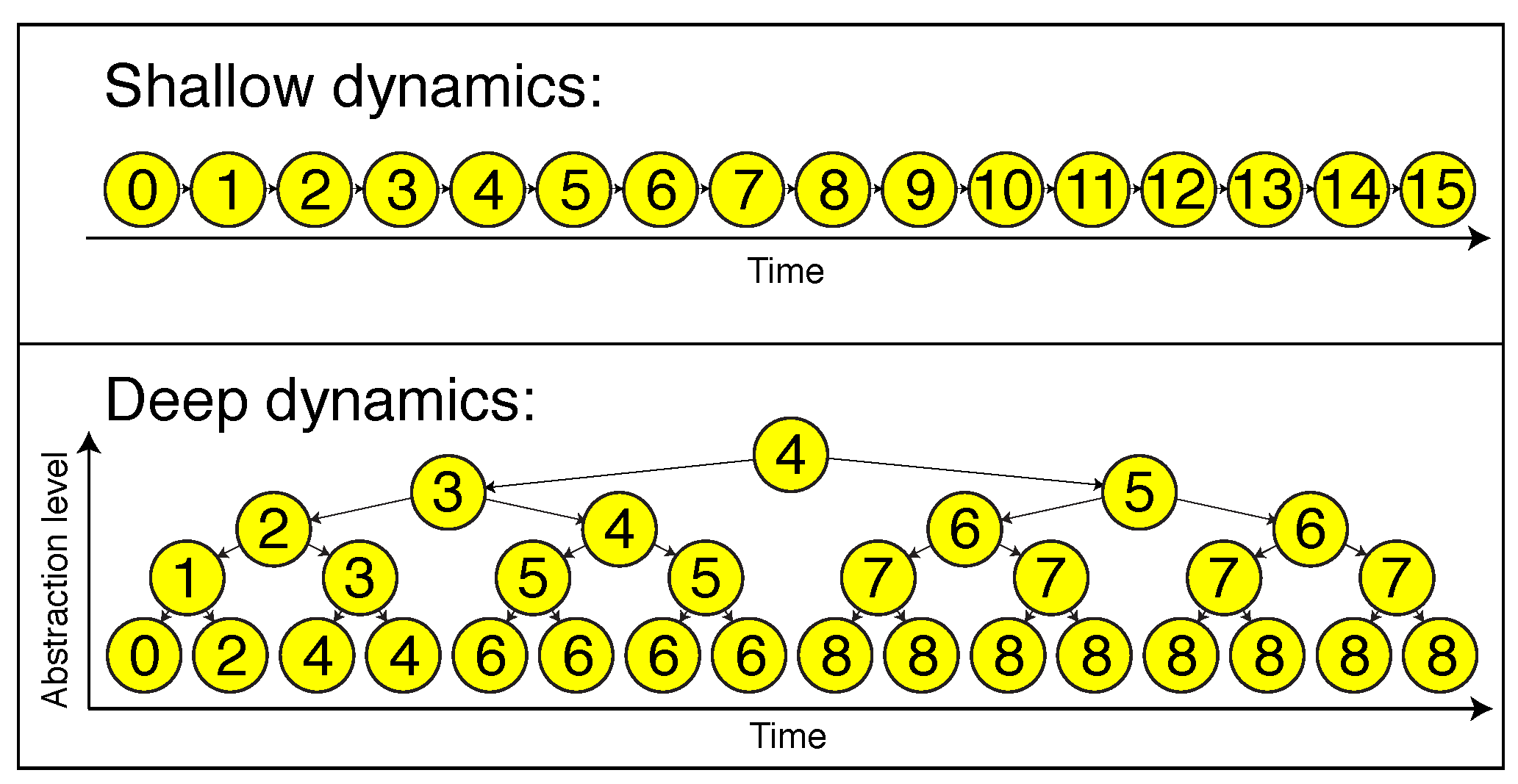
generations. Hence, in the tree graph shown in
Figure 2, which illustrates the special case
, the number of edges
between
X and
Y is about
. Hence, by the previous result for Markov processes, we expect an exponential decay of the mutual information in the variable
. This means that
should be of the form:
where
is controlled by the second-largest eigenvalue of
, the matrix of conditional probabilities
. However, this exponential decay in
is exactly a power law decay in
! This intuitive argument is transformed into a rigorous proof in
Appendix C.
3.2. Further Generalization: Strongly Correlated Characters in Words
In the model we have been describing so far, all nodes emanating from the same parent can be freely permuted since they are conditionally independent. In this sense, characters within a newly-generated word are uncorrelated. We call models with this property weakly correlated. There are still arbitrarily large correlations between words, but not inside of words. If a weakly correlated grammar allows , it must allow for with the same probability. We now wish to relax this property to allow for the strongly-correlated case where variables may not be conditionally independent given the parents. This allows us to take a big step towards modeling realistic languages: in English, god significantly differs in meaning and usage from dog.
In the previous computation, the crucial ingredient was the joint probability
. Let us start with a seemingly trivial remark. This joint probability can be re-interpreted as a conditional joint probability. Instead of
X and
Y being random variables at specified sites
and
, we can view them as random variables at randomly chosen locations, conditioned on their locations being
and
. Somewhat pedantically, we write
. This clarifies the important fact that the only way that
depends on
and
is via a dependence on
. Hence,
This equation is specific to weakly-correlated models and does not hold for generic strongly-correlated models.
In computing the mutual information as a function of separation, the relevant quantity is the right-hand side of Equation (
7). The reason is that in practical scenarios, we estimate probabilities by sampling a sequence at fixed separation
, corresponding to
, but varying
and
(the
term is discussed in Appendix C).
Now, whereas
will change when strong correlations are introduced,
will retain a very similar form. This can be seen as follows: knowledge of the geodesic distance corresponds to knowledge of how high up the closest parent node is in the hierarchy (see
Figure 2). Imagine flowing down from the parent node to the leaves. We start with the stationary distribution
at the parent node. At the first layer below the parent node (corresponding to a causal distance
), we get
, where the symmetrized probability
comes into play because knowledge of the fact that
are separated by
gives no information about their order. To continue this process to the second stage and beyond, we only need the matrix
The reason is that since we only wish to compute the two-point function at the bottom of the tree, the only place where a three-point function is ever needed is at the very top of the tree, where we need to take a single parent into two children nodes. After that, the computation only involves evolving a child node into a grand-child node, and so forth. Hence, the overall two-point probability matrix
is given by the simple equation:
As we can see from the above formula, changing to the strongly-correlated case essentially reduces to the weakly correlated case where:
except for a perturbation near the top of the tree. We can think of the generalization as equivalent to the old model except for a different initial condition. We thus expect on intuitive grounds that the model will still exhibit power law decay. This intuition is correct, as we will prove in
Appendix C. Our result can be summarized by the following theorem:
Theorem 3. There exist probabilistic context-free grammars (PCFGs) such that the mutual information between two symbols A and B in the terminal strings of the language decay like , where d is the number of symbols in between A and B.
In
Appendix C, we give an explicit formula for
k, as well as the normalization of the power law for a particular class of grammars.
3.3. Further Generalization: Bayesian Networks and Context-Free Grammars
Just how generic is the scaling behavior of our model? What if the length of the words is not constant? What about more complex dependencies between layers? If we retrace the derivation in the above arguments, it becomes clear that the only key feature of all of our models considered so far is that the rational mutual information decays exponentially with the causal distance
:
This is true for (hidden) Markov processes and the hierarchical grammar models that we have considered above. So far, we have defined in terms of quantities specific to these models; for a Markov process, is simply the time separation. Can we define more generically? In order to do so, let us make a brief aside about Bayesian networks. Formally, a Bayesian net is a directed acyclic graph (DAG), where the vertices are random variables and conditional dependencies are represented by the arrows. Now, instead of thinking of X and Y as living at certain times , we can think of them as living at vertices of the graph.
We define
as follows. Since the Bayesian net is a DAG, it is equipped with a partial order ≤ on vertices. We write
iff there is a path from
k to
l, in which case, we say that
k is an ancestor of
l. We define the
to be the number of edges on the shortest directed path from
k to
l. Finally, we define the causal distance
to be:
It is easy to see that this reduces to our previous definition of
for Markov processes and recursive generative trees (see
Figure 2).
Is it true that our exponential decay result from Equation (
14) holds even for a generic Bayesian net? The answer is yes, under a suitable approximation. The approximation is to ignore long paths in the network when computing the mutual information. In other words, the mutual information tends to be dominated by the shortest paths via a common ancestor, whose length is
. This is generally a reasonable approximation, because these longer paths will give exponentially weaker correlations, so unless the number of paths increases exponentially (or faster) with length, the overall scaling will not change.
With this approximation, we can state a key finding of our theoretical work. Deep models are important because without the extra “dimension” of depth/abstraction, there is no way to construct “shortcuts” between random variables that are separated by large amounts of time with short-range interactions; 1D models will be doomed to exponential decay. Hence, the ubiquity of power laws may partially explain the success of applications of deep learning to natural language processing. In fact, this can be seen as the Bayesian net version of the important result in statistical physics that there are no phase transitions in 1D [
48,
49].
One might object that while the requirement of short-ranged interactions is highly motivated in physical systems, it is unclear why this restriction is necessary in the context of natural languages. Our response is that allowing for a generic interaction between say k-nearest neighbors will increase the number of parameters in the model exponentially with k.
There are close analogies between our deep recursive grammar and more conventional physical systems. For example, according to the emerging standard model of cosmology, there was an early period of cosmological inflation when density fluctuations were getting added on a fixed scale as space itself underwent repeated doublings, combining to produce an excellent approximation to a power law correlation function. This inflationary process is simply a special case of our deep recursive model (generalized from 1–3 dimensions). In this case, the hidden “depth” dimension in our model corresponds to cosmic time, and the time parameter that labels the place in the sequence of interest corresponds to space. A similar physical analogy is turbulence in a fluid, where energy in the form of vortices cascades from large scales to ever smaller scales through a recursive process where larger vortices create smaller ones, leading to a scale-invariant power spectrum. There is also a close analogy to quantum mechanics: Equation (
13) expresses the exponential decay of the mutual information with geodesic distance through the Bayesian network; in quantum mechanics, the correlation function of a many body system decays exponentially with the geodesic distance defined by the tensor network, which represents the wavefunction [
50].
It is also worth examining our model using techniques from linguistics. A generic PCFG consists of three ingredients:
An alphabet , which consists of non-terminal symbols A and terminal symbols T.
A set of production rules of the form , where the left-hand side is always a single non-terminal character and B is a string consisting of symbols in .
Probabilities associated with each production rule , such that for each , .
It is a remarkable fact that any stochastic-context free grammars can be put in Chomsky normal form [
27,
45]. This means that given
, there exists some other grammar
, such that all of the production rules are either of the form
or
, where
and
and the corresponding languages
. In other words, given some complicated grammar
, we can always find a grammar
such that the corresponding statistics of the languages are identical and all of the production rules replace a symbol by at most two symbols (at the cost of increasing the number of production rules in
).
This formalism allows us to strengthen our claims. Our model with a branching factor is precisely the class of all context-free grammars that are generated by the production rules of the form . While this might naively seem like a very small subset of all possible context-free grammars, the fact that any context-free grammar can be converted into Chomsky normal form shows that our theory deals with a generic context-free grammar, except for the additional step of producing terminal symbols from non-terminal symbols. Starting from a single symbol, the deep dynamics of the PCFG in normal form are given by a strongly-correlated branching process with , which proceeds for a characteristic number of productions before terminal symbols are produced. Before most symbols have been converted to terminal symbols, our theory applies, and power law correlations will exist amongst the non-terminal symbols. To the extent that the terminal symbols that are then produced from non-terminal symbols reflect the correlations of the non-terminal symbols, we expect context-free grammars to be able to produce power law correlations.
From our corollary to Theorem 2, we know that regular grammars cannot exhibit power law decays in mutual information. Hence, context-free grammars are the simplest grammars that support criticality, e.g., they are the lowest in the Chomsky hierarchy that support criticality. Note that our corollary to Theorem 2 also implies that not all context-free grammars exhibit criticality since regular grammars are a strict subset of context-free grammars. Whether one can formulate an even sharper criterion should be the subject of future work.