1. Introduction
Random fluctuation (also called noise) is inevitable in dynamical systems. Due to the interactions between nonlinearity and stochasticity, in nonlinear dynamical systems many phenomena with new regimes can be induced by even weak fluctuations. For the systems far from equilibrium, fluctuation plays an important role in self-organization induced order phenomena [
1]. The various fluctuation-induced behaviors, like stochastic resonance [
2,
3], noise-induced synchronization [
4], coherence resonance [
5], noise-induced chaos [
6], fluctuation-induced escape [
7], and noise-induce bifurcation [
8] have attracted the attention of a large number of researchers from various fields as central problems in modern nonlinear dynamics theories.
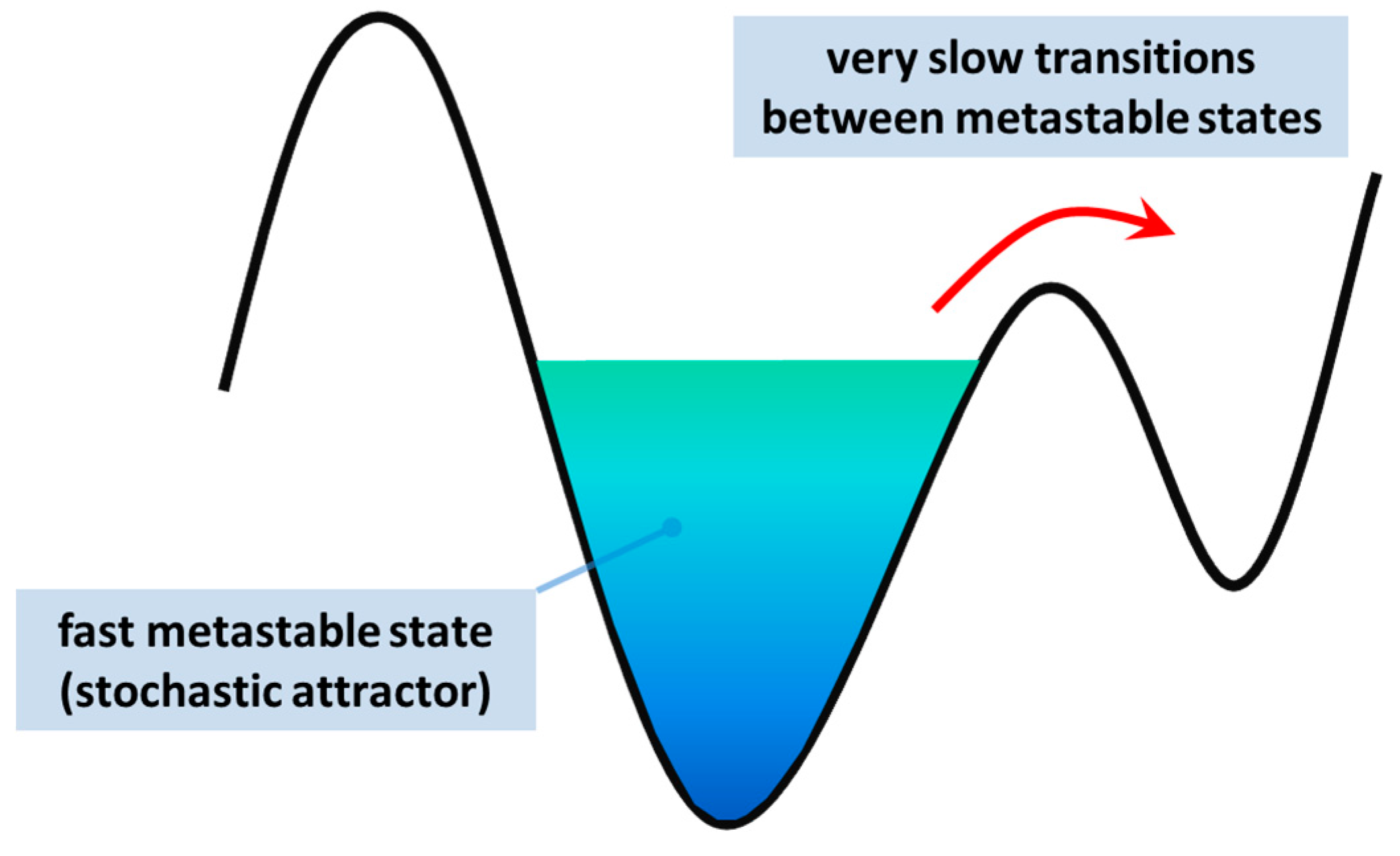
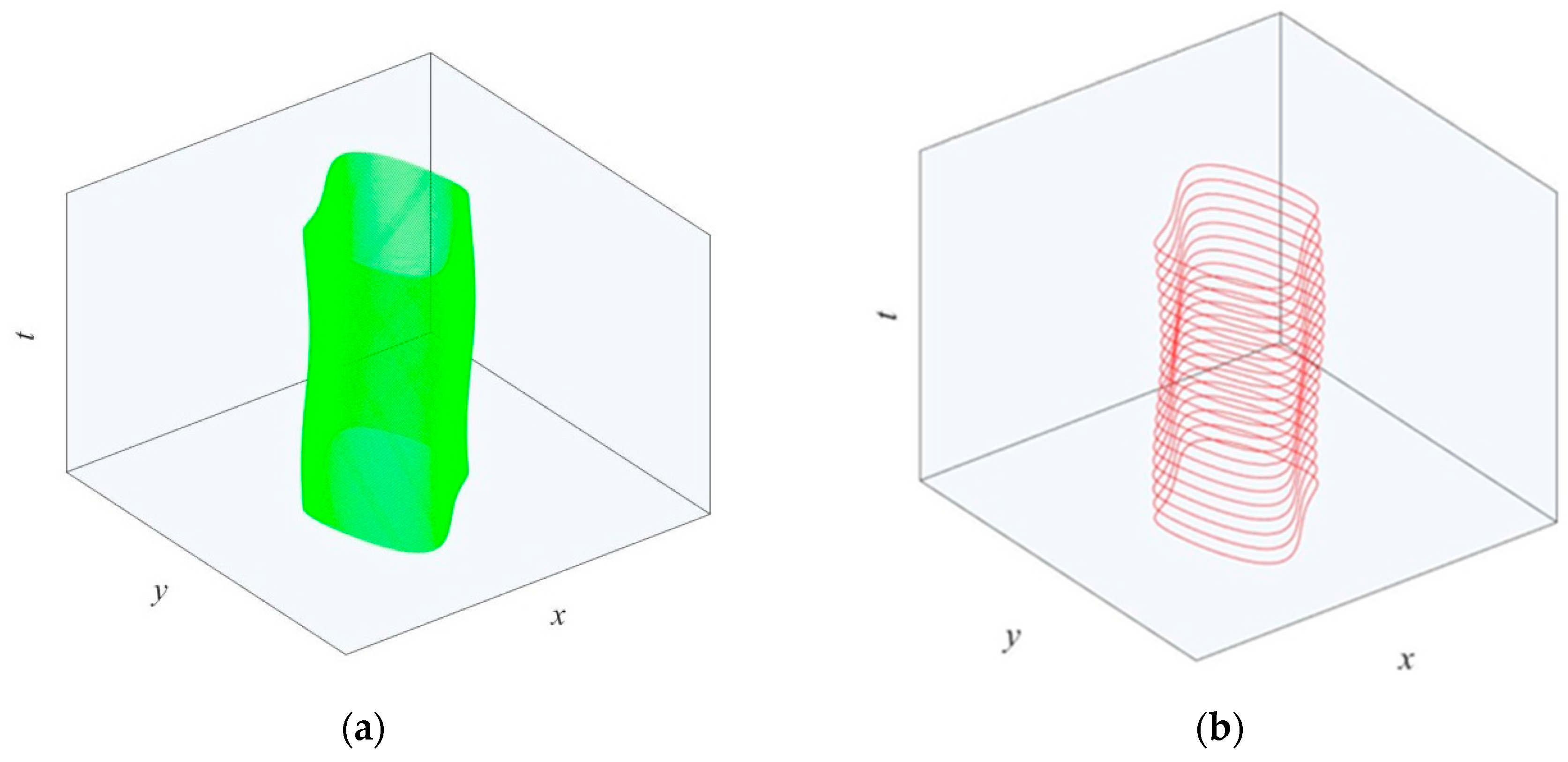
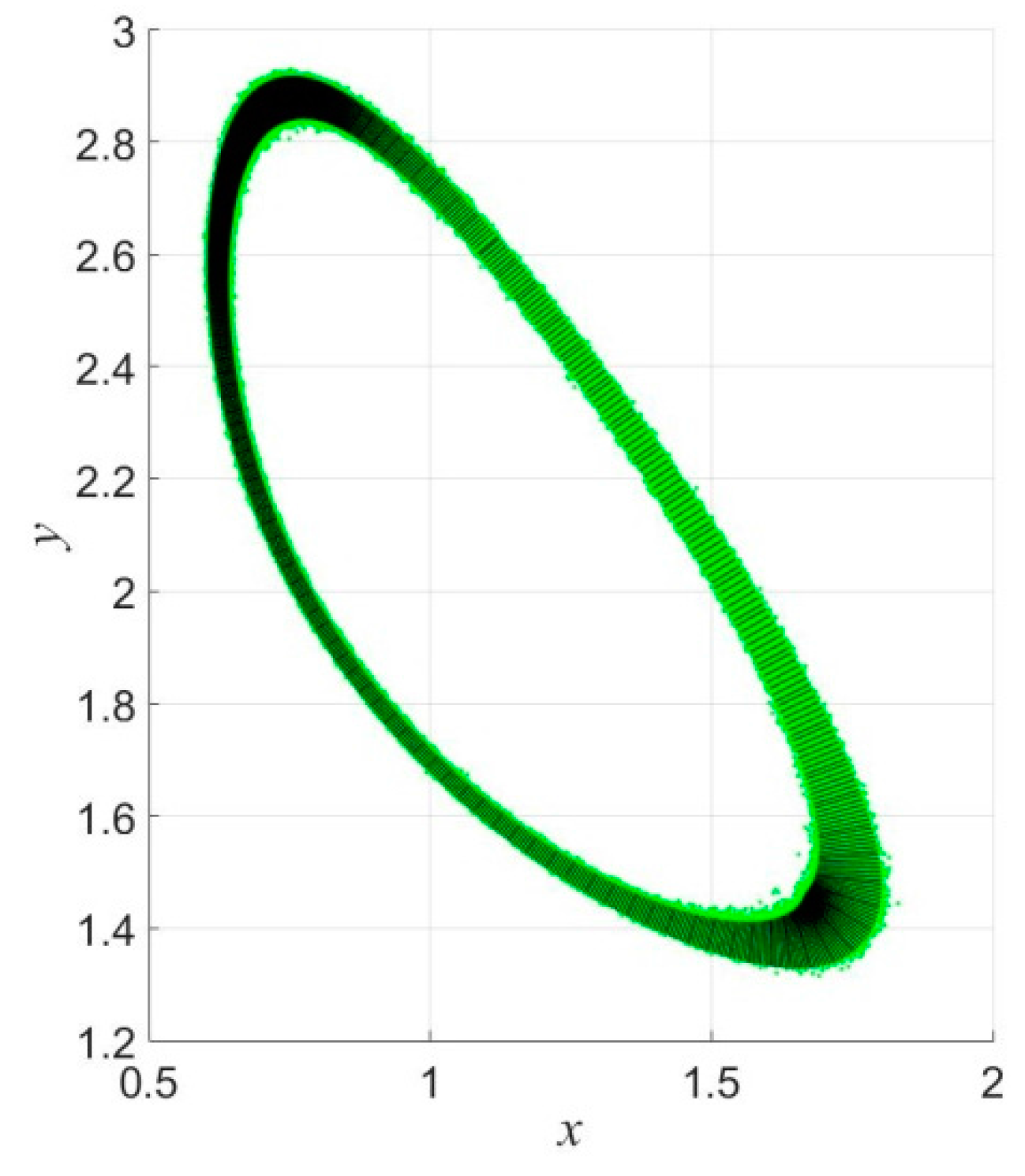
The stationary state, which is called an attractor in nonlinear dynamical system theory, plays the central role in the analysis of the nonlinear systems. Fluctuation can drive the trajectory of the attractor, leave it, and form a "blurred" state around it (
Figure 1). This state is named a stochastic attractor [
9], which is one kind of almost invariant sets in mathematical language [
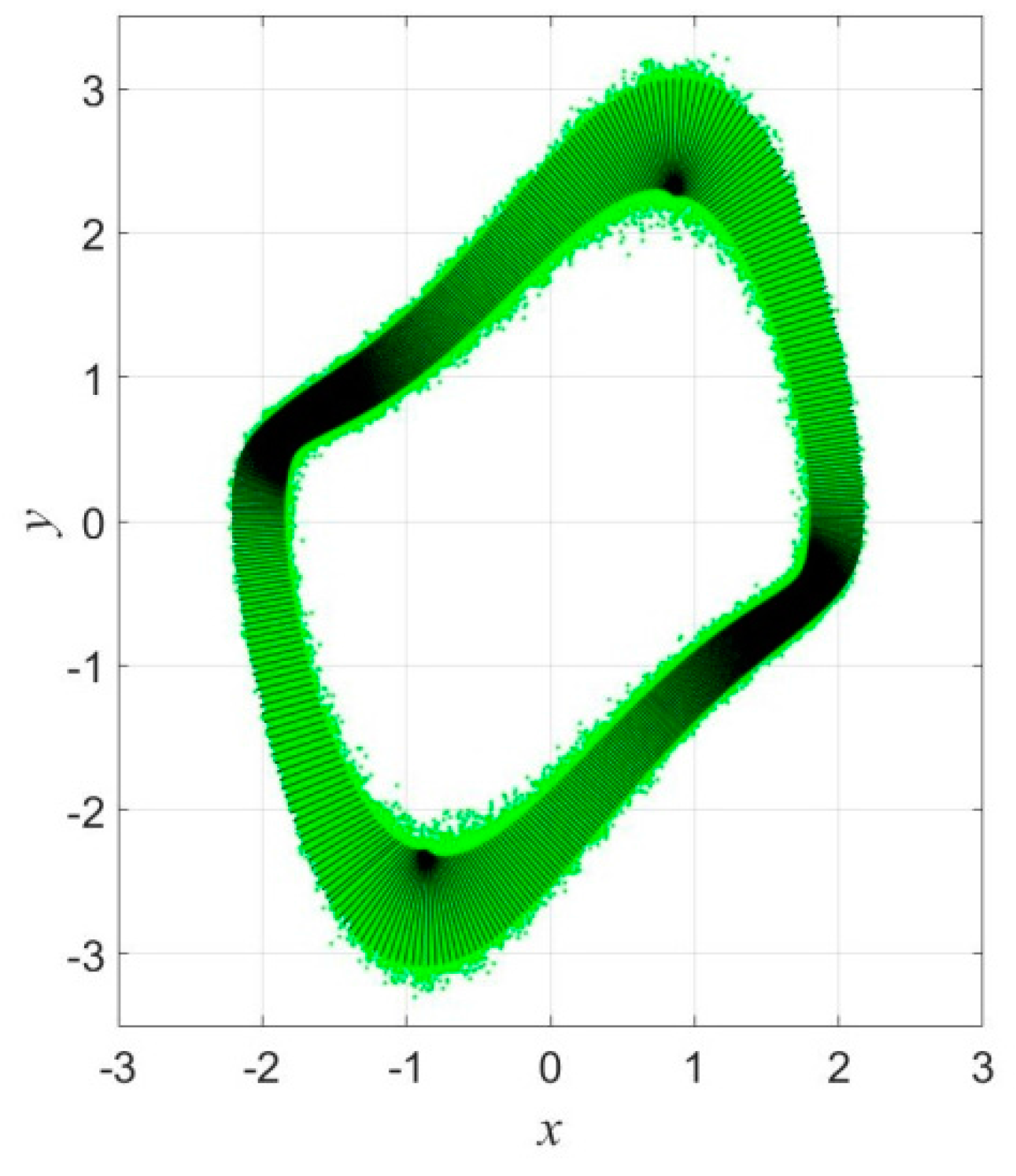
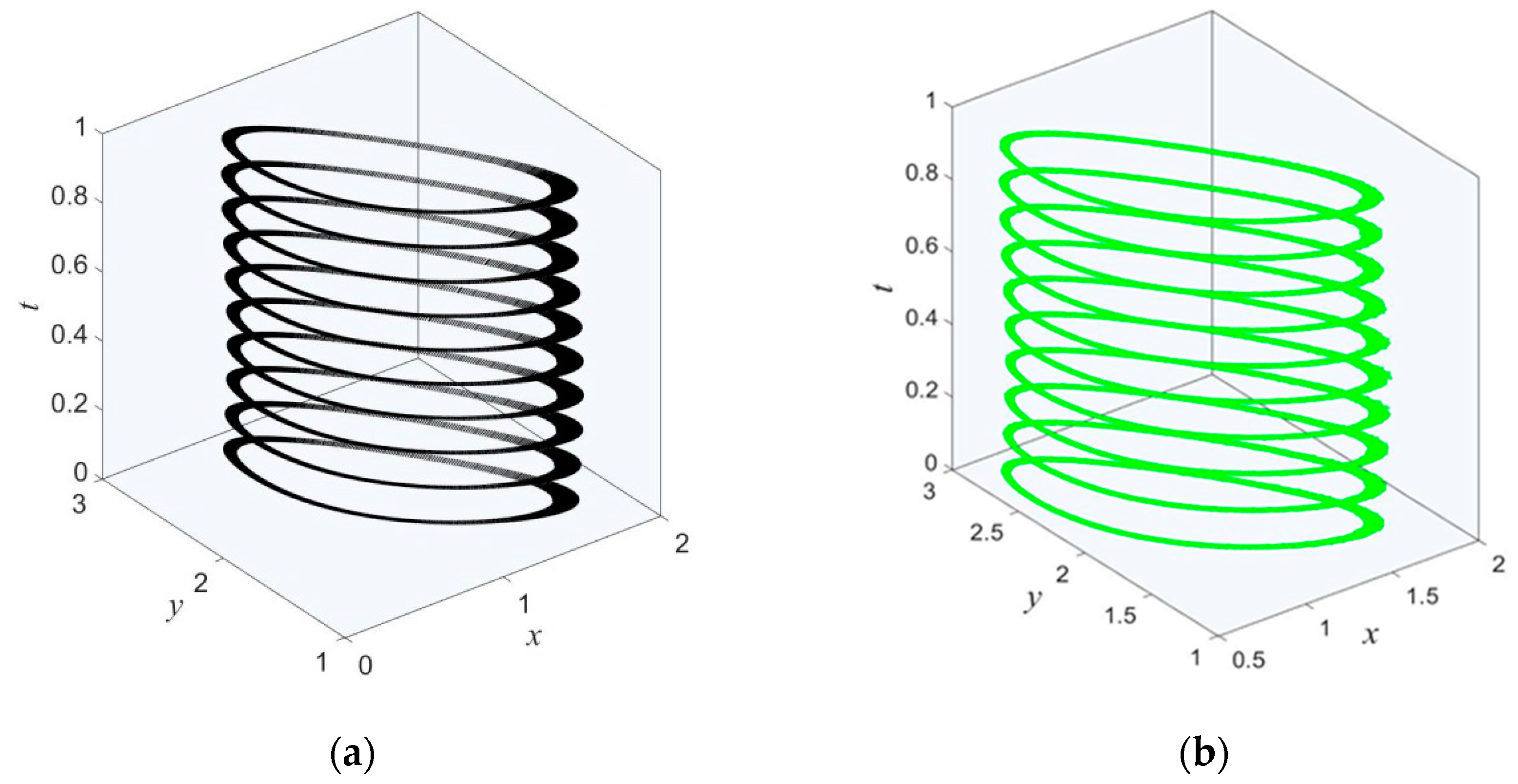
10]. When multi-stable systems are disturbed by additive Gaussian white noise, all deterministic attractors become metastable stochastic attractors. Thereby, the responses of the disturbed systems can be seen as combinations of stochastic attractors and hopping between them. When noise is weak, the lifetime of metastable states is very long, although this metastable state will finally escape to other metastable states. Thus, if we choose initial conditions in the vicinity of the deterministic attractor, a very long transient probability density distribution will form that can be considered as a steady state probability density distribution for a finite observation time (
Figure 2). Thus, picking initial conditions in the vicinity of the underlying deterministic attractor, the probability density function (PDF) of stochastic attractor can be computed by a Monte Carlo simulation. Monte Carlo simulations are very time consuming, analytical methods that are still indispensable. For differential dynamical systems, the Fokker-Planck equation (FPE) [
11] gives the most detailed description of PDF evolution, but it is difficult to get close-form solutions of FPE for systems without detailed balance except for some special systems [
12]. Thus, until now, many approximate methods have been raised to solve FPE under various specific circumstances, such as the stochastic average method [
13], path-integral method [
14], finite element method [
15], Galerkin-Ulam-like method [
16], cell-mapping method [
8], etc. Most of these methods are proposed to solve the response of systems with weak nonlinearities. For stronger nonlinear systems, they cannot work well.
Based on quasi-potential (also called pseudo-potential) theory [
17,
18,
19], Bashkirtseva [
20] proposed the stochastic sensitivity function (SSF) method to describe the transverse dispersion of stochastic attractors. In this method, distribution of stochastic attractor is expressed by confidence ellipse or confidence band around the deterministic attractor. The original deterministic attractor is calculated numerically so the problem of nonlinearity is evaded. The SSF method provides an idea for the construction of a PDF of weak fluctuation generated stochastic attractors, especially a stochastic periodic attractor [
21].
The simplest kind of non-equilibrium stationary state is the limit cycle attractor (see
Figure 3). Based on the understanding that weak additive noise cannot change the probability distribution along the closed curve type attractors, a PDF decomposition method [
22] is proposed by the authors to construct an
n-dimensional PDF of the stochastic closed-curve attractor using a one-dimensional in-attractor PDF and an (
n − 1)-dimensional out-of-attractor PDF. The former is calculated in the deterministic system numerically and the latter can be quantified by the SSF method. Consequently, the
n-dimensional PDF of the stochastic closed-curve attractor can be expressed by production of a one-dimensional in-attractor PDF and an (
n − 1)-dimensional out-of-attractor PDF. In the SSF method, only a weak noise condition is required, so it can be used in strongly nonlinear systems.
Periodic force is a common kind of excitation which widely exists in various systems. When a limit cycle attractor suffers periodic excitation, the system becomes non-autonomous and the response is quasi-periodic for non-degenerate conditions. In the augmented phase space the quasi-periodic attractor takes the form of an invariant torus. The quasi-periodic attractor is of great significance in many fields, like celestial mechanics, mechanical vibrations, and lasers, etc. While the excitation contains both periodic component and random fluctuation, the quasi-periodic attractor diffuses to a stochastic attractor. Thus, it is of great significance to obtain a PDF of the stochastic quasi-periodic attractor in periodic and random excited non-equilibrium systems. A theoretical investigation of the SSF of the quasi-periodic attractor in autonomous systems is given in [
23]. In this paper, for quasi-periodic attractors in non-autonomous systems, a simpler method is used to obtain the SSF based on the SSF of discrete-time systems proposed in [
24]. Compared with the works in [
24], a kind of 1/
N-stroboscopic map is used in this paper to discretize the torus of the non-autonomous system into quasi-periodic circles in stroboscopic sections, so that the SSF method for circles in discrete-time systems is extended to tori in non-autonomous systems. Furthermore, not only confidence intervals, but also PDF of the circles in observed stroboscopic sections, can be approximately obtained in this paper using a kind of PDF decomposition method for weak additive noise-disturbed systems.
If the rotation number of the response is rational, the attractor degenerates, becoming periodic. Note that in this situation the method proposed in this paper can also be used. In fact, in order to obtain the SSF of the quasi-periodic circle with an irrational rotation number, the circle is just an approximate with a periodic one with a rational rotation number. Since periodicity can be considered as a special case of quasi-periodicity, the term “quasi-periodic” is used in the title of the paper.
This paper is structured as follows: In
Section 2 the PDF decomposition method of closed curve attractors is introduced.
Section 3 covers the method to get SSF of stochastic quasi-periodic attractor in non-autonomous systems by the periodic approximation method and 1/
N-stroboscopic map. In
Section 4 the procedure to construct a PDF of a stochastic quasi-periodic attractor in stroboscopic Sections is listed. The validity of the proposed method is verified by van der Pol oscillator and Brusselator in
Section 5. Conclusions are drawn in the final section.
2. Density Distribution of the Stochastic Attractor
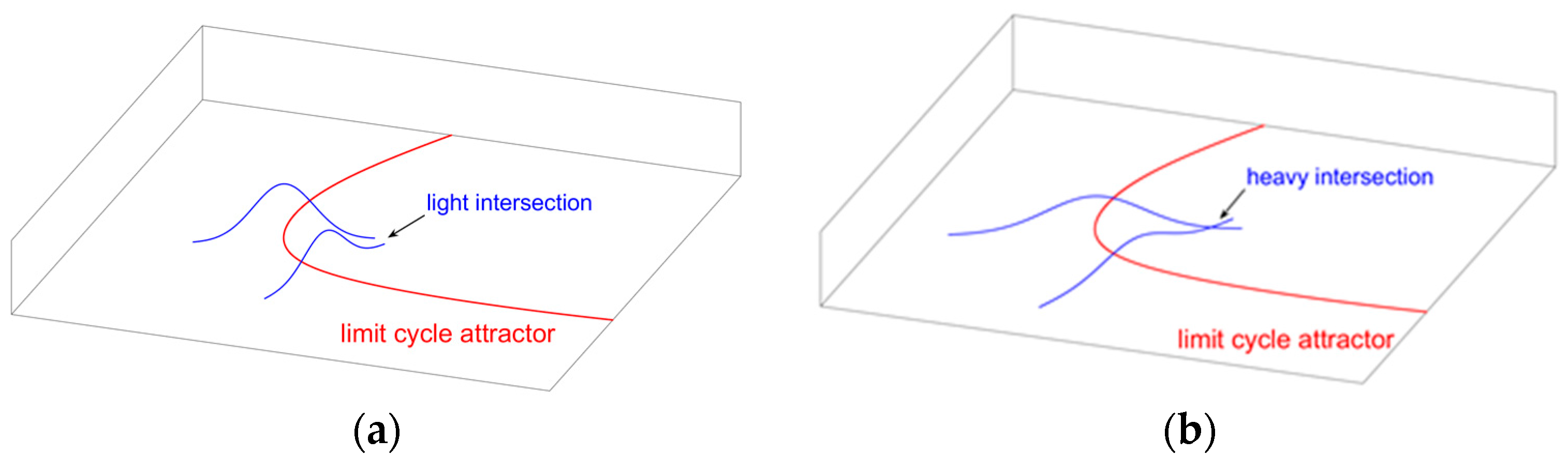
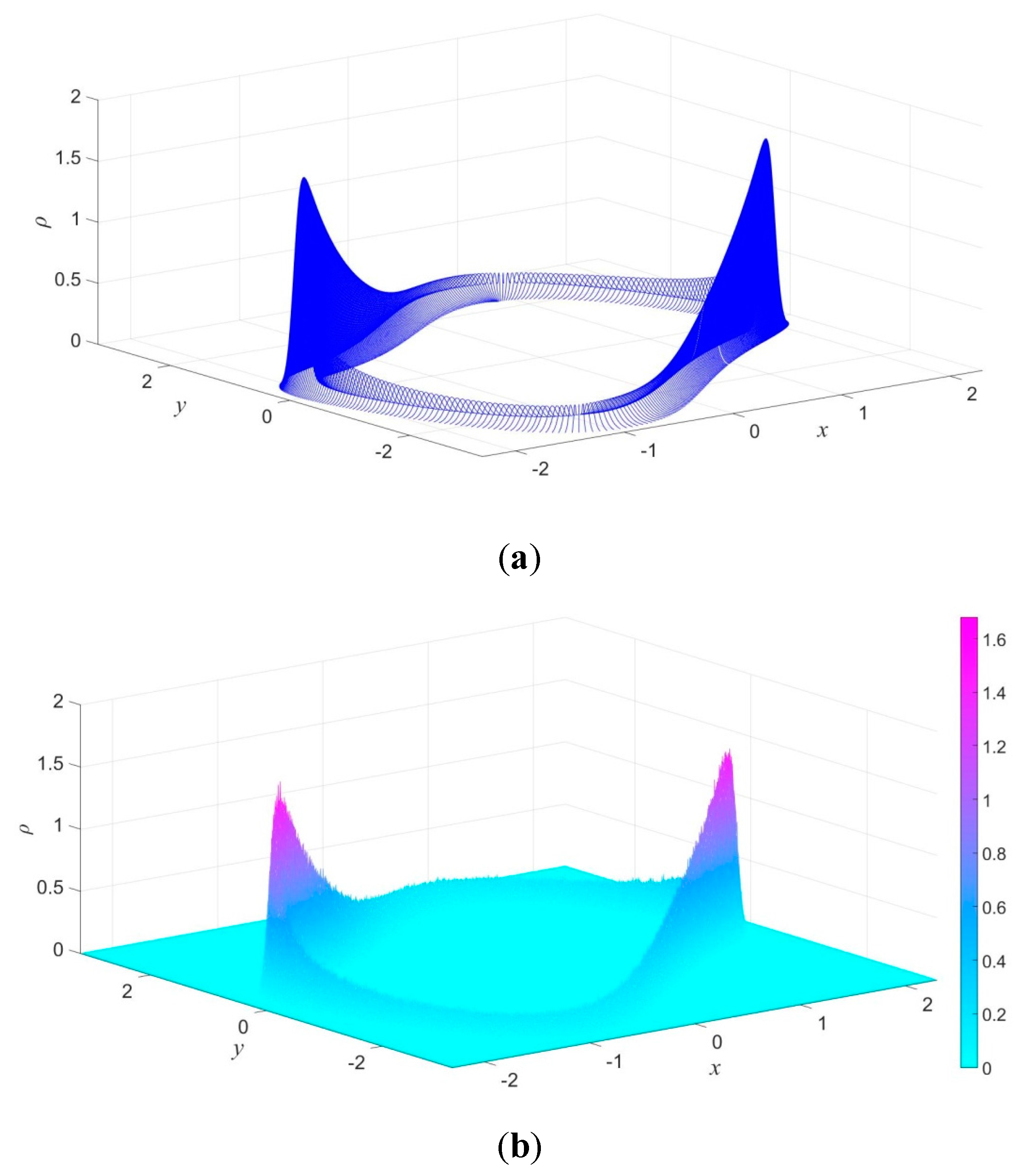
When noise is vanishingly small, the probability of finding the state in the direction "along" an attractor (called in-attractor PDF) is independent of the intensity of the noise and coincides with the deterministic invariant measure. When an attractor suffers additive Gaussian noise, points deviate from it and form a Gaussian distribution in the orthogonal hyperplane. It was found in [
22] that, although the Gaussian distributions in different parts of the attractor can intersect each other (
Figure 4b), which means hopping between different parts of the attractor and, thus, changing the invariant measure along this attractor, when the noise is weak, due to the Gaussian shape of orthogonal distribution, the intersection only happens in the tails of the Gaussian distributions (
Figure 4a) and the hopping between different parts can be considered as a rare event. Thus, it can be considered that weak additive Gaussian noise just drives points away from the deterministic attractor in the transverse direction [
17] because the in-attractor probability flux reaches a dynamical balance, and the points of stochastic attractor form a Gaussian distribution around the deterministic attractor in the transverse direction (called out-of-attractor PDF). Note that whether the noise is weak or not depends on the attractors. If the attractor is not sensitive to noise, the “weak” noise can have a relatively larger intensity.
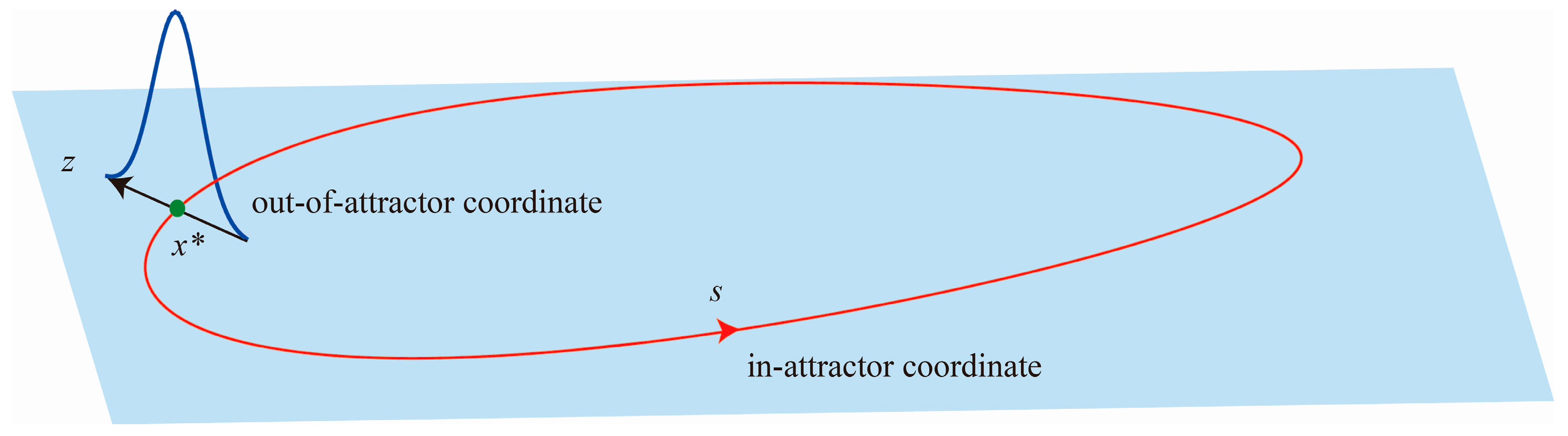
Therefore, for the stochastic attractor generated by weak additive Gaussian noise: (1) the in-attractor PDF equals the distribution of the original deterministic attractor; and (2) the out-of-attractor PDF is Gaussian. Based on these understanding, a PDF decomposition method can be used to construct PDF of stochastic attractors. Suppose the dimension of the system and deterministic attractor is
n and
na, respectively. Two kinds of coordinates are needed in this method. One is the global in-attractor
na-dimensional coordinate presenting the location of point
x* in the deterministic attractor which is nearest to the studied point
x, the other is the local (
n −
na)-dimensional out-of-attractor coordinate which is defined in the transverse direction at point
x* (see
Figure 5 for planar limit cycle attractors). Thus, the
n-dimensional PDF of stochastic attractor can now be decomposed into two independent low-dimensional PDF approximately. One is the
na-dimensional PDF,
ρτ, which describes the in-attractor PDF, and the other is the (
n −
na)-dimensional Gaussian form PDF,
ρn, that represents the out-of-attractor PDF, namely:
From above discussion, the in-attractor PDF of stochastic attractor can be determined from the deterministic systems, while the out-of-attractor PDF takes the Gaussian form:
where
M is (
n −
na) × (
n −
na) covariance matrix of this Gaussian distribution. In the following section, approaches to obtain matrix
M based on the SSF will be detailed.
3. The SSF of Stochastic Quasi-Periodic Attractor in Non-Autonomous Systems
3.1. 1/N-Period Stroboscopic Map
Consider a continuous-time non-autonomous dynamical system:
where
f(
x,t) is n-dimensional non-autonomous vector field depending on both state vector
x and time t.
For periodic-driven non-autonomous systems (Equation (3)) with period T, the phase of the driving force is introduced as:
Considering θ as a new variable, the non-autonomous systems (Equation (3)) can be rewritten as an (n + 1)-dimensional augmented autonomous system:
Thus, the state of this extended system is determined by x and θ.
Stroboscopic map is often used to observe the response of system (Equation (5)). Taking snapshots of the trajectory of Equation (5) at discrete phases θ
i = i△θ (i is a natural number and △θ is the sampling phase interval) and registering the state
x at each instant, a series of points {
xi} is generated. Point
xi+1 is determined only by the previous point
xi, thus a discrete map can be defined as:
which M
si is the so-called stroboscopic map. In fact, the points {
xi} are the intersections between the trajectory and the stroboscopic sections, which are defined as:
where S
1 means a one-dimensional circle space.
Often the sampling phase interval △θ is chosen to be 2π, and this kind of stroboscopic map will be called a one-period stroboscopic map in this article. There is only one stroboscopic section in a one-period stroboscopic map. In this case, M
si is identical in every iteration step i and often lacks an analytical formula. Further, the information of the system in the phase interval [0, 2π] is lost. Thus, in order to solve these problems and consider persistent fluctuation along the trajectory, a kind of 1/N-period stroboscopic map is introduced [
25].
Note from Equation (4) that if △θ→0, the time interval △t also tends to zero, the linear approximation of the map (Equation (6)) can be used to estimate the one-step map of Equation (6) from (θ
0 + i△θ) to (θ
0 + (i + 1)△θ); that is:
where:
is the Jacobian matrix of Equation (3) at point
xi and time t
0 + i△t. t
0 is the initial time.
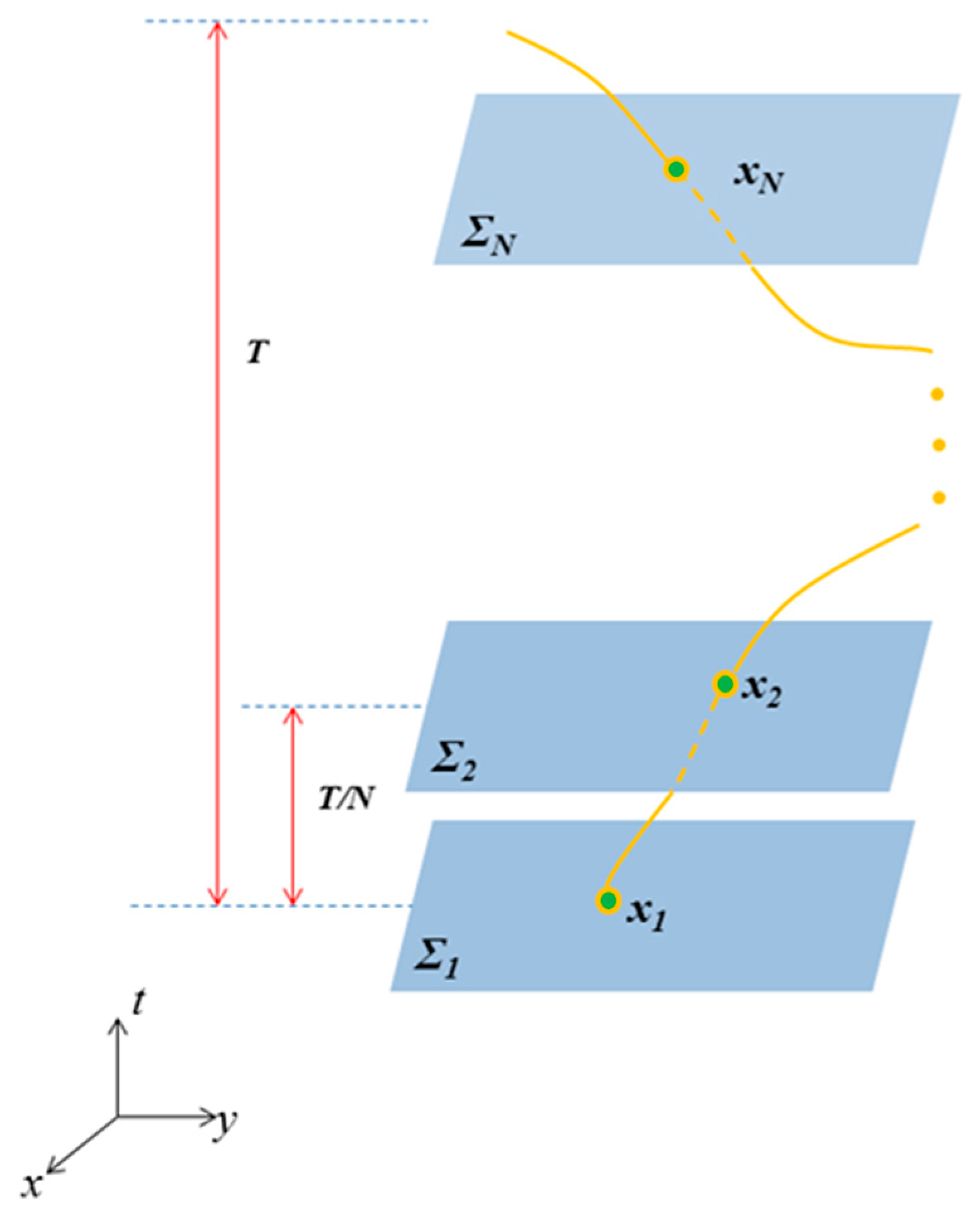
Thus, suppose N is a large positive integer, the sampling phase interval of the stroboscopic map can be set to:
Consequently, the sampling time interval is:
Thus, a new stroboscopic map can be written in the form of Equation (8), approximately. This new map is named the 1/N-period stroboscopic map (see
Figure 6). Since the phase θ is in S
1 and Σ
i = Σ
i+N, there are totally N stroboscopic sections to be considered.
Through this new map, a torus attractor of Equation (3) is discretized into N closed curves {Г
1, …, Г
N} by N stroboscopic sections {Σ
1, …, Σ
N} (see
Figure 7).
Now consider the case that Equation (3) suffers additive Gaussian white noise disturbances:
where
ξ is n-dimensional Gaussian white noise,
σ is an n × n matrix which indicates the disturbed states, and ε is the noise intensity.
The 1/N-period stroboscopic map of Equation (12) can be approximately written as:
where:
is the increment of Wiener process within the time interval [t
0 + i△t, t
0 + (i + 1)△t].
3.2. Periodic Approximation of Quasi-Periodic Attractor
From
Section 3.1, the distribution of a stochastic torus can be expressed by distributions of stochastic circles in the stroboscopic sections. Usually the winding number of torus is irrational so the circle in any stroboscopic section is quasi-periodic. If the winding number of the torus is rational, the torus is in resonance and degenerate to periodic solution. The circles in stroboscopic sections also degenerate to periodic points, in which case the circles {
Г1, … ,
ГN} are often called invisible attractors [
26]. This kind of degeneration is called resonance or synchronization. In this situation the SSF method in [
24] can be used directly and will not be discussed in this section.
The SSF method can be used to obtain the transverse density distribution of circles {Гi} in stroboscopic sections. In order to adapt the SSF method to quasi-periodic circles, periodic approximation is used to approximate the quasi-periodic circle into a periodic one.
A simple method in [
9] is utilized to implement this approximation. First, we generate a long series of points {
xГi} along the circle, then find the point
xГk which has the minimal distance from the first point
xГ1. Finally, the quasi-periodic circle is approximated by a resonant one containing periodic-
k points on it. Note that the points are periodic-
k in a one-period stroboscopic map and, thus, period-
kN in a 1/
N-period stroboscopic map.
If one circle Гi in {Г1, …, ГN} has been approximated by a periodic one, this means that all of the closed curves {Гi} are in resonance and the quasi-periodic torus attractor degenerates to periodic.
3.3. Transverse Distribution of the Closed Curves in Stroboscopic Sections
In
Section 3.2 the method to approximate quasi-periodic circles by a resonant one is stated. For the quasi-periodic attractor, the torus is exponentially stable and so are all circles {
Гi} in stroboscopic sections. Thus, the SSF method can be used. In this section, SSF method of resonant circle in discrete maps [
24] is detailed. Rewriting the 1/
N-period stroboscopic map (13) as:
where:
while
σ has the same meaning as in Equation (15),
ξk is
n-dimensional Gaussian white noise which satisfies:
where
E is expectation operation, and
I is the unit matrix. Equation (13) is rewritten in a simpler form for convenience:
Suppose a quasi-periodic closed curve has been approximated by a period-k one in a one-period stroboscopic map. Thus, in 1/N-period stroboscopic map (Equation (20)), all circles {Гi} are periodic-kN, and all points in them are considered to be periodic-kN. For convenience, the range of phase θ is extended from [θ0, θ0 + 2π] to [θ0, θ0 + 2kπ], therefore, the number of circles and stroboscopic sections are also extended to kN. However, note that circle {Гi} and {Гi + αN} are the same, as are {Σi} and {Σi + αN}, where α = 1, 2, ..., k.
Consider the periodic –
kN points are {
xГi} (
i =1, 2, …,
kN), each
xГi belongs to a circle
Гi in stroboscopic section Σ
i. If a point
xГi deviates as:
where
υi is a vector orthogonal to circle
Гi at point
xГi with random length. For small values of
η, the evolution of
υi satisfies the linear iterative relation:
where:
is the Jacobian matrix at
xГi.
Pi+1 is the projection matrix onto the hyperplane which is orthogonal to circle
Гi+1 at
xГ(i + 1). Since
ξi is weak and Gaussian, the distribution of
υi is considered to be Gaussian, approximately, and its first two order moments follow the iterative relations:
Combining Equation (24) with the periodic condition, the SSF of any periodic point on any circle can be calculated. Pick a point arbitrarily in the circle
Г1 as
xГ1, it can be proved that the mean of
υ1 is zero. Applying the second formula of Equation (24)
kN times, and using the periodic condition
MkN+1 =
M1, it can be deduced that the covariance matrix
M1 follows the algebraic equation:
where:
Matrix
Q1 can be obtained recurrently:
Through the matrix algebraic equation (Equation (25)), M1 can be calculated directly. Matrix M1 is named the stochastic sensitivity function (SSF) of xГ1 because it represents the covariance of out-of-attractor distribution of stochastic attractor at xГ1 with unity noise intensity.
Based on the recurrence relation (25), Mi (i = 2, ..., kN) can be calculated and the dispersion character of any circle can be quantified. If the circle under analysis is Гm, the periodic points on it are xГm, xГ(m + N), xГ(m + 2N), ...,xГ(m + (k − 1)N). Through calculating SSF of these points, the sensitivity of the circle can be approximately depicted.
When the stroboscopic map is planar, every circle is 2D and the SSF can be decomposed as:
where
pi is normalized vector of
υi. Scalar
μi quantifies the out-of-circle variance at point
xГi with unity noise intensity, which has an explicit form [
24]:
Therefore, SSF of 2D circles degenerates into a scalar
μi, which is the function of point
xГi, and the out-of-circle variance of the distribution at point
xГi is
η2μi. The out-of-circle 1D distribution in a point
x is thus given by:
4. Procedure of Construct PDF of Stochastic Quasi-Periodic Attractors
From above sections, the procedure to construct approximate expression of the PDF of quasi-periodic torus in a given stroboscopic section is summarized as:
(1) Determine the number N of 1/N stroboscopic map and the closed curve to be studied (i of Гi, i=1, 2, ..., N). Without loss of generality, suppose the studied circle is Гm.
(2) Replace the quasi-periodic circle by an approximate periodic-k one using periodic approximation method. Extend the number of stroboscopic section from N to kN and the scope of indice i is also extended to [1, kN]. Thus, the circle is discretized into k points {xГi}, i = m, m + N, ..., m + kN.
(3) Calculate the in-attractor PDF of discretized
Гm numerically, say, PDF at points {
xГi},
i =
m,
m +
N, ...,
m +
kN. To do this, divide
Гm into
k tiny sections each contains only one point
xГi,
i =
m,
m +
N, ...,
m+
kN. Generate a large number of points in this circle to compute the probability to visit every section, and the in-attractor PDF at point
xГi is approximated as:
where
P[
△s(
xГi)] is the probability of the section which contains
xГi and
△s(
xГi) is the length of it.
(4) Calculate SSF at points {xГi} using Formula (24)–(27), i=m, m + N, ..., m + kN. Using SSF, confidence intervals (n = 2) or confidence ellipses (for n > 2) at points {xГi} can be drawn. Increase N and repeat (1)–(4) until the result converges.
(5) PDF of the studied circle
Гm can be expressed utilizing formula:
or
for planar circles.
In order to visualize the PDF of the studied circle, the out-of-circle distributions at chosen points on the circle can be plotted within confidence intervals (n = 2) or confidence ellipses (for n > 2) at given confidence probability. Because the PDF is difficult to visualize when n>2, only n=2 cases are taken as examples in this article. PDF or confidence intervals of all the circles {Гi} (i = 1, 2, .., N) in stroboscopic sections can be drawn to get a global view of the stochastic torus attractor.
5. Examples
The first example is the forced van der Pol oscillator:
where
ξ is Gaussian white noise and
ε is its intensity. The values of parameters are:
δ = 1,
F = 1,
ω = 2, and
ε = 0.15. The response of this system is quasi-periodic.
This quasi-periodic attractor is approximated by a periodic-593 attractor (attractor with the period which is 593 times that of the forcing period). The time step of integration is finally determined as 1/500, so
N = 500. In
Figure 8 three-sigma confidence intervals and the stochastic attractor obtained by the Monte Carlo method in stroboscopic section
Σ1 (θ = 2
kπ,
k = 0, 1, ...) is shown. It is calculated that 98.6% of the points are in these intervals, which is very close to 99.73% (three-sigma). To obtain a global and clear view, three-sigma confidence intervals and stochastic attractors in 10 different stroboscopic sections are depicted in
Figure 9. It is shown that there is no severe variance of the dispersion of the stochastic closed curves in different stroboscopic sections.
Combining with the in-attractor density, the 2D PDF of stochastic attractors in stroboscopic sections can be obtained.
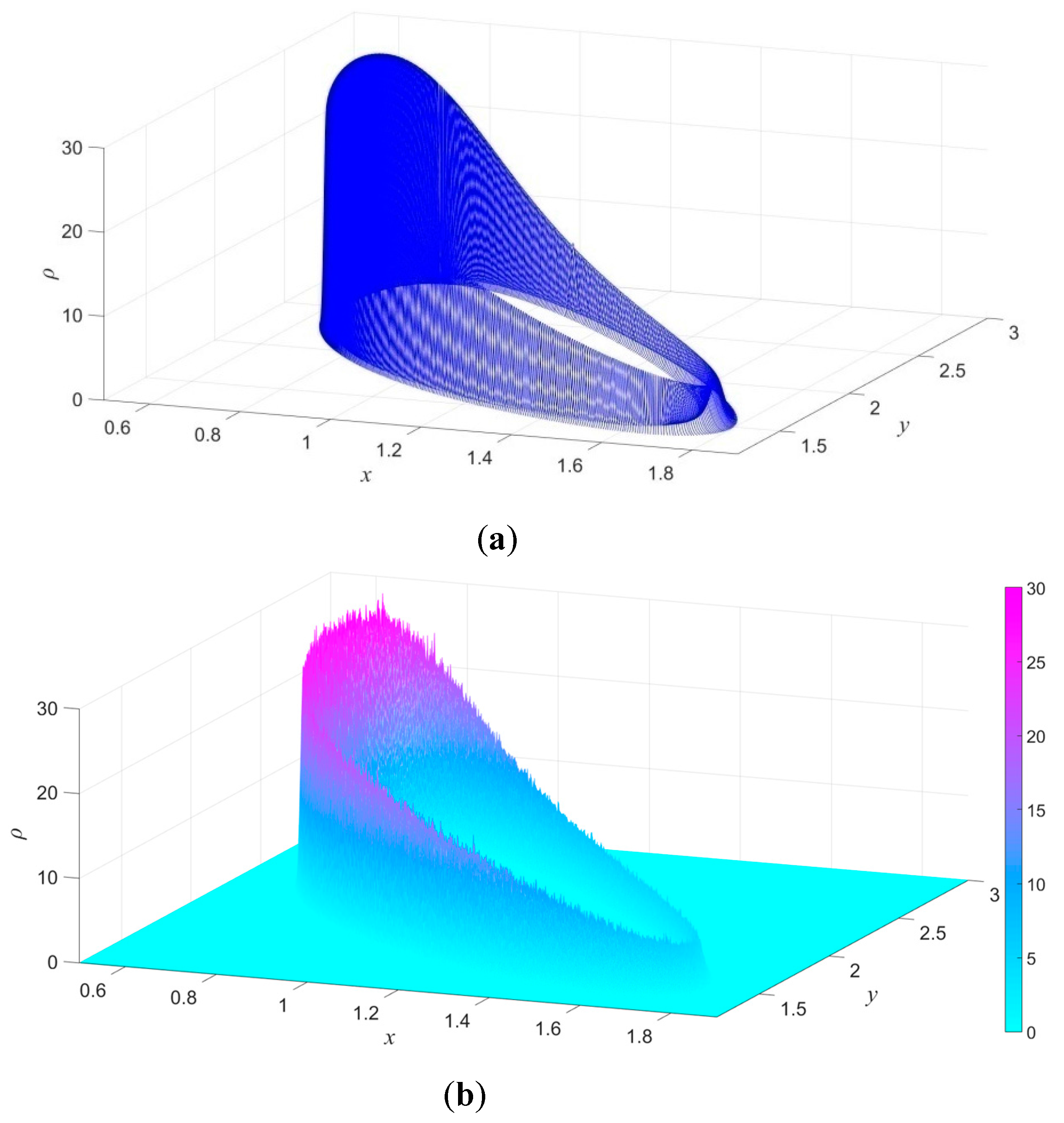
Figure 10a illustrates the 2D PDF of stochastic attractor in stroboscopic section
Σ1 which is drawn within the three-sigma intervals of out-of-attractor Gaussian distributions. The Monte Carlo method is also used to get this PDF (1000 × 1000 grids and 10
7 points), which is shown in
Figure 10b. We can see that the shapes of PDF in
Figure 10a,b are almost the same, but the computing time of the proposed method is only 95.78 s, while the Monte Carlo method is 150,732 s.
The second example is the forced Brusselator:
where
ξ is Gaussian white noise and
ε is its intensity. In [
20] the disturbed Brusselator was also studied, but the periodic force is tackled as a weak disturbance; thus, the combined action of periodic and random excitation were not studied. In this paper, the parameters of Equation (35) are:
a = 1,
b = 2.2,
F = 0.1, and
ε = 0.005. The intensity of noise is chosen as 0.005 because when noise is larger, some out-of-attractor distributions will intersect each other obviously and this means the proposed method no longer works well.
When the forcing frequency
ω = 2, this system possesses a quasi-periodic torus attractor. This quasi-periodic attractor is approximated by a periodic-777 attractor. In order to build a 1/
N-periodic stroboscopic map, set
N = 500. Three-sigma confidence intervals and the stochastic attractor obtained by the Monte Carlo simulation in stroboscopic section
Σ1 are depicted in
Figure 11, and 97.4% of the points are in the intervals. Three-sigma confidence intervals and stochastic attractors in 10 different stroboscopic sections are drawn in
Figure 12. It can be seen that there is also no obvious change of the dispersion character of the closed curves in different stroboscopic sections. The PDF of the stochastic attractor in stroboscopic section
Σ1 is drawn in
Figure 13a using the proposed method. Compared with the result obtained by the Monte Carlo method (1000 × 1000 grids and 10
7 points,
Figure 13b), it can be seen that the proposed method gives a simple and accurate illustration of the PDF in the forced Brusselator. In this example, the computing time of the proposed method is 102 s while the Monte Carlo method is 154,523 s.
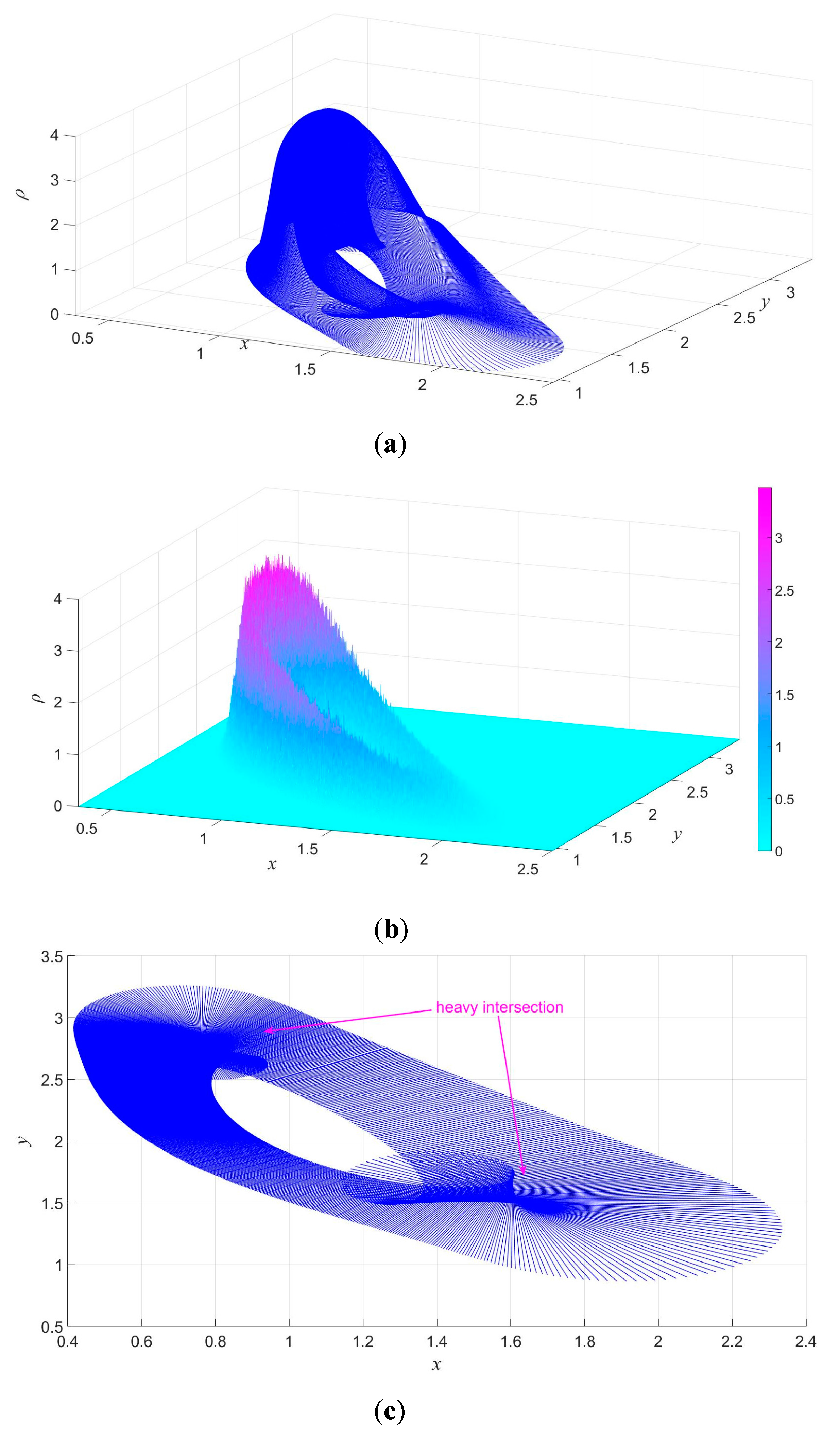
In order to show the limitation of the proposed method, the noise intensity of the Brusselator is increased into 0.05. The results are illustrated in
Figure 14. The root mean square (RMS) errors between the proposed method and the Monte Carlo method are calculated for
ε = 0.005 and
ε = 0.05, which are listed in
Table 1. It can be seen from
Figure 14 that the value of the PDF using the proposed method (
Figure 14a) is not consistent with the Monte Carlo simulation result (
Figure 14b). From
Table 1 it is shown that the RMS error, when
ε = 0.05, is 23.67%, which is much larger than when ε = 0.005 (7.57%). The reason is that the Gaussian distributions of some parts intersect with each other heavily (
Figure 14c) so Equation (1) does not work well.