1. Introduction
The wind turbine is an important piece of equipment in modern agricultural production. The health status of the gearbox directly affects the working condition of the wind turbine system. In the event of failure, it will cause huge economic losses and casualties. Therefore, technology that can diagnose its faults is highly valued [
1,
2,
3]. Among them, the prompt fault diagnosis of the bearing is particularly important, and the bearing system’s faults mainly occur in the inner race, outer race, and rolling elements. When the bearing failure occurs, it produces periodic impulses whose characteristics depend on the location of the fault. In general, the rotational frequency or frequency multiplication of the shaft is the modulation frequency, while the fault frequency of the inner and outer race or the rolling element of the bearing is the carrier frequency. In the fault diagnosis of the actual rotating machinery and equipment, the site’s environment is relatively poor, and the measured vibration signals contain substantial noise interference besides useful characteristics. Especially for the early failure of mechanical equipment, the characteristic signals are relatively weak and often submerged by strong noise, which greatly affects the accurate acquisition of equipment status information. In order to extract the early fault features of the bearing accurately and eliminate the interference of the noise from the signal, it is necessary to suppress the noise and improve the signal-to-noise ratio.
Common denoising methods include traditional filters, wavelet denoising and Empirical Mode Decomposition (EMD), etc. With the development of wavelet theory, wavelet denoising technology can achieve a high signal-to-noise ratio in the process of signal denoising. However, the effect of wavelet denoising is largely determined by the choice of basic functions and thresholds, which often require the designer to have rich experience, and it is a non-adaptive signal processing method. Donoho and Johnstone [
4,
5] first proposed a scalar wavelet threshold denoising method and proved its effectiveness. However, this method ignores the correlation between the wavelet coefficients and fault features, and cannot extract the weak fault features accurately. Cai and Silverman [
6] proposed a thresholding scheme that considers the nearest neighbor coefficients. The experimental results showed that the performance of the neighborhood coefficient thresholding on denoising is superior to the traditional wavelet denoising method. Ming et al. [
7] proposed a method based on a cyclic Wiener filter and envelope spectrum analysis. The cyclic Wiener filter exploited the spectral coherence theory induced by the second-order cyclostationary signal. The noise component was optimally filtered by a filter-bank. The filtered signal was analyzed as an envelope spectrum. The effectiveness of the method was demonstrated on both simulated signals and actual data from a rolling bearing accelerated life test. It could be concluded that the proposed method held a great advantage in detecting early faults over single envelope analysis. Park [
8] provided a method based on minimum variance cepstrum (MVC), which was introduced for the observation of periodic impulse signals under noisy environments. Using the proposed method, they found that four out of twelve newly-made bearings that passed a conventional acceptance test had small early faults in them. Moreover, comparison between these results and those obtained using other fault detection methods indicated that the MVC method was much more capable of detecting early faults under the given conditions. EMD is an adaptive signal processing method. The complex signal can be decomposed into several intrinsic mode functions (IMFs) whose instantaneous frequencies have physical significance, however, this method has the end effect, as well as modal aliasing and other shortcomings. The simulation results showed that IMFs with high frequency components after EMD are mainly composed of noise components and fault features. In the strong noise environment, the noise often affects the sensitive IMFs, and the high frequency weak characteristics can easily be submerged in the intrinsic mode function with noise. Van [
9] proposed a fault feature extraction method for rolling bearing vibration signals based on non-local means (NLM) denoising, EMD and envelope detection. NLM was used as a pre-filter to filter the noise component. The denoised signal was then decomposed into a finite number of stationary IMFs by EMD. The hybrid feature extraction technique of NLM denoising, EMD, and envelope analyses successfully extracted impulsive features from noise signals.
Ensemble empirical mode decomposition (EEMD) and local mean decomposition (LMD) based denoising techniques have been widely employed recently [
10,
11,
12,
13]. LMD is an adaptive time-frequency analysis method proposed by Jonathan S. Smith. The LMD method decomposes a complex multi-component signal into a number of physical functions (PFs) from which instantaneous frequencies with physical significance can be obtained [
14]. Each PF component is obtained by multiplying an envelope signal and a purely frequency modulated (FM) signal. The envelope signal is the instantaneous amplitude of the product function, and the instantaneous frequency of the product function can be obtained from the purely FM signal. The LMD method was compared with the EMD method for decomposition efficiency by Cheng [
11], and the results showed the superiority of the LMD method. Then, the LMD method was applied to gear and roller bearing fault diagnosis. The analysis results demonstrated that the diagnosis approach based on LMD could identify gear and roller bearing work condition accurately and effectively. Liu [
15] applied the LMD method to condition monitoring and fault diagnosis of wind turbines, and the effectiveness of the method was verified by analyzing the vibrational signals of wind turbines. However, in the strong noise environment, the actual signal is often mixed with a lot of noise which is also involved in the process of LMD decomposition, resulting in the original fault feature information and noise mixed together, so that it is not easy to extract the fault features. Moreover, the noise component increases the number of decomposition layers of LMD, which may cause the algorithm to not converge and aggravate the boundary effect. In severe cases, the LMD decomposition will lose its physical meaning, leading to misdiagnosis or leakage diagnosis. As a strong noise reduction method, MED uses the maximum kurtosis as the termination condition of the algorithm, which can highlight the strong impact component of the original signal and weaken the effect of noise on LMD.
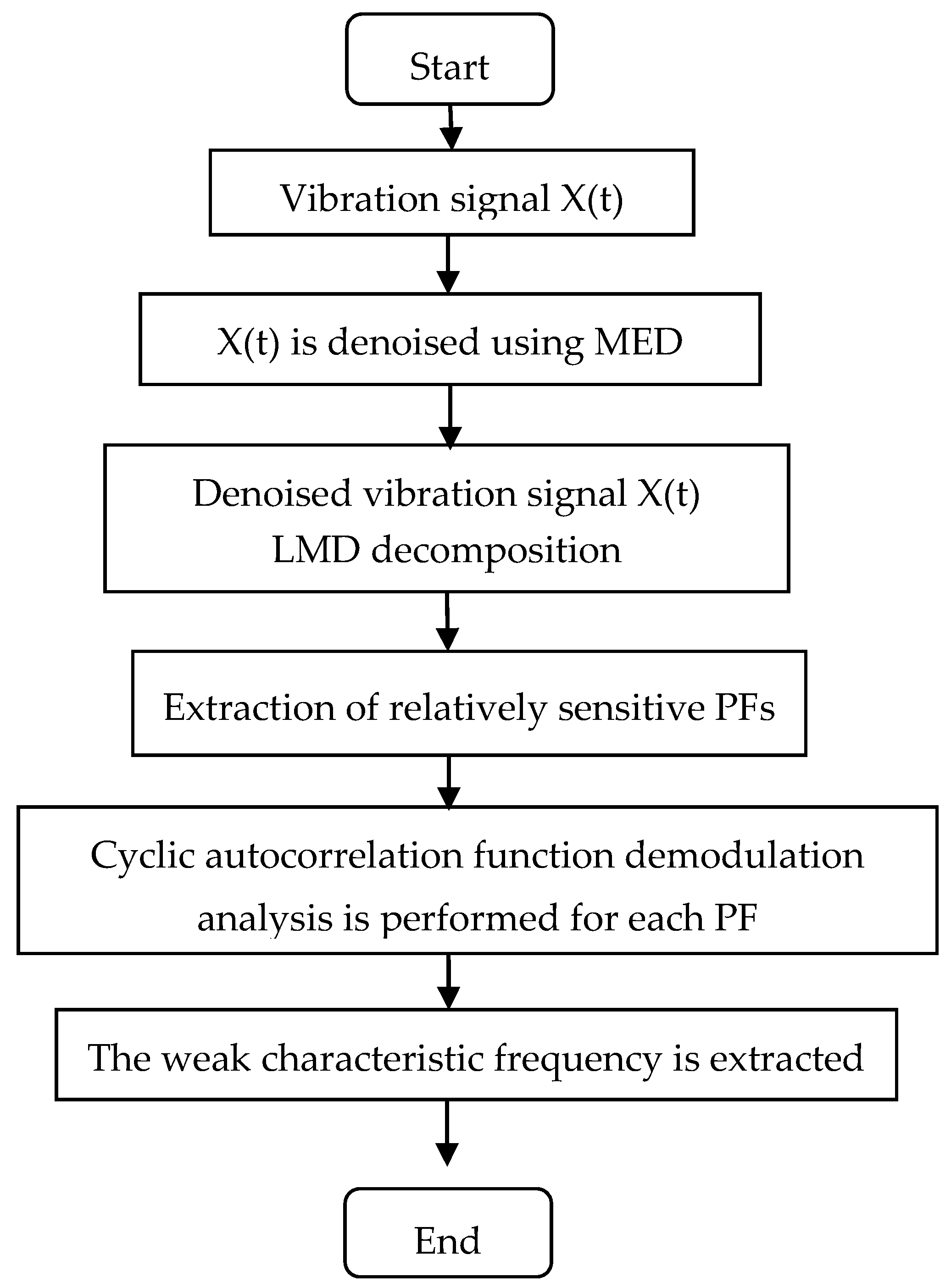
In this approach, the MED-based denoising method is used to reduce the effect of the measurement’s noise signal. The denoised signal is then decomposed by LMD to eliminate the noise because of the effects of other components. In this paper, for the poor performance of weak signal feature extraction of rolling bearing by LMD in a strong noise environment, a method of combining of MED-based denoising and LMD has been proposed. The MED method is first employed as the pretreatment to denoise the weak signal, and the purified signal obtained through MED denoising is then decomposed by LMD into PFs. Finally, the PFs corresponding to the faulty feature signal are analyzed by cyclic autocorrelation function demodulation and the fault features are extracted.
3. A Bearing Fault Diagnosis Method Based on MED-LMD
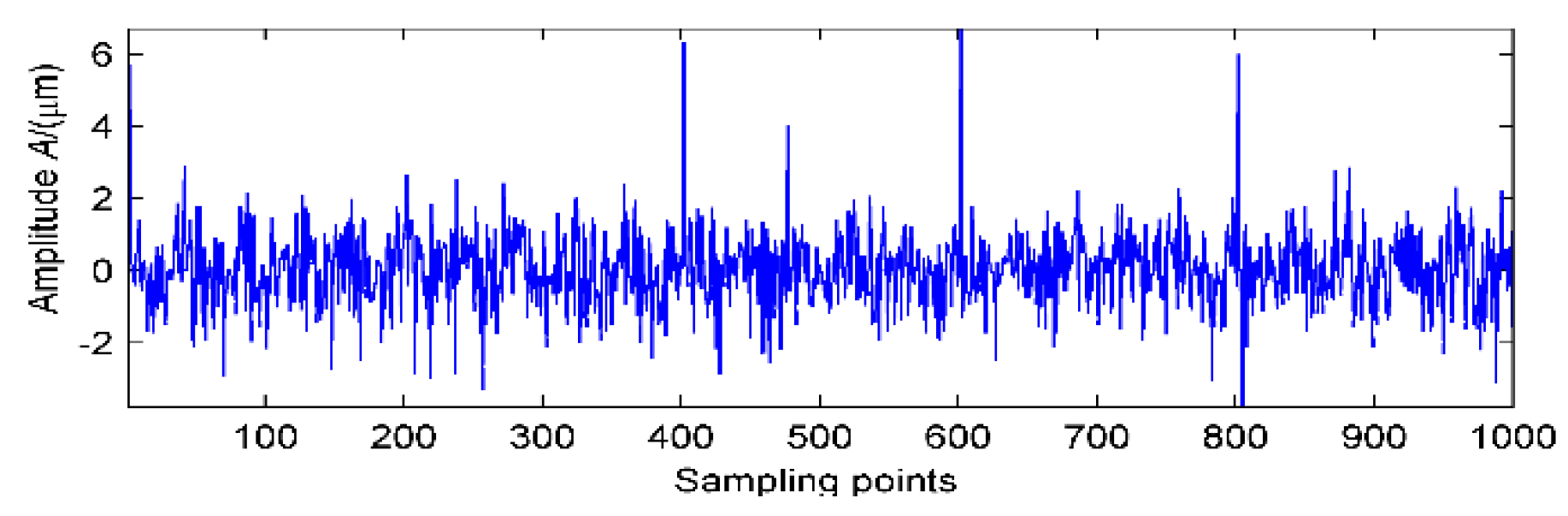
In view of the problem that the early fault vibration signal of the rolling bearing is weak and the fault feature is difficult to extract in the strong white noise environment, a hybrid method is proposed in this paper. The MED method is first employed as the pretreatment to denoise the weak signal, and the purified signal obtained through the MED denoising is then decomposed by LMD to eliminate the noise arising from the effects of other components. The merit of the MED method is that it has a strong denoising ability in a strong noise environment, and it has obvious self-adaptability. The purpose of the MED method is to deconvolute the results to highlight a few large spikes, with the maximum kurtosis value as the termination condition of the calculation. The weak early fault feature extraction is not ideal because early fault features can easily be submerged in the denoised signal. In order to reflect the noise reduction capability of this method, we took the simulation signal containing strong noise as an example, and analyzed it. The time-domain signal is shown in
Figure 1 which contains a noise signal, a sinusoidal signal, a weak impact (signal 1), and a strong impact (signal 2). After filtering the simulation signal using MED, the kurtosis value increased from 1.47 to 5.562. The results are shown in
Figure 2. Most of the strong shock signals are highlighted, while the weak shock signal was still submerged in the noise.
LMD is a very effective fault signal processing method because of its high efficiency of decomposition and good processing of non-stationary signals. However, due to the strong noise interference, the number of decomposed layers of LMD will increase in the decomposition process of the actual vibration signal, and even lead to a greater deviation between the decomposition result and the ideal result, thus affecting the fault diagnosis analysis as shown in the third part of the simulation signal. Therefore, there is an urgent need to find a suitable signal denoising method to improve the decomposition accuracy of LMD, reduce the number of decomposition layers, and increase the signal-to-noise ratio of the input signal.
In order to improve the signal-to-noise ratio and highlight the weak fault impact component, the signal is pretreated with the MED method to weaken the effect of noise on the weak impact component, that is, the effect of the decomposition efficiency of LMD. The LMD algorithm is then used for secondary noise reduction. Considering that each PF component is obtained by multiplying an envelope signal with a pure FM signal, the cyclic autocorrelation function is used to process the denoised sensitive PF components. This method overcomes the limitations of LMD in strong background noise. An example analysis is shown in
Section 3 and
Section 4, and the specific flow chart is illustrated in
Figure 3.
4. Modulation Signal Analysis Based on MED-EEMD and Cyclic Autocorrelation Function
When a bearing fails, the vibration signal is often expressed as the modulation signal [
6]. The fault signal demodulation analysis is designed to extract the vibration signal fault characteristics. For example, given a modulation signal (23), the carrier signal is weaker than the noise signal, the signal is digitized at a sampling frequency
of 2000 Hz and the number of data samples is 1000. The two modulation frequencies
,
are 50 Hz and 30 Hz, respectively, and the carrier frequency
is 180 Hz.
The simulation signal is represented in
Figure 4a. It can be seen from the graph that the carrier and the modulation signal are completely submerged by noise. In order to extract the frequency components of these signals, the simulation signal is denoised by the MED method. The kurtosis values before and after noise reduction were 0.1192 and 1.9154, respectively. The kurtosis value increased 16-fold, and the noise reduction effect is obvious. There are only individual peaks in the signal, and no clear periodic components appear, which is the limitation of MED. Simultaneously, the cyclic autocorrelation demodulation of the simulation signal and the MED-based denoised signal were performed, as shown in
Figure 4b. The spectrum peak does not appear at the high and low frequencies of the carrier frequency and the modulation frequency, but after MED noise reduction and then cyclic autocorrelation function demodulation analysis, the spectrum peak has increased in the case of
= 50 Hz and
Hz. However, the carrier frequency at high frequencies still cannot be distinguished. In the case of strong noise, MED noise reduction and cyclic autocorrelation function demodulation cannot extract the characteristic frequency accurately.
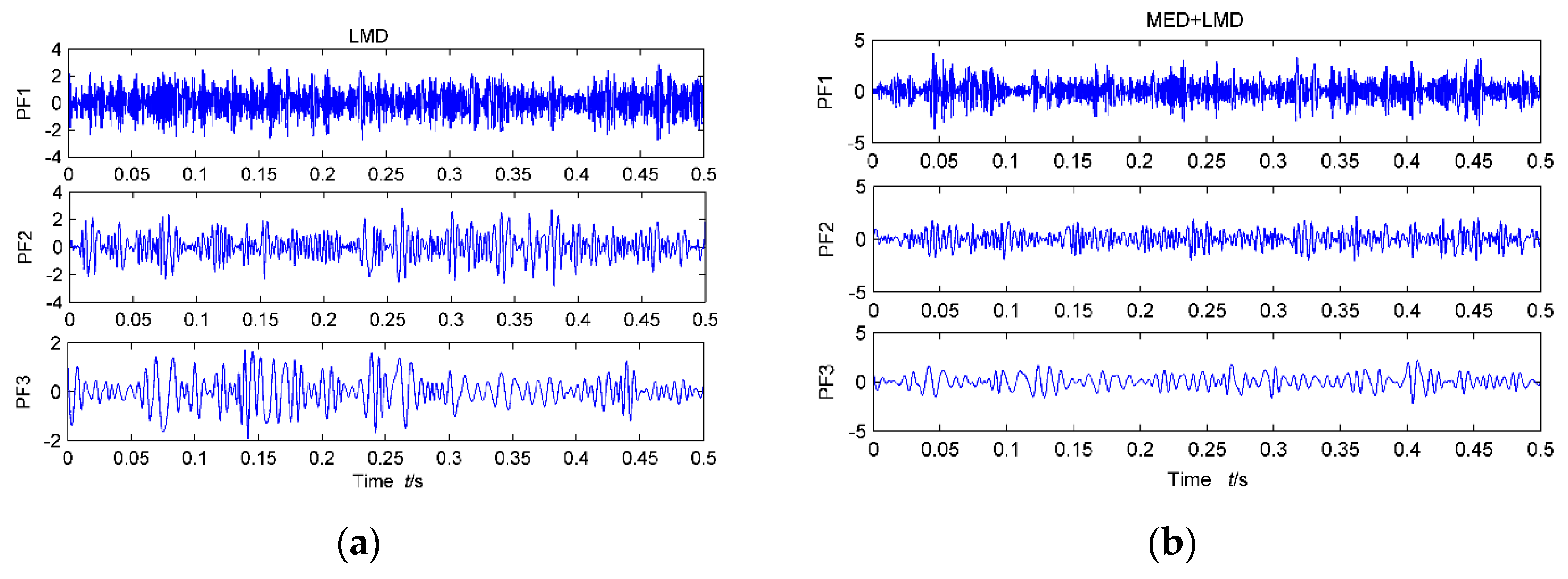
In order to show the interference of the noise to the weak signal in the original signal by EEMD decomposition, the original signal is decomposed by LMD, as shown in
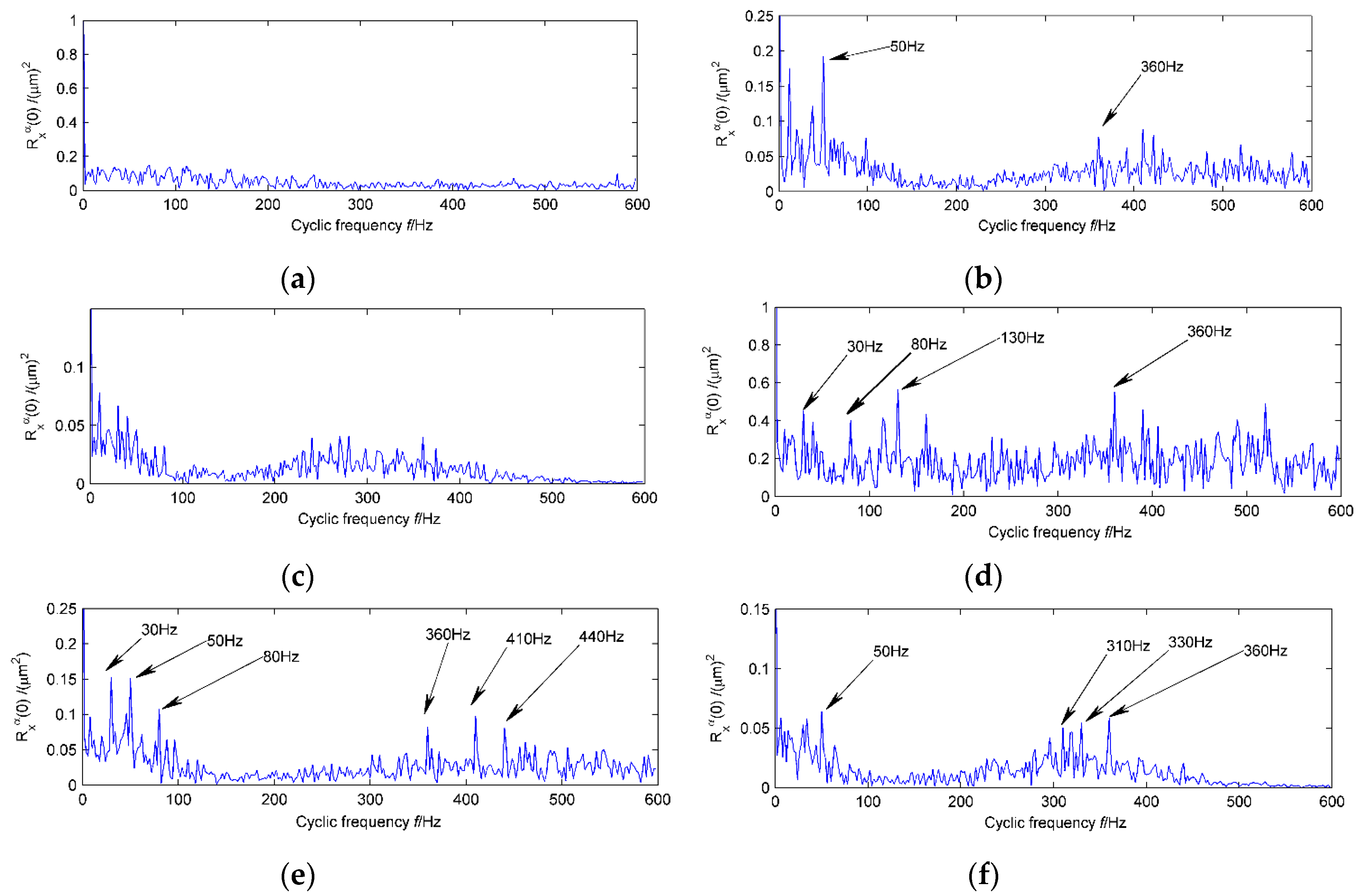
Figure 5a. The first three layers of PFs which have the strongest correlation with the original signal were obtained, and cyclic autocorrelation demodulation analysis was carried out on them, as shown in
Figure 6a–c. The modulation frequency
= 50 Hz and the carrier frequency
= 360 Hz only appear in the second layer. And the spectrum peak
is not so prominent that it can be easily confused with other components. At the same time, the modulation frequency
= 30 Hz also does not appear. It is clear that the original signal denoising processing is necessary. The results of LMD decomposition of the signal after MED noise reduction are shown in
Figure 5b. The first three layers are analyzed by cyclic autocorrelation function, and the results are shown in
Figure 6d–f. In the high frequency zone, the carrier frequency
= 360 Hz is obviously prominent, 310 Hz, 330 Hz, 410 Hz are side frequencies of the frequency 360 Hz, respectively. Their spacing is the modulation frequency
= 50 Hz and
= 30 Hz. In the low frequency zone,
= 50 Hz and
= 30 Hz are the modulation frequencies of the original signal. Therefore, noise reduction by MED can not only avoid the effect of noise on the weak features, but also does not affect the decomposition effect of LMD. Although the MED method cannot extract the weak feature frequency signal directly, using its noise reduction ability to eliminate the influence of the original signal noise on LMD decomposition effect helps the LMD method to identify the weak feature components. This method is not only unique in that the original signals are analyzed by cyclic autocorrelation function demodulation, but is also superior to the method in which MED-based and LMD-based de-noising signals are analyzed by cyclic autocorrelation function demodulation.
5. Vibration Signal Analysis
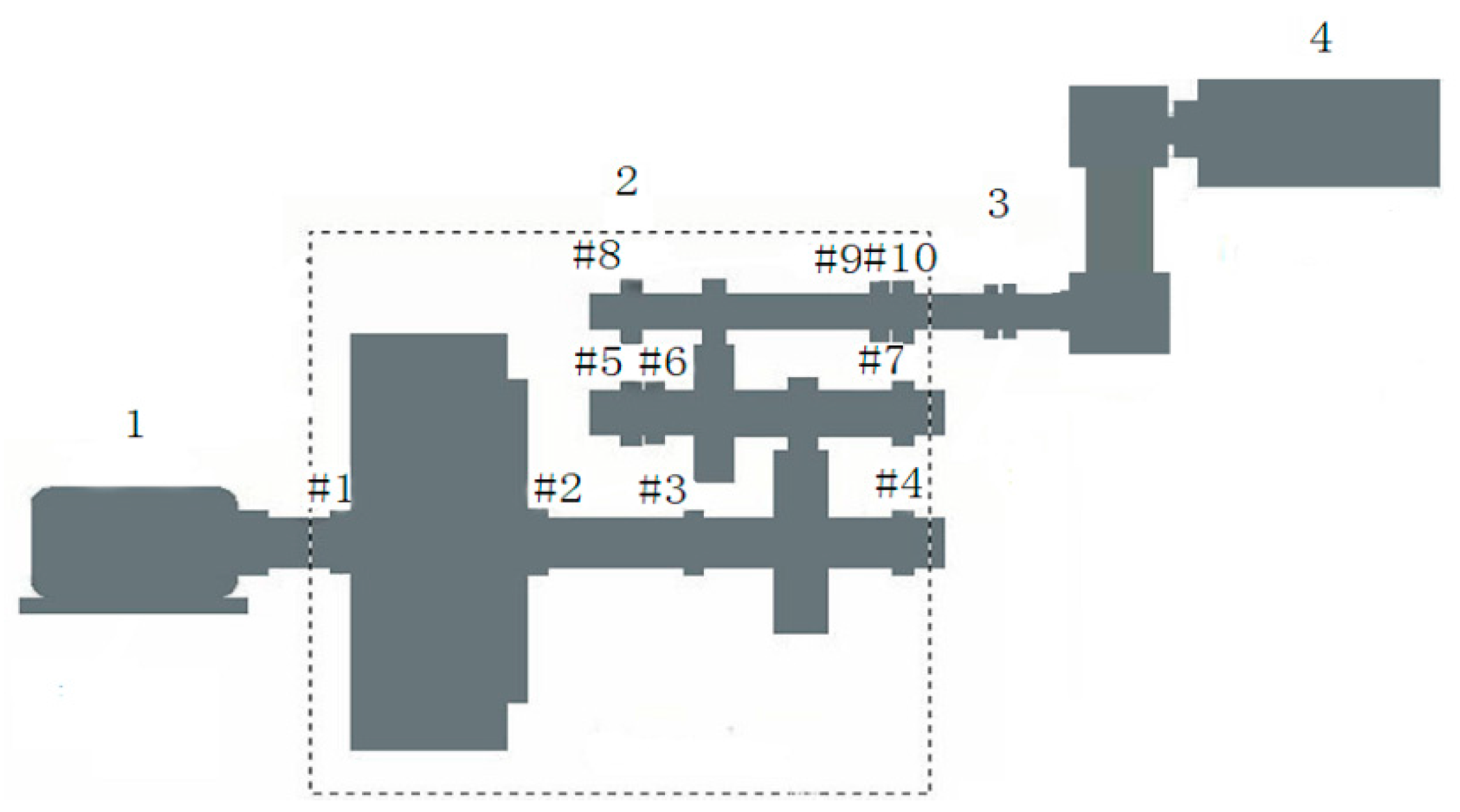
The method is further demonstrated with a vibration signal from a wind turbine. The test bench sketch of a wind turbine gearbox is shown in
Figure 7. The speed-increasing gear transmission system has a three-stage gear transmission device with the generator as the load of the gearbox. During the test, as the power of the generator increases, the vibration and noise of the gearbox are continuously strengthened, and the temperature of the high-speed shaft continues to rise. In order to determine the fault location, we use acceleration sensors and a dynamic signal analyzer for measurement and data acquisition. The sampling points are located in the bearing block of the high-speed shaft gearbox. The signal is digitized at a sampling frequency of 10,000 Hz and the number of data sample is 2048. The rotating speed of the output gear shaft is 1728 r/min and the rotating frequency
of the shaft is 28.8 Hz (modulation frequency). The position of the high-speed shaft, the speed of the bearing and the frequency of the fault are shown in
Table 1The original vibration signal shown in
Figure 8a is chaotic and has no obvious periodic component. After cyclic autocorrelation demodulation analysis, no significant carrier and modulation frequencies appear in
Figure 8b. The results of noise reduction of the original signal by MED are shown in
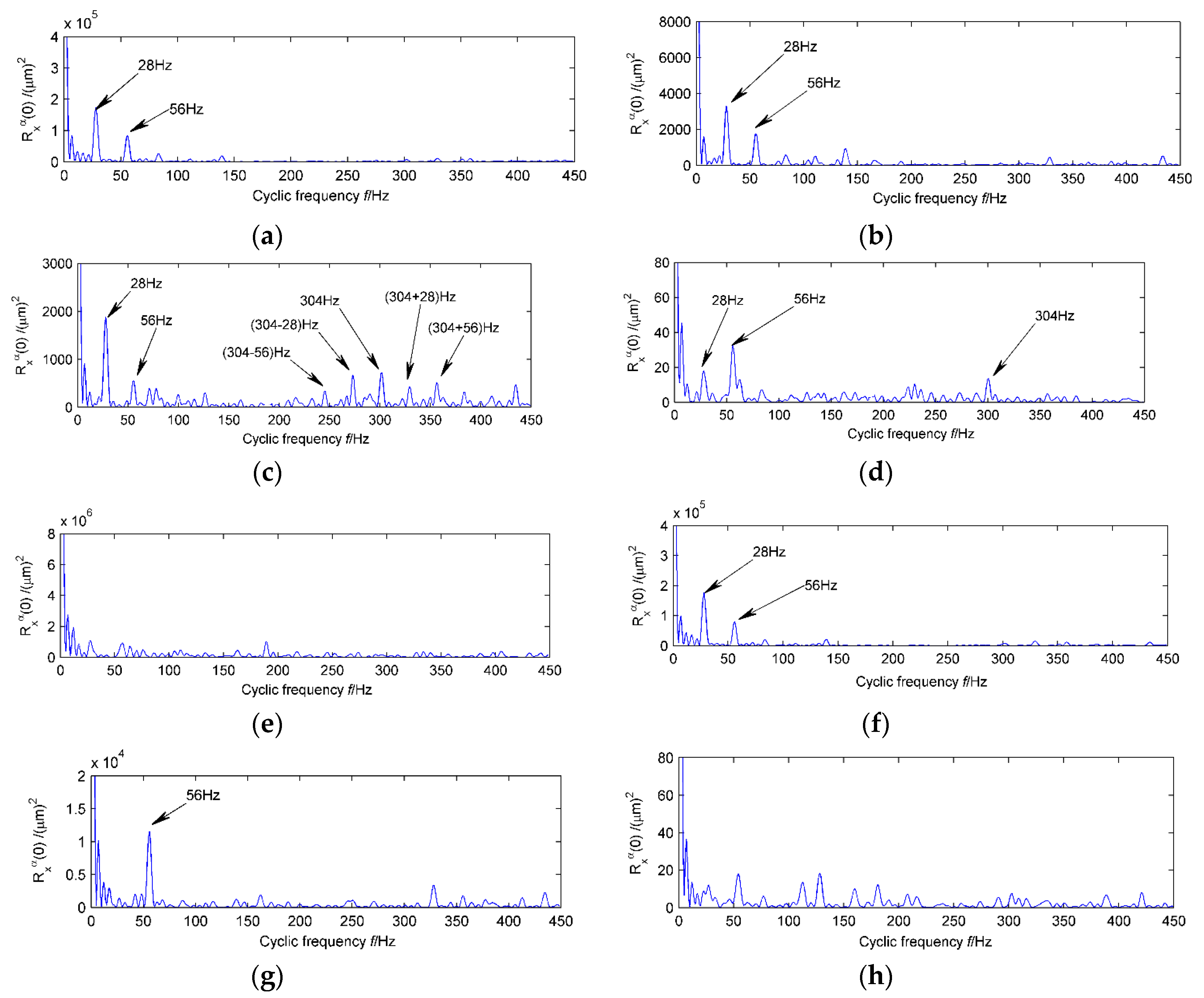
Figure 8c. It can be seen from the figure that the signal-to-noise ratio is obviously increased after denoising and the periodic impulse is prominent. There are about 357 sampling points between the two adjacent impulse signals. The corresponding frequency 1/0.0357 = 28.01 Hz is the rotation frequency of the high-speed shaft. The cyclic autocorrelation function of the vibration signal, illustrated in
Figure 8d, consists of two main frequency components at 28 Hz and 56 Hz, which correspond respectively to the high-speed shaft rotational frequency and its second-order harmonics. It can be initially determined that there appears to be a weak bending on the high-speed shaft.
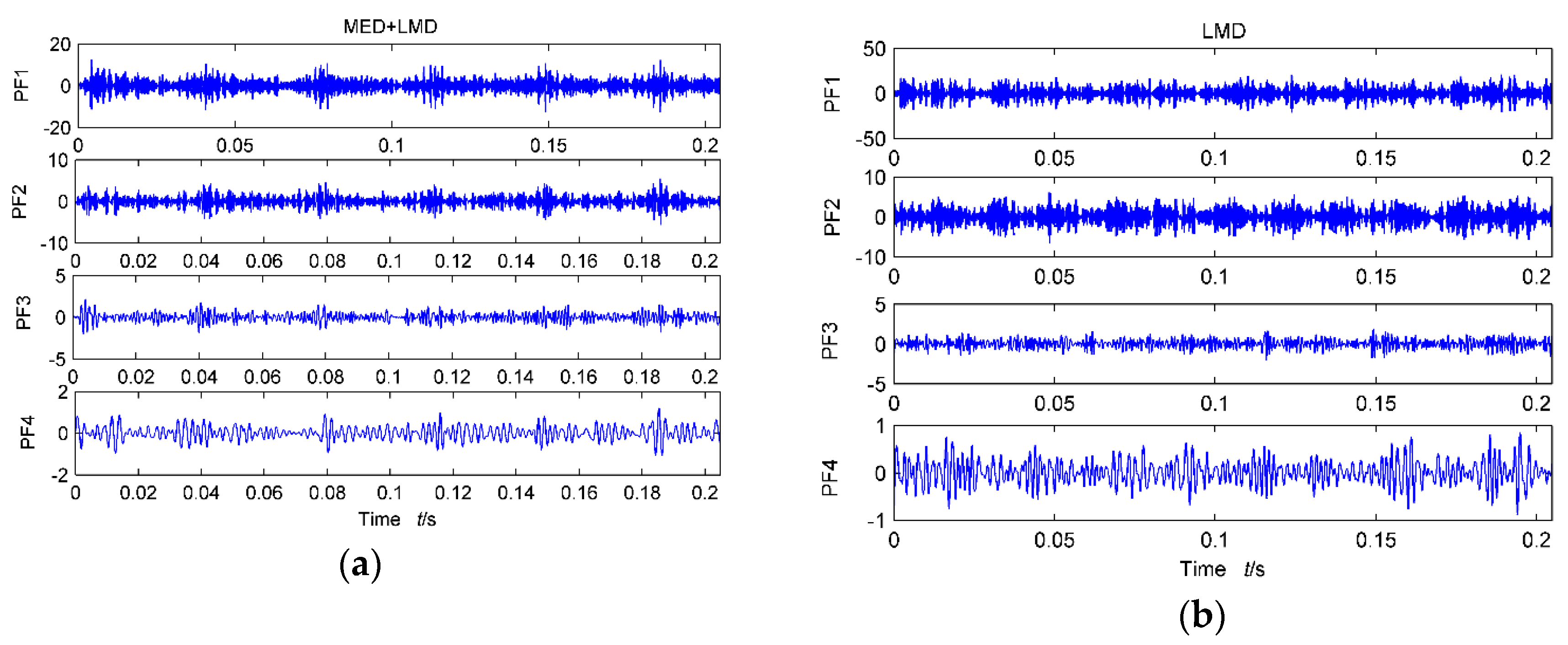
In order to further determine the characteristic frequency of the fault, the signal after MED noise reduction is decomposed by LMD, and the decomposition result is shown in
Figure 9a. The main energy of the original signal is concentrated in the first four layers, among which the first layer is of the strongest correlation with the original signal. The first four PFs are analyzed by cyclic autocorrelation function demodulation, and the result is represented in
Figure 10a–d. The first four PFs contain the strong impact component of the original signal, that is, the high-speed shaft rotational frequency and its second order harmonics. Modulation frequency (high-speed shaft rotating frequency) is still the main frequency in the low frequency zone in the second two layers. A frequency cluster with a center frequency of 304 Hz and a rotational frequency of the high-speed shaft as a side band appears in the high frequency zone. The frequency of 304 Hz is also second-order harmonics of the fault frequency of the bearing outer ring at the output end of the #10 bearing. The presence of these prominent frequency components indicates that there is slight pitting on the face of outer rings of the #10 bearings at the end of the of high-speed shaft.
When opening the box, it can be found that the high-speed shaft has a small bending deformation and there is pitting on the face of outer rings of the #10 bearings at one side end of the high-speed shaft. Thus, the diagnosis result has been confirmed. As the vibration signal generated by the bearing outer ring pitting is weak, it is easily submerged by the noise. The first four layers of PFs of the measured signal are analyzed by LMD, and the results are shown in
Figure 9b. The cyclic autocorrelation functions of first four PFs are shown in
Figure 10e–h. As can be seen from the figures, the low frequency is still dominated by the modulation frequencies, but the fault frequency of the bearing outer ring at the output end of the #10 bearing is not reflected in the high frequency zone. Therefore, it is not ideal to use only the LMD decomposition method to extract the weak fault signal in a strong noise background. However, a hybrid fault diagnosis method based on the MED denoising, LMD, and the cyclic autocorrelation function can successfully extract the weak characteristic frequency. The analyzed results demonstrate that the proposed method is an effective approach in identifying multiple faults in rotating machinery.
In order to compare and analyze the proposed method, an adaptive noise reduction method, variational mode decomposition (VMD), is used to further analyze the vibration signals, and the results were compared with EMD, EEMD, and other adaptive methods. VMD has the advantages of fast convergence, good noise robustness, and so on. In addition, this method has different frequency bands for each layer of intrinsic modal functions, so it is suitable for multi-fault feature extraction. Similarly, a MED + VMD secondary noise reduction method was used to process the original signal and the result is shown in
Figure 11. Through the analysis of the first four layers of IMFs, each layer corresponds to a periodic component, of which the first two layers correspond to the fault characteristics. The corresponding frequencies of the other two layers are pseudo frequencies, however, belonging to the noise components. Although this method can also identify the fault characteristics, the efficiency of VMD noise reduction is affected by two factors; one is the penalty factor and the other is the number of decomposition layers. Too few layers will cause modal aliasing, too many layers will result in energy leakage. The penalty factor was set to 5000, and the number of decomposition layers was set to 4. The results are shown in
Figure 11. The rationality of the proposed method is verified by the comparison of the two methods.
6. Conclusions
(1) The PFs obtained by LMD decomposition not only contain the characteristic frequency, but also the noise components. In the strong noise background, the weak feature information is still submerged in the noise and is difficult to extract.
(2) MED has a strong capability for noise reduction and filtering, but can only highlight a few large spikes. Thus, the original signal through the MED filter, can only increase the kurtosis value of the signal and the weak characteristic frequency still cannot be extracted.
(3) A hybrid fault diagnosis method based on MED denoising and the LMD method is proposed in this paper. The filtering with MED reduces the influence of noise on LMD, and through cyclic autocorrelation demodulation analysis, the weak feature is successfully extracted. The proposed method was applied to analyze measured vibration signals and simulated signals. The results demonstrate the feasibility of the proposed method. In general, the MED-LMD method provides a new idea for weak fault diagnosis of rotating machinery, which is helpful for further research and has certain reference value.