Noise Enhancement for Weighted Sum of Type I and II Error Probabilities with Constraints
Abstract
:1. Introduction
- Formulation of the optimization problem for minimizing the noise modified weighted sum of type I and II error probabilities under the constraints on the two error probabilities is presented.
- Derivations of the optimal noise that minimizes the weighted sum and sufficient conditions for improvability and nonimprovability for a general composite hypothesis testing problem are provided.
- Analysis of the characteristics of the optimal additive noise that minimizes the weighted sum for a simple hypothesis testing problem is studied and the corresponding algorithm to solve the optimization problem is developed.
- Numerical results are presented to verify the theoretical results and to demonstrate the superior performance of the proposed detector.
2. Noise Enhanced Composite Hypothesis Testing
2.1. Problem Formulation
2.2. Sufficient Conditions for Improvability and Non-improvability
- (1)
- , , ;
- (2)
- , , ;
- (3)
- , , .
2.3. Optimal Additive Noise
3. Noise Enhanced Simple Hypothesis Testing
3.1. Problem Formulation
3.2. Algorithm for the Optimal Additive Noise
- (1)
- If , then and such that .
- (2)
- If and are true, then we have , , , and .
- (3)
- If , then is obtained when , and the corresponding achieves the minimum and .
- (4)
- If , then is achieved when , and the corresponding and reaches the minimum.
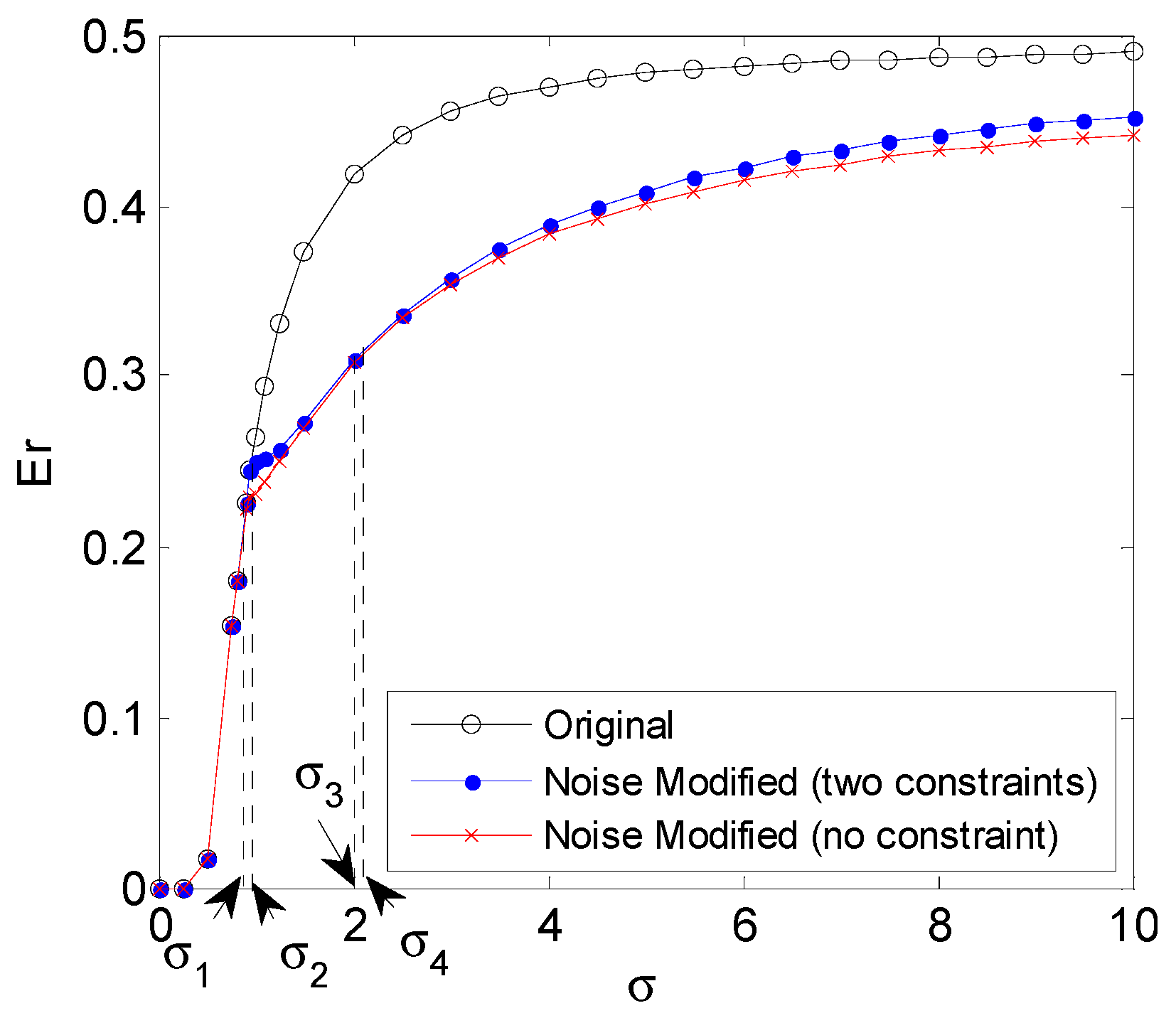
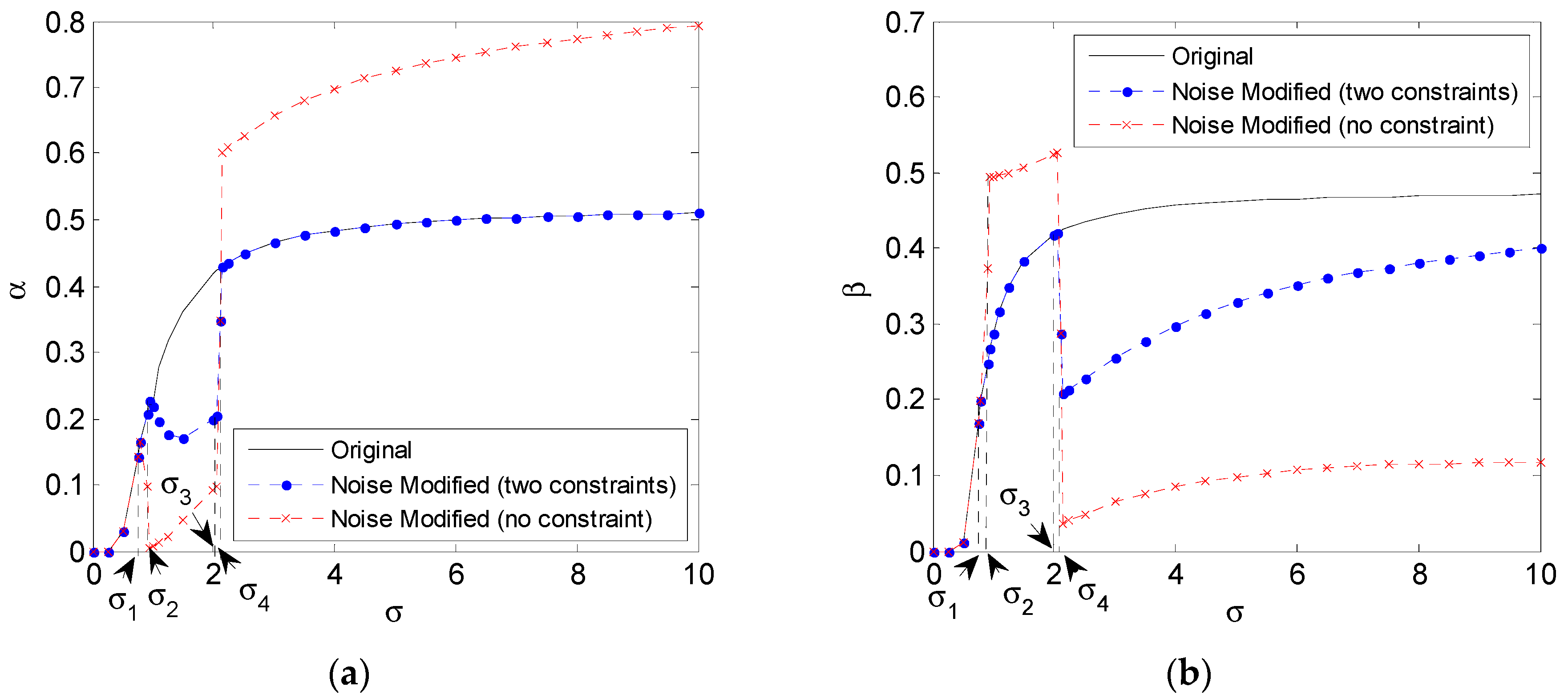
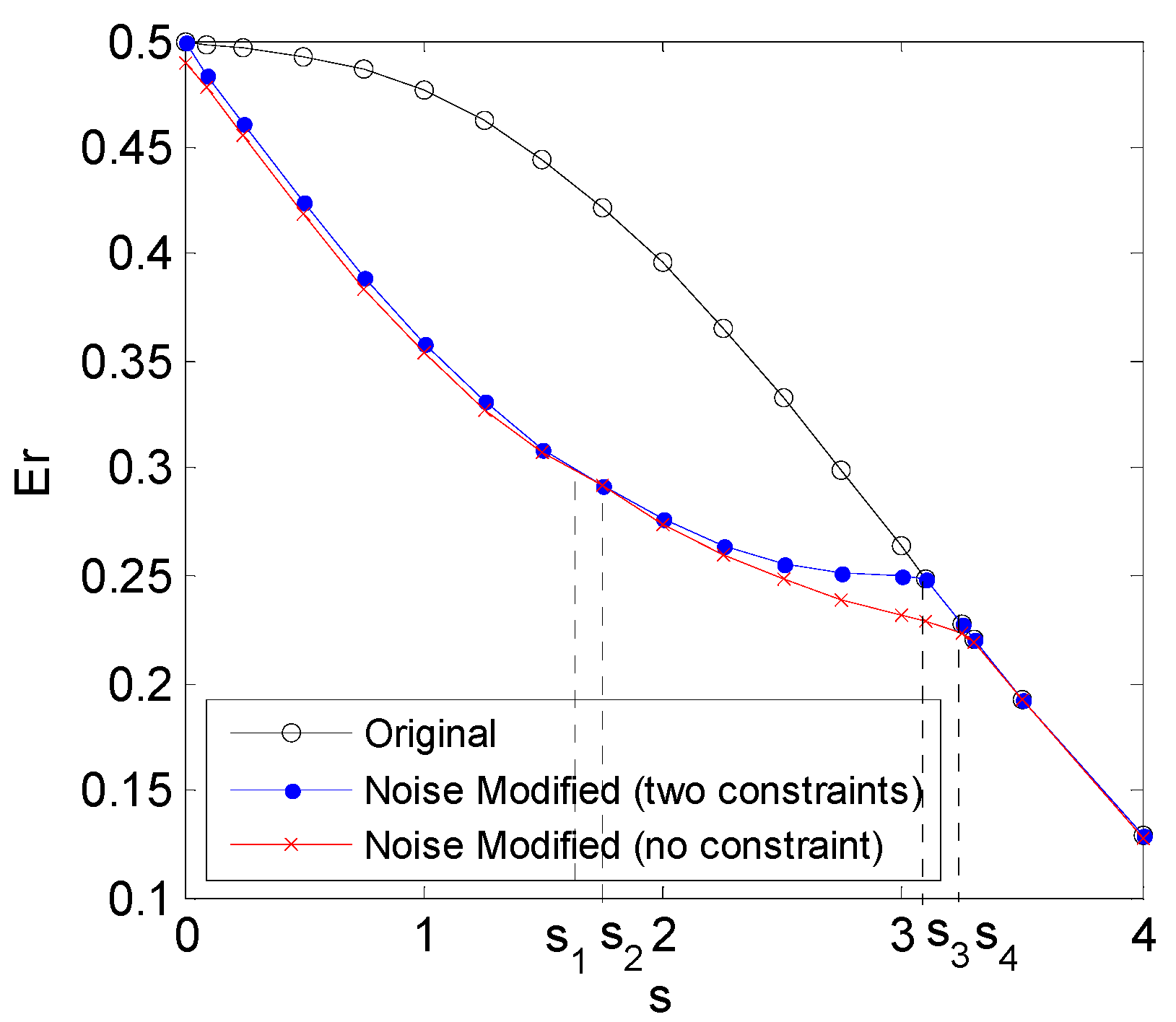
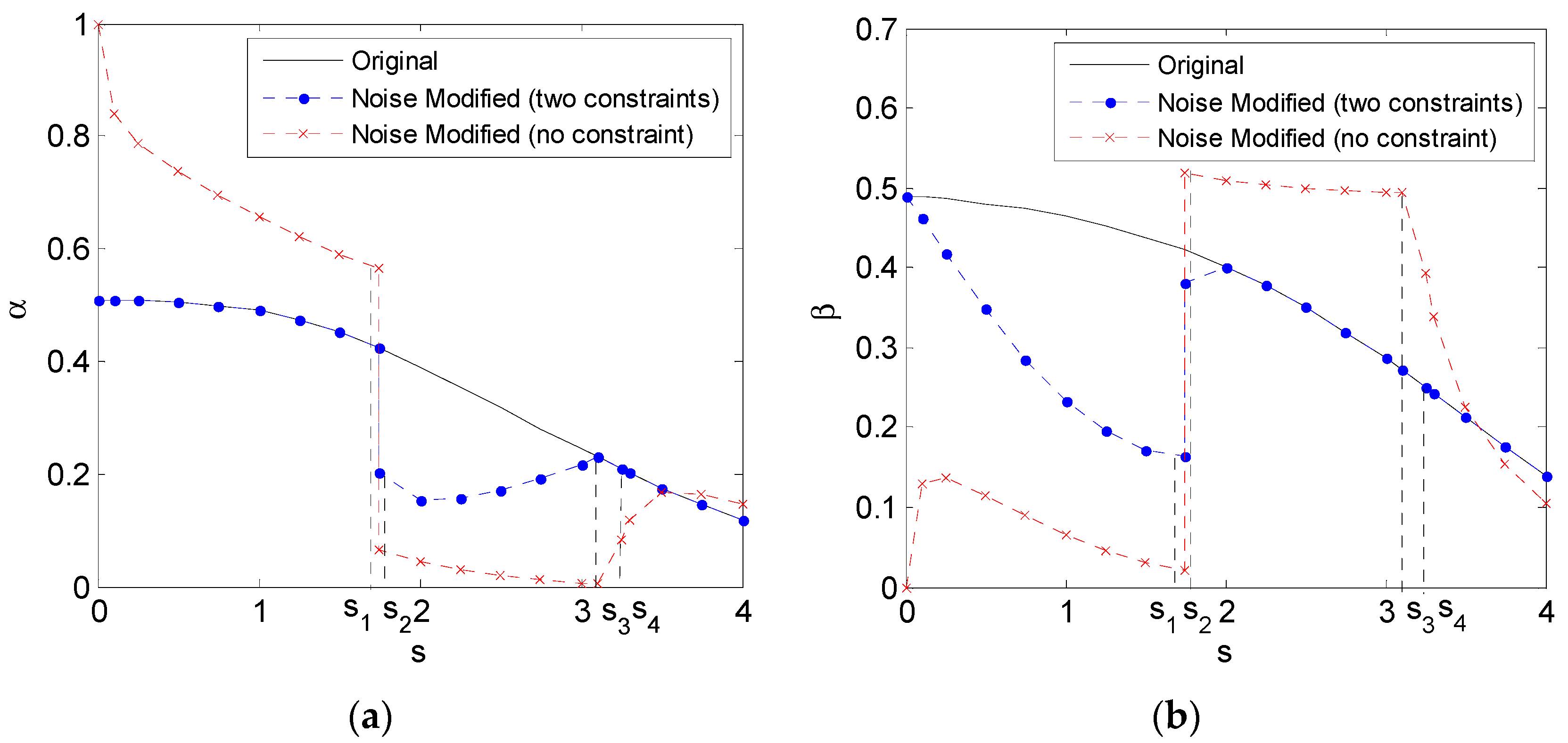
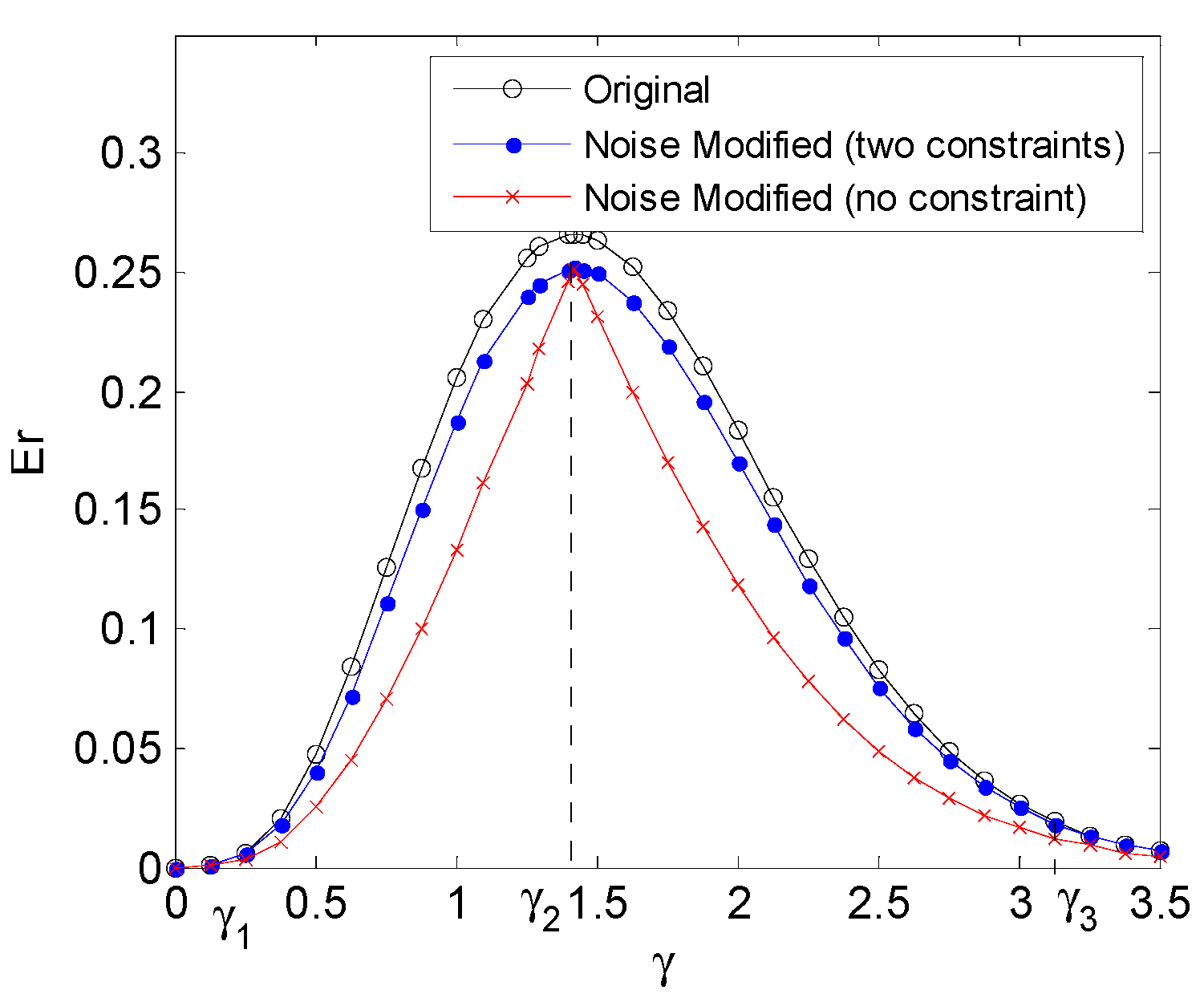
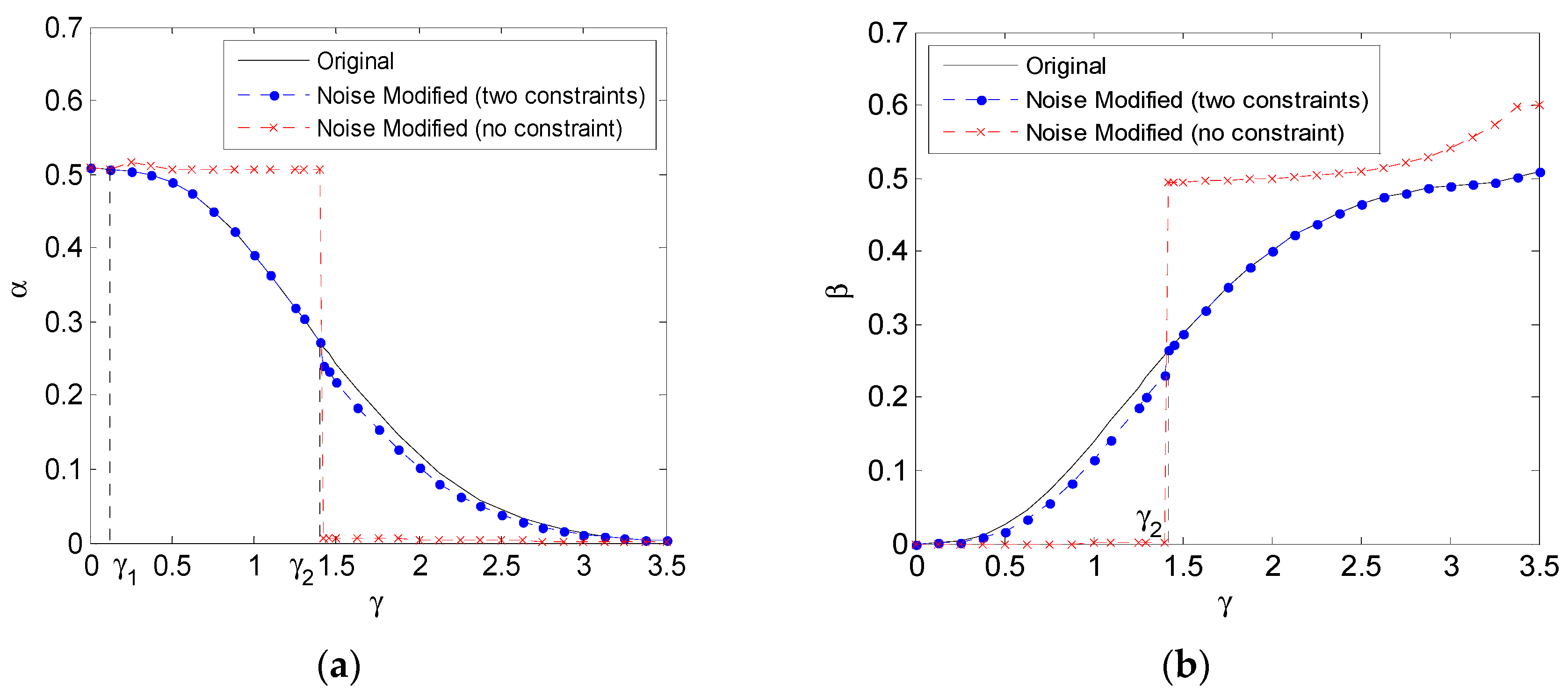
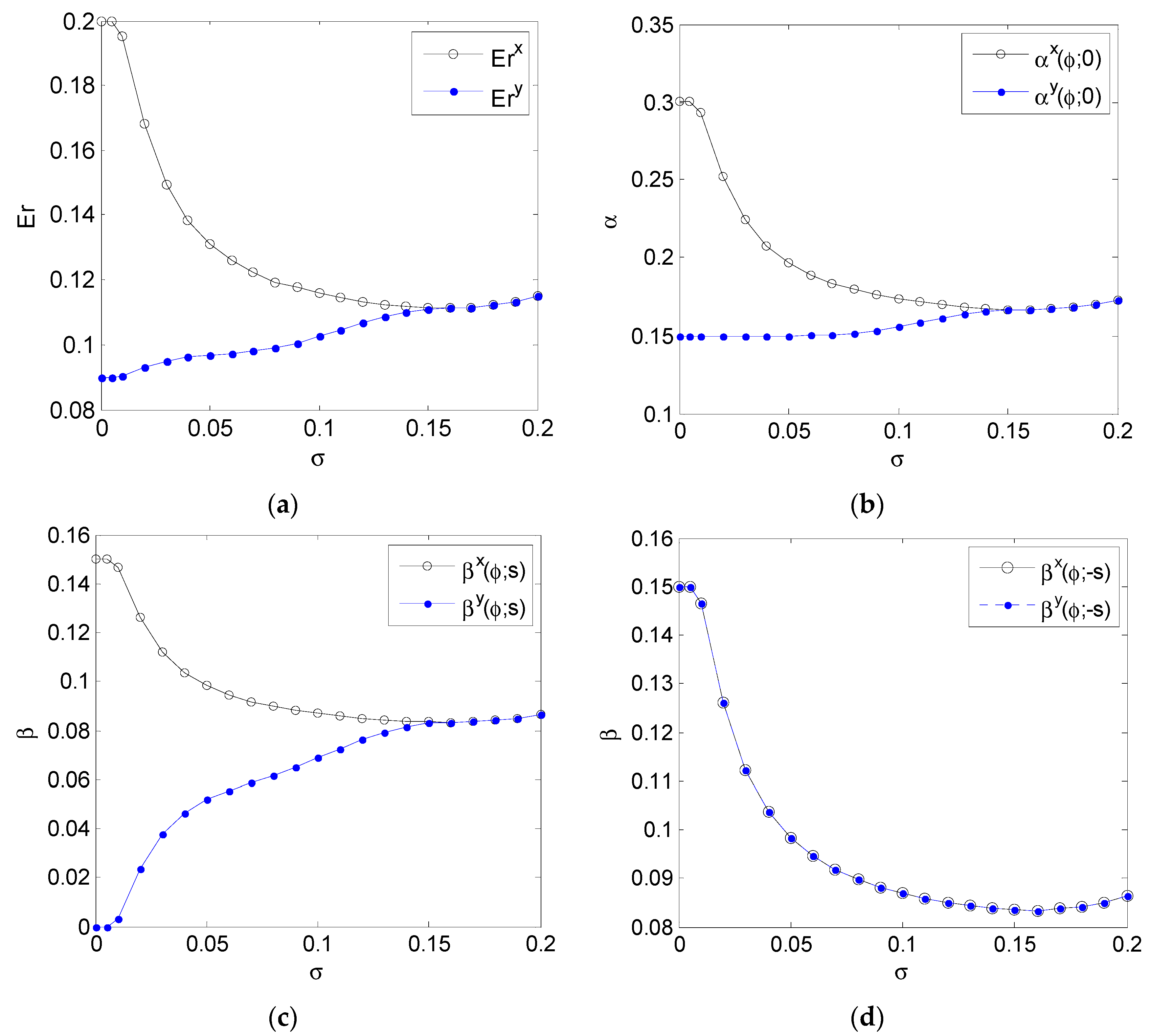
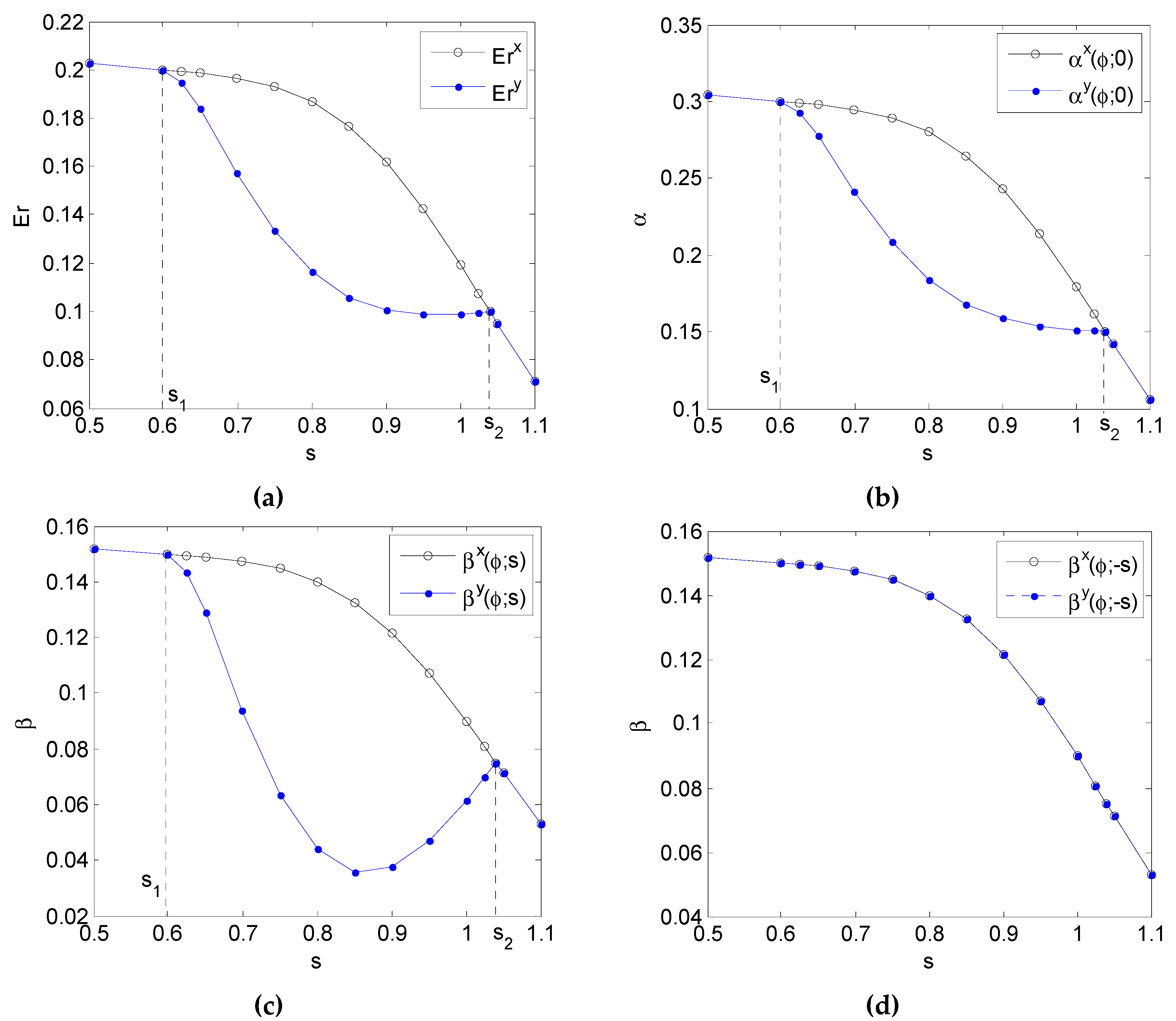
4. Numerical Results
4.1. Rayleigh Distribution Background Noise
4.2. Gaussian Mixture Background Noise
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
- (1)
- Inequalities (A15)–(A17) can be satisfied by setting as a sufficiently large positive number, if , , hold.
- (2)
- Inequalities (A15)–(A17) can be satisfied by setting as a sufficiently large negative number, if , , hold.
- (3)
- Inequalities (A15)–(A17) can be satisfied by setting as zero, if , , hold. □
Appendix C. Proof of Theorem 3
Appendix D. Proof of Theorem 5
References
- DeGroot, M.H.; Sxhervish, M.J. Probability and Statistics, 4nd ed.; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Pericchi, L.; Pereira, C. Adaptative significance levels using optimal decision rules: Balancing by weighting the error probabilities. Braz. J. Probab. Stat. 2016, 30, 70–90. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. 1981, 14, 453–457. [Google Scholar] [CrossRef]
- Patel, A.; Kosko, B. Noise benefits in quantizer-array correlation detection and watermark decoding. IEEE Trans. Signal Process. 2011, 59, 488–505. [Google Scholar] [CrossRef]
- Han, D.; Li, P.; An, S.; Shi, P. Multi-frequency weak signal detection based on wavelet transform and parameter compensation band-pass multi-stable stochastic resonance. Mech. Syst. Signal Process. 2016, 70–71, 995–1010. [Google Scholar] [CrossRef]
- Addesso, P.; Pierro, V.; Filatrella, G. Interplay between detection strategies and stochastic resonance properties. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 15–31. [Google Scholar] [CrossRef]
- Gingl, Z.; Makra, P.; Vajtai, R. High signal-to-noise ratio gain by stochastic resonance in a double well. Fluct. Noise Lett. 2001, 1, L181–L188. [Google Scholar] [CrossRef]
- Makra, P.; Gingl, Z. Signal-to-noise ratio gain in non-dynamical and dynamical bistable stochastic resonators. Fluct. Noise Lett. 2002, 2, L147–L155. [Google Scholar] [CrossRef]
- Makra, P.; Gingl, Z.; Fulei, T. Signal-to-noise ratio gain in stochastic resonators driven by coloured noises. Phys. Lett. A 2003, 317, 228–232. [Google Scholar] [CrossRef]
- Duan, F.; Chapeau-Blondeau, F.; Abbott, D. Noise-enhanced SNR gain in parallel array of bistable oscillators. Electron. Lett. 2006, 42, 1008–1009. [Google Scholar] [CrossRef]
- Mitaim, S.; Kosko, B. Adaptive stochastic resonance in noisy neurons based on mutual information. IEEE Trans. Neural Netw. 2004, 15, 1526–1540. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.; Kosko, B. Mutual-Information Noise Benefits in Brownian Models of Continuous and Spiking Neurons. In Proceedings of the 2006 International Joint Conference on Neural Network, Vancouver, BC, Canada, 16–21 July 2006; pp. 1368–1375. [Google Scholar]
- Chen, H.; Varshney, P.K.; Kay, S.M.; Michels, J.H. Theory of the stochastic resonance effect in signal detection: Part I – fixed detectors. IEEE Trans. Signal Process. 2007, 55, 3172–3184. [Google Scholar] [CrossRef]
- Patel, A.; Kosko, B. Optimal noise benefits in Neyman–Pearson and inequality constrained signal detection. IEEE Trans. Signal Process. 2009, 57, 1655–1669. [Google Scholar]
- Bayram, S.; Gezici, S. Stochastic resonance in binary composite hypothesis-testing problems in the Neyman–Pearson framework. Digit. Signal Process. 2012, 22, 391–406. [Google Scholar] [CrossRef]
- Bayrama, S.; Gultekinb, S.; Gezici, S. Noise enhanced hypothesis-testing according to restricted Neyman–Pearson criterion. Digit. Signal Process. 2014, 25, 17–27. [Google Scholar] [CrossRef]
- Bayram, S.; Gezici, S.; Poor, H.V. Noise enhanced hypothesis-testing in the restricted Bayesian framework. IEEE Trans. Signal Process. 2010, 58, 3972–3989. [Google Scholar] [CrossRef]
- Bayram, S.; Gezici, S. Noise enhanced M-ary composite hypothesis-testing in the presence of partial prior information. IEEE Trans. Signal Process. 2011, 59, 1292–1297. [Google Scholar] [CrossRef]
- Chen, H.; Varshney, L.R.; Varshney, P.K. Noise-enhanced information systems. Proc. IEEE 2014, 102, 1607–1621. [Google Scholar] [CrossRef]
- Weber, J.F.; Waldman, S.D. Stochastic Resonance is a Method to Improve the Biosynthetic Response of Chondrocytes to Mechanical Stimulation. J. Orthop. Res. 2015, 34, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Duan, F.; Chapeau-Blondeau, F.; Abbott, D. Non-Gaussian noise benefits for coherent detection of narrow band weak signal. Phys. Lett. A 2014, 378, 1820–1824. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, L.; Brennan, M.J.; Yang, T.; Ding, H.; Liu, Z. Stochastic resonance in a nonlinear mechanical vibration isolation system. J. Sound Vib. 2016, 370, 221–229. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Ekman, T.; Dong, H. Energy Detection for MIMO Decision Fusion in Underwater Sensor Networks. IEEE Sen. J. 2015, 15, 1630–1640. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Kansanen, K.; Ekman, T. Performance Analysis of Energy Detection for MIMO Decision Fusion in Wireless Sensor Networks Over Arbitrary Fading Channels. IEEE Trans. Wirel. Commun. 2016, 15, 7794–7806. [Google Scholar] [CrossRef]
- Ciuonzo, D.; de Maio, A.; Rossi, P.S. A Systematic Framework for Composite Hypothesis Testing of Independent Bernoulli Trials. IEEE Signal Proc. Lett. 2015, 22, 1249–1253. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle Swarm Optimization Method for Constrained Optimization Problems; IOS Press: Amsterdam, The Netherlands, 2002; pp. 214–220. [Google Scholar]
- Hu, X.; Eberhart, R. Solving constrained nonlinear optimization problems with particle swarm optimization. In Proceedings of the sixth world multiconference on systemics, cybernetics and informatics, Orlando, FL, USA, 14–18 July 2002. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: New York, NY, USA, 2005. [Google Scholar]
| Two Constraints | No Constraints | |||
|---|---|---|---|---|
| 0.950 | - | - | - | −1.7089 |
| 1.250 | −1.9082 | 1.7963 | 0.6950 | −1.9218 |
| 2.125 | −2.5136 | 3.1896 | 0.7862 | −2.5136/3.1896 |
| 3.000 | −3.3771 | 4.6942 | 0.3770 | 4.7449 |
| Two Constraints | No Constraints | |||
|---|---|---|---|---|
| 1.25 | −1.3682 | 1.7327 | 0.2918 | 1.7474 |
| 1.75 | −1.4408 | 1.6563 | 0.7265 | −1.4408/1.6563 |
| 2.5 | −1.6052 | 1.4690 | 0.6983 | −1.6201 |
| 3.25 | - | - | - | −0.5866 |
| Two Constraints | No Constraints | |||
|---|---|---|---|---|
| 0.050 | - | - | - | - |
| 1.100 | −2.1213 | 0.9341 | 0.2878 | 0.9691 |
| 1.425 | −1.7947 | 1.2585 | 0.5355 | −1.7957 |
| 2.250 | −0.9693 | 2.0836 | 0.8867 | −1.1763 |
| 3.375 | - | - | - | −0.5775 |
| 0.0001 | 0.2286 | - | - | 1.0000 | - | - |
| 0.02 | 0.2286 | −0.2255 | - | 0.8413 | 0.1587 | - |
| 0.05 | 0.2287 | −0.2208 | 0.2421 | 0.5310 | 0.3446 | 0.1244 |
| 0.08 | 0.2180 | −0.2185 | −0.2168 | 0.5943 | 0.2449 | 0.1608 |
| 0.65 | 0.1613 | −0.1613 | - | 0.6267 | 0.3733 | - |
| 0.75 | 0.2026 | −0.2026 | - | 0.7949 | 0.2051 | - |
| 0.85 | 0.2148 | −0.2149 | -0.2150 | 0.8262 | 0.1300 | 0.0438 |
| 0.95 | 0.2195 | −0.2196 | -0.2190 | 0.7006 | 0.1916 | 0.1078 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yang, T.; Zhang, K. Noise Enhancement for Weighted Sum of Type I and II Error Probabilities with Constraints. Entropy 2017, 19, 276. https://doi.org/10.3390/e19060276
Liu S, Yang T, Zhang K. Noise Enhancement for Weighted Sum of Type I and II Error Probabilities with Constraints. Entropy. 2017; 19(6):276. https://doi.org/10.3390/e19060276
Chicago/Turabian StyleLiu, Shujun, Ting Yang, and Kui Zhang. 2017. "Noise Enhancement for Weighted Sum of Type I and II Error Probabilities with Constraints" Entropy 19, no. 6: 276. https://doi.org/10.3390/e19060276
APA StyleLiu, S., Yang, T., & Zhang, K. (2017). Noise Enhancement for Weighted Sum of Type I and II Error Probabilities with Constraints. Entropy, 19(6), 276. https://doi.org/10.3390/e19060276




