Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis
Abstract
:1. Introduction
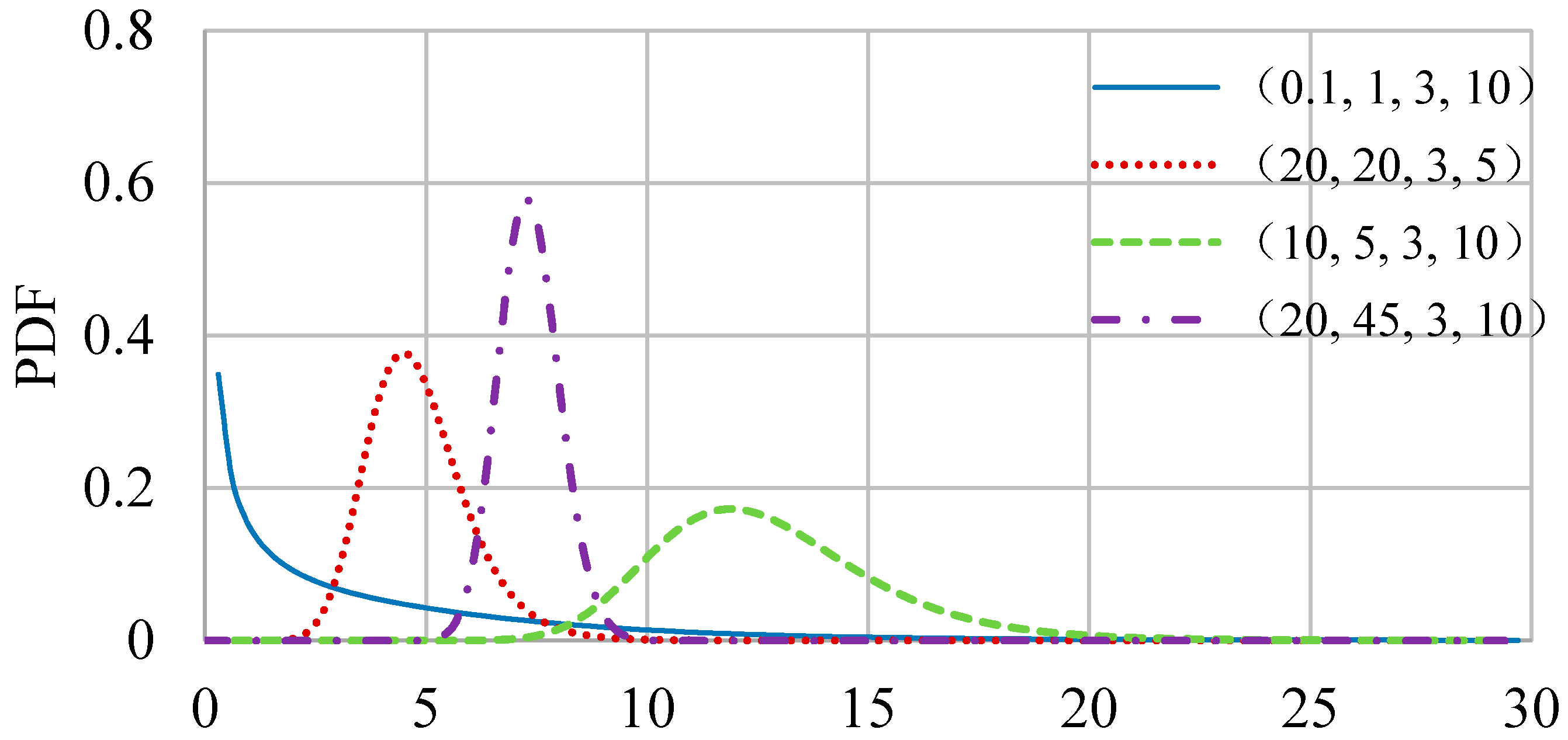
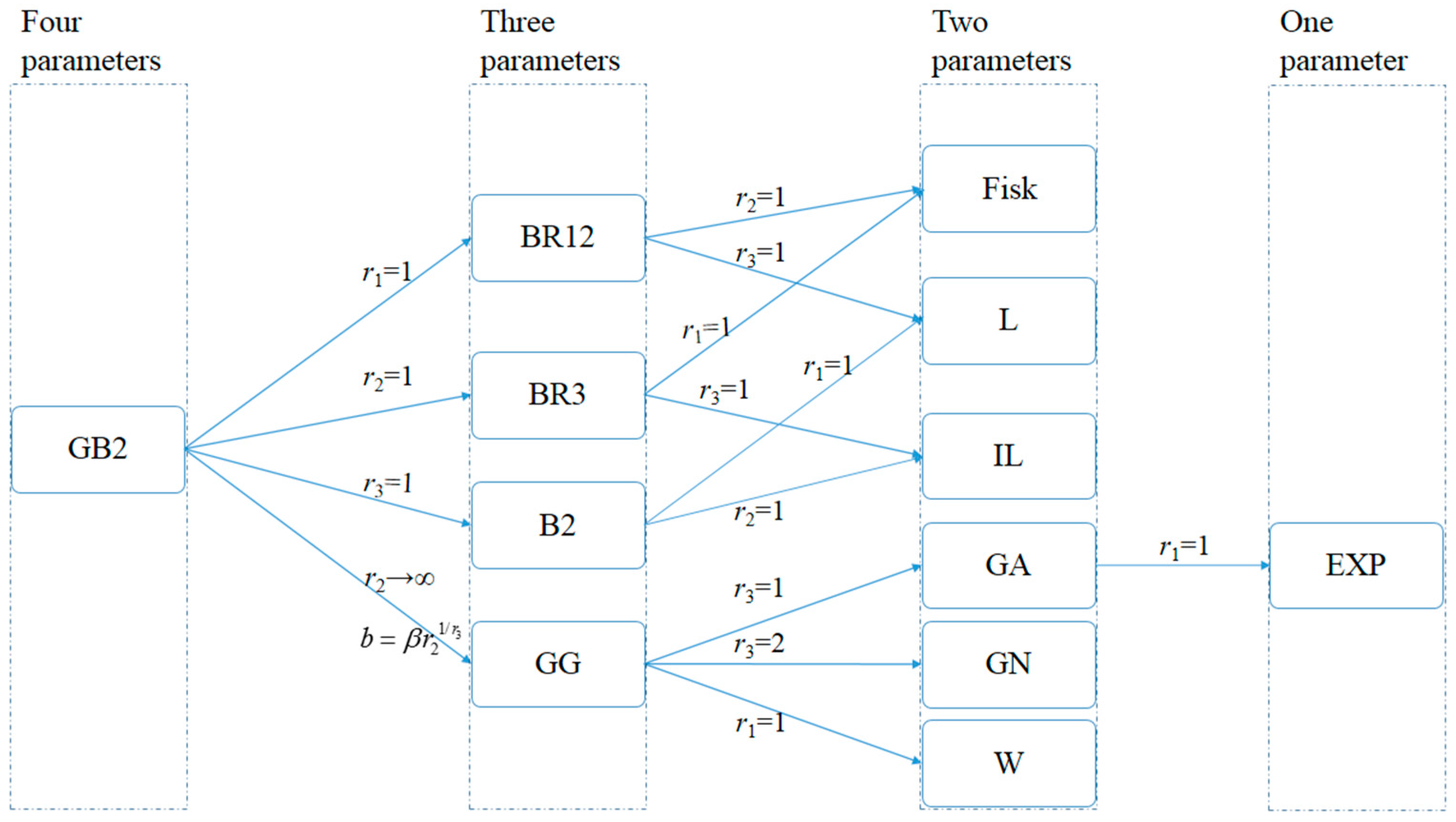
2. GB2 Distribution
3. Estimation of Parameters of GB2 Distribution by POME Method
4. Flood Frequency Analysis
4.1. Flood Data
4.2. Performance Measures
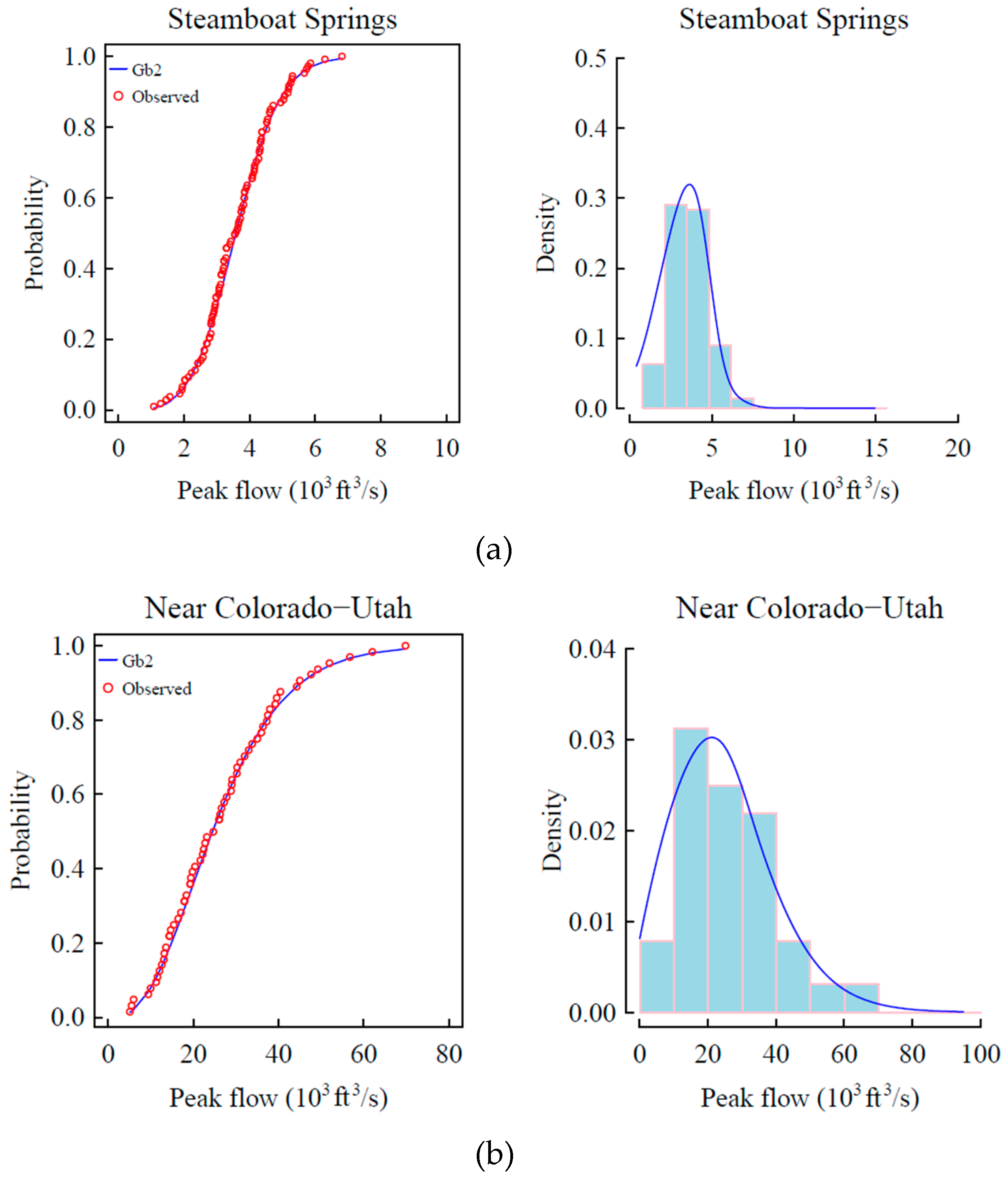
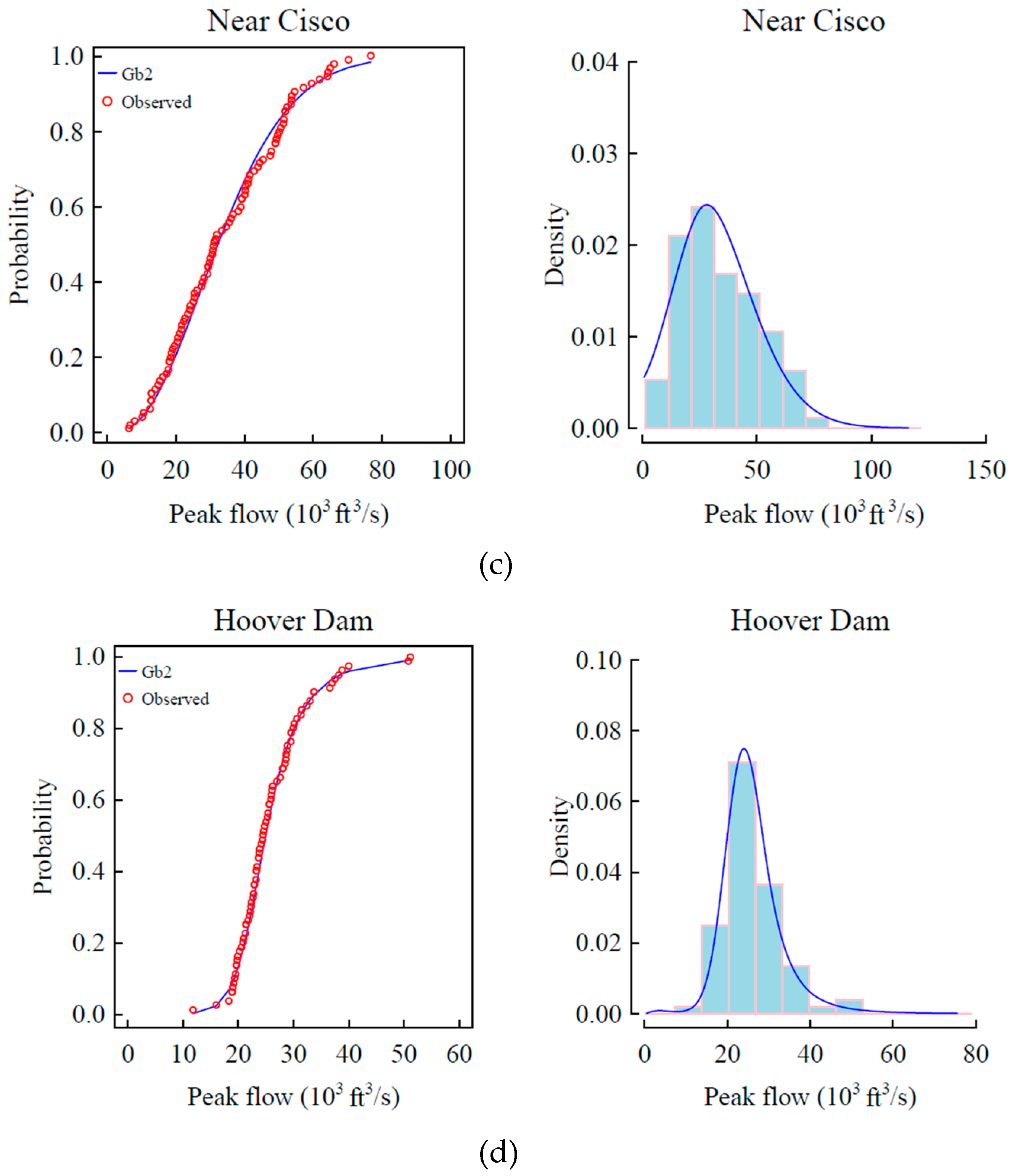
4.3. Evaluation of GB2 Distribution
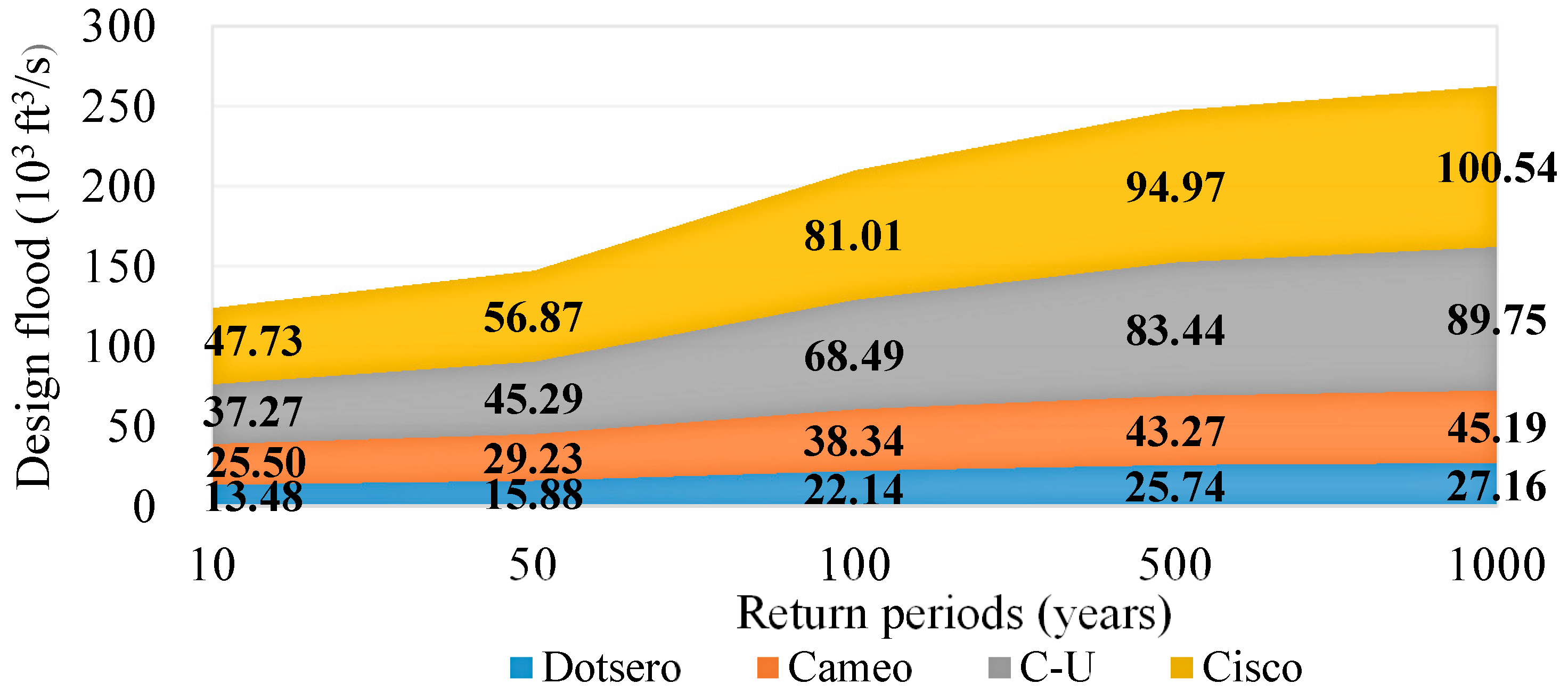
4.4. Flood Frequency Analysis
4.5. Change in Flood Frequency Distribution with Change in Drainage Area
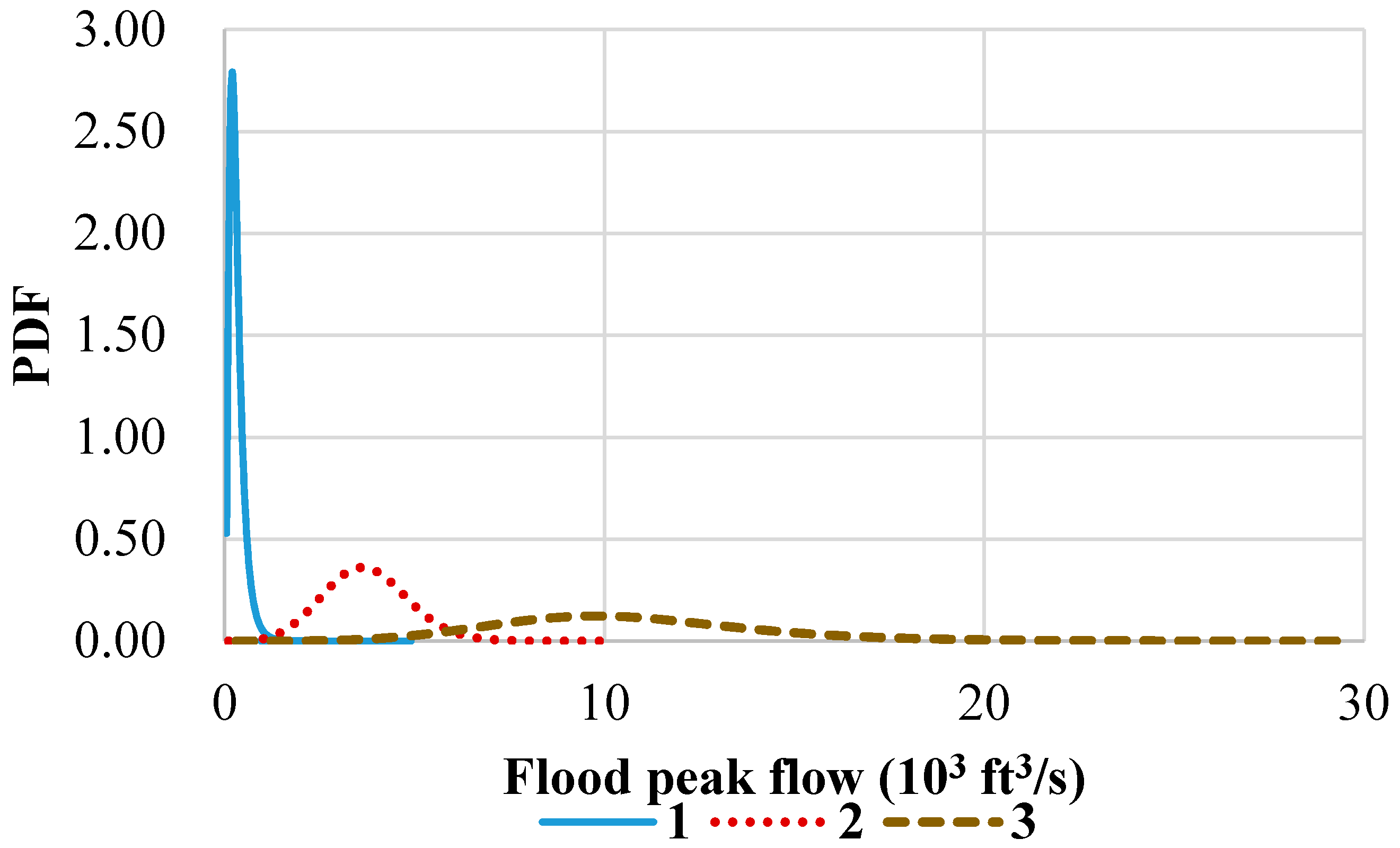
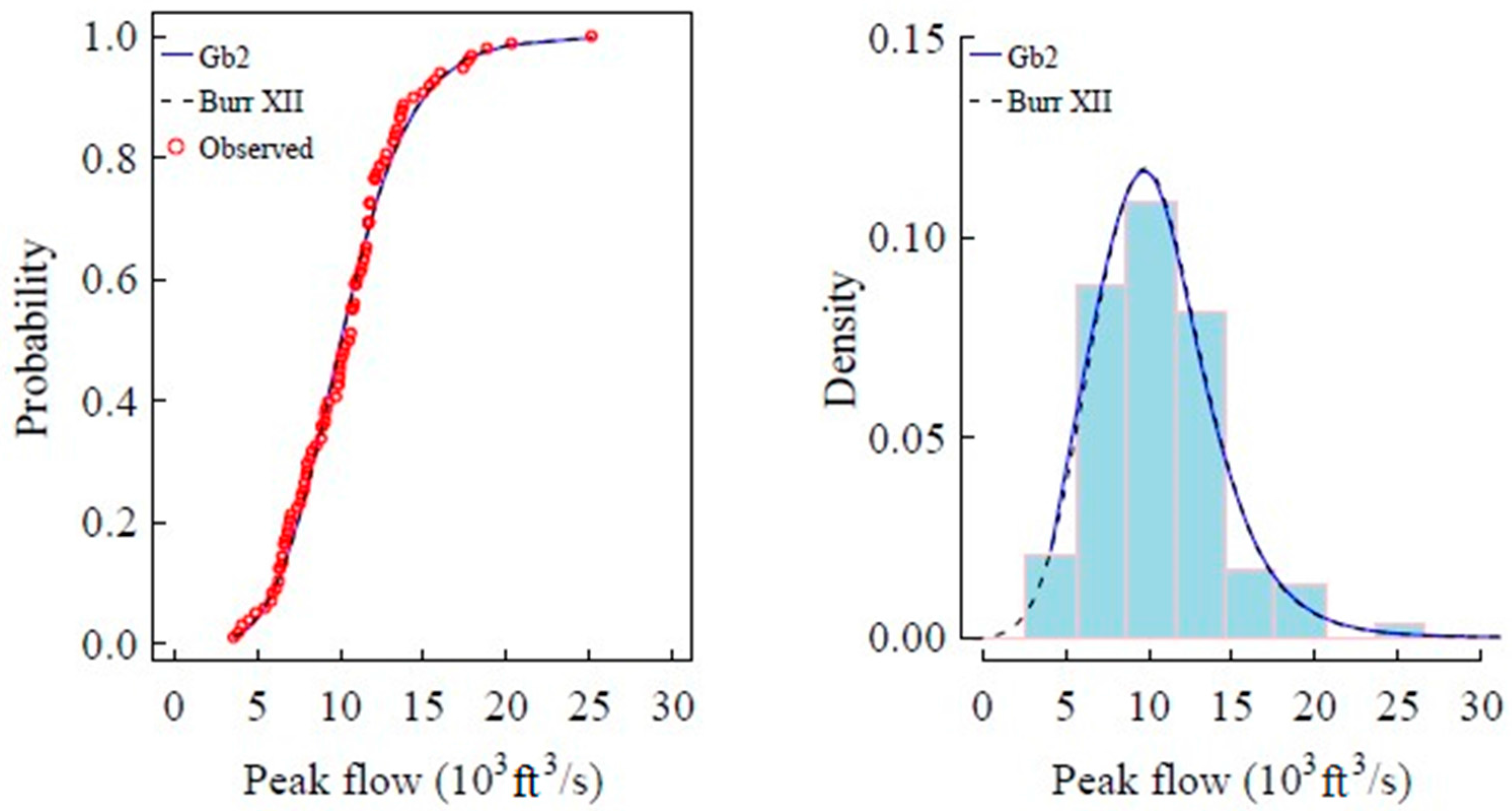
4.6. Evolution of Frequency Distribution along Stream
5. Conclusions
- (1)
- Results demonstrate that the GB2 is appealing for FFA, since it has four parameters which allows the distribution to be able to fit data having very different histogram shapes, such as the J-shaped and bell-shaped distributions. And by fixing certain parameters, the GB2 distribution can yield some well-known distributions, such as the beta distribution of the second kind (B2), the Burr type XII, generalized gamma (GG), and so on.
- (2)
- The parameters estimated by POME method are found reasonable. Both the marginal distributions and histograms indicates that the GB2 distribution can successfully be fitted to empirical values using the POME method.
- (3)
- The performance of the GB2 distribution is better than that of the widely used distributions in hydrology. For the site streamboat springs, the GB2 and generalized normal distributions have the smallest RMSD values. For the site Near Cisco, the GB2 has the smallest RMSE values. For the site Near Colorado-Utah, the GB2 and gamma distributions have the smallest RMSE value. For the site Hoover dam, the GB2 distribution has the smallest RMSE value. Since the GB2 distribution have more parameters, the AIC values of GB2 distribution are larger than those of generalized normal, Gamma and GEV distributions. Thus, generally GB2 distribution gives a getter fit.
- (4)
- When using different distributions for FFA, significant different design flood values are obtained. It concludes that if the wrong distribution were used, the design flood would be underestimated and potential flood risk would be higher.
- (5)
- The design flood value increase with the drainage area. For a given return period, the design flood value of the downstream gauging stations is larger than that of the upstream gauging stations. In this study, the percentage increase of the drainage area was nearly the same as that of the design flood values. It seems that in a mountainous watershed, the upstream the reach is, the greater the impact the drainage area has on flood. This may be because that the runoff coefficient is generally larger in the steep area.
- (6)
- There is an evolution of distribution along this river. Along the Yampa River, the distribution for FFA changes from the four-parameter GB2 distribution to the three-parameter Burr XII distribution. And both r1 and r2 decrease along the stream, which demonstrates that both the left and right tails become fatter, and the PDF values become larger in these areas and lower in the central area, which means that when the drainage area become larger, the flood magnitudes has a more significant variation.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Estimation of Parameters of GB2 Distribution
References
- Beven, K.J.; Hornberger, G.M. Assessing the effect of spatial pattern of precipitation in modeling streamflow hydrographs. J. Am. Water Resour. Assoc. 1982, 18, 823–829. [Google Scholar] [CrossRef]
- Shao, Q.; Wong, H.; Xia, J.; Ip, W. Models for extremes using the extended three-parameter Burr XII system with application to flood frequency analysis. Hydrol. Sci. J. 2004, 49, 685–702. [Google Scholar] [CrossRef]
- Chen, L.; Guo, S.L.; Yan, B.W.; Liu, P.; Fang, B. A new seasonal design flood method based on bivariate joint distribution of flood magnitude and date of occurrence. Hydrol. Sci. J. 2010, 55, 1264–1280. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Hao, Z.; Li, T. Flood coincidence risk analysis using multivariate copula functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Mielke, P.W., Jr.; Johnson, E.S. Some generalized beta distributions of the second kind having desirable application features in hydrology and meteorology. Water Resour. Res. 1974, 10, 223–226. [Google Scholar] [CrossRef]
- Wilks, D.S. Comparison of three-parameter probability distributions for representing annual extreme and partial duration precipitation series. Water Resour. Res. 1993, 29, 3543–3549. [Google Scholar] [CrossRef]
- Perreault, L.; Bobée, B.; Rasmussen, P. Halphen distribution system. I: Mathematical and statistical properties. J. Hydrol. Eng. 1999, 4, 189–199. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Based Parameter Estimation in Hydrology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation Hydrology; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Singh, V.P.; Guo, H. Parameter estimation for 3-parameter generalized Pareto distribution by the principle of maximum entropy (POME). Hydrol. Sci. J. 1995, 40, 165–181. [Google Scholar] [CrossRef]
- Karim, A.; Chowdhury, J.U. A comparison of four distributions used in flood frequency analysis in Bangladesh. Hydrol. Sci. J. 1995, 40, 55–66. [Google Scholar] [CrossRef]
- Natural Environment Research Council. Flood Studies Report; Natural Environment Research Council: London, UK, 1975; Volumes 1–5. [Google Scholar]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Ross, R. Graphical method for plotting and evaluating weibull distribution data. In Proceedings of the 4th International Conference on Properties and Application of Dielectric Materials, Brisbane, Austrialia, 3–8 July 1994; pp. 250–253. [Google Scholar]
- Cunnane, C. Unbiased plotting positions—A review. J. Hydrol. 1978, 37, 205–222. [Google Scholar] [CrossRef]
- Makkonen, L. Notes and correspondence plotting positions in extreme value analysis. J. Appl. Meteorol. Clim. 2006, 45, 334–340. [Google Scholar] [CrossRef]
- Shabri, A. A Comparison of plotting formulas for the pearson type III distribution. J. Technol. 2002, 36, 61–74. [Google Scholar] [CrossRef]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813–814. [Google Scholar] [CrossRef]
- Dagum, C. A New Model of Personal Income Distribution: Specification and Estimation. In Modeling Income Distributions and Lorenz Curves; Springer: New York, NY, USA, 2008; pp. 3–25. [Google Scholar]
- Mehdi, F.; Mehdi, J. Determination of plotting position formula for the normal, log-normal, pearson(III), log-pearson(III) and gumble distribution hypotheses using the probability plot correlation coefficient test. World Appl. Sci. J. 2011, 15, 1181–1185. [Google Scholar]
- Kim, S.; Shin, H.; Kim, T.; Taesoon, K.; Heo, J. Derivation of the probability plot correlation coefficient test statistics for the generalized logistic distribution. In Proceedings of the International Workshop Advances in Statistical Hydrology, Taormina, Italy, 23–25 May 2010; pp. 1–8. [Google Scholar]
- Singh, V.P.; Guo, H. Parameter estimation for 2-parameter log-logistic distribtuion distribution (LLD2) by maximum entropy. Civ. Eng. Syst. 1995, 12, 343–357. [Google Scholar] [CrossRef]
- Singh, V.P.; Guo, H. Parameter estimations for 2-parameter Pareto distribution by pome. Stoch. Hydrol. Hydraul. 1980, 9, 81–93. [Google Scholar]
- Burr, I.W. Cumulative Frequency Functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Singh, S.K.; Maddala, G.S. A function for size distribution of incomes. Econometrica 1976, 44, 963–970. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Entropy-based parameter estimation for extended Burr XII distribution. Stoch. Environ. Res. Risk Assess. 2008, 23, 1113–1122. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
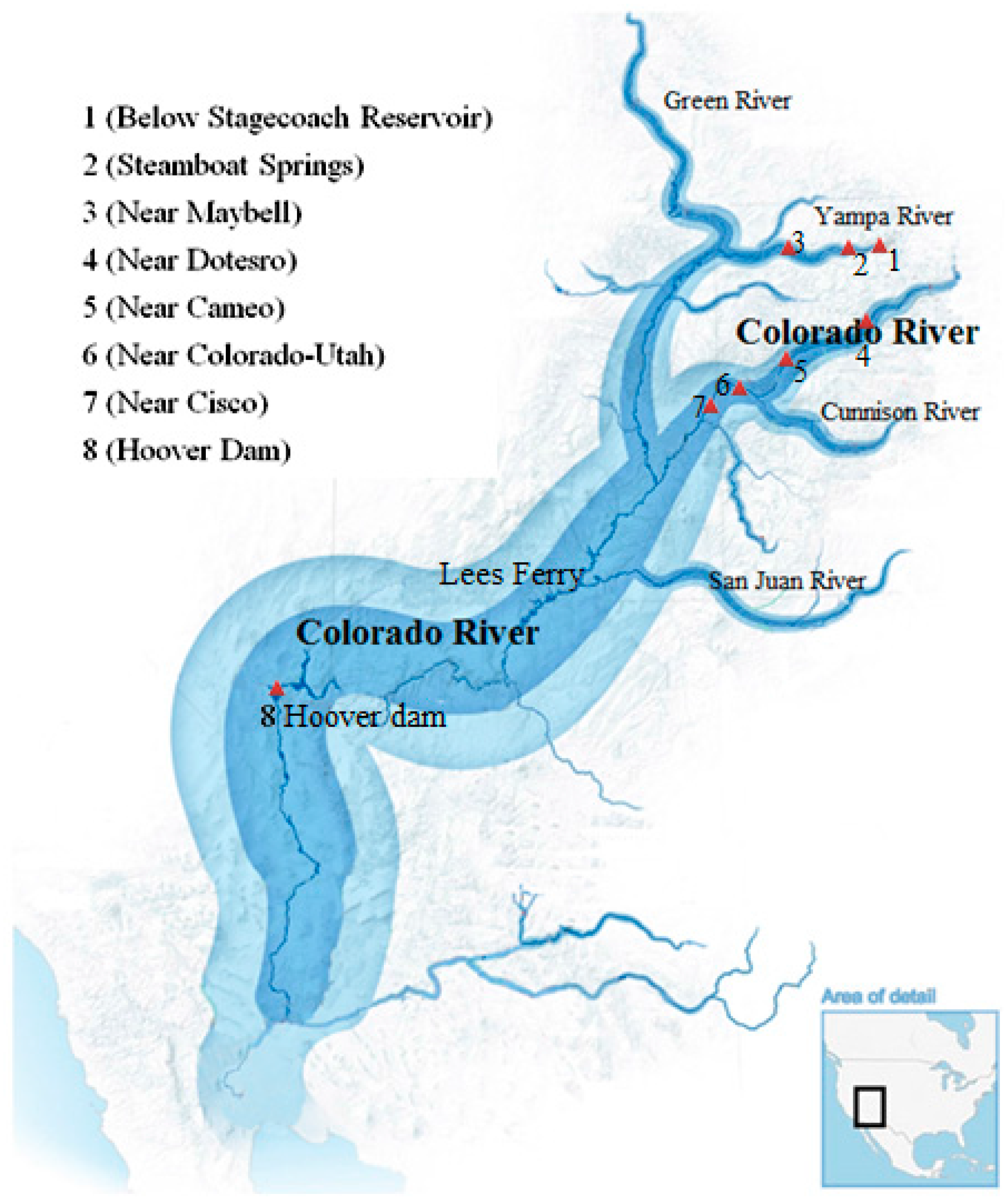
| River | No. | Gaging Station | Drainage Area (Square Miles) | Length of Data | Mean Value (ft3/s) | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| Yampa River | 1 | Below Stagecoach Reservoir | 228 | 1957–2014 | 315 | 189 | 0.91 | 3.49 |
| 2 | Steamboat Springs | 567 | 1904–2013 | 3630 | 1115 | 0.26 | 2.94 | |
| 3 | Near Maybell | 3383 | 1904–2013 | 10,419 | 3657 | 0.90 | 4.88 | |
| Colorado River | 4 | Near Dotsero | 4390 | 1941–2013 | 9870 | 4450 | 0.39 | 2.59 |
| 5 | Near Cameo | 7986 | 1934–2013 | 19,049 | 7687 | 0.26 | 2.68 | |
| 6 | Near Colorado-Utah | 17,847 | 1951–2013 | 26,714 | 13,936 | 0.84 | 3.53 | |
| 7 | Near Cisco | 24,100 | 1884–2013 | 34,329 | 16,520 | 0.36 | 2.31 | |
| 8 | Hoover Dam | 171,700 | 1934–2013 | 26,131 | 6831 | 1.37 | 5.83 |
| Number | Location | r1 | r2 | r3 | β |
|---|---|---|---|---|---|
| 4 | Near Dotsero | 1.58 | 60.30 | 1.75 | 85.11 |
| 5 | Near Cameo | 1.12 | 77.57 | 2.53 | 112.93 |
| 6 | Near Colorado-Utah | 3.94 | 83.08 | 0.94 | 69.05 |
| 7 | Near Cisco | 2.73 | 76.82 | 1.07 | 80.90 |
| 8 | Hoover Dam | 10.59 | 434.72 | 1.31 | 43.62 |
| Number | Distribution | Steamboat Springs | Near Cisco | Near Colorada-Utah | Hoover Dam | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-Value | RMSE | AIC | p-Value | RMSE | AIC | p-Value | RMSE | AIC | p-Value | RMSE | AIC | ||
| 1 | GB2 | 0.976 | 0.025 | 924.1 | 0.991 | 0.061 | 1384.1 | 1 | 0.047 | 852.7 | 1 | 0.036 | 1098.8 |
| 2 | Normal | 0.926 | 0.043 | 992.9 | 0.787 | 0.194 | 1502 | 0.839 | 0.221 | 1031 | 0.436 | 0.081 | 1236.2 |
| 3 | Exponential | 0.409 | 0.122 | 1306.8 | 0.336 | 0.171 | 1669.6 | 0.839 | 0.145 | 1036.4 | 0.919 | 0.055 | 1152.6 |
| 4 | Gamma | 1 | 0.045 | 1005.1 | 0.959 | 0.064 | 1512.8 | 1 | 0.047 | 842.5 | 0.692 | 0.057 | 1192.9 |
| 5 | Gumbel | 0.976 | 0.066 | 1143.5 | 0.959 | 0.088 | 1546.2 | 1 | 0.107 | 869.1 | 0.978 | 0.039 | 1122.3 |
| 6 | Generalized normal | 0.844 | 0.025 | 922.9 | 0.991 | 0.137 | 1455.5 | 1 | 0.083 | 852.8 | 0.978 | 0.039 | 1106.7 |
| 7 | Pearson type III | 0.976 | 0.035 | 953.2 | 0.991 | 0.1 | 1425 | 1 | 0.054 | 895.6 | 1 | 0.058 | 1146.8 |
| 8 | Log Pearson type III | 0.976 | 0.034 | 951.3 | 0.991 | 0.106 | 1431.5 | 1 | 0.054 | 893.1 | 1 | 0.052 | 1133 |
| 9 | Generalized Pareto | 0.976 | 0.078 | 1158 | 0.991 | 0.062 | 1386.1 | 1 | 0.09 | 960.2 | 1 | 0.054 | 1169 |
| 10 | GEV | 0.976 | 0.027 | 929.6 | 0.991 | 0.138 | 1450.1 | 1 | 0.128 | 865.5 | 1 | 0.036 | 1096.8 |
| Methods | r1 | r2 | r3 | β | p-Value | RMSE | AIC |
|---|---|---|---|---|---|---|---|
| POME | 2.14 | 24.78 | 1.40 | 157.18 | 1 | 0.0169 | −357.76 |
| ML | 2.26 | 30.85 | 1.35 | 158.55 | 1 | 0.0170 | −357.80 |
| Number | Return Period | 1000 | 500 | 100 | 50 | 10 |
|---|---|---|---|---|---|---|
| 1 | GB2 | 76.702 | 67.914 | 51.198 | 34.138 | 30.125 |
| 2 | Normal | 45.800 | 44.451 | 40.938 | 34.288 | 31.488 |
| 3 | Exponential | 68.561 | 63.583 | 52.024 | 35.486 | 30.508 |
| 4 | Gamma | 50.485 | 48.424 | 43.314 | 34.613 | 31.320 |
| 5 | Gumbel | 58.926 | 55.332 | 46.973 | 34.799 | 30.912 |
| 6 | Generalized normal | 50.513 | 49.271 | 45.325 | 35.732 | 31.485 |
| 7 | Pearson type III | 60.025 | 56.451 | 47.985 | 35.145 | 30.926 |
| 8 | Log Pearson type III | 69.568 | 64.494 | 52.713 | 35.639 | 31.858 |
| 9 | Generalized Pareto | 64.809 | 59.870 | 49.084 | 34.893 | 30.695 |
| 10 | GEV | 57.809 | 54.766 | 47.324 | 35.270 | 31.072 |
| Number | Locations | Drainage Area (Square Miles) | Increase in Drainage Area (%) | Increase in in Flood Value (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1000 | 500 | 100 | 50 | 10 | Mean | ||||
| 4 | Near Dotsero | 11370 | 45 | 40 | 41 | 42 | 47 | 46 | 43 |
| 5 | Near Cameo | 20683 | 55 | 50 | 48 | 44 | 32 | 35 | 42 |
| 6 | Near Colorado-Utah | 46228 | 26 | 11 | 12 | 15 | 22 | 20 | 16 |
| 7 | Near Cisco | 62419 | |||||||
| Number | Location | r1 | r2 | r3 | β |
|---|---|---|---|---|---|
| 1 | Below stagecoach Reservoir | 17.44 | 15.25 | 0.55 | 2.10 |
| 2 | Steamboat springs | 1.20 | 5.49 | 3.59 | 5.81 |
| 3 | Near Maybell | 1.14 | 2.07 | 3.92 | 12.11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Singh, V.P. Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis. Entropy 2017, 19, 254. https://doi.org/10.3390/e19060254
Chen L, Singh VP. Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis. Entropy. 2017; 19(6):254. https://doi.org/10.3390/e19060254
Chicago/Turabian StyleChen, Lu, and Vijay P. Singh. 2017. "Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis" Entropy 19, no. 6: 254. https://doi.org/10.3390/e19060254
APA StyleChen, L., & Singh, V. P. (2017). Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis. Entropy, 19(6), 254. https://doi.org/10.3390/e19060254






