Ruling out Higher-Order Interference from Purity Principles
Abstract
:1. Introduction
2. Framework
2.1. States, Transformations, and Effects
- as the set of states of system ,
- as the set of effects on ,
- as the set of transformations from to , and as the set of transformations from to ,
- (or , for short) as the sequential composition of two transformations and , with the input of matching the output of ,
- as the parallel composition (or tensor product) of the transformations and .
2.2. Tests and Channels
2.3. Pure Transformations
2.4. Causality
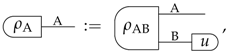
3. Higher-Order Interference
4. Sharp Theories with Purification
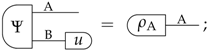
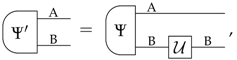
Properties of Sharp Theories With Purifications
5. Sharp Theories with Purification Have No Higher-Order Interference
5.1. Self-Duality
5.2. Existence of Pure Orthogonal Projectors
- ;
- ,
- if , then ;
- if , then .
- if
- if
5.3. Main Result
5.4. Jordan-Algebraic Structure
6. Discussion and Conclusions
Finding Higher Order Interference
- The transformations corresponding to blocking slits satisfy: . By this we mean that they share several properties with the projectors of Section 5: if we define the effects and the faces and as in Section 5.2, i.e., as the 1-set and 0-set of , then the are assumed to be orthogonal projectors in the sense of Definition 8, and to be both idempotent and “orthogonal” () if and are disjoint (as in Proposition 7).
- The ’s map pure states to pure states
- The ’s are self-adjoint.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Norms and Fidelity
Appendix A.1. Operational Norm and Dagger Norm
Appendix A.2. Dagger Fidelity
- ;
- if and only if ρ and σ are perfectly distinguishable;
- if and only if ;
- , for every reversible channel .
- Recall that , whence . Moreover, by Schwarz inequality, , so .
- Suppose and are perfectly distinguishable, then by Lemma A1 , implying . Now suppose ; then . Let be a diagonalisation of , with , for all , and . We have , which means that for . This means that we can build an observation-test that distinguishes and perfectly by taking , where .
- Clearly, if , , whence . Conversely, suppose . This means that . By Schwarz inequality, this is true if and only if , for some . Since both states are normalised, , yielding .
- This property follows by Proposition 4, because the inner product and the dagger norm are invariant under reversible channels.
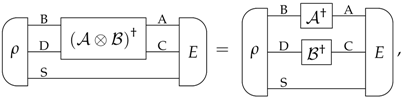
Appendix B. Dagger of All Transformations
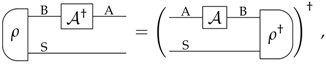
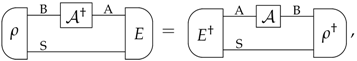
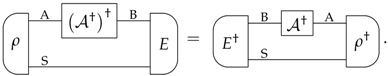
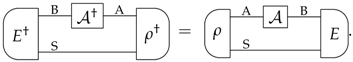
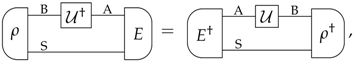
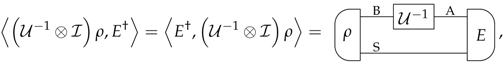
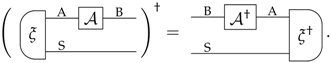



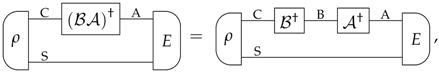

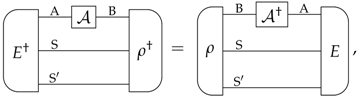




References
- Feynman, R.P.; Leighton, R.; Sands, M. The Feynman Lectures on Physics. The Definitive and Extended Edition; Addison Wesley: Boston, MA, USA, 2005. [Google Scholar]
- Sorkin, R.D. Quantum mechanics as quantum measure theory. Mod. Phys. Lett. A 1994, 9, 3119–3127. [Google Scholar] [CrossRef]
- Sorkin, R.D. Quantum Classical Correspondence: The 4th Drexel Symposium on Quantum Nonintegrability; Chapter Quantum Measure Theory and Its Interpretation; International Press: Boston, MA, USA, 1997; pp. 229–251. [Google Scholar]
- Barnum, H.; Müller, M.P.; Ududec, C. Higher-order interference and single-system postulates characterizing quantum theory. New J. Phys. 2014, 16, 123029. [Google Scholar] [CrossRef]
- Bolotin, A. On the ongoing experiments looking for higher-order interference: What are they really testing? arXiv 2016. [Google Scholar]
- Dakić, B.; Paterek, T.; Brukner, Č. Density cubes and higher-order interference theories. New J. Phys. 2014, 16, 023028. [Google Scholar] [CrossRef]
- Lee, C.M.; Selby, J.H. Deriving grover’s lower bound from simple physical principles. New J. Phys. 2016, 18, 093047. [Google Scholar] [CrossRef]
- Lee, C.M.; Selby, J.H. Generalised phase kick-back: The structure of computational algorithms from physical principles. New J. Phys. 2016, 18, 033023. [Google Scholar] [CrossRef]
- Lee, C.M.; Selby, J.H. Higher-order interference in extensions of quantum theory. Found. Phys. 2017, 47, 89–112. [Google Scholar] [CrossRef]
- Niestegge, G. Three-slit experiments and quantum nonlocality. Found. Phys. 2013, 43, 805–812. [Google Scholar] [CrossRef]
- Ududec, C. Perspectives on the Formalism of Quantum Theory. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2012. [Google Scholar]
- Ududec, C.; Barnum, H.; Emerson, J. Probabilistic Interference in Operational Models. 2009; in preparation. [Google Scholar]
- Ududec, C.; Barnum, H.; Emerson, J. Three slit experiments and the structure of quantum theory. Found. Phys. 2011, 41, 396–405. [Google Scholar] [CrossRef]
- Lee, C.M.; Selby, J.H. A no-go theorem for theories that decohere to quantum mechanics. arXiv 2017. [Google Scholar]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Generalized no-broadcasting theorem. Phys. Rev. Lett. 2007, 99, 240501. [Google Scholar] [CrossRef] [PubMed]
- Barnum, H.; Wilce, A. Information processing in convex operational theories. Electron. Notes Theor. Comput. Sci. 2011, 270, 3–15. [Google Scholar] [CrossRef]
- Barrett, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75, 032304. [Google Scholar] [CrossRef]
- Barrett, J.; de Beaudrap, N.; Hoban, M.J.; Lee, C.M. The computational landscape of general physical theories. arXiv 2017. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Probabilistic theories with purification. Phys. Rev. A 2010, 81, 062348. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Chiribella, G.; Spekkens, R.W. (Eds.) Quantum Theory: Informational Foundations and Foils; Fundamental Theories of Physics; Springer: Dordrecht, The Netherlands, 2016; Volume 181. [Google Scholar]
- Dakić, B.; Brukner, Č. Quantum Theory and Beyond: Is Entanglement Special; Cambridge University Press: Cambridge, UK, 2011; pp. 365–392. [Google Scholar]
- Hardy, L. Quantum Theory From Five Reasonable Axioms. arXiv 2001. [Google Scholar]
- Hardy, L. Foliable Operational Structures for General Probabilistic Theories; Cambridge University Press: Cambridge, UK, 2011; pp. 409–442. [Google Scholar]
- Lee, C.M.; Barrett, J. Computation in generalised probabilistic theories. New J. Phys. 2015, 17, 083001. [Google Scholar] [CrossRef]
- Lee, C.M.; Hoban, M.J. Bounds on the power of proofs and advice in general physical theories. Proc. R. Soc. A 2016, 472, 20160076. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.M.; Hoban, M.J. The information content of systems in general physical theories. In Proceedings of the 7th International Workshop on Physics and Computation, Manchester, UK, 14 July 2016; Volume 214, pp. 22–28. [Google Scholar]
- Masanes, L.; Müller, M.P. A derivation of quantum theory from physical requirements. New J. Phys. 2011, 13, 063001. [Google Scholar] [CrossRef]
- Hardy, L. Reformulating and reconstructing quantum theory. arXiv 2011. [Google Scholar]
- Chiribella, G.; Scandolo, C.M. Entanglement as an axiomatic foundation for statistical mechanics. arXiv 2016. [Google Scholar]
- Krumm, M.; Barnum, H.; Barrett, J.; Müller, M.P. Thermodynamics and the structure of quantum theory. New J. Phys. 2017, 19, 043025. [Google Scholar] [CrossRef]
- Jin, F.; Liu, Y.; Geng, J.; Huang, P.; Ma, W.; Shi, M.; Duan, C.; Shi, F.; Rong, X.; Du, J. Experimental test of born’s rule by inspecting third-order quantum interference on a single spin in solids. Phys. Rev. A 2017, 95, 012107. [Google Scholar] [CrossRef]
- Kauten, T.; Keil, R.; Kaufmann, T.; Pressl, B.; Brukner, Č.; Weihs, G. Obtaining tight bounds on higher-order interferences with a 5-path interferometer. New J. Phys. 2017, 19, 033017. [Google Scholar] [CrossRef]
- Park, D.K.; Moussa, O.; Laflamme, R. Three path interference using nuclear magnetic resonance: A test of the consistency of born’s rule. New J. Phys. 2012, 14, 113025. [Google Scholar] [CrossRef]
- Sinha, A.; Vijay, A.H.; Sinha, U. On the superposition principle in interference experiments. Sci. Rep. 2015, 5, 10304. [Google Scholar] [CrossRef] [PubMed]
- Sinha, U.; Couteau, C.; Jennewein, T.; Laflamme, R.; Weihs, G. Ruling out multi-order interference in quantum mechanics. Science 2010, 329, 418–421. [Google Scholar] [CrossRef] [PubMed]
- Barnum, H.; Graydon, M.; Wilce, A. Composites and categories of Euclidean Jordan algebras. arXiv 2016. [Google Scholar]
- Chiribella, G. Dilation of states and processes in operational-probabilistic theories. In Proceedings of the 11th workshop on Quantum Physics and Logic, Kyoto, Japan, 4–6 June 2014; Volume 172, pp. 1–14. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Quantum Theory: Informational Foundations and Foils; Chapter Quantum from Principles; Springer: Dordrecht, The Netherlands, 2016; pp. 171–221. [Google Scholar]
- Hardy, L. Quantum Theory: Informational Foundations and Foils; Chapter Reconstructing Quantum Theory; Springer: Dordrecht, The Netherlands, 2016; pp. 223–248. [Google Scholar]
- Abramsky, S.; Coecke, B. A categorical semantics of quantum protocols. In Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science, Turku, Finland, 13–17 July 2004; pp. 415–425. [Google Scholar]
- Coecke, B. Kindergarten quantum mechanics: Lecture notes. AIP Conf. Proc. 2006, 810, 81–98. [Google Scholar]
- Coecke, B. Quantum picturalism. Contemp. Phys. 2010, 51, 59. [Google Scholar] [CrossRef]
- Coecke, B.; Duncan, R.; Kissinger, A.; Wang, Q. Quantum Theory: Informational Foundations and Foils; Chapter Generalised Compositional Theories and Diagrammatic Reasoning; Springer: Dordrecht, The Netherlands, 2016; pp. 309–366. [Google Scholar]
- Coecke, B.; Kissinger, A. Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Selinger, P. A survey of graphical languages for monoidal categories. In New Structures for Physics; Coecke, B., Ed.; Springer: Berlin, Germany, 2011; pp. 289–356. [Google Scholar]
- Wootters, W.K. Local accessibility of quantum states. In Complexity, Entropy and the Physics of Information; Zurek, W.H., Ed.; Westview Press: Boulder, CO, USA, 1990; pp. 39–46. [Google Scholar]
- Chiribella, G.; Scandolo, C.M. Entanglement and thermodynamics in general probabilistic theories. New J. Phys. 2015, 17, 103027. [Google Scholar] [CrossRef]
- Chiribella, G.; Scandolo, C.M. Purity in microcanonical thermodynamics: A tale of three resource theories. arXiv 2016. [Google Scholar]
- Gour, G.; Müller, M.P.; Narasimhachar, V.; Spekkens, R.W.; Yunger Halpern, N. The resource theory of informational nonequilibrium in thermodynamics. Phys. Rep. 2015, 583, 1–58. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Oppenheim, J. Reversible transformations from pure to mixed states and the unique measure of information. Phys. Rev. A 2003, 67, 062104. [Google Scholar] [CrossRef]
- Selby, J.H.; Coecke, B. Leaks: Quantum, classical, intermediate, and more. Entropy 2017, 19, 174. [Google Scholar] [CrossRef]
- Coecke, B. Terminality implies non-signalling. In Proceedings of the 11th workshop on Quantum Physics and Logic, Kyoto, Japan, 4–6 June 2014; Volume 172, pp. 27–35. [Google Scholar]
- Chiribella, G.; Scandolo, C.M. Operational axioms for diagonalizing states. In Proceedings of the 12th International Workshop on Quantum Physics and Logic, Oxford, UK, 15–17 July 2015; Volume 195, pp. 96–115. [Google Scholar]
- Chiribella, G.; Scandolo, C.M. Conservation of information and the foundations of quantum mechanics. EPJ Web Conf. 2015, 95, 03003. [Google Scholar] [CrossRef]
- Disilvestro, L.; Markham, D. Quantum protocols within Spekkens’ toy model. Phys. Rev. A 2017, 95, 052324. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Manessi, F.; Perinotti, P.; Tosini, A. Fermionic computation is non-local tomographic and violates monogamy of entanglement. Europhys. Lett. 2014, 107, 20009. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Manessi, F.; Perinotti, P.; Tosini, A. The Feynman problem and fermionic entanglement: Fermionic theory versus qubit theory. Int. J. Mod. Phys. A 2014, 29, 1430025. [Google Scholar] [CrossRef]
- Chiribella, G.; Yuan, X. Bridging the gap between general probabilistic theories and the device-independent framework for nonlocality and contextuality. Inf. Comput. 2016, 250, 15–49. [Google Scholar] [CrossRef]
- Pfister, C.; Wehner, S. An information-theoretic principle implies that any discrete physical theory is classical. Nat. Commun. 2013, 4, 1851. [Google Scholar] [CrossRef] [PubMed]
- Alfsen, E.M.; Shultz, F.W. Geometry of State Spaces of Operator Algebras; Mathematics Theory & Applications; Birkhäuser: Basel, Switzerland, 2003. [Google Scholar]
- Barnum, H.; Barrett, J.; Krumm, M.; Müller, M.P. Entropy, majorization and thermodynamics in general probabilistic theories. In Proceedings of the 12th International Workshop on Quantum Physics and Logic, Oxford, UK, 15–17 July 2015; Volume 195, pp. 43–58. [Google Scholar]
- Chiribella, G.; Yuan, X. Measurement sharpness cuts nonlocality and contextuality in every physical theory. arXiv 2014. [Google Scholar]
- Alfsen, E.M.; Shultz, F.W. State spaces of Jordan algebras. Acta Math. 1978, 140, 155–190. [Google Scholar] [CrossRef]
- Iochum, B. Cônes Autopolaires et Algèbres de Jordan; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1358; Volume 1049, (In French). [Google Scholar] [CrossRef]
- Coecke, B.; Selby, J.; Tull, S. Two roads to classicality. arXiv 2017. [Google Scholar]
- Barnum, H. Spectrality as a Tool for Quantum Reconstruction: Higher-Order Interference, Jordan State Space Characterizations, Aug. 2009. Talk Given at the Conference “Reconstructing Quantum Theory”, August 9–11, Perimeter Institute for Theoretical Physics. Available online: http://pirsa.org/09080016/ (accessed on 26 May 2017).
- Niestegge, G. Conditional probability, three-slit experiments, and the jordan algebra structure of quantum mechanics. Adv. Math. Phys. 2012, 2012, 156573. [Google Scholar] [CrossRef]
- Selby, J.H.; Coecke, B. Process-theoretic characterisation of the hermitian adjoint. arXiv 2016. [Google Scholar]
- Müller, M.P.; Oppenheim, J.; Dahlsten, O.C.O. The black hole information problem beyond quantum theory. J. High Energy Phys. 2012, 2012, 9. [Google Scholar] [CrossRef]
- Müller, M.P.; Ududec, C. Structure of reversible computation determines the self-duality of quantum theory. Phys. Rev. Lett. 2012, 108, 130401. [Google Scholar] [CrossRef] [PubMed]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Springer Series in Statistics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Müller, M.P.; Dahlsten, O.C.O.; Vedral, V. Unifying typical entanglement and coin tossing: On randomization in probabilistic theories. Commun. Math. Phys. 2012, 316, 441–487. [Google Scholar] [CrossRef]
- Wilde, M.M. Quantum Information Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Selinger, P. Dagger compact closed categories and completely positive maps. Electron. Notes Theor. Comput. Sci. 2007, 170, 139–163. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barnum, H.; Lee, C.M.; Scandolo, C.M.; Selby, J.H. Ruling out Higher-Order Interference from Purity Principles. Entropy 2017, 19, 253. https://doi.org/10.3390/e19060253
Barnum H, Lee CM, Scandolo CM, Selby JH. Ruling out Higher-Order Interference from Purity Principles. Entropy. 2017; 19(6):253. https://doi.org/10.3390/e19060253
Chicago/Turabian StyleBarnum, Howard, Ciarán M. Lee, Carlo Maria Scandolo, and John H. Selby. 2017. "Ruling out Higher-Order Interference from Purity Principles" Entropy 19, no. 6: 253. https://doi.org/10.3390/e19060253
APA StyleBarnum, H., Lee, C. M., Scandolo, C. M., & Selby, J. H. (2017). Ruling out Higher-Order Interference from Purity Principles. Entropy, 19(6), 253. https://doi.org/10.3390/e19060253





