Glassy States of Aging Social Networks
Abstract
:1. Introduction
”Yesterdays’ friend (enemy) rarely become tomorrows’ enemy (friend).”
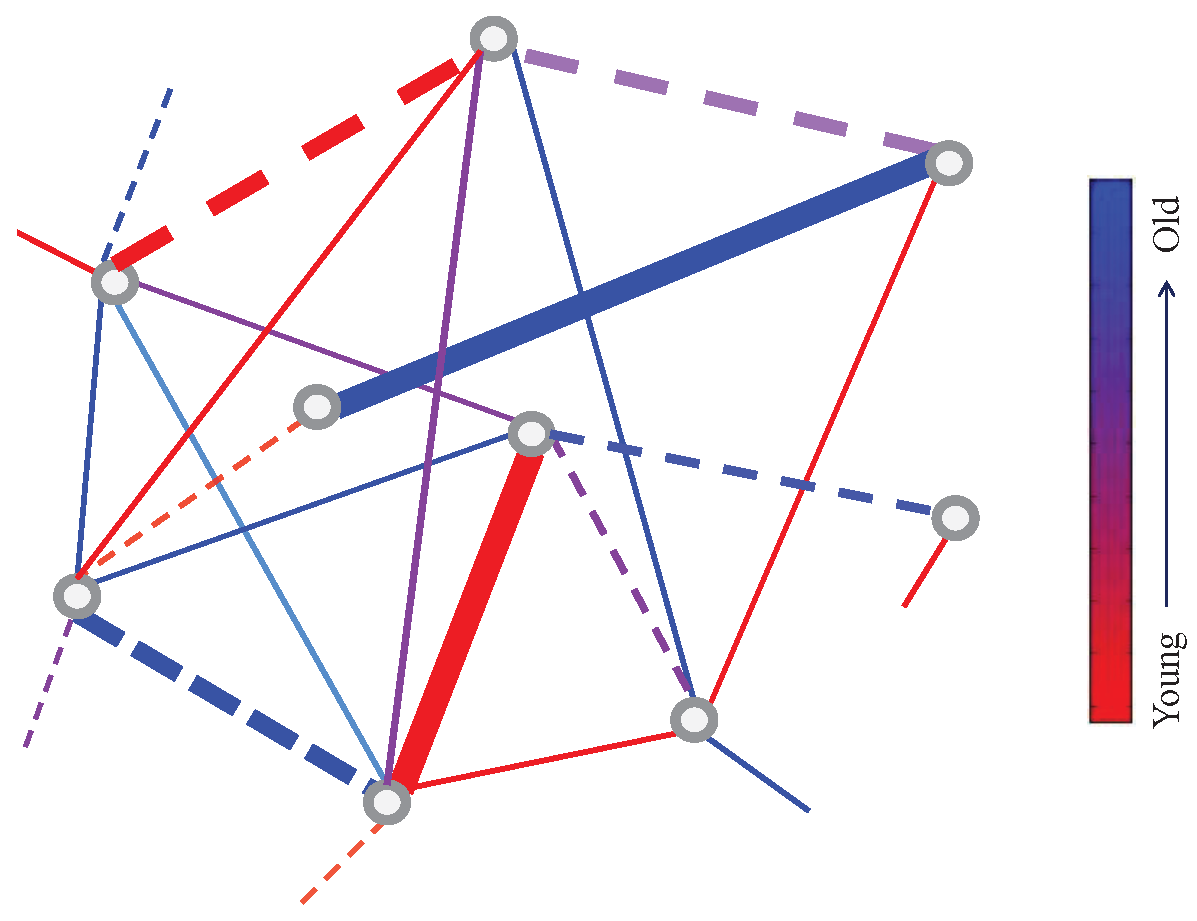
2. The Evolving Network
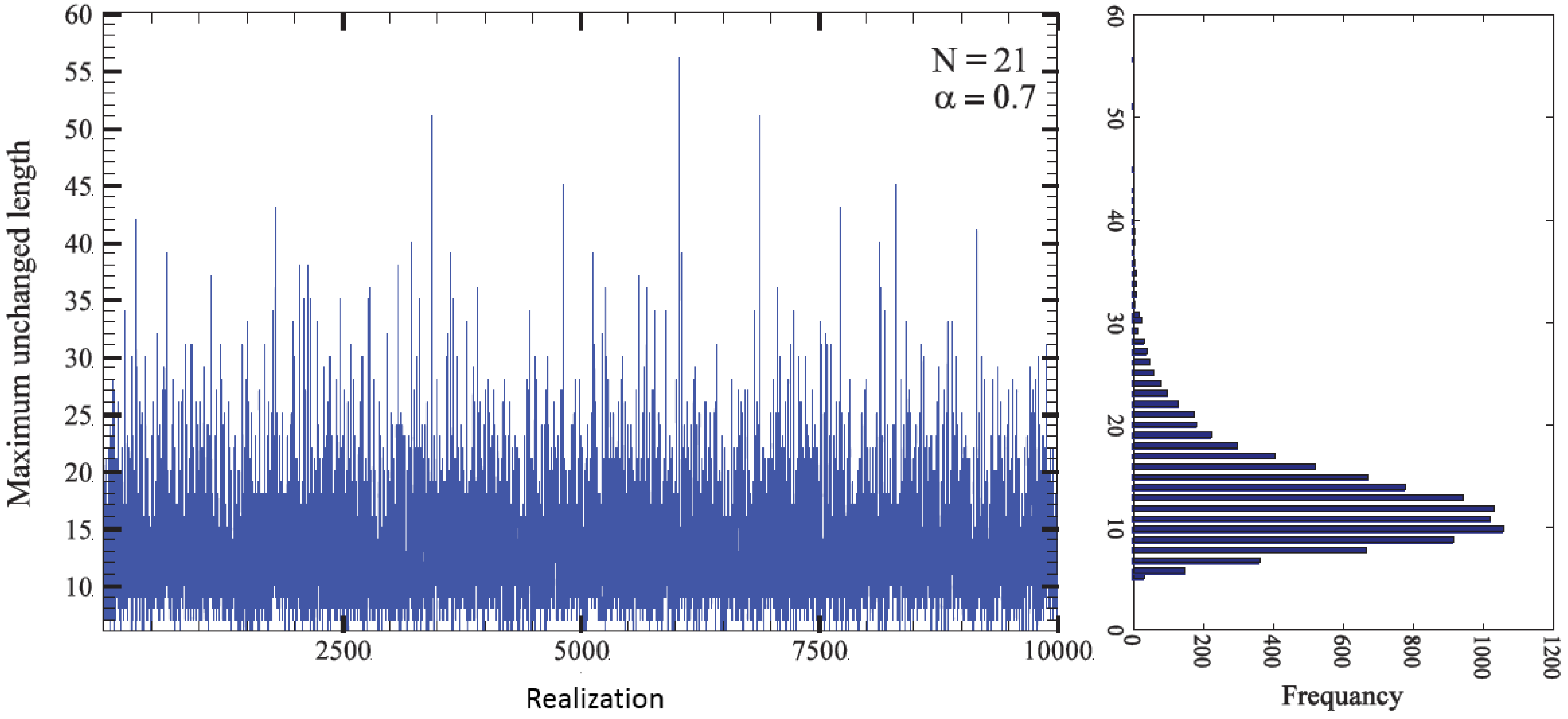
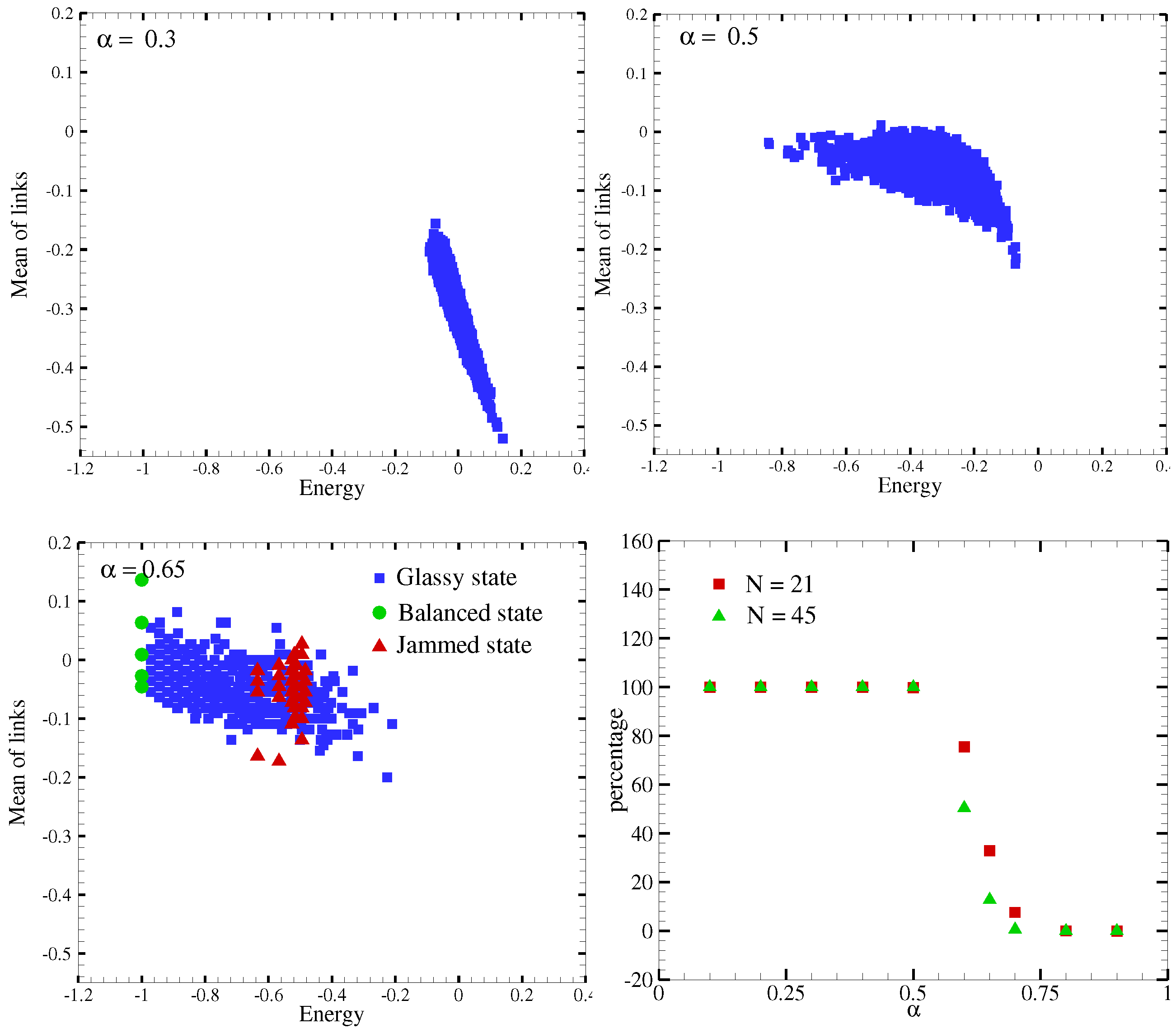
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heider, F. Attitudes and cognitive organization. J. Psychol. 1946, 21, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Szolnoki, A.; Perc, M. Self-organization towards optimally interdependent networks by means of coevolution. New J. Phys. 2014, 16, 033041. [Google Scholar] [CrossRef]
- Perca, M.; Szolnokib, A. Coevolutionary games—A mini review. BioSystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Kirman, A.; Markose, S.; Giansante, S.; Pin, P. Marginal contribution, reciprocity and equity in segregated groups: Bounded rationality and self-organization in social networks. J. Econ. Dyn. Control 2007, 31, 2085–2107. [Google Scholar] [CrossRef]
- Ramasco, J.J.; Dorogovtsev, S.N.; Pastor-Satorras, R. Self-organization of collaboration networks. Phys. Rev. E 2004, 70, 036106. [Google Scholar] [CrossRef] [PubMed]
- Becker, H.S. Notes on the concept of commitment. Am. J. Sociol. 1960, 66, 32–40. [Google Scholar] [CrossRef]
- Stanley, S.M.; Markman, H.J. Assessing commitment in personal relationships. J. Marriage Fam. 1992, 54, 595–608. [Google Scholar] [CrossRef]
- Clements, R.; Swensen, C.H. Commitment to one’s spouse as a predictor of marital quality among older couples. Curr. Psychol. 2000, 19, 110–119. [Google Scholar] [CrossRef]
- Granovetter, M. The strength of weak ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Stehlé, J.; Barrat, A.; Bianconi, G. Dynamical and bursty interactions in social networks. Phys. Rev. E 2010, 81, 035101–035104. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Stehlé, J.; Bianconi, G.; Barrat, A. Social network dynamics of face-to-face interactions. Phys. Rev. E 2011, 83, 056109–056127. [Google Scholar] [CrossRef] [PubMed]
- Karsai, M.; Kaski, K.; Kertész, J. Correlated Dynamics in Egocentric Communication Networks. PLoS ONE 2012, 7, e40612. [Google Scholar] [CrossRef] [PubMed]
- Rybski, D.; Buldyrev, S.; Havlin, S.; Liljeros, F.; Makse, H. Communication Activity in a Social Network: Relation Between Long-Term Correlations and Inter-Event Clustering; Scientific Reports; Nature Publishing Group: London, UK, 2012; Volume 2, p. 560. [Google Scholar]
- Shirazi, A.H.; Namaki, A.; Roohi, A.A.; Jafari, G.R. Transparency effect in emergence of monopolies in social networks. J. Artif. Soc. Soc. Simul. 2013, 6, 1–10. [Google Scholar] [CrossRef]
- Karsai, M.; Kaski, K.; Barabási, A.; Kertész, J. Universal Features of Correlated Bursty Behavior; Scientific Reports; Nature Publishing Group: London, UK, 2012; Volume 2, p. 397. [Google Scholar]
- Vestergaard, C.; Génois, M.; Barrat, A. How memory generates heterogeneous dynamics in temporal networks. Phys. Rev. Lett. 2014, 90, 042805. [Google Scholar] [CrossRef] [PubMed]
- Karsai, M.; Perra, N.; Vespignani, A. Time Varying Networks and the Weakness of Strong Ties; Scientific Reports; Nature Publishing Group: London, UK, 2014; Volume 4, pp. 4001–4007. [Google Scholar]
- Saeedian, M.; Khaliqi, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef] [PubMed]
- Dezso, Z.; Almaas, E.; Lukacs, A.; Racz, B.; Szakadat, I.; Barabási, A. Dynamics of information access on the web. Phys. Rev. E 2008, 73, 066132–066137. [Google Scholar] [CrossRef] [PubMed]
- Ebadi, E.; Saeedian, M.; Ausloos, M.; Jafari, G.R. Effect of memory in non-Markovian Boolean networks illustrated with a case study: A cell cycling process. EPL 2016, 116, 30004. [Google Scholar] [CrossRef]
- Lipowski, A.; Gontarek, K.; Ausloos, M. Statistical mechanics approach to a reinforcement learning model with memory. Physica A 2009, 388, 1849–1856. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M.; Szabó, G.; Stark, H.-U. Impact of aging on the evolution of cooperation in the spatial prisoner’s dilemma game. Phys. Rev. E 2009, 80, 021901. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, F.; Parravano, A. Tolerating the Intolerant: Homophily, Intolerance, and Segregation in Social Balanced Networks. J. Confl. Resolut. 2013, 59, 29–50. [Google Scholar] [CrossRef]
- Van de Rijt, A. The Micro-Macro Link for the Theory of Structural Balance. J. Math. Sociol. 2011, 35, 94–113. [Google Scholar] [CrossRef]
- Summers, T.H.; Shames, I. Active influence in dynamical models of structural balance in social networks. Europhys. Lett. 2013, 103, 18001. [Google Scholar] [CrossRef]
- Hassanibesheli, F.; Hedayatifar, L.; Gawroński, P.; Stojkow, M.; Żuchowska-Skiba, D.; Kulakowski, K. Gain and loss of esteem, direct reciprocity and Heider balance. Physica A 2017, 468, 334–339. [Google Scholar] [CrossRef]
- Moore, M. An international application of Heider’s balance theory. Eur. J. Soc. Psychol. 1978, 8, 401–405. [Google Scholar] [CrossRef]
- Esmailian, P.; Abtahi, S.E.; Jalili, M. Mesoscopic analysis of online social networks: The role of negative ties. Phys. Rev. E 2014, 90, 042817. [Google Scholar] [CrossRef] [PubMed]
- Szell, M.; Lambiotte, R.; Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 2010, 107, 13636–13641. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Zeng, D.; Wang, F.Y. Social balance in signed networks. Inf. Syst. Front. 2014, 17, 1–19. [Google Scholar] [CrossRef]
- Kunegis, J.; Lommatzsch, A.; Bauckhage, C. The slashdot zoo: Mining a social network with negative edges. In Proceedings of the 18th International Conference on World Wide Web—WWW 2009, Madrid, Spain, 20–24 April 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 741–750. [Google Scholar]
- Doreian, P. Evolution of Human Signed Networks. Metodol. Zv. 2004, 1, 277–293. [Google Scholar]
- Guha, R.V.; Kumar, R.; Raghavan, P.; Tomkins, A. Propagation of trust and distrust. In Proceedings of the 13th International Conference on World Wide Web, New York, NY, USA, 17–20 May 2004. [Google Scholar]
- Marvel, S.A.; Kleinberg, J.; Strogatz, S.H. The energy landscape of social balance. Phys. Rev. Lett. 2009, 103, 198701. [Google Scholar] [CrossRef] [PubMed]
- Antal, T.; Krapivsky, P.; Redner, S. Social balance on networks: The dynamics of friendship and enmity. Physica D 2006, 224, 130–136. [Google Scholar] [CrossRef]
- Hedayatifar, L.; Hassanibesheli, F.; Shirazi, A.H.; Vasheghani Farahani, S.; Jafari, G.R. Pseudo paths toward minimum energy states in network dynamics. Physica A 2017. [Google Scholar] [CrossRef]
- Safdari, H.; Chechkin, A.V.; Jafari, G.R.; Metzler, R. Aging Scaled Brownian Motion. Phys. Rev. E 2015, 91, 042107. [Google Scholar] [CrossRef] [PubMed]
- Gallos, L.K.; Rybski, D.; Liljeros, F.; Havlin, S.; Makse, H.A. How People Interact in Evolving Online Affiliation Networks. Phys. Rev. X 2012, 2, 031014. [Google Scholar] [CrossRef]
- Livina, V.; Havlin, S.; Bunde, A. Memory in the Occurrence of Earthquakes. Phys. Rev. Lett. 2005, 95, 208501. [Google Scholar] [CrossRef] [PubMed]
- Kemuriyama, T.; Ohta, H.; Sato, Y.; Maruyama, S.; Tandai-Hiruma, M. A power-law distribution of inter-spike intervals in renal sympathetic nerve activity in salt-sensitive hypertension-induced chronic heart failure. Biosystems 2010, 101, 144–147. [Google Scholar] [CrossRef] [PubMed]
- Siwy, Z.; Ausloos, M.; Ivanova, K. Correlation studies of open and closed states fluctuations in an ion channel: Analysis of ion current through a large-conductance locust potassium channel. Phys. Rev. E 2002, 65, 031907. [Google Scholar] [CrossRef] [PubMed]
- Kułakowski, K. Some recent attempts to simulate the Heider balance problem. Comput. Sci. Eng. 2007, 9, 80–85. [Google Scholar] [CrossRef]
- Kułakowski, K.; Gawronski, P.; Gronek, P. The Heider balance-a continuous approach. Int. J. Mod. Phys. C 2005, 16, 707–716. [Google Scholar] [CrossRef]
- Marvel, S.A.; Kleinberg, J.; Kleinberg, R.D.; Strogatz, S.H. Continuous-time model of structural balance. Proc. Natl. Acad. Sci. USA 2011, 108, 1771–1776. [Google Scholar] [CrossRef] [PubMed]
- Altafini, C. Dynamics of Opinion Forming in Structurally Balanced Social Networks. PLoS ONE 2012, 7, e38135. [Google Scholar] [CrossRef] [PubMed]
- Ausloos, M.; Petroni, F. Threshold Model for Triggered Avalanches on Networks; Stock Markets, F., Prattico, P.F., D’Amico, G., Eds.; Nova Scotia: New York, NY, USA, 2013; pp. 83–101. [Google Scholar]
- Sousa, A.O.; Yu-Song, T.; Ausloos, M. Propaganda spreading or running away from frustration effects in Sznajd model. Eur. Phys. J. B 2008, 66, 115–124. [Google Scholar] [CrossRef]
- Newcomb, T.M.; Turner, R.H.; Converse, P.E. Social Psychology: The Study of Human Interaction; Holt, Rinehart and Winston: New York, NY, USA, 1965. [Google Scholar]
- Cartwright, D.; Harary, F. Structure balance: A generalization of Heider’s theory. Psychol. Rev. 1956, 63, 277–293. [Google Scholar] [CrossRef] [PubMed]
- Saeedian, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Kertesz, J. Epidemic spreading on evolving signed networks. Phys. Rev. E 2017, 95, 022314. [Google Scholar] [CrossRef] [PubMed]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
- Horvath, S. Weighted Network Analysis. Applications in Genomics and Systems Biology; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gligor, M.; Ausloos, M. Clusters in weighted macroeconomic networks: The EU case. Introducing the overlapping index of GDP/capita fluctuation correlations. Eur. Phys. J. B 2008, 63, 533–539. [Google Scholar] [CrossRef]
- Goychuk, I. Viscoelastic subdiffusion: From anomalous to normal. Phys. Rev. E 2009, 80, 046125. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.H.; Metzler, R. Fractional Brownian motion and motion governed by the fractional Langevin equation in confined geometries. Phys. Rev. E 2010, 81, 021103. [Google Scholar] [CrossRef] [PubMed]
- West, B.J.; Turalska, M.; Grigolini, P. Fractional calculus ties the microscopic and macroscopic scales of complex network dynamics. New J. Phys. 2015, 17, 045009. [Google Scholar] [CrossRef]
- Safdari, H.; Kamali, M.Z.; Shirazi, A.H.; Khaliqi, M.; Jafari, G.R.; Ausloos, M. Fractional Dynamics of Network Growth Constrained by Aging Node Interactions. PLoS ONE 2016, 11, e0154983. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Garrappa, R. On linear stability of predictor-corrector algorithms for fractional differential equations. Int. J. Comput. Math. 2010, 87, 2281–2290. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen; Heinzel, S., Plesser, T., Eds.; Gessellschaft für Wissenschaftliche Datenverarbeitung: Göttingen, Germany, 1998; pp. 57–71. [Google Scholar]
- Lubich, C. A stability analysis of convolution quadratures for Abel-Volterra integral equations. IMA J. Numer. Anal. 1986, 6, 87–101. [Google Scholar] [CrossRef]
- Traag, V.; Van Dooren, P.; De Leenheer, P. Dynamical Models Explaining Social Balance and Evolution of Cooperation. PLoS ONE 2013, 8, e60063. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, M.J.; Castillo-Mussot, M.; Hernández-Ramírez, E.; Naumis, G.G.; Kułakowski, K. Heider balance, asymmetric ties, and gender segregation. Physica A 2015, 439, 66–74. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanibesheli, F.; Hedayatifar, L.; Safdari, H.; Ausloos, M.; Jafari, G.R. Glassy States of Aging Social Networks. Entropy 2017, 19, 246. https://doi.org/10.3390/e19060246
Hassanibesheli F, Hedayatifar L, Safdari H, Ausloos M, Jafari GR. Glassy States of Aging Social Networks. Entropy. 2017; 19(6):246. https://doi.org/10.3390/e19060246
Chicago/Turabian StyleHassanibesheli, Foroogh, Leila Hedayatifar, Hadise Safdari, Marcel Ausloos, and G. Reza Jafari. 2017. "Glassy States of Aging Social Networks" Entropy 19, no. 6: 246. https://doi.org/10.3390/e19060246
APA StyleHassanibesheli, F., Hedayatifar, L., Safdari, H., Ausloos, M., & Jafari, G. R. (2017). Glassy States of Aging Social Networks. Entropy, 19(6), 246. https://doi.org/10.3390/e19060246





