A Study of the Transfer Entropy Networks on Industrial Electricity Consumption
Abstract
:1. Introduction
2. Methodology Statement
2.1. Transfer Entropy
2.2. Symbolization
2.3. Minimum Spanning Tree
3. Data Description
4. Empirical Results on Transfer Entropy Networks
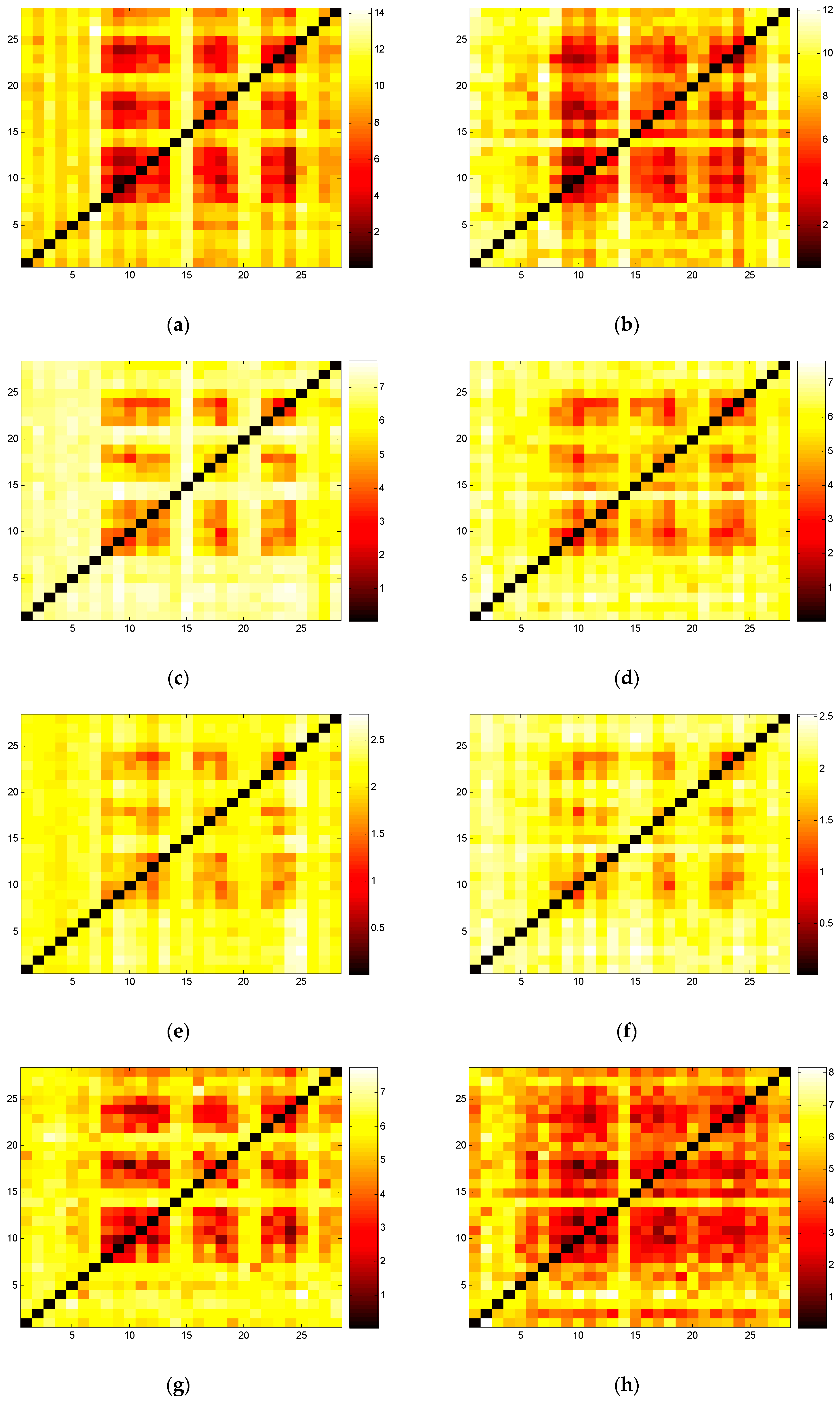
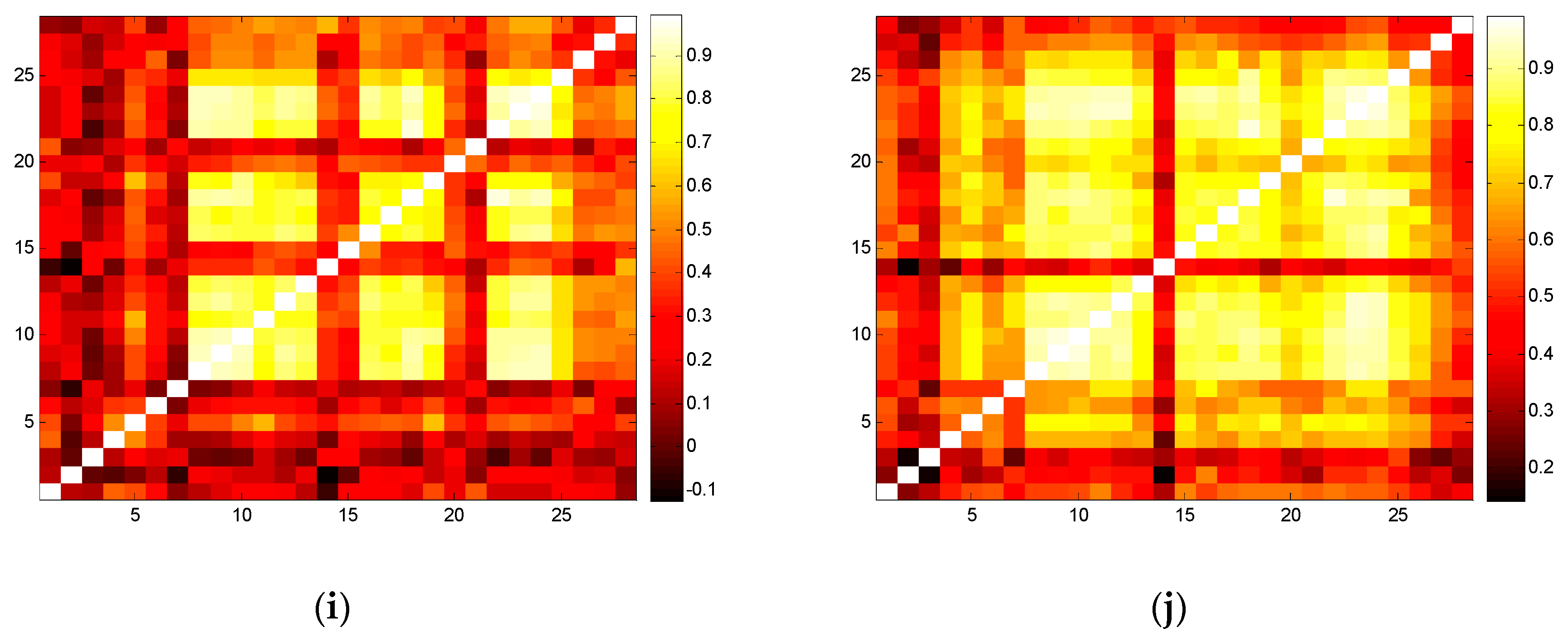
4.1. Industrial Analysis
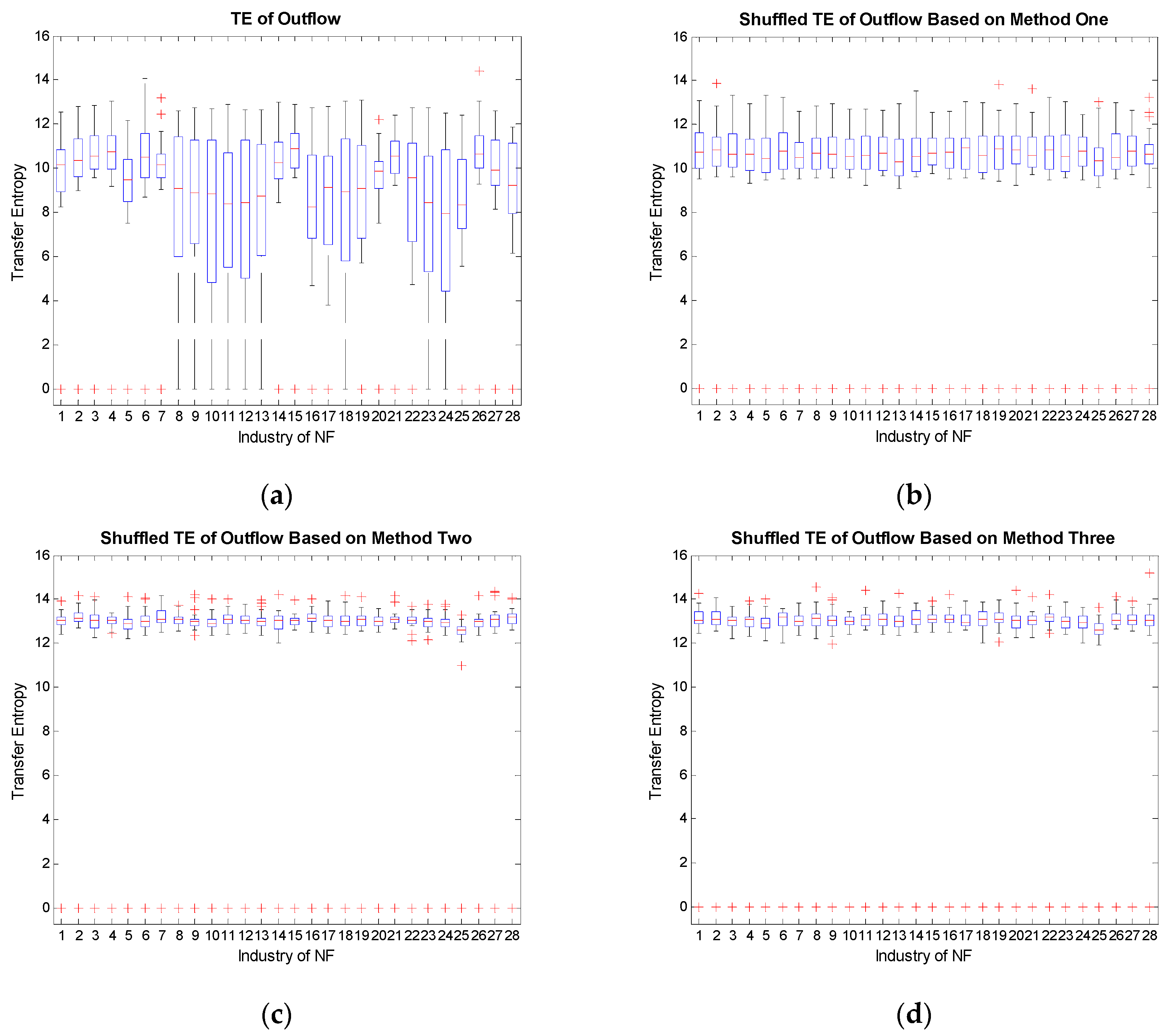
4.2. Reshuffled Analysis
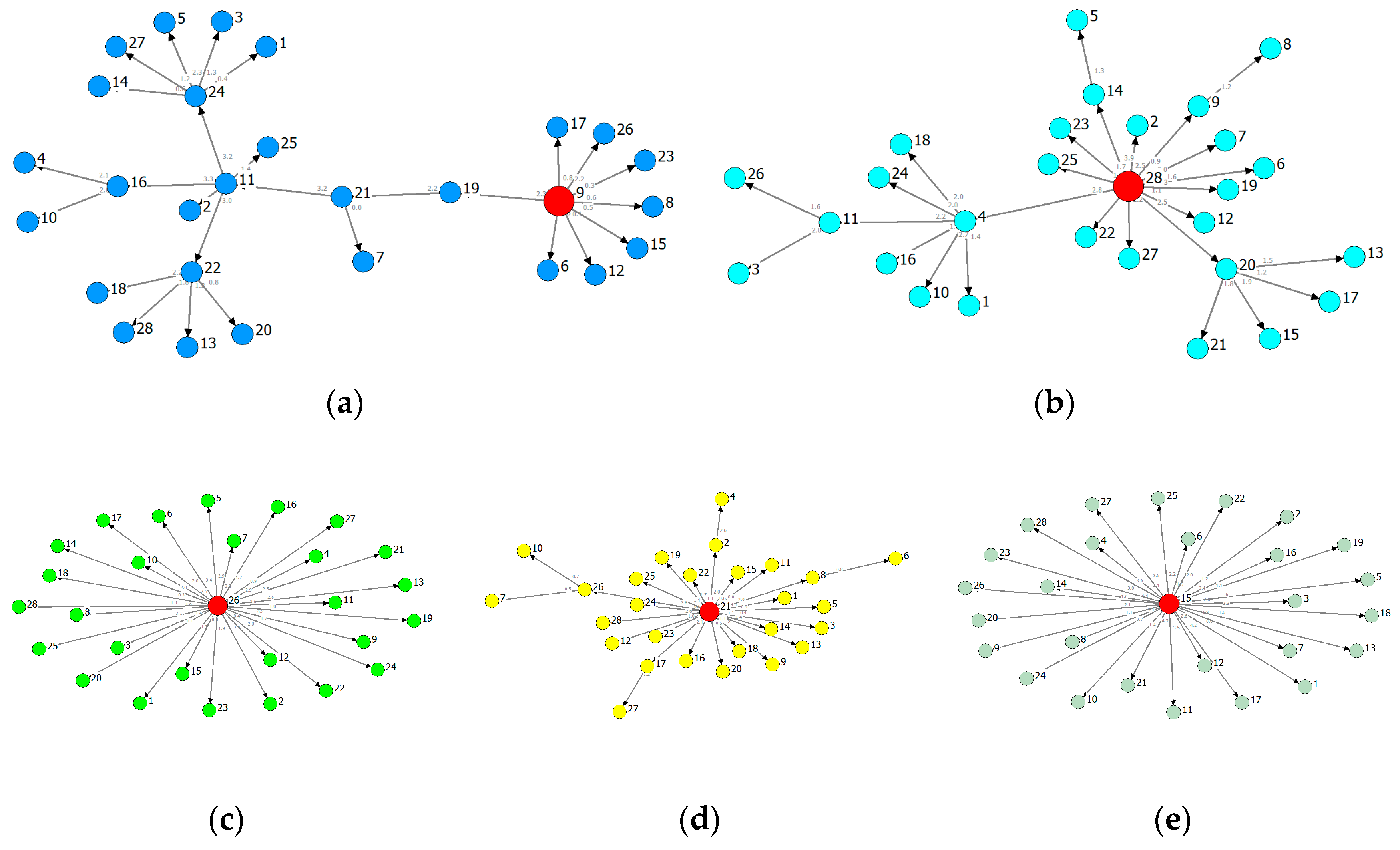
5. Route Extraction of the Causality Structure and Dynamics
5.1. Analysis of a Single Province
5.2. Inter-Provincial Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Miśkiewicz, J.; Ausloos, M. Influence of Information Flow in the Formation of Economic Cycles. Underst. Complex. Syst. 2006, 9, 223–238. [Google Scholar]
- Zhang, Q.; Liu, Z. Coordination of Supply Chain Systems: From the Perspective of Information Flow. In Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar]
- Eom, C.; Kwon, O.; Jung, W.S.; Kim, S. The effect of a market factor on information flow between stocks using the minimal spanning tree. Phys. A Stat. Mech. Appl. 2009, 389, 1643–1652. [Google Scholar] [CrossRef]
- Shi, W.; Shang, P. Cross-sample entropy statistic as a measure of synchronism and cross-correlation of stock markets. Nonlinear Dyn. 2012, 71, 539–554. [Google Scholar] [CrossRef]
- Gao, F.J.; Guo, Z.X.; Wei, X.G. The Spatial Autocorrelation Analysis on the Regional Divergence of Economic Growth in Guangdong Province. Geomat. World 2010, 4, 29–34. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Song, H.L.; Zhang, Y.; Li, C.L.; Wang, C.P. Analysis and evaluation of structural complexity of circular economy system’s industrial chain. J. Coal Sci. Eng. 2013, 19, 427–432. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 4652–4657. [Google Scholar] [CrossRef] [PubMed]
- Amblard, P.O.; Michel, O.J.J. The Relation between Granger Causality and Directed Information Theory: A Review. Entropy 2012, 15, 113–143. [Google Scholar] [CrossRef]
- Liu, L.; Hu, H.; Deng, Y.; Ding, N.D. An Entropy Measure of Non-Stationary Processes. Entropy 2014, 16, 1493–1500. [Google Scholar] [CrossRef]
- Liang, X.S. The Liang-Kleeman Information Flow: Theory and Applications. Entropy 2013, 1, 327–360. [Google Scholar] [CrossRef]
- Prokopenko, M.; Lizier, J.T.; Price, D.C. On Thermodynamic Interpretation of Transfer Entropy. Entropy 2013, 15, 524–543. [Google Scholar] [CrossRef]
- Materassi, M.; Consolini, G.; Smith, N.; de Marco, R. Information Theory Analysis of Cascading Process in a Synthetic Model of Fluid Turbulence. Entropy 2014, 16, 1272–1286. [Google Scholar] [CrossRef]
- Steeg, G.V.; Galstyan, A. Information transfer in social media. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012. [Google Scholar]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Shew, W.L.; Yang, H.; Yu, S.; Roy, R. Information Capacity and Transmission are Maximized in Balanced Cortical Networks with Neuronal Avalanches. J. Neurosci. 2011, 31, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Compensated Transfer Entropy as a Tool for Reliably Estimating Information Transfer in Physiological Time Series. Entropy 2013, 15, 198–219. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Mahoney, J.R. Moving Frames of Reference, Relativity and Invariance in Transfer Entropy and Information Dynamics. Entropy 2013, 15, 177–197. [Google Scholar] [CrossRef]
- Lizier, J.T.; Heinzle, J.; Horstmann, A.; Haynes, J.D. Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. J. Comput. Neurosci. 2011, 30, 85–107. [Google Scholar] [CrossRef] [PubMed]
- Lam, L.; Mcbride, J.W.; Swingler, J. Renyi’s information transfer between financial time series. Phys. A Stat. Mech. Appl. 2011, 391, 2971–2989. [Google Scholar]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Dimpfl, T.; Peter, F.J. The impact of the financial crisis on transatlantic information flows: An intraday analysis. J. Int. Financ. Mark. Inst. Money 2014, 31, 1–13. [Google Scholar] [CrossRef]
- Melzer, A.; Schella, A. Symbolic transfer entropy analysis of the dust interaction in the presence of wakefields in dusty plasmas. Phys. Rev. E 2014, 89, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Lobier, M.; Siebenhühner, F.; Palva, S.; Palva, J.M. Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions. Neuroimage 2014, 85, 853–872. [Google Scholar] [CrossRef] [PubMed]
- Daugherty, M.S.; Jithendranathan, T. A study of linkages between frontier markets and the U.S. equity markets using multivariate GARCH and transfer entropy. J. Multinatl. Financ. Manag. 2015, 32, 95–115. [Google Scholar] [CrossRef]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Kwon, O.; Yang, J.S. Information flow between stock indices. Europhys. Lett. 2008, 82, 68003. [Google Scholar] [CrossRef]
- Kwon, O.; Oh, G. Asymmetric information flow between market index and individual stocks in several stock markets. Europhys. Lett. 2012, 97, 28007–28012. [Google Scholar] [CrossRef]
- Sandoval, L. Structure of a Global Network of Financial Companies Based on Transfer Entropy. Entropy 2014, 16, 110–116. [Google Scholar] [CrossRef]
- Bekiros, S.; Nguyen, D.K.; Junior, L.S.; Uddin, G.S. Information diffusion, cluster formation and entropy-based network dynamics in equity and commodity markets. Eur. J. Oper. Res. 2017, 256, 945–961. [Google Scholar] [CrossRef]
- Harré, M. Entropy and Transfer Entropy: The Dow Jones and the Build Up to the 1997 Asian Crisis. In Proceedings of the International Conference on Social Modeling and Simulation, plus Econophysics Colloquium 2014; Springer: Zurich, Switzerland, 2015. [Google Scholar]
- Oh, G.; Oh, T.; Kim, H.; Kwon, O. An information flow among industry sectors in the Korean stock market. J. Korean Phys. Soc. 2014, 65, 2140–2146. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, H. Complex network-based time series analysis. Phys. A Stat. Mech. Appl. 2008, 387, 1381–1386. [Google Scholar] [CrossRef]
- Trancoso, T. Emerging markets in the global economic network: Real(ly) decoupling? Phys. A Stat. Mech. Appl. 2014, 395, 499–510. [Google Scholar] [CrossRef]
- Zheng, Z.; Yamasaki, K.; Tenenbaum, J.N.; Stanley, H.E. Carbon-dioxide emissions trading and hierarchical structure in worldwide finance and commodities markets. Phys. Rev. E 2012, 87, 417–433. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Podobnik, B.; Kenett, D.Y.; Stanley, H.E. Systemic risk and causality dynamics of the world international shipping market. Phys. A Stat. Mech. Appl. 2014, 415, 43–53. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L. Rejoinder: Brownian distance covariance. Ann. Appl. Stat. 2010, 3, 1303–1308. [Google Scholar] [CrossRef]
- Yao, C.Z.; Lin, J.N.; Liu, X.F. A study of hierarchical structure on South China industrial electricity-consumption correlation. Phys. A Stat. Mech. Appl. 2016, 444, 129–145. [Google Scholar] [CrossRef]
- Yao, C.Z.; Lin, Q.W.; Lin, J.N. A study of industrial electricity consumption based on partial Granger causality network. Phys. A Stat. Mech. Appl. 2016, 461, 629–646. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Olivares, S.; Paris, M.G.A. Quantum estimation via the minimum Kullback entropy principle. Phys. Rev. A 2007, 76, 538. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. Using Transfer Entropy to Measure Information Flows Between Financial Markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102. [Google Scholar] [CrossRef]
- Teng, Y.; Shang, P. Transfer entropy coefficient: Quantifying level of information flow between financial time series. Phys. A Stat. Mech. Appl. 2016, 469, 60–70. [Google Scholar] [CrossRef]
- Nichols, J.M.; Seaver, M.; Trickey, S.T.; Todd, M.D.; Olson, C. Detecting nonlinearity in structural systems using the transfer entropy. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 046217. [Google Scholar] [CrossRef] [PubMed]
- Boba, P.; Bollmann, D.; Schoepe, D.; Wester, N. Efficient computation and statistical assessment of transfer entropy. Front. Phys. 2015, 3, 267–278. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, 3136–3140. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Xie, L.; Chu, J. Measuring causality by taking the directional symbolic mutual information approach. Chin. Phys. B 2013, 22, 556–560. [Google Scholar] [CrossRef]
- Onnela, J.P.; Chakraborti, A.; Kaski, K.; Kertesz, J. Dynamic Asset Trees and Black Monday. Phys. A Stat. Mech. Appl. 2002, 324, 247–252. [Google Scholar] [CrossRef]
- Chu, Y.J.; Liu, T.H. On the Shortest Arborescence of a Directed Graph. Sci. Sin. 1965, 14, 1396–1400. [Google Scholar]
- Edmonds, J. Optimum branchings. J. Res. Natl. Bur. Stand. B 1967, 71, 233–240. [Google Scholar] [CrossRef]
- Yao, C.Z.; Lin, J.N.; Lin, Q.W.; Zheng, X.Z.; Liu, X.F. A study of causality structure and dynamics in industrial electricity consumption based on Granger network. Phys. A Stat. Mech. Appl. 2016, 462, 297–320. [Google Scholar] [CrossRef]
- Sensoy, A.; Sobaci, C.; Sensoy, S.; Alali, F. Effective transfer entropy approach to information flow between exchange rates and stock markets. Chaos Solitons Fractals 2014, 68, 180–185. [Google Scholar] [CrossRef]






| Code | Industry |
|---|---|
| V1 | Mining and Washing of Coal |
| V2 | Extraction of Petroleum and Natural Gas |
| V3 | Mining and Dressing of Ferrous Metal Ores |
| V4 | Mining and Dressing of Nonferrous Metal Ores |
| V5 | Mining and Dressing of Nonmetal Ores |
| V6 | Mining and Dressing of Other Ores |
| V7 | Manufacture of Food, Beverage, and Tobacco |
| V8 | Textile Industry |
| V9 | Manufacture of Textile Garments, Fur, Feather, and Related Products |
| V10 | Timber Processing, Products, and Manufacture of Furniture |
| V11 | Papermaking and Paper Products |
| V12 | Printing and Record Medium Reproduction |
| V13 | Manufacture of Cultural, Educational, Sports, and Entertainment Articles |
| V14 | Petroleum Refining, Coking, and Nuclear Fuel Processing |
| V15 | Manufacture of Raw Chemical Materials and Chemical Products |
| V16 | Manufacture of Medicines |
| V17 | Manufacture of Chemical Fibers |
| V18 | Rubber and Plastic Products |
| V19 | Nonmetal Mineral Products |
| V20 | Smelting and Pressing of Ferrous Metals |
| V21 | Smelting and Pressing of Nonferrous Metals |
| V22 | Metal Products |
| V23 | Manufacture of General-purpose and Special-purpose Machinery |
| V24 | Manufacture of Transport, Electrical, and Electronic Machinery |
| V25 | Other Manufactures |
| V26 | Comprehensive Utilization of Waste |
| V27 | Production and Supply of Gas |
| V28 | Production and Supply of Water |
| Code | Mean | STD | Skewness | Kurtosis | JB-Statistic | Probability |
|---|---|---|---|---|---|---|
| V1 | 0.028593 | 0.159676 | 0.022191 | 3.728845 | 2.377116 | 0.304660 |
| V2 | 0.050715 | 0.325692 | 1.383137 | 6.100709 | 76.98059 | 0.000000 |
| V3 | 0.030155 | 0.194552 | 0.753318 | 6.280401 | 58.09648 | 0.000000 |
| V4 | 0.022994 | 0.141241 | 0.113567 | 3.899567 | 3.837782 | 0.146770 |
| V5 | 0.02181 | 0.186587 | 1.930843 | 14.32913 | 638.7092 | 0.000000 |
| V6 | 0.068385 | 0.321179 | 1.665988 | 8.443783 | 181.6184 | 0.000000 |
| V7 | 0.014926 | 0.159499 | 0.827264 | 5.225815 | 34.29224 | 0.000000 |
| V8 | 0.031674 | 0.284571 | 3.837147 | 26.56859 | 2739.081 | 0.000000 |
| V9 | 0.033462 | 0.257691 | 3.051374 | 21.80968 | 1743.420 | 0.000000 |
| V10 | 0.025657 | 0.209002 | 2.190527 | 14.91872 | 718.9044 | 0.000000 |
| V11 | 0.014068 | 0.131022 | 1.103867 | 6.753926 | 84.55699 | 0.000000 |
| V12 | 0.021448 | 0.222096 | 1.316007 | 12.19274 | 407.6430 | 0.000000 |
| V13 | 0.02337 | 0.246749 | 2.609256 | 21.83432 | 1702.926 | 0.000000 |
| V14 | 0.024322 | 0.172692 | 1.40529 | 11.33782 | 345.1580 | 0.000000 |
| V15 | 0.017798 | 0.116727 | −0.23907 | 3.183362 | 1.169192 | 0.557331 |
| V16 | 0.022083 | 0.135479 | 1.56146 | 8.714324 | 189.0606 | 0.000000 |
| V17 | 0.016444 | 0.193304 | 2.335657 | 13.33235 | 573.2465 | 0.000000 |
| V18 | 0.032043 | 0.236534 | 2.773104 | 18.81172 | 1251.771 | 0.000000 |
| V19 | 0.022901 | 0.160858 | 1.515492 | 9.312477 | 218.6109 | 0.000000 |
| V20 | 0.020431 | 0.135593 | 0.646182 | 4.847269 | 22.65996 | 0.000012 |
| V21 | 0.017874 | 0.121844 | 0.397835 | 6.999253 | 74.12922 | 0.000000 |
| V22 | 0.036121 | 0.24267 | 2.783564 | 18.11194 | 1156.329 | 0.000000 |
| V23 | 0.024369 | 0.177941 | 2.167856 | 15.36133 | 765.0540 | 0.000000 |
| V24 | 0.025961 | 0.180863 | 1.461672 | 9.638931 | 234.6035 | 0.000000 |
| V25 | 0.032045 | 0.233692 | 0.967952 | 5.123345 | 36.80940 | 0.000000 |
| V26 | 0.043833 | 0.367526 | 4.013498 | 29.4557 | 3407.669 | 0.000000 |
| V27 | 0.020359 | 0.180185 | −0.43386 | 8.581308 | 142.2384 | 0.000000 |
| V28 | 0.02955 | 0.286529 | 6.398114 | 58.17704 | 14303.45 | 0.000000 |
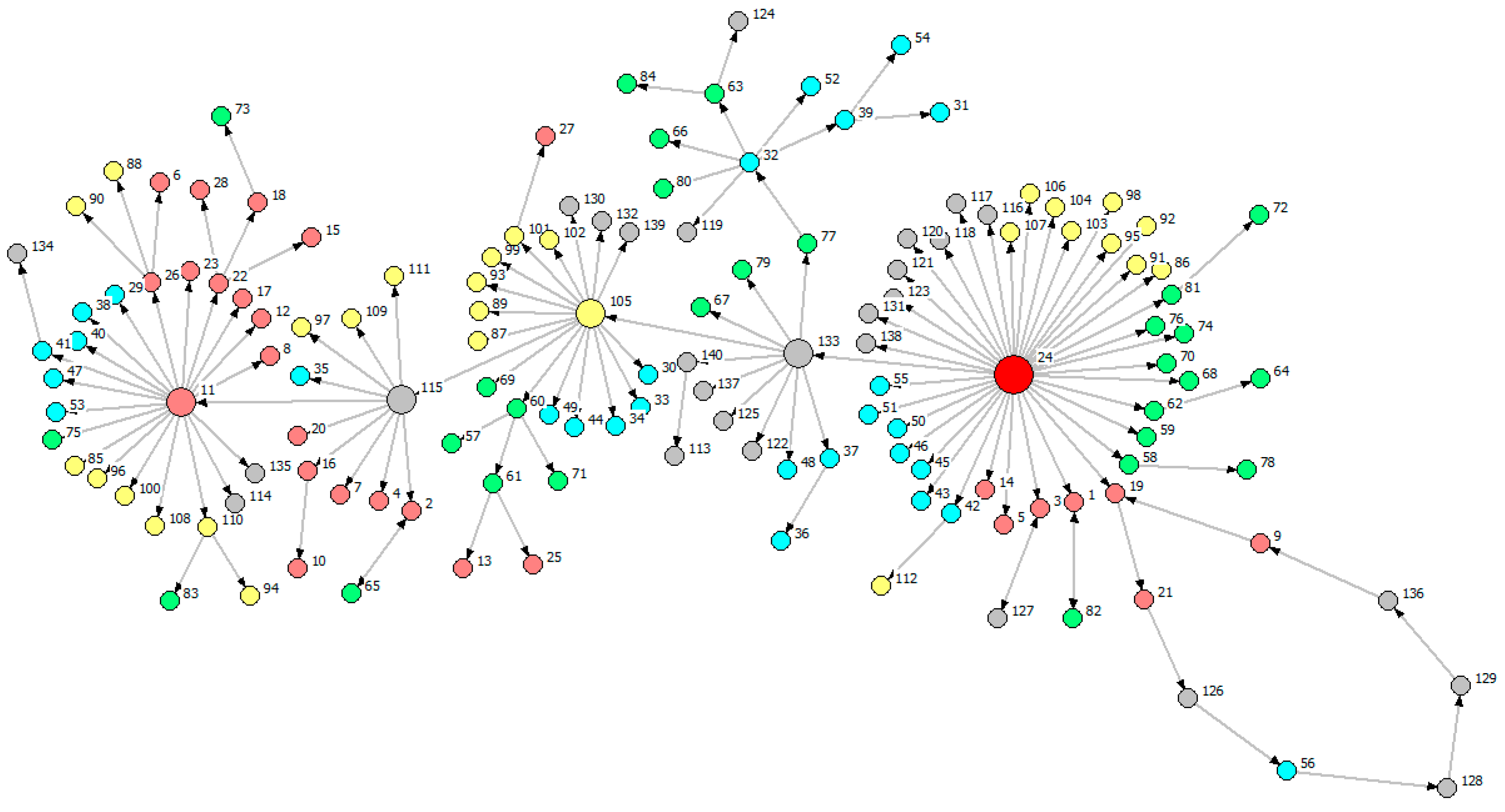
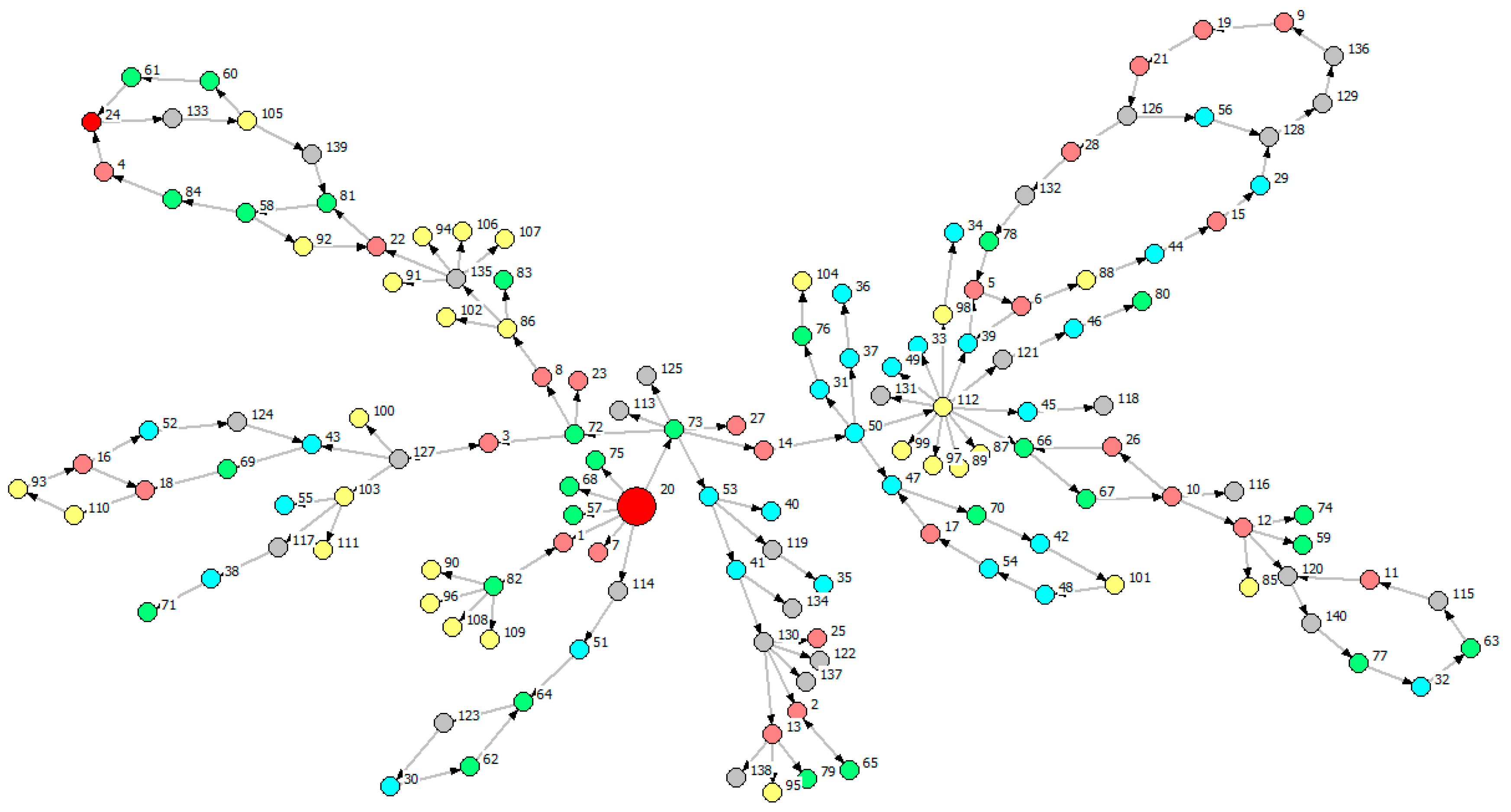
| Root | Key Nodes | Number of Feedback Loop | |
|---|---|---|---|
| Figure 8 | V24 | Radial nodes of hierarchical structure (V133, V105, V115, V11) | 1 |
| Figure 9 | V20 | Nodes with an out-degree more than 3 (V12, V13, V50, V53, V72,V73, V82,V86, V103, V112, V127, V130,V135) | 12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.-Z.; Kuang, P.-C.; Lin, Q.-W.; Sun, B.-Y. A Study of the Transfer Entropy Networks on Industrial Electricity Consumption. Entropy 2017, 19, 159. https://doi.org/10.3390/e19040159
Yao C-Z, Kuang P-C, Lin Q-W, Sun B-Y. A Study of the Transfer Entropy Networks on Industrial Electricity Consumption. Entropy. 2017; 19(4):159. https://doi.org/10.3390/e19040159
Chicago/Turabian StyleYao, Can-Zhong, Peng-Cheng Kuang, Qing-Wen Lin, and Bo-Yi Sun. 2017. "A Study of the Transfer Entropy Networks on Industrial Electricity Consumption" Entropy 19, no. 4: 159. https://doi.org/10.3390/e19040159
APA StyleYao, C.-Z., Kuang, P.-C., Lin, Q.-W., & Sun, B.-Y. (2017). A Study of the Transfer Entropy Networks on Industrial Electricity Consumption. Entropy, 19(4), 159. https://doi.org/10.3390/e19040159





