1. Introduction
In this paper, the relevance index (RI) is applied to the task of identifying critical states in complex systems (more precisely, we identify regions near critical points; however, in order not to overload the writing, in the following, we use the expression “critical states”). This index had been originally introduced for a different purpose, i.e., as a way to identify key features of the organization of complex dynamical systems, and it has proven able to provide useful results in various kinds of models, including, e.g., those of gene regulatory networks and protein-protein interactions.
Moreover, the method can be applied directly to data, without any need to resort to models, possibly helping to uncover some non-obvious or hidden features of the underlying dynamical organization. As an example, let us mention the discovery of coordinated behaviors of different social and economic agents from the analysis of time series alone, without any a priori knowledge of their interactions.
Essentially, the RI is based on Shannon entropies and can be used to identify groups of variables that change in a coordinated fashion, while they are less integrated with the rest of the system. These groups of integrated variables may form the basis for an aggregate description of the system, at levels higher than that of the single variables. Since the RI allows a variable to belong to more than one group, it can be applied also to “tangled” organizations, which are widespread in complex biological and social systems and which do not have the clean tree-like topology of pure hierarchies.
The RI will be reviewed in detail in
Section 2.
The availability of quantitative variables that allow one to identify critical states in complex systems is of utmost importance, and we have found that the RI can also be used to locate critical states with good results, as will be shown below. Moreover, since the RI is affected by the distance of the present state from critical states, it can also be used to identify situations that approach criticality, thus providing early warning signals that can be extremely useful for controlling the behavior of a system.
The use of information-theoretical measures for studying criticality has already been documented in previous studies, such as [
1,
2], in which Fisher information is used to identify the critical state in both the Ising model and Boolean networks, and [
3,
4]. However, we remark that the aim of the paper is to show that the RI can be effectively used to identify critical states, rather than to compare different measures of criticality (we also deliberately avoid discussing the tight and intricate relation between criticality and complexity, as it is out of the scope of the paper).
The RI has been applied in two different kinds of systems, where the word “criticality” takes somewhat different meanings. In general, criticality refers to the existence of two qualitatively different behaviors that the same system can show, depending on the values of some parameters. Criticality is then associated with parameter values that separate the qualitatively different behaviors. However, slightly different meanings of the word can be found in the literature, two major cases being (i) the one related to phase transitions and (ii) dynamical criticality, sometimes called the “edge of chaos”. In the former case, the two different behaviors refer to equilibrium states that can be observed by varying the value of, e.g., temperature, or of other macroscopic external parameters. In the latter case, the two different behaviors are characterized by their dynamical properties: the attractors that describe the asymptotic behavior of the system can be ordered states, like, e.g., fixed points or limit cycles, or chaotic states. These two meanings are related, but not identical (see [
5] for a more detailed discussion).
It is therefore important to understand which kind of critical states can be identified by the RI. That is why we have examined two important models that exhibit the two different meanings of criticality: the Ising model for phase transitions and the random Boolean network model for dynamical criticality. Both are well known, and it will suffice to recall their main properties and notations (in
Section 3).
It is also important to stress that the two cases above do not differ only for the different kinds of criticality they show, but also for other important physical and mathematical properties: the Ising model is an ergodic system close to equilibrium, while the random Boolean networks (RBNs) are dissipative, non-ergodic systems. Moreover, the Ising model is inherently stochastic, while the RBN model is deterministic. It is remarkable that the RI is able to satisfactorily locate the critical points in both cases, notwithstanding their differences, as shown in
Section 4 and
Section 5.
Finally, the main results will be summarized in the final section, alongside with indications for further work.
2. The Relevance Index
The roots of the RI can be traced back to the work on biological neural networks by Edelman and Tononi [
6], who introduced several system-level measures, based on recordings of neural activity, among them the cluster index. The RI is an extension of this latter measure, which can be applied to dynamical systems, while the cluster index had been conceived of for fluctuations around a steady state.
The reasons why the RI has originally been introduced were related to the difficulty in understanding the actual organization of dynamical systems, which requires (i) a proper identification of meaningful organizational “levels” that emerge from the interactions of lower level entities (and possibly also of higher-level entities, such as groups of interacting chemical species inprotocells [
7,
8]) and (ii) a mapping of the interactions between these meso-levels. In some cases, they can be properly described by a quite familiar tree-like hierarchical structure, as happens in several physical systems where the levels can be identified with the space-time scales of the phenomena (microscopic and macroscopic or micro-meso-macro), in inclusion hierarchies (e.g., a cell that comprises a nucleus that comprises chromosomes that comprise
…), in social organizations and others. However, one sometimes finds cases where the interactions among the high levels are of the network type, and their organization cannot be satisfactorily described by a hierarchical structure.
The first step towards understanding these complex organizations is the identification of the meso-level structures, a process that can be far from trivial whenever the interactions are unknown or only partly known. Think for example of a gene regulatory network, where some genes may be known to regulate the expression of a particular gene, but several other interactions are unknown; or of a social or economic organization, where some activities can be observed, but the complete pattern of reciprocal influences cannot (some may be even deliberately hidden, due, e.g., to economic interests).
The purpose of the RI is that of identifying sets of variables that behave in a somehow coordinated way in a dynamical system; the variables that belong to the set are integrated with the other variables of the set, much more than with the others. Since these subsets are possible candidates as higher-level entities, to be used to describe the system organization, they will be called relevant subsets (omitting the specification that they are candidates). A quantitative measure, well suited for identifying them, is defined as follows (the presentation below follows the one given in [
9]).
Let us consider a system
U whose elements are discrete variables that change in time, and let us suppose that the time series of their values are known. According to information theory, the Shannon entropy of an element
is defined as:
where
is the set of the possible values of
and
the probability of occurrence of symbol
v. In this work, dealing with observational data, probabilities will be estimated by relative frequencies.
The entropy of a pair of elements
and
is defined by means of their joint probabilities:
Equation (
2) can obviously be extended to sets composed of more than two elements.
Let us now consider a subset
S of
U composed of
k elements. Its integration
is defined as (the integration is also known as intrinsic information or multi-information):
represents the deviation from statistical independence of the
k elements in
S. The integration alone could be used to try to identify the relevant subsets, but it turns out that a more accurate identification requires considering the ratio between
and the mutual information between
S and the rest of the universe. The mutual information
between
S and the rest of the system
is defined as usual as:
where
is the conditional entropy and
the joint entropy.
Finally, the relevance index
r(S) is defined as:
This is the measure that will be used below to identify critical states. Note that it is undefined in all of those cases where vanishes. In these cases, however, the subset S is statistically independent from the rest of the system, and it should therefore be analyzed separately (these cases should be screened out in advance).
In our first papers on this subject, following the terminology of Tononi [
6], we called the quantity
the dynamical cluster index. However, when applied to time series, this term may be misleading: think for example of two variables that take constant and equal values at all times; one usually tends to think that they (can) belong to the same cluster, but their
value vanishes, since it is based on Shannon entropy, that is zero for states whose probability is one (remember that we estimate probabilities with relative frequencies). Therefore, the measure defined in Equation (
5) misses some quite obvious clusters, and in order to avoid ambiguities, we prefer to avoid using that word and refer to it as the relevance index (since it can be used to identify relevant subsets of variables).
When the RI is applied to identify relevant subsets, it is necessary to compare sets of different sizes. However, entropies scale with system size, so this requires considerable ingenuity. Following the original work of Tononi, an “RI method” has been developed for this purpose, where the variable is first normalized with respect to a reference case, and a statistical index is computed that allows meaningful comparisons of sets of different sizes [
6,
9,
10]. However, quite often, these sets overlap, so the actual organization of the system remains opaque; for example, a variable may belong to a set of three variables and also to one of its four-element supersets, both endowed with fairly high values of the statistical index. The RI has been developed to decide which set to consider as a basis for deciphering the system structure, as described in [
8,
11].
However, in order to identify critical states, it turns out that the comparisons among subsystems of different sizes are not required, and one can directly use the RI as defined in Equation (
5), as will be done in
Section 4 and
Section 5.
3. Models
As has been discussed in
Section 1, one can find in the literature slightly different meanings of the word criticality; critical states are always located in-between different regimes, but the nature of these regimes might differ. Here, we will consider two among the most important cases, namely phase transitions and dynamical criticality. To this end, we will apply the RI to the Ising model (for phase transitions) and the random Boolean network (RBN) model of gene regulation for dynamical criticality.
3.1. Ising Model
The Ising model (according to Brush [
12], the model was first proposed by Lenz in 1920, as also pointed out by Ising in 1925 in its seminal paper) was originally presented with the aim of reproducing simplified ferromagnetic phenomena in materials, but was then recognized as a notable example of a system that can undergo a phase transition as a function of a control parameter. In this section, we briefly recall its main properties; detailed descriptions of the model may be found in the survey paper by Brush [
12] and statistical physics books, such as [
13,
14].
Let us consider a
d-dimensional lattice of
N atoms characterized by a spin, which can be either up (
) or down (
). The atoms exert short-range forces on each other, and each atom tends to align its spin according to the values of its first neighbors. An external field may also be considered, which biases the orientation of the atoms. The energy of the system is defined as follows:
where
is the spin of atom
i,
is a parameter accounting for the coupling between atoms,
denotes the set of all neighboring pairs and
B is a parameter playing the role of an external field.
The system can be studied by means of usual statistical mechanics methods, and it can be assessed whether it undergoes a phase transition. Ising proved that the
case does not have phase transitions, while the
model can undergo a phase transition, as proven by Onsager [
15] under the hypothesis that
.
In this work, we consider the two-dimensional model, with
. We performed Monte Carlo simulations at constant temperature
T; in this case, the system tends to minimize the value of the free energy
(where
S is the entropy), and there is competition between the energy term, which tends to align the spins, and the entropy term that accounts for thermal disorder. The Monte Carlo algorithm used is a classical Metropolis algorithm with a Boltzmann distribution:
| Algorithm 1 Monte Carlo simulation of a 2D Ising model. Adapted from [16]. |
while maximum number of iterations not reached do Choose a random atom Compute the energy change associated to the flip Generate a random number r in [0,1] with uniform distribution if then end if end while
|
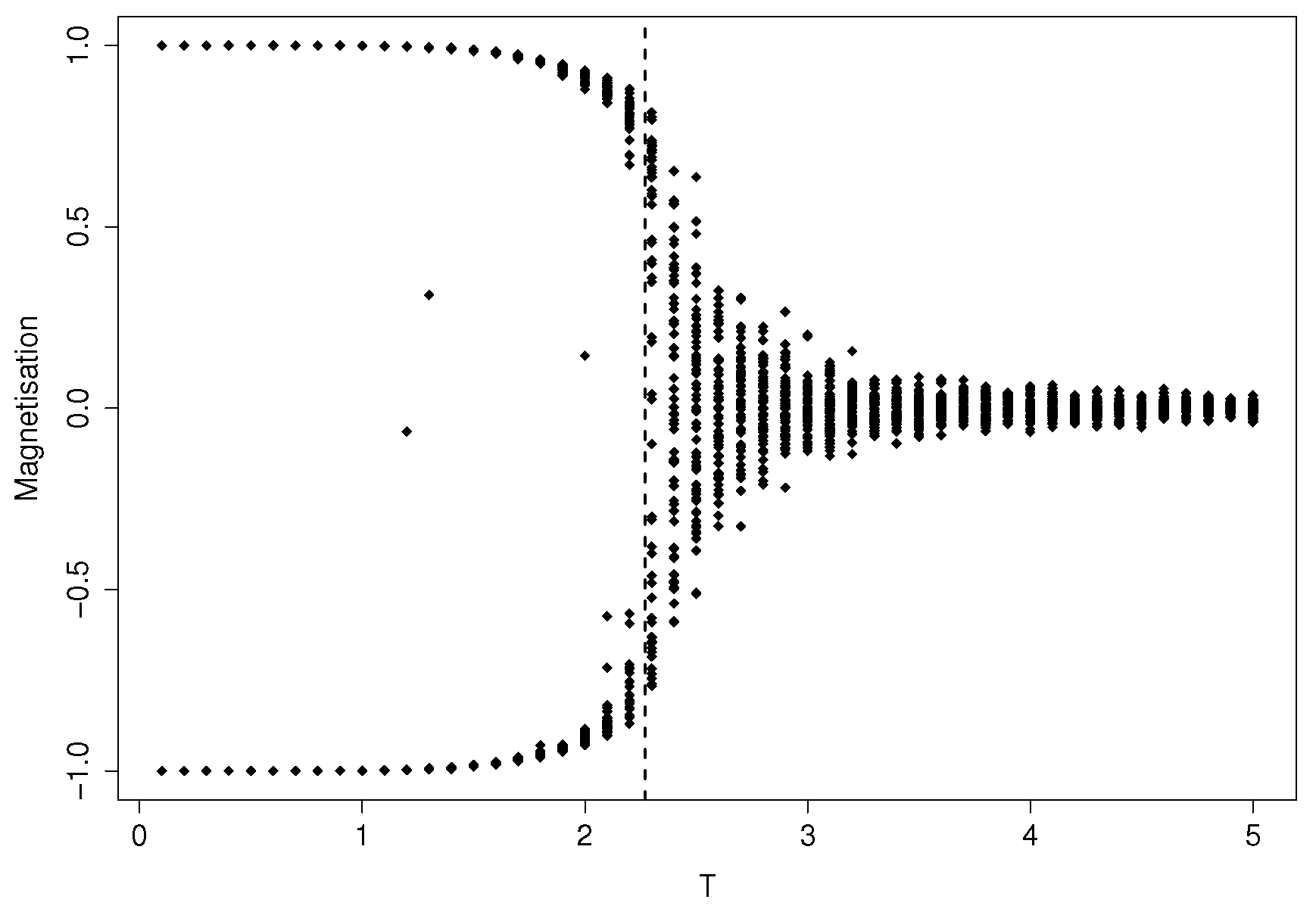
The temperature is the control parameter, while the order parameter is the so-called magnetization:
For low values of
T, the steady state of the system will be composed of atoms mostly frozen at the same spin, and the time average of the magnetization
will be close either to one or
; for high values of
T, the spins will randomly flip, and it will be
. For values close to the critical temperature
, a phase transition occurs: the system magnetization undergoes a change in its possible steady state values, as depicted in
Figure 1.
3.2. Random Boolean Networks
Let us now describe RBNs in a very synthetic way, referring the reader to [
17,
18,
19,
20] for a more detailed account. Several variants of the model have been presented and discussed, but we will restrict our attention here to the “classical” model. A classical RBN is a dynamical system composed of
N genes, or nodes, which can take either the value zero (inactive) or one (active). Let
be the activation value of node
i at time t, and let
be the vector of activation values of all of the genes.
The activation of a gene may affect that of other genes; these relationships are represented by directed links and Boolean functions, which model the response of each node to the values of its input nodes. In a classical RBN, each node has the same number of incoming connections K, and its K input nodes are chosen at random with uniform probability among the remaining nodes. The Boolean functions can be chosen in different ways: in this paper, we will only consider the case where they are chosen by assigning, to each combination of K input values, an output value one or zero according to a Bernoulli distribution with parameter p. The various outputs are chosen independently from each other, and the probability that the output is one (i.e., the bias p) is the same for all of the inputs and for all of the nodes.
In the so-called quenched model, neither the topology nor the Boolean function associated with each node change in time. The network dynamics is discrete and synchronous, so fixed points and cycles are the only possible asymptotic states in finite networks (a single RBN can have, and usually has, more than one attractor). The model shows two main dynamical regimes, ordered and disordered, depending on the degree of connectivity and on the Boolean functions: typically, the average cycle length grows as a power law with the number of nodes
N in the ordered region and increases exponentially in the disordered region [
17]. The dynamically-disordered region also shows sensitive dependence on the initial conditions (that is why disordered states are often called “chaotic”, although the asymptotic states are cycles of finite length in the case of finite networks) not observed in the ordered one.
A well-known method to determine the dynamical regime of an RBN directly measures the spreading of perturbations through the network, by comparing two parallel runs of the same system, whose initial states differ for only a small fraction of the units. This difference is measured by the Hamming distance , defined as the number of units that have different activations on the two runs at the same time step (the measure is performed on many different initial condition realizations, so one actually considers the average value , but we will omit below the somewhat pedantic brackets). If the two runs converge to the same state, i.e., , then the dynamics of the system are robust with respect to small perturbations (a signature of the ordered regime), while if grows in time (at least initially), then the system is in a disordered state. The critical states are those where remains initially constant. If a single node is perturbed, the average number of different nodes that differ in the two cases at the following time step is sometimes called the Derrida parameter λ, so characterizes disordered states, ordered states, and identifies critical states.
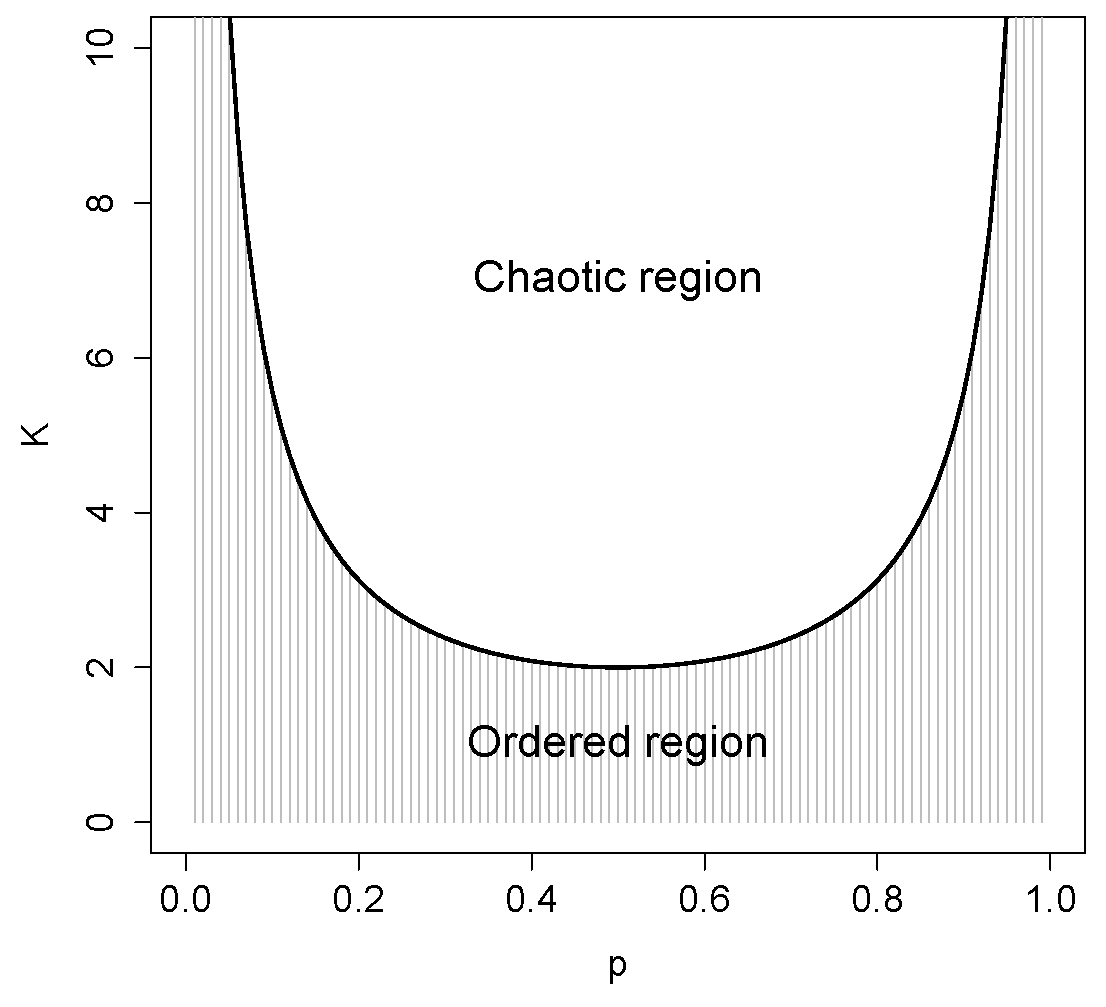
In a
p–
K diagram, ordered regimes are separated from those where the dynamics is chaotic by a critical line, whose equation can be shown [
19] by:
where
is the critical value of the connectivity corresponding to a given value of the bias
p (see
Figure 2).
The knowledge of the value of
is extremely important (Equation (
8) can be rigorously derived in the so-called annealed approximation, that is able to provide analytical estimates of the behavior of some variables in RBNs), as it allows us to precisely locate the critical states and to verify how close the RI comes to that value.
4. Results on the Ising Model
We run Monte Carlo simulations of Ising models with toroidal boundary connections. The neighbors of an atom are its horizontal and vertical first neighbors, i.e., the four adjacent cells in the lattice. We set
and
, for which
(the first analytical result on the phase transition in the 2D Ising model has been presented by Onsager [
15]). The values of
T span the range
at steps of
. For each value of
T, 10 runs are performed starting from random initial conditions chosen with
spin probability equal to
, so as to start with an intermediate condition between
and
(we also ran experiments with different biases in the initial condition and did not observe any difference in the results). We run experiments for lattices of size
, with
. For each run,
steps were executed, with
; we skipped the first steps so as to reach a steady state, so only the last
steps were considered and recorded every
steps.
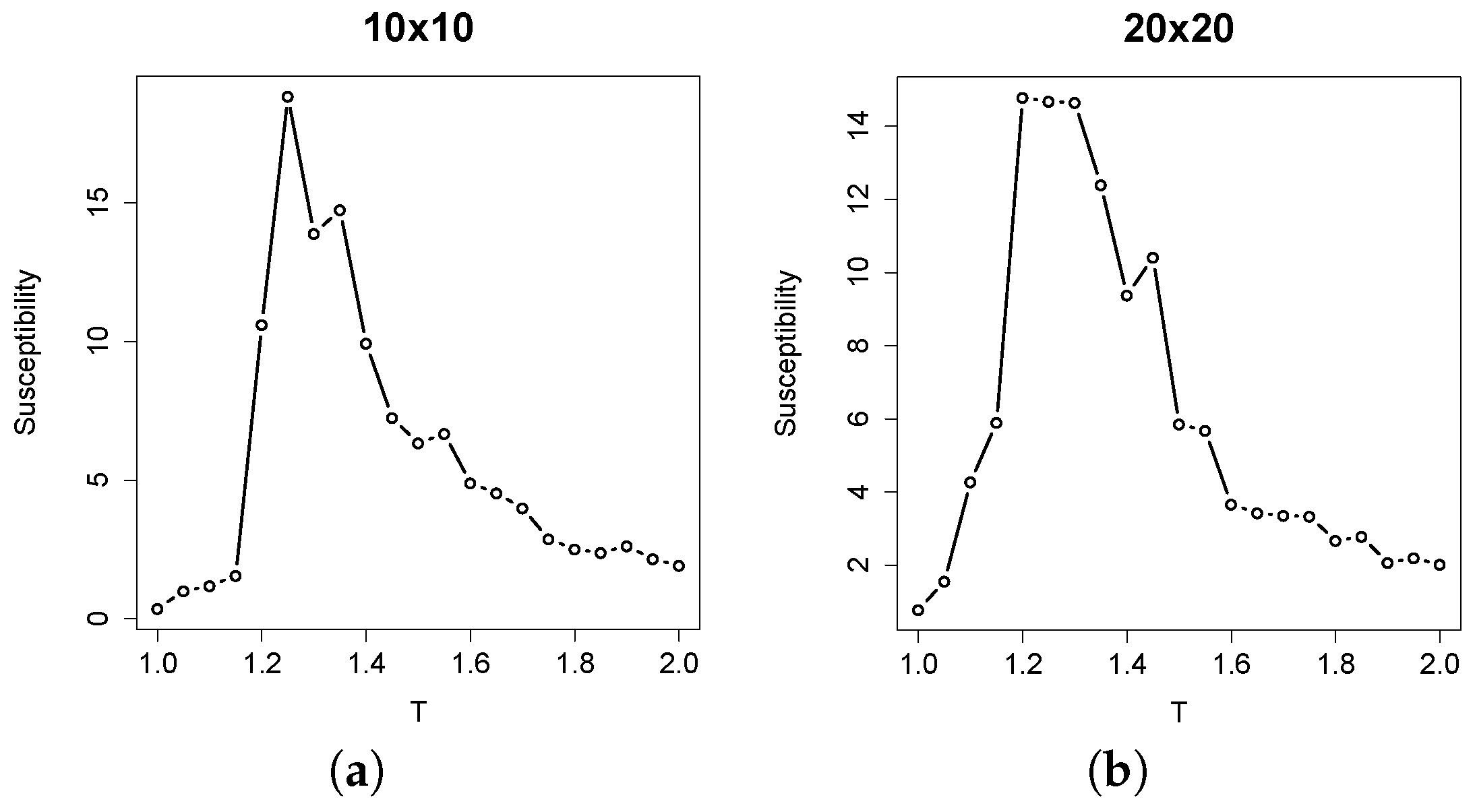
In finite-sized Ising models, the critical value of temperature is expected to deviate from the theoretical value. Therefore, the actual critical temperature value was estimated by computing the susceptibility [
21], defined as:
where
T is the temperature,
N the number of atoms,
μ the magnetization of the system at a given time step and angular brackets denote the time average. The peak of
χ may be used to identify the actual critical temperature value for finite instances. In
Figure 3, the median values of susceptibility of ten replicas are plotted against the temperature value. As we can observe, the critical values are around
for both lattice sizes considered, which is slightly higher than the theoretical one. This discrepancy is due to the finite size of the systems. This specific value will be taken as the critical one in the Ising models of our experiments.
Relevance Index in the 2D-Ising Model
For each simulation of the Ising model, we computed the RI for 1000 random subsets of the atoms of size . Subsets of larger cardinality would require an impractical number of samples to avoid undersampling in the evaluation of the entropies. However, this is not a limitation of the method, as we will show in the following.
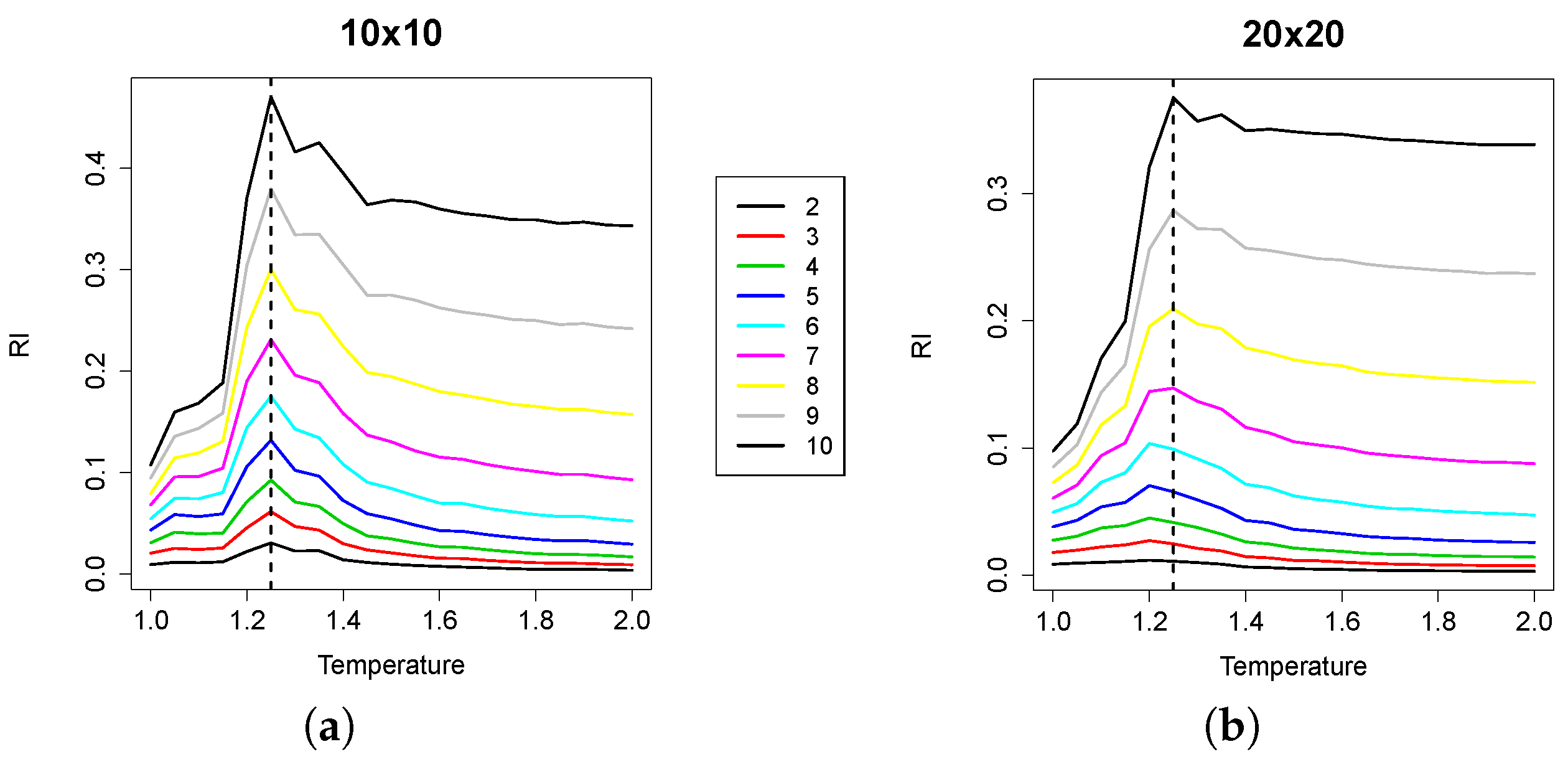
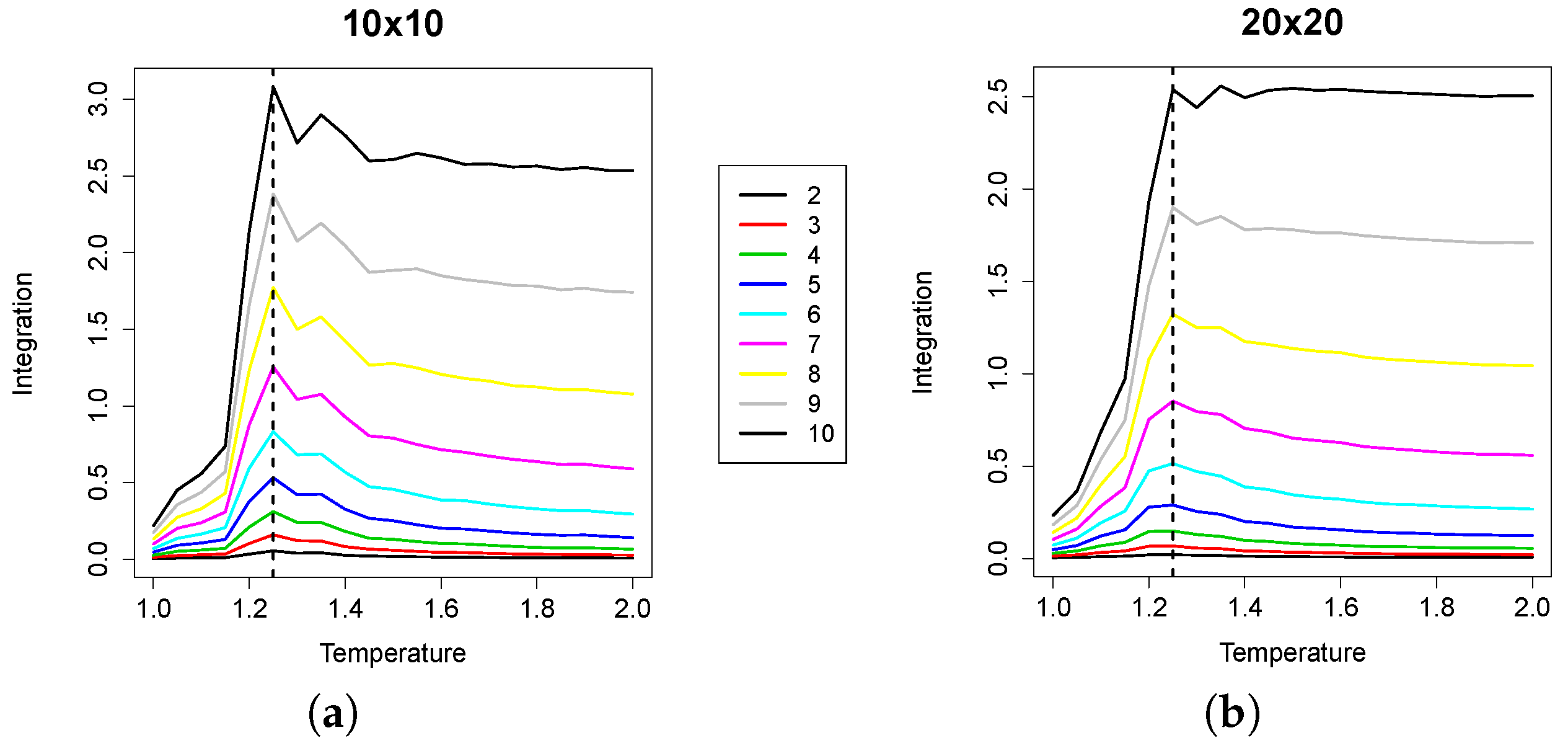
In
Figure 4, the median values of RI (averaged over the 1000 samples for each replica) are plotted, against temperature values. For the sake of space, we plotted all of the curves corresponding to all group sizes in the same plot. As
increases, the curves shift towards the upper part of the plot, because the (non-normalized) RI values increase with group size. We can observe that the maximum value of RI is attained at a temperature value that corresponds with high precision to the empirically-derived critical value. The effect of undersampling starts to be visible for group sizes approximately greater than 10; indeed, as the cardinality of the groups evaluated increases, the RI peak tends to flatten. However, small group sizes are enough to locate the critical point.
A question may arise as to what extent the individual contribution of the integration might impact the overall results. To assess this, we also considered the statistics of the integration only, which are summarized in the plots in
Figure 5.
From the plots, we can observe that the integration profiles across temperature values show a peak in correspondence with the critical temperature. Nevertheless, the larger the group considered, the less sharp the peak, especially in the
instances. Therefore, even if integration alone could provide useful indications to locate the critical temperature, its combination with the mutual information into the RI makes it possible to detect the phase transition with higher precision. The reason for this phenomenon is that the mutual information still moderately grows after
(see
Figure 6), thus reducing the RI value after the critical point.
5. Results on RBNs
In this section, we show the results of the application of the RI to the task of identifying critical states in RBNs, which have been described in
Section 3. There, it was shown that the dynamical behavior of RBNs depends mainly on the values of two parameters, which are (i) their connectivity
K and (ii) the bias
p of the Boolean functions that rule the responses of their nodes. Since individual network realizations can show different behaviors, the study of the RBN dynamics is based on averages computed on ensembles of networks sharing the same values of connectivity and bias.
The computation of the RI requires a collection of the states of each variable; these have been obtained by collecting in a single series all of the states encountered by a specific RBN starting from
random initial conditions. Each time point corresponds to an
N-dimensional Boolean vector of simultaneous values of the
N nodes, and each run continues until an attractor is found or up to a maximum of 1000 steps. The raw data series contain all of the time points, while the attractors series contains only those states that belong to an attractor, and the transients series contains only the states that do not belong to the attractor. In order to avoid excessive computing times, for each series, the analysis is limited to a subset of 1000 randomly-chosen states. The possibility to link together the various time series is directly related to the fact that the RI is based only on relative frequencies of equal-time values and does not depend on states at different times. Note that the choice of random initial conditions implies that the various attractors contribute in a way that is proportional to their basin of attraction. In order to characterize the behavior of families of networks sharing the same parameter values, different random realizations are analyzed; details can be found in
Table 1, which summarizes the parameters of the series that have been considered. Since we are interested in their typical dynamical behaviors at different scales, we compute the average of RI for different group sizes; then, the median is taken among all of the systems with the same connectivity and bias.
5.1. A Bird’s Eye View of the Dynamical Behavior of Families of RBNs
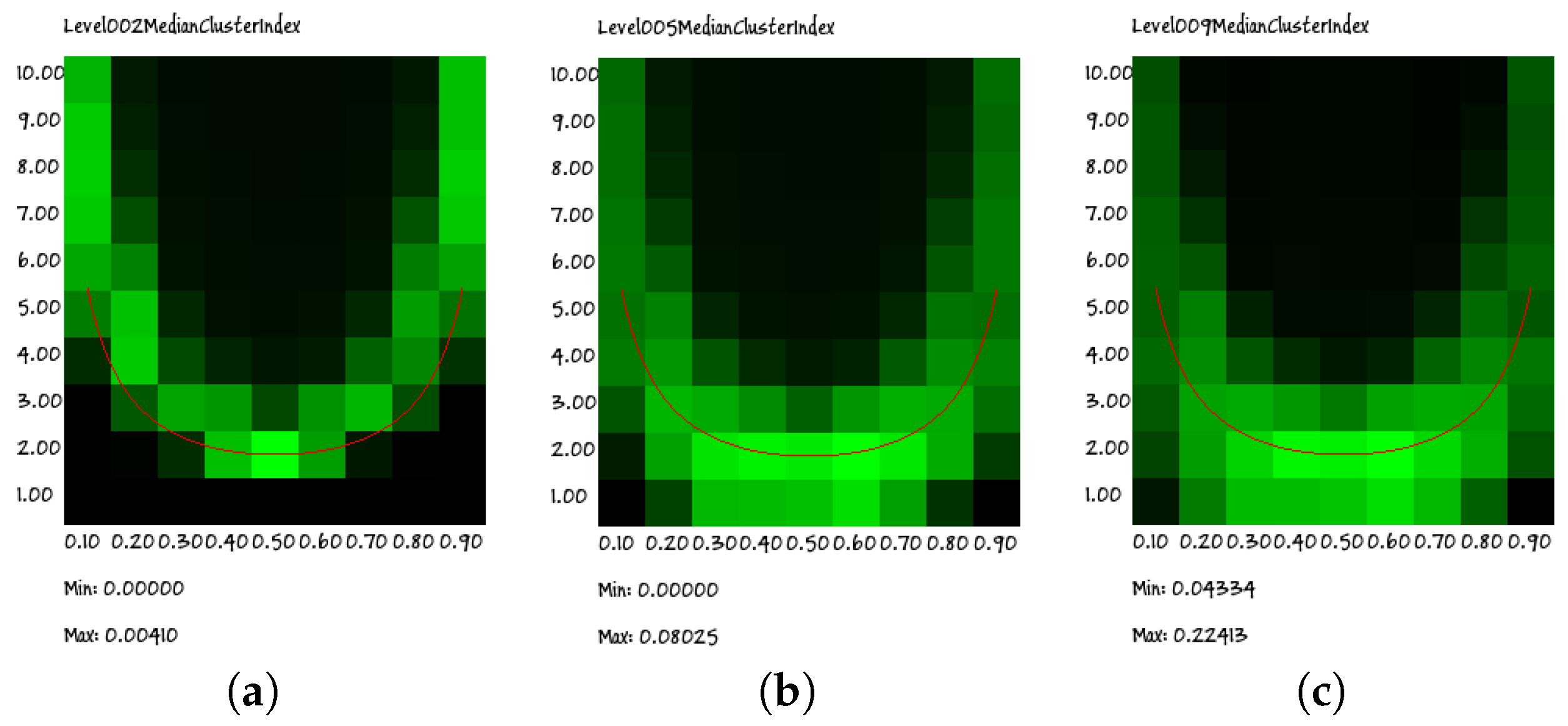
Let us first of all consider the behavior of the RI on a wide set of values of network parameters. As described in
Section 3, in a
p–
K diagram, the critical curve is U-shaped (
Figure 2); this curve will be called here the Kauffman–Aldana curve [
17,
19]. Interestingly, the same U-shaped behavior can be observed in
Figure 7, where the value of the RI is shown for different
p–
K points. It is also remarkable that the same behavior is observed for different group sizes.
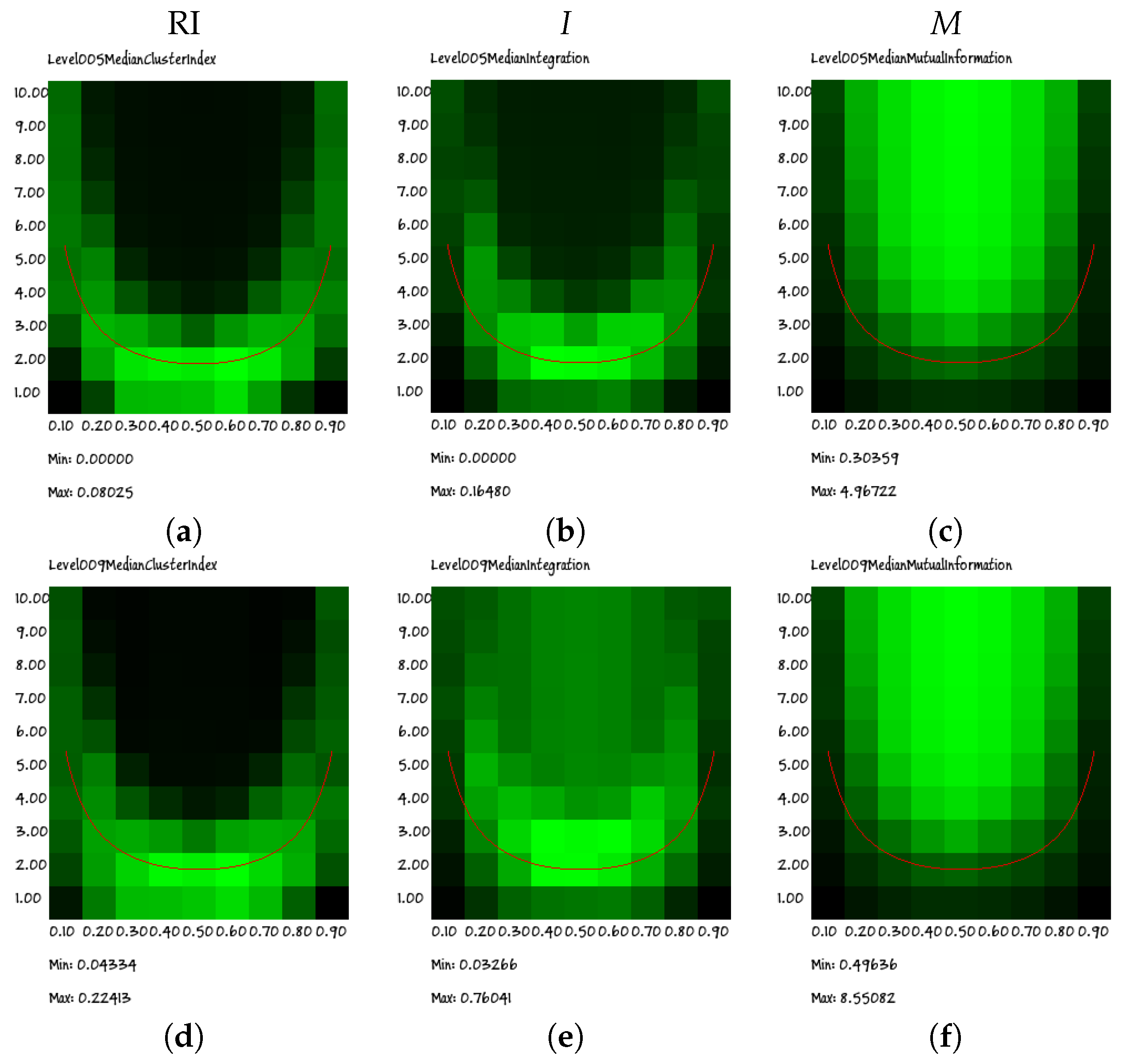
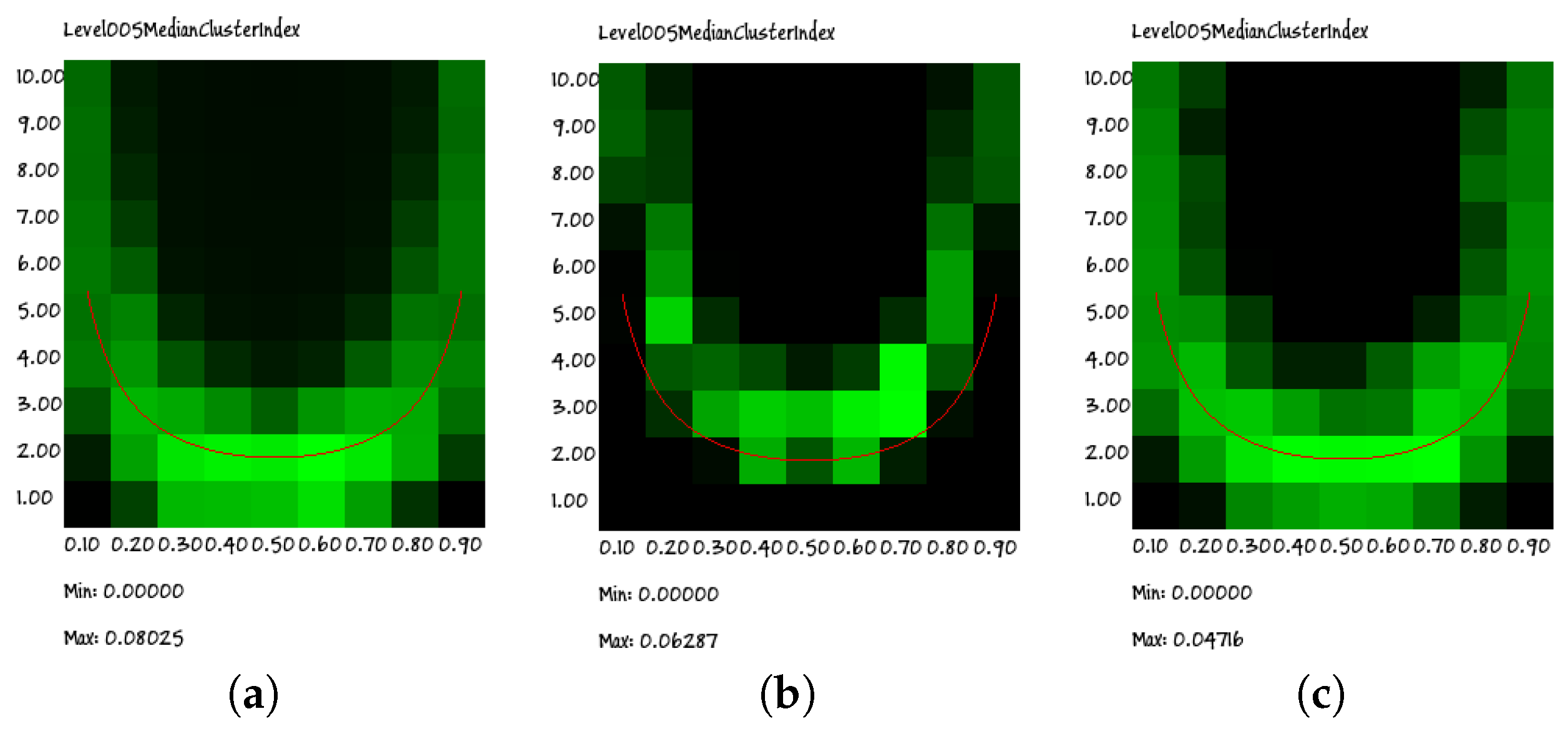
The heat maps indeed show a cloud that surrounds the Kauffman–Aldana curve, indicated by the U-shaped red line superimposed on the plots. Moreover, the position and dispersion of the clouds are similar in all of the group sizes (for clarity, in this section, we present only the results regarding groups of sizes 2, 5 and 9; similar results have been obtained for all groups having sizes from 3 to 10), the only exception being that of the size of two group: actually, as will be shown in the following section, this visual impression is an effect of the low granularity of the wide-range data rather than the signature of a truly different behavior.
Indeed, due to computational limitations and to the attempt to cover a wide range of parameter values, the resolution of the plots in
Figure 7 is quite low. However, if we perform a higher resolution search for the peaks of the RI, we find that they actually approach the correct theoretical values (see Equation (
8)). An example of such a high-resolution analysis is described in the following section.
Note also that the extremal values of the RI are not the same for all of the critical states, as shown in
Figure 8. While this might seem surprising, it should be recalled that critical states share some properties, but there may be differences. Indeed, it has already been shown elsewhere [
23] that RBNs can show heterogeneous behaviors in different positions along the critical line (even maintaining critical dynamics).
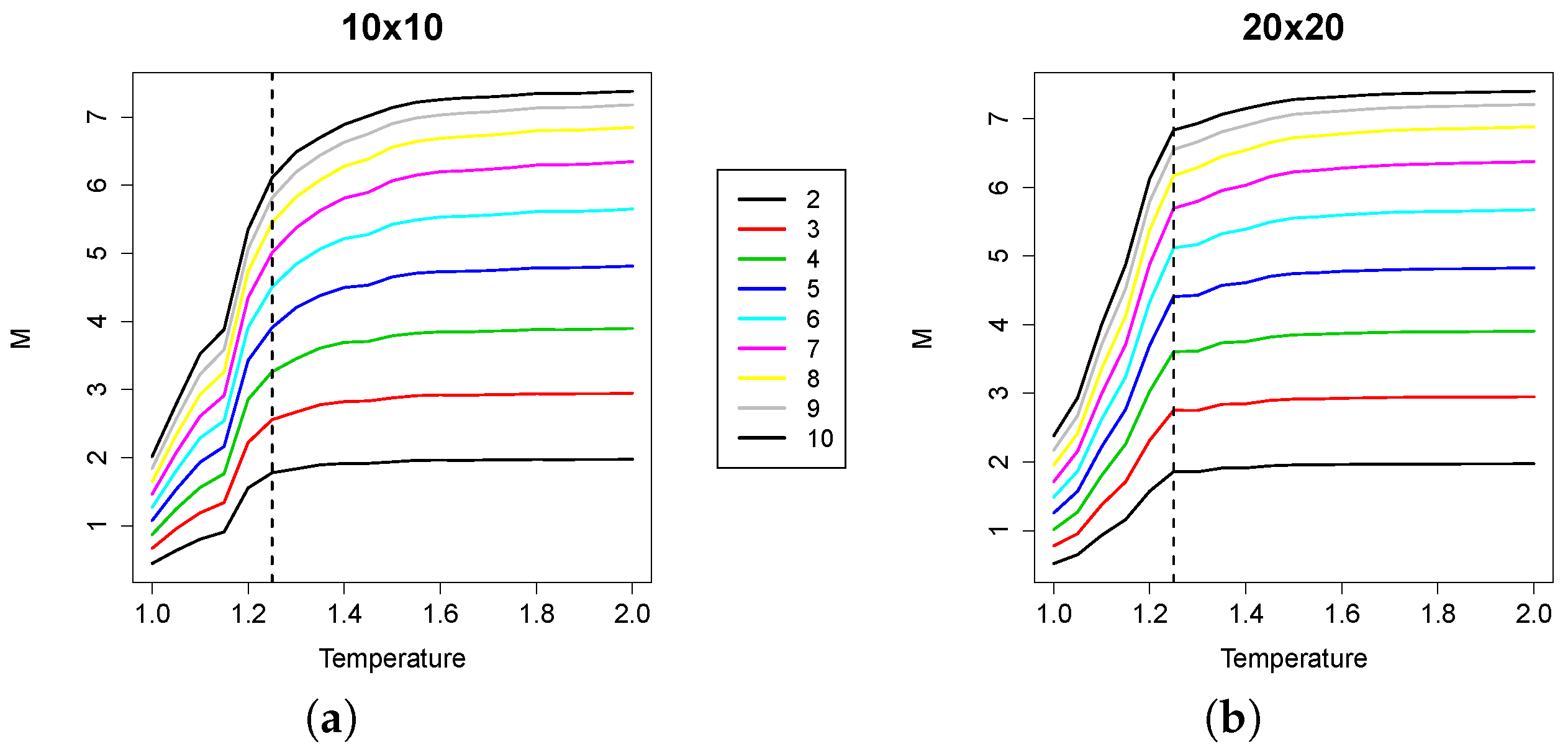
Besides studying the RI, it is interesting to observe the separate contributions of integration (
I) and mutual information (
M): as shown in
Figure 9, RI and
I are both close to the edge of chaos region, but the RI cloud provides a better estimation of the critical curve, especially in the zone of large biases. Moreover, the integration tends to worsen in identifying the chaotic region as the size of the groups increase; it seems indeed that the RI, i.e., the ratio between integration and mutual information, allows a better identification of the chaotic region.
5.2. A High-Resolution Analysis
As anticipated, in this section, we show small sections of the whole bias-connectivity diagrams, with a finer sampling of the values of the independent variables and with larger RBNs.
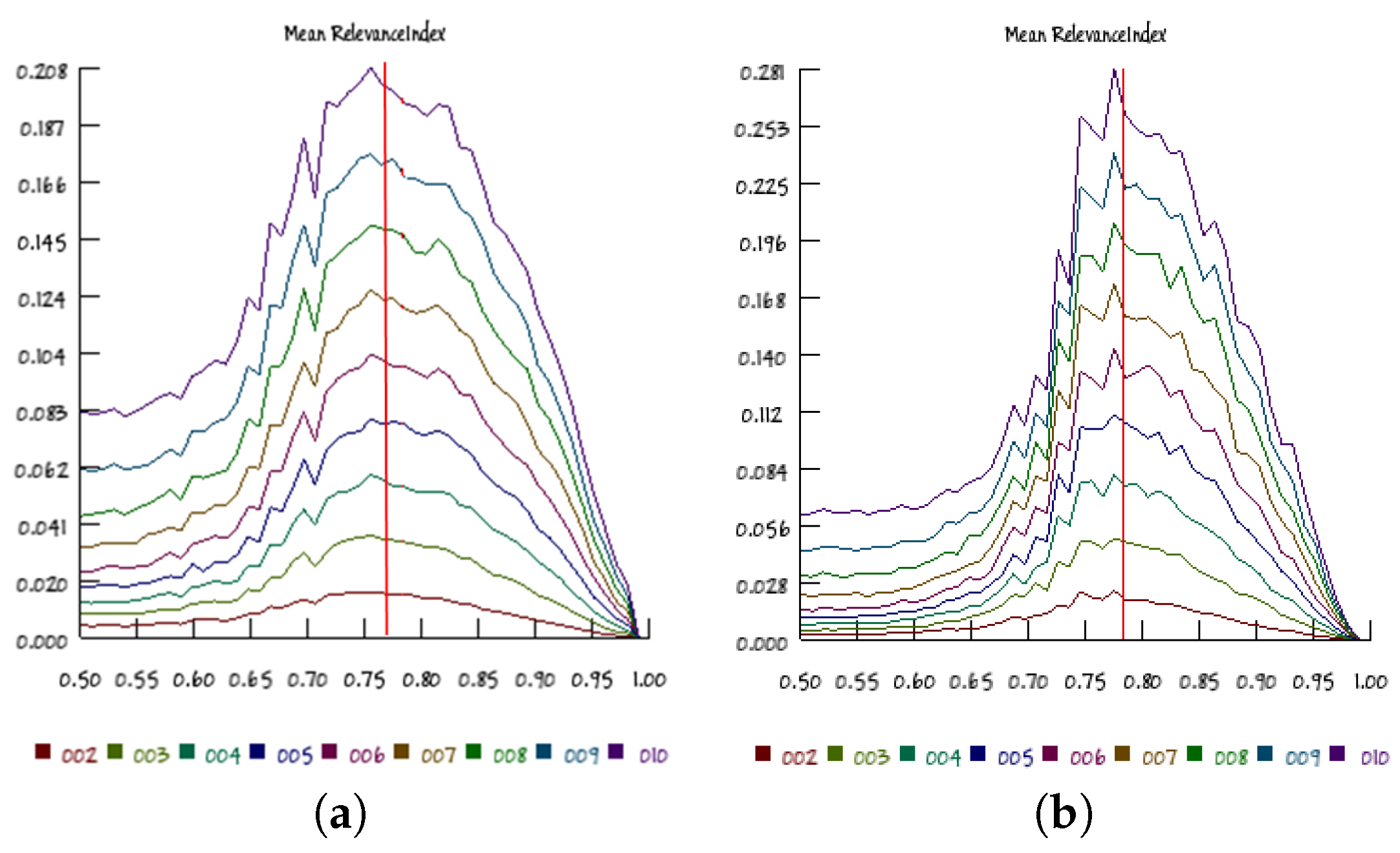
Figure 10 shows the RI results obtained from a section of the
p–
K diagram at
, in nets having 100 and 500 nodes: it is possible to note that the RI maximum value is attained for values that are very close to those predicted by the Kauffman–Aldana curve, for all of the investigated group sizes. This observation supports the idea that a similar distribution of organizations is present at many scales (represented here by different group sizes). Moreover, series involving larger RBNs identify more precisely the critical point (a fact already observed in the literature, as for example in [
24]) and have narrower RI distributions. Similar observations can be made for other
p–
K diagram sections (data not shown).
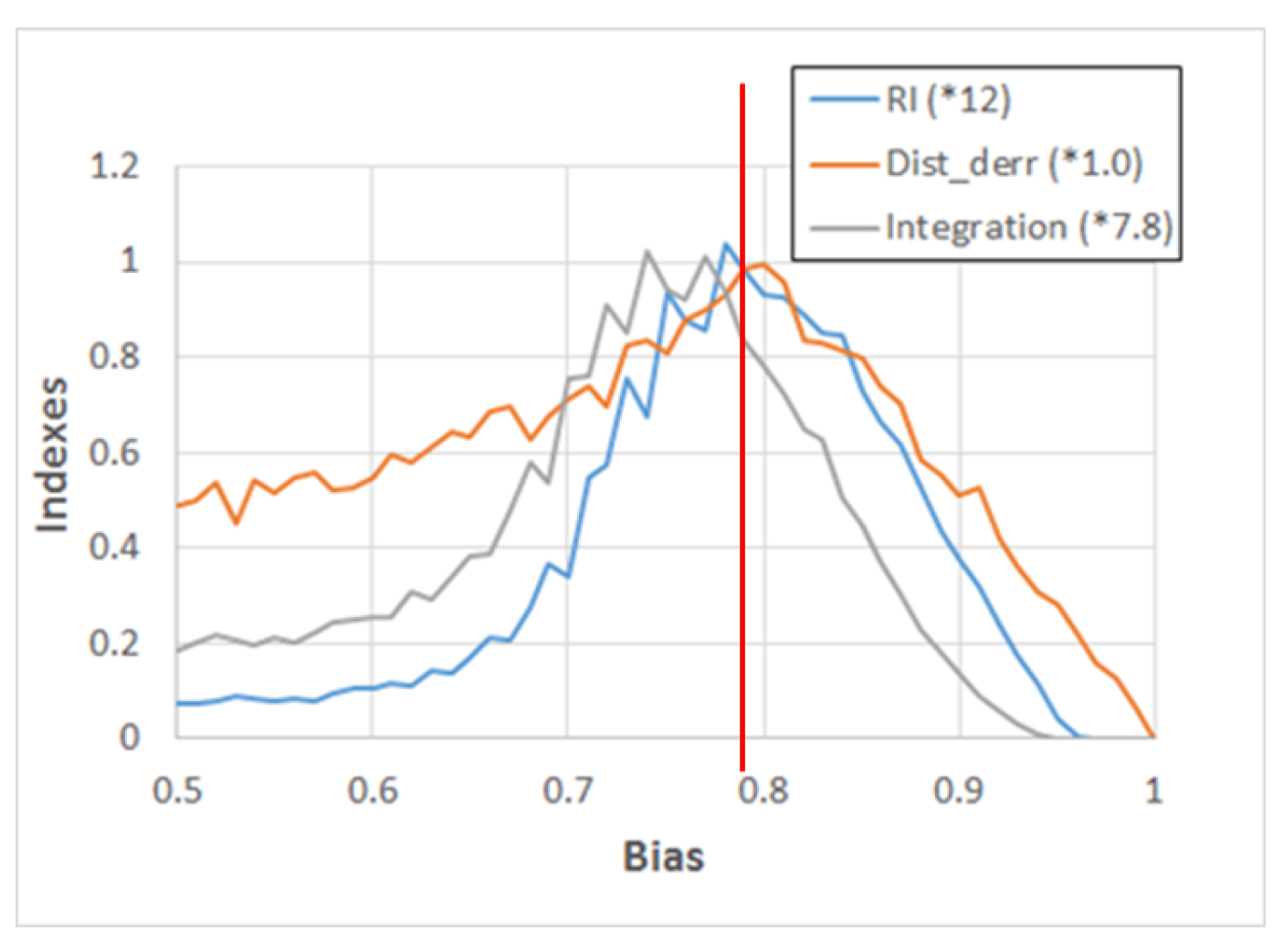
The high-resolution analysis confirms that the RI locates the critical region more precisely than integration alone, as shown in
Figure 11. Moreover, in the same figure, a measure
λ’, closely related to the Derrida parameter and described in the legend, is also shown. It is interesting to observe that
λ’ has a maximum close to the theoretical critical value of Equation
8, but that its distribution is not sharply peaked. On the other hand, the plot of the RI has also a very close maximum, but the width of its distribution is narrower, so that it can better help to localize the critical value.
Transients and Attractors
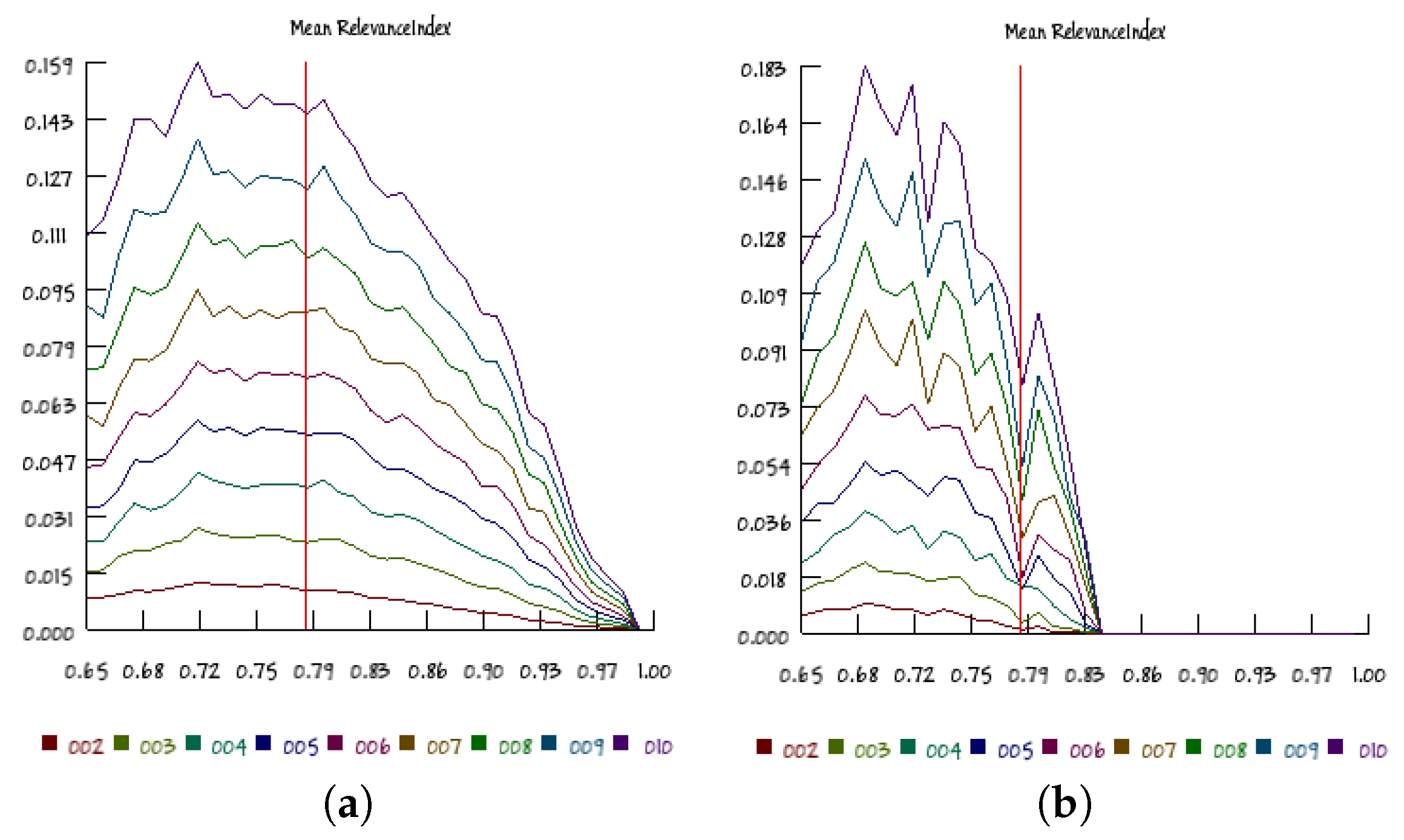
Differently from ergodic systems (like those represented by the Ising model), RBNs are highly dissipative systems; their asymptotic states are a very small subset of the ensemble of all of the possible states. Therefore, an interesting question regards the dynamical organization of these systems when they reach their attractors: is it significantly different from the organization expressed when the systems are traveling along their transients?
In order to address this question, we split the low-resolution data of 20-node networks and the high-resolution data of 100-node networks into series containing respectively only the states belonging to transients and those that belong to attractors, and we compute the RI separately (while the results of the previous sections refer to complete raw data series). Interestingly, the results are quite different, as shown in
Figure 12: the transients of critical systems show RI values close to their maxima, as was the case in the raw data series, although with a relatively wider dispersion, but the attractors’ series show peaks of the RI distributions significantly far from the theoretical expectations. In spite of these quantitative difference, the general U-shape of the cloud on the
p–
K diagram is still observed (as shown in
Figure 13).
One might guess that the difference may be due to the fact that many feedbacks strongly constrain the attractor states, while transients should be able to explore a broader set of conditions. Indeed, the theoretical curve of Equation (
8) had been rigorously obtained in the so-called annealed model, where at every time step, connections and Boolean functions are redrawn at random. Physical systems like gene regulatory networks are however much better described by the quenched model, where the links and the Boolean functions are constant in time, and it is this model that has been used in the simulations described here. While the annealed model may provide useful estimates of some properties of the quenched one, it is likely to fail when the analysis considers only dynamical attractors that do not exist in the annealed case; and this seems to happen here, looking at the plots in
Figure 12.
It has also been observed elsewhere that the Derrida plots computed by perturbing a subset of all of the possible initial states (for example, those belonging to some attractor) can be very different from the theoretical ones [
23]. The phenomena related to the peculiarities of restricting the set of states of an RBN require further studies, as the differences shown here confirm.
6. Conclusions and Future Work
The results discussed in the previous sections support the statement that the RI can be effectively used to identify critical states in different kinds of complex systems, both in terms of phase transition and dynamical criticality. Our experimental analysis concerned two prominent classes of complex systems, which stands in favor of the hypothesis that the results may hold in general. The results show also that the RI behaves robustly against sampling effort and system size. Results on both the Ising model and RBN ensembles show that the RI identifies the criticality profile with high precision. In addition, a detailed analysis shows also that, while still detecting critical states, the RI varies across RBN critical ensembles, providing further evidence to the observation that critical RBNs exhibit a spectrum of different behaviors. Moreover, our analysis also supports the statement that the information provided by the dynamics of an RBN along its transients might considerably differ from that of its attractors. Preliminary results in this direction were obtained in [
23,
25].
It is worth emphasizing that, whilst the index was originally proposed with a different aim, it has been proven able to detect features of criticality. One can imagine possible reasons for this interesting phenomenon, but further investigation is required.
Finally, we plan to study the possibility of applying this method to detect early warning signals of change in complex systems, with the aim of identifying in advance dynamical changes toward or away from criticality.