Characterisation of the Effects of Sleep Deprivation on the Electroencephalogram Using Permutation Lempel–Ziv Complexity, a Non-Linear Analysis Tool
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Lempel–Ziv Complexity
- (1)
- The original signal X = x(i), x(i + 1), …, x(n), is symbolised according to the value of the original time series sample compared to the median value (Td) of the time series as:
- (2)
- The symbol series, P = s(1), s(2), …, s(n), is created. P is then parsed and used for the calculation of the complexity measure where,
- (3)
- S and Q (substrings of the symbol series) are allocated with the first and second symbols of the symbol series respectively and complexity counter c(n) is set to 1.
- (4)
- S and Q are merged together to form SQ and, SQv by deleting the last character of the string SQ. For example if, S = x(1), x(2), …, x(i) and Q = x(i + 1), …, x(i + j − 1), x(i + j), then SQ = x(1), x(2), …, x(i), x(i + 1), …, x(i + j) and SQv = x(1), x(2), …, x(i + j − 1).
- (5)
- Substring Q is sought in SQv. If Q is found in SQv, Q is updated by adding next symbol from the symbol series and step 4 is repeated. If not, S is updated to be SQ and Q is set to be the next symbol of {P(n)} and complexity counter is increased by one, lastly step 4 and 5 are repeated until all the series is parsed.
- (6)
- c(n) is the complexity counter of symbol sequence {P(n)} which denotes the number of distinct words found in the sequence. The total number of substrings present in {P(n)} has an upper bound [37] denoted as b(n):
2.3. Permutation Lempel–Ziv Complexity
2.4. Surrogate Data Analysis
2.5. Statistical Analysis
3. Results
3.1. Non-Linear Complexity Measures-Surrogate Data Analysis
3.2. Effects of Sleep Deprivation
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Muto, V.; Jaspar, M.; Meyer, C.; Kusse, C.; Chellappa, S.L.; Degueldre, C.; Balteau, E.; Shaffii-Le Bourdiec, A.; Luxen, A.; Middleton, B.; et al. Local modulation of human brain responses by circadian rhythmicity and sleep debt. Science 2016, 353, 687–690. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Sanchis, C.; Brock, O.; Winsky-Sommerer, R.; Thuret, S. Modulation of Adult Hippocampal Neurogenesis by Sleep: Impacts on Mental Health. Front. Neural Circuits 2017, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Raven, F.; Van der Zee, E.A.; Meerlo, P.; Havekes, R. The role of sleep in regulating structural plasticity and synaptic strength: Implications for memory and cognitive function. Sleep Med. Rev. 2017, in press. [Google Scholar] [CrossRef] [PubMed]
- Baglioni, C.; Navoska, S.; Regen, W.; Spiegelhalder, K.; Feige, B.; Nissen, C.; Reynolds, C.F.; Riemann, D. Sleep and mental disorders: A meta-analysis of polysomnographic research. Psychol. Bull. 2016, 142, 969–990. [Google Scholar] [CrossRef] [PubMed]
- Mander, B.A.; Winer, J.R.; Jagust, W.J.; Walker, M.P. Sleep: A novel mechanistic pathway, biomarker and treatment target in the pathology of Alzheimer’s disease. Trends Neurosci. 2016, 39, 552–566. [Google Scholar] [CrossRef] [PubMed]
- Dijk, D.J. Regulation and functional correlates of slow wave sleep. J. Clin. Sleep Med. 2009, 5 (Suppl. 2), 6–15. [Google Scholar]
- Scammell, T.E.; Arrigoni, E.; Lipton, J.O. Neural circuitry of wakefulness and sleep. Neuron 2017, 93, 747–765. [Google Scholar] [CrossRef] [PubMed]
- Rechtschaffen, A.; Kales, A. A Manual of Standardized Terminology, Techniques, and Scoring Systems for Sleep Stages of Human Subjects; University of California: Los Angeles, CA, USA, 1968. [Google Scholar]
- American Academy of Sleep Medicine. The AASM manual for the scoring of sleep and associated events: Rules. In Terminology and Technical Specifications; AASM: Westchester, NY, USA, 2007. [Google Scholar]
- Winsky-Sommerer, R.; Vyazovskiy, V.V.; Homanics, G.E.; Tobler, I. The effects of THIP (Gabaxadol) on sleep and waking are mediated by the GABAAδ-subunit-containing receptors. Eur. J. Neurosci. 2007, 25, 1893–1899. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, A.; Loomis, S.; Eastwood, B.; Wafford, K.A.; Winsky-Sommerer, R. Gilmour, G. Modelling maintenance of wakefulness in rats: Comparing potential non-invasive sleep-restriction methods and theirs effects on sleep and attentional performance. J. Sleep Res. 2017, 26, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Prerau, M.J.; Brown, R.E.; Bianchi, M.T.; Ellenbogen, M.J.; Purdon, P.L. Sleep neurophysiological dynamics through the lens of multitaper spectral analysis. Physiology 2017, 32, 60–92. [Google Scholar] [CrossRef] [PubMed]
- Borbély, A.A.; Tobler, I.; Hanagasioglu, H. Effect of sleep deprivation on sleep and EEG power spectra in the rat. Behav. Brain Res. 1984, 14, 171–182. [Google Scholar]
- Franken, P.; Malafosse, A.; Tafti, M. Genetic variation in EEG activity during sleep in inbred mice. Am. J. Physiol. 1998, 275 Pt 2, 1127–1137. [Google Scholar]
- Borbély, A.A.; Neuhaus, N.U. Sleep-deprivation: Effects on sleep and EEG in the rat. J. Comp. Physiol. 1979, 133, 71–87. [Google Scholar] [CrossRef]
- Rechtschaffen, A.; Gilliland, M.A.; Bergmann, B.M.; Winter, J.B. Physiological correlates of prolonged sleep deprivation in rats. Science 1983, 221, 182–184. [Google Scholar] [CrossRef] [PubMed]
- Akay, M. Detection and Estimation Methods for Biomedical Signals; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Meyer-Lindenberg, A. The evolution of complexity in human brain development: An EEG study. Electroencephalogr. Clin. Neurophysiol. 1996, 99, 405–411. [Google Scholar] [CrossRef]
- Pijn, J.P.; Van Neerven, J.; Noest, A.; Lopes da Silva, F.H. Chaos or noise in EEG signals; dependence on state and brain site. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 371–381. [Google Scholar] [CrossRef]
- Röschke, J.; Fell, J.; Beckmann, P. The calculation of the first positive Lyapunov exponent in sleep EEG data. Electroencephalogr. Clin. Neurophysiol. 1993, 86, 348–352. [Google Scholar] [CrossRef]
- Güler, N.F.; Übeyli, E.D.; Güler, I. Recurrent neural networks employing Lyapunov exponents for EEG signals classification. Expert Syst. Appl. 2005, 29, 506–514. [Google Scholar] [CrossRef]
- Pardey, J.; Roberts, S.; Tarassenko, L. A review of parametric modelling techniques for EEG analysis. Med. Eng. Phys. 1996, 18, 2–11. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, W.; Peng, C.; Yang, A.C. Nonlinear dynamical analysis of sleep electroencephalography using fractal and entropy approaches. Sleep Med. Rev. 2017, in press. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Tung, W.; Gao, J.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef] [PubMed]
- Turchetti, C.; Crippa, P.; Pirani, M.; Biagetti, G. Representation of nonlinear random transformations by non-Gaussian stochastic neural networks. IEEE Trans. Neural Netw. 2008, 19, 1033–1060. [Google Scholar] [CrossRef] [PubMed]
- Grech, R.; Cassar, T.; Muscat, J.; Camilleri, K.P.; Fabri, S.G.; Zervakis, M.; Xanthopoulos, P.; Sakkalis, V.; Vanrumste, B. Review on solving the inverse problem in EEG source analysis. J. NeuroEng. Rehab. 2008, 5, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Liang, Z.; Li, X. A permutation Lempel–Ziv complexity measure for EEG analysis. Biomed. Signal Process. Control 2015, 19, 102–114. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Ibáñez-Molina, A.J.; Iglesias-Parro, S.; Soriano, M.F.; Aznarte, J.I. Multiscale Lempel–Ziv complexity for EEG measures. Clin. Neurophysiol. 2015, 126, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Hasan, S.; van der Veen, D.R.; Winsky-Sommerer, R.; Dijk, D.J.; Archer, S.N. Altered sleep and behavioural activity phenotypes in PER3-deficient mice. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2011, 301, 1821–1830. [Google Scholar] [CrossRef] [PubMed]
- Palchykova, S.; Winsky-Sommerer, R.; Shen, H.Y.; Boison, D.; Gerling, A.; Tobler, I. Manipulation of adenosine kinase affects sleep regulation in mice. J. Neurosci. 2010, 30, 13157–13165. [Google Scholar] [CrossRef] [PubMed]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Aboy, M.; Hornero, R.; Abasolo, D.; Alvarez, D. Interpretation of the Lempel-Ziv complexity measure I the context of biomedical signal analysis. IEEE Trans. Biomed. Eng. 2006, 53, 2282–2288. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R. Quantifying physiological data with Lempel-Ziv complexity-certain issues. IEEE Trans. Biomed. Eng. 2002, 49, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Abasolo, D.; Simons, S.; Morgado da Silva, R.; Tononi, G.; Vyazovskiy, V.V. Lempel-Ziv complexity of cortical activity during sleep and waking in rats. J. Neurophysiol. 2015, 113, 2742–2752. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Gao, J.; Principe, J.C. Analysis of biomedical signals by the Lempel-Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Qin, C.; Ma, Q.D.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85, 0219061. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal patterns, entropy, and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anaesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Olofsen, E.; Sleigh, J.W.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Unakafova, V.A.; Keller, K. Efficiently measuring complexity on the basis of real-world data. Entropy 2013, 15, 4392–4415. [Google Scholar] [CrossRef]
- King, J.; Sitt, J.D.; Faugeras, F.; Rohaut, B.; El Karoui, I.; Cohen, L.; Naccache, L.; Dehaene, S. Information sharing in the brain indexes consciousness in noncommunicative patients. Curr. Biol. 2013, 23 (Suppl. 1), 1914–1919. [Google Scholar] [CrossRef] [PubMed]
- Dolan, K.T.; Spano, M.L. Surrogate for nonlinear time series analysis. Phys. Rev. E 2001, 64, 046128. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T.; Schmitz, A. Surrogate time series. Physics D 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Palus, M.; Hoyer, D. Detecting nonlinearity and phase synchronization with surrogate data. IEEE Eng. Med. Biol. Mag. 1998, 17, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Achermann, P.; Hartmann, R.; Gunzinger, A.; Guggenbüh, W.; Borbély, A.A. Correlation dimension of the human sleep electroencephalogram: Cyclic changes in the course of the night. Eur. J. Neurosci. 1994, 6, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Rapp, P.; Zimmerman, I.; Albano, A.; Deguzman, G.; Greenbaun, N. Dynamics of spontaneous neural activity in the simian motor cortex: The dimension of chaotic neurons. Phys. Lett. A 1985, 110, 335–338. [Google Scholar] [CrossRef]
- Acharya, R.; Faust, O.; Kannathal, N.; Chua, T.; Laxminarayan, S. Non-linear analysis of EEG signals at various sleep stages. Comput. Methods Programs Biomed. 2005, 80, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Achermann, P.; Hartmann, R.; Gunzinger, A.; Guggenbühl, W.; Borbély, A.A. All-night sleep EEG and artificial stochastic control signals have similar correlation dimensions. Electroencephalogr. Clin. Neurophysiol. 1994, 90, 384–387. [Google Scholar] [CrossRef]
- Fell, J.; Röschke, J.; Mann, K.; Schäffner, C. Discrimination of sleep stages: A comparison between spectral and nonlinear EEG measures. Electroencephalogr. Clin. Neurophysiol. 1996, 98, 401–410. [Google Scholar] [CrossRef]
- Weiss, B.; Clemens, Z.; Bódizs, R.; Vágó, Z.; Halász, P. Spatio-temporal analysis of monofractal and multifractal properties of the human sleep EEG. J. Neurosci. Methods 2009, 185, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Kim, D.; Kim, I.; Park, K.S.; Kim, S.I. Nonlinear-analysis of human sleep EEG using detrended fluctuation analysis. Med. Eng. Phys. 2004, 26, 773–776. [Google Scholar] [CrossRef] [PubMed]
- Dai-Jin Kim, M. Effect of total sleep deprivation on the dimensional complexity of the waking EEG. Sleep 2001, 24, 197–202. [Google Scholar]
- Nicolaou, N.; Georgiou, J. The use of permutation entropy to characterize sleep electroencephalograms. Clin. EEG Neurosci. 2011, 42, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Bruhn, J.; Röpcke, H.; Rehberg, B.; Bouillon, T.; Hoeft, A. Electroencephalogram approximate entropy correctly classifies the occurrence of burst suppression pattern as increasing anaesthetic drug effect. J. Am. Soc. Anesthesiol. 2000, 93, 981–985. [Google Scholar] [CrossRef]
- Burioka, N.; Miyata, M.; Cornélissen, G.; Halberg, F.; Takeshima, T.; Kaplan, D.T. Approximate entropy in the electroencephalogram during wake and sleep. Clin. EEG Neurosci. 2005, 36, 21–24. [Google Scholar] [CrossRef] [PubMed]
- Bruce, E.N.; Bruce, M.C.; Vennelaganti, S. Sample entropy tracks changes in electroencephalogram power spectrum with sleep state and aging. J. Clin. Neurophysiol. 2009, 26, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Franken, P.; Dijk, D.J.; Tobler, I.; Borbély, A.A. Sleep deprivation in rats: Effects on EEG power spectra, vigilance states, and cortical temperature. Am. J. Physiol. 1991, 261 Pt 2, 198–208. [Google Scholar]
- Tobler, I.; Borbély, A.A. The effect of 3-h and 6-h sleep deprivation on sleep and EEG spectra of the rat. Behav. Brain Res. 1990, 36, 73–78. [Google Scholar] [CrossRef]
- Steriade, M. The corticothalamic system in sleep. Front. Biosci. 2003, 878–899. [Google Scholar] [CrossRef]
- Timofeev, I.; Bazhenov, M.; Seigneur, J.; Sejnowski, T. Neuronal synchronization and thalamocortical rhythms in sleep, wake and epilepsy. In Jasper’s Basic Mechanisms of the Epilepsies, 4th ed.; Noebels, J.L., Avoli, M., Rogawski, M.A., Olsen, R.W., Delgado-Escueta, A.V., Eds.; National Centre for Biotechnology Information (US): Bethesda, MD, USA, 2012. [Google Scholar]
- Amigo, J.M.; Szczepanski, J.; Wajnryb, E.; Sanchez-Vives, M.V. Estimating the entropy rate of spike trains via Lempel-Ziv complexity. Neural Comput. 2004, 16, 717–736. [Google Scholar] [CrossRef] [PubMed]
- Amigo, J.M.; Szczepanski, J.; Wajnryb, E.; Sanchez-Vives, M.V. On the number of states of the neuronal sources. Biosystems 2003, 68, 57–66. [Google Scholar] [CrossRef]
- Arnold, M.M.; Szczepanski, J.; Montejo, N.; Amigo, J.M.; Sanchez-Vives, M.V. Information content in cortical spike trains during brain state transitions. J. Sleep Res. 2013, 22, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Szczepański, J.; Amigo, J.M.; Wajnryb, E.; Sanchez-Vives, M.V. Application of Lempel–Ziv complexity to the analysis of neural discharges. Network 2003, 14, 335–350. [Google Scholar] [CrossRef] [PubMed]
- Szczepański, J.; Amigo, J.M.; Wajnryb, E.; Sanchez-Vives, M.V. Characterizing spike trains with Lempel–Ziv complexity. Neurocomputing 2004, 58 (Suppl. C), 79–84. [Google Scholar] [CrossRef]
- Tononi, G.; Edelman, G.M.; Sporns, O. Complexity and coherency: Integrating information in the brain. Trends Cogn. Sci. 1998, 2, 474–484. [Google Scholar] [CrossRef]
- Bai, Y.; Liang, Z.; Li, X.; Voss, L.J.; Sleigh, J.W. Permutation Lempel-Ziv complexity measure of electroencephalogram in GABAergic anaesthetics. Physiol. Meas. 2015, 36, 2483–2501. [Google Scholar] [CrossRef] [PubMed]
- Mateos, D.M.; Guevara Erra, R.; Wennberg, R.; Perez Velaquez, J.L. Measures of entropy and complexity in altered states of consciousness. arXiv, 2017; arXiv:1701.07061. [Google Scholar]
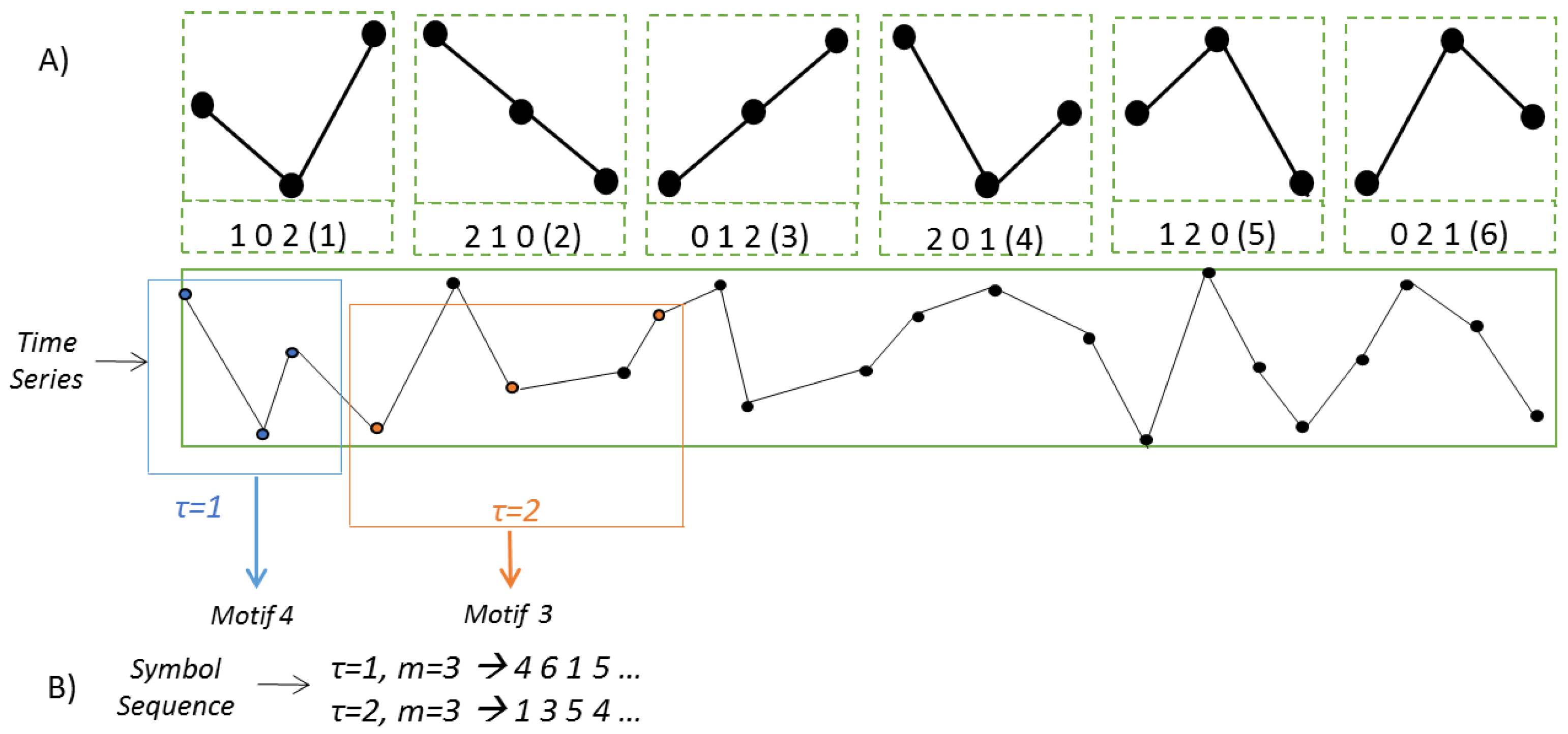
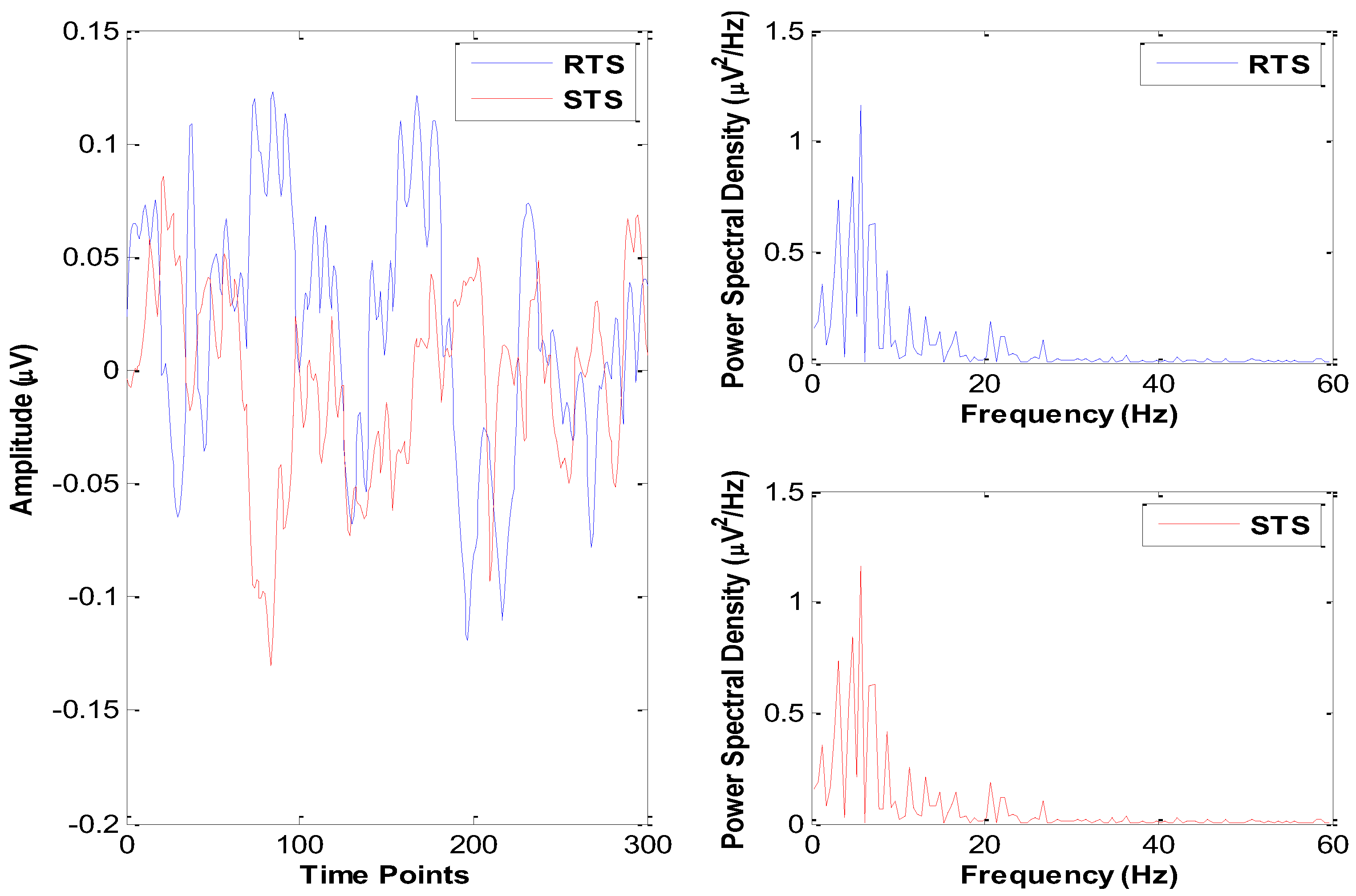
 ), NREM sleep (
), NREM sleep ( ) and REM sleep (
) and REM sleep ( ). Recordings start at light onset (Baseline Light) and continued with Baseline Dark followed by recovery sleep at light (Recovery Light) and dark (Recovery Dark). Lower panels (A) and (B): LZC and PLZC values (Mean ± SEM; red in RTS, black in STS) in each vigilance state during the course of baseline. * p < 0.05 (Related Samples Wilcoxon Signed Test between RTS and STS).
). Recordings start at light onset (Baseline Light) and continued with Baseline Dark followed by recovery sleep at light (Recovery Light) and dark (Recovery Dark). Lower panels (A) and (B): LZC and PLZC values (Mean ± SEM; red in RTS, black in STS) in each vigilance state during the course of baseline. * p < 0.05 (Related Samples Wilcoxon Signed Test between RTS and STS).
 ), NREM sleep (
), NREM sleep ( ) and REM sleep (
) and REM sleep ( ). Recordings start at light onset (Baseline Light) and continued with Baseline Dark followed by recovery sleep at light (Recovery Light) and dark (Recovery Dark). Lower panels (A) and (B): LZC and PLZC values (Mean ± SEM; red in RTS, black in STS) in each vigilance state during the course of baseline. * p < 0.05 (Related Samples Wilcoxon Signed Test between RTS and STS).
). Recordings start at light onset (Baseline Light) and continued with Baseline Dark followed by recovery sleep at light (Recovery Light) and dark (Recovery Dark). Lower panels (A) and (B): LZC and PLZC values (Mean ± SEM; red in RTS, black in STS) in each vigilance state during the course of baseline. * p < 0.05 (Related Samples Wilcoxon Signed Test between RTS and STS).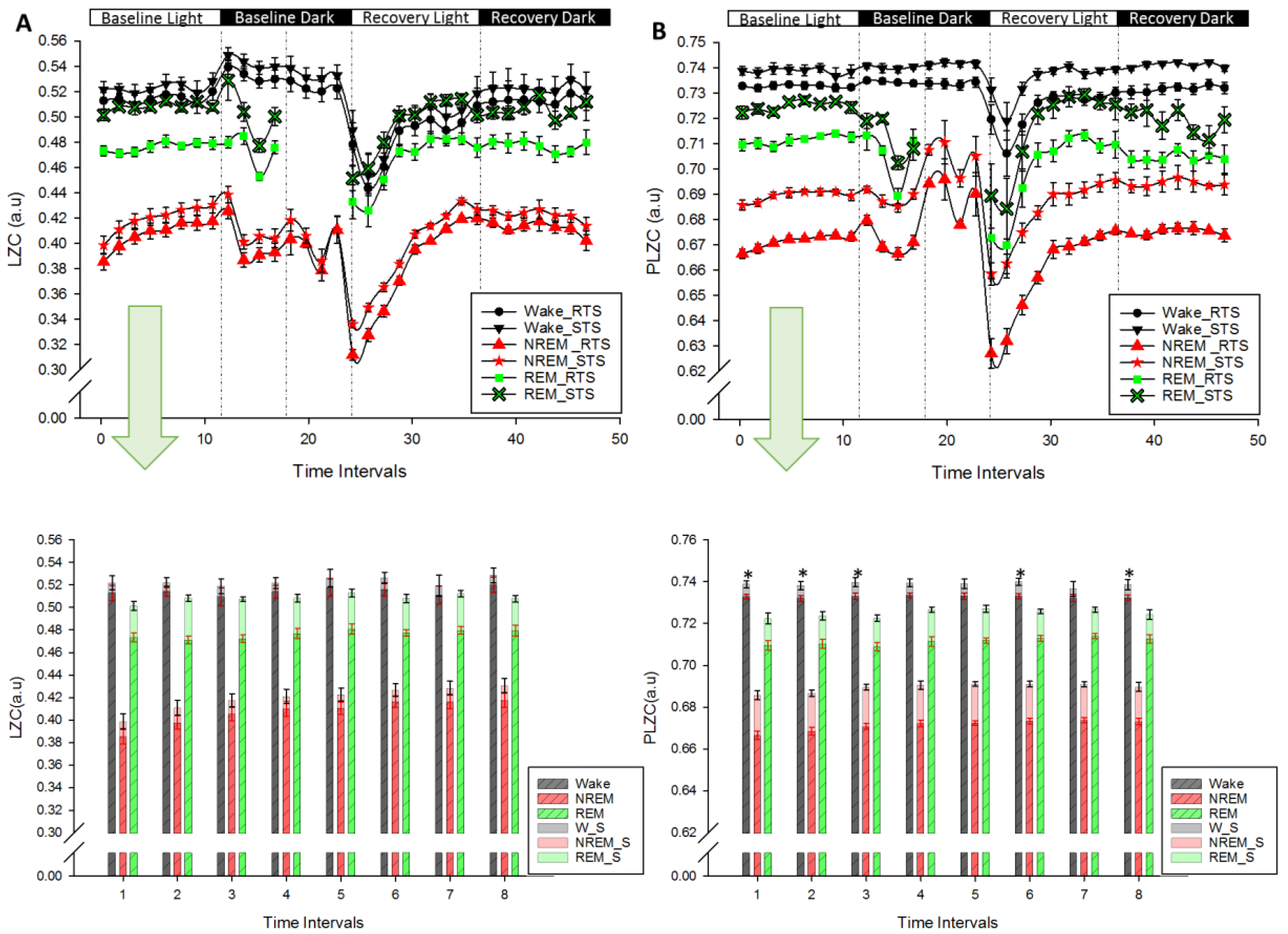
 left panel graphs,
left panel graphs,  right panels) BL; Baseline Dark (
right panels) BL; Baseline Dark ( ) BD; Recovery Light (
) BD; Recovery Light ( ) RL; Recovery Dark (
) RL; Recovery Dark ( ) RD. (A–C): Changes at complexity in wakefulness, NREM and REM sleep respectively were plotted over the bout of periods. (D–F): Significant changes in complexity in the time intervals were marked (Repeated measures ANOVA, Factors: “Time Intervals”, “VS”, “Period”), Bonferroni comparisons in time intervals #1 to 4 (** p < 0.01, *** p < 0.001).
) RD. (A–C): Changes at complexity in wakefulness, NREM and REM sleep respectively were plotted over the bout of periods. (D–F): Significant changes in complexity in the time intervals were marked (Repeated measures ANOVA, Factors: “Time Intervals”, “VS”, “Period”), Bonferroni comparisons in time intervals #1 to 4 (** p < 0.01, *** p < 0.001).
 left panel graphs,
left panel graphs,  right panels) BL; Baseline Dark (
right panels) BL; Baseline Dark ( ) BD; Recovery Light (
) BD; Recovery Light ( ) RL; Recovery Dark (
) RL; Recovery Dark ( ) RD. (A–C): Changes at complexity in wakefulness, NREM and REM sleep respectively were plotted over the bout of periods. (D–F): Significant changes in complexity in the time intervals were marked (Repeated measures ANOVA, Factors: “Time Intervals”, “VS”, “Period”), Bonferroni comparisons in time intervals #1 to 4 (** p < 0.01, *** p < 0.001).
) RD. (A–C): Changes at complexity in wakefulness, NREM and REM sleep respectively were plotted over the bout of periods. (D–F): Significant changes in complexity in the time intervals were marked (Repeated measures ANOVA, Factors: “Time Intervals”, “VS”, “Period”), Bonferroni comparisons in time intervals #1 to 4 (** p < 0.01, *** p < 0.001).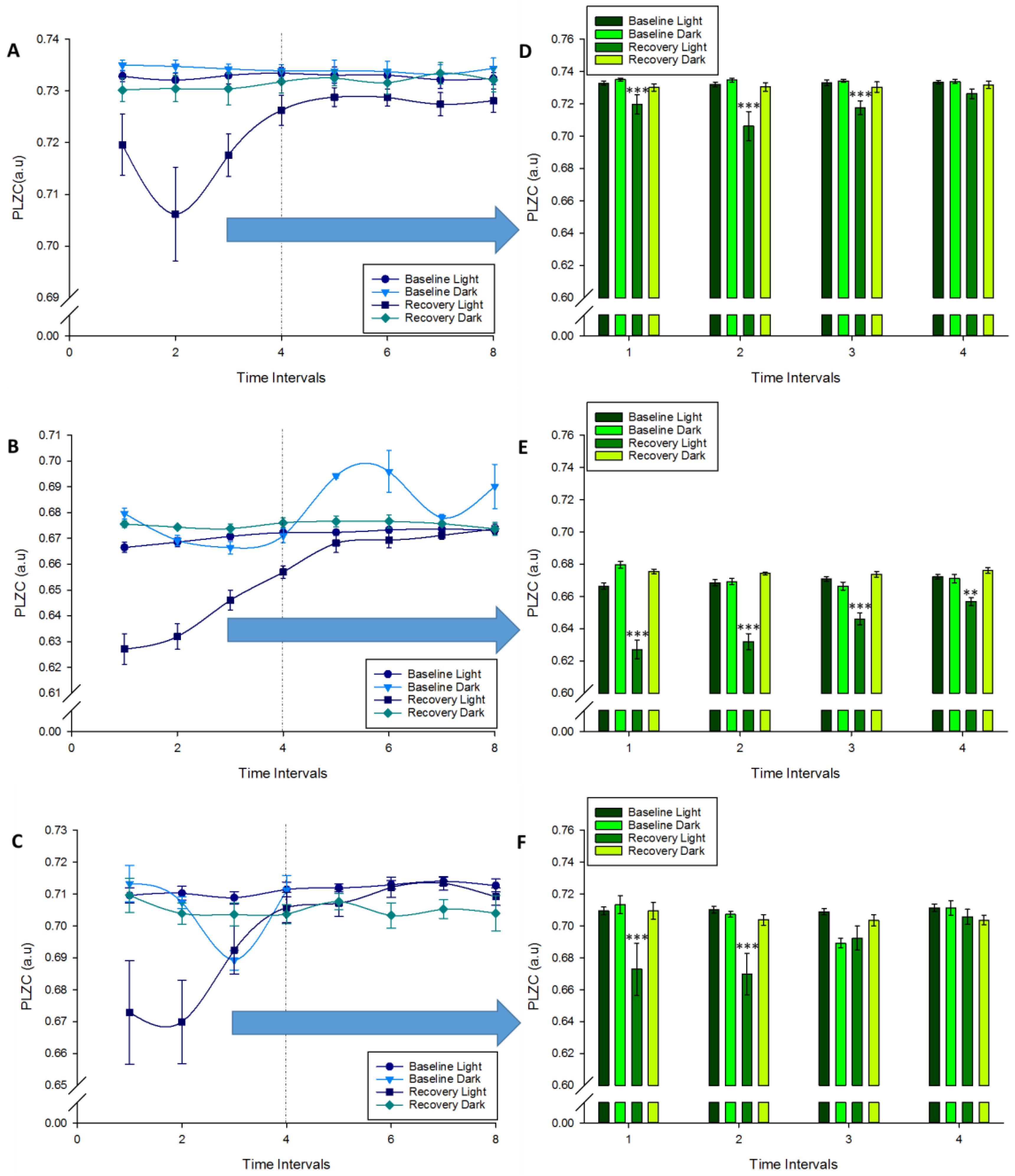
| Input Parameters/Periods | BL (% of Epochs) | BD (% of Epochs) | RL (% of Epochs) | RD (% of Epochs) |
|---|---|---|---|---|
| m = 3 and τ = 1 | 91.67 | 84.21 | 85.25 | 82.14 |
| m = 4 and τ = 1 | 100 | 94.74 | 96.72 | 94.05 |
| m = 5 and τ = 1 | 95.83 | 92.11 | 95.08 | 94.05 |
| m = 6 and τ = 1 | 100 | 94.74 | 96.72 | 96.43 |
| Lempel–Ziv Complexity | Permutation Lempel–Ziv Complexity | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Period | BL | BD | RL | RD | BL | BD | RL | RD | |
| Time Intervals | 1 | 0.098 | 0.240 | 0.018 | 0.129 | 0.029 * | 0.039 * | 0.051 | 0.042 * |
| 2 | 0.166 | 0.039 * | 0.117 | 0.093 | 0.046 * | 0.028 * | 0.092 | 0.073 | |
| 3 | 0.164 | 0.065 | 0.118 | 0.090 | 0.033 * | 0.016 * | 0.060 | 0.072 | |
| 4 | 0.151 | 0.073 | 0.091 | 0.124 | 0.066 | 0.206 | 0.008 * | 0.018 * | |
| 5 | 0.145 | N/A | 0.130 | 0.216 | 0.069 | N/A | 0.057 | 0.021 * | |
| 6 | 0.140 | N/A | 0.115 | 0.122 | 0.032 * | N/A | 0.031 * | 0.043 * | |
| 7 | 0.166 | N/A | 0.133 | 0.136 | 0.063 | N/A | 0.046 * | 0.101 | |
| 8 | 0.130 | N/A | 0.166 | 0.121 | 0.029 * | N/A | 0.047 * | 0.027 * | |
| Period/VS | Wakefulness | NREM Sleep | REM Sleep |
|---|---|---|---|
| Baseline Light (Mean ± SEM) | 0.733 ± 0.001 | 0.671 ± 0.002 | 0.711 ± 0.002 |
| Baseline Dark (Mean ± SEM) | 0.734 ± 0.002 | 0.681 ± 0.004 | 0.705 ± 0.004 |
| Recovery Light (Mean ± SEM) | 0.723 ± 0.004 | 0.656 ± 0.003 | 0.698 ± 0.007 |
| Recovery Dark (Mean ± SEM) | 0.732 ± 0.002 | 0.675 ± 0.002 | 0.705 ± 0.004 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tosun, P.D.; Abásolo, D.; Stenson, G.; Winsky-Sommerer, R. Characterisation of the Effects of Sleep Deprivation on the Electroencephalogram Using Permutation Lempel–Ziv Complexity, a Non-Linear Analysis Tool. Entropy 2017, 19, 673. https://doi.org/10.3390/e19120673
Tosun PD, Abásolo D, Stenson G, Winsky-Sommerer R. Characterisation of the Effects of Sleep Deprivation on the Electroencephalogram Using Permutation Lempel–Ziv Complexity, a Non-Linear Analysis Tool. Entropy. 2017; 19(12):673. https://doi.org/10.3390/e19120673
Chicago/Turabian StyleTosun, Pinar Deniz, Daniel Abásolo, Gillian Stenson, and Raphaelle Winsky-Sommerer. 2017. "Characterisation of the Effects of Sleep Deprivation on the Electroencephalogram Using Permutation Lempel–Ziv Complexity, a Non-Linear Analysis Tool" Entropy 19, no. 12: 673. https://doi.org/10.3390/e19120673
APA StyleTosun, P. D., Abásolo, D., Stenson, G., & Winsky-Sommerer, R. (2017). Characterisation of the Effects of Sleep Deprivation on the Electroencephalogram Using Permutation Lempel–Ziv Complexity, a Non-Linear Analysis Tool. Entropy, 19(12), 673. https://doi.org/10.3390/e19120673






