Capturing Causality for Fault Diagnosis Based on Multi-Valued Alarm Series Using Transfer Entropy
Abstract
1. Introduction
2. Alarm Series and Its Extended Form
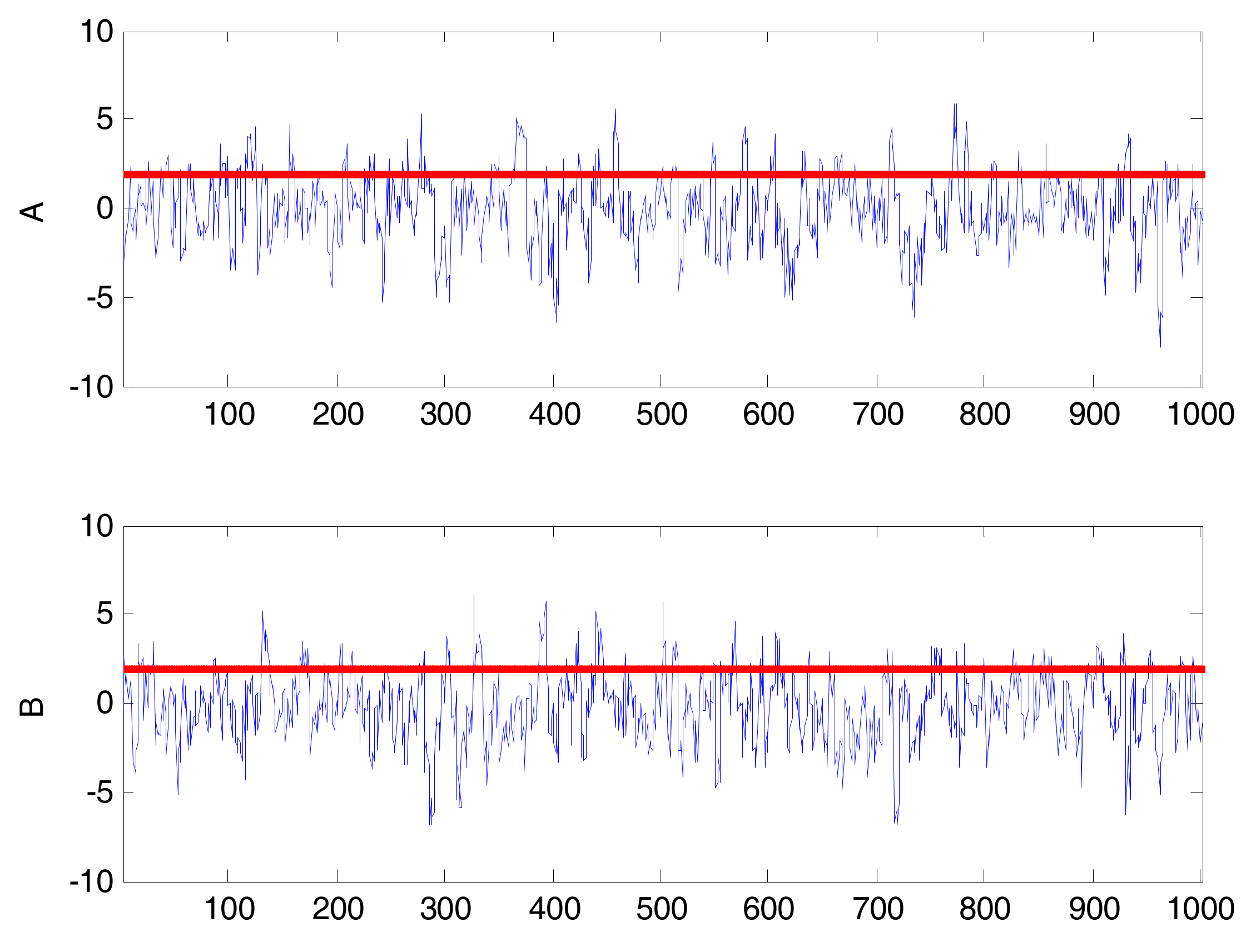
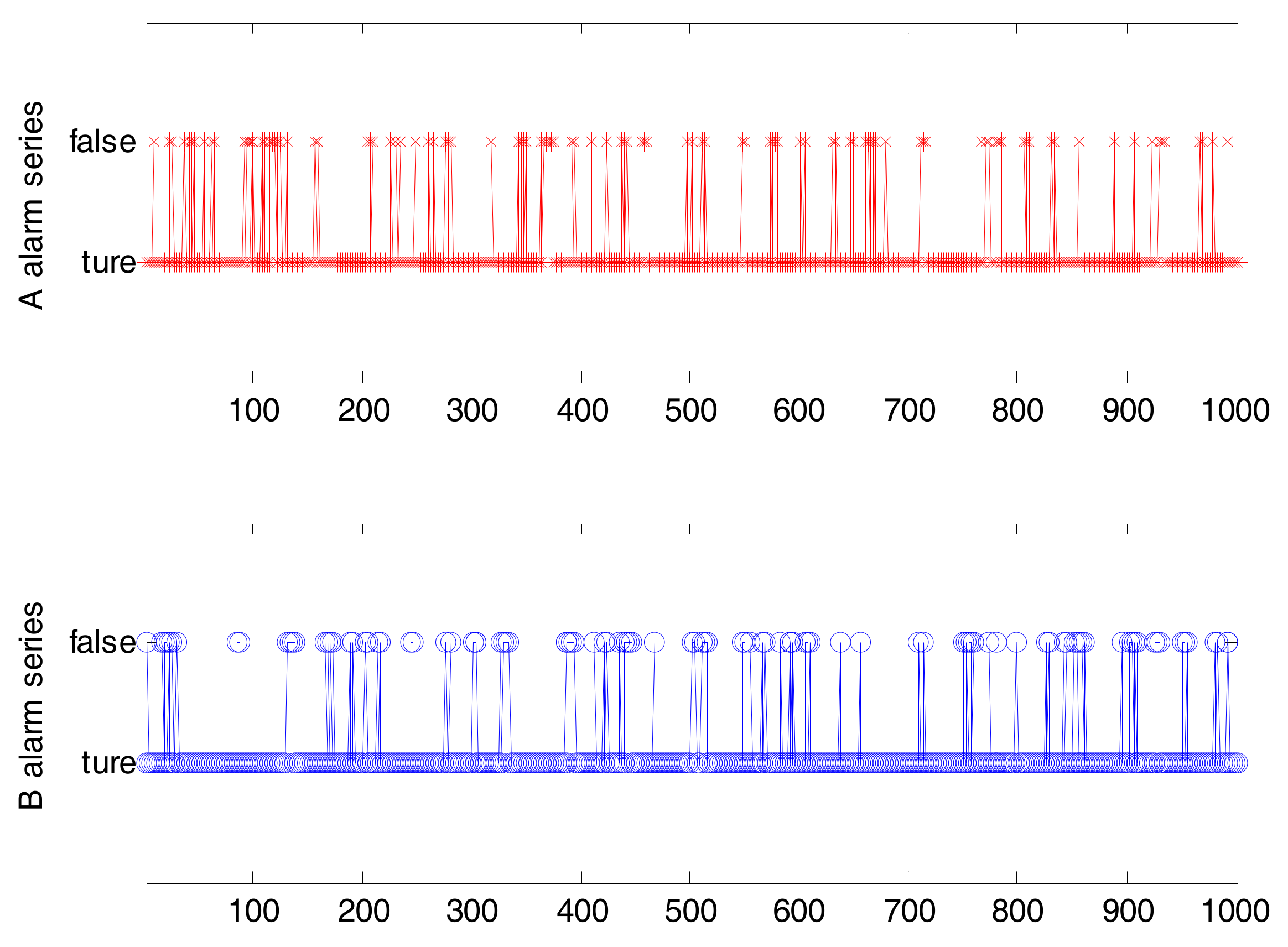
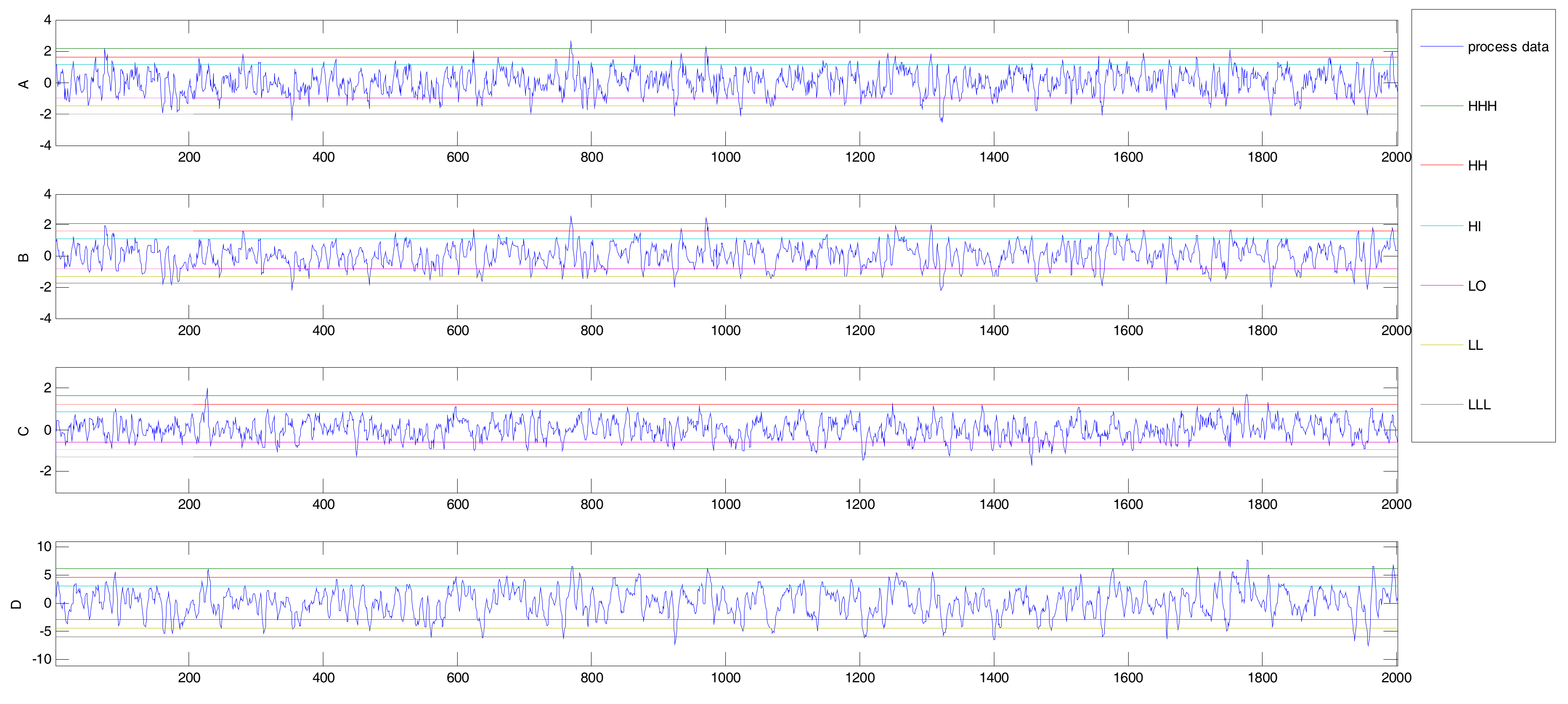
2.1. Binary Alarm Series
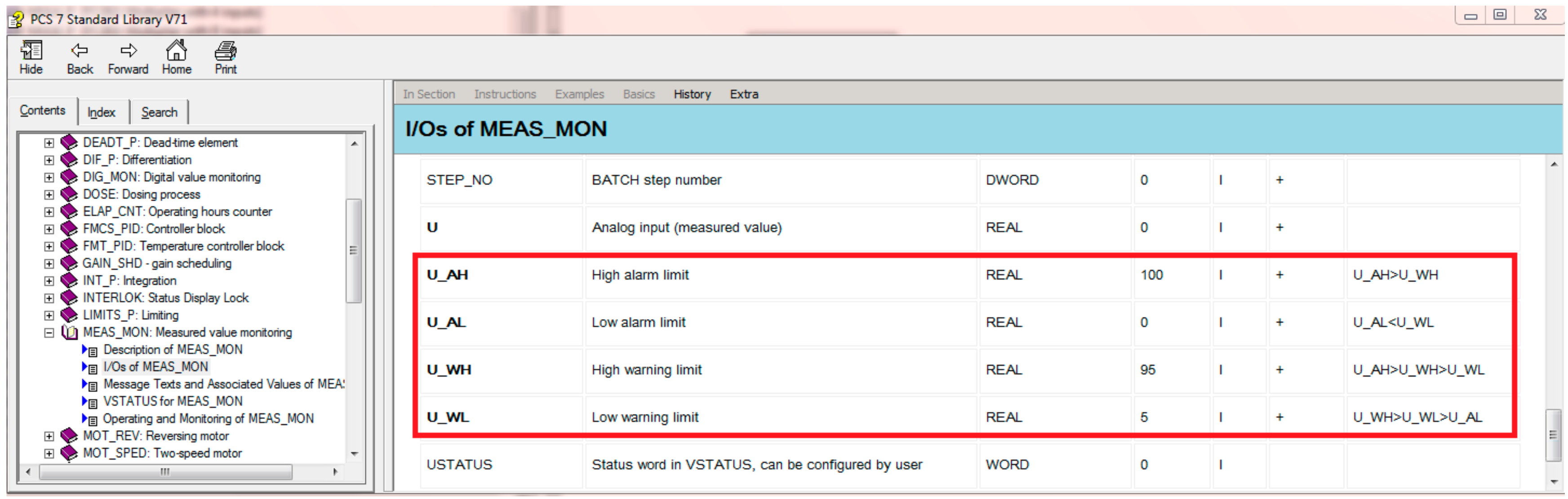
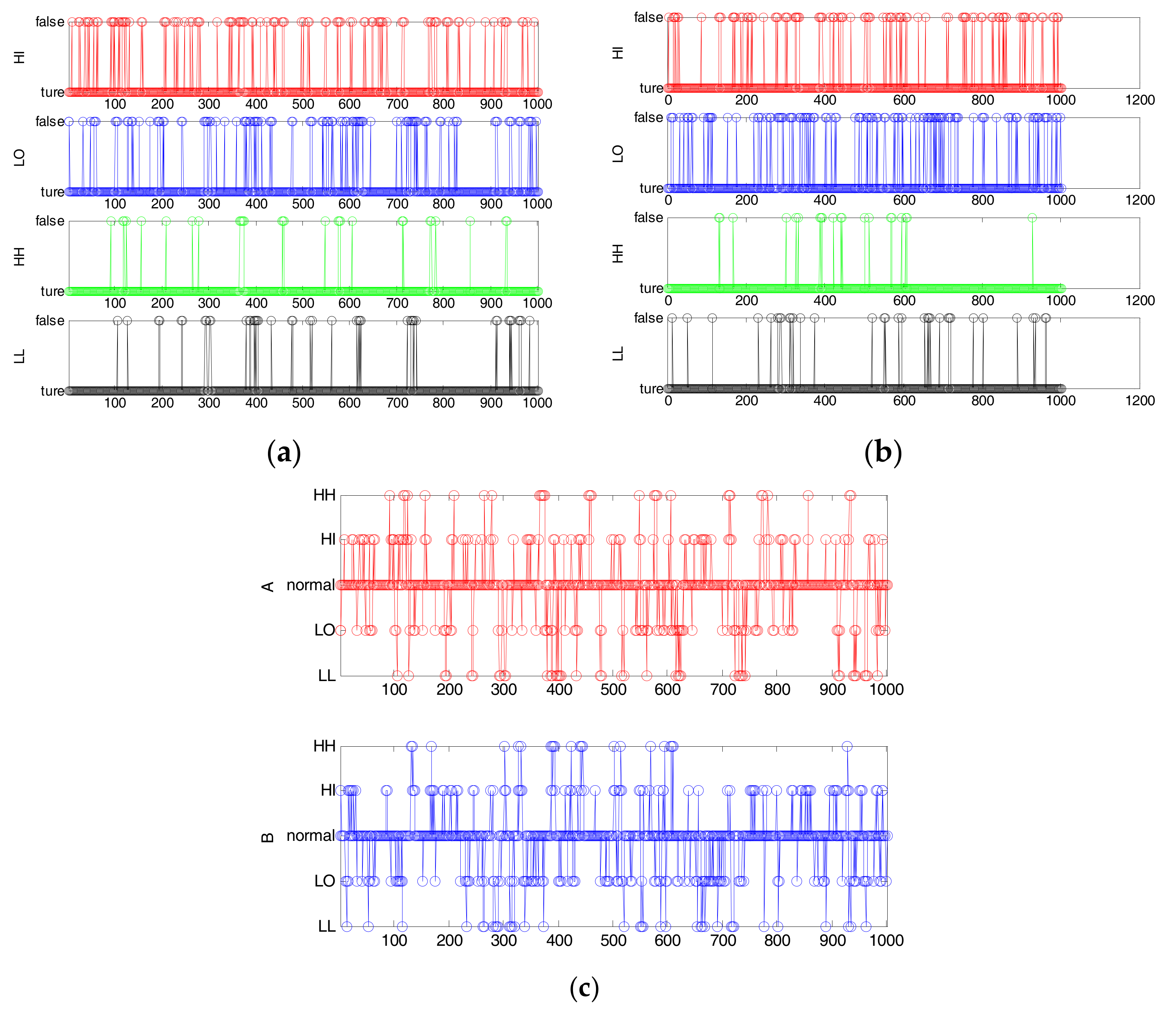
2.2. Multi-Valued Alarm Series
3. Transfer Entropy and Mutual Information
3.1. Transfer Entropy
3.2. Conditional Mutual Information
3.2.1. Mutual Information
3.2.2. Conditional Mutual Information
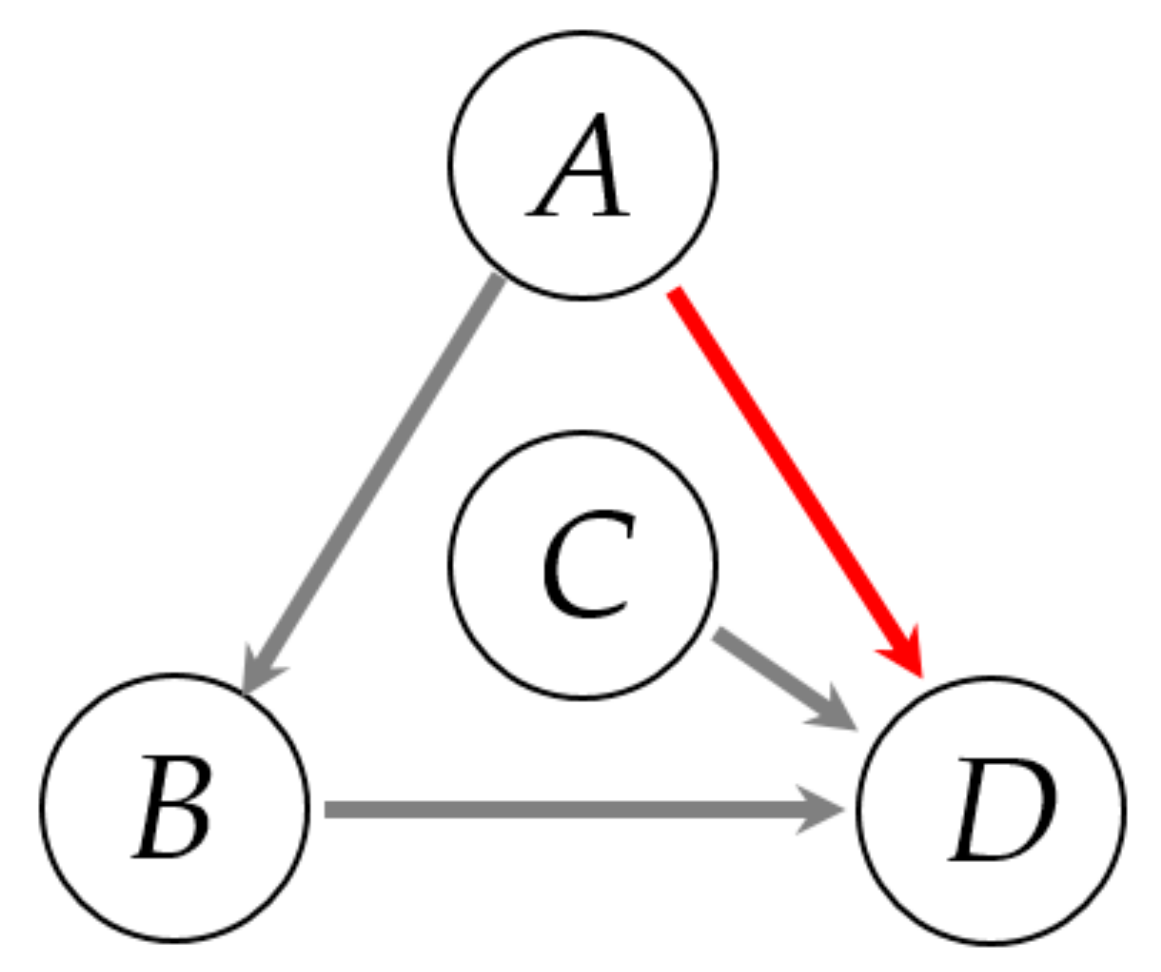
4. Detection of Direct Causality via Multi-Valued Alarm Series
4.1. Detection of Causality via TE
4.2. Detection of Direct Causality via CMI
5. Significance Test
6. Case Studies
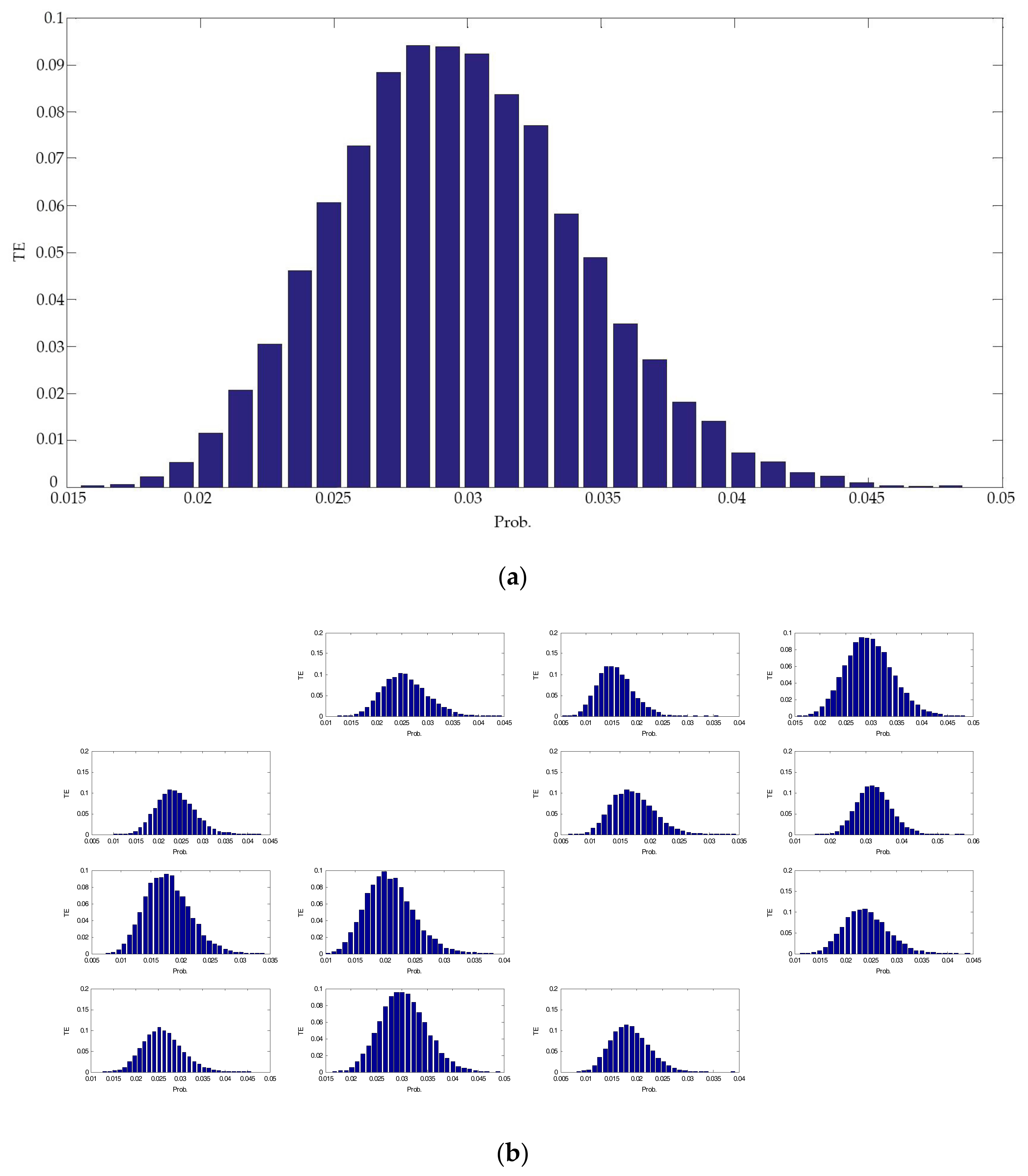
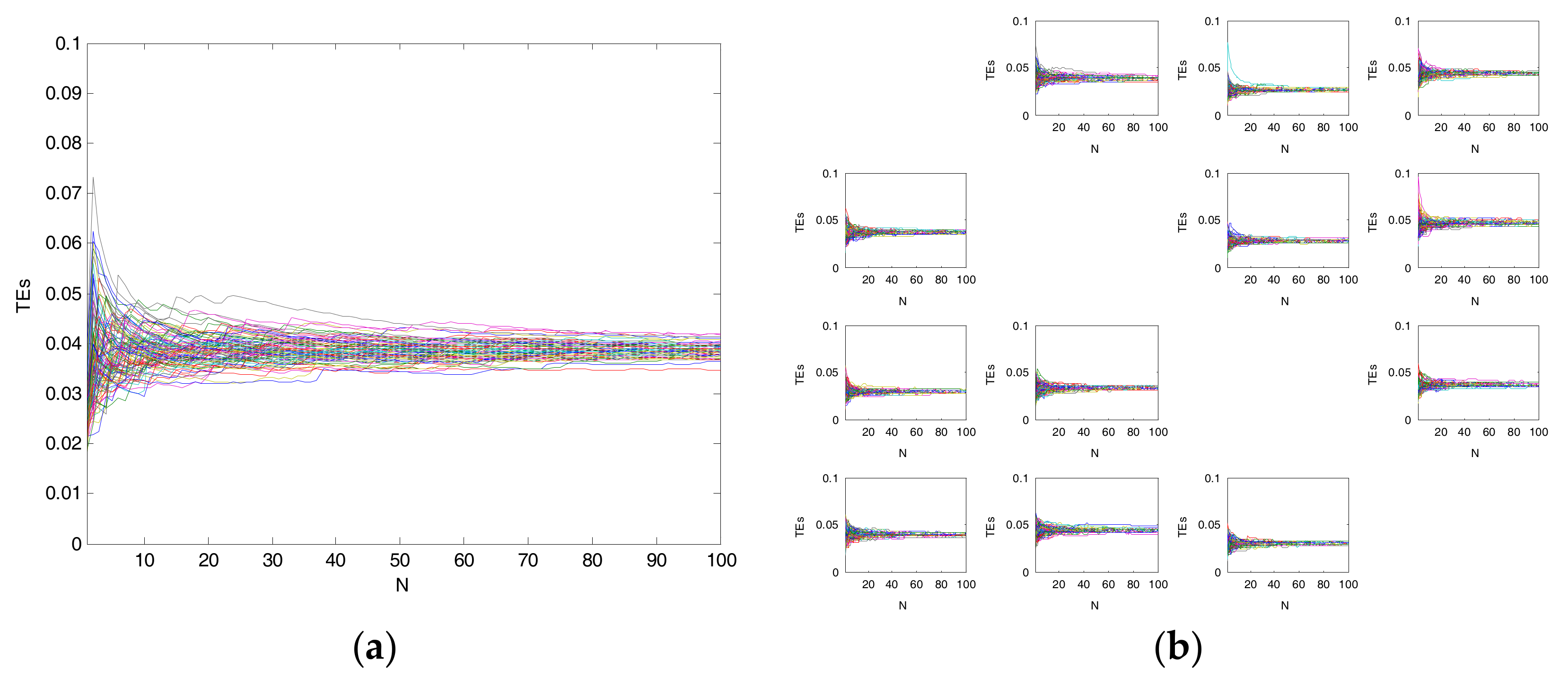
6.1. Numerical Example
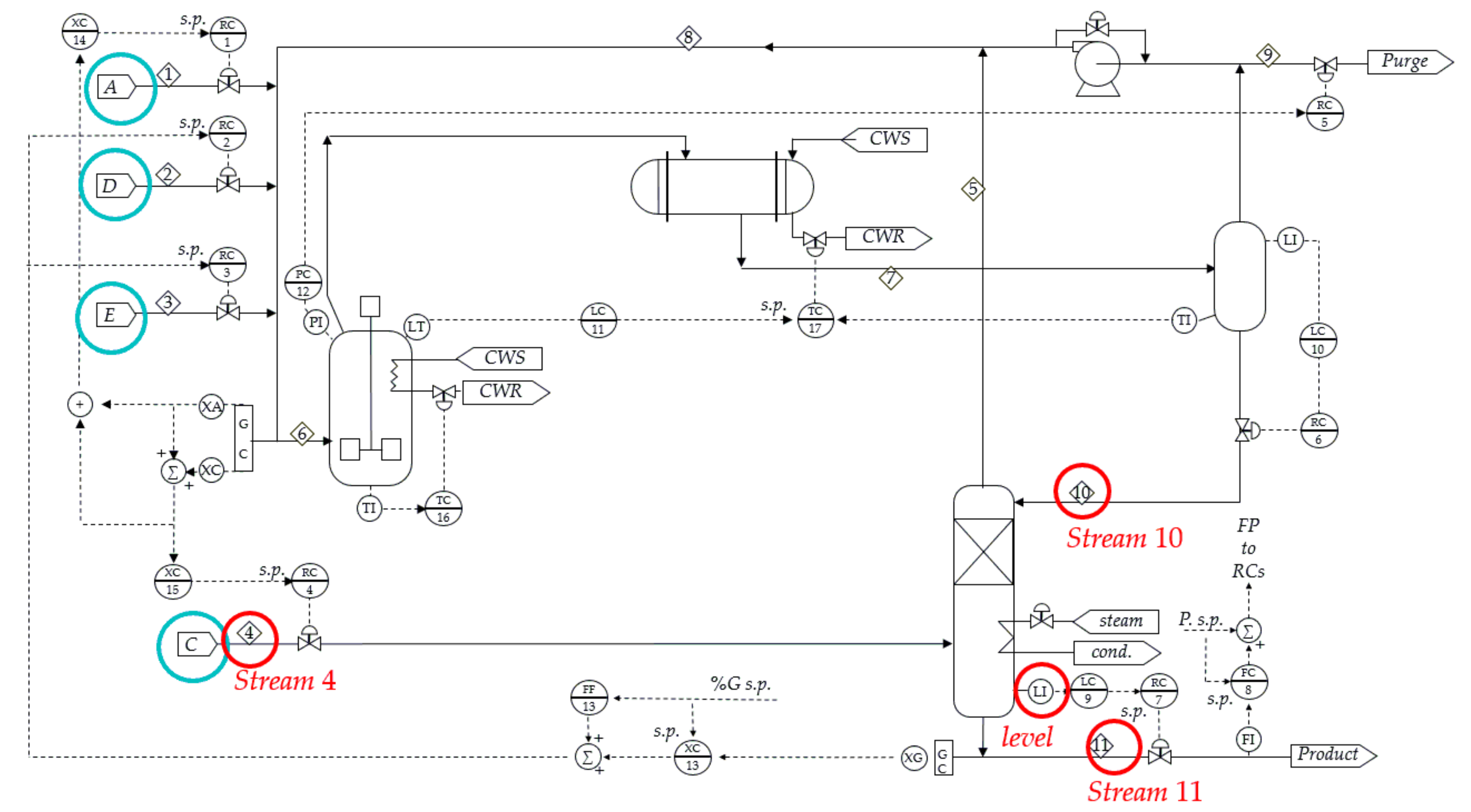
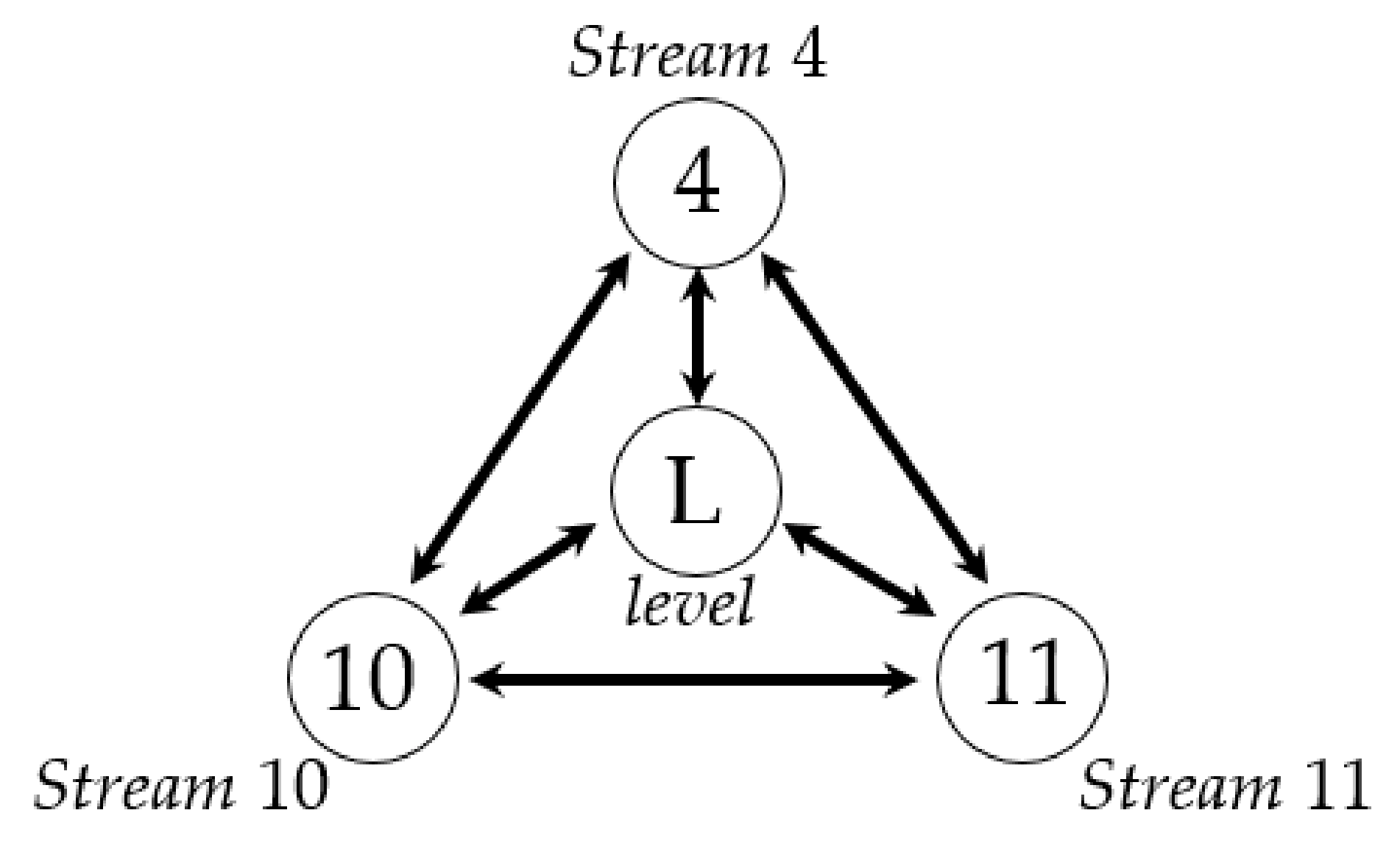
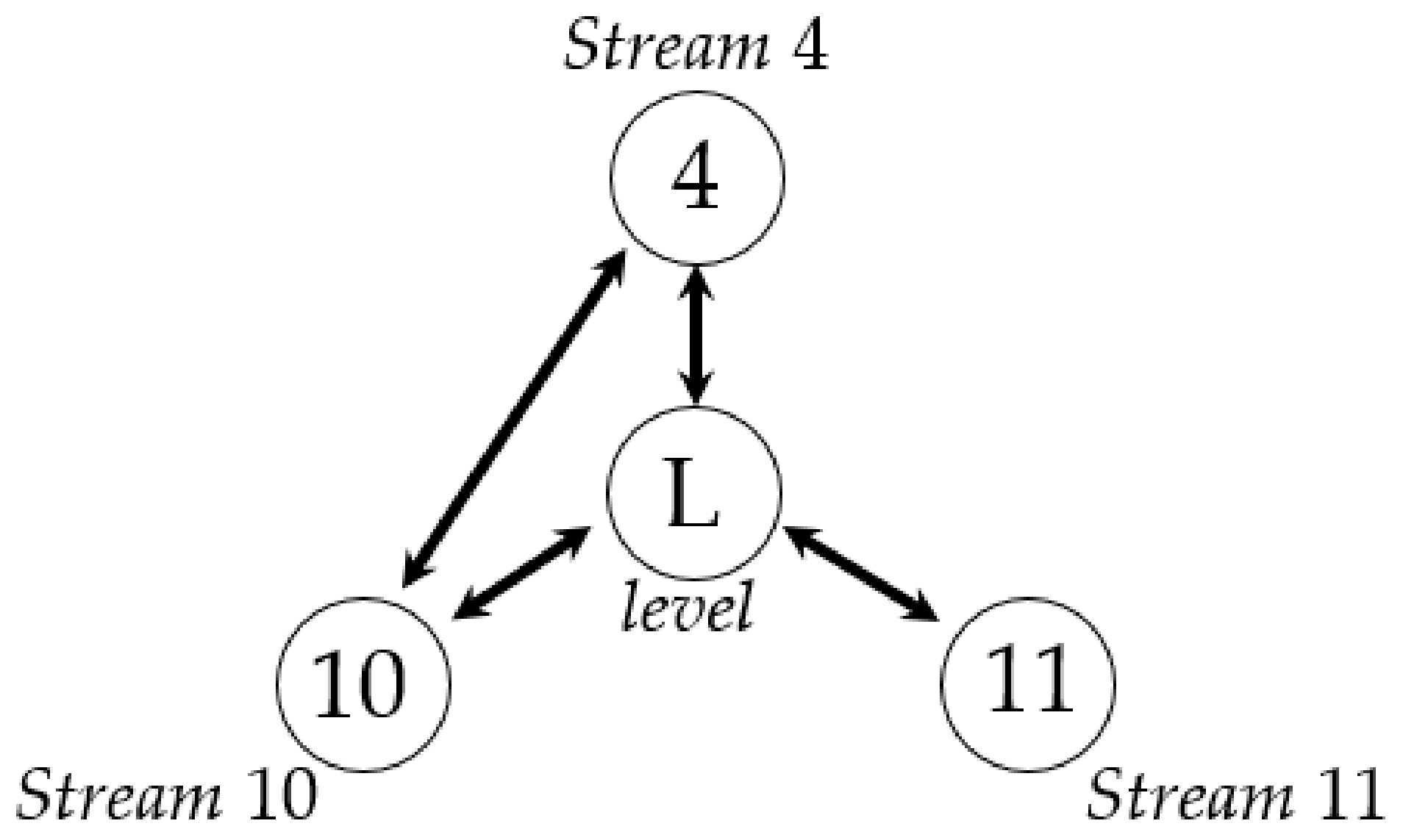
6.2. Industrial Example
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, F.; Duan, P.; Shah, S.L.; Chen, T.W. Capturing Causality from Process Data. In Capturing Connectivity and Causality in Complex Industrial Processes; Springer: New York, NY, USA, 2014; pp. 57–62. [Google Scholar]
- Khandekar, S.; Muralidhar, K. Springerbriefs in applied sciences and technology. In Dropwise Condensation on Inclined Textured Surfaces; Springer: New York, NY, USA, 2014; pp. 17–72. [Google Scholar]
- Pant, G.B.; Rupa Kumar, K. Climates of south asia. Geogr. J. 1998, 164, 97–98. [Google Scholar]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Hiemstra, C.; Jones, J.D. Testing for linear and nonlinear granger causality in the stock price-volume relation. J. Financ. 1994, 49, 1639–1664. [Google Scholar]
- Wang, W.X.; Yang, R.; Lai, Y.C.; Kovanis, V.; Grebogi, C. Predicting catastrophes in nonlinear dynamical systems by compressive sensing. Phys. Rev. Lett. 2011, 106, 154101. [Google Scholar] [CrossRef] [PubMed]
- Hlavackova-Schindler, K.; Palus, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information. Phys. Rep. 2007, 441. [Google Scholar] [CrossRef]
- Duggento, A.; Bianciardi, M.; Passamonti, L.; Wald, L.L.; Guerrisi, M.; Barbieri, R.; Toschi, N. Globally conditioned granger causality in brain-brain and brain-heart interactions: A combined heart rate variability/ultra-high-field (7 t) functional magnetic resonance imaging study. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-K.; Wu, G.-H.; Xie, C.-L.; Duan, Z.-Y.; Peng, M.-J.; Li, M.-K. A fault diagnosis method based on signed directed graph and matrix for nuclear power plants. Nucl. Eng. Des. 2016, 297, 166–174. [Google Scholar] [CrossRef]
- Maurya, M.R.; Rengaswamy, R.; Venkatasubramanian, V. A systematic framework for the development and analysis of signed digraphs for chemical processes. 2. Control loops and flowsheet analysis. Ind. Eng. Chem. Res. 2003, 42, 4811–4827. [Google Scholar] [CrossRef]
- Bauer, M.; Thornhill, N.F. A practical method for identifying the propagation path of plant-wide disturbances. J. Process Control 2008, 18, 707–719. [Google Scholar] [CrossRef]
- Chen, W.; Larrabee, B.R.; Ovsyannikova, I.G.; Kennedy, R.B.; Haralambieva, I.H.; Poland, G.A.; Schaid, D.J. Fine mapping causal variants with an approximate bayesian method using marginal test statistics. Genetics 2015, 200, 719–736. [Google Scholar] [CrossRef] [PubMed]
- Ghysels, E.; Hill, J.B.; Motegi, K. Testing for granger causality with mixed frequency data. J. Econom. 2016, 192, 207–230. [Google Scholar] [CrossRef]
- Yang, F.; Fan, N.J.; Ye, H. Application of PDC method in causality analysis of chemical process variables. J. Tsinghua Univ. (Sci. Technol.) 2013, 210–214. [Google Scholar]
- Bauer, M.; Cox, J.W.; Caveness, M.H.; Downs, J.J. Finding the direction of disturbance propagation in a chemical process using transfer entropy. IEEE Trans. Control Syst. Technol. 2007, 15, 12–21. [Google Scholar] [CrossRef]
- Duan, P.; Yang, F.; Chen, T.; Shah, S.L. Direct causality detection via the transfer entropy approach. IEEE Trans. Control Syst. Technol. 2013, 21, 2052–2066. [Google Scholar] [CrossRef]
- Duan, P.; Yang, F.; Shah, S.L.; Chen, T. Transfer zero-entropy and its application for capturing cause and effect relationship between variables. IEEE Trans. Control Syst. Technol. 2015, 23, 855–867. [Google Scholar] [CrossRef]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, 158101. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Yang, F. Detection of causality between process variables based on industrial alarm data using transfer entropy. Entropy 2015, 17, 5868–5887. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Chen, T. Detection of correlated alarms based on similarity coefficients of binary data. IEEE Trans. Autom. Sci. Eng. 2013, 10, 1014–1025. [Google Scholar] [CrossRef]
- Yang, F.; Shah, S.L.; Xiao, D.; Chen, T. Improved correlation analysis and visualization of industrial alarm data. ISA Trans. 2012, 51, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Dehnad, K. Density Estimation for Statistics and Data Analysis by Bernard Silverman; Chapman and Hall: London, UK, 1986; pp. 296–297. [Google Scholar]
- Cover, T. Information Theory and Statistics. In Proceedings of the IEEE-IMS Workshop on Information Theory and Statistics, Alexandria, VA, USA, 27–29 October 1994; p. 2. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Tsinghua University Press: Beijing, China, 2003; pp. 1600–, 1601. [Google Scholar]
- Palus, M.; Komárek, V.; Hrncír, Z.; Sterbová, K. Synchronization as adjustment of information rates: Detection from bivariate time series. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 63, 046211. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 1997; p. 491. [Google Scholar]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Ricker, N.L. Decentralized control of the tennessee eastman challenge process. J. Process Control 1996, 6, 205–221. [Google Scholar] [CrossRef]


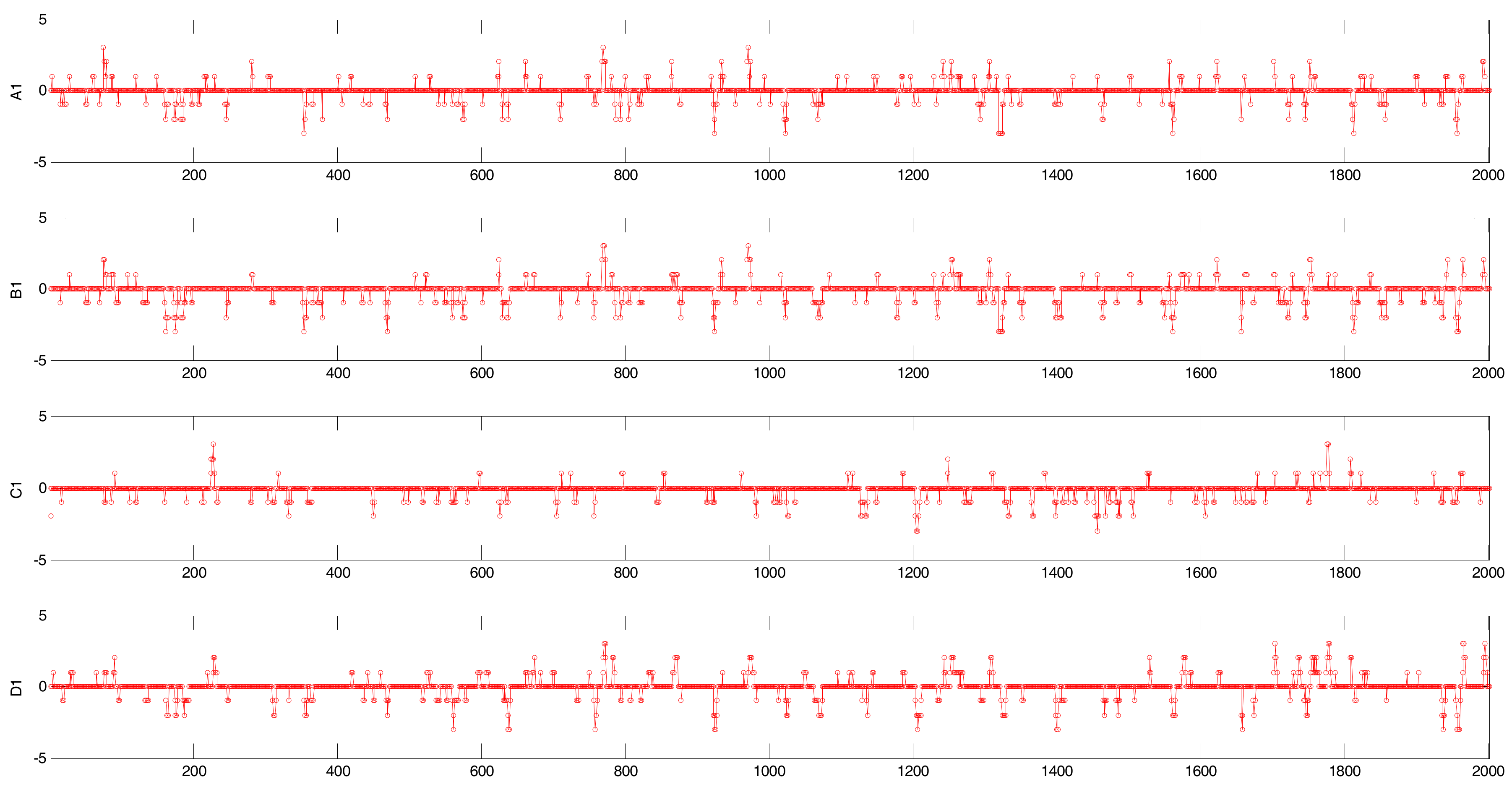
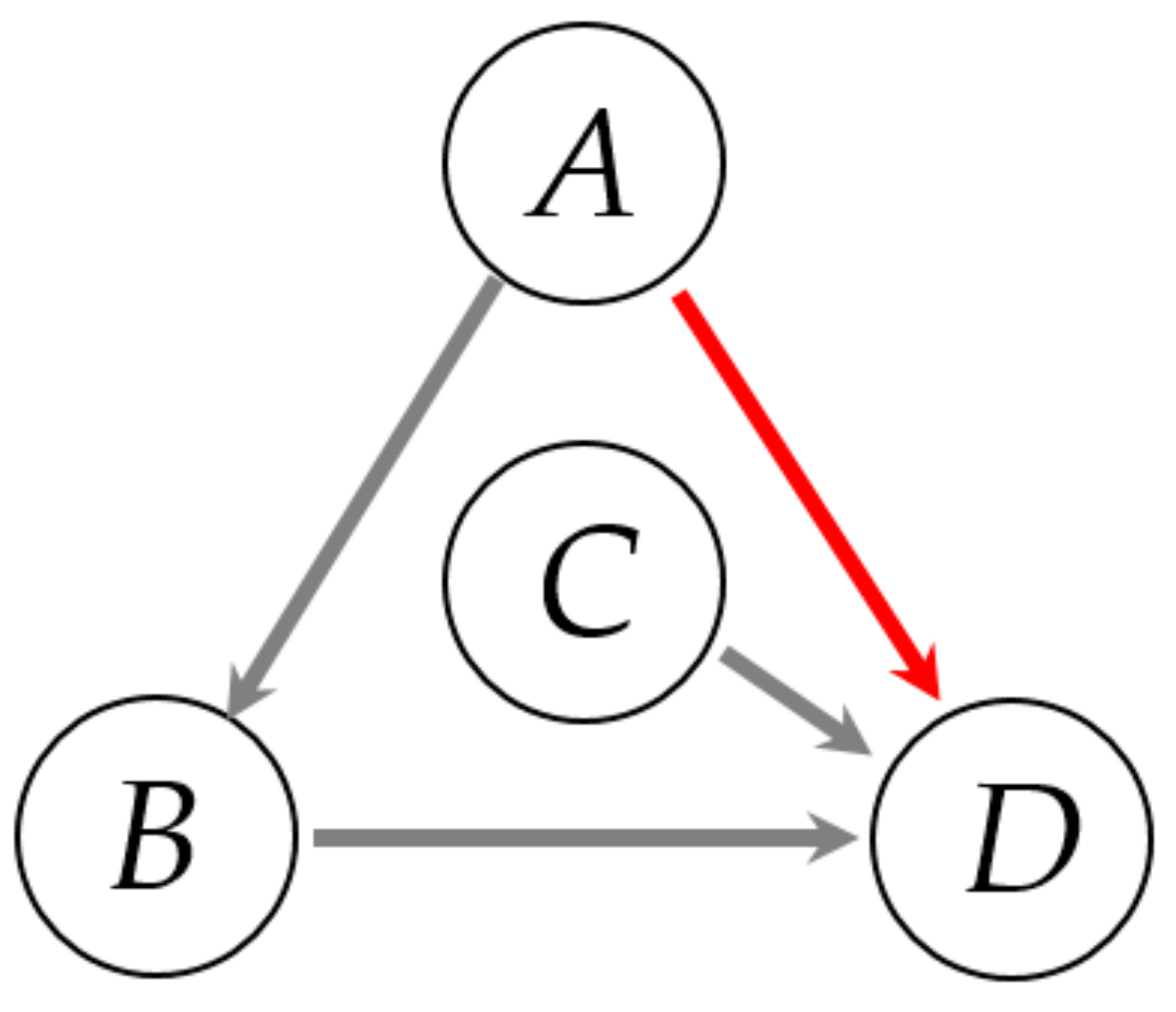
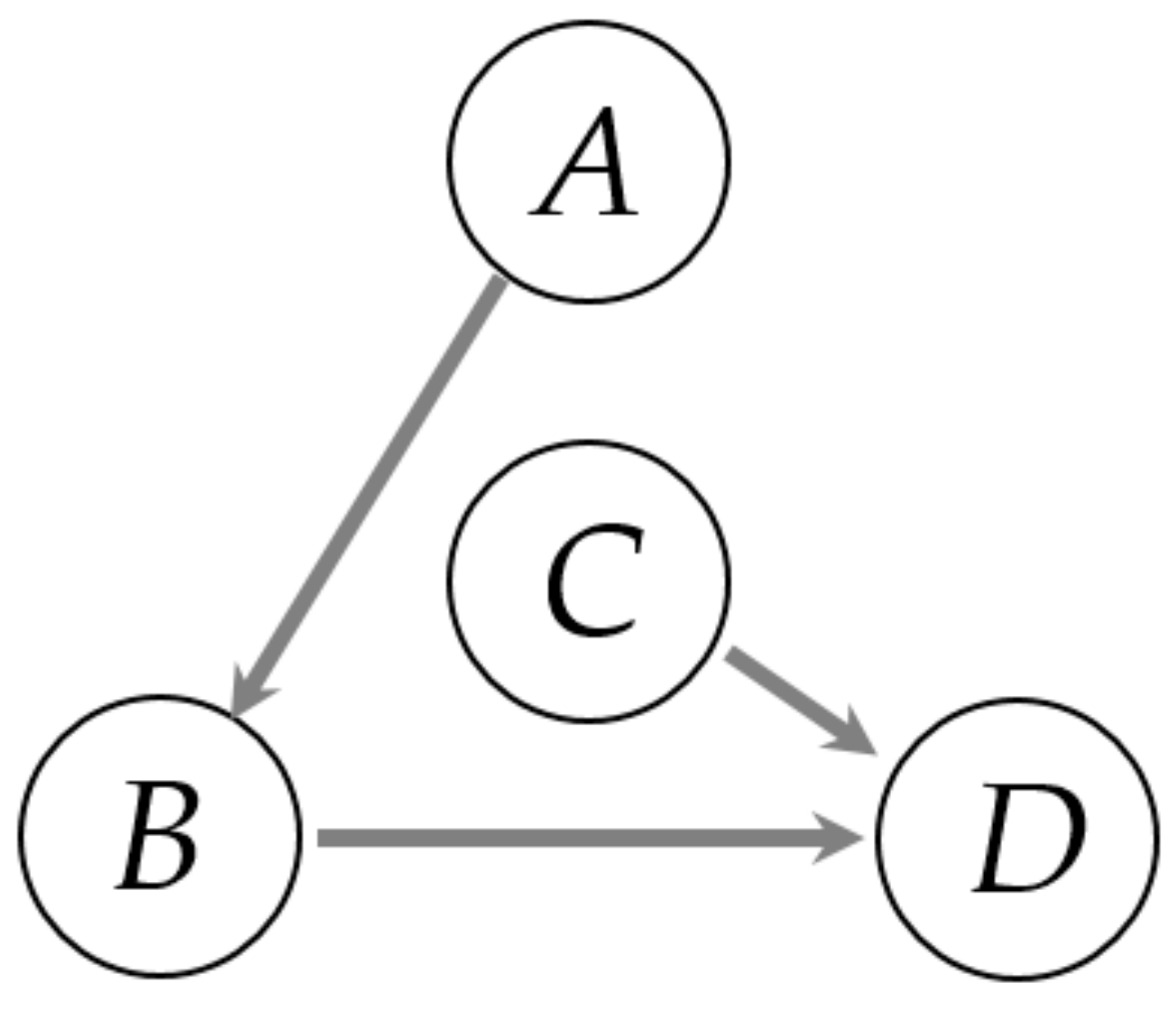
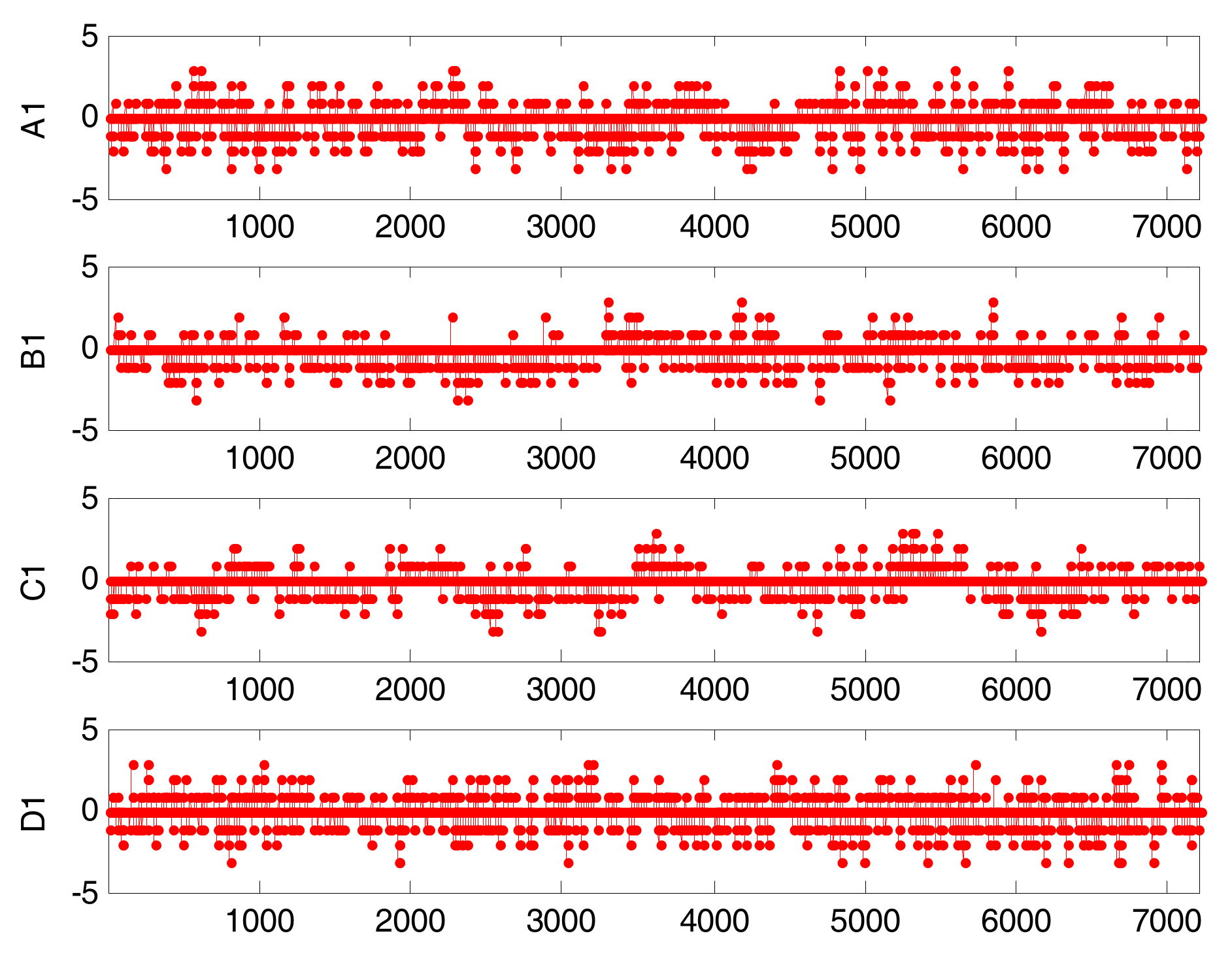
| CCF | Original Time Series | Binary Alarm Series | Multi-Valued Alarm Series |
|---|---|---|---|
| value | 0.15080 | 0.24580 | 0.14663 |
| Lag | 245 | −71 | 245 |
| To A | To B | To C | To D | |
|---|---|---|---|---|
| From A | - | 0.041(0.036) | 0.016(0.025) | 0.159(0.046) |
| From B | 0.031(0.035) | - | 0.021(0.026) | 0.175(0.049) |
| From C | 0.021(0.029) | 0.023(0.030) | - | 0.055(0.041) |
| From D | 0.028(0.037) | 0.035(0.045) | 0.027(0.030) |
| To Stream 4 | To Stream 10 | To Level | To Stream 11 | |
|---|---|---|---|---|
| From stream 4 | 0.456(0.027) | 0.290(0.025) | 0.182(0.019) | |
| From stream 10 | 0.379(0.028) | 0.423(0.021) | 0.257(0.016) | |
| From level | 0.028(0.027) | 0.289(0.022) | 0.139(0.015) | |
| From stream 11 | 0.152(0.023) | 0.030(0.019) | 0.035(0.018) |
| Condition | To Stream 4 | |
|---|---|---|
| From stream 11 | Stream 4 and level | 0.026(0.036) |
| From stream 11 | Stream 10 and level | 0.016(0.038) |
| From stream 10 | Stream 4 | 0.119(0.020) |
| From stream 10 | Stream 4 and stream 11 | 0.027(0.037) |
| From stream 4 | level | 0.018(0.021) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Wang, D.; Zhang, Y.; Yang, F.; Zhao, Y.; Pang, X. Capturing Causality for Fault Diagnosis Based on Multi-Valued Alarm Series Using Transfer Entropy. Entropy 2017, 19, 663. https://doi.org/10.3390/e19120663
Su J, Wang D, Zhang Y, Yang F, Zhao Y, Pang X. Capturing Causality for Fault Diagnosis Based on Multi-Valued Alarm Series Using Transfer Entropy. Entropy. 2017; 19(12):663. https://doi.org/10.3390/e19120663
Chicago/Turabian StyleSu, Jianjun, Dezheng Wang, Yinong Zhang, Fan Yang, Yan Zhao, and Xiangkun Pang. 2017. "Capturing Causality for Fault Diagnosis Based on Multi-Valued Alarm Series Using Transfer Entropy" Entropy 19, no. 12: 663. https://doi.org/10.3390/e19120663
APA StyleSu, J., Wang, D., Zhang, Y., Yang, F., Zhao, Y., & Pang, X. (2017). Capturing Causality for Fault Diagnosis Based on Multi-Valued Alarm Series Using Transfer Entropy. Entropy, 19(12), 663. https://doi.org/10.3390/e19120663






