Abstract
Foam systems have been attracting extensive attention due to their importance in a variety of applications, e.g., in the cleaning industry, and in bubble flotation. In the context of flotation chemistry, flotation performance is strongly affected by bubble coalescence, which in turn relies significantly on the surface forces upon the liquid film between bubbles. Conventionally, unusual short-range strongly repulsive surface interactions for Newton black films (NBF) between two interfaces with thickness of less than 5 nm were not able to be incorporated into the available classical Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory. The non-DLVO interaction would increase exponentially with the decrease of film thickness, as it plays a crucial role in determining liquid film stability. However, its mechanism and origin are still unclear. In the present work, we investigate the surface interaction of free-standing sodium dodecyl-sulfate (SDS) nanoscale black films in terms of disjoining pressure using the molecular simulation method. The aqueous nanoscale film, consisting of a water coating with SDS surfactants, and with disjoining pressure and film tension of SDS-NBF as a function of film thickness, were quantitatively determined by a post-processing technique derived from film thermodynamics.
1. Introduction
The stability of foam depends a great deal on thin liquid films between the bubbles. A better understanding of the function and behavior of bubble coalescence requires detailed knowledge of the surface interaction of the liquid films. Surface force is one of the most fundamental thermodynamic properties that characterize the stability of thin films. The film thickness has great influence on the surface force. As liquid films become thinner (Figure 1a), these films begin to exhibit a black color, as there is nearly no light been reflected. These black films can be divided into two types based on their thickness ranges: common black films, with thickness 10~100 nm; and Newton black films, which are usually are much thinner, with thicknesses below 5 nm.
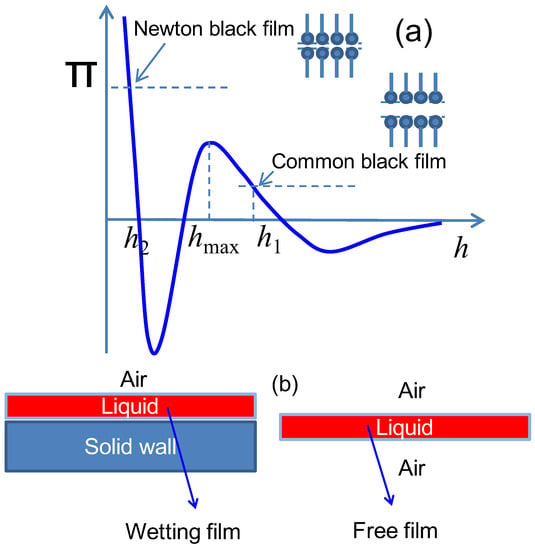
Figure 1.
Typical isotherm of disjoining pressure vs. film thickness (a); when an external pressure is applied, the liquid film thins and reaches an equilibrium value [4]; and illustration of wetting thin film and free-standing thin films (b).
Experiments [1,2] have indicated that Newton black films (NBF) can be fairly stable in the absence of water evaporation and mechanical disturbances. Classical DLVO theory can successfully predict and explain the stability for CBF based on the contributions of electrostatic double layer (EDL) and attractive van der Waals (VDW) interactions, and CBF thickness with salt concentration could be well quantified [3] by the Poisson-Boltzmann theory. However, NBF with <5 nm thickness is sometimes not possible to interpret on the basis of EDL + VDW as suggested by conventional DLVO theory, because a remarkable repulsive interaction is observed within short range for NBFs that cannot be classified.
As an important quantity governing film stability, it is possible to determine disjoining pressure (Π) based on the sum of the so-called attractive component, e.g., VDW or hydrophobic interaction, and the repulsive part, e.g., EDL, according to extended-DLVO theory [5]. On the other hand, disjoining pressure Π (shown in Figure 2) can be regarded as the difference between the normal pressure of the film and pressure of the homogeneous bulk liquid. In fact, disjoining pressure could be regarded as the molecular interaction within the liquid film. From the perspective of molecular modeling, the molecular interaction using molecular simulation can represent the sum of the surface force components, as in classical DLVO theory.
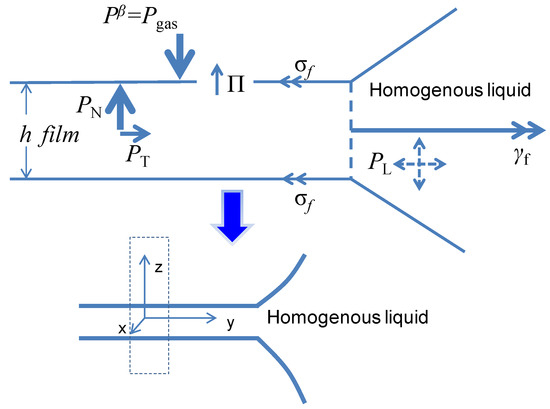
Figure 2.
Pressure balance within liquid film. PL is bulk liquid pressure.
To be specific, the net (or total) disjoining pressure of a liquid film, according to classical DLVO theory, can be divided into several components, depending on its molecular types,
where Π is the disjoining pressure, and Πvw, Πel, and Πhb are the VDW, electrostatic, and hydrophobic components, respectively. The VDW can be written as:
where A232 is the Hamaker constant between two gas phases and the liquid phase, H is thickness. The hydrophobic force has a similar form:
where K232 is hydrophobic interaction parameter between the phases. For the component of electrostatic double-layer (EDL), the weak-overlap expression can be used:
where R is the gas constant, T is temperature, Cs is electrolyte concentration, and ψmid is the potential at the mid-plane of the film. At equilibration [6], Pc is the capillary pressure.
Classical DLVO theory does not consider the factors that arise from the microstructure of water molecules [7], and regards water as a uniform medium, which does not accurately identify the role of this short-ranged and strongly repulsive interaction. It has been proposed previously that such “non-conventional” interactions [8] are rooted in the density profiles of the molecules that form the double-layer NBF, and exhibit entropy characteristics. Such an interpretation provides a reasonable benchmark account for the strong stability of NBFs. With the fast advancement by computational resources, a wide range of applications related to complicated subjects has become examinable with simulation methods, e.g., Molecular Dynamics (MD) techniques, which can be applied to investigating a range of systems [9,10,11] such as carbon nanotubes or diamond nano-thread, and under various conditions (e.g., compounds onto water droplets) [12,13,14]. It has been reported [15] that, by using MD simulations, electrostatic energy could be obtained based on electrostatic potential profile, by taking into account the uniform characteristic of water. The electrostatic contribution of disjoining pressure [16,17] can thus be derived, and its value is in similar order of magnitude to that of the VDW component from experimental evaluation.
Certain quantities and liquid film properties [18,19,20,21] can be readily observed or calculated using computational simulations. Determination of disjoining pressure would be of great interest in liquid film research. However, it is one of the most challenging tasks in molecular simulations. Winter et al. [22] and Bhatt [23,24,25] developed a methodology for determining disjoining pressure, and studied the disjoining pressure isotherm for thin films with LJ fluid, water and surfactant. Their results showed that the disjoining pressure of LJ fluid and water were purely negative. However, disjoining pressure was positive for surfactant, and decreases with an increase in film thickness.
Classical DLVO theory is usually applied to interpret the stability of foams and films, and it has been commonly regarded as the sum of the van der Waals (VDW) component and electrostatic double layer (EDL) component. However, discrepancies between DLVO theory and experimental observations (e.g., the existence of Newton black films not predicted by DLVO theory, or even some common black films) have been found, indicating that DLVO forces alone are not able to explain the results. Thus, non-DLVO forces, such as steric force, hydration force and hydrophobic force have been proposed. This insufficiency is significant, especially for very thin thicknesses (e.g., 1–2 nm), as the classical Hamaker theory neglects fluid structure and entropy completely, and assumes a slab density [24]. VDW interaction, as in DLVO, is based on Hamaker theory (or, the classical Hamaker constant was estimated from Lifshitz’s formulation). Therefore, rigorous calculation of disjoining pressures requires detailed molecular simulations with physical molecular profiles.
Previously, Π-h of liquid film with salt [26] has been calculated, and it was found that VDW + EDL from DLVO theory were not able to explain the simulation results, with Π from DLVO theory being 1–2 × 106 Pa lower than the results obtained from the MD simulations for film thickness at 1~3 nm. Furthermore, it was suggested that hydration force could be contributing to the difference between the simulation results and the classical DLVO theory using SPC/E-ions model. In this study, SDS is applied, as this molecule serves as a popular model for computational studies. The difference between wetting film and free film is shown in Figure 1b; in this study free-standing liquid film with SDS was investigated, to examine the disjoining pressure and film tension using a convenient alternative method to MD simulations. This provides a basis for validation of such systems and the further interpretation for experimental measurements.
2. Methodology
2.1. Theoretical Approach from Film Thermodynamics
For an aqueous thin film [27], the Gibbs free energy differential of thin film can be written as:
Here, h is film thickness, is the excess entropy of the thin film, is the surface tension of the thin film, is chemical potential of the ith component and is mole number of component i. From the point of energy change, disjoining pressure could be thermodynamically regarded as the change of Gibbs free energy [28,29,30] within the thin film, that is:
For the surface tension of the film σf, it could be written as:
By integrating Equation (6), there is the Gibbs-Duhem type Equation (9),
It can be seen from Equation (9) that disjoining pressure has following relationship:
Integrating Equation (10), the corresponding film tension can be given in Equation (11).
A key equation based on Equation (6) (also seen from Figure 2, pressure balance) can be obtained:
Here γf is film tension of the liquid film; σ∞ is surface tension of bulk liquid. There is also another correlation:
Combining Equations (11) and (12), disjoining pressure can be obtained, and the key process is as described below. It can be seen that the two types (energy, pressure balance) would lead to the same inner relationship for disjoining pressure and surface tension.
By performing derivation directly on both sides of Equation (13), then Equation (14) could be obtained. Please note that σ∞ is the surface tension of bulk liquid, and it is a constant; thus, its derivation is zero. From Equation (14), disjoining pressure has a relationship with the surface tension of thin film (σf) and film thickness. To be more specific, the 2σf (double surface tension) at varied thicknesses needs to be obtained first; then, there was 2σf vs. h. After that, a derivative procedure was conducted on the curve of 2σf vs. h; subtraction of the result would result in the final disjoining pressure isotherm (Π-h). Surface tension was determined by the usual pressure tensor way [31] within GROMACS, i.e., given by
where PN and PT are pressure tensors, at normal and tangential directions, respectively.
2.2. Computational Modeling System
The schematic simulation setup is shown in Figure 3, the thin film contains SDS and water molecules. The lateral dimension of the simulation box is Lx = Ly (~13 nm), and Lz = 3 Lx, two vapor areas were placed in the Z direction to form the film structure. The vapor size on the Z-axis is big enough to avoid possible interaction between the up and bottom surface.
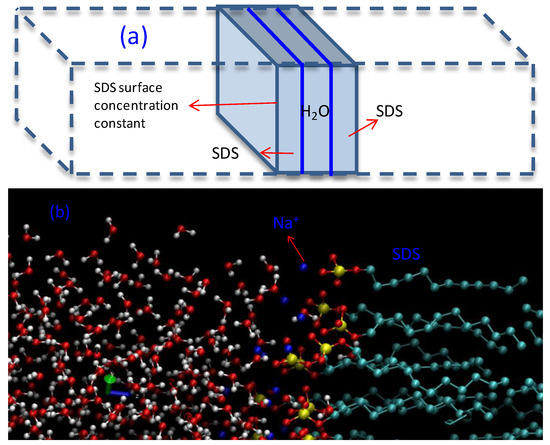
Figure 3.
Schematic diagram of MD modeling, (a) slab geometry and (b) molecular configuration.
Water model TIP4P/2005 [32] was applied using GROMACS 4.5.3 [33,34,35] under periodic boundary conditions (PBC) in all directions. Long-range corrections to the Coulomb interactions adopted the particle mesh Ewald (PME) [36] method; both Lennard-Jones (LJ) and Coulomb terms had a potential cut-off 1.4 nm. The Nose-Hoover method was applied to keep the system temperature at T = 298 K, with each running step set as 2 fs. Surface tension was obtained by running in the NVT (number of molecules, volume and temperature were kept constant). SDS was modeled by united atom force fields [16], the parameters of the SDS head group were from the AMBER force-field [37], Na+ parameters were from Dang [38]. The TIP4P/2005 water model was suggested to be better for describing water surface tension. Film thickness, h, was determined as the thickness (from configuration) within the NVT running process, in order to keep consistent.
To well equilibrate the simulation system and minimize the potential, 10 ns were first run, and another 10 ns trajectory for calculating average properties. Each result presented is the average of at least 3 simulations, each with a different initial configuration. Surface concentration of SDS was fixed at ~33 Å2, as previous verified by X-ray experimental data [39] and suggested that film usually contains between two and four H2O for one SDS molecule. The value is in agreement with observation in the spontaneous formation of the SDS-NBF. Water molecules were placed at the middle of the SDS surfactants, forming a sandwiched slab geometry (Figure 3a), and Na+ could move around the SDS (Figure 3b), and can also interact with water molecules. The film thickness changes with the change of ratio of Nwater/NSDS, e.g., ratio of Nwater/NSDS = 3, for each monolayer 256 SDS (NSDS = 256 for each surface, and 512 for two surfaces), Nwater = 1536 is total. With the changing of Nwater/NSDS from 2 to 3.5, film thickness and the corresponding disjoining pressure and film tension will change.
3. Results and Discussion
3.1. Disjoining Pressure Isotherms
Surface tension and disjoining pressure are the key parameters that can be applied to obtain the film tension of a liquid thin film. In molecular modeling, film tension cannot be directly obtained; the surface tension and disjoining pressure need to be determined firstly. It is noted that the disjoining pressure is crucial to understanding the behavior of drainage and rupture processes of surfactant and non-surfactant thin films. In addition, the understanding of the effects of specific ions on film- or bubble-related problems [40,41,42,43] also needs a better, more concise description for the tensions within these thin liquid films. By molecular simulation, it is possible to calculate the surface tension of bulk liquids, and also possible to calculate the surface tension of thin films (i.e., of smaller thickness). However, it is not possible to calculate film tension directly by simulation.
One methodology for Π was developed by Bhatt [23,24,25], under the same chemical potential, by comparing the difference between the normal pressure and the surrounding bulk liquid pressure. This study applied film thermodynamics, and derived disjoining pressure using 2σf vs. h; the obtained 2σf vs. h curve and corresponding fitting line are shown in Figure 4.
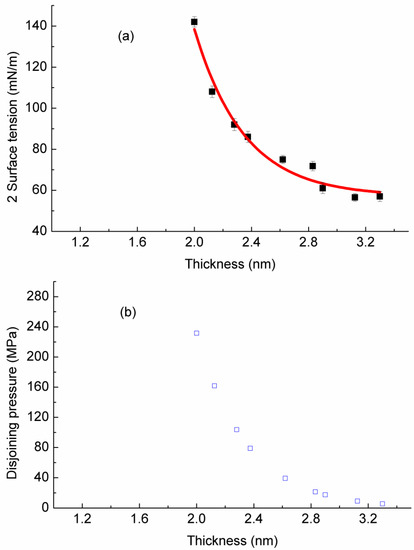
Figure 4.
Variation of (2 surface tension) versus thickness (a); the red line represents fitting results, and disjoining pressure isotherm (b) for these nanoscale liquid films.
The curve of 2σf vs. h is empirically fitted (shown in Figure 4a) using a single exponential decay model with three parameters, and the obtained parameters for SDS-stabilized films are given by Equation (16), below, with R = 0.99.
For very thin films, e.g., nanoscale black films, the surface interaction becomes stronger with a decrease in film thickness, and the corresponding surface force (in terms of disjoining pressure) will not be zero. Surface tension for SDS-stabilized nano-film was observed to decrease with increasing film thickness; this is opposite to the case of pure water film, as σf of water films would increase with increasing film thickness. Please note that, for liquid films with very large thickness, their σf is very similar to the value of the bulk liquid (i.e., very thick film with film thickness ∞). However, with the decrease in film thickness, its surface tension would change accordingly, and this change is more pronounced for thinner films, as can be seen in Figure 4a.
Equation (14) is used for the determination of Π; the corresponding Π-h below 5 nm thickness is obtained and shown in Figure 4b. In turn, the disjoining pressure isotherm derived by 2σf vs. h can be expressed as:
the units of σf, h, and Π are mN/m, nm, and in MPa (i.e., ×106 Pa), respectively. The disjoining pressure is positive across the entire given thickness range. For films with thickness range 30–100 nm, the disjoining pressure is below 105 Pa, i.e., ≤1 bar, at such film thicknesses, their Π is easy to detect and measure, and cannot be negligible under experimental conditions. However, at film thicknesses of 30–100 nm, due to the small Π (≤1 bar), it is not possible for MD to capture its accurate Π value. Molecular simulations can only simulate very thin films (usually ~10 nm, below 100 nm).
The disjoining pressure can be studied from different perspectives, as shown in Figure 5. In this study, we applied a non-polarizable model, i.e., Equation (18) was applied:
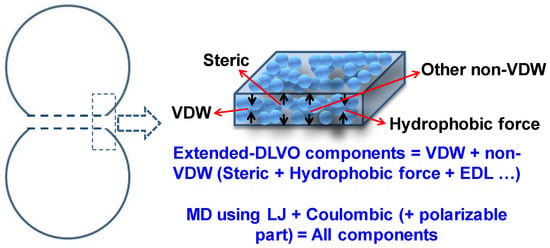
Figure 5.
Molecular interaction by interpretation from the perspective of molecular modeling or extended-DLVO theory.
LJ fluid thin film has only attractive components, that is to say, there are no other components. For LJ fluid, there is no Coulombic interaction in Equation (18). However, for non-LJ fluid, water molecules coated with SDS have LJ and Coulombic interactions (plus polarizable interactions, when the polarizable model is applied). The LJ term and Coulombic term cannot provide further insight into the surface force components. It has been reported [44] that, by fitting Electrostatic Helmholtz free energy exponentially, it is possible to derive the electrostatic contribution of Π. Disjoining pressure in Figure 4b contains all of the contributions. There is no solid theory to divide the so-called various components, and these interactions cannot be distinguished in MD simulations.
Classical theory can well interpret the observed results for most cases in usual ranges. However, that is not always satisfactory, especially under some extreme conditions, where it may, for example, underestimate VDW interactions by 1–2 orders of magnitude compared to the molecular simulation results for water films with 1–2 nm thickness.
3.2. Film Tension
Usually, there is very small (and sometimes negligible, in the case of very thick films) difference between film tension and 2σ∞ for common free liquid films, or for CBF. Hence, experimental measurements of film tension can be within the margin of uncertainty for these relatively thick liquid films. The important properties of the liquid bulk solution from which the aqueous film is produced dictate the final state, and the corresponding tension values (surface tension, film tension, disjoining pressure) change with variations in temperature and concentration. For these CBFs, indirect measurement can be preferable, as the relationship (cosθ = γ/2σ∞) defines the ratio of film tension with that of the surface tension of bulk solution. For NBFs, direct measurement for γ is possible. The surface tension, Π, and film tension are mainly dependent on film thickness.
The obtained disjoining pressure profile was subsequently employed to investigate the film tension for the thin films; Equation (12) is applied to determine film tension, and the results are shown in Figure 6. It can be seen that film tension decreased gradually as the film thickness increased, and the decreasing trend was more pronounced in the small thickness range. Moreover, the film tensions thus determined were positive values across the entire given thickness range. The film tension is great in the small thickness range, and becomes much smaller in the large thickness region, indicating that thick film tends to gradually fall into the bulk solution zone.
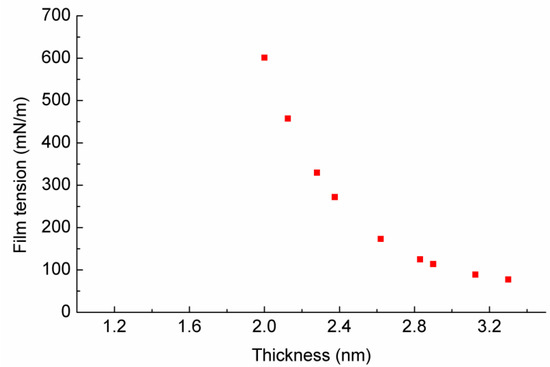
Figure 6.
Film tension of SDS nanoscale liquid films.
4. Conclusions
The disjoining pressure isotherm is an important thermodynamic property for aqueous thin films, and surface interaction is not zero when the liquid film is sufficiently thin, especially when it is nanoscale. Disjoining pressure was determined in this study for SDS-stabilized nanoscale liquid film by deriving the curve of 2σf vs. h based on film thermodynamics. The σf was different for varying film thicknesses, which indicates that surface interaction plays an important role at the nanoscale level. The determined Π for nanoscale liquid films with SDS was positive (the total Π is repulsive) at all film thicknesses studied, and of comparable magnitude to previous simulation results.
This paper is the first determination of NBF film tension and disjoining pressure using a convenient method, without complicated process, by molecular simulations using a post-processing method. However, it is not possible to separate the total interaction into various components at this stage. We have no solid theory to separate these components, and sometimes these individual components may not be additive. The present study has potential implications for the interpretation and validation of similar experimental measurements.
Acknowledgments
The authors thank Natural Science Foundation of China (Grant No. 51704047, 51506013), Doctoral Foundation of Southwest University of Science and Technology, and innovation team (17LZXT05).
Author Contributions
Tiefeng Peng and Qibin Li conceived and designed the simulations; Tiefeng Peng performed the simulations; Tiefeng Peng, Qibin Li, Longhua Xu, Chao He and Liqun Luo analyzed the data; Tiefeng Peng, Qibin Li, Longhua Xu, Chao He and Liqun Luo wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barthélémy, P.; Cuvillier, N.; Chaudier, Y.; Benattar, J.-J.; Pucci, B. Stability of Newton black films of highly fluorinated non-ionic surfactants. J. Fluor. Chem. 2000, 105, 95–102. [Google Scholar] [CrossRef]
- Muruganathan, R.M.; Müller, H.J.; Möhwald, H.; Krastev, R. Effect of Headgroup Size on Permeability of Newton Black Films. Langmuir 2005, 21, 12222–12228. [Google Scholar] [CrossRef] [PubMed]
- Bergeron, V.; Waltermo, Å.; Claesson, P.M. Disjoining Pressure Measurements for Foam Films Stabilized by a Nonionic Sugar-Based Surfactant. Langmuir 1996, 12, 1336–1342. [Google Scholar] [CrossRef]
- Langevin, D.; Marquez-Beltran, C.; Delacotte, J. Surface force measurements on freely suspended liquid films. Adv. Colloid Interface Sci. 2011, 168, 124–134. [Google Scholar] [CrossRef] [PubMed]
- Ninham, B. On progress in forces since the DLVO theory. Adv. Colloid Interface 1999, 83, 1–17. [Google Scholar] [CrossRef]
- Wang, L.; Yoon, R.-H. Effect of pH and NaCl concentration on the stability of surfactant-free foam films. Langmuir 2008, 25, 294–297. [Google Scholar] [CrossRef] [PubMed]
- Paunov, V.N.; Dimova, R.I.; Kralchevsky, P.A.; Broze, G.; Mehreteab, A. The Hydration Repulsion between Charged Surfaces as an Interplay of Volume Exclusion and Dielectric Saturation Effects. J. Colloid Interface Sci. 1996, 182, 239–248. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Wennerstroem, H. Entropic forces between amphiphilic surfaces in liquids. J. Phys. Chem. 1992, 96, 520–531. [Google Scholar] [CrossRef]
- Hu, H.; Weinberger, C.R.; Sun, Y. Effect of Nanostructures on the Meniscus Shape and Disjoining Pressure of Ultrathin Liquid Film. Nano Lett. 2014, 14, 7131–7137. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Chen, X. Liquid flow-induced energy harvesting in carbon nanotubes: A molecular dynamics study. Phys. Chem. Chem. Phys. 2013, 15, 1164–1168. [Google Scholar] [CrossRef] [PubMed]
- Zhan, H.; Zhang, G.; Tan, V.B.C.; Gu, Y. The best features of diamond nanothread for nanofibre applications. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Jian, C.; Liu, Q.; Zeng, H.; Tang, T. Effect of Model Polycyclic Aromatic Compounds on the Coalescence of Water-in-Oil Emulsion Droplets. J. Phys. Chem. C 2017, 121, 10382–10391. [Google Scholar] [CrossRef]
- Jian, C.; Zeng, H.; Liu, Q.; Tang, T. Probing the Adsorption of Polycyclic Aromatic Compounds onto Water Droplets Using Molecular Dynamics Simulations. J. Phys. Chem. C 2016, 120, 14170–14179. [Google Scholar] [CrossRef]
- Taherian, F.; Marcon, V.; Bonaccurso, E.; van der Vegt, N.F.A. Vortex formation in coalescence of droplets with a reservoir using molecular dynamics simulations. J. Colloid Interface Sci. 2016, 479, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Faraudo, J.; Bresme, F. Anomalous dielectric behavior of water in ionic newton black films. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef] [PubMed]
- Faraudo, J.; Bresme, F. Origin of the short-range, strong repulsive force between ionic surfactant layers. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.S.; Goddard, W.A. Structures and properties of Newton black films characterized using molecular dynamics simulations. J. Phys. Chem. B 2006, 110, 7992–8001. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Yang, X. Molecular Dynamics Study of the Influence of Calcium Ions on Foam Stability. J. Phys. Chem. B 2010, 114, 10066–10074. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Yang, X. Molecular Dynamics Study of the Foam Stability of a Mixed Surfactant/Water System with and without Calcium Ions. J. Phys. Chem. B 2011, 115, 4645–4653. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Nguyen, A.V.; Peng, H.; Dang, L.X. Quantitative Analysis of Aqueous Nanofilm Rupture by Molecular Dynamic Simulation. J. Phys. Chem. B 2012, 116, 1035–1042. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Chang, T.-M. Molecular processes of ion effects on aqueous nanofilm rupture. J. Mol. Liq. 2014, 193, 139–151. [Google Scholar] [CrossRef]
- Winter, S.J. Computer Simulation of Free, Thin-Liquid Films and Disjoining Pressures; University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Bhatt, D.; Newman, J.; Radke, C. Molecular simulation of disjoining-pressure isotherms for free liquid, Lennard-Jones thin films. J. Phys. Chem. B 2002, 106, 6529–6537. [Google Scholar] [CrossRef]
- Bhatt, D.; Newman, J.; Radke, C. Molecular simulation of disjoining-pressure isotherms for free aqueous thin films. J. Phys. Chem. B 2003, 107, 13076–13083. [Google Scholar] [CrossRef]
- Bhatt, D.; Newman, J.; Radke, C. Monte Carlo simulations of disjoining-pressure isotherms for Lennard-Jones surfactant-stabilized free thin films. J. Phys. Chem. B 2004, 108, 13412–13418. [Google Scholar] [CrossRef]
- Peng, T.; Firouzi, M.; Li, Q.; Peng, K. Surface force at the nano-scale: Observation of non-monotonic surface tension and disjoining pressure. Phys. Chem. Chem. Phys. 2015, 17, 20502–20507. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, J.C.; Toshev, B.V. Disjoining pressure in soap film thermodynamics. Colloids Surf. 1982, 5, 241–264. [Google Scholar] [CrossRef]
- Ivanov, I. Thin Liquid Films; CRC Press: Boca Raton, FL, USA, 1988; Volume 29. [Google Scholar]
- Radke, C.J. Film and membrane-model thermodynamics of free thin liquid films. J. Colloid Interface Sci. 2015, 449, 462–479. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, I.; Toshev, B. Thermodynamics of thin liquid films. Colloid Polym. Sci. 1975, 253, 593–599. [Google Scholar] [CrossRef]
- Brown, D.; Neyertz, S. A general pressure tensor calculation for molecular dynamics simulations. Mol. Phys. 1995, 84, 577–595. [Google Scholar] [CrossRef]
- Abascal, J.L.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Lindahl, E.; Hess, B.; Van Der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Model. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Peng, T.; Chang, T.M.; Sun, X.; Nguyen, A.V.; Dang, L.X. Development of ions-TIP4P-Ew force fields for molecular processes in bulk and at the aqueous interface using molecular simulations. J. Mol. Liq. 2012, 173, 47–54. [Google Scholar] [CrossRef]
- Bélorgey, O.; Benattar, J.J. Structural properties of soap black films investigated by X-ray reflectivity. Phys. Rev. Lett. 1991, 66. [Google Scholar] [CrossRef] [PubMed]
- Christenson, H.K.; Bowen, R.E.; Carlton, J.A.; Denne, J.R.M.; Lu, Y. Electrolytes that Show a Transition to Bubble Coalescence Inhibition at High Concentrations. J. Phys. Chem. C 2007, 112, 794–796. [Google Scholar] [CrossRef]
- Marrucci, G.; Nicodemo, L. Coalescence of gas bubbles in aqueous solutions of inorganic electrolytes. Chem. Eng. Sci. 1967, 22, 1257–1265. [Google Scholar] [CrossRef]
- Craig, V.S.J.; Ninham, B.W.; Pashley, R.M. Effect of electrolytes on bubble coalescence. Nature 1993, 364, 317–319. [Google Scholar] [CrossRef]
- Craig, V.S.J. Bubble coalescence and specific-ion effects. Curr. Opin. Colloid Interface 2004, 9, 178–184. [Google Scholar] [CrossRef]
- Chen, M.; Lu, X.; Liu, X.; Hou, Q.; Zhu, Y.; Zhou, H. Molecular Dynamics Simulation of the Effects of NaCl on Electrostatic Properties of Newton Black Films. J. Phys. Chem. C 2012, 116, 21913–21922. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).