Radially Excited AdS5 Black Holes in Einstein–Maxwell–Chern–Simons Theory
Abstract
1. Introduction
2. AdS Black Holes in Einstein–Maxwell–Chern–Simons Theory
2.1. The Theory
2.2. Ansatz, Asymptotics and Charges
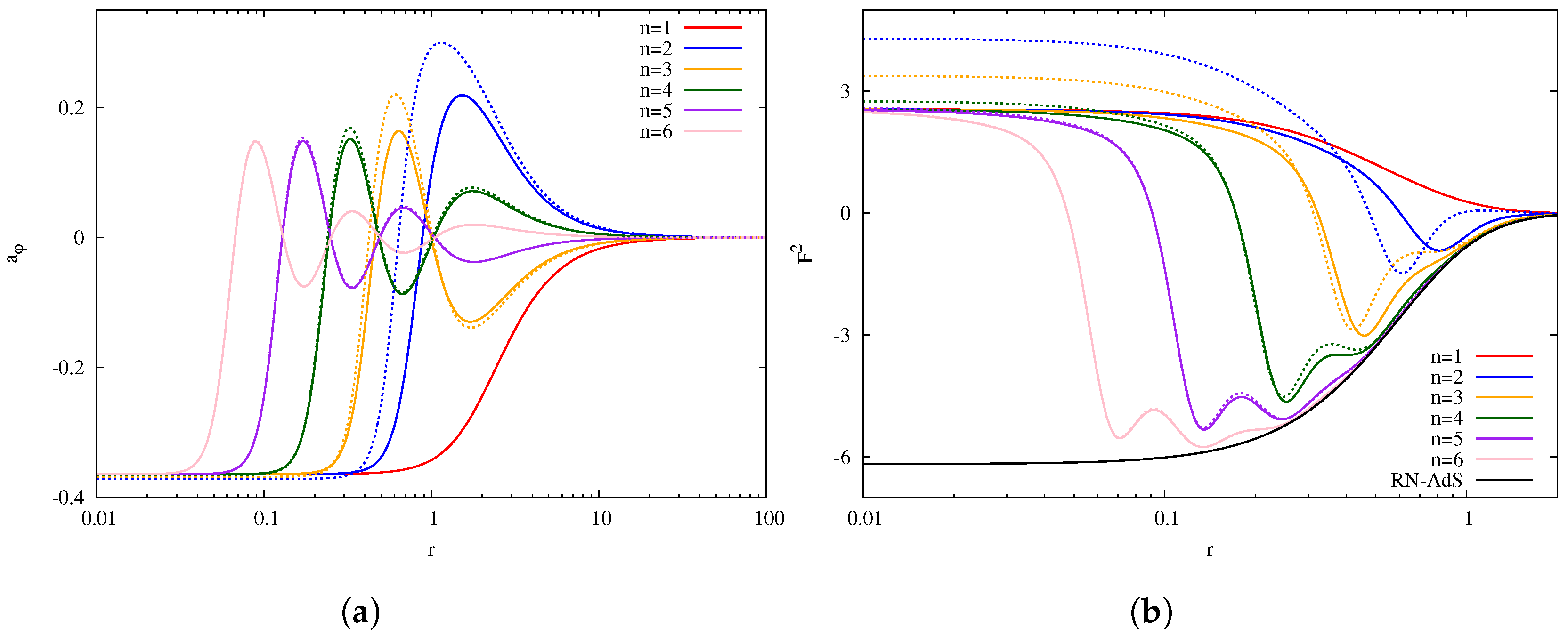
3. Excited Black Holes
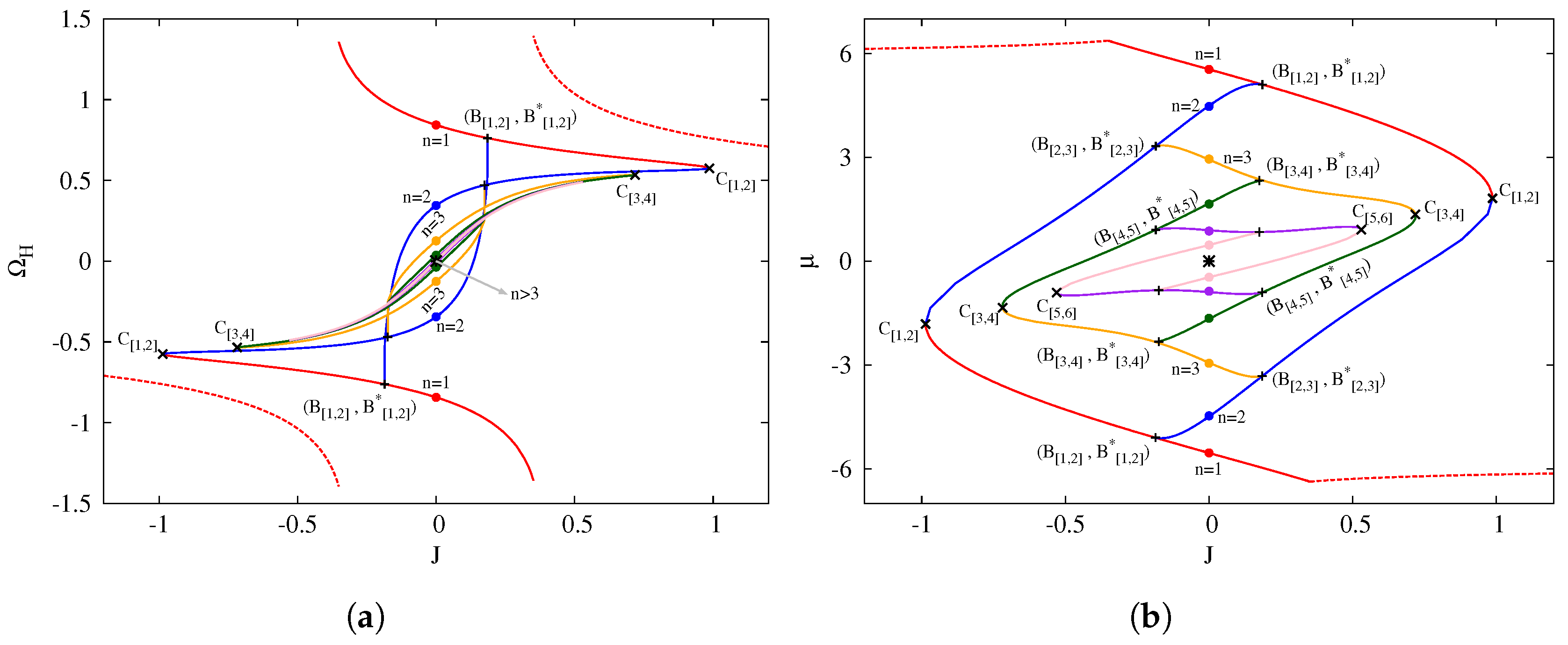
3.1. Branch Structure of the Black Holes for
- The branch (with ) connects with the branch via a single solution, the cusp .
- Every branch of number n contains a branching point at some . At these points, there is non-uniqueness with respect to the global quantities (Q, M, J) of extremal black holes, but the solutions can be distinguished by their horizon properties. This means it is possible to jump from branch n to through a branching point keeping all global quantities continuous, but this requires a jump of the entropy .
- Each branch of number contains one non-static solution, which can be labeled by the number n of the branch.
- Similarly, each branch of number also contains one non-static solution, which can also be labeled with the n number.
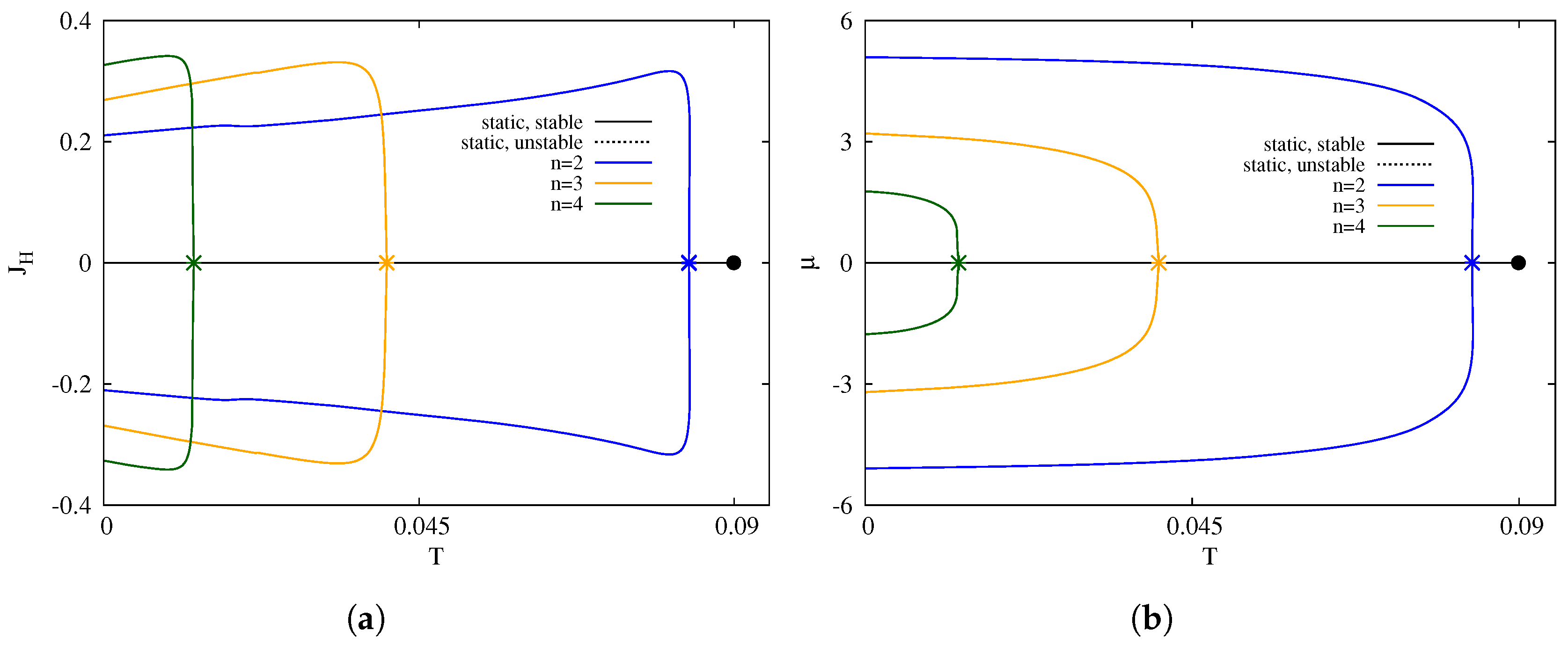
3.2. Thermodynamic Properties of the Non-Extremal Excited Black Holes
3.2.1. Non-Static Black Holes
3.2.2. The Case for Non-Static Black Holes
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Witten, E. Anti de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hunter, C.J.; Taylor-Robinson, M.M. Rotation and the AdS-CFT correspondence. Phys. Rev. D 1999, 59, 064005. [Google Scholar] [CrossRef]
- Mitra, P. Thermodynamics of charged anti-de Sitter black holes in canonical ensemble. Phys. Lett. B 1999, 459, 119–124. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Holography, thermodynamics, and fluctuations of charged AdS black holes. Phys. Rev. D 1999, 60, 104026. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Static Einstein–Maxwell magnetic solitons and black holes in an odd dimensional AdS spacetime. Entropy 2016, 18, 438. [Google Scholar]
- Kunz, J.; Navarro-Lérida, F.; Radu, E. Higher dimensional rotating black holes in Einstein–Maxwell theory with negative cosmological constant. Phys. Rev. B 2007, 649, 463–471. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Charged rotating black holes in Einstein–Maxwell–Chern–Simons theory with a negative cosmological constant. Phys. Rev. D 2017, 95, 064018. [Google Scholar] [CrossRef]
- Figueras, P.; Tunyasuvunakool, S. Black rings in global anti-de Sitter space. J. High Energy Phys. 2015. [Google Scholar] [CrossRef]
- Cvetic, M.; Lu, H.; Pope, C.N. Charged Kerr-de Sitter black holes in five dimensions. Phys. Rev. B 2004, 598, 273–278. [Google Scholar] [CrossRef]
- Gutowski, J.B.; Reall, H.S. Supersymmetric AdS5 black holes. J. High Energy Phys. 2004, 2, 6. [Google Scholar] [CrossRef]
- Chong, Z.W.; Cvetic, M.; Lu, H.; Pope, C.N. General nonextremal rotating black holes in minimal five-dimensional gauged supergravity. Phys. Rev. Lett. 2005, 95, 161301. [Google Scholar] [CrossRef] [PubMed]
- Chong, Z.W.; Cvetic, M.; Lu, H.; Pope, C.N. Non-extremal rotating black holes in five-dimensional gauged supergravity. Phys. Lett. B 2007, 644, 192–197. [Google Scholar] [CrossRef]
- Chong, Z.W.; Cvetic, M.; Lu, H.; Pope, C.N. Five-dimensional gauged supergravity black holes with independent rotation parameters. Phys. Rev. D 2005, 72, 041901. [Google Scholar] [CrossRef]
- Cvetic, M.; Lu, H.; Pope, C.N. Charged rotating black holes in five dimensional U(1) 3 gauged N = 2 supergravity. Phys. Rev. D 2004, 70, 081502. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. AdS 5 magnetized solutions in minimal gauged supergravity. Phys. Rev. B 2007, 771, 52–58. [Google Scholar] [CrossRef]
- Grunau, S.; Neumann, H. Thermodynamics of a rotating black hole in minimal five-dimensional gauged supergravity. Class. Quantum Gravity 2015, 32, 175004. [Google Scholar] [CrossRef]
- Mir, M.; Mann, R.B. Charged rotating AdS black holes with Chern–Simons coupling. Phys. Rev. D 2017, 95, 024005. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Sequences of extremal radially excited rotating black holes. Phys. Rev. Lett. 2014, 112, 011101. [Google Scholar] [CrossRef] [PubMed]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Radially excited rotating black holes in Einstein–Maxwell–Chern–Simons theory. Phys. Rev. D 2015, 92, 044025. [Google Scholar] [CrossRef]
- Ashtekar, A.; Magnon, A. Asymptotically anti-de Sitter space-times. Class. Quant. Grav. 1984, 1, L39. [Google Scholar] [CrossRef]
- Ashtekar, A.; Das, S. Asymptotically anti-de Sitter spacetimes: Conserved quantities. Class. Quant. Grav. 2000, 17, L17. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Kraus, P. A stress tensor for anti-de Sitter gravity. Commun. Math. Phys. 1999, 208, 413–428. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the mechanics of AdS black holes. Class. Quantum Gravity 2009, 26, 195011. [Google Scholar] [CrossRef]
- Cvetic, M.; Gibbons, G.W.; Kubiznak, D.; Pope, C.N. Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Dolan, B.P.; Kastor, D.; Kubiznak, D.; Mann, R.B.; Traschen, J. Thermodynamic volumes and isoperimetric inequalities for de Sitter black holes. Phys. Rev. D 2013, 87, 104017. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Thermodynamics of rotating black holes and black rings: Phase transitions and thermodynamic volume. Galaxies 2014, 2, 89–159. [Google Scholar] [CrossRef]
- Ascher, U.; Christiansen, J.; Russell, R.D. A collocation solver for mixed order systems of boundary value problems. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
- Ascher, U.; Christiansen, J.; Russell, R.D. Collocation software for boundary-value ODEs. ACM Trans. 1981, 7, 209–222. [Google Scholar] [CrossRef]
- Sen, A. Black hole entropy function and the attractor mechanism in higher derivative gravity. J. High Energy Phys. 2005, 9, 038. [Google Scholar] [CrossRef]
- Astefanesei, D.; Goldstein, K.; Jena, R.P.; Sen, A.; Trivedi, S.P. Rotating attractors. J. High Energy Phys. 2006, 10, 058. [Google Scholar] [CrossRef]
- Goldstein, K.; Jena, R.P. One entropy function to rule them all... J. High Energy Phys. 2007, 11, 049. [Google Scholar] [CrossRef]
- Kunduri, H.K.; Lucietti, J. Near-horizon geometries of supersymmetric AdS5 black holes. J. High Energy Phys. 2007, 12, 015. [Google Scholar] [CrossRef]
- Cai, R.G.; Yang, R.Q. Paramagnetism-ferromagnetism phase transition in a dyonic black hole. Phys. Rev. D 2014, 90, 081901. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quantum Gravity 2000, 17, 399. [Google Scholar] [CrossRef]
- Dolan, B.P. On the thermodynamic stability of rotating black holes in higher dimensions–a comparison of thermodynamic ensembles. Class. Quantum Gravity 2014, 31, 135012. [Google Scholar] [CrossRef]





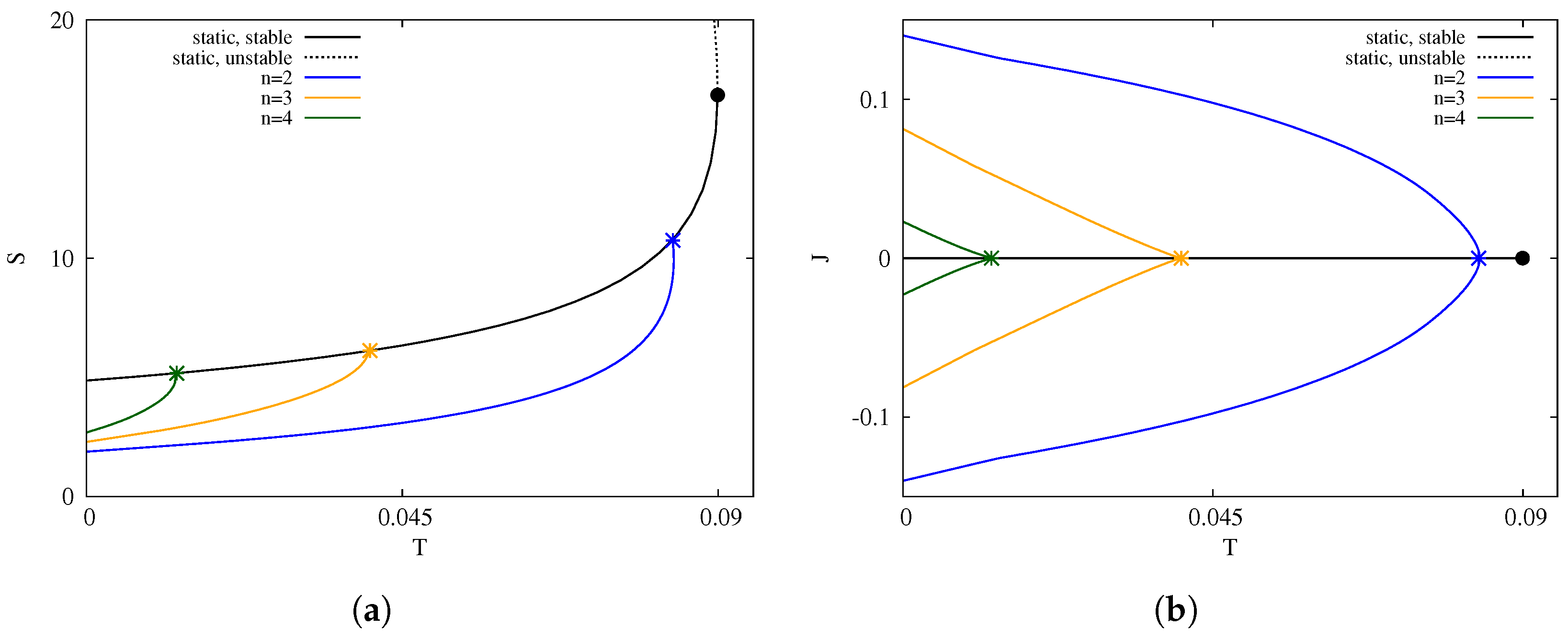
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Salcedo, J.L. Radially Excited AdS5 Black Holes in Einstein–Maxwell–Chern–Simons Theory. Entropy 2017, 19, 567. https://doi.org/10.3390/e19100567
Blázquez-Salcedo JL. Radially Excited AdS5 Black Holes in Einstein–Maxwell–Chern–Simons Theory. Entropy. 2017; 19(10):567. https://doi.org/10.3390/e19100567
Chicago/Turabian StyleBlázquez-Salcedo, Jose Luis. 2017. "Radially Excited AdS5 Black Holes in Einstein–Maxwell–Chern–Simons Theory" Entropy 19, no. 10: 567. https://doi.org/10.3390/e19100567
APA StyleBlázquez-Salcedo, J. L. (2017). Radially Excited AdS5 Black Holes in Einstein–Maxwell–Chern–Simons Theory. Entropy, 19(10), 567. https://doi.org/10.3390/e19100567




