Comparative Statistical Mechanics of Muscle and Non-Muscle Contractile Systems: Stationary States of Near-Equilibrium Systems in A Linear Regime
Abstract
:1. Introduction
2. Results
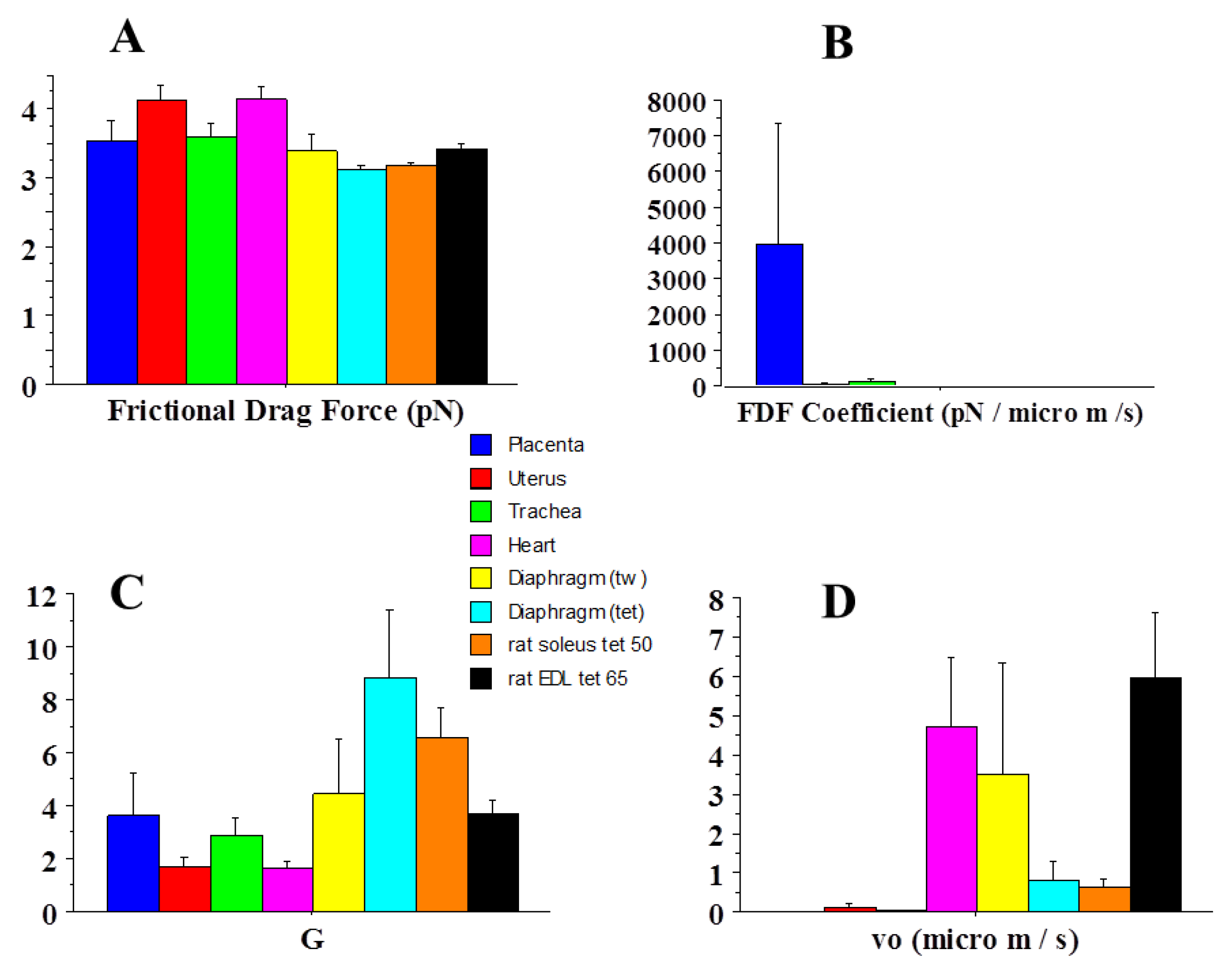
2.1. General Mechanical Parameters
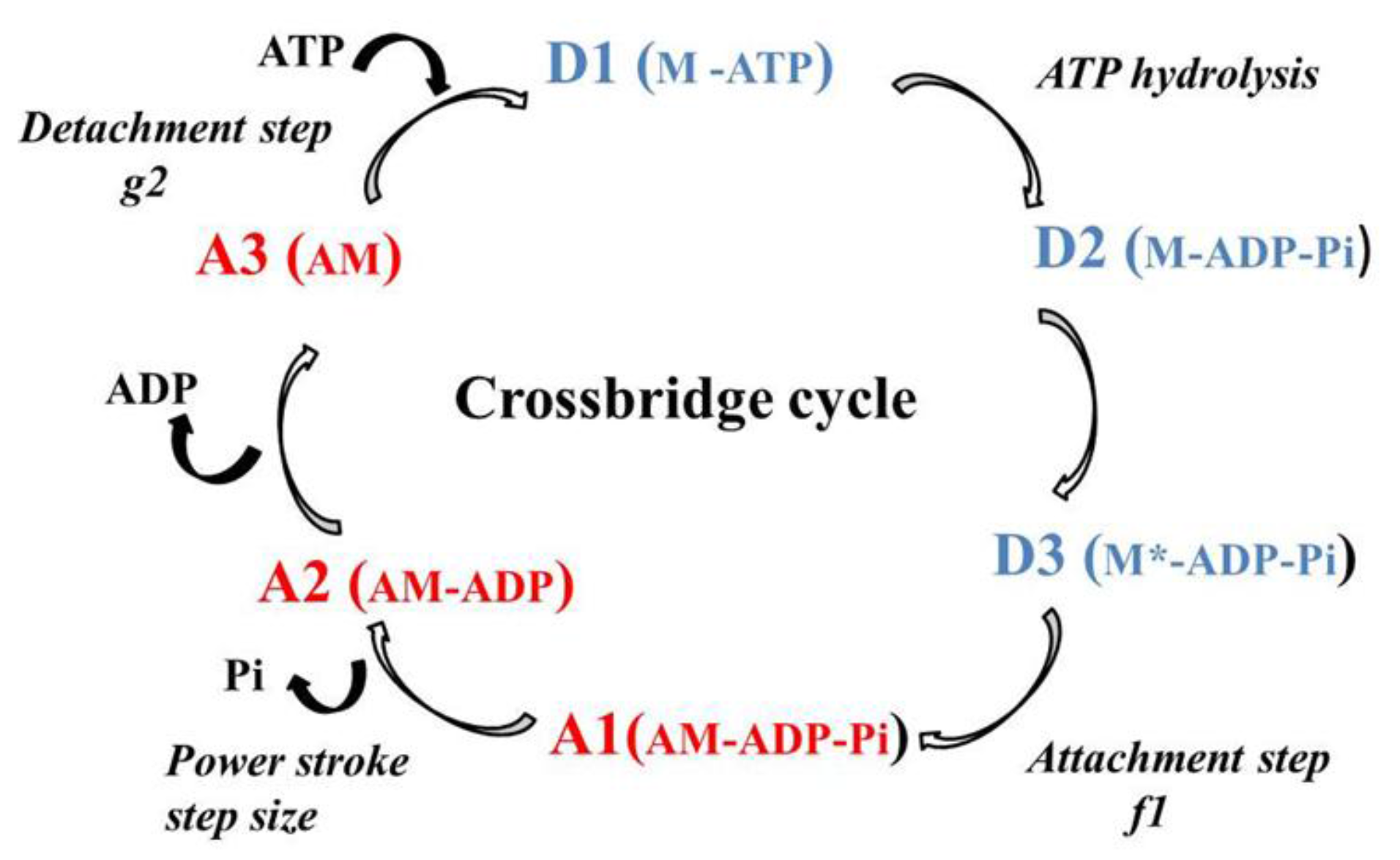
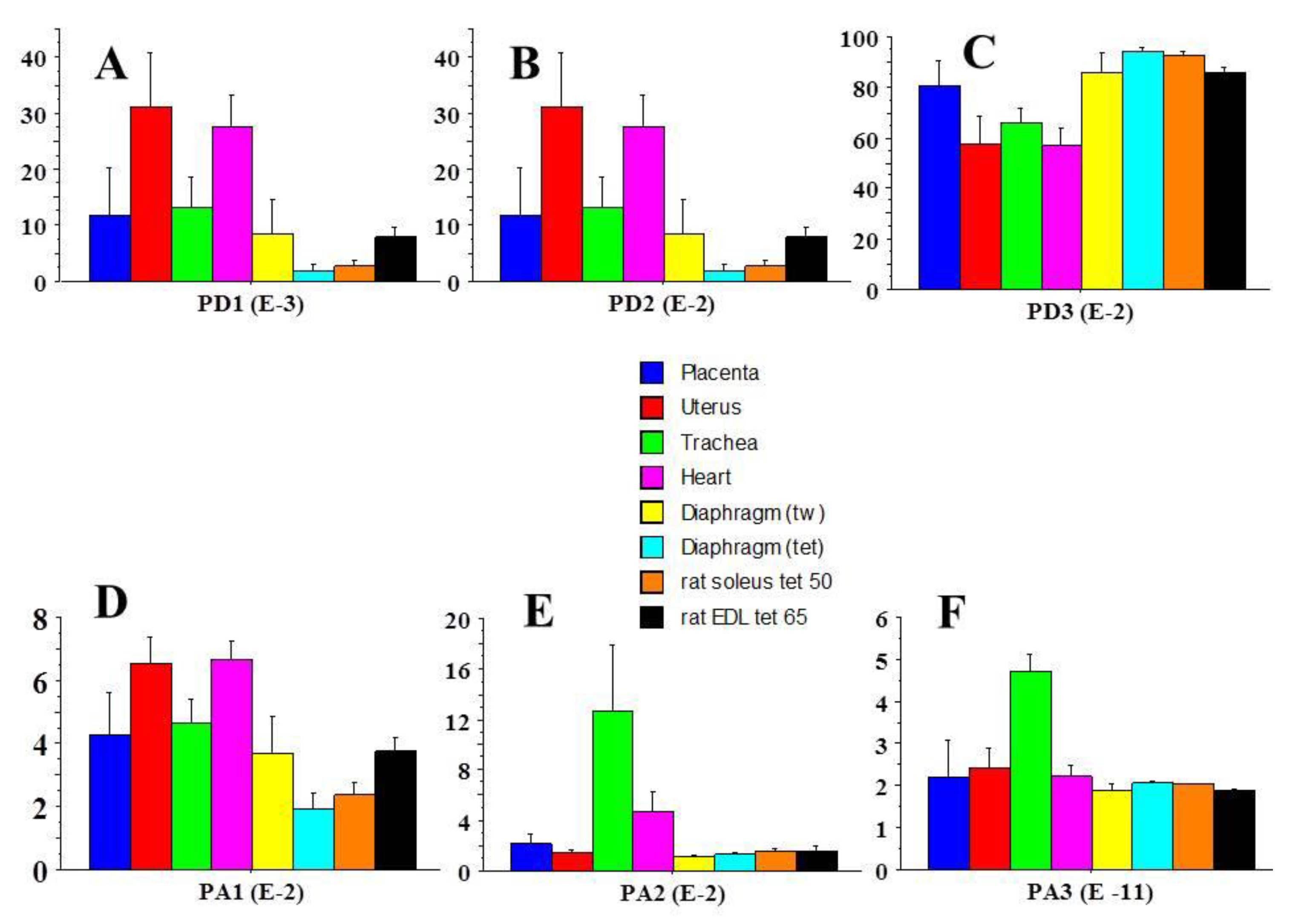
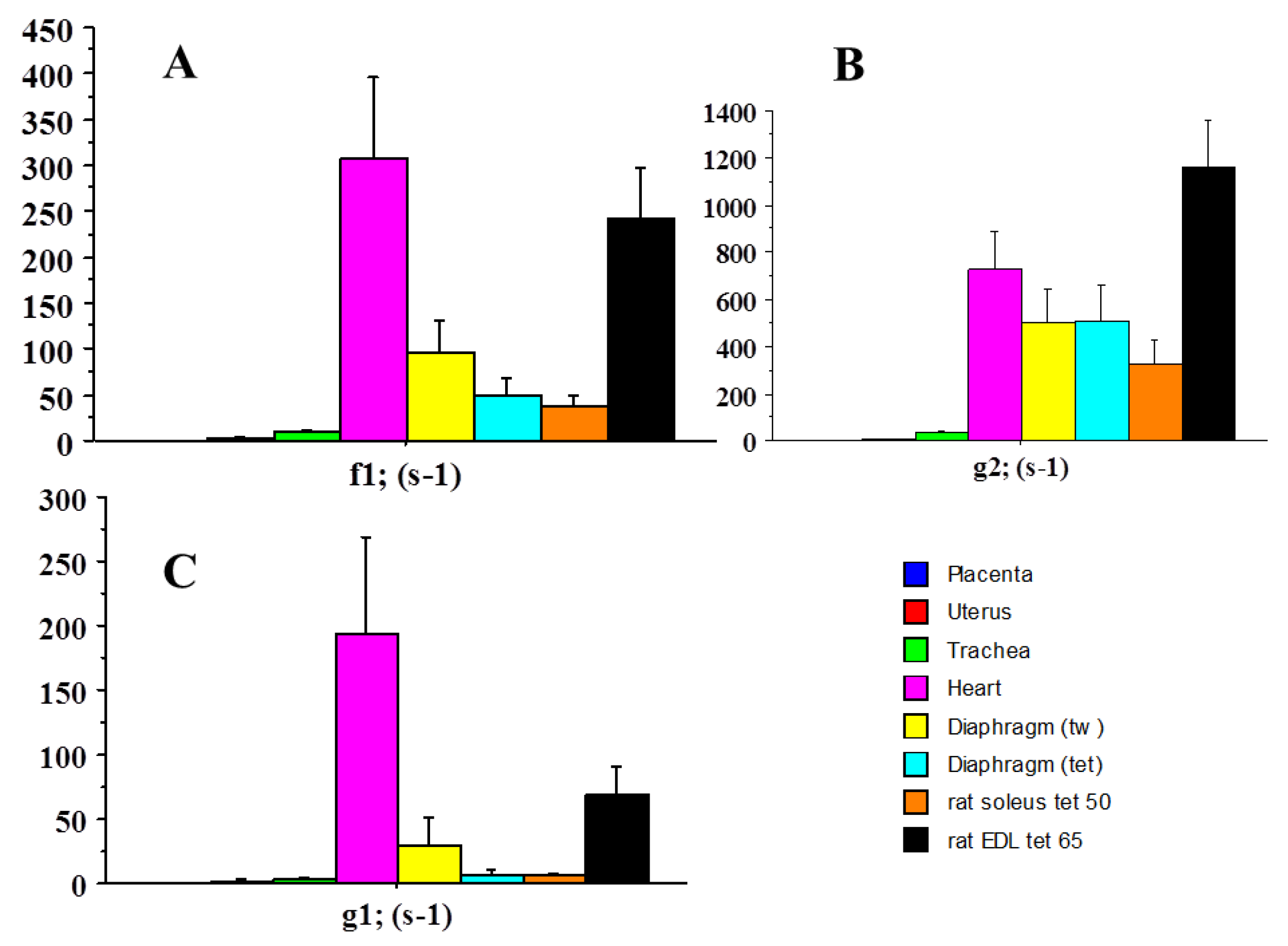
2.2. Molecular Mechanics of Actin–Myosin Molecular Motors
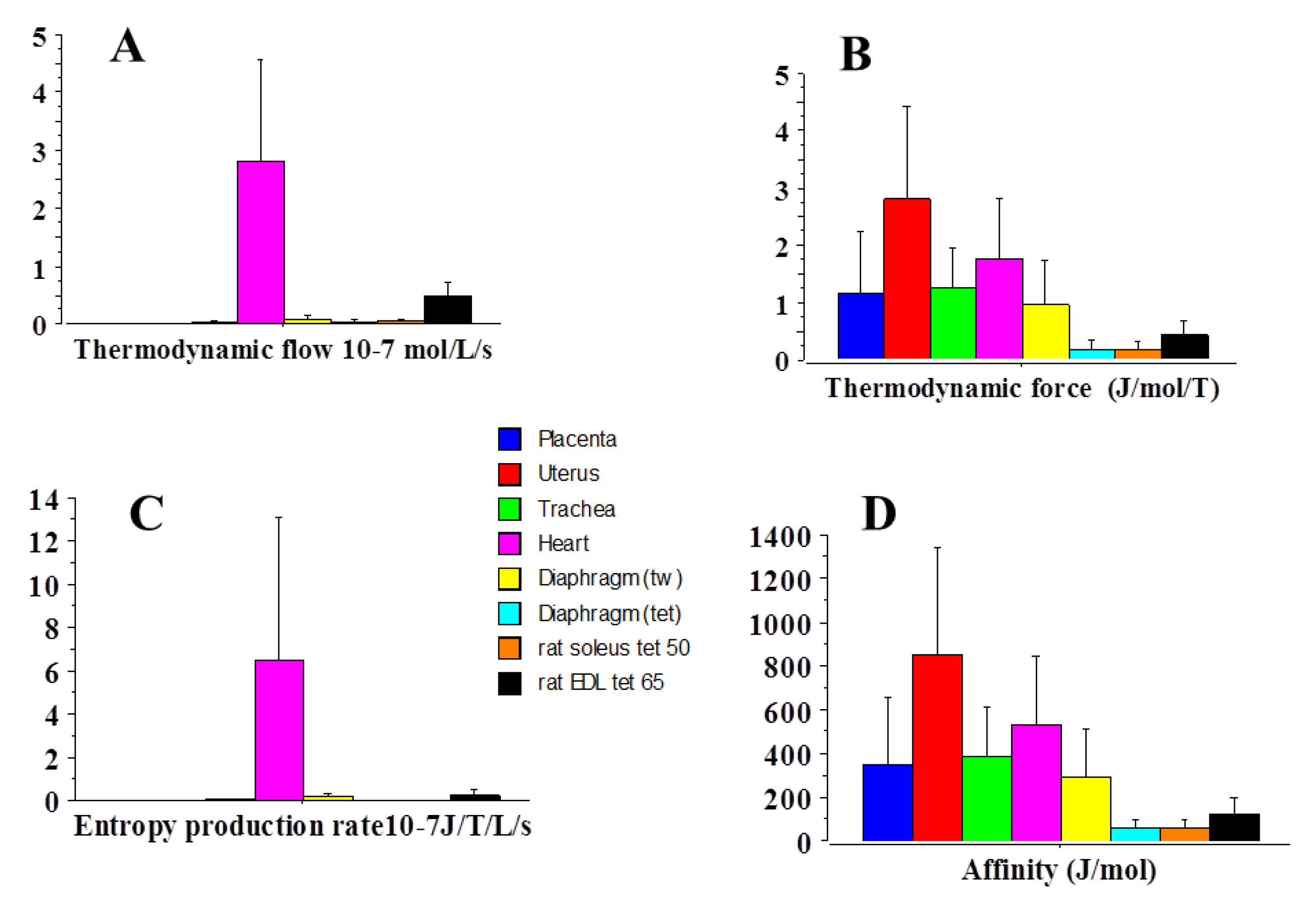
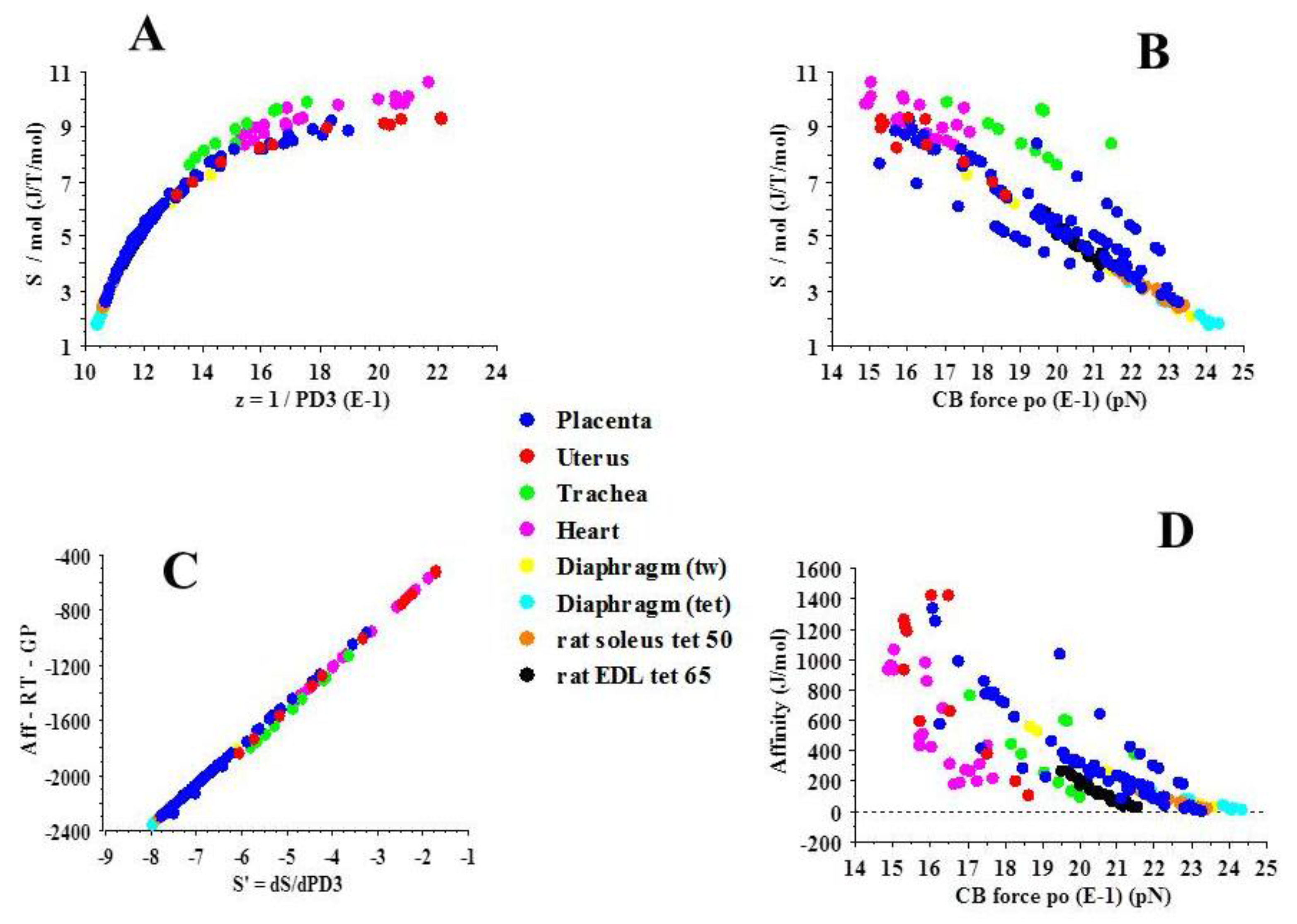
2.3. Statistical Mechanics
3. Discussion
4. Materials and Methods
4.1. Experimental Procedure
4.2. Experimental Set-Up
4.3. Huxley Formalism
4.4. Determination of CB Probabilities of the Six States
4.5. Statistical Mechanics
5. Statistical Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cooke, R. Actomyosin interaction in striated muscle. Physiol. Rev. 1997, 77, 671–697. [Google Scholar] [PubMed]
- Krantz, E.K.; Parker, J.C. Contractile properties of the smooth muscle in the human placenta. Clin. Obstet. Gynecol. 1963, 6, 26–38. [Google Scholar] [CrossRef]
- Farley, A.E.; Graham, C.H.; Smith, G.N. Contractile properties of human placental anchoring villi. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2004, 287, R680–R685. [Google Scholar] [CrossRef] [PubMed]
- Hinz, B. Formation and function of the myofibroblast during tissue repair. J. Investig. Dermatol. 2007, 127, 526–537. [Google Scholar] [CrossRef] [PubMed]
- Conti, M.A.; Adelstein, R.S. Nonmuscle myosin II moves in new directions. J. Cell Sci. 2008, 121, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, S.; Sakurai, K.; Shinomiya, T.; Fujitani, N.; Key, K.; Ohashi, M. Biochemical and immunohistochemical characterization of the isoforms of myosin and actin in human placenta. Placenta 2011, 32, 347–355. [Google Scholar] [CrossRef] [PubMed]
- Huxley, A.F. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957, 7, 255–318. [Google Scholar] [PubMed]
- Atkins, P.W. Physical Chemistry, 5th ed.; Oxford University Press: Oxford, UK; Melbourne, Australia; Tokio, Japan, 1990. [Google Scholar]
- Levine, I.N. Physical Chemistry, 5th ed.; McGraw-Hill International Edition: New York, NY, USA, 2003. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience Publishers: New York, NY, USA, 1967. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics from Heat Engines to Dissipative Structures; Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Lecarpentier, Y.; Claes, V.; Lecarpentier, E.; Blanc, F.X.; Joseph, T.; Geraets, B.; Krokidis, X.; Hebert, J.L. Comparative statistical mechanics of myosin molecular motors in rat heart, diaphragm and tracheal smooth muscle. Comptes Rendus Biol. 2011, 334, 725–736. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, Y.; Blanc, F.X.; Quillard, J.; Hebert, J.L.; Krokidis, X.; Coirault, C. Statistical mechanics of myosin molecular motors in skeletal muscles. J. Theor. Biol. 2005, 235, 381–392. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, Y.; Claes, V.; Hebert, J.L.; Krokidis, X.; Blanc, F.X.; Michel, F.; Timbely, O. Statistical Mechanics of the Human Placenta: A Stationary State of a Near-Equilibrium System in a Linear Regime. PLoS ONE 2015, 10, e0142471. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. Biol. Sci. 1938, 126, 136–195. [Google Scholar] [CrossRef]
- Hill, A.V. Thermodynamics of muscle. Nature 1951, 167, 377–380. [Google Scholar] [CrossRef] [PubMed]
- Leibler, S.; Huse, D.A. Porters versus rowers: A unified stochastic model of motor proteins. J. Cell Biol. 1993, 121, 1357–1368. [Google Scholar] [CrossRef] [PubMed]
- Howard, J. Molecular motors: Structural adaptations to cellular functions. Nature 1997, 389, 561–567. [Google Scholar] [CrossRef] [PubMed]
- Spudich, J.A. How molecular motors work. Nature 1994, 372, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, Y.; Chemla, D.; Pourny, J.C.; Blanc, F.X.; Coirault, C. Myosin cross bridges in skeletal muscles: “Rower” molecular motors. J. Appl. Physiol. 2001, 91, 2479–2486. [Google Scholar] [PubMed]
- Tawada, K.; Sekimoto, K. A physical model of ATP-induced actin-myosin movement in vitro. Biophys. J. 1991, 59, 343–356. [Google Scholar] [CrossRef]
- Lecarpentier, Y.; Chemla, D.; Blanc, F.X.; Pourny, J.C.; Joseph, T.; Riou, B.; Coirault, C. Mechanics, energetics, and crossbridge kinetics of rabbit diaphragm during congestive heart failure. FASEB J. 1998, 12, 981–989. [Google Scholar] [PubMed]
- Lecarpentier, Y.; Coirault, C.; Riou, B.; Chemla, D.; Mercadier, J.J. Diaphragm strength and cross-bridge properties during chronic growth hormone hypersecretion. Eur. Respir. J. 1999, 13, 1070–1077. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, Y.; Krokidis, X.; Martin, P.; Pineau, T.; Hebert, J.L.; Quillard, J.; Cortes-Morichetti, M.; Coirault, C. Increased entropy production in diaphragm muscle of PPAR alpha knockout mice. J. Theor. Biol. 2008, 250, 92–102. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.E.; Omachi, A. Measured and calculated NAD+-NADH ratios in human erythrocytes. Biochim. Biophys. Acta 1974, 354, 1–10. [Google Scholar] [CrossRef]
- Veech, R.L.; Kashiwaya, Y.; Gates, D.N.; King, M.T.; Clarke, K. The energetics of ion distribution: The origin of the resting electric potential of cells. IUBMB Life 2002, 54, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Veech, R.L.; Lawson, J.W.; Cornell, N.W.; Krebs, H.A. Cytosolic phosphorylation potential. J. Biol. Chem. 1979, 254, 6538–6547. [Google Scholar] [PubMed]
- Masuda, T.; Dobson, G.P.; Veech, R.L. The Gibbs-Donnan near-equilibrium system of heart. J. Biol. Chem. 1990, 265, 20321–20334. [Google Scholar] [PubMed]
- Demirel, Y.; Sandler, S.I. Thermodynamics and bioenergetics. Biophys. Chem. 2002, 97, 87–111. [Google Scholar] [CrossRef]
- Rigoulet, M.; Guerin, B.; Denis, M. Modification of flow-force relationships by external ATP in yeast mitochondria. Eur. J. Biochem. 1987, 168, 275–279. [Google Scholar] [CrossRef] [PubMed]
- Stucki, J.W. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem. 1980, 109, 269–283. [Google Scholar] [CrossRef] [PubMed]
- Kedem, O.; Katchalsky, A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim. Biophys. Acta 1958, 1000, 413–430. [Google Scholar] [CrossRef]
- Dewey, T.G.; Delle Donne, M. Non-equilibrium thermodynamics of molecular evolution. J. Theor. Biol. 1998, 193, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.L.; Eisenberg, E.; Chen, Y.D.; Podolsky, R.J. Some self-consistent two-state sliding filament models of muscle contraction. Biophys. J. 1975, 15, 335–372. [Google Scholar] [CrossRef]
- Chen, Y.D.; Hill, T.L. Analysis of a simple prototypal muscle model near to and far from equilibrium. Proc. Natl. Acad. Sci. USA 1974, 71, 1982–1986. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.L.; Chen, Y.D. Further analysis of a simple prototypal muscle model near to and far from equilibrium. Proc. Natl. Acad. Sci. USA 1974, 71, 2478–2481. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.L. Studies in irreversible thermodynamics, vii. Proc. Natl. Acad. Sci. USA 1966, 56, 840–844. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.L. Studies in irreversible thermodynamics, IV. Diagrammatic representation of steady state fluxes for unimolecular systems. J. Theor. Biol. 1966, 10, 442–459. [Google Scholar] [CrossRef]
- Hill, T.L.; Simmons, R.M. Free energy levels and entropy production in muscle contraction and in related solution systems. Proc. Natl. Acad. Sci. USA 1976, 73, 336–340. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, E.; Claes, V.; Timbely, O.; Hebert, J.L.; Arsalane, A.; Moumen, A.; Guerin, C.; Guizard, M.; Michel, F.; Lecarpentier, Y. Role of both actin-myosin cross bridges and NO-cGMP pathway modulators in the contraction and relaxation of human placental stem villi. Placenta 2013, 34, 1163–1169. [Google Scholar] [CrossRef] [PubMed]
- Woledge, R.C.; Curtin, A.N.; Homsher, E. Energetic Aspects of Muscle Contraction; Academic Press: London, UK, 1985; Volume 41. [Google Scholar]
- Sheterline, P.; Clayton, J.; Sparrow, J. Protein Profile, 3rd ed.; Academic Press: London, UK, 1996. [Google Scholar]
- Huxley, A.F.; Simmons, R.M. Mechanical properties of the cross-bridges of frog striated muscle. J. Physiol. 1971, 218, 59P–60P. [Google Scholar] [PubMed]
- Rayment, I.; Holden, H.M.; Whittaker, M.; Yohn, C.B.; Lorenz, M.; Holmes, K.C.; Milligan, R.A. Structure of the actin-myosin complex and its implications for muscle contraction. Science 1993, 261, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, R.; Freyzon, Y.; Trybus, K.M.; Cohen, C. Crystal structure of a vertebrate smooth muscle myosin motor domain and its complex with the essential light chain: Visualization of the pre-power stroke state. Cell 1998, 94, 559–571. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes II. Phys. Rev. 1931, 38, 405–426. [Google Scholar] [CrossRef]
- De Donder, T. L’Affinité; Gauthiers-Villars: Paris, France, 1927. [Google Scholar]
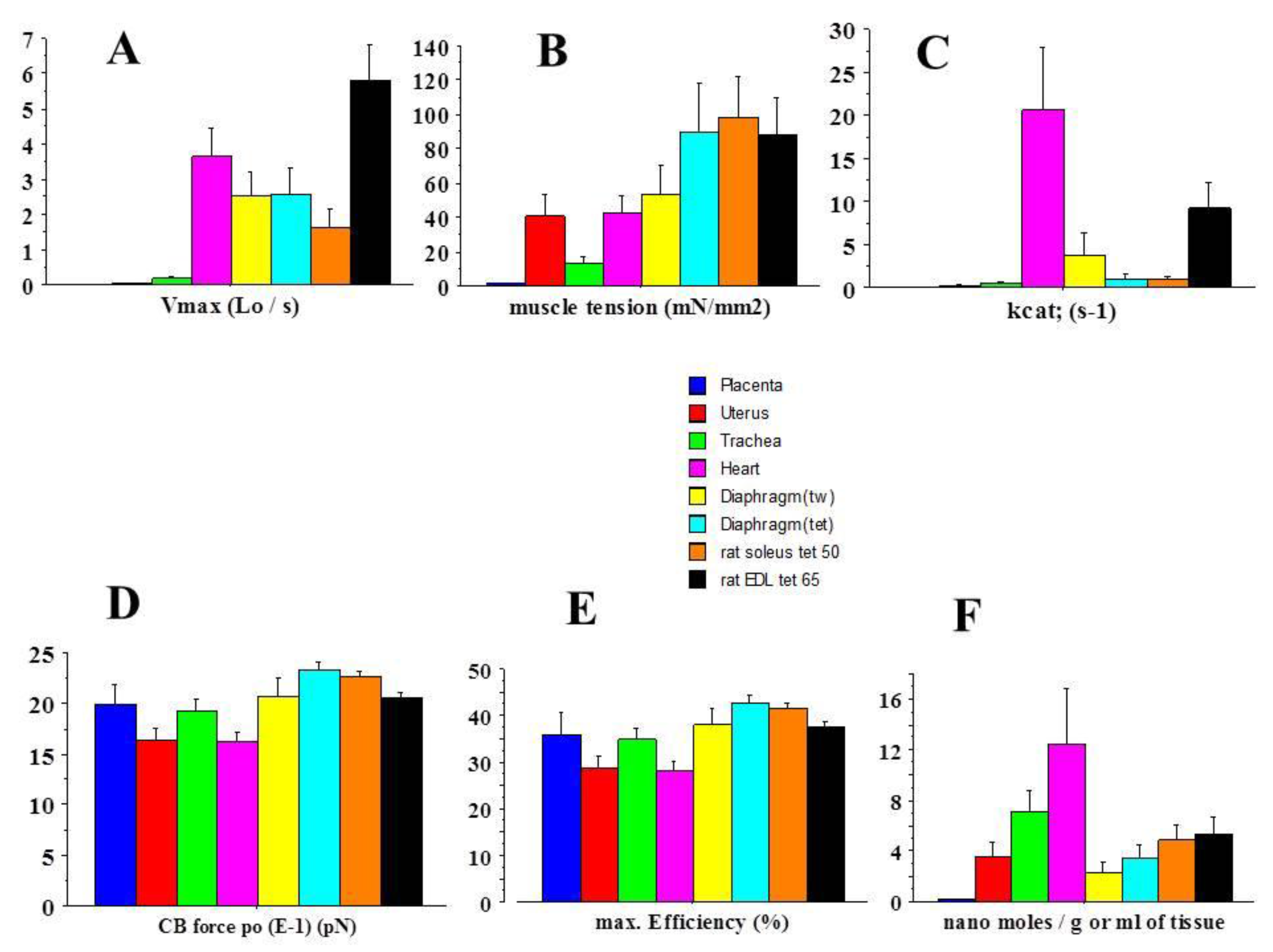

| Placenta (Mean) | Heart (Mean) | Heart/Placenta Ratio | |
|---|---|---|---|
| Vmax | 0.002 | 3.7 | 1850 |
| Tension | 1.5 | 42 | 28 |
| Kcat | 0.003 | 20.6 | 6866 |
| Unitary CB force | 2.0 | 1.6 | 0.80 |
| max Efficiency (%) | 36 | 28 | 0.78 |
| Myosin content | 0.14 | 12.5 | 89 |
| Frictional drag force (FDF) | 3.5 | 4.1 | 1.2 |
| FDF coefficient | 3943 | 1 | 0.0003 |
| Vo | 0.002 | 4.7 | 2350 |
| G | 3.7 | 1.6 | 0.43 |
| f1 | 0.075 | 306 | 4080 |
| g1 | 0.028 | 194 | 6928 |
| g2 | 0.341 | 731 | 2143 |
| Statistical entropy | 5.6 | 9.3 | 1.7 |
| Internal energy | 1097 | 1401 | 1.3 |
| Affinity | 354 | 535 | 1.5 |
| Thermodynamic force | 1.2 | 1.8 | 1.5 |
| Thermodynamic flow | 4.8 × 10−6 | 2.8 | 0.58 × 106 |
| Entropy Production Rate | 8.2 × 10−13 | 6.5 × 10−7 | 0.8 × 106 |
| Slope | R | P | |
|---|---|---|---|
| PLACENTA | 2.4 × 1013 | 0.85 | 0.001 |
| UTERUS | 1.6 × 1010 | 0.61 | 0.04 |
| TRACHEA | 4.9 × 109 | 0.76 | 0.01 |
| HEART | 5.2 × 107 | 0.89 | 0.0001 |
| DIAPHRAGM (tw) | 1.1 × 109 | 0.91 | 0.0001 |
| DIAPHRAGM (TET) | 4.2 × 108 | 0.85 | 0.002 |
| SOLEUS | 3.5 × 108 | 0.60 | 0.0001 |
| EDL | 7.9 × 107 | 0.71 | 0.0001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lecarpentier, Y.; Claes, V.; Krokidis, X.; Hébert, J.-L.; Timbely, O.; Blanc, F.-X.; Michel, F.; Vallée, A. Comparative Statistical Mechanics of Muscle and Non-Muscle Contractile Systems: Stationary States of Near-Equilibrium Systems in A Linear Regime. Entropy 2017, 19, 558. https://doi.org/10.3390/e19100558
Lecarpentier Y, Claes V, Krokidis X, Hébert J-L, Timbely O, Blanc F-X, Michel F, Vallée A. Comparative Statistical Mechanics of Muscle and Non-Muscle Contractile Systems: Stationary States of Near-Equilibrium Systems in A Linear Regime. Entropy. 2017; 19(10):558. https://doi.org/10.3390/e19100558
Chicago/Turabian StyleLecarpentier, Yves, Victor Claes, Xénophon Krokidis, Jean-Louis Hébert, Oumar Timbely, François-Xavier Blanc, Francine Michel, and Alexandre Vallée. 2017. "Comparative Statistical Mechanics of Muscle and Non-Muscle Contractile Systems: Stationary States of Near-Equilibrium Systems in A Linear Regime" Entropy 19, no. 10: 558. https://doi.org/10.3390/e19100558
APA StyleLecarpentier, Y., Claes, V., Krokidis, X., Hébert, J.-L., Timbely, O., Blanc, F.-X., Michel, F., & Vallée, A. (2017). Comparative Statistical Mechanics of Muscle and Non-Muscle Contractile Systems: Stationary States of Near-Equilibrium Systems in A Linear Regime. Entropy, 19(10), 558. https://doi.org/10.3390/e19100558





