Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems
Abstract
1. Introduction
2. Method
2.1. Entropy of Entropy (EoE) Method
2.2. Data Description
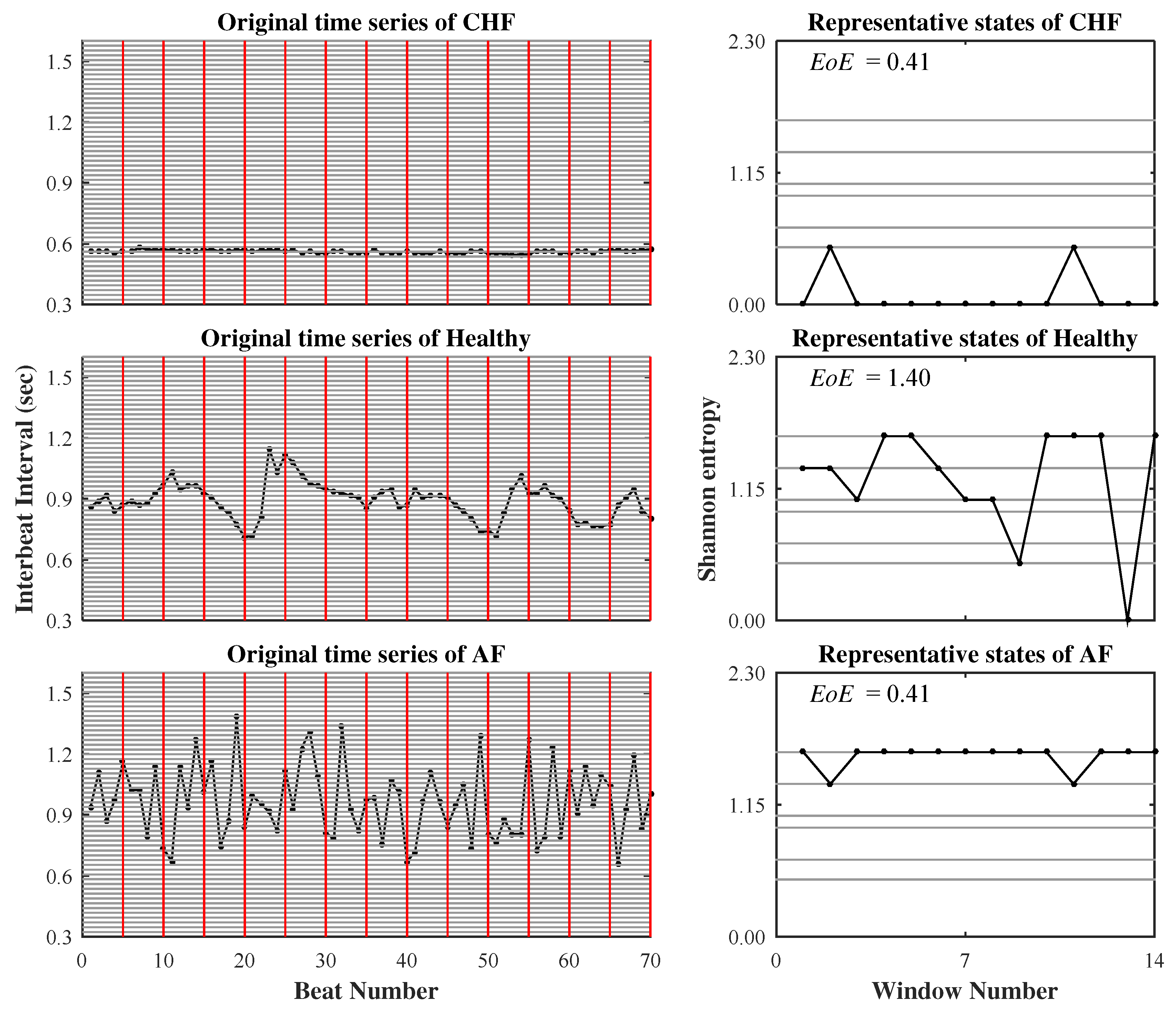
2.3. An Example in Analyzing Cardiac Interbeat Interval Time Series
3. Results
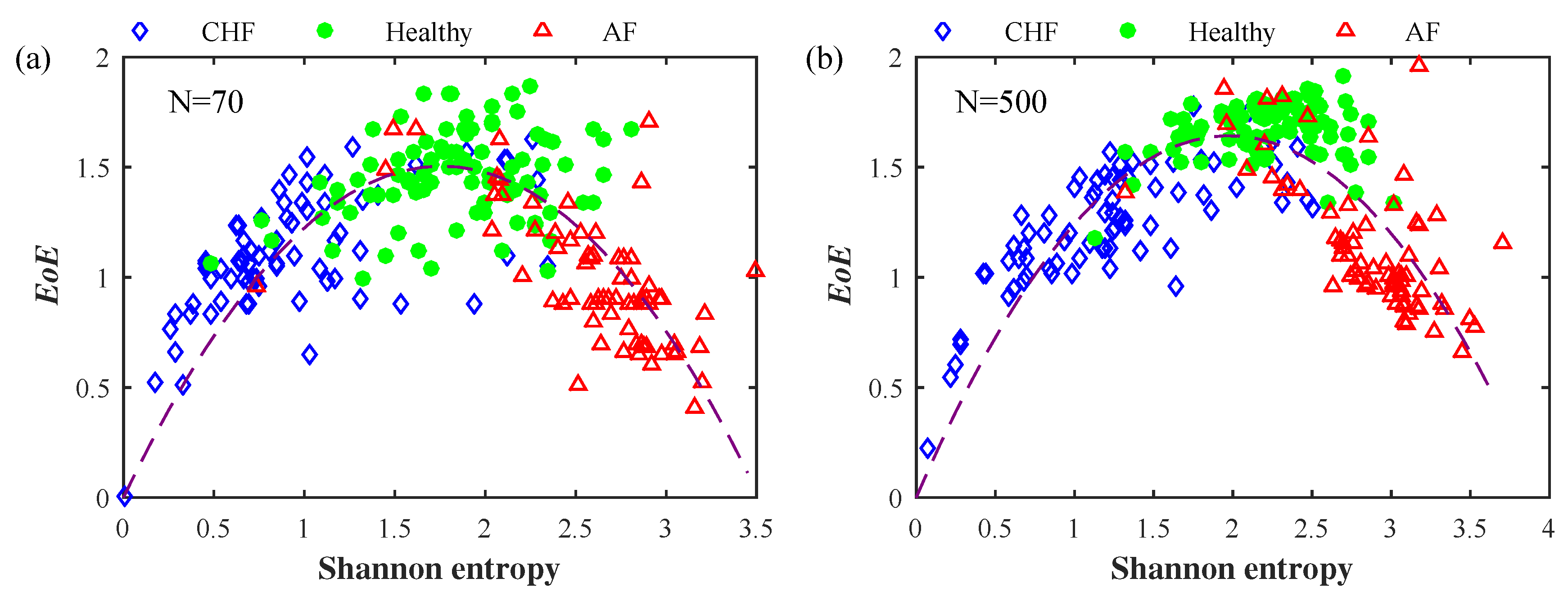
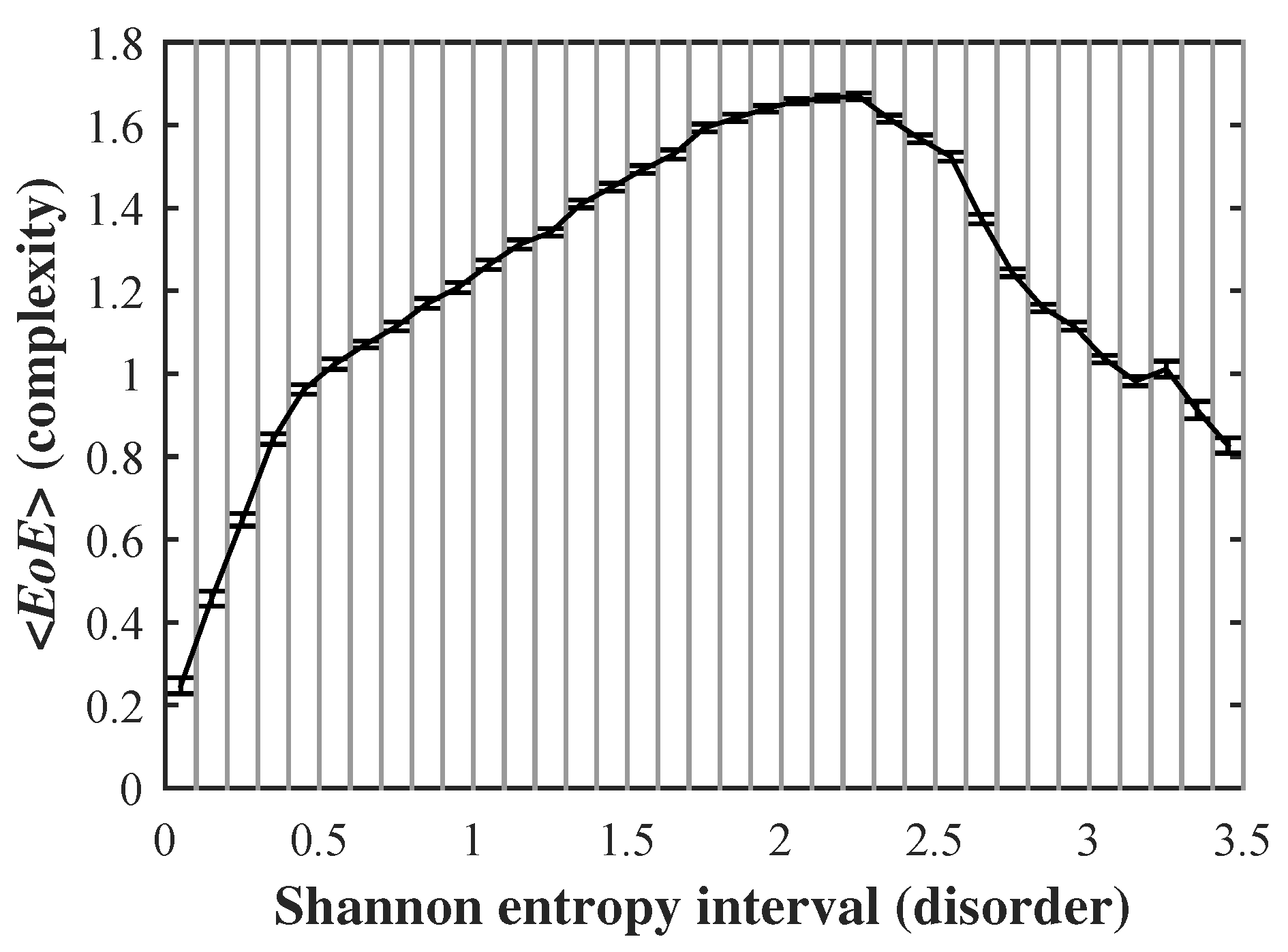
3.1. Inverted U Curve
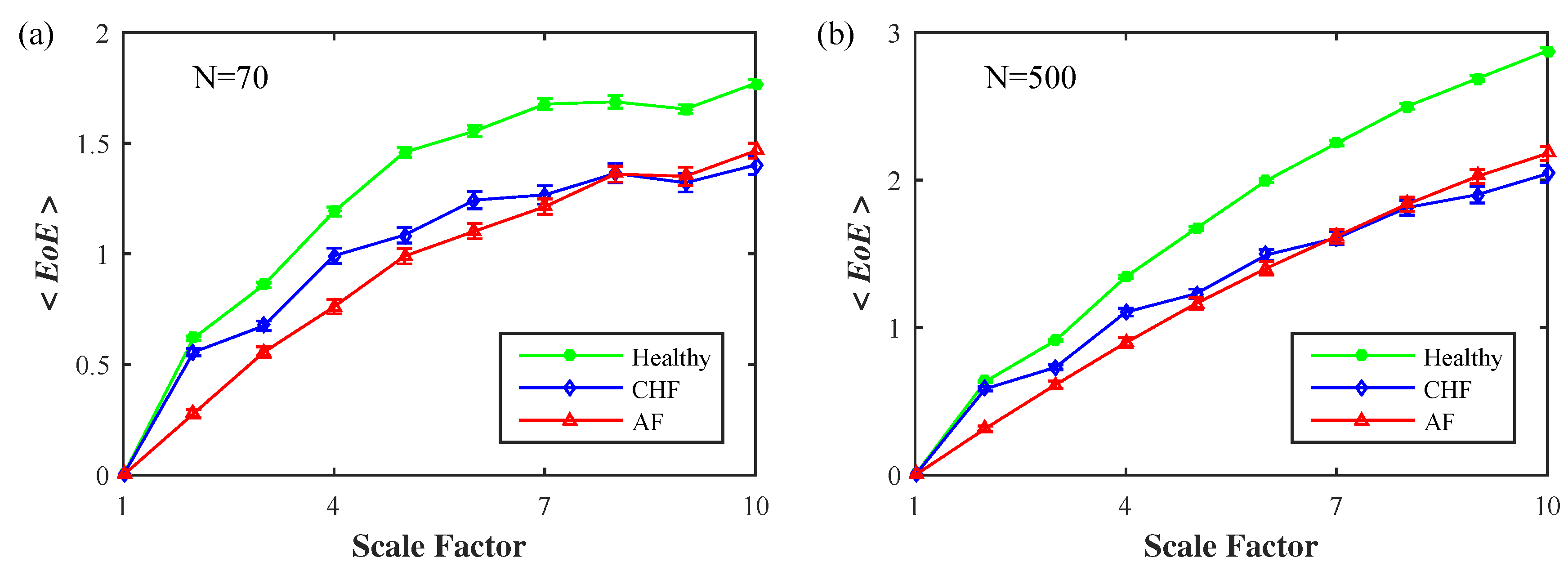
3.2. Accuracy of EoE
4. Discussion
4.1. Parameters and Setup
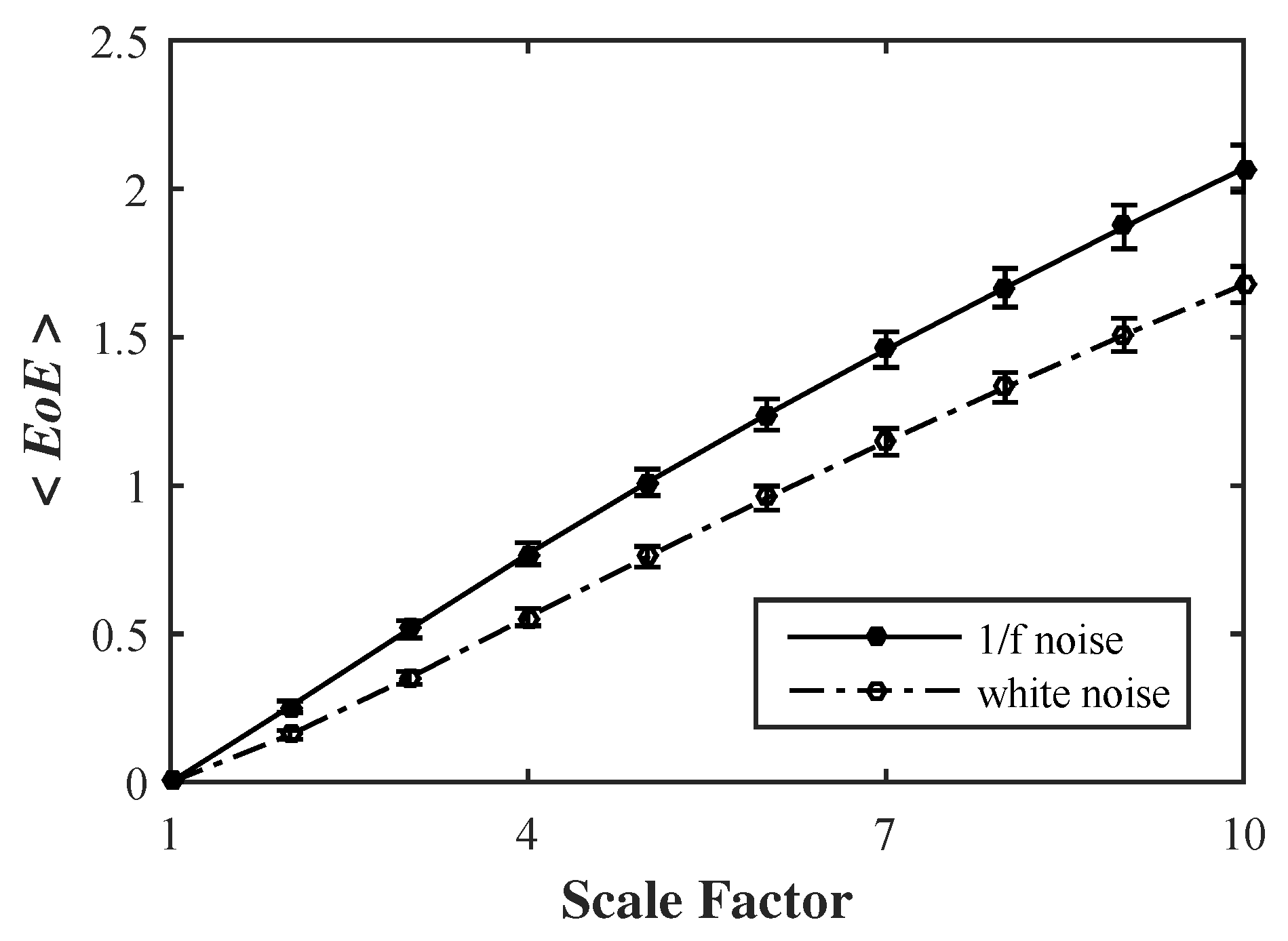
4.2. Simulated 1/f Noise and Gaussian Distributed White Noise
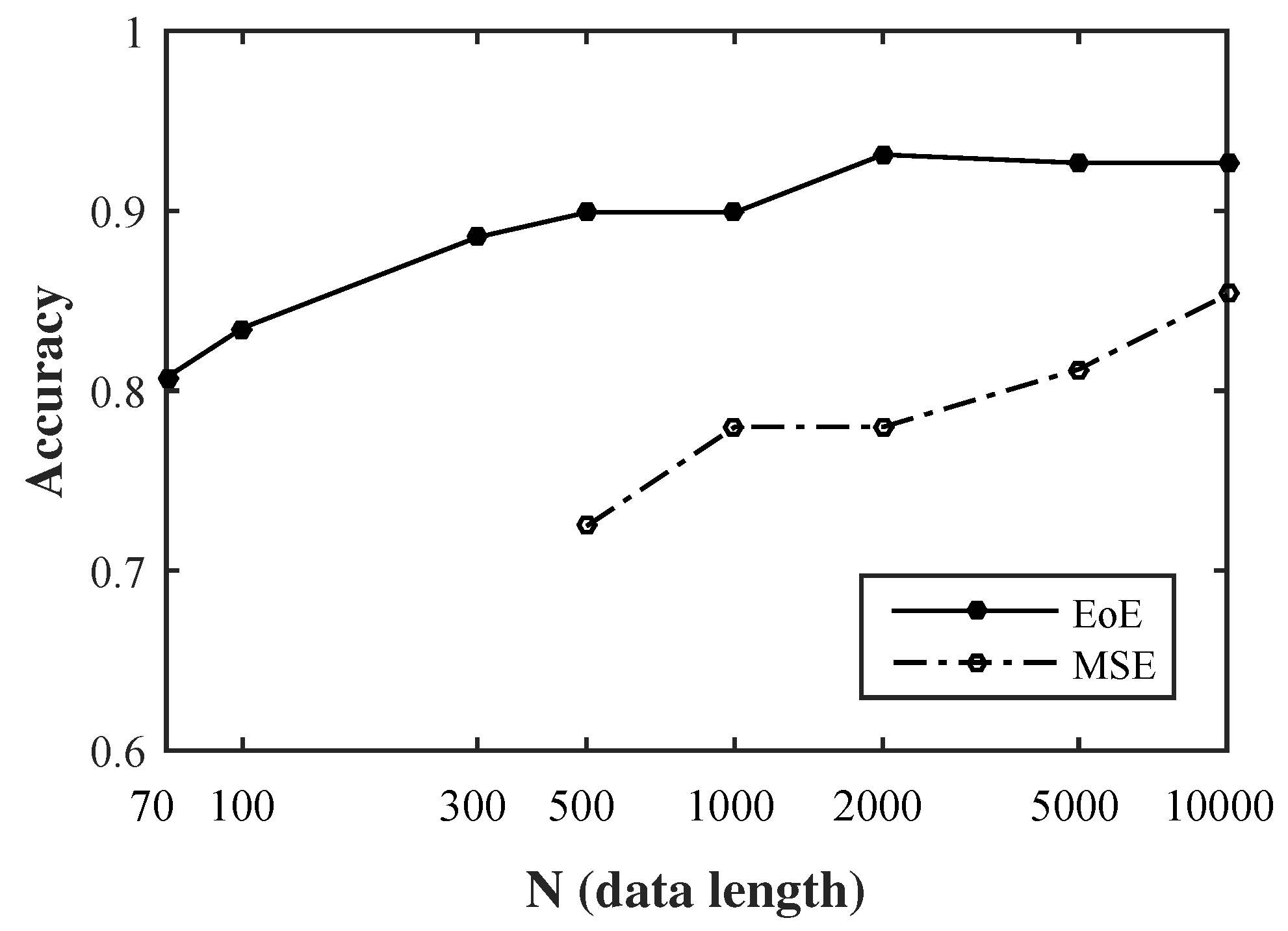
4.3. Comparison between MSE and EoE
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mitchell, M. Complexity A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 68102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.-K.; Costa, M.; Goldberger, A.L. Adaptive data analysis of complex fluctuations in physiologic time series. World Sci. 2009, 1, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Gell-Mann, M. What is complexity. Complexity 1995, 1, 16–19. [Google Scholar] [CrossRef]
- Huberman, B.A.; Hogg, T. Complexity and Adaptation. Physica D 1986, 22, 376–384. [Google Scholar] [CrossRef]
- Zhang, Y.-C. Complexity and 1/f noise. A phase space approach. J. Phys. I EDP Sci. 1991, 1, 971–977. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Cabella, B.C.T.; Neves, U.P.D.C.; Murta Junior, L.O. Multiscale entropy-based methods for heart rate variability complexity analysis. Physica A 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Beisbart, C.; Hartmann, S. Probabilities in Physics; Oxford University Press: Oxford, UK, 2011; p. 117. [Google Scholar]
- Shannon, C.E. Prediction and ntropy of printed english. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Mathematics 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Hear. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Castiglioni, P.; Bari, V.; Bassani, T.; Marchi, A.; Cividjian, A.; Quintin, L.; DiRienzo, M. K-nearest-neighbor conditional entropy approach for the assessment of the short-term complexity of cardiovascular control. Physiol. Meas. 2013, 34, 17–33. [Google Scholar] [CrossRef] [PubMed]
- Hou, F.-Z.; Wang, J.; Wu, X.-C.; Yan, F.-R. A dynamic marker of very short-term heartbeat under pathological states via network analysis. Europhys. Lett. 2014, 107, 58001. [Google Scholar] [CrossRef]
- Bose, R.; Chouhan, S. Alternate measure of information useful for DNA sequences. Phys. Rev. E 2011, 83, 1–6. [Google Scholar] [CrossRef] [PubMed]
- BIDMC Congestive Heart Failure Database, MIT-BIH Normal Sinus Rhythm Database, and Long Term AF Database. Available online: http://www.physionet.org/physiobank/database/#ecg (accessed on 5 December 2016).
- VonTscharner, V.; Zandiyeh, P. Multi-scale transitions of fuzzy sample entropy of RR-intervals and their phase-randomized surrogates: A possibility to diagnose congestive heart failure. Biomed. Signal Process. Control 2017, 31, 350–356. [Google Scholar] [CrossRef]
- Liu, C.; Gao, R. Multiscale entropy analysis of the differential RR interval time series signal and its application in detecting congestive heart failure. Entropy 2017, 19, 3. [Google Scholar] [CrossRef]
- Dao, Q.; Krishnaswamy, P.; Kazanegra, R.; Harrison, A.; Amirnovin, R.; Lenert, L.; Clopton, P.; Alberto, J.; Hlavin, P.; Maisel, A.S. Utility of b-type natriuretic peptide in the diagnosis of congestive heart failure in an urgent-care setting. J. Am. Coll. Cardiol. 2001, 37, 379–385. [Google Scholar] [CrossRef]
- Lin, Y.H.; Huang, H.C.; Chang, Y.C.; Lin, C.; Lo, M.T.; Liu, L.Y.; Tsai, P.R.; Chen, Y.S.; Ko, W.J.; Ho, Y.L.; et al. Multi-scale symbolic entropy analysis provides prognostic prediction in patients receiving extracorporeal life support. Crit. Care 2014, 18, 548. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Broken asymmetry of the human heartbeat: Loss of time irreversibility in aging and disease. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Cho, R.Y.; Mizuno, T.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Antipsychotics reverse abnormal EEG complexity in drug-naive schizophrenia: A multiscale entropy analysis. Neuroimage 2010, 51, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Garrett, D.D.; Samanez-Larkin, G.R.; MacDonald, S.W.S.; Lindenberger, U.; McIntosh, A.R.; Grady, C.L. Moment-to-moment brain signal variability: A next frontier in human brain mapping? Neurosci. Biobehav. Rev. 2013, 37, 610–624. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Lo, M.; Yang, A.C.; Peng, C.; Cheng, S.; Tseng, P.; Juan, C. NeuroImage Revealing the brains adaptability and the transcranial direct current stimulation facilitating effect in inhibitory control by multiscale entropy. Neuroimage 2014, 90, 218–234. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Huang, C.C.; Yeh, H.L.; Liu, M.E.; Hong, C.J.; Tu, P.C.; Chen, J.F.; Huang, N.E.; Peng, C.K.; Lin, C.P.; et al. Complexity of spontaneous BOLD activity in default mode network is correlated with cognitive function in normal male elderly: A multiscale entropy analysis. Neurobiol. Aging 2013, 34, 428–438. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, T.T.; Jirsa, V.K.; Spiegler, A.; McIntosh, A.R.; Deco, G. Bottom up modeling of the connectome: Linking structure and function in the resting brain and their changes in aging. Neuroimage 2013, 80, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, J.; Edwards, J.; Mamelak, A.N.; Schuman, E.M. Long-range temporal correlations in the spontaneous spiking of neurons in the hippocampal-amygdala complex of humans. Neuroscience 2005, 131, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Liu, D.H.; Wang, K.H.; Liu, Q.; Abbod, M.F.; Jiang, B.C.; Chen, K.P.; Wu, C.; Shieh, J.S. Multivariate multiscale entropy applied to center of pressure signals analysis: An effect of vibration stimulation of shoes. Entropy 2012, 14, 2157–2172. [Google Scholar] [CrossRef]
- Kang, H.G.; Costa, M.D.; Priplata, A.A.; Starobinets, O.V.; Goldberger, A.L.; Peng, C.K.; Kiely, D.K.; Cupples, L.A.; Lipsitz, L.A. Frailty and the degradation of complex balance dynamics during a dual-task protocol. J. Gerontol.-Ser. A Biol. Sci. Med. Sci. 2009, 64, 1304–1311. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.-W.; Czosnyka, M.; Shieh, J.-S.; Smielewska, A.; Pickard, J.D.; Smielewski, P. Complexity of intracranial pressure correlates with outcome after traumatic brain injury. Brain 2012, aws155. [Google Scholar] [CrossRef] [PubMed]
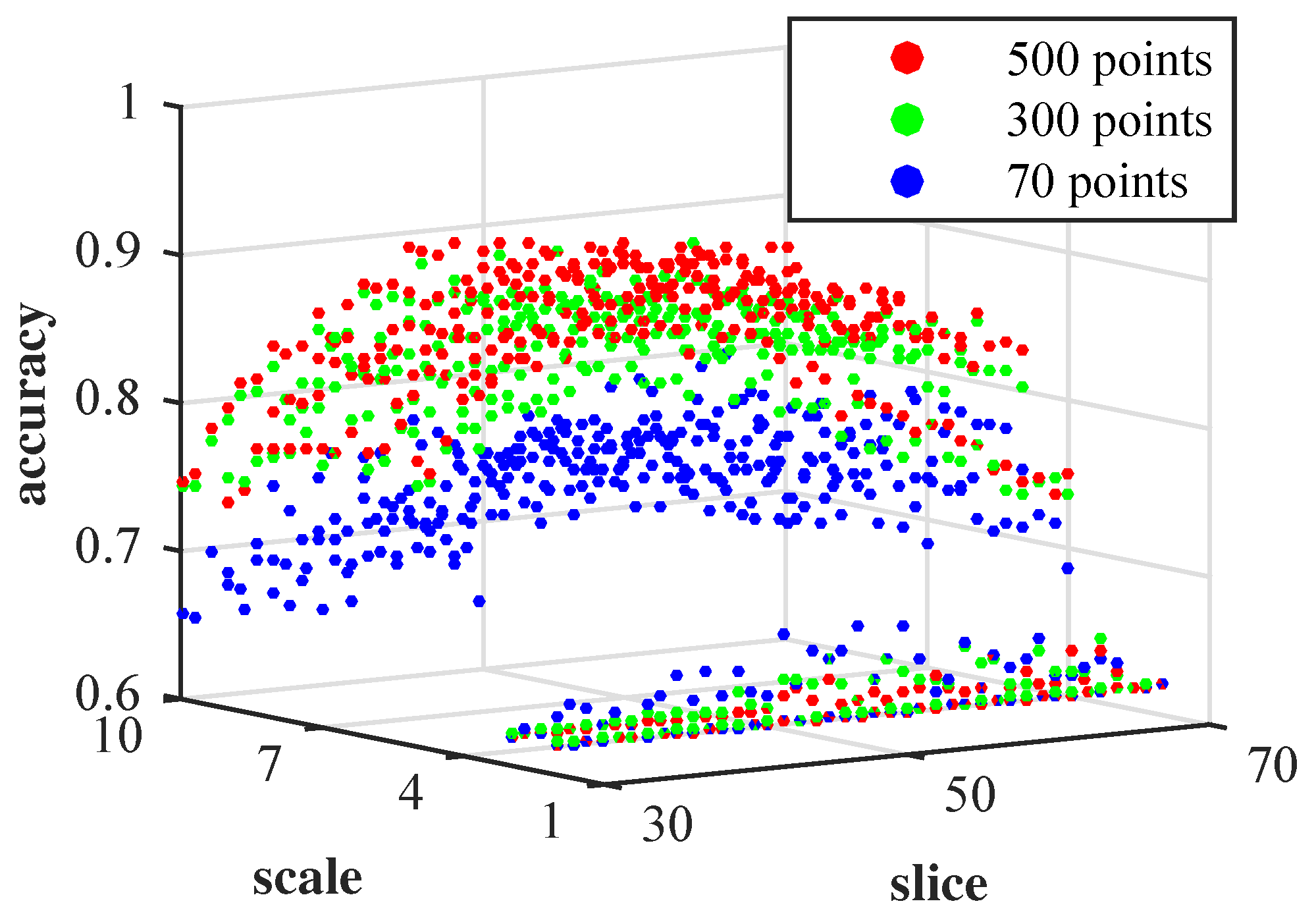
| Date Length | 70 Points | 300 Points | 500 Points | |
|---|---|---|---|---|
| Group | ||||
| NSR (Specificity) | 0.86 | 0.93 | 0.91 | |
| CHF (Sensitivity) | 0.72 | 0.81 | 0.92 | |
| AF (Sensitivity) | 0.83 | 0.83 | 0.86 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, C.F.; Wei, S.-Y.; Huang, H.-P.; Hsu, L.; Chi, S.; Peng, C.-K. Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems. Entropy 2017, 19, 550. https://doi.org/10.3390/e19100550
Hsu CF, Wei S-Y, Huang H-P, Hsu L, Chi S, Peng C-K. Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems. Entropy. 2017; 19(10):550. https://doi.org/10.3390/e19100550
Chicago/Turabian StyleHsu, Chang Francis, Sung-Yang Wei, Han-Ping Huang, Long Hsu, Sien Chi, and Chung-Kang Peng. 2017. "Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems" Entropy 19, no. 10: 550. https://doi.org/10.3390/e19100550
APA StyleHsu, C. F., Wei, S.-Y., Huang, H.-P., Hsu, L., Chi, S., & Peng, C.-K. (2017). Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems. Entropy, 19(10), 550. https://doi.org/10.3390/e19100550






