Solution of Higher Order Nonlinear Time-Fractional Reaction Diffusion Equation
Abstract
:1. Introduction
2. Definitions
- (a)
- A real function , is said to be in the space , if a real number , such that , where . Clearly if .
- (b)
- A function , is said to be in the space , m if
- (c)
- The (left sided) Riemann–Liouville fractional integral of order of a function , is defined as , , where .
- (d)
- The (left sided) Riemann–Liouville fractional derivative of , , of order , is defined by , , .
- (e)
- The (left sided) Caputo fractional derivative of , , is defined as
3. Basic Idea of HAM
4. Solution of the Problem
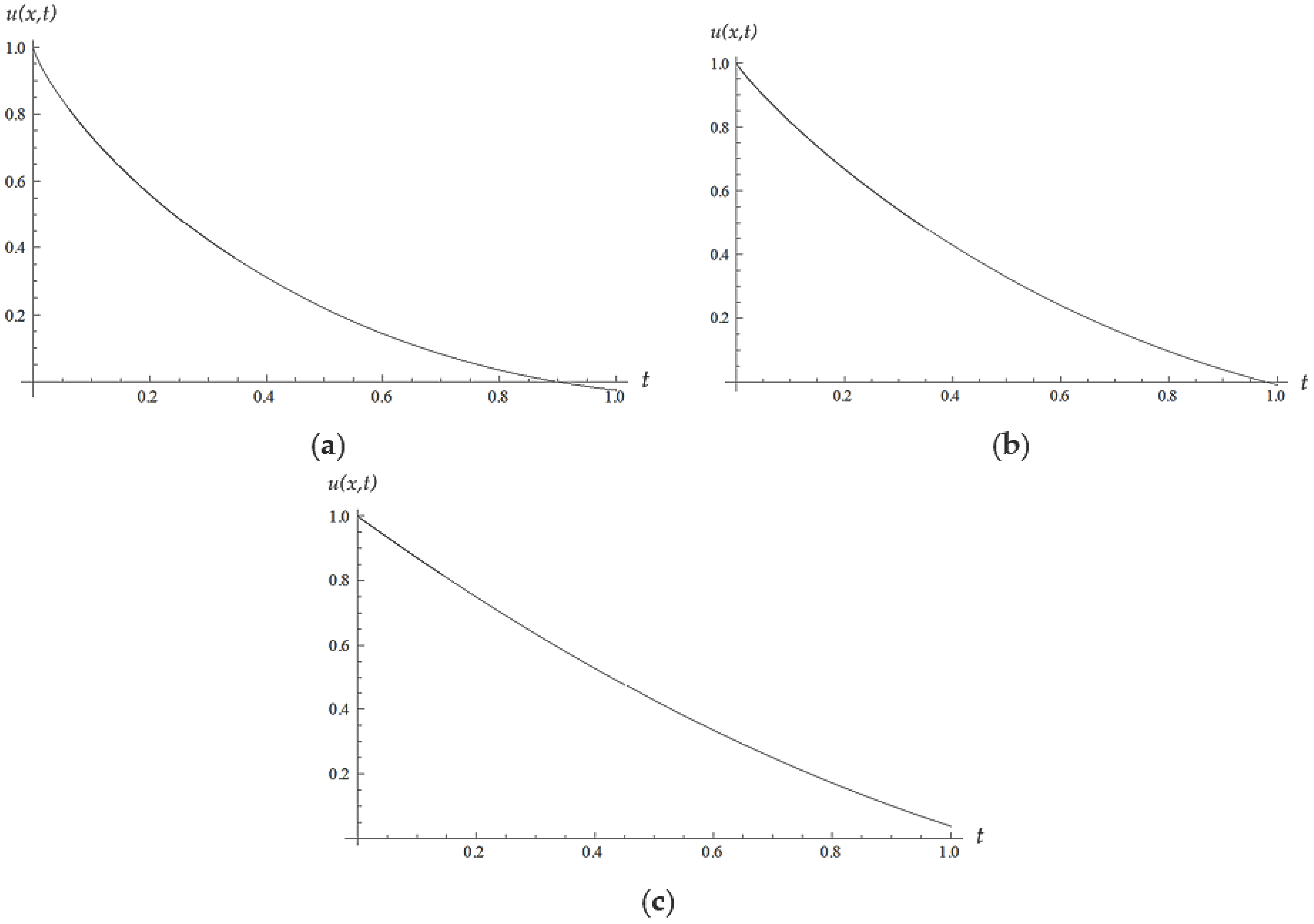
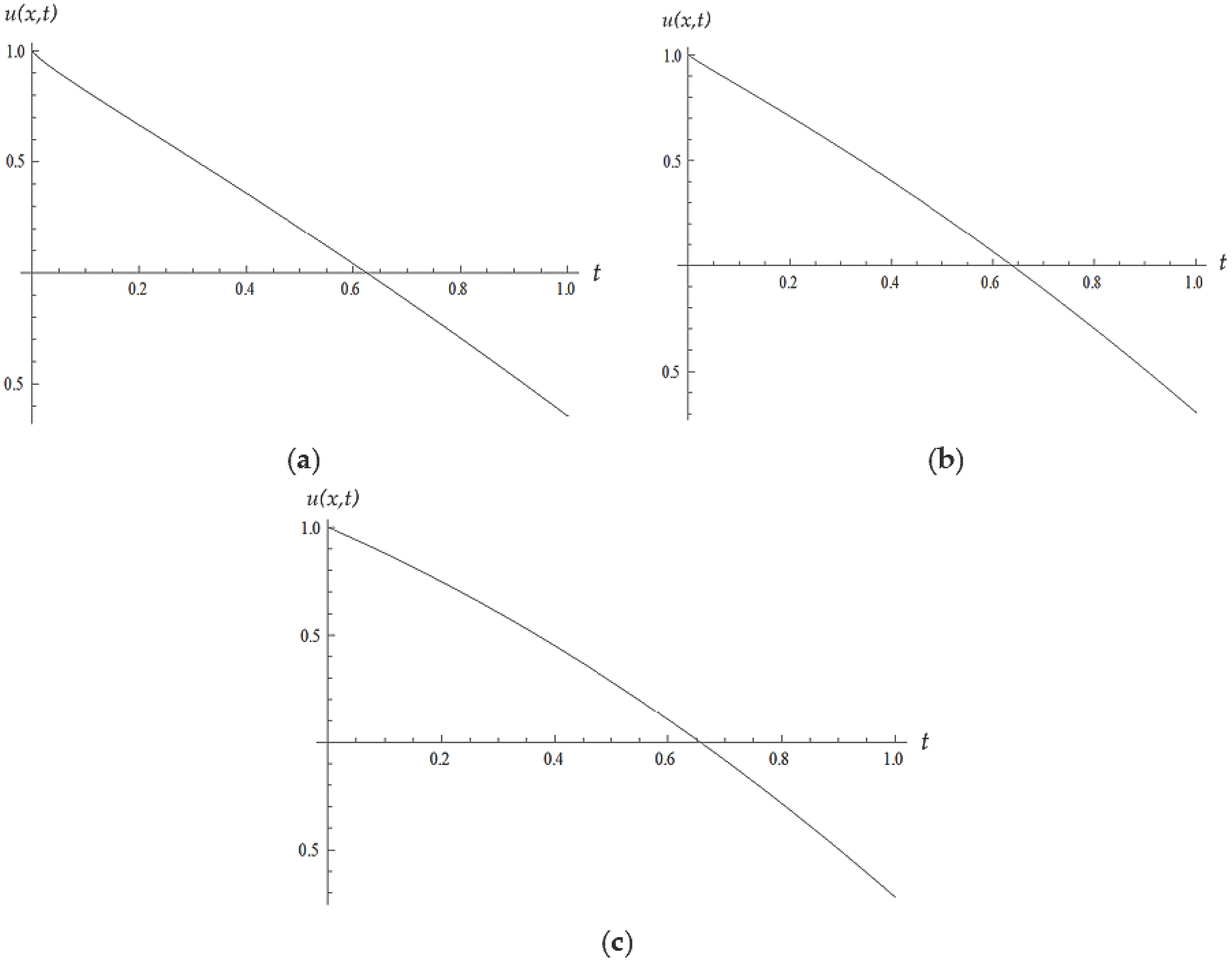
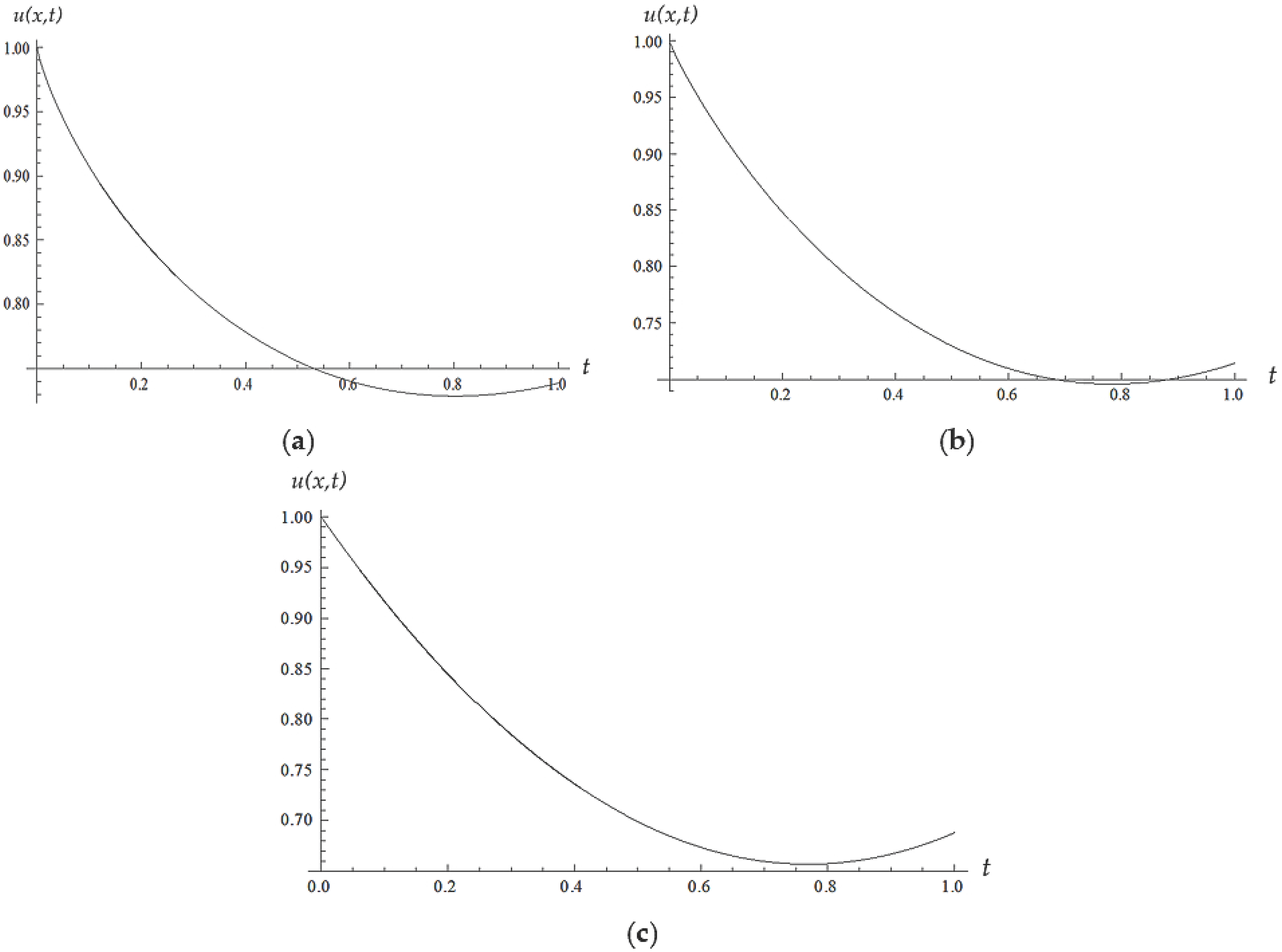
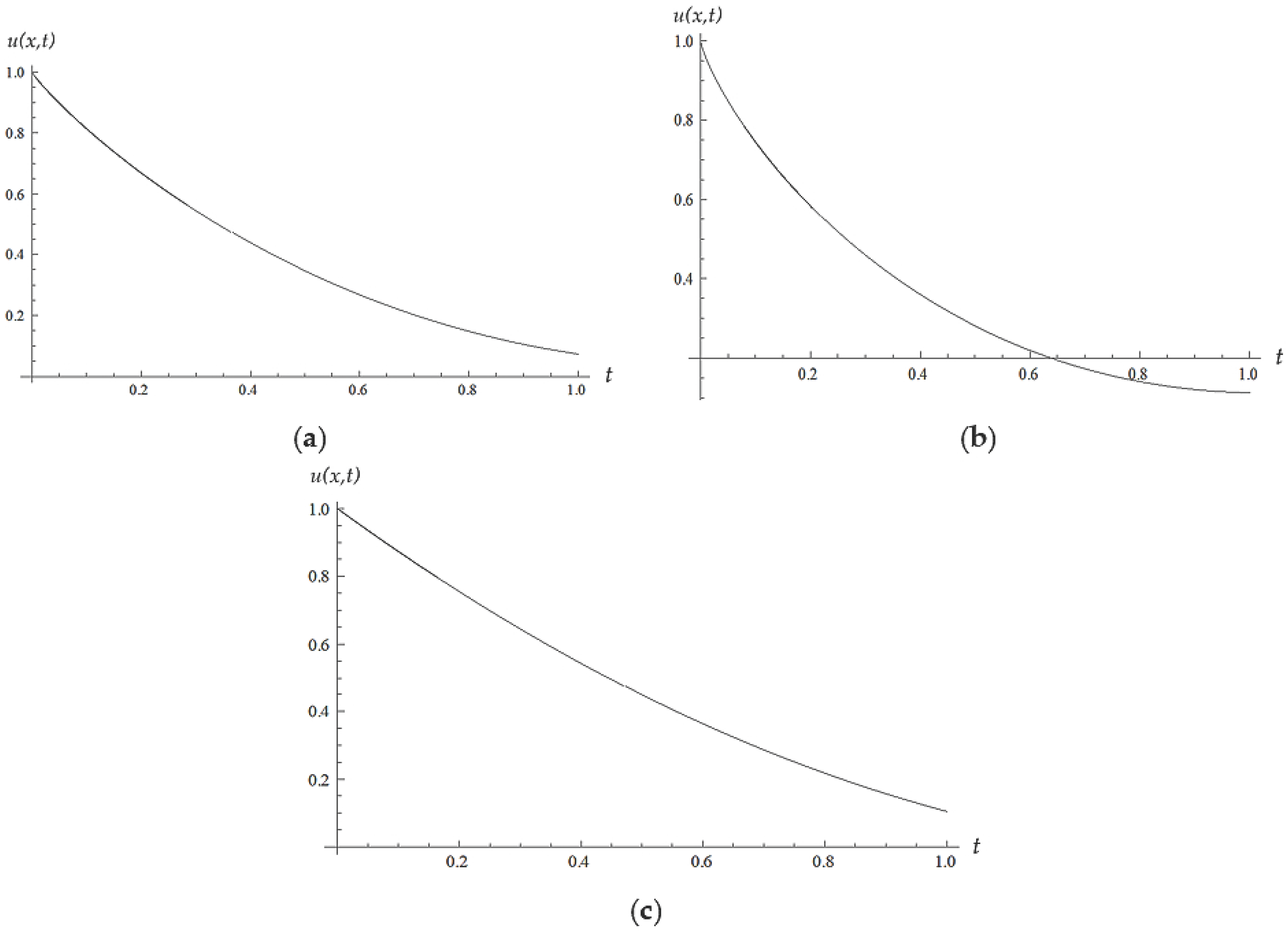
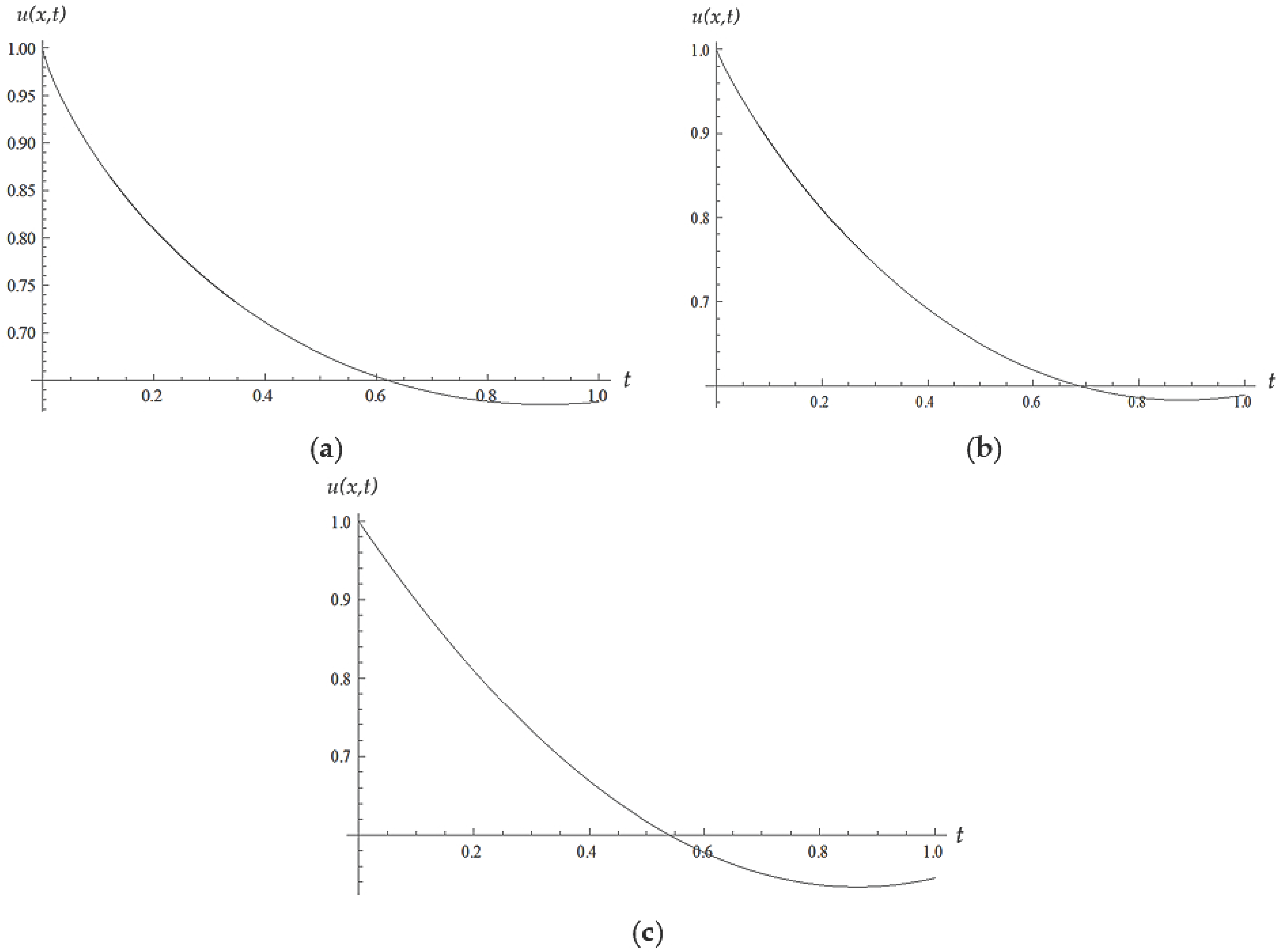
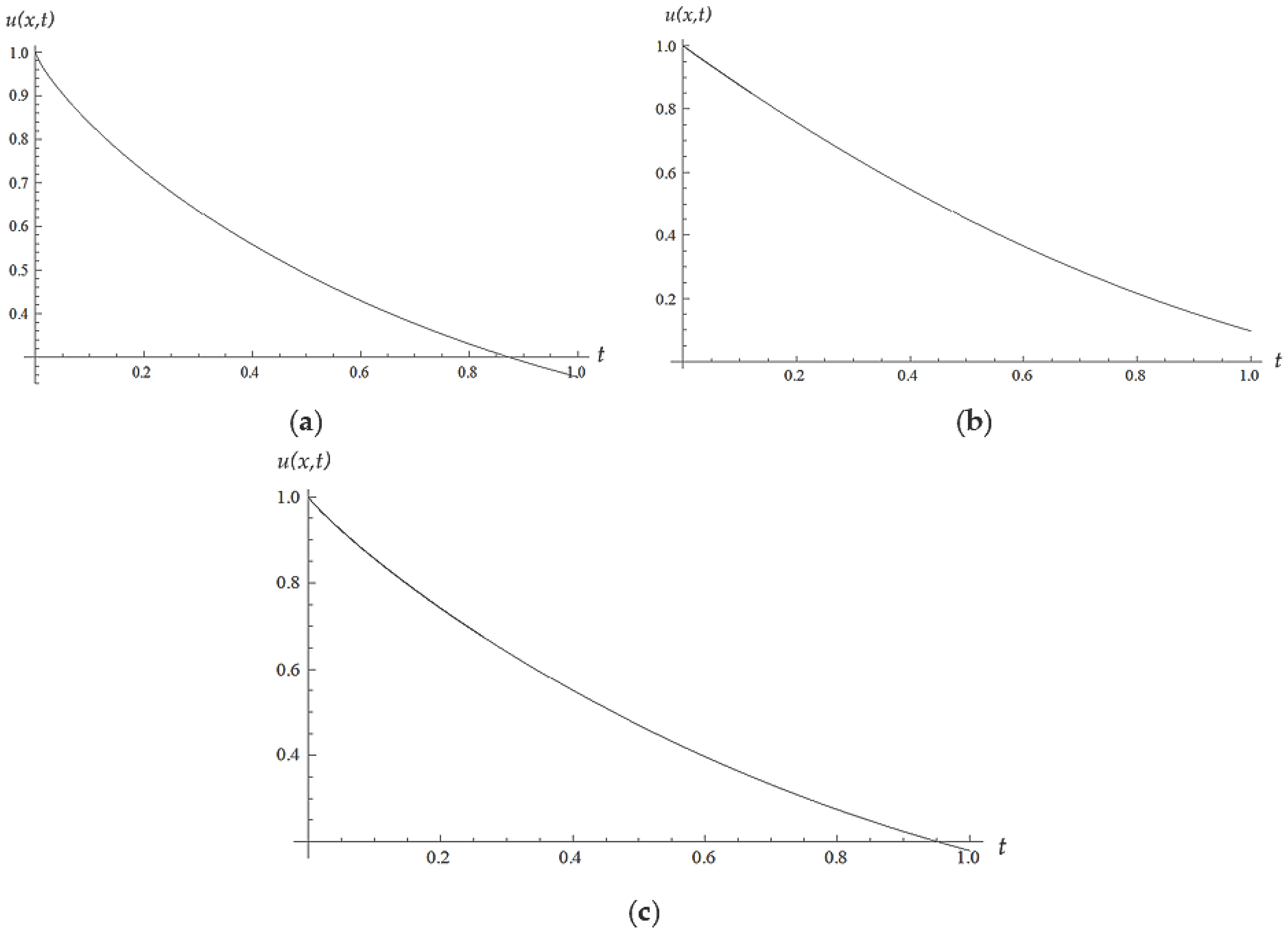
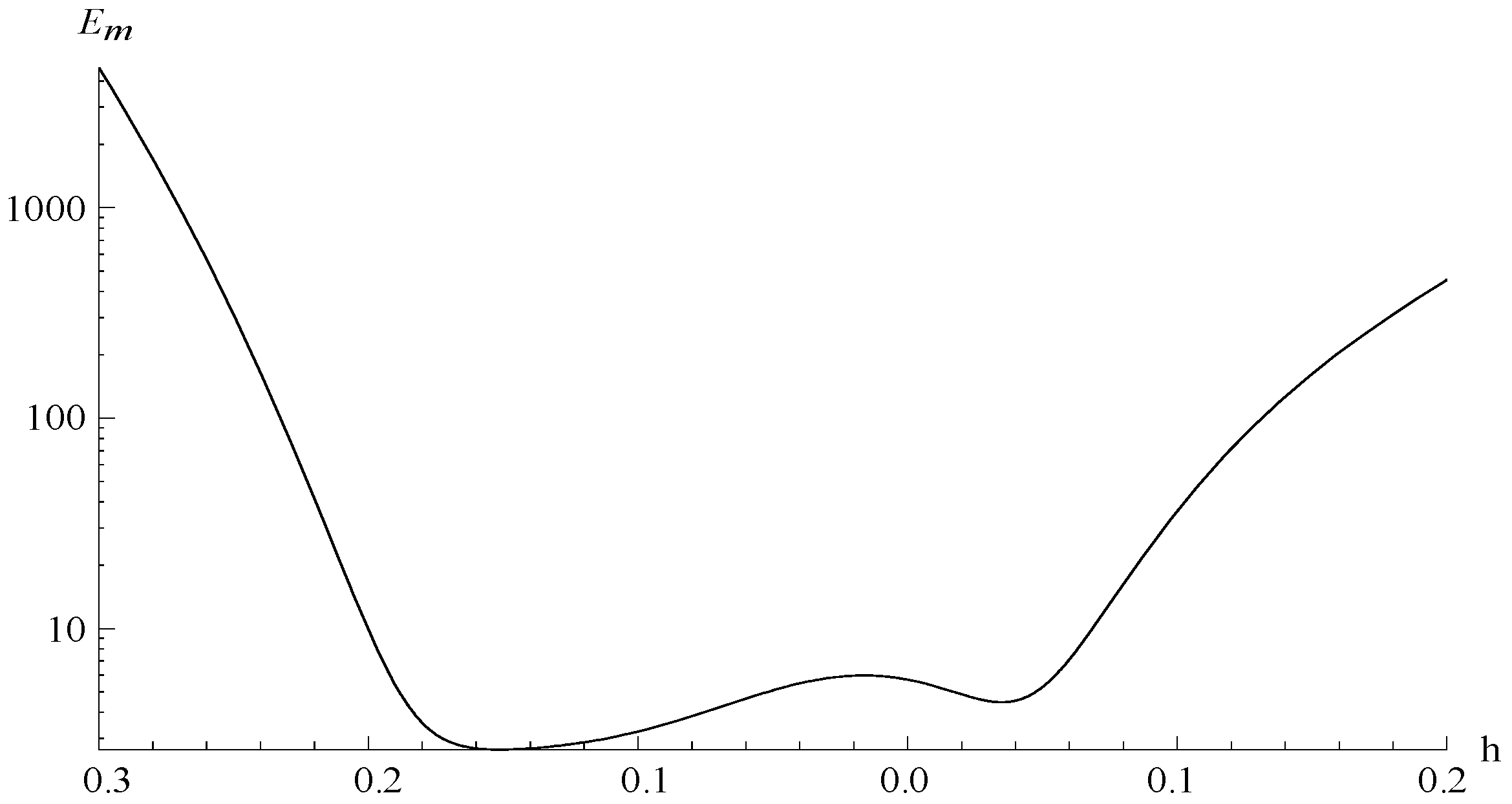
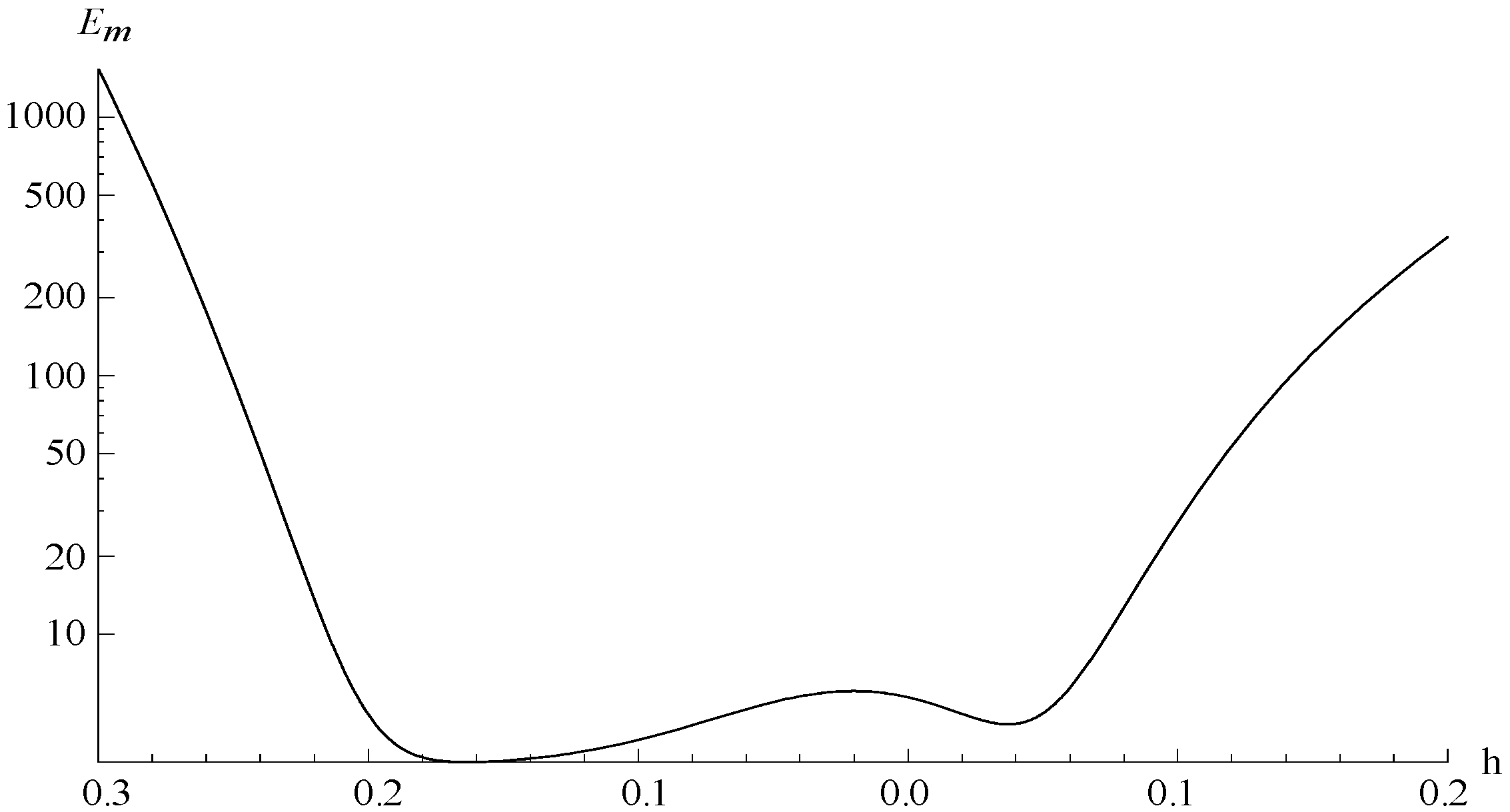
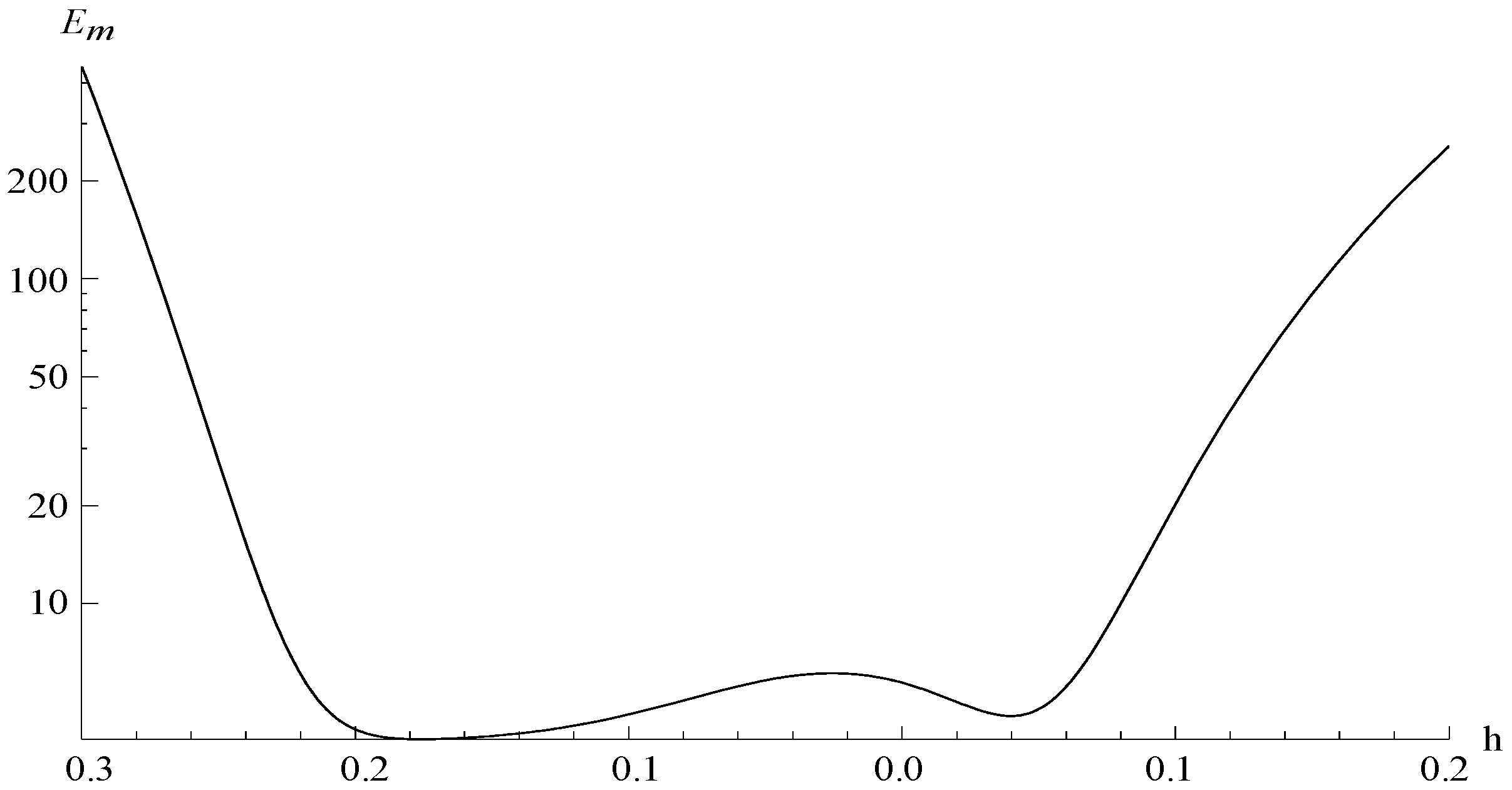
5. Numerical Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| constants | |
| space and time coordinates respectively | |
| field variable |
Greek Letters
| fractional derivative |
References
- Zhang, S. Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365, 448–453. [Google Scholar] [CrossRef]
- Misirli, E.; Gurefe, Y. Exp-function method to solve the generalized Burgers-Fisher equation. Nonlinear Sci. Lett. A 2010, 1, 1323–1328. [Google Scholar]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Yan, Z. Abundant families of Jacobi elliptic function solutions of the (2 + 1)-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Tascan, F.; Bekir, A.; Koparan, M. Travelling wave solutions of nonlinear evolution equations by using the first integral method. Commun. Nonlinear Sci. Numer. Simul. 2009, 10, 1810–1815. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shirzadi, A. The first integral method for modified Benjamin-Bona-Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1759–1765. [Google Scholar] [CrossRef]
- Wanga, M.; Lia, X.; Zhanga, J. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A. 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Salas, A.H.; Gomez, C.A. Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math. Probl. Eng. 2010. [Google Scholar] [CrossRef] [PubMed]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Liao, S.J. The Proposed Homotopy Analysis Technique for Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. Notes on the Homotopy analysis method: Some definitions and theorems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 983–997. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J.; Cheung, A.T. Application of homotopy analysis method in nonlinear oscillations. ASME J. Appl. Mech. 1998, 65, 914–922. [Google Scholar] [CrossRef]
- Liao, S.J. A challenging nonlinear problem for numerical techniques. J. Comput. Appl. Mech. 2005, 181, 467–472. [Google Scholar] [CrossRef]
- Liao, S.J.; Cheung, K.F. Homotopy analysis of nonlinear progressive waves in deep water. J. Eng. Math. 2003, 45, 105–116. [Google Scholar] [CrossRef]
- Liao, S.J.; Tan, Y. A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 2007, 119, 254–297. [Google Scholar] [CrossRef]
- Das, S.; Vishal, K.; Gupta, P.K. Solution of the nonlinear fractional diffusion equation with absorbent term and external force. Appl. Math. Model. 2011, 35, 3970–3979. [Google Scholar] [CrossRef]
- Das, S. Approximate solution of fractional diffusion equation revisited. Int. Rev. Chem. Eng. 2012, 4, 501–504. [Google Scholar]
- Zhang, Y.; Cattani, C.; Yang, X.J. Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy 2015, 17, 6753–6764. [Google Scholar] [CrossRef]
- Das, S. Analytical solution of a fractional diffusion equation by variational iteration method. Comput. Math. Appl. 2009, 57, 483–487. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equation; Springer: Berlin, Germany, 2004. [Google Scholar]
- El-Sayed, A.M.A. On the fractional differential equations. Appl. Math. Comput. 1992, 49, 205–213. [Google Scholar] [CrossRef]
- Grin’ko, A.P. Solution of a nonlinear differential equation with a generalized fractional derivative. Dokl. Akad. Navnk BSSR 1991, 35, 27–31. [Google Scholar]
- Atangana, A. Numerical Analysis of Time Fractional Three Dimensional. Therm. Sci. 2015, 19, 7–12. [Google Scholar] [CrossRef]
- Baleanu, D.; Khan, H.; Jafari, H.; Khan, R.A. On the Exact Solution of Wave Equations on Cantor Sets. Entropy 2015, 17, 6229–6237. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Iqbal, M.A.; Hassan, S.M. Modified Legendre Wavelets Technique for Fractional Oscillation Equations. Entropy 2015, 17, 6925–6936. [Google Scholar] [CrossRef]
- Vishal, K.; Das, S. Solution of the nonlinear fractional diffusion equation with absorbent term and external force using optimal homotopy analysis method. Z. Naturforsch. A 2012, 67, 203–209. [Google Scholar] [CrossRef]
- Jafari, H. Numerical Solution of Time-Fractional Klein–Gordon Equation by Using the Decomposition Methods. J. Comput. Nonlinear Dyn. 2016, 11. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; López-López, M.G.; Alvarado-Martínez, V.M.; Reyes-Reyes, J.; Adam-Medina, M. Modeling diffusive transport with a fractional derivative without singular kernel. Physica A 2016, 447, 467–481. [Google Scholar] [CrossRef]
- Liu, X.; Lou, B. On a reaction–diffusion equation with Robin and free boundary conditions. J. Differ. Equ. 2015, 259, 423–453. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Baleanu, D.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H. Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Adv. Differ. Equ. 2016. [Google Scholar] [CrossRef]
- Morgado, M.L.; Rebelo, M. Numerical approximation of distributed order reaction–diffusion equations. J. Comput. Appl. Math. 2015, 275, 216–227. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Miranda-Hernández, M.; López-López, M.G.; Alvarado-Martínez, V.M.; Baleanu, D. Modeling and simulation of the fractional space-time diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 115–127. [Google Scholar] [CrossRef]
- LenziE, K.; Mendes, G.A.; Mendes, R.S.; Da Silva, L.R.; Lucena, L.S. Exact solutions to nonlinear non-autonomous space-fractional diffusion equations with absorption. Phys. Rev. E 2003, 67, 051109. [Google Scholar] [CrossRef] [PubMed]
- Zola, R.S.; Lenzi, M.K.; Evangelista, L.R.; Lenzi, E.K.; Lucena, L.S.; Da Silva, L.R. Exact solutions for a diffusion equation with a nonlinear external force. Phys. Lett. A 2008, 372, 2359–2363. [Google Scholar] [CrossRef]
- Mathew, T.P.A. Domain Decomposition Methods for the Numerical Solution of Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; Volume 61. [Google Scholar]
- Gong, C.; Bao, W.; Tang, G.; Jiang, Y.; Liu, J. A Domain Decomposition Method for Time Fractional Reaction-Diffusion Equation. Sci. World J. 2014, 2014, 681–707. [Google Scholar] [CrossRef] [PubMed]
- Liao, S. Advances in the Homotopy Analysis Method; World Scientific: Singapore, 2014. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tripathi, N.K.; Das, S.; Ong, S.H.; Jafari, H.; Al Qurashi, M. Solution of Higher Order Nonlinear Time-Fractional Reaction Diffusion Equation. Entropy 2016, 18, 329. https://doi.org/10.3390/e18090329
Tripathi NK, Das S, Ong SH, Jafari H, Al Qurashi M. Solution of Higher Order Nonlinear Time-Fractional Reaction Diffusion Equation. Entropy. 2016; 18(9):329. https://doi.org/10.3390/e18090329
Chicago/Turabian StyleTripathi, Neeraj Kumar, Subir Das, Seng Huat Ong, Hossein Jafari, and Maysaa Al Qurashi. 2016. "Solution of Higher Order Nonlinear Time-Fractional Reaction Diffusion Equation" Entropy 18, no. 9: 329. https://doi.org/10.3390/e18090329
APA StyleTripathi, N. K., Das, S., Ong, S. H., Jafari, H., & Al Qurashi, M. (2016). Solution of Higher Order Nonlinear Time-Fractional Reaction Diffusion Equation. Entropy, 18(9), 329. https://doi.org/10.3390/e18090329






