Abstract
In the last few decades, a wide variety of instruments with laser-based techniques have been developed that enable experimentally measuring particle velocity and fluid velocity separately in particle-laden flow. Experiments have revealed that stream-wise particle velocity is different from fluid velocity, and this velocity difference is commonly known as “velocity lag” in the literature. A number of experimental, as well as theoretical investigations have been carried out to formulate deterministic mathematical models of velocity lag, based on several turbulent features. However, a probabilistic study of velocity lag does not seem to have been reported, to the best of our knowledge. The present study therefore focuses on the modeling of velocity lag in open channel turbulent flow laden with sediment using the entropy theory along with a hypothesis on the cumulative distribution function. This function contains a parameter η, which is shown to be a function of specific gravity, particle diameter and shear velocity. The velocity lag model is tested using a wide range of twenty-two experimental runs collected from the literature and is also compared with other models of velocity lag. Then, an error analysis is performed to further evaluate the prediction accuracy of the proposed model, especially in comparison to other models. The model is also able to explain the physical characteristics of velocity lag caused by the interaction between the particles and the fluid.
1. Introduction
Fluid-particle interaction in open channel flow has long been a topic of interest in hydraulics. The sediment particle velocity plays an important role in the computation of the suspended sediment transport rate. Due to the complexity of the turbulence mechanism of the flow field, it is often assumed that stream-wise particle velocity is the same as fluid velocity, which implies that the stream-wise fluid-particle relative velocity is zero, even though in reality, this is not so (Bagnold [1]). More than four decades ago, Bagnold [1] recognized that the particle velocity was less than the velocity of the fluid carrying the particle, but was unable to measure the difference between the two velocities because of instrumental limitations. Several advanced measurement techniques, such as particle image velocimetry (PIV), laser-Doppler anemometry (LDA) and discriminator laser-Doppler velocimetry (DLDV), that enable measuring the particle and fluid velocities separately, have been developed. These techniques allow one to develop models of particle and fluid velocity lag.
Laboratory experiments have been carried out to determine the influence of flow parameters on the lag. In their open channel experiments, Muste and Patel [2] observed that the stream-wise sediment velocity of 0.22-mm natural sand was less than that of water by 4%. Best et al. [3] applied phase Doppler anemometry (PDA) to determine the turbulent characteristics of water and glass spheres and reported that velocity lag became greater towards the bed. With different measurement techniques, Rashidi et al. [4], Taniere et al. [5] and Kiger and Pan [6] reported similar results. However, when the sediment concentration is high, this may give rise to a more significant velocity lag owing to the interaction of particles with each other, as well as with boundaries.
Using a two-phase flow theory, Chauchat and Guillou [7], Bombardelli and Jha [8] and Jha and Bombardelli [9] discussed the velocity lag. However, it is important to numerically calculate the results with this theory. Starting from a two-phase flow theory, Greimann et al. [10] and Jiang et al. [11] derived analytical solutions of velocity lag, but their solutions were confined to verification with limited experimental data. Cheng [12] presented a model of velocity lag, based on a hindered drag force in sediment-laden flow and stated that the model may not be well applicable when the velocity and concentration gradients were significant in the flow. Based on the hindered drag force on particle impact and viscous shear stress, particle-liquid and particle-particle interactions and the dispersion of sediment due to these interactions, Pal et al. [13] developed a model of velocity lag and verified it with a wide range of experimental data. Apart from this, in recent years, researchers have investigated particle-fluid and particle-particle interactions in particulate turbulent flow using direct numerical simulations (DNS) (Vowinckel et al. [14]). Shao et al. [15] used a fictitious domain method to perform fully-resolved numerical simulations of particle-laden turbulent flow in a horizontal channel. They found that the average velocities of the particle were smaller in the lower half-channel and larger in the upper half-channel than the local fluid velocities in the presence of gravity effects. Three-dimensional, time-dependent simulations have been reported for a granular bed consisting of non-cohesive spherical particles by Derksen [16]. The simulations were performed by means of a lattice-Boltzmann scheme to show the effect of the Shields number on the mobility of the sediment particles at the top and above the bed. A detailed review of these methods has been provided by Finn and Li [17] recently.
A survey of the literature shows that stream-wise velocity difference or velocity lag between fluid and particle in particle-laden flow has been studied either experimentally or theoretically using deterministic approaches. These approaches say nothing about the uncertainty associated with the velocity lag in sediment-laden flow. To the best of our knowledge, a probabilistic treatment of velocity lag based on entropy theory has not been reported. For the past 25 years, entropy theory has been advantageously applied in fluvial hydraulics. Using this theory, several models of velocity (Chiu [18], Cui and Singh [19,20], Kumbhakar and Ghoshal [21,22]), sediment concentration (Chiu et al. [23], Cui and Singh [24]), debris flow (Singh and Cui [25]), etc., have been developed. The objective of this study therefore is to model velocity lag using the entropy theory, verify the model using a wide range of twenty-two experimental datasets obtained from the literature and compare the proposed model with the existing velocity lag models.
2. Entropy Theory-Based Methodology
We consider sediment-laden open channel flow with flow depth D. Let and be the time-averaged stream-wise velocities of fluid and sediment particles, respectively, at a vertical distance y from the reference level, and be the corresponding time-averaged stream-wise velocity lag or velocity difference. For convenience, the velocity lag is non-dimensionalized as (=), where is the shear velocity. From the experimental results, Rashidi et al. [4] and Righetti and Romano [26] proposed a monotonic variation of velocity-lag along the vertical direction in open channel flow. Based on this proposition, it is assumed that the velocity lag increases monotonically from the water surface to the channel bed, having a zero value at the water surface and at the reference level (above the bed) , where a is the vertical distance from the bed to the reference level. It is argued that temporally-averaged dimensionless velocity lag can be considered as a random variable.
2.1. Definition of Entropy
Let the dimensionless velocity lag be a continuous random variable, having a probability density function (PDF) . Then, the Shannon [27] entropy in continuous form can be written as:
where is the dimensionless maximum velocity lag in which is the maximum value of velocity lag. Equation (1) expresses a measure of uncertainty of or the average information content of sampled . The objective is to derive the least-biased PDF of velocity lag, subject to known information. The known information can be codified in terms of constraints.
2.2. Specification of Constraints
If observations on velocity lag are available, then we can express information on this random variable in terms of constraints. First, the total probability law must be satisfied for the probability density function . Therefore, the first constraint is given as:
which follows from the total probability rule.
Second, to keep things simple, another constraint is taken as the mean of expressed as:
Equation (2) is the mean constraint or the first (raw) moment of dimensionless velocity lag values.
2.3. Maximization of Entropy
Theoretically, maximum entropy can be achieved when the probability distribution is uniform within its limits. Therefore, due to the presence of constraints, it often cannot be uniform. In accord with the principle of maximum entropy (POME) developed by Jaynes [28,29,30], the probability distribution is as uniform as possible while satisfying the constraints. To determine the least biased towards what is not known regarding the velocity lag, POME is applied, which requires the specification of known information, called constraints, on velocity lag. According to POME, the most appropriate probability distribution is the one that has the maximum entropy or uncertainty, subject to constraint Equations (2) and (3). To that end the method of Euler–Lagrange calculus of variation is used. Hence, the Lagrangian function can be constructed as follows:
where , are the Lagrange multipliers to be determined from constraint equations based on experimental data. Differentiating Equation (4) with respect to and equating the derivative to zero, the probability density function of the velocity lag is obtained as:
Therefore, the cumulative distribution function (CDF), of is obtained by using Equation (5) as:
Equation (7) is a measure of uncertainty associated with velocity lag. One can observe from Equations (5)–(7) that the probability density function, cumulative distribution function and the Shannon entropy function depend on the values of Lagrange multipliers and . Therefore, these parameters need to be determined.
2.4. Calculation of Lagrange Multipliers
Substitution of from Equation (5) in the constraints given in Equations (2) and (3) leads to the system of non-linear equations for Lagrange multipliers as:
Equations (8) and (9) can be solved numerically to get the values of the Lagrange multipliers. However, for computing these unknown multipliers, the value of is required, and there seems no formulae available in the literature for its determination. Therefore, in this study, this value was taken from the available experimental data. Then, Equations (8) and (9) were solved in MATLAB (R2012b version) by using the non-linear equation solver.
2.5. Cumulative Distribution Function
In order to express the velocity lag in the real (space) domain, an equation connecting the probability domain to the space domain is needed. Therefore, a hypothesis on the CDF of in terms of flow depth was formulated as follows:
where D is the maximum depth, a is the reference level, y is the vertical height from the channel bed having a range from a to D and η is a fitting parameter. This hypothesis on the CDF is based on two important assumptions: (1) all of the values of y between a and D are equally likely; and (2) the velocity lag increases monotonically from the water surface to the reference level. Exponent η in Equation (10) represents the shape parameter and declination of the CDF. The declination of the proposed CDF curve with the change of exponent η is shown in Figure 1 from which it can be seen that the CDF is linear for and is non-linear for other values of η. It is also observed that at a fixed height from the bed, the value of CDF increases with the increase of parameter η. The proposed CDF was validated with the experimental data R1 of Rashidi et al. [4] and SL01 of Muste and Patel [2], presented in Figure 2 and Figure 3, respectively. Despite the fact that there is the zigzag nature of the experimental results of velocity lag, the proposed model CDF in Equation (10) agrees well with the values of CDF computed from Equation (6).
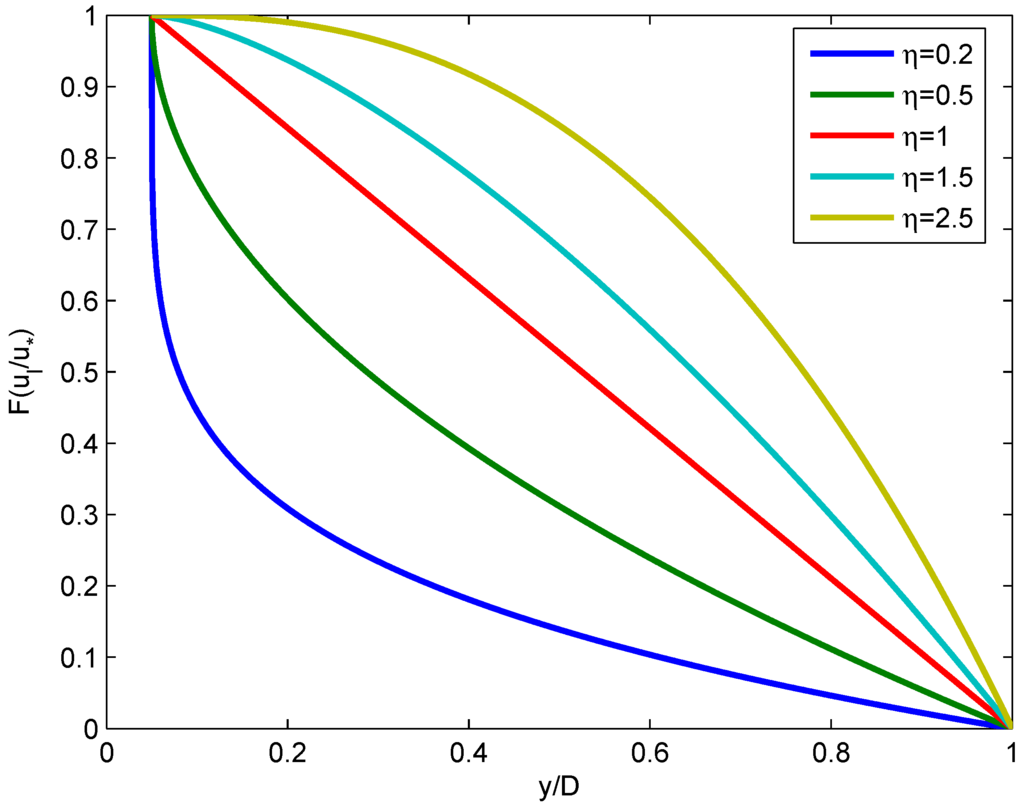
Figure 1.
Variation of the proposed CDF with fitting parameter η.
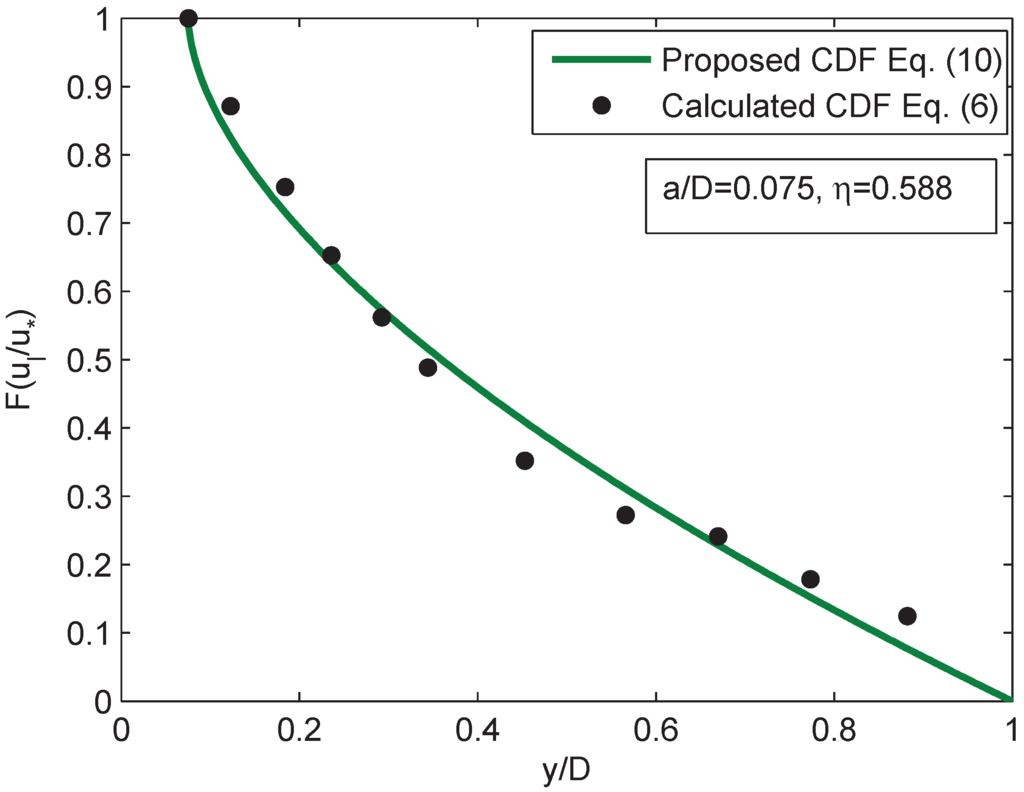
Figure 2.
Validation of the proposed CDF for the R1 data of Rashidi et al. [4].
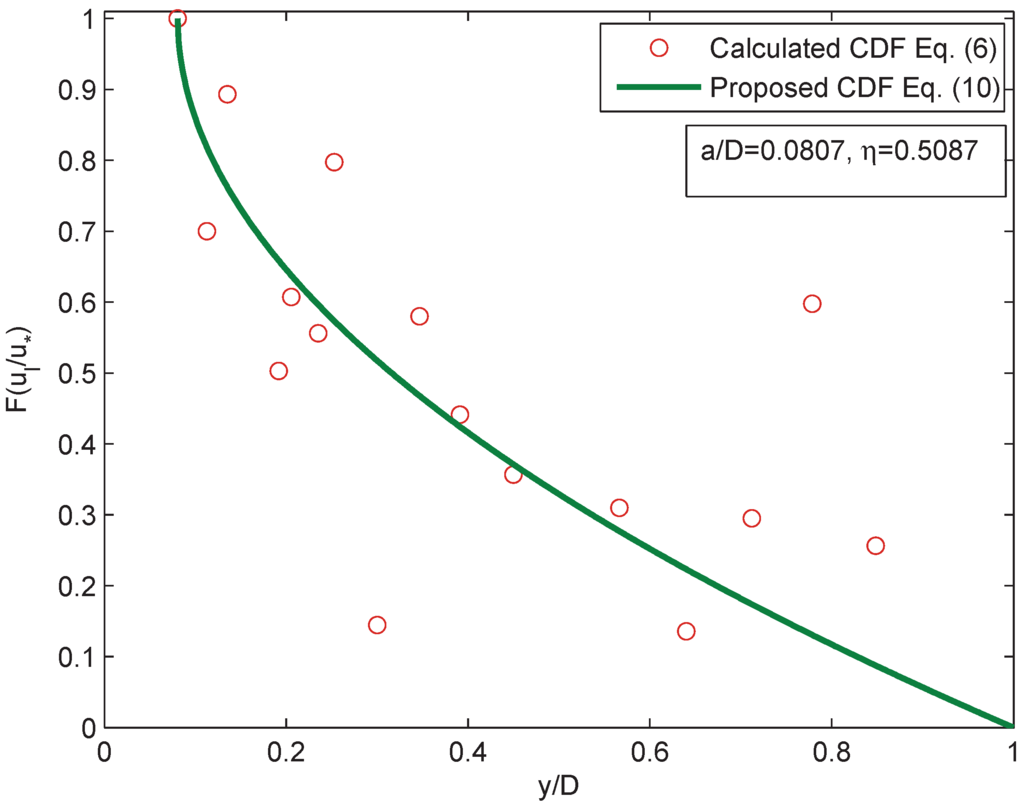
Figure 3.
Validation of the proposed CDF for the SL01 data of Muste and Patel [2].
2.6. Derivation of Velocity Lag
2.7. Re-Parametrization
To represent the proposed model in a simple-to-use form, a dimensionless parameter L was introduced here as the entropy parameter. The parameter L was defined as:
Substituting Equation (12) into Equation (11), the velocity lag equation can be written in terms of the parameter L as:
The variation of the velocity lag with the change of entropy parameter L is shown in Figure 4 for fixed values of the parameters , and /. The values of these parameters were taken from the experimental observation of run R1 of Rashidi et al. [4]. Figure 4 shows that a change in the L value changes the declination of the velocity lag profile. Furthermore, it can be observed that at a fixed height from the channel bed, the velocity lag of a particle increases with the increase of parameter L.
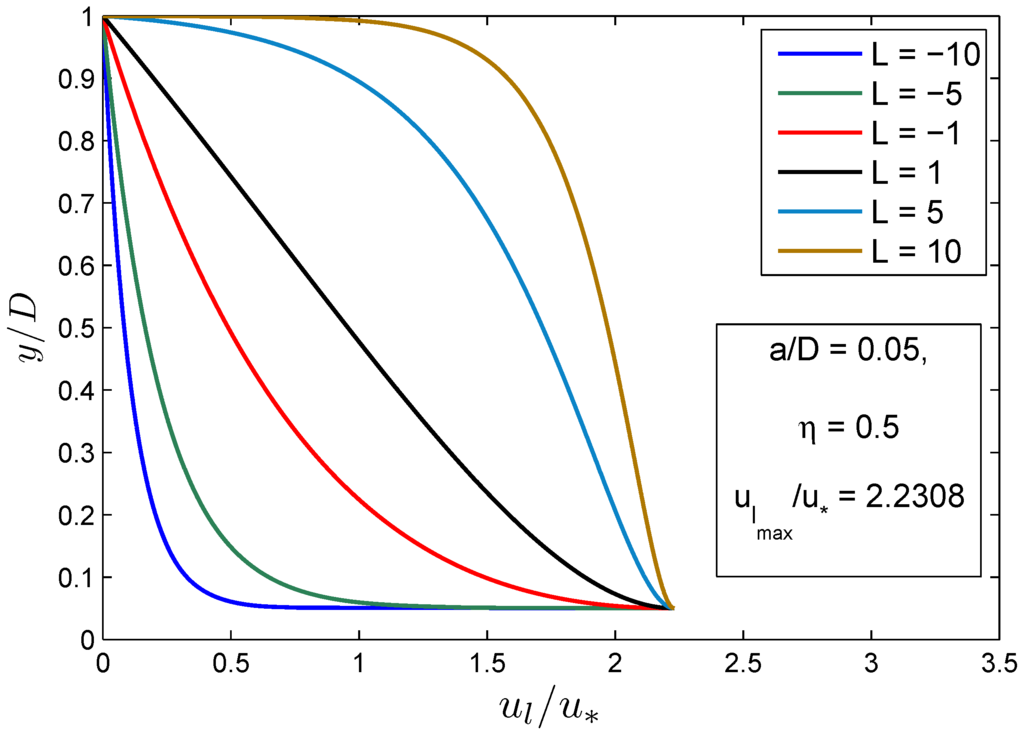
Figure 4.
Variation of the velocity lag equation with different L values.
In a similar manner, the dimensionless entropy function H given in Equation (7) can be expressed in terms of the parameter L as:
In Figure 5, the variation of entropy H with parameter L is plotted for the range of L from to 10. From the figure, it is found that the entropy value increases when L increases from to zero, and then, entropy decreases when L further increases from zero to 10. It is also observed from Figure 5 that the curve is symmetrical about the vertical axis. In the range of L from zero to 10, it is observed that the maximum value of entropy occurs when L is close to zero, and with the increase of L, entropy decreases. Thus, parameter L, as an index of velocity lag, gives the entropy value for the distribution. This means that the probability distribution will have more uniformity for smaller L values than for larger L values. Furthermore, the probability density function can be expressed in terms of parameter L from Equations (5) and (8) as:
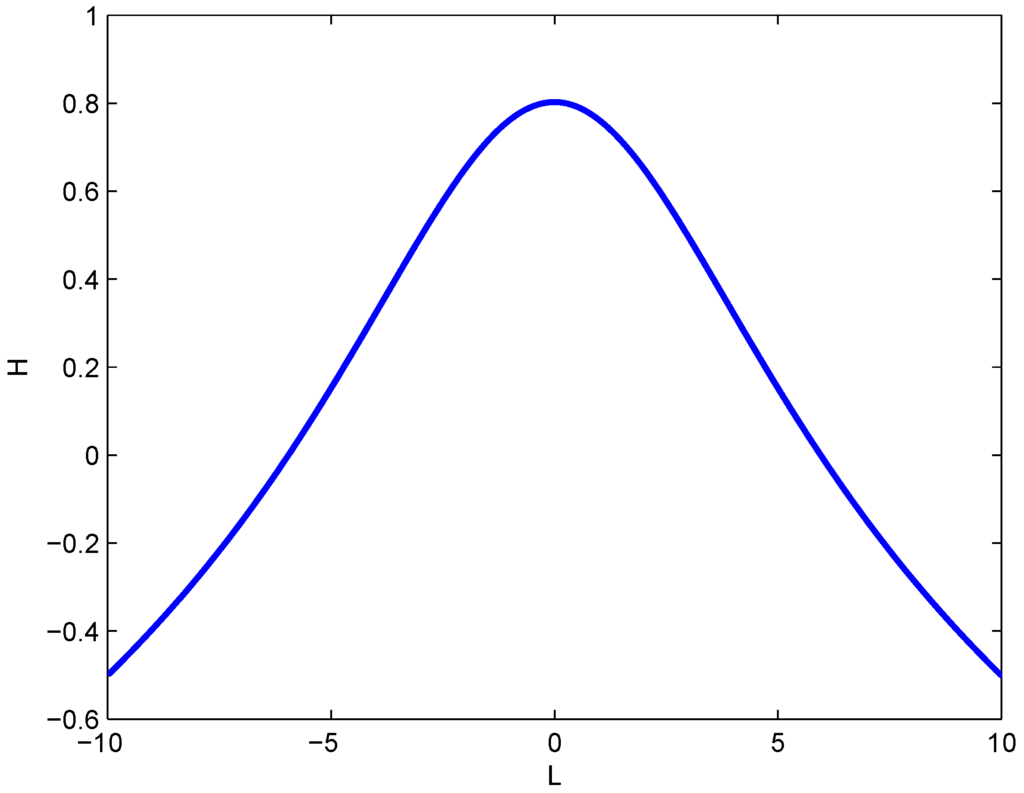
Figure 5.
Variation of the dimensionless entropy with entropy parameter L.
From Equation (15), we have:
Equation (16) shows that if , , and therefore, the probability density function would tend to be uniform. As the value of L increases, the denominator becomes larger, tends to infinity and the probability density function becomes non-uniform.
It can be observed from Equation (13) that to find the velocity lag, the determination of entropy parameter L and, hence, the determination of Lagrange multiplier are needed, which can be achieved by solving the system of non-linear Equations (2) and (3). Here, we present a graphical method to determine the L value, which is related to . Simple algebraic calculation of Equations (2) and (3) gives the following equation as:
Equation (17) shows that the value of parameter L can be determined for given values of , without solving the system of non-linear equations. Variation of the with L is presented in Figure 6, which shows that the ratio of mean and maximum velocity lags continuously increase with the increase of entropy parameter L.
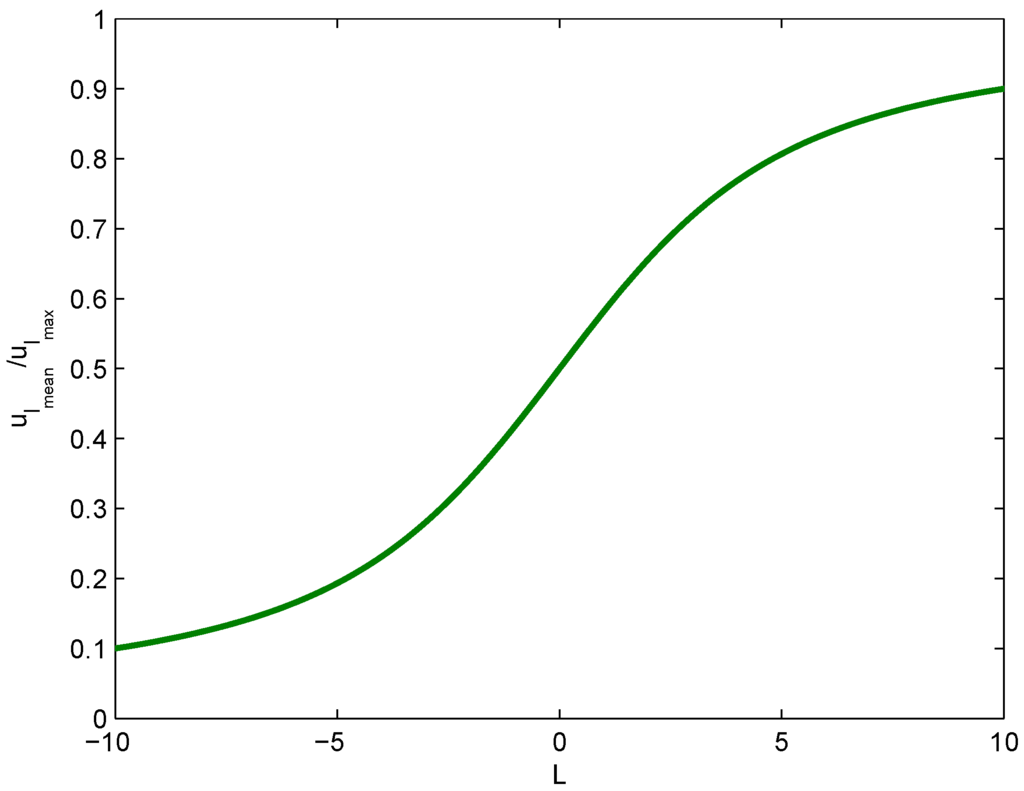
Figure 6.
Ratio of the mean-max velocity lag with entropy parameter L.
3. Comparison with Experimental Data and Other Models
The proposed model of velocity lag, based on the entropy theory, was validated with experimental observations available in the literature. To test the validity of this model, i.e., Equation (13) with a wide range of sediment-laden flow conditions and different types of particles, experimental data from Rashidi et al. [4] and Kaftori et al. [31] for polystyrene particles, Best et al. [3] and Righetti and Romano [26] for glass particles and Muste and Patel [2] and Muste et al. [32] for natural sand particles were selected. A summary of these data with flow conditions and other flow characteristics is given in Table 1. We can find from the table that the flow parameters vary for a broad range in these experimental runs. We calculated averaged Reynolds number () where is the mean flow velocity of sediment-laden fluid over the flow depth, is the kinematic viscosity of fluid and denotes the particle diameter. Shields parameter θ (=) is presented in the table, where g is the gravitational acceleration, and s denotes the specific gravity of particles. Table 1 shows the reasonable ranges of the and θ values. Therefore, the present study considered a wide range of experimental runs for verification of the velocity lag model.

Table 1.
Summary of the experimental data.
The proposed model was also compared with other existing models reported in the literature. The models of velocity lag selected were the models of Cheng [12], Greimann et al. [10] and Pal et al. [13]. These models are deterministic. The Cheng [12] model can be expressed as:
Similarly, the model of Greimann et al. [10] can be expressed as:
and the model of Pal et al. [13] can be given as:
where and M and N are given by:
and:
in which:
Using regression, they proposed the value of as:
where , and are the mass densities of fluid, particle and sediment-fluid mixture, respectively. is the relative viscosity, in which and are the dynamic viscosities of sediment-laden and sediment-free fluid, respectively; c denotes the sediment concentration by volume; denotes the specific gravity of particles; is the settling velocity of sediment particles; and denotes the von Karman coefficient of mixture. For the purposes of discussion of the model comparison, the models proposed in the present study and by Cheng [12], Greimann et al. [10] and Pal et al. [13] were denoted, respectively, as PM, CM, GM and DM. Hence, onwards, throughout the present study, we use these acronyms to refer to the corresponding models on velocity lag.
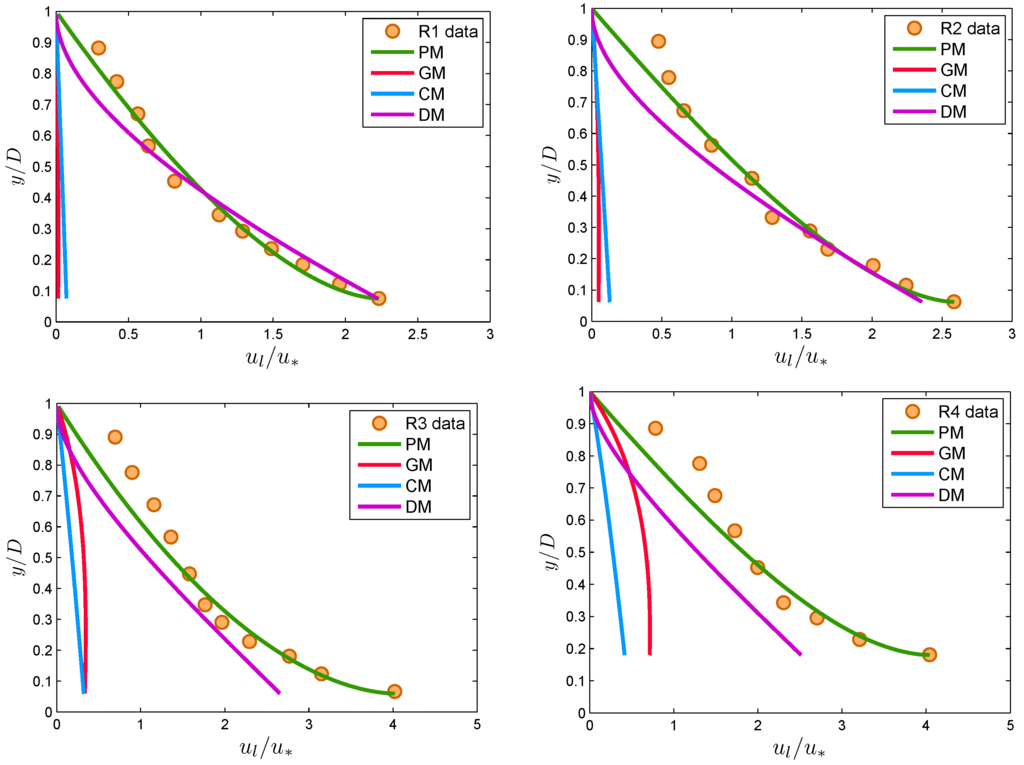
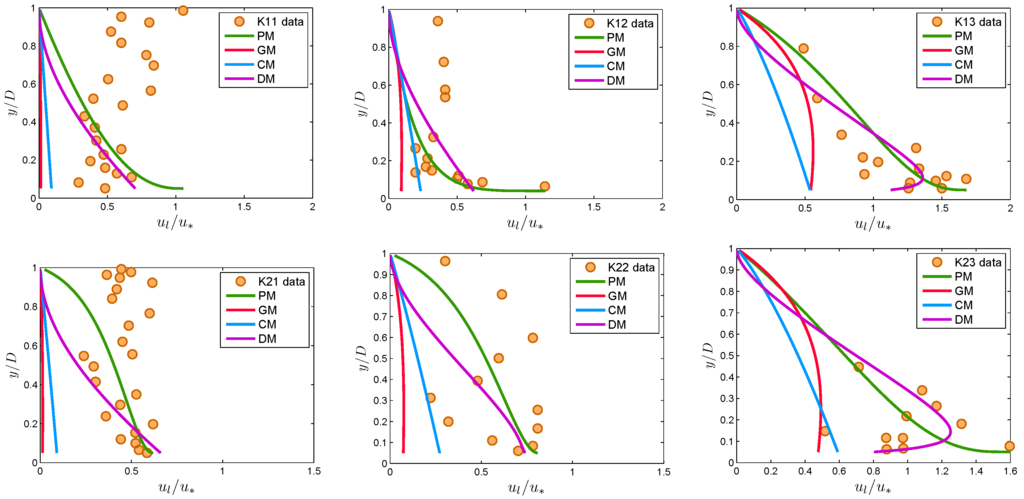
Figure 7 and Figure 8 compare the proposed model Equation (13) with the experimental data of Rashidi et al. [4] and Kaftori et al. [31] for polystyrene particles, respectively. The model parameters were computed as follows: exponent η was obtained after fitting the CDF in Equation (10) to the experimental data; the value of L was computed from Equation (12) after computing the Lagrange multiplier by solving the non-linear equations given in Equations (8) and (9). In Figure 7 and Figure 8, the models of CM, GM and DM are also shown for comparison. It can be observed from Figure 7 that the proposed model showed a good agreement with experimental data, whereas models CM, GM and DM underestimated the experimental results over the whole flow depth. Despite the scattered nature of the data, in Figure 8, the present model also showed a favorably good agreement with the experimental data. It can be observed from Figure 8 that the results of PM and DM are comparable to each other. To get a quantitative idea about the goodness of fit, the root-mean-square error was computed, as discussed in the next section.
To test the proposed model for glass particles, the computed values of velocity lag were compared with the observed data of Best et al. [3] and Righetti and Romano [26]. In all cases, the model parameters were computed as mentioned earlier. Figure 9 compares the Best et al. [3] data, and Figure 10 shows the Righetti and Romano [26] data. From Figure 9, it can be seen that all theoretical models gave almost similar results. This indicates that the adoption of an entropy-based approach for modeling velocity lag between fluid and particles in sediment-laden flow is reasonable. It can be seen that PM and DM agreed favorably well with the data, but CM and GM underestimated the velocity lag near the channel bed.

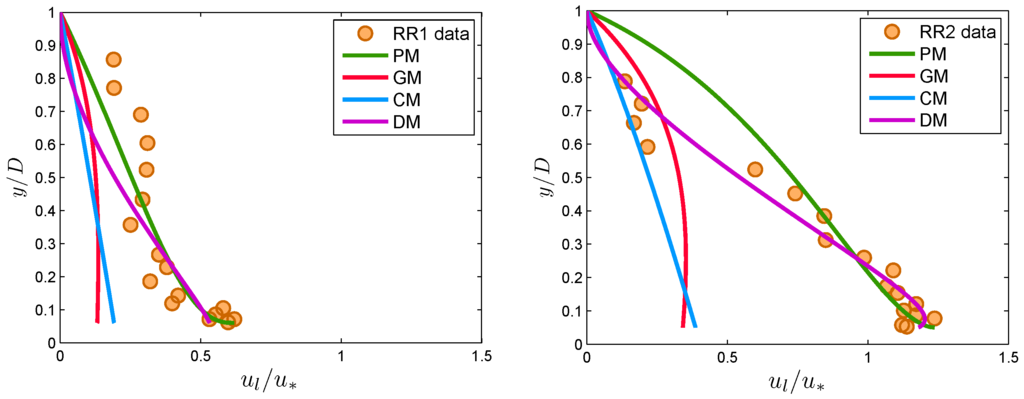
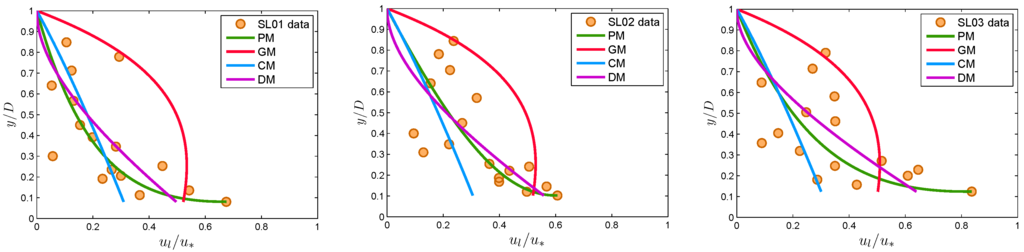
Figure 11 and Figure 12 compare the computed and observed values of velocity lag for natural sand particles with the data from Muste and Patel [2] and Muste et al. [32]. From Figure 11, it is found that PM, CM and DM predicted the results well, but GM overestimated the velocity in all of the test cases, SL01, SL02 and SL03. Figure 12 shows the results due to Muste et al. [32]. It has been found that in run NS1, CM and GM agreed with the observations up to 50% of the flow height from the free surface, but underestimated the lag close to the channel bed; whereas PM and DM predicted well the dataset. In the case of runs NS2 and NS3, the proposed model showed more accurate matching results than did all other models.

It can be seen from the figures that in all of the cases, the entropy-based model derived in the present study dominated over the deterministic models regarding the prediction accuracy of the models. However, entropy-based derivations have some limitations, though not that serious. In this approach, some experimental observations like the , values should be known to us in order to compute the Lagrange multipliers. Furthermore, the model behavior depends on the hypothesis of the CDF, which is defined by looking into the flow configuration. In this study, the CDF decreases from the reference level to the water surface, and hence, the derived model of velocity lag also behaves in the same manner. Therefore, the present model can predict those types of experimental observations on velocity lag, which decrease from the reference level to the water surface. This is not only the case for the present model, but also for the other deterministic models with which we are comparing and can be seen from the figures. These discrepancies do not arise due to the theoretical models presented, rather they can be treated as an experimental error commonly found in the experiments related to open channel turbulent flow. Therefore, discrepancies in a few subfigures of Figure 8 and Figure 12 do not prove the weakness of the derived model globally.
Entropy-based derivation does not incorporate explicit fluid mechanics processes; the only physical basis is through the constraints and data. To compute the velocity lag from the proposed model, the unknown parameter η is required, which was computed by fitting the CDF to the experimental data. Now, we try to link the fitting parameter η to some known quantities of flow. For that purpose, a regression analysis was carried out. It is noted that the value of η depends on the particle diameter , shear velocity , settling velocity , flow depth D and specific gravity s of particles. From regression analysis of the fitted values of η, the following formula was obtained:
The fitted values were compared with the values computed from the regression relation, as shown in Figure 13, except for the negative values of parameter L. The value of the coefficient of regression was obtained as 0.4317. The value is low due to the scatter of data points in the original velocity lag data. To get more accurate results, more velocity lag data are required.

To examine the prediction accuracy of the derived model as compared to the other models considered in this study, an error analysis was carried out. As the experimental data of velocity lag are highly scattered, we needed a suitable error formula. In all of these twenty-two selected datasets, to get an idea about the goodness of fit, the root-mean-square error was computed for all of the models. The root-mean-square error is calculated form the following formula as:
where and are the computed and observed values of the i-th data point of dimensionless velocity lag () in a run and N is the total number of data points in that run. For each of the experimental runs, the computed values of E from PM, GM, CH and DM are shown in Table 2, where the asterisk (*) denotes the least error for that run. It is observed from Table 2 that the proposed model provided the least error for twenty test cases out of twenty-two experimental runs considered here. This result shows the superiority of the entropy-based model to the existing deterministic models of Cheng [12], Greimann et al. [10] and Pal et al. [13].

Table 2.
Calculation of error E from different models ( corresponds to minimum error).
4. Discussion
While comparing with experimental data and other models in Section 3, we observed from Equation (27) that the physical quantities of flow, such as particle diameter , specific gravity s and shear velocity , play a significant role in the proposed model on velocity lag. Therefore, this section discusses the effect of these parameters on the derived velocity lag model, as well as uncertainty.
To perform this analysis, we arbitrarily choose an experimental run and varied each of the parameters mentioned above by keeping others fixed. Figure 14, Figure 15 and Figure 16 show the effect of particle diameter , shear velocity and the specific gravity s, respectively, on the velocity lag. It follows from Figure 14 that velocity lag increases with increasing . As increases, the mass and surface area of a particle increases; thus, the particle accelerates less with the flow velocity, which results in increased . Rashidi et al. [4] obtained the same characteristics in their experiment, which can be observed from Figure 7 and Table 1. Again, Figure 15 demonstrates the effect of shear velocity on the velocity lag profile. It is observed from the figure that the velocity lag decreases with increasing . The reason is that shear stress increases with the increase of fluid velocity in terms of , which leads the particle to follow fluid velocity, and hence, velocity lag decreases. This characteristic was also observed in the work of Pal et al. [13]. On the other hand, Figure 16 suggests that the velocity lag decreases with the increase of specific gravity s. This characteristic is also matched with the analysis of Cheng [12]. The aforementioned discussion delineates that our present model on velocity lag, which is based on entropy, is able to describe the characteristics of velocity lag caused by the interaction between particle and fluid in open channel sediment-laden turbulent flow, and hence, the model is also justified.
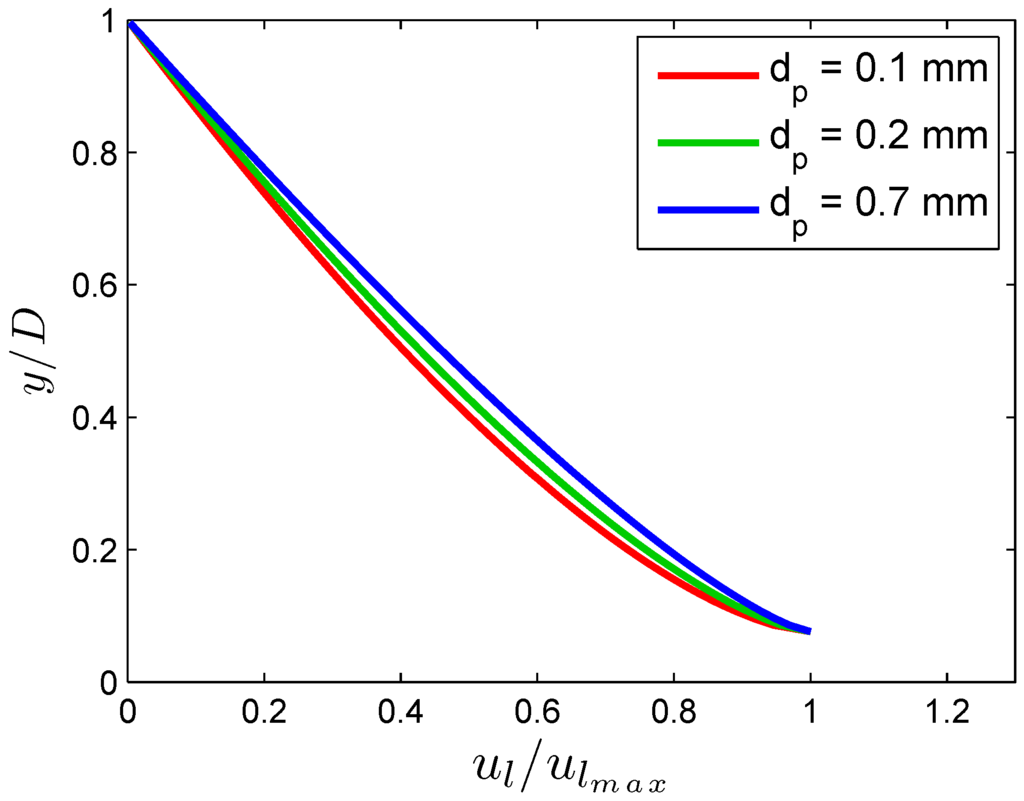
Figure 14.
Effect of particle diameter on velocity lag.
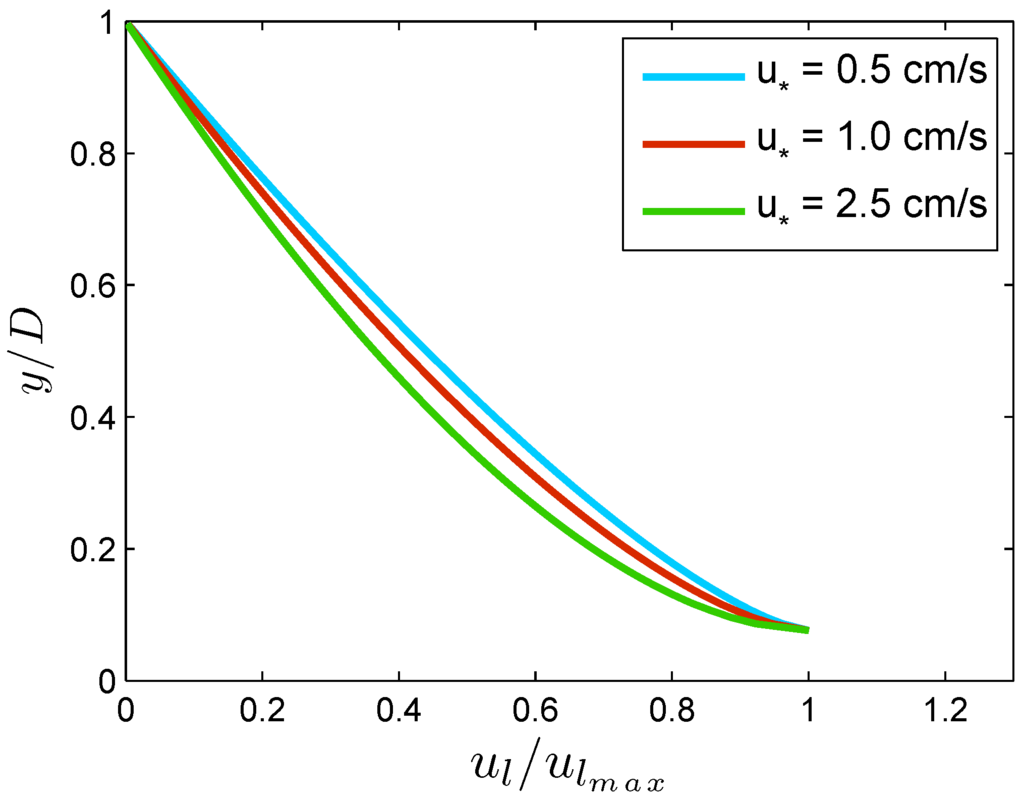
Figure 15.
Effect of shear velocity on velocity lag.
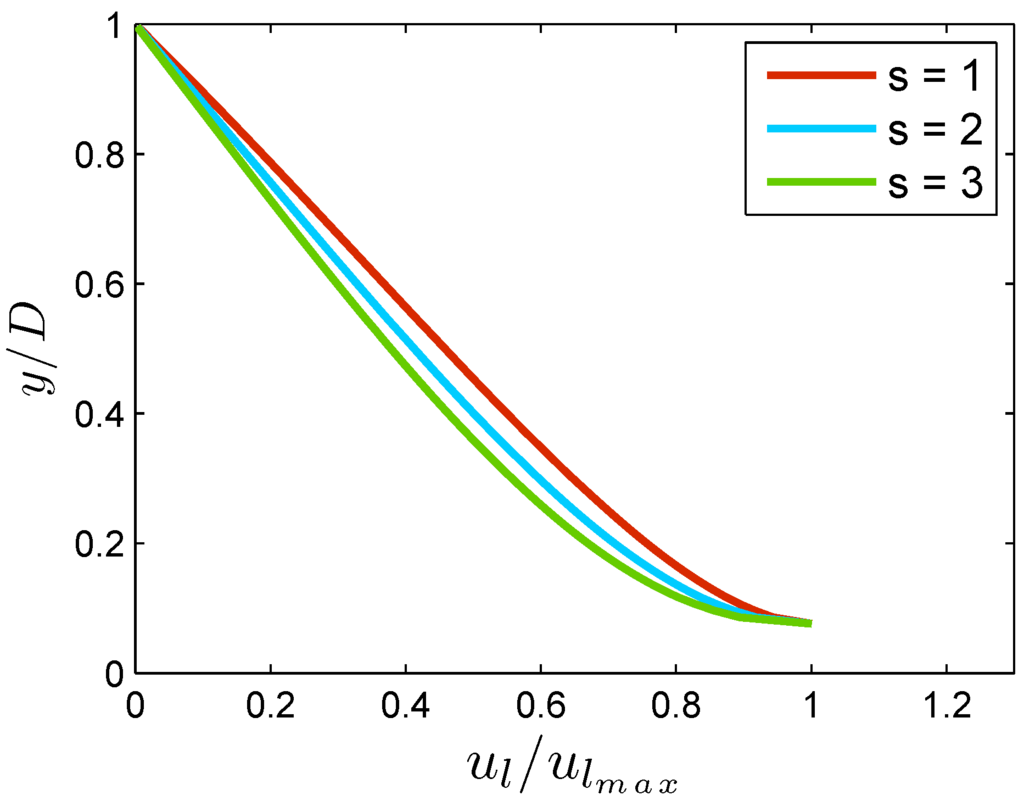
Figure 16.
Effect of specific gravity on velocity lag.
The maximum entropy H can be obtained from Equation (14). Figure 17 gives the relation between maximum entropy H and dimensionless maximum velocity lag . The relation is obtained from regression analysis as:
with a coefficient of regression . Figure 17 shows that the higher the value of the maximum dimensionless velocity lag , the higher the value of entropy H; physically larger means that more complexity is involved in the flow; hence, more uncertainty can be expected, which is expressed as a linear relation in Equation (29).
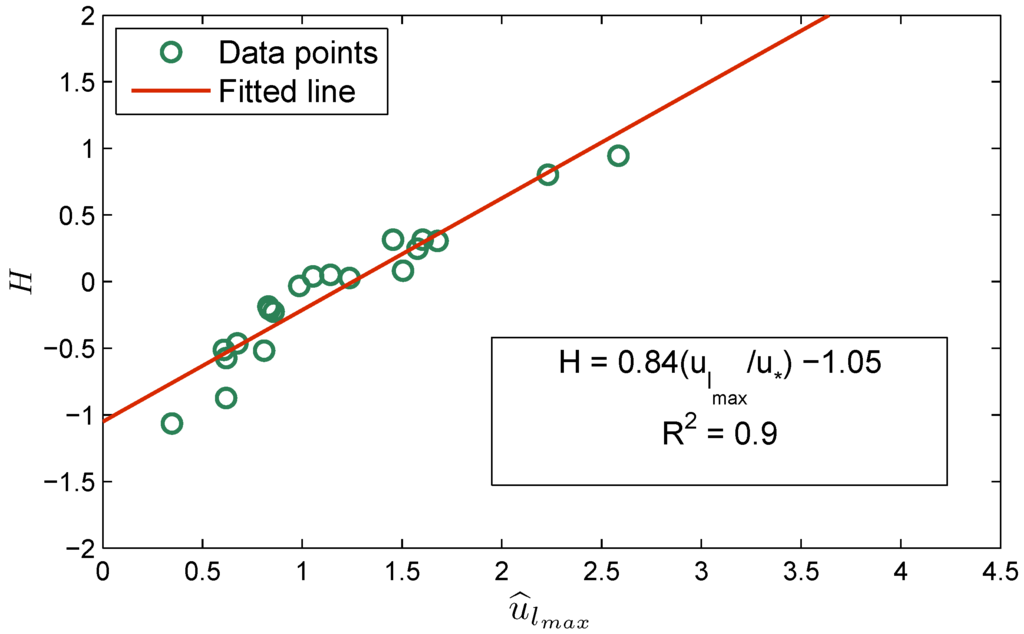
Figure 17.
Relationship of with .
5. Conclusions
In this study, the velocity lag between fluid and sediment particles in a sediment-laden flow is modeled using entropy theory. The model is validated with a wide range of twenty-two sets of experimental data published in the literature. The validation results show that the model predicts the velocity lag between particle and fluid well over the whole flow depth of the open-channel in spite of the scattered nature of the data points. Significance and utilization of the present model can be addressed satisfactorily in the area of sediment transport. Apart from the rigorous numerical solution procedures using the two-phase flow approach, the present model can predict velocity lag for a wide range of flow conditions. Furthermore, if the stream-wise velocity profile u of fluid is known, then we can calculate the stream-wise velocity profile of particles without any difficulty. The model is also compared with three existing models. To measure the accuracy of these models, the root-mean-square error is computed, and it is found that the proposed model gives the best approximation of the velocity lag of particles among the models investigated. The effect of different flow parameters on the derived model of velocity lag is also evaluated. To that end, the model is verified by comparing to the previous models of velocity lag.
Author Contributions
All authors contributed extensively to the work presented in this paper. Manotosh Kumbhakar and Koeli Ghoshal had the original idea of this study. Snehasis Kundu and Manotosh Kumbhakar formulated the model and discussed the analysis of the study. Vijay P. Singh and Koeli Ghoshal made editing corrections and improvements to the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bagnold, R.A. The nature of saltation and bedload transport in water. Proc. R. Soc. Lond. Ser. A 1973, 332, 473–504. [Google Scholar] [CrossRef]
- Muste, M.; Patel, V.C. Velocity profiles for particles and liquid in open-channel flow with suspended sediment. J. Hydraul. Eng. 1997, 123, 742–751. [Google Scholar] [CrossRef]
- Best, J.; Bennett, S.; Bridge, J.; Leeder, M. Turbulence modulation and particle velocities over flat sand beds at low transport rates. J. Hydraul. Eng. 1997, 123, 1118–1129. [Google Scholar] [CrossRef]
- Rashidi, M.; Hetsroni, G.; Banerjee, S. Particle-turbulence interaction in a boundary layer. Int. J. Multiph. Flow 1990, 16, 935–949. [Google Scholar] [CrossRef]
- Taniere, A.; Oesterle, B.; Monnier, J.C. On the behavior of solid particles in a horizontal boundary layer with turbulence and saltation effects. Exp. Fluids 1997, 23, 463–471. [Google Scholar]
- Kiger, K.T.; Pan, C. Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 2002. [Google Scholar] [CrossRef]
- Chauchat, J.; Guillou, S. On turbulence closures for two-phase sediment-laden flow models. J. Geophys. Res. Oceans 2008. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Jha, S.K. Hierarchical modeling of the dilute transport of suspended sediment in open channels. Environ. Fluid Mech. 2009, 9, 207–235. [Google Scholar] [CrossRef]
- Jha, S.K.; Bombardelli, F.A. Toward two-phase flow modeling of nondilute sediment transport in open channels. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Greimann, B.P.; Muste, M.; Holly, F.M. Two-phase formulation of suspended sediment transport. J. Hydraul. Res. 1999, 37, 479–500. [Google Scholar] [CrossRef]
- Jiang, J.S.; Law, A.W.K.; Cheng, N.S. Two-phase modeling of suspended sediment distribution in open channel flows. J. Hydraul. Res. 2004, 42, 273–281. [Google Scholar] [CrossRef]
- Cheng, N.S. Analysis of velocity lag in sediment-laden open channel flows. J. Hydraul. Eng. 2004, 130, 657–666. [Google Scholar] [CrossRef]
- Pal, D.; Jha, S.K.; Ghoshal, K. Velocity lag between particle and liquid in sediment-laden open channel turbulent flow. Eur. J. Mech. B Fluids 2016, 56, 130–142. [Google Scholar] [CrossRef]
- Vowinckel, B.; Kempe, T.; Fröhlich, J. Fluid–particle interaction in turbulent open channel flow with fully-resolved mobile beds. Adv. Water Resour. 2014, 72, 32–44. [Google Scholar] [CrossRef]
- Shao, X.; Wu, T.; Yu, Z. Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. J. Fluid Mech. 2012, 693, 319–344. [Google Scholar] [CrossRef]
- Derksen, J.J. Simulations of granular bed erosion due to a mildly turbulent shear flow. J. Hydraul. Res. 2015, 53, 622–632. [Google Scholar] [CrossRef]
- Finn, J.R.; Li, M. Regimes of sediment-turbulence interaction and guidelines for simulating the multiphase bottom boundary layer. Int. J. Multiph. Flow 2016, 85, 278–283. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Two-dimensional velocity distribution in open channels using the Tsallis entropy. J. Hydrol. Eng. 2012, 18, 331–339. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. One-dimensional velocity distribution in open channels using Tsallis entropy. J. Hydrol. Eng. 2013, 19, 290–298. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K. One-Dimensional velocity distribution in open channels using Renyi entropy. Stoch. Environ. Res. Risk Assess. 2016. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K. Two dimensional velocity distribution in open channels using Renyi entropy. Phys. A Stat. Mech. Appl. 2016, 450, 546–559. [Google Scholar] [CrossRef]
- Chiu, C.; Jin, W.; Chen, Y. Mathematical models for distribution of sediment concentration. J. Hydraul. Eng. 2000, 126, 16–23. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Suspended sediment concentration in open channels using Tsallis entropy. J. Hydrol. Eng. 2013, 19, 966–977. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H. Modeling sediment concentration in debris flow by Tsallis entropy. Phys. A Stat. Mech. Appl. 2015, 420, 49–58. [Google Scholar] [CrossRef]
- Righetti, M.; Romano, G.P. Particle-fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 2004, 505, 93–121. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communications, I and II. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics: I. Phys. Rev. 1957, 106, 620–930. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics: II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Kaftori, D.; Hetsroni, G.; Banerjee, S. Particle behavior in the turbulent boundary layer velocity and distribution profiles. Phys. Fluids 1995, 7, 1107–1121. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Fujita, I.; Ettema, R. Two-phase versus mixed-flow perspective on suspended sediment transport in turbulent channel flows. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).