Combinatorial Intricacies of Labeled Fano Planes
Abstract
:1. Introduction
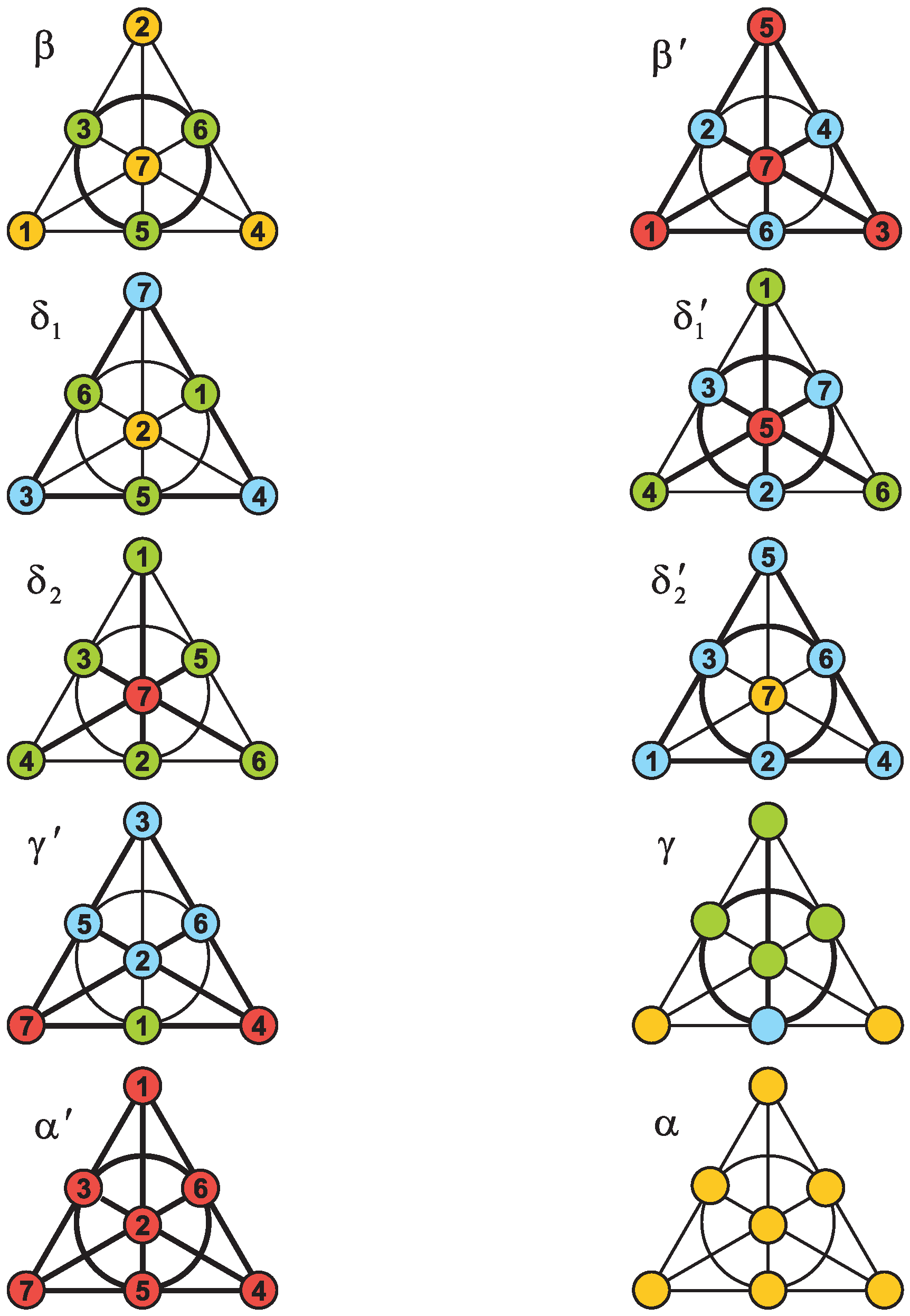
2. Refined Structure of Numbered Fano Planes
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hall, J.I. On identifying PG(3,2) and the complete 3-design on seven points. Ann. Discret. Math. 1980, 7, 131–141. [Google Scholar]
- Lindner, C.C.; Rosa, A. Steiner triple systems having a prescribed number of triples in common. Can. J. Math. 1975, 27, 1166–1175. [Google Scholar] [CrossRef]
- Polster, B. Yea why try her raw wet hat: A tour of the smallest projective space. Math. Intell. 1999, 21, 38–43. [Google Scholar] [CrossRef]
- Polster, B. A Geometrical Picture Book; Springer: New York, NY, USA, 1998; pp. 77–79. [Google Scholar]
- Saniga, M.; Holweck, F.; Pracna, P. From Cayley–Dickson algebras and finite geometry. Mathematics 2015, 3, 1192–1221. [Google Scholar] [CrossRef]
- Grannell, M.J.; Griggs, T.S.; Rosa, A. Three-line chromatic indices of Steiner triple systems. Australas. J. Comb. 2000, 21, 67–84. [Google Scholar]
- Horak, P.; Phillips, N.; Wallis, W.D.; Yucas, J. Counting frequencies of configurations in Steiner triple systems. Ars Comb. 1997, 46, 65–75. [Google Scholar]
- Forbes, A.D.; Grannell, M.J.; Griggs, T.S. Configurations and trades in Steiner triple systems. Australas. J. Comb. 2004, 29, 75–84. [Google Scholar]
- Brown, E. The many names of (7,3,1). Math. Mag. 2002, 75, 83–94. [Google Scholar] [CrossRef]
- Brown, E. Many more names of (7,3,1). Math. Mag. 2015, 88, 103–120. [Google Scholar]
- Baez, J. The Octonions. Bull. Am. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Honold, T.; Kiermaier, M. On putative q-analogues of the Fano plane and related combinatorial structures. 2015. [Google Scholar]

| Type | Points of Order | |||
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |
| (α) | (7) | (0) | (0) | (0) |
| 0 | 0 | 0 | 7 | |
| β | 4 | 3 | 0 | 0 |
| 0 | 0 | 3 | 4 | |
| (γ) | (2) | (4) | (1) | (0) |
| 0 | 1 | 4 | 2 | |
| 1 | 3 | 3 | 0 | |
| 0 | 3 | 3 | 1 | |
| 0 | 6 | 0 | 1 | |
| 1 | 0 | 6 | 0 | |
| Plane | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | β |
| Plane | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type |
| Type | (α) | β | (γ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Set | - | 1 | - | 0 | 1 | 1 | 7 | 5 | 0 | 0 |
| Set | - | 0 | - | 2 | 0 | 5 | 0 | 5 | 1 | 2 |
| Total | - | 1 | - | 2 | 1 | 6 | 7 | 10 | 1 | 2 |
| Line | (α) | β | (γ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 123 | - | 1 | - | 1 | 0 | 0 | 1 | 2 | 0 | 1 |
| 145 | - | 1 | - | 1 | 0 | 0 | 1 | 2 | 0 | 1 |
| 257 | - | 1 | - | 1 | 0 | 0 | 1 | 2 | 0 | 1 |
| 347 | - | 1 | - | 1 | 0 | 0 | 1 | 2 | 0 | 1 |
| 156 | - | 0 | - | 1 | 1 | 0 | 0 | 4 | 0 | 0 |
| 235 | - | 0 | - | 1 | 1 | 0 | 0 | 4 | 0 | 0 |
| 246 | - | 1 | - | 2 | 1 | 0 | 1 | 0 | 1 | 0 |
| 167 | - | 1 | - | 0 | 0 | 0 | 1 | 1 | 1 | 2 |
| 134 | - | 0 | - | 0 | 1 | 0 | 1 | 3 | 1 | 0 |
| 124 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 236 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 247 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 346 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 357 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 456 | - | 0 | - | 0 | 0 | 1 | 1 | 3 | 0 | 1 |
| 136 | - | 0 | - | 1 | 0 | 2 | 2 | 1 | 0 | 0 |
| 147 | - | 0 | - | 1 | 0 | 2 | 2 | 1 | 0 | 0 |
| 345 | - | 0 | - | 1 | 0 | 2 | 2 | 1 | 0 | 0 |
| 567 | - | 0 | - | 1 | 0 | 2 | 2 | 1 | 0 | 0 |
| 126 | - | 0 | - | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
| 157 | - | 0 | - | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
| 245 | - | 0 | - | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
| 467 | - | 0 | - | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
| 135 | - | 0 | - | 0 | 0 | 2 | 3 | 0 | 0 | 1 |
| 237 | - | 0 | - | 0 | 0 | 2 | 3 | 0 | 0 | 1 |
| 256 | - | 0 | - | 0 | 0 | 2 | 3 | 0 | 0 | 1 |
| 127 | - | 0 | - | 1 | 1 | 1 | 2 | 1 | 0 | 0 |
| 367 | - | 0 | - | 1 | 1 | 1 | 2 | 1 | 0 | 0 |
| 146 | - | 0 | - | 0 | 0 | 3 | 2 | 1 | 0 | 0 |
| 234 | - | 0 | - | 0 | 0 | 3 | 2 | 1 | 0 | 0 |
| 137 | - | 0 | - | 0 | 0 | 2 | 0 | 4 | 0 | 0 |
| 267 | - | 0 | - | 0 | 0 | 2 | 0 | 4 | 0 | 0 |
| 356 | - | 1 | - | 0 | 0 | 1 | 1 | 2 | 1 | 0 |
| 457 | - | 0 | - | 0 | 1 | 2 | 1 | 1 | 1 | 0 |
| 125 | - | 0 | - | 0 | 0 | 3 | 1 | 1 | 1 | 0 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saniga, M. Combinatorial Intricacies of Labeled Fano Planes. Entropy 2016, 18, 312. https://doi.org/10.3390/e18090312
Saniga M. Combinatorial Intricacies of Labeled Fano Planes. Entropy. 2016; 18(9):312. https://doi.org/10.3390/e18090312
Chicago/Turabian StyleSaniga, Metod. 2016. "Combinatorial Intricacies of Labeled Fano Planes" Entropy 18, no. 9: 312. https://doi.org/10.3390/e18090312
APA StyleSaniga, M. (2016). Combinatorial Intricacies of Labeled Fano Planes. Entropy, 18(9), 312. https://doi.org/10.3390/e18090312






