An Efficient Method to Construct Parity-Check Matrices for Recursively Encoding Spatially Coupled LDPC Codes † †
Abstract
:1. Introduction
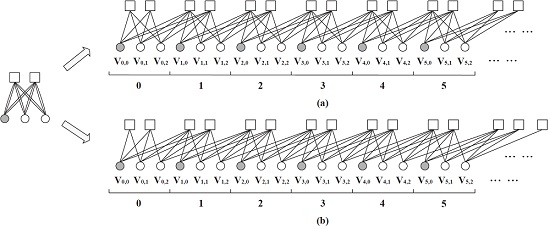
2. Overview of Spatially Coupled LDPC Codes
- The number of ones in each row is .
- The number of ones in each column is , except the beginning and the terminating ends of the chain.
- , for and ,.
- There exists l such that .
- has full rank .
- 6.
- The last rows of is a identity matrix.
3. Recursive Encoding of Spatially Coupled LDPC Codes with Arbitrary Node Degrees
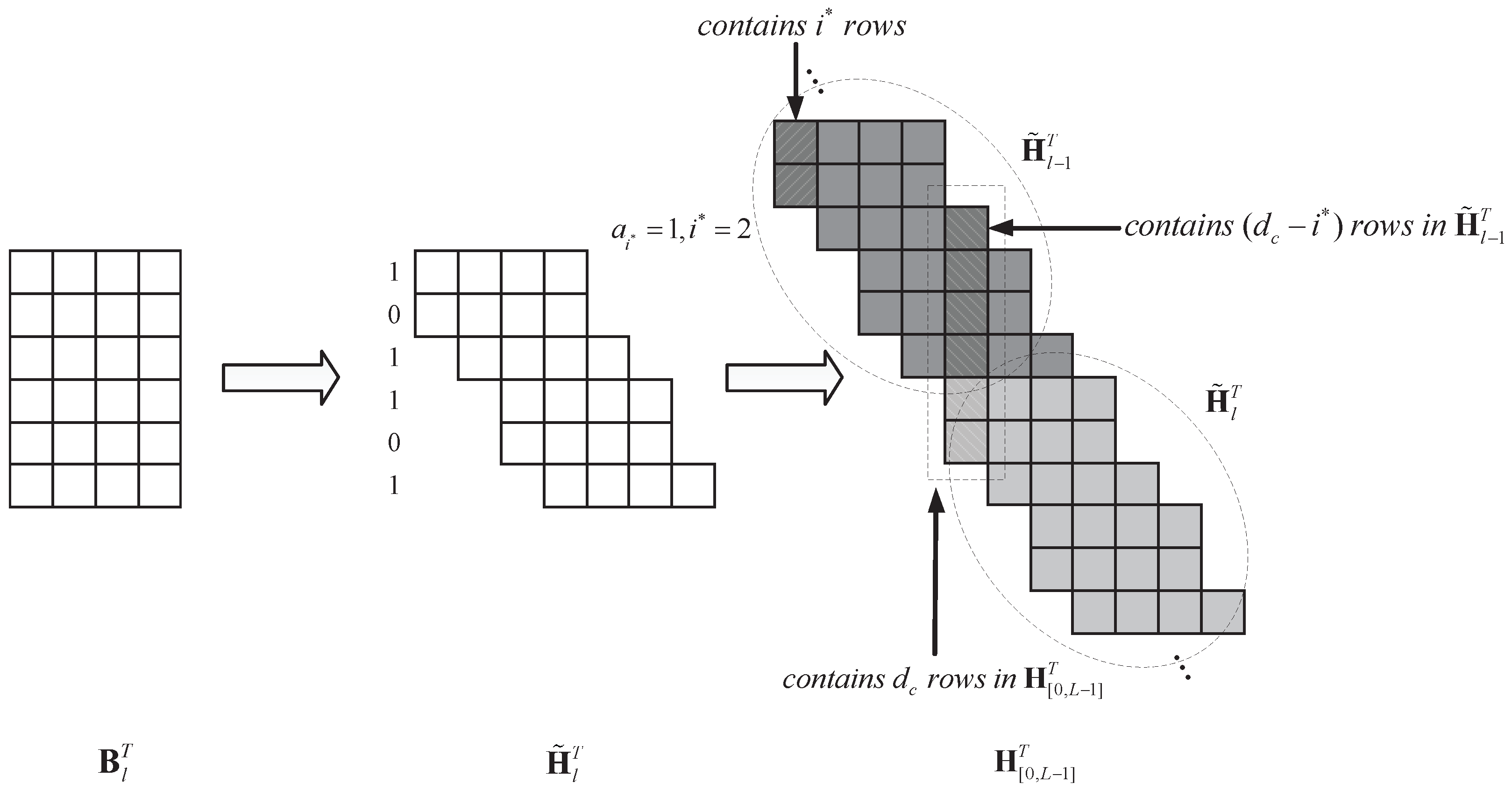
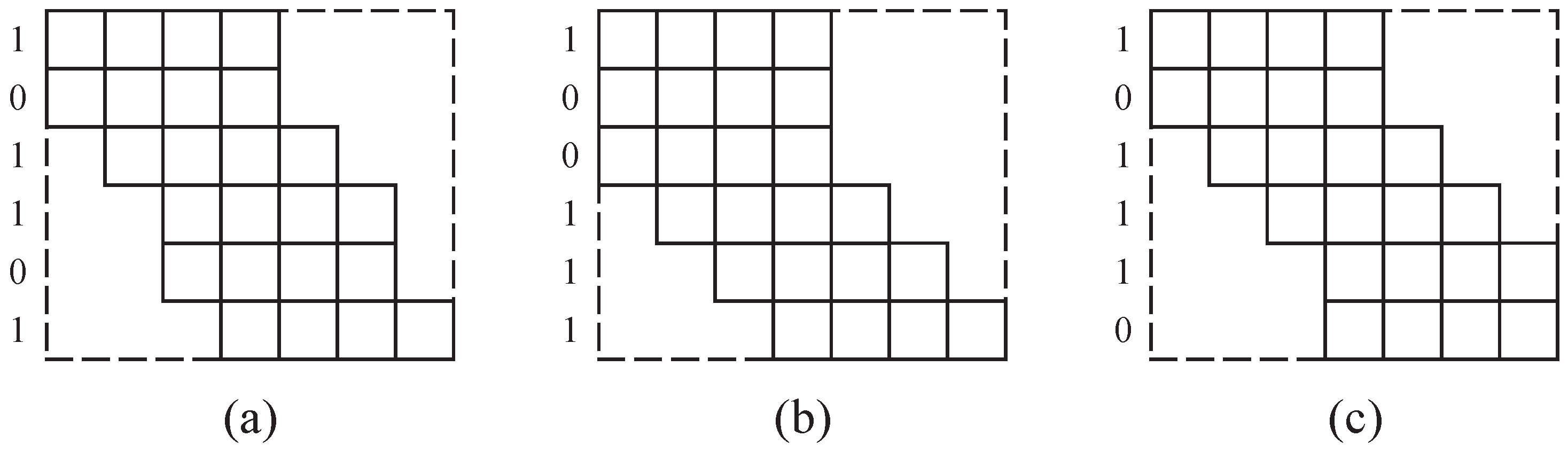
3.1. General Principle on Constructing Parity-Check Matrices
3.2. Implementation of Recursive Encoding
4. Theoretical Analysis
4.1. Design Rate
4.2. Density Evolution
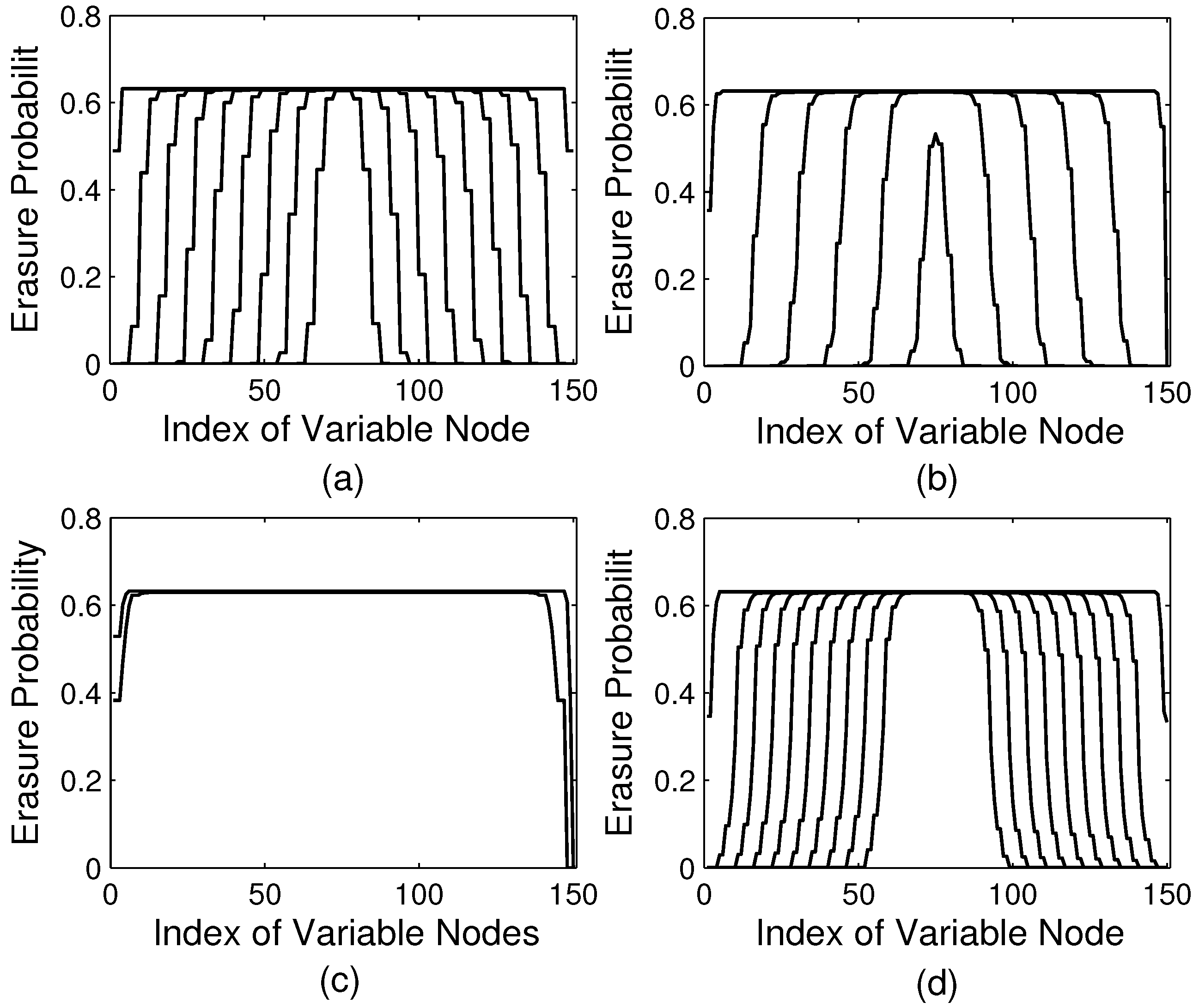
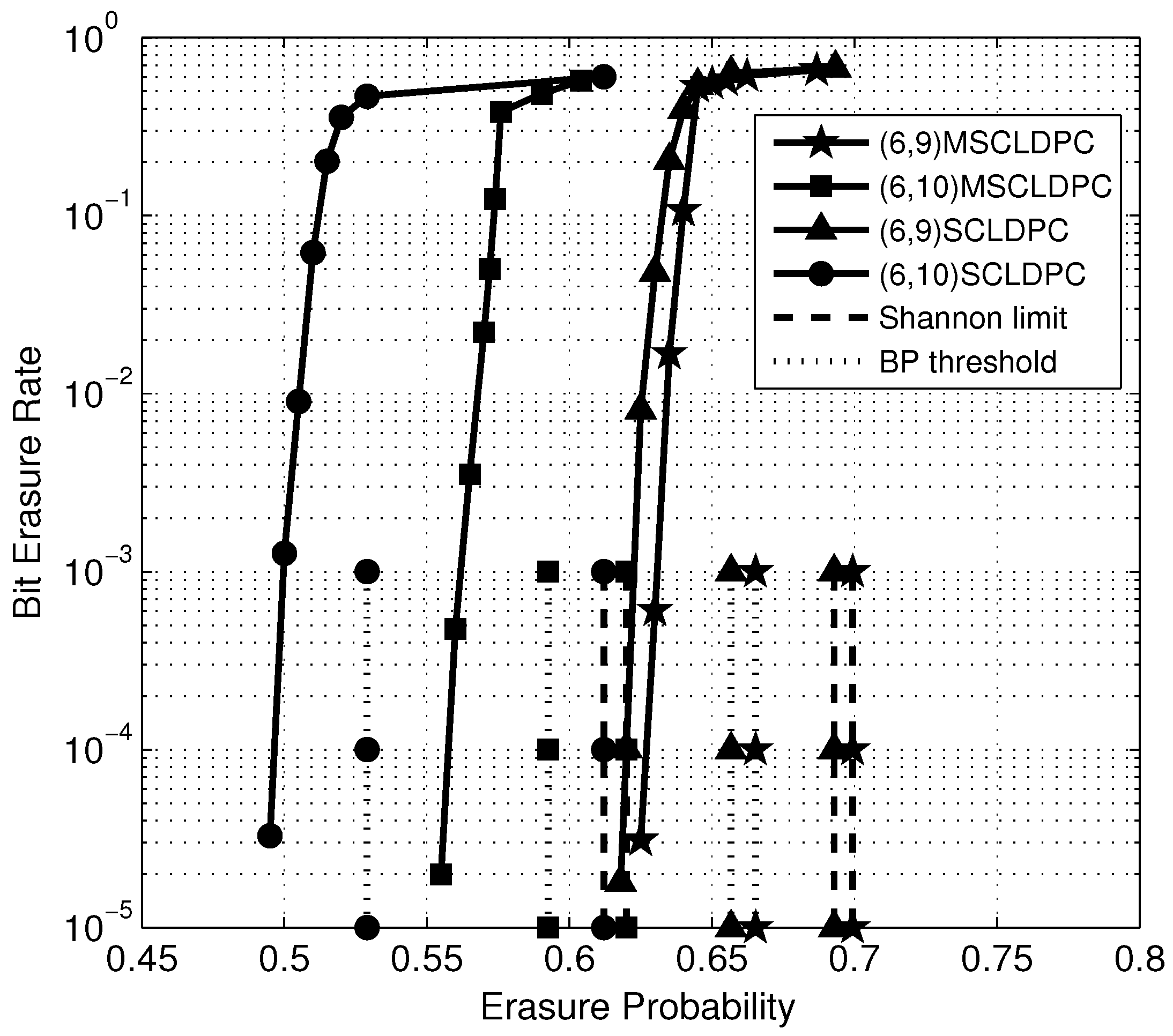
5. Simulation Results and Discussions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gallager, R.G. Low Density Parity Check Codes; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Jimenez-Feltström, A.; Zigangirov, K.S. Time-varying periodic convolutional codes with low-density parity-check matrix. IEEE Trans. Inf. Theory 1999, 45, 2181–2191. [Google Scholar] [CrossRef]
- Lentmaier, M.; Sridharan, A.; Costello, D.J., Jr.; Zigangirov, K.S. Iterative decoding threshold analysis for LDPC convolutional codes. IEEE Trans. Inf. Theory 2010, 56, 5274–5289. [Google Scholar] [CrossRef]
- Kudekar, S.; Richardson, T.; Urbanke, R. Threshold saturation via spatial coupling: Why convolutional LDPC ensembles perform so well over the BEC. IEEE Trans. Inf. Theory 2011, 57, 803–834. [Google Scholar] [CrossRef]
- Mitchell, D.G.M.; Pusane, A.E.; Zigangirov, K.S.; Costello, D.J., Jr. Asymptotically good LDPC convolutional codes based on protograph. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1030–1034.
- Pusane, A.E.; Jimenez-Felström, A.; Sridharan, A.A.; Lentmaier, M.M.; Zigangirov, K.S.; Costello, D.J., Jr. Implementation aspects of LDPC convolutional codes. IEEE Trans. Commun. 2008, 56, 1060–1069. [Google Scholar] [CrossRef]
- Tanner, R.M.; Sridhara, D.; Sridharan, A.; Fuja, T.E.; Costello, D.J., Jr. LDPC block and convolutional codes based on circulant matrices. IEEE Trans. Inf. Theory 2004, 50, 2966–2984. [Google Scholar] [CrossRef]
- Sridharan, A.; Truhachev, D.V.; Lentmaier, M.; Costello, D.J.; Zigangirov, K.S. Distance bounds for an ensemble of LDPC convolutional codes. IEEE Trans. Inf. Theory 2007, 53, 4537–4555. [Google Scholar] [CrossRef]
- Tazoe, K.; Kasai, K.; Sakaniwa, K. Efficient termination of spatially-coupled code. In Proceedings of the 2012 IEEE Information Theory Workshop, Lausanne, Switzerland, 3–7 September 2012; pp. 30–34.
- Yedla, A.; Jian, Y.-Y.; Nguyen, P.S.; Pfister, H.D. A simple proof of threshold saturation for coupled scalar recursions. In Proceedings of the 2012 IEEE International Symposium on Turbo Codes and Iterative Information Processing, Gothenburg, Sweden, 27–31 August 2012; pp. 51–55.
- Yedla, A.; Jian, Y.-Y.; Nguyen, P.S.; Pfister, H.D. A simple proof of threshold saturation for coupled vector recursions. In Proceedings of the 2012 IEEE Information Theory Workshop, Lausanne, Switzerland, 3–7 September 2012; pp. 25–29.
- Kudekar, S.; Richardson, T.; Urbanke, R. Spatially coupled ensembles universally achieve capacity under belief propagation. In Proceedings of the 2012 IEEE International Symposium on Information Theory, Cambridge, UK, 1–6 July 2012; pp. 453–457.
- Kumar, S.; Young, A.J.; Macris, N.; Pfister, H.D. Threshold saturation for spatially coupled LDPC and LDGM codes on BMS channels. IEEE Trans. Inf. Theory 2014, 60, 7389–7415. [Google Scholar] [CrossRef]
- Kudekar, S.; Pfister, H.D. The effect of spatial coupling on compressive sensing. In Proceedings of the Allerton Conference on Communications, Control, and Computing, Monticello, NY, USA, 29 September–1 October 2010; pp. 347–353.
- Si, Z.; Thobaben, R.; Skoglund, M. Rate-compatible LDPC convolutional codes achieving the capacity of the BEC. IEEE Trans. Inf. Theory 2012, 58, 4021–4029. [Google Scholar] [CrossRef]
- Nitzold, W.; Lentmaier, M.; Fettweis, G.P. Spatially coupled protograph-based LDPC codes for incremental redundancy. In Proceedings of the International Symposium on Turbo Codes and Iterative Information Processing, Gothenburg, Sweden, 27–31 August 2012; pp. 155–159.
- Si, Z.; Thobaben, R.; Skoglund, M. Bilayer LDPC convolutional codes for decode-and-forward relaying. IEEE Trans. Commun. 2013, 61, 3086–3099. [Google Scholar]
- Schwandter, S.; Amat, A.G.; Matz, G. Spatially coupled LDPC codes for two-user decode-and-forward relaying. In Proceedings of the International Symposium on Turbo Codes and Iterative Information Processing, Gothenburg, Sweden, 27–31 August 2012; pp. 46–50.
- Rathi, V.; Urbanke, R.; Andersson, M.; Skoglund, M. Rate-equivocation optimally spatially coupled LDPC codes for the BEC wiretap channel. In Proceedings of the 2011 IEEE International Symposium on Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 2393–2397.
- Kudekar, S.; Kasai, K. Spatially coupled codes over the multiple access channel. In Proceedings of the 2011 IEEE International Symposium on Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 2816–2820.
- Schlegel, C.; Truhachev, D. Multiple access demodulation in the lifted signal graph with spatial coupling. IEEE Trans. Inf. Theory 2013, 59, 2459–2470. [Google Scholar] [CrossRef]
- Yedla, A.; Pfister, H.D.; Narayanan, K.R. Universality for the noisy Slepian-Wolf problem via spatial coupling. In Proceedings of the 2011 IEEE International Symposium on Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 2567–2571.
- Iyengar, A.R.; Papaleo, M.; Siegel, P.H.; Wolf, J.K.; Vanelli-Coralli, A.; Corazza, G.E. Windowed decoding of protograph-based LDPC convolutional codes over erasure channels. IEEE Trans. Inf. Theory 2012, 58, 2303–2320. [Google Scholar] [CrossRef]
- Ma, J.; Si, Z.; He, Z.; Niu, K. Recursive encoding of spatially coupled LDPC codes with arbitrary rates. In Proceedings of the 2015 IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Hong Kong, China, 30 August–2 September 2015; pp. 127–131.
- Mitchell, D.; Lentmaier, M.; Costello, D.J. Spatially coupled LDPC codes constructed from protographs. IEEE Trans. Inf. Theory 2015, 61, 4866–4889. [Google Scholar] [CrossRef]
- Stinner, M.; Olmos, P.M. On the waterfall performance of finite-length SC-LDPC codes constructed from protographs. IEEE J. Sel. Areas Commun. 2016, 34, 345–361. [Google Scholar] [CrossRef]
- Johnson, S.; Lechner, G. Spatially coupled repeat-accumulate codes. IEEE Commun. Lett. 2013, 17, 373–376. [Google Scholar] [CrossRef]
- Divsalar, D.; Dolinar, S.; Jones, C.R.; Andrews, K. Capacity approaching protograph codes. IEEE J. Sel. Areas Commun. 2009, 27, 876–888. [Google Scholar] [CrossRef]
- Kasai, K.; Sakaniwa, K. Spatially-coupled MacKay–Neal codes and Hsu–Anastasopoulos codes. In Proceedings of the 2011 IEEE International Symposium on Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 747–751.
- Divsalar, D. Ensemble weight enumerators for protograph LDPC codes. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, MA, USA, 9–14 July 2006; pp. 1554–1558.
- Abu-Surra, S.; Divsalar, D.; Ryan, W.E. Enumerators for Protograph-based ensembles of LDPC and generalized LDPC codes. IEEE Trans. Inf. Theory 2011, 57, 858–886. [Google Scholar] [CrossRef]



| Pattern a | Design Rate | |||
|---|---|---|---|---|
| Original | 0.3200 | 0.6800 | 0.6567 | 0.0233 |
| (101101) | 0.3133 | 0.6867 | 0.6646 | 0.0221 |
| (100111) | 0.3133 | 0.6867 | 0.6364 | 0.0503 |
| (101110) | 0.3133 | 0.6867 | 0.6479 | 0.0388 |
| Pattern a | Design Rate | |||||
|---|---|---|---|---|---|---|
| (4, 6) | (101101) | 0.3133 | 0.6867 | 0.6646 | 0.0221 | 0.0233 |
| (6, 9) | (101101101) | 0.3007 | 0.6993 | 0.6653 | 0.0340 | 0.0361 |
| (8, 12) | (101101101101) | 0.2885 | 0.7115 | 0.6653 | 0.0462 | 0.0484 |
| (6, 10) | (1001110011) | 0.3800 | 0.6200 | 0.5925 | 0.0275 | 0.0830 |
| (9, 15) | (100111001110011) | 0.3686 | 0.6314 | 0.5925 | 0.0389 | 0.0945 |
| (12, 20) | (10011100111001110011) | 0.3577 | 0.6423 | 0.5925 | 0.0498 | 0.1055 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, Z.; Wang, S.; Ma, J. An Efficient Method to Construct Parity-Check Matrices for Recursively Encoding Spatially Coupled LDPC Codes †. Entropy 2016, 18, 305. https://doi.org/10.3390/e18080305
Si Z, Wang S, Ma J. An Efficient Method to Construct Parity-Check Matrices for Recursively Encoding Spatially Coupled LDPC Codes †. Entropy. 2016; 18(8):305. https://doi.org/10.3390/e18080305
Chicago/Turabian StyleSi, Zhongwei, Sijie Wang, and Junyang Ma. 2016. "An Efficient Method to Construct Parity-Check Matrices for Recursively Encoding Spatially Coupled LDPC Codes †" Entropy 18, no. 8: 305. https://doi.org/10.3390/e18080305
APA StyleSi, Z., Wang, S., & Ma, J. (2016). An Efficient Method to Construct Parity-Check Matrices for Recursively Encoding Spatially Coupled LDPC Codes †. Entropy, 18(8), 305. https://doi.org/10.3390/e18080305