Heat Transfer and Entropy Generation of Non-Newtonian Laminar Flow in Microchannels with Four Flow Control Structures
Abstract
:1. Introduction
2. Solution Method
2.1. Governing Equations
- Continuity equation:
- X-momentum equation:
- Y-momentum equation:
- Z-momentum equation:
- Energy equation:
2.2. Data Reduction
2.3. Working Substances
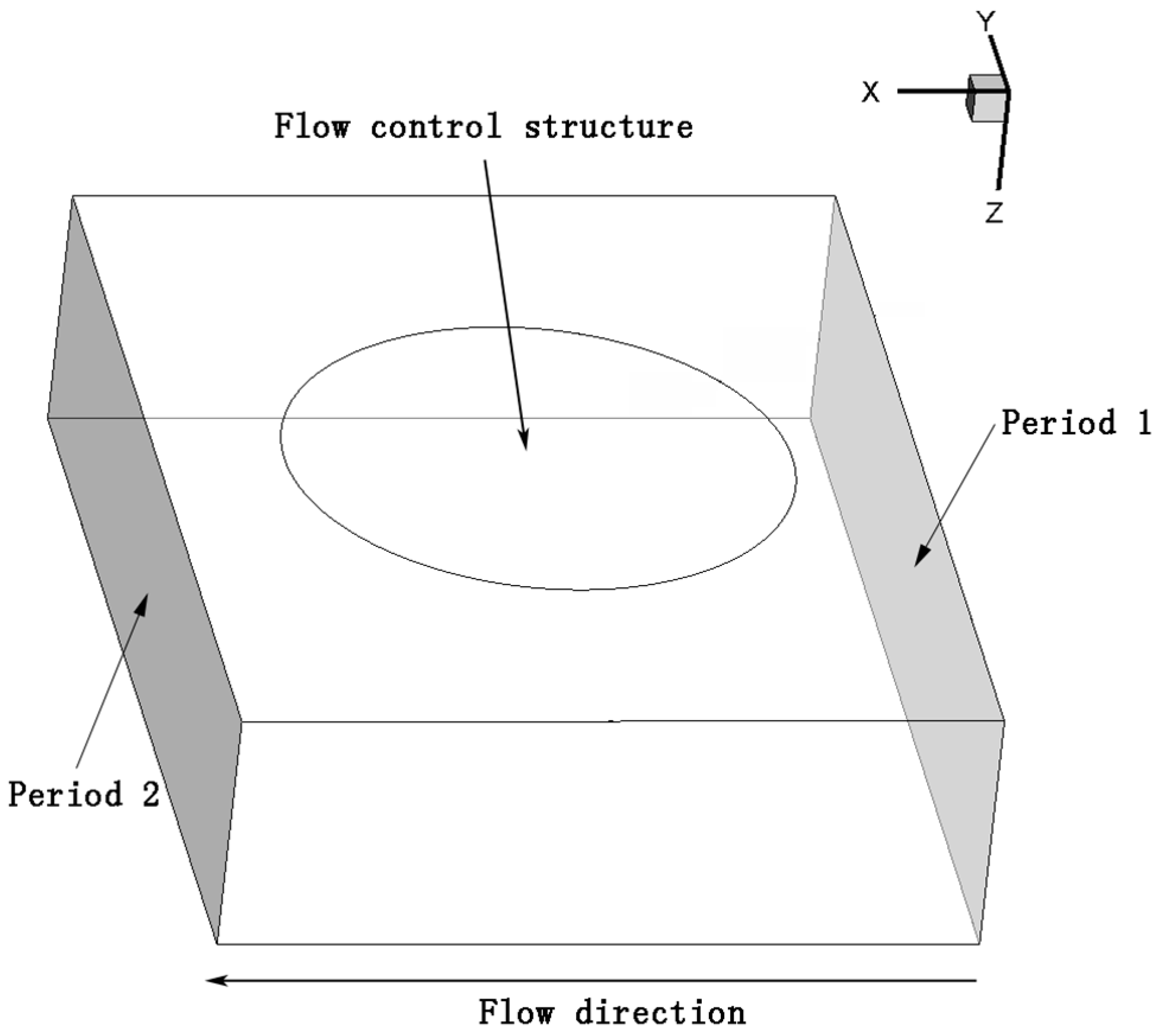
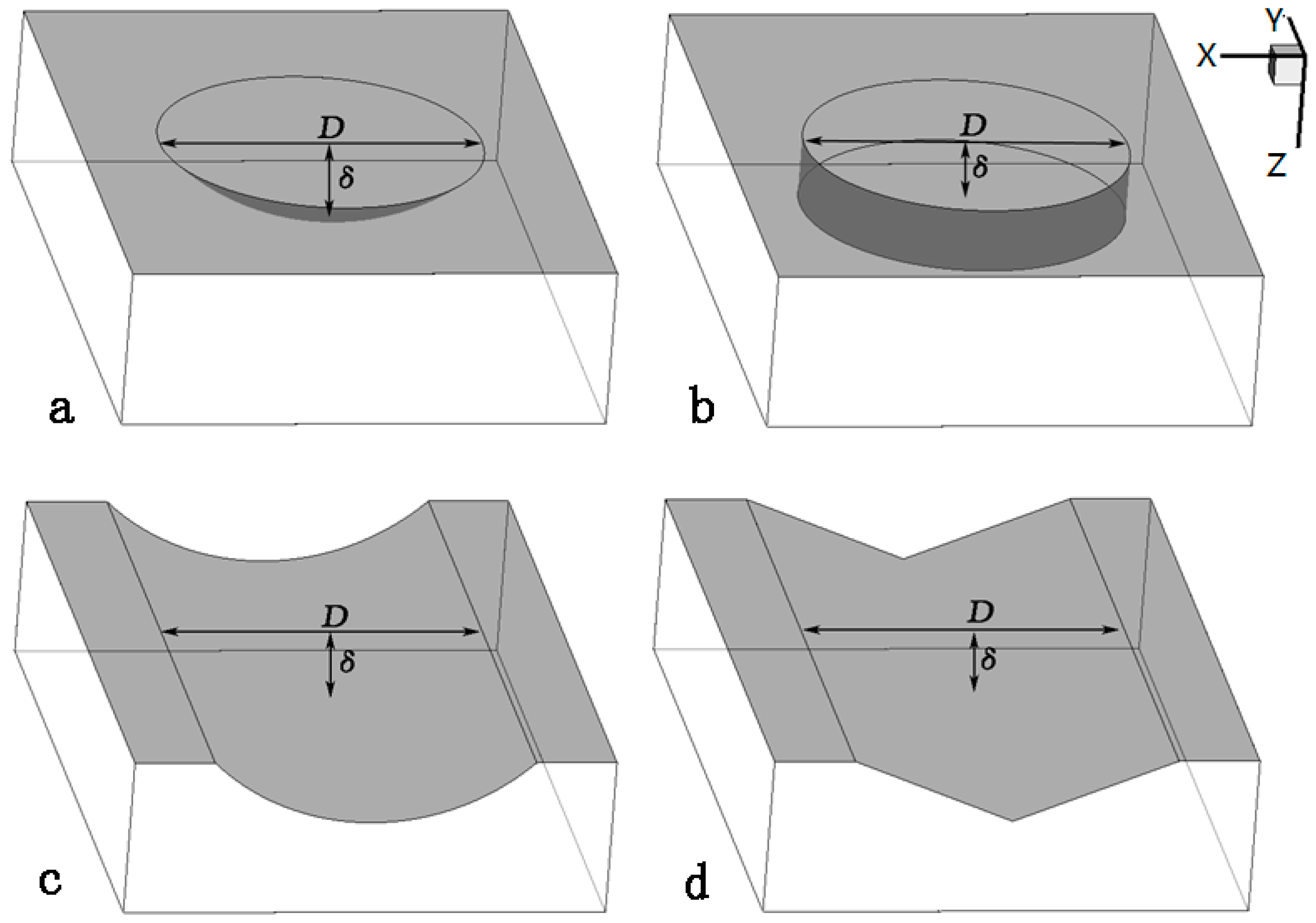
2.4. Physical Model and Boundary Conditions
2.5. Model Validation
3. Results and Discussion
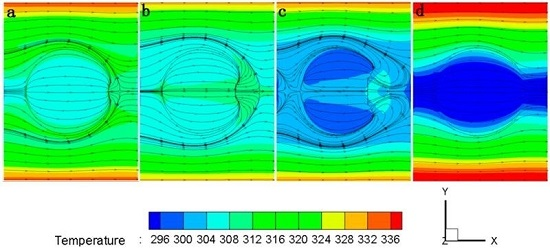
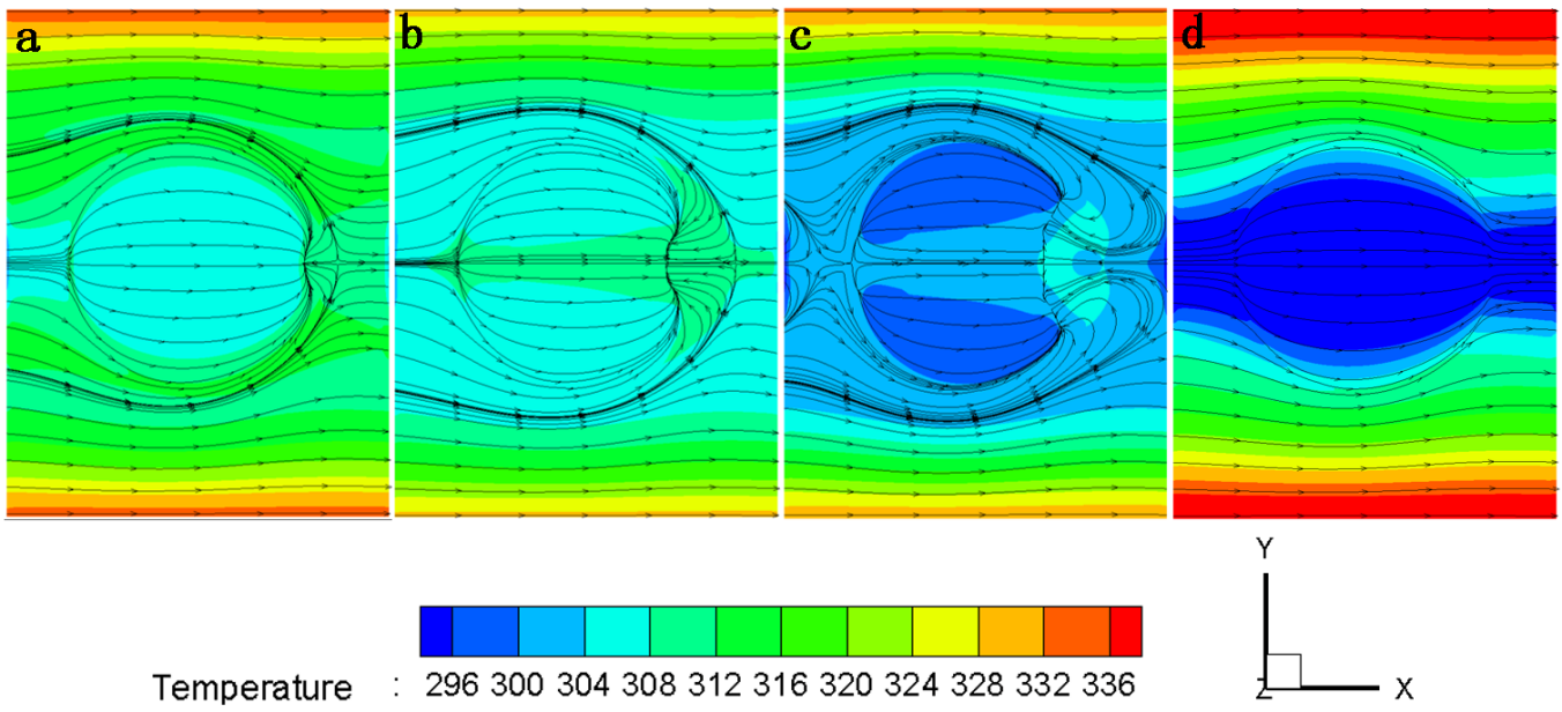
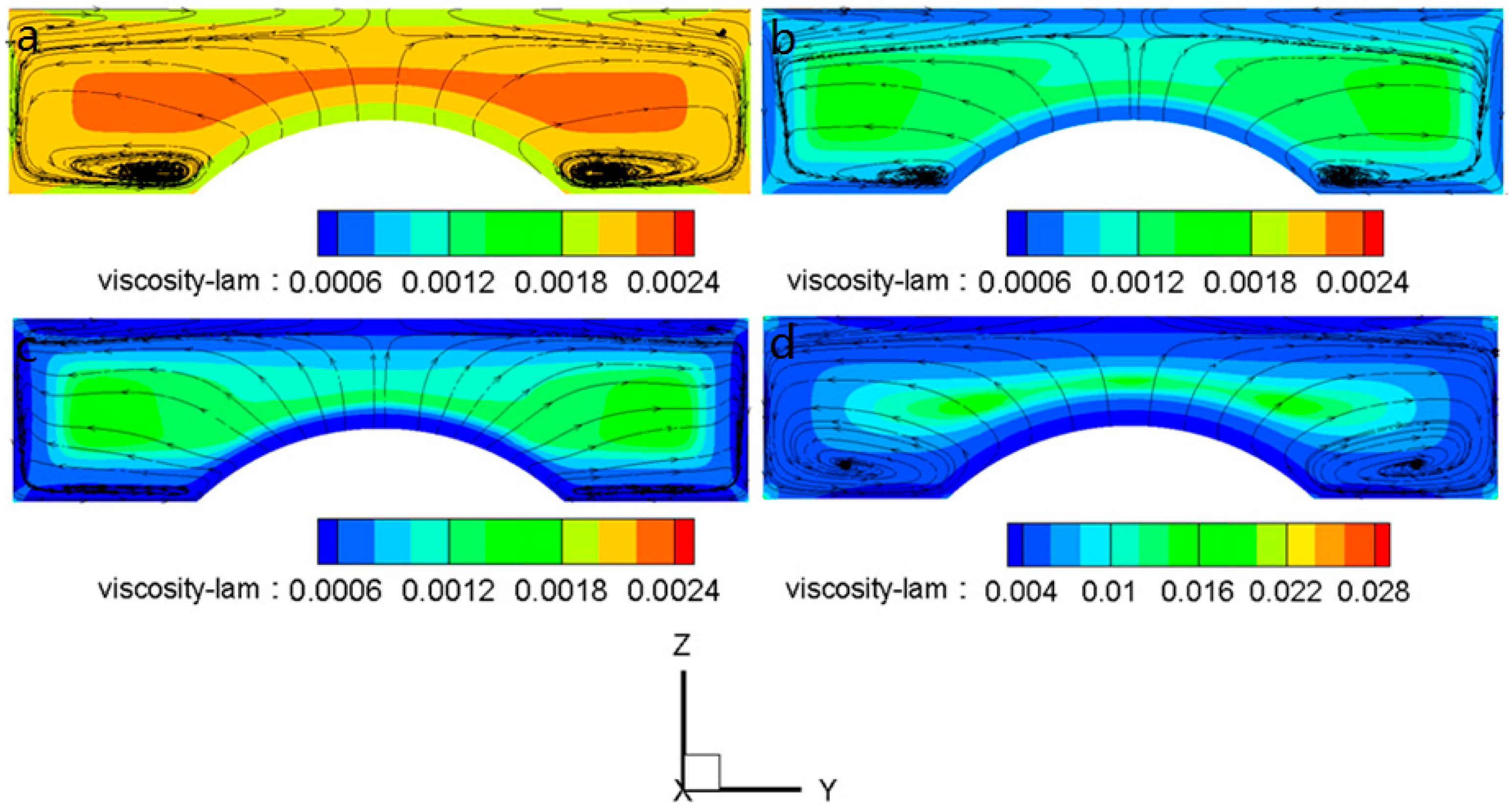
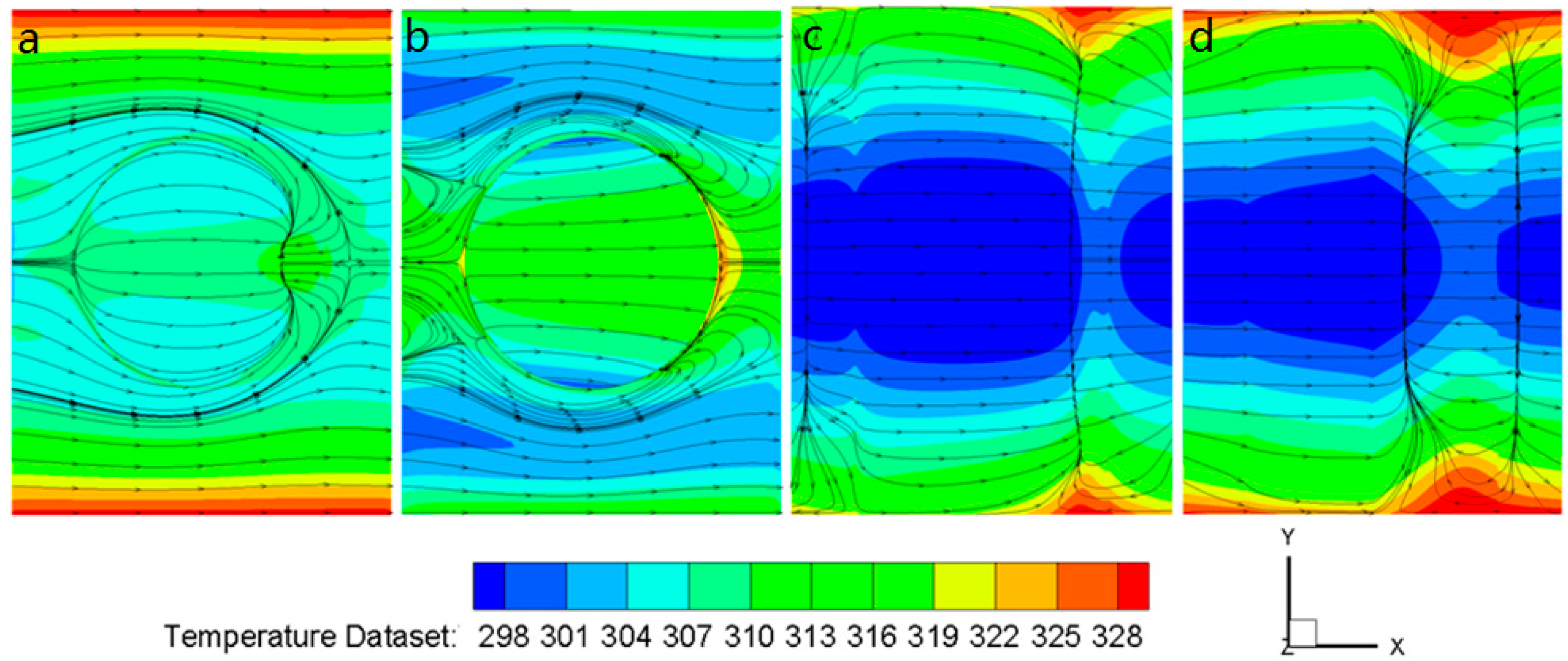
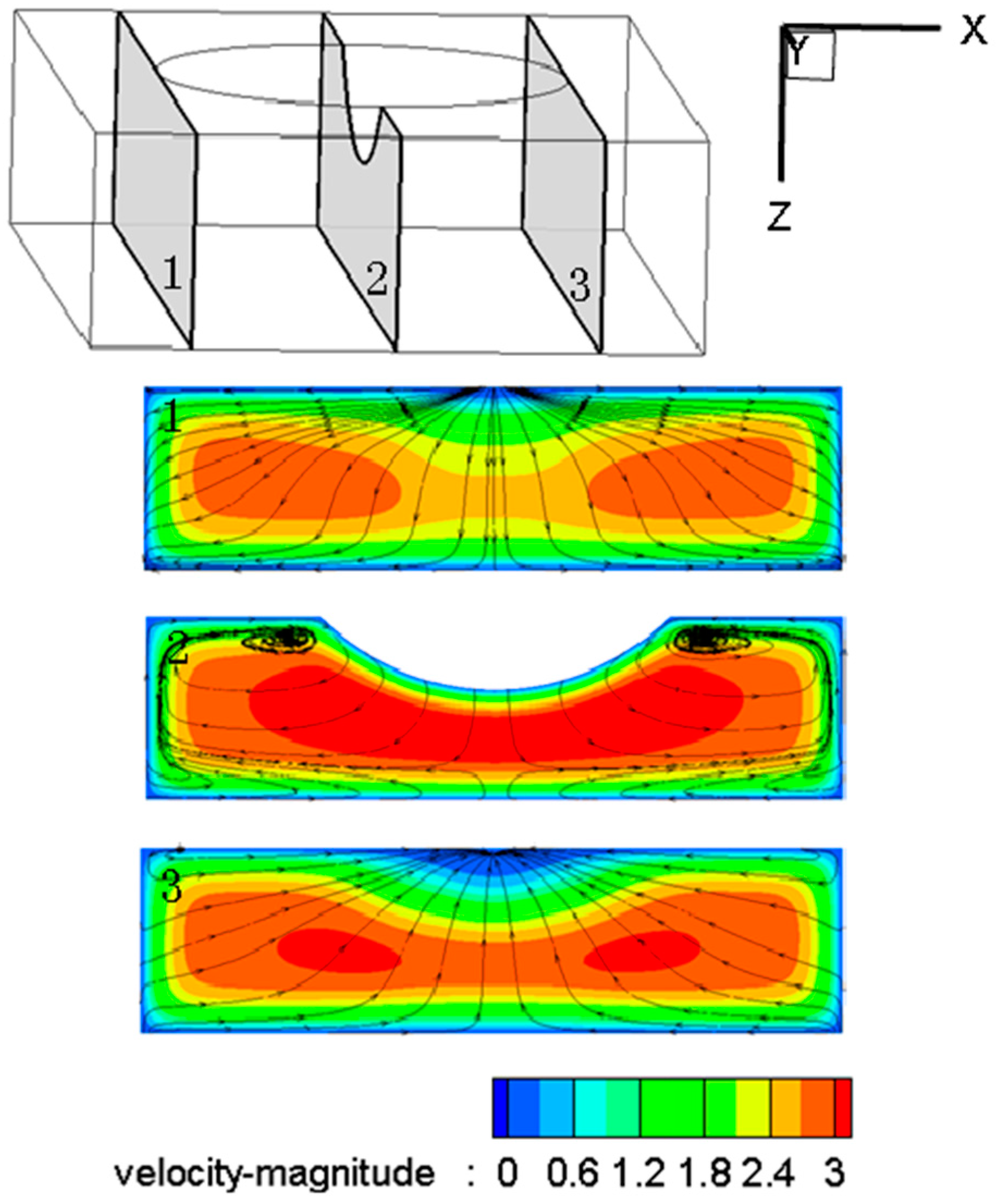
3.1. Flow Structures and Temperature Distribution
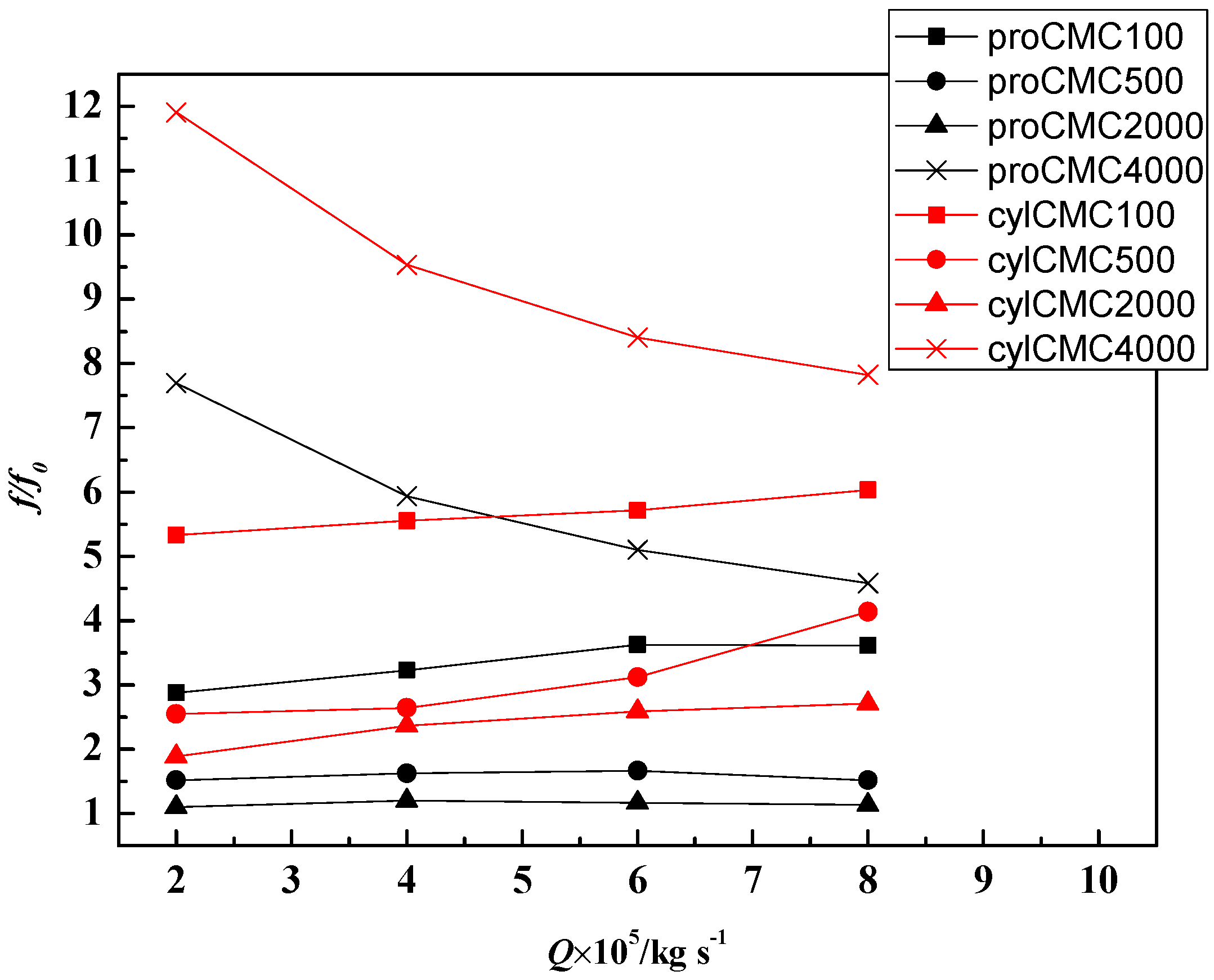
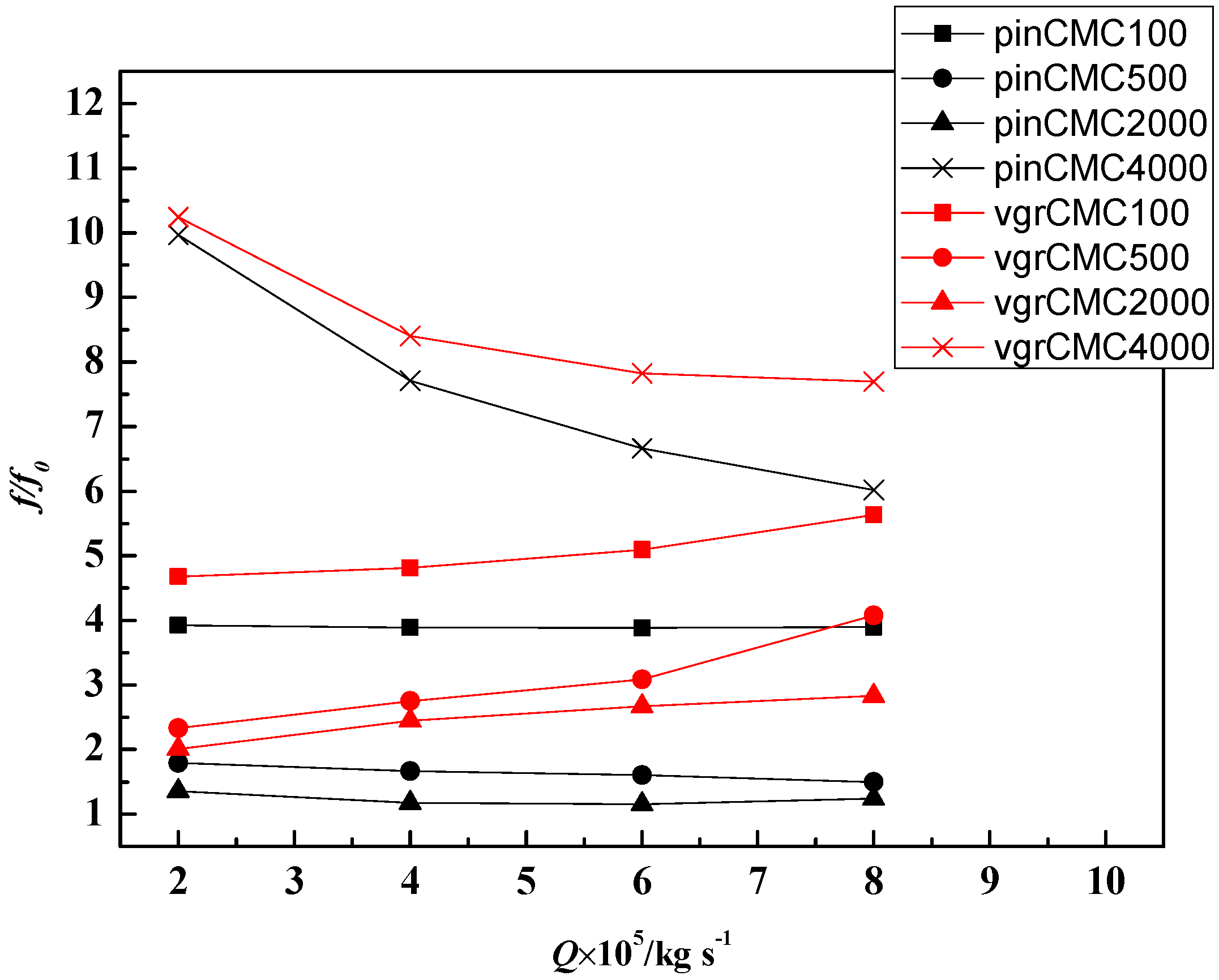
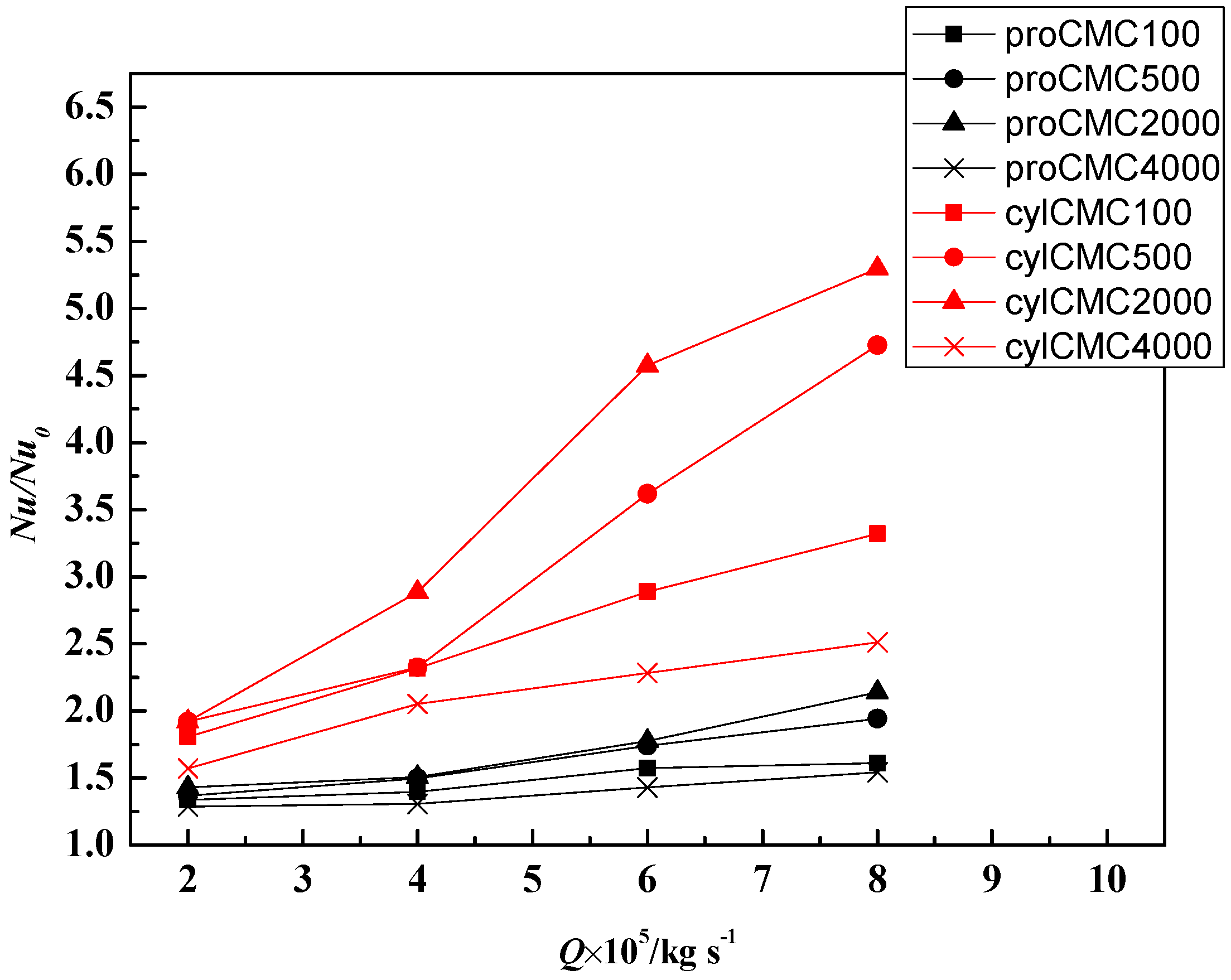
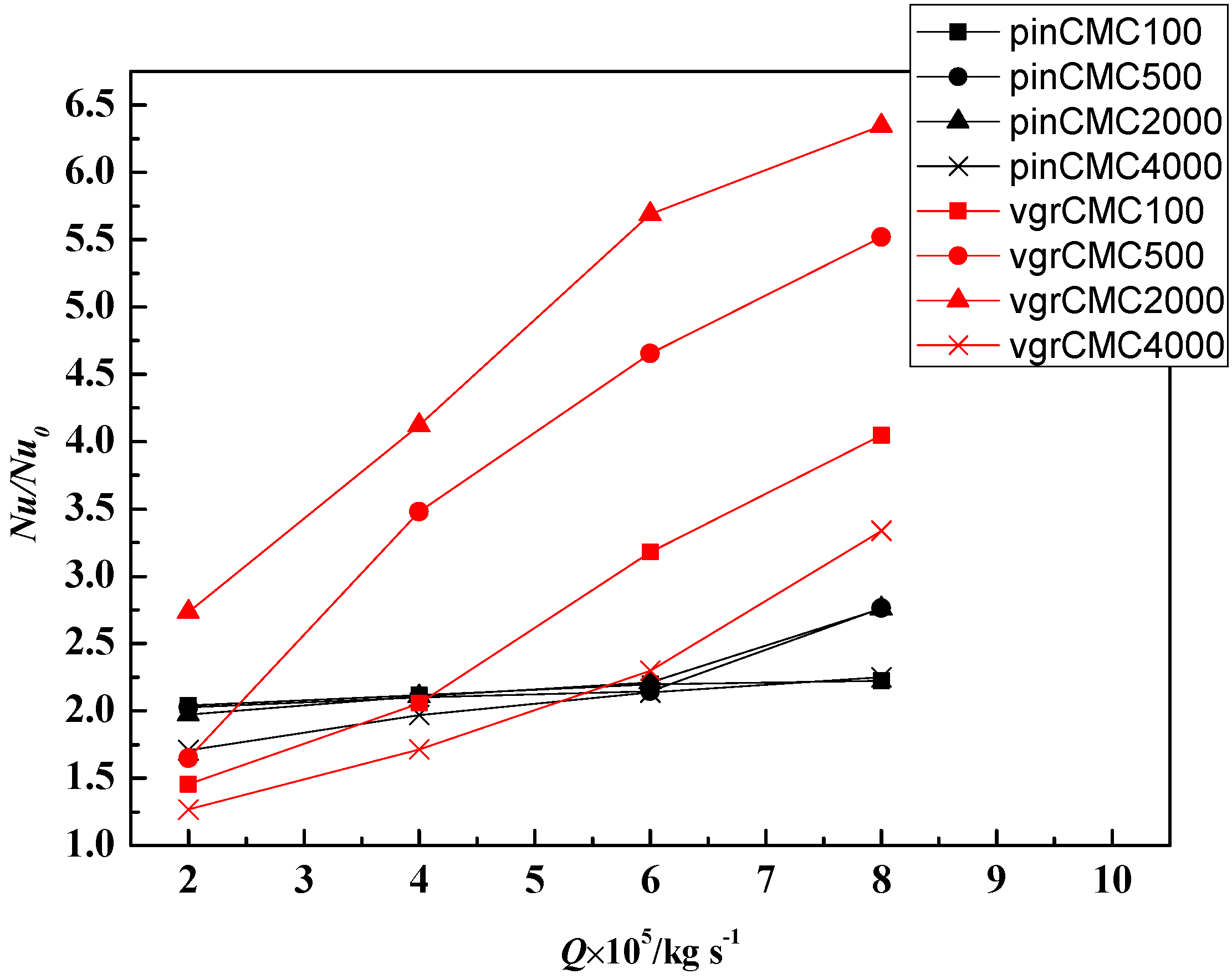
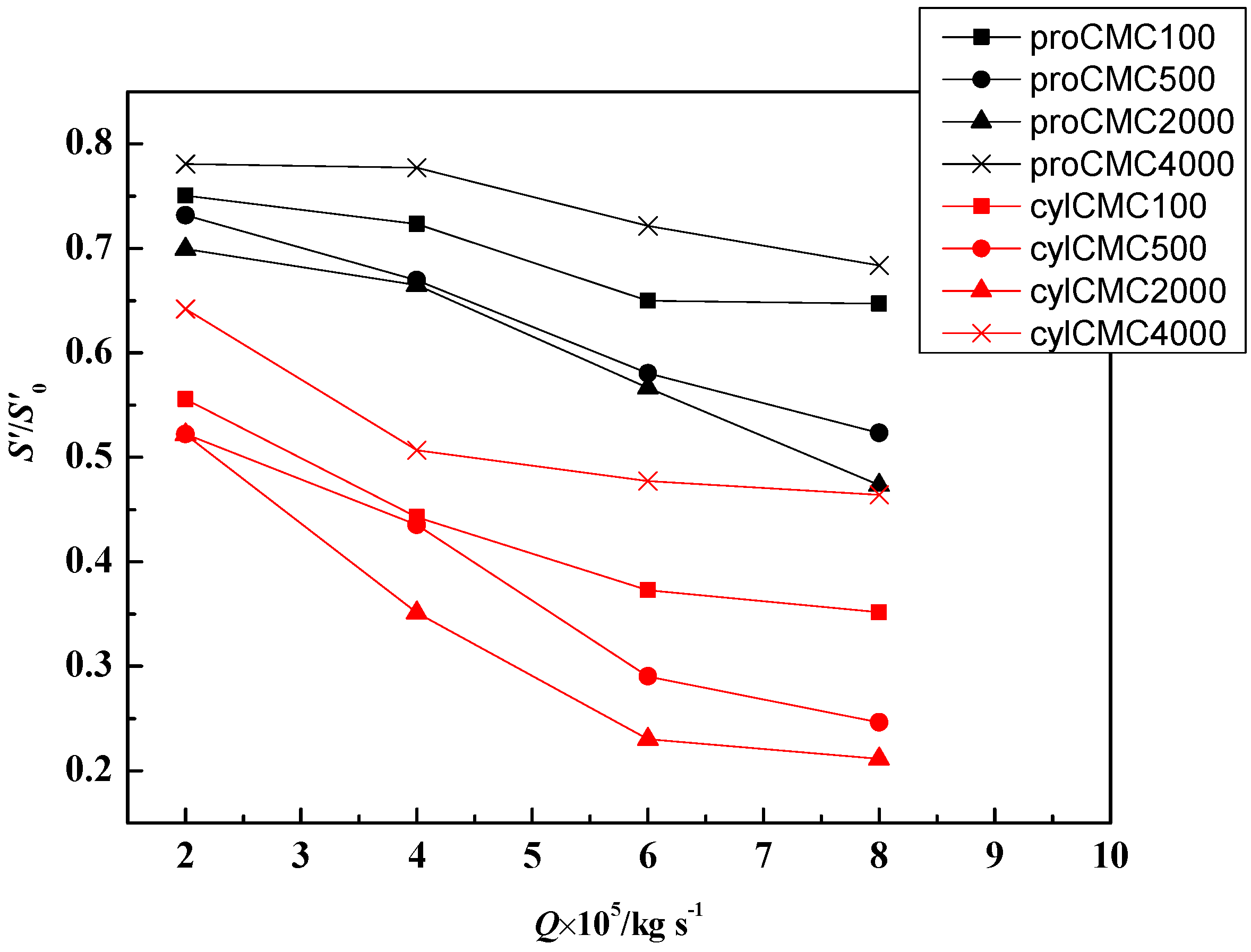
3.2. Flow Friction and Heat Transfer Performance Analysis
4. Conclusions
- (1)
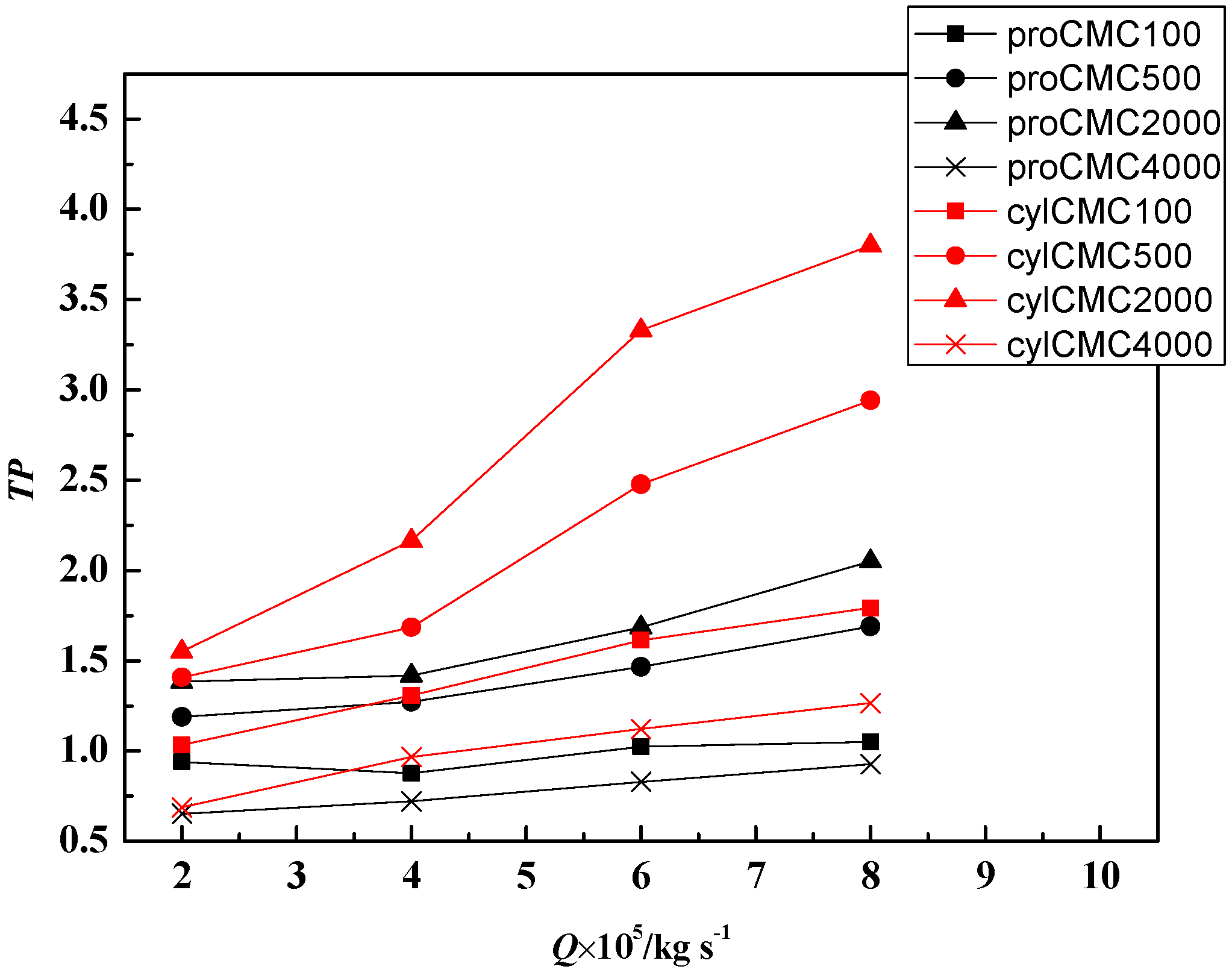
- The pin-fin microchannel has the most uniform temperature distribution on the structured walls and the area-average temperature of the pin-finned wall reaches the lowest point in the four different flow control structures at different CMC concentrations when the flow rate equals 2 × 10−5 kg/s. What’s more, as the flow rate further decreases, pin-finned microchannel should have the largest TP in the four flow control structures and is preferred to be selected.
- (2)
- The microchannel with protrusion has the minimum relative Fanning friction factor f/f0 that just slightly larger than smoothing rectangular microchannel with water, but Nu/Nu0 increases up to 2 in these cases, so protrusion can be selected if the pressure drops are strictly limited in some cases. And also, the protrusion is preferred to be selected in low flow rate cases.
- (3)
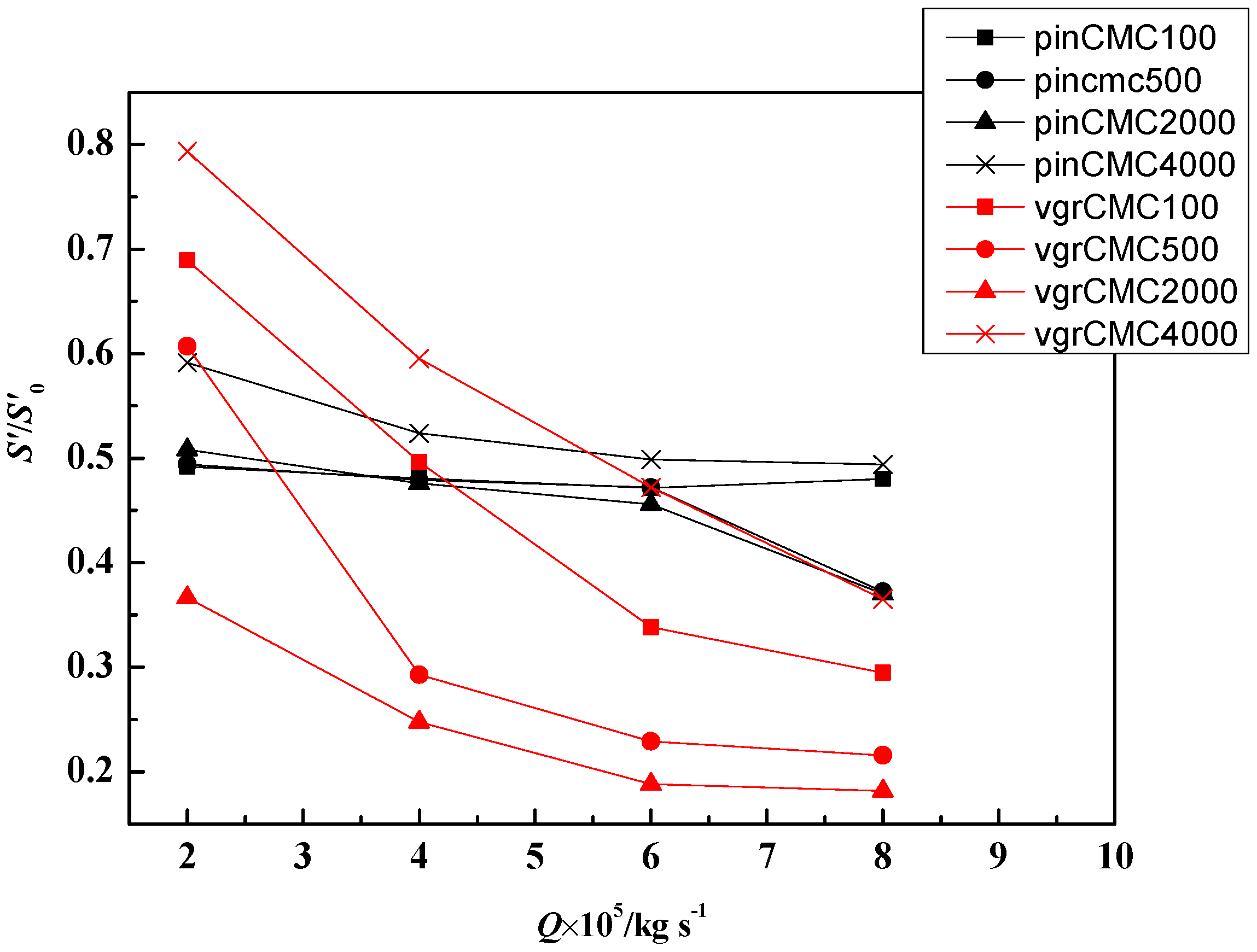
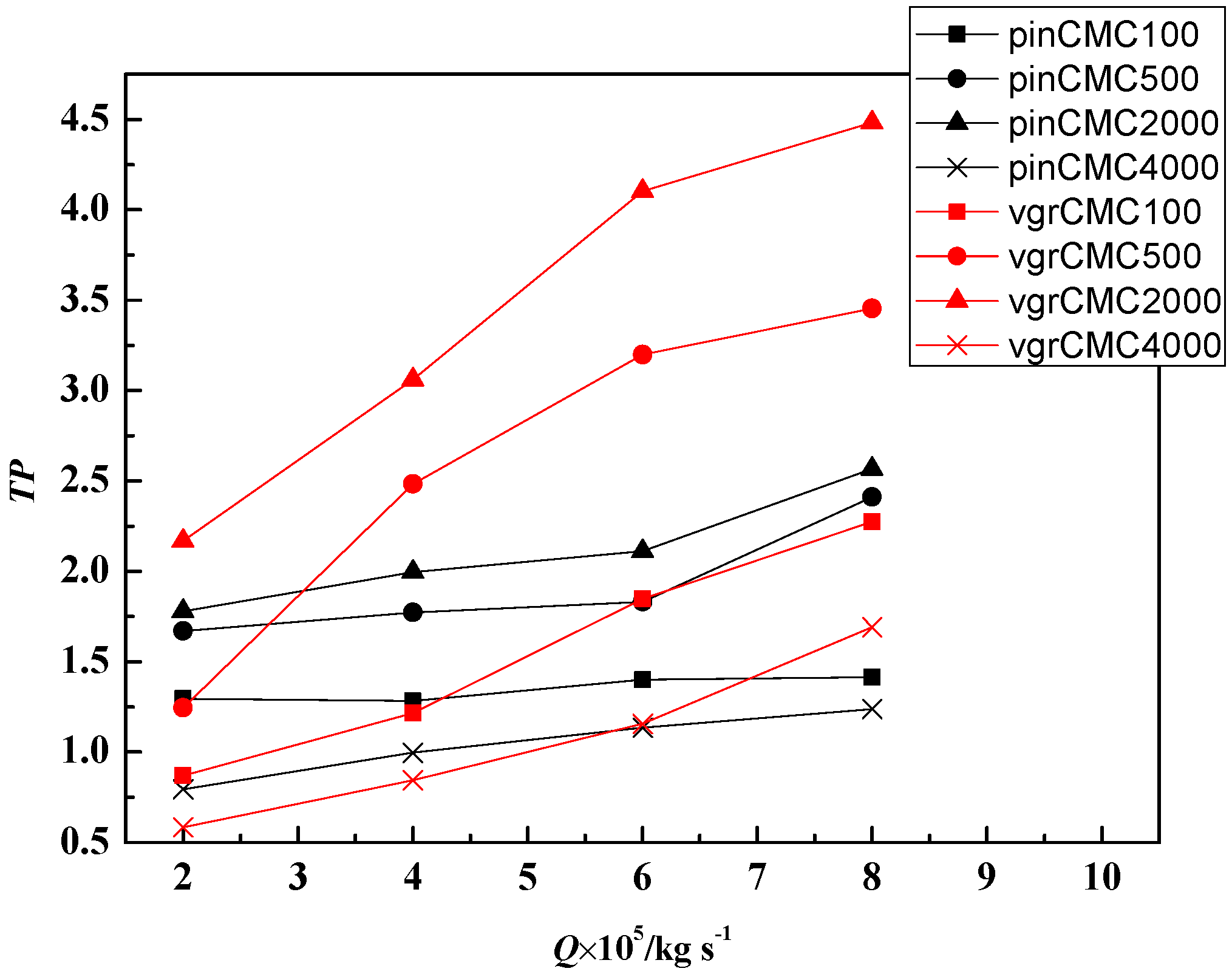
- The V-groove microchannel has the minimum S’/S0’ and maximum TP when flow rates larger than 2 × 10−5 kg/s at different CMC concentrations, and can be selected in some cases need large heat removal with high flow rate and pressure drop.
- (4)
- The relative Fanning friction factor f/f0 has a minimum value when the CMC concentration increases and the minimum value of f/f0 is reached at CMC2000 in this study, and also, the Nu/Nu0 of CMC2000 cases is larger than that of other working substances in the four different structured microchannels. Combined with these two effects, 2000 ppm is the best CMC concentration in the four different microchannel and has both minimum f/f0 and maximum Nu/Nu0, and then minimum S’/S0’ and highest TP.
Author Contributions
Conflicts of Interest
Abbreviations
| Cp | specific heat (J·kg−1·K−1) |
| D | microchannel height (m) |
| Dh | hydraulic diameter (m) |
| f | fanning friction factor |
| K | consistency index (Pa·sn) |
| L | periodic length (m) |
| n | flow behavior index |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Q | mass flow rate (kg·s−1) |
| Q” | heat flux (W·m−2) |
| Re | Reynolds number |
| S’ | entropy generation (W·K−1·m−1) |
| SF’ | friction entropy generation (W·K−1·m−1) |
| ST’ | heat transfer entropy generation (W·K−1·m−1) |
| T | temperature (K) |
| TP | thermal performance |
| ∆P | pressure drop (Pa) |
| ∆T | temperature difference (K) |
| Greek Characters | |
| δ | flow control structures depth (m) |
| η | fluid viscosity |
| λ | thermal conductivity (W·m−1·K−1) |
| ρ | fluid density (kg·m−3) |
| Subscripts | |
| ave | average value |
| f | fluid |
| w | wall |
References
- Kandlikar, S.; Garimella, S.; Li, D.; Colin, S.; King, M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zhang, D.; Zheng, L.; Xie, G.; Xie, Y. An experimental study on heat transfer enhancement of non-newtonian fluid in a rectangular channel with dimples/protrusions. J. Electron. Packag. 2014, 136, 021005. [Google Scholar] [CrossRef]
- Li, P.; Xie, Y.; Zhang, D. Laminar flow and forced convective heat transfer of shear-thinning power-law fluids in dimpled and protruded microchannels. Int. J. Heat Mass Transf. 2016, 99, 372–382. [Google Scholar] [CrossRef]
- Naphon, P.; Kornkumjayrit, K. Numerical analysis on the fluid flow and heat transfer in the channel with V-shaped wavy lower plate. Int. Commun. Heat Mass Transf. 2008, 35, 839–843. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Peng, H.-S. Numerical study of pin-fin heat sink with un-uniform fin height design. Int. J. Heat Mass Transf. 2008, 51, 4788–4796. [Google Scholar] [CrossRef]
- Liu, M.; Liu, D.; Xu, S.; Chen, Y. Experimental study on liquid flow and heat transfer in micro square pin fin heat sink. Int. J. Heat Mass Transf. 2011, 54, 5602–5611. [Google Scholar] [CrossRef]
- Huang, C.-H.; Chen, Y.-H. An impingement heat sink module design problem in determining simultaneously the optimal non-uniform fin widths and heights. Int. J. Heat Mass Transf. 2014, 73, 627–633. [Google Scholar] [CrossRef]
- Mamourian, M.; Shirvan, K.M.; Ellahi, R.; Rahimi, A.B. Optimization of mixed convection heat transfer with entropy generation in a wavy surface square lid-driven cavity by means of Taguchi approach. Int. J. Heat Mass Transf. 2016, 102, 544–554. [Google Scholar] [CrossRef]
- Gong, L.; Kota, K.; Tao, W.; Joshi, Y. Parametric numerical study of flow and heat transfer in microchannels with wavy walls. J. Heat Transf. 2011, 133, 051702. [Google Scholar] [CrossRef]
- Gong, L.J.; Kota, K.; Tao, W.; Joshi, Y. Thermal performance of microchannels with wavy walls for electronics cooling. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 1029–1035. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Z.; Shen, Z.; Zhang, D. Numerical Investigation of Non-Newtonian Flow and Heat Transfer Characteristics in Rectangular Tubes with Protrusions. Math. Probl. Eng. 2015, 2015, 121048. [Google Scholar] [CrossRef]
- Roth, R.; Lenk, G.; Cobry, K.; Woias, P. Heat transfer in freestanding microchannels with in-line and staggered pin fin structures with clearance. Int. J. Heat Mass Transf. 2013, 67, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Yuan, S.; Tan, S.K. Flow development in curved rectangular ducts with continuously varying curvature. Exp. Therm. Fluid Sci. 2016, 75. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A.; Ellahi, R.; Aziz, S. Non-newtonian nanofluid flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Barkhordari, M.; Etemad, S.G. Numerical study of slip flow heat transfer of non-Newtonian fluids in circular microchannels. Int. J. Heat Fluid Flow 2007, 28, 1027–1033. [Google Scholar] [CrossRef]
- Peixinho, J.; Desaubry, C.; Lebouche, M. Heat transfer of a non-Newtonian fluid (Carbopol aqueous solution) in transitional pipe flow. Int. J. Heat Mass Transf. 2008, 51, 198–209. [Google Scholar] [CrossRef]
- Ternik, P. Planar sudden symmetric expansion flows and bifurcation phenomena of purely viscous shear-thinning fluids. J. Non-Newton. Fluid Mech. 2009, 157, 15–25. [Google Scholar] [CrossRef]
- Manica, R.; De Bortoli, A. Simulation of sudden expansion flows for power-law fluids. J. Non-Newton. Fluid Mech. 2004, 121, 35–40. [Google Scholar] [CrossRef]
- Ellahi, R.; Shivanian, E.; Abbasbandy, S.; Hayat, T. Numerical study of magnetohydrodynamics generalized Couette flow of Eyring-Powell fluid with heat transfer and slip condition. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1433–1445. [Google Scholar] [CrossRef]
- Ellahi, R.; Rahman, S.U.; Gulzar, M.M.; Nadeem, S.; Vafai, K. A Mathematical Study of Non-Newtonian Micropolar Fluid in Arterial Blood Flow Through Composite Stenosis. Appl. Math. Inf. Sci. 2014, 8, 1567–1573. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Nitiapiruk, P.; Mahian, O. Performance characteristics of a microchannel heat sink using TiO2/water nanofluid and different thermophysical models. Int. Commun. Heat Mass Transf. 2013, 47, 98–104. [Google Scholar] [CrossRef]
- Nejat, A.; Mirzakhalili, E.; Aliakbari, A.; Niasar, M.S.F.; Vahidkhah, K. Non-Newtonian power-law fluid flow and heat transfer computation across a pair of confined elliptical cylinders in the line array. J. Non-Newton. Fluid Mech. 2012, 171, 67–82. [Google Scholar] [CrossRef]
- Soares, A.; Ferreira, J.; Chhabra, R. Flow and forced convection heat transfer in crossflow of non-Newtonian fluids over a circular cylinder. Ind. Eng. Chem. Res. 2005, 44, 5815–5827. [Google Scholar] [CrossRef]
- Xie, Y.; Zheng, L.; Zhang, D.; Xie, G. Entropy Generation and Heat Transfer Performances of Al2O3-Water Nanofluid Transitional Flow in Rectangular Channels with Dimples and Protrusions. Entropy 2016, 18, 148. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Endoscopic Effects with Entropy Generation Analysis in Peristalsis for the Thermal Conductivity of H2O + Cu Nanofluid. J. Appl. Fluid Mech. 2016, 9, 1721–1730. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Li, P.; Xie, Y.; Zhang, D.; Xie, G. Heat Transfer Enhancement and Entropy Generation of Nanofluids Laminar Convection in Microchannels with Flow Control Devices. Entropy 2016, 18, 134. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A.; Khan, A.A. The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl. Nanosci. 2016, 6, 641–651. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Peristaltic flow with thermal conductivity of H2O + Cu nanofluid and entropy generation. Results Phys. 2015, 5, 115–124. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Li, P.; Zhang, D.; Xie, Y. Heat transfer and flow analysis of Al2O3-water nanofluids in microchannel with dimple and protrusion. Int. J. Heat Mass Transf. 2014, 73, 456–467. [Google Scholar] [CrossRef]

| Property | Value |
|---|---|
| Density (ρ) | 1000/kg·m−3 |
| Specific heat (Cp) | 4100/J·kg−1·K−1 |
| Thermal conductivity (λ) | 0.7/W·m−1·K−1 |
| Concentration/ppm | K × 103/Pa·sn | n |
|---|---|---|
| 100 | 3.83 | 0.9512 |
| 500 | 8.49 | 0.8229 |
| 2000 | 27.92 | 0.7051 |
| 4000 | 657.2 | 0.6161 |
| Nodes | Nu | Difference % | f | Difference % | |
|---|---|---|---|---|---|
| 1 | 387,840 | 5.617 | 2.831 | 0.0542 | 3.15 |
| 2 | 794,880 | 5.776 | 1.143 | 0.0559 | 2.15 |
| 3 | 1,160,493 | 5.842 | 0.068 | 0.0571 | 0.35 |
| 4 | 1,608,960 | 5.846 | - | 0.0573 | - |
| fluids | CMC100 | CMC500 | CMC2000 | CMC4000 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q × 105/kg·s−1 | 2 | 4 | 6 | 8 | 2 | 4 | 6 | 8 | 2 | 4 | 6 | 8 | 2 | 4 | 6 | 8 |
| protrusion | n | y | y | y | y | y | y | y | y | y | y | y | n | n | n | y |
| Item | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Q × 105/kg·s−1 | 2.0 | 4.0 | 6.0 | 8.0 |
| ∆p0/Pa | 1713 | 3436 | 5174 | 6930 |
| Nu0 | 4.30 | 4.33 | 4.35 | 4.38 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Zhang, D.; Xie, Y.; Xie, G. Heat Transfer and Entropy Generation of Non-Newtonian Laminar Flow in Microchannels with Four Flow Control Structures. Entropy 2016, 18, 302. https://doi.org/10.3390/e18080302
Yang K, Zhang D, Xie Y, Xie G. Heat Transfer and Entropy Generation of Non-Newtonian Laminar Flow in Microchannels with Four Flow Control Structures. Entropy. 2016; 18(8):302. https://doi.org/10.3390/e18080302
Chicago/Turabian StyleYang, Ke, Di Zhang, Yonghui Xie, and Gongnan Xie. 2016. "Heat Transfer and Entropy Generation of Non-Newtonian Laminar Flow in Microchannels with Four Flow Control Structures" Entropy 18, no. 8: 302. https://doi.org/10.3390/e18080302
APA StyleYang, K., Zhang, D., Xie, Y., & Xie, G. (2016). Heat Transfer and Entropy Generation of Non-Newtonian Laminar Flow in Microchannels with Four Flow Control Structures. Entropy, 18(8), 302. https://doi.org/10.3390/e18080302