1. Introduction
The Expectation Maximization (EM) algorithm is a well-known method for calculating the maximum likelihood estimator of a model where incomplete data is considered. For example, when working with mixture models in the context of clustering, the labels or classes of observations are unknown during the training phase. Several variants of the EM algorithm were proposed (see [
1]). Another way to look at the EM algorithm is as a proximal point problem (see [
2,
3]). Indeed, one may rewrite the conditional expectation of the complete log-likelihood as a sum of the log-likelihood function and a distance-like function over the conditional densities of the labels provided an observation. Generally, the proximal term has a regularization effect in the sense that a proximal point algorithm is more stable and frequently outperforms classical optimization algorithms (see [
4]). Chrétien and Hero [
5] prove superlinear convergence of a proximal point algorithm derived from the EM algorithm. Notice that EM-type algorithms usually enjoy no more than linear convergence.
Taking into consideration the need for robust estimators, and the fact that the maximum likelihood estimator (MLE) is the least robust estimator among the class of divergence-type estimators that we present below, we generalize the EM algorithm (and the version of Tseng [
2]) by replacing the log-likelihood function by an estimator of a
divergence between the
true distribution of the data and the model. A
–divergence in the sense of Csiszár [
6] is defined in the same way as [
7] by:
where
is a nonnegative strictly convex function. Examples of such divergences are: the Kullback–Leibler (KL) divergence , the modified KL divergence, the Hellinger distanceamong others. All these well-known divergences belong to the class of Cressie-Read functions [
8] defined by
for
respectively. For
, the limit is calculated, and we denote
for the case of the modified KL and
for the KL.
Since the
divergence calculus uses the unknown true distribution, we need to estimate it. We consider the dual estimator of the divergence introduced independently by [
9,
10]. The use of this estimator is motivated by many reasons. Its minimum coincides with the MLE for
. In addition, it has the same form for discrete and continuous models, and does not consider any partitioning or smoothing.
Let
be a parametric model with
, and denote
as the
true set of parameters. Let
be the Lebesgue measure defined on
. Suppose that
, the probability measure
is absolutely continuous with respect to
and denote
the corresponding probability density. The dual estimator of the
divergence given an
sample
is given by:
with
. Al Mohamad [
11] argues that this formula works well under the model; however, when we are not, this quantity largely underestimates the divergence between the true distribution and the model, and proposes the following modification:
where
is the Rosenblatt–Parzen kernel estimate with window parameter
w. Whether it is
, or
, the minimum dual
divergence estimator (MD
DE) is defined as the argument of the infimum of the dual approximation:
Asymptotic properties and consistency of these two estimators can be found in [
7,
11]. Robustness properties were also studied using the influence function approach in [
11,
12]. The kernel-based MD
DE (5) seems to be a
better estimator than the classical MD
DE (4) in the sense that the former is robust whereas the later is generally not. Under the model, the estimator given by (4) is, however, more efficient, especially when the true density of the data is unbounded. More investigation is needed in the context of unbounded densities, since we may use asymmetric kernels in order to improve the efficiency of the kernel-based MD
DE, see [
11] for more details.
In this paper, we propose calculation of the MD
DE using an iterative procedure based on the work of Tseng [
2] on the log-likelihood function. This procedure has the form of a proximal point algorithm, and extends the EM algorithm. Our convergence proof demands some regularity (continuity and differentiability) of the estimated divergence with respect to the parameter vector
φ) which is not simply checked using (2). Recent results in the book of Rockafellar and Wets [
13] provide sufficient conditions to prove continuity and differentiability of supremal functions of the form of (2) with respect to
φ. Differentiability with respect to
φ still remains a very hard task; therefore, our results cover cases when the objective function is not differentiable.
The paper is organized as follows: in
Section 2, we present the general context. We also present the derivation of our algorithm from the EM algorithm and passing by Tseng’s generalization. In
Section 3, we present some convergence properties. We discuss in
Section 4 a variant of the algorithm with a theoretical global infimum, and an example of the two-Gaussian mixture model and a convergence proof of the EM algorithm in the spirit of our approach. Finally,
Section 5 contains simulations confirming our claim about the efficiency and the robustness of our approach in comparison with the MLE. The algorithm is also applied to the so-called minimum density power divergence (MDPD) introduced by [
14].
3. Some Convergence Properties of
We show here how, according to some possible situations, one may prove convergence of the algorithm defined by (11). Let
be a given initialization, and define
which we suppose to be a subset of
. The idea of defining this set in this context is inherited from the paper Wu [
16], which provided the first
correct proof of convergence for the EM algorithm. Before going any further, we recall the following definition of a (generalized) stationary point.
Definition 1. Let be a real valued function. If f is differentiable at a point such that , we then say that is a stationary point of f. If f is not differentiable at but the subgradient of f at , say , exists such that , then is called a generalized stationary point of f.
Remark 1. In the whole paper, the subgradient is defined for any function not necessarily convex (see Definition 8.3) in [13] for more details. We will be using the following assumptions:
- A0.
Functions are lower semicontinuous;
- A1.
Functions and are defined and continuous on, respectively, and ;
- AC.
Function is defined and continuous on Φ;
- A2.
is a compact subset of int;
- A3.
for all .
Recall also that we suppose that We relax the convexity assumption of function ψ. We only suppose that ψ is nonnegative and iff . In addition, if .
Continuity and differentiability assumptions of function
for the case of (3) can be easily checked using Lebesgue theorems. The continuity assumption for the case of (2) can be checked using Theorem 1.17 or Corollary 10.14 in [
13]. Differentiability can also be checked using Corollary 10.14 or Theorem 10.31 in the same book. In what concerns
, continuity and differentiability can be obtained merely by fulfilling Lebesgue theorems conditions. When working with mixture models, we only need the continuity and differentiability of
ψ and functions
. The later is easily deduced from regularity assumptions on the model. For assumption A2, there is no universal method, see
Section 4.2 for an Example. Assumption A3 can be checked using Lemma 2 in [
2].
We start the convergence properties by proving that the objective function decreases alongside the the sequence , and give a possible set of conditions for the existence of the sequence .
Proposition 1. (a) Assume that the sequence is well defined in Φ, then , and (b) . (c) Assume A0 and A2 are verified, then the sequence is defined and bounded. Moreover, the sequence converges.
Proof. We prove
. We have by definition of the arginf:
We use the fact that
for the right-hand side and that
for the left-hand side of the previous inequality. Hence,
.
We prove using the decreasing property previously proved in (a). We have by recurrence . The result follows directly by definition of .
We prove
by induction on
k. For
, clearly
is well defined since we choose it. The choice of the initial point
of the sequence may influence the convergence of the sequence. See the Example of the Gaussian mixture in
Section 4.2. Suppose, for some
, that
exists. We prove that the infimum is attained in
. Let
be any vector at which the value of the optimized function has a value less than its value at
, i.e.,
. We have:
The first line follows from the non negativity of . As , then . Thus, the infimum can be calculated for vectors in instead of Φ. Since is compact and the optimized function is lower semicontinuous (the sum of two lower semicontinuous functions), then the infimum exists and is attained in . We may now define to be a vector whose corresponding value is equal to the infimum.
Convergence of the sequence comes from the fact that it is non increasing and bounded. It is non increasing by virtue of (a). Boundedness comes from the lower semicontinuity of . Indeed, . The infimum of a proper lower semicontinuous function on a compact set exists and is attained on this set. Hence, the quantity exists and is finite. This ends the proof. □
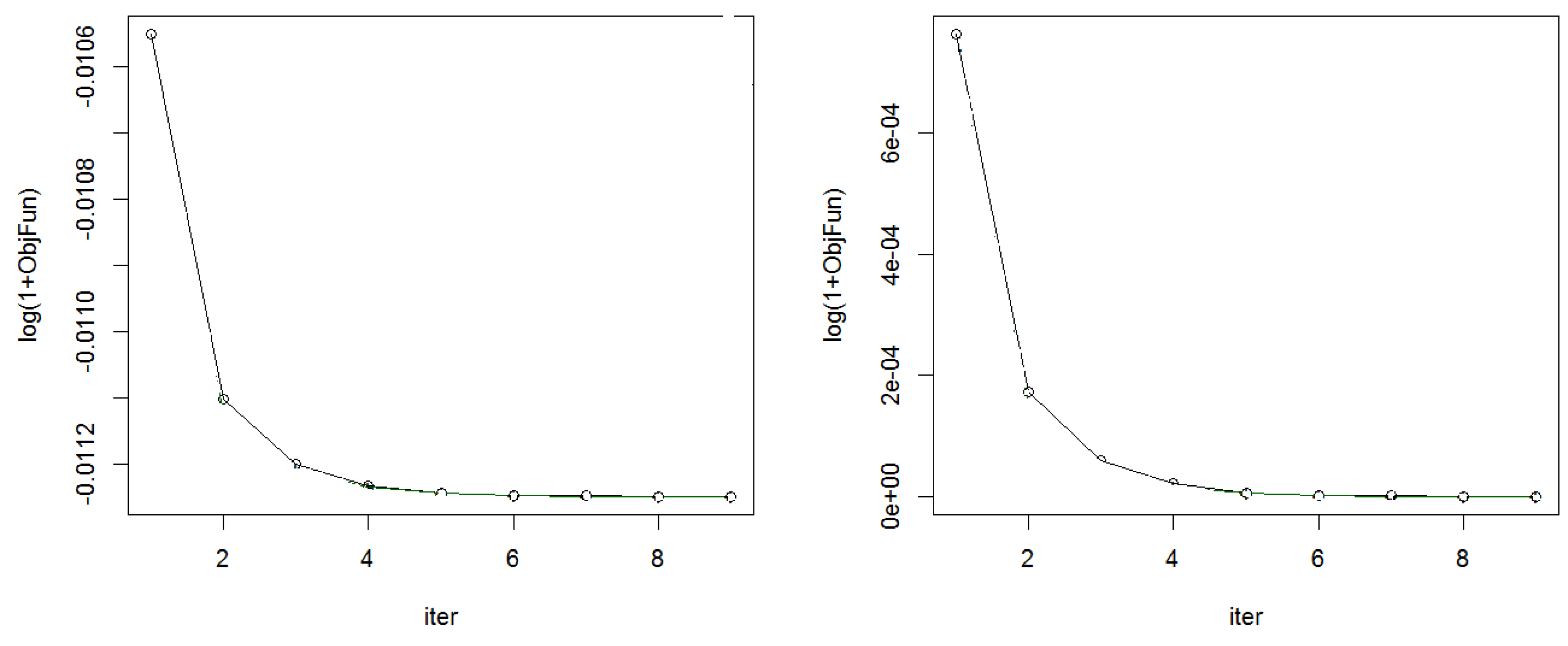
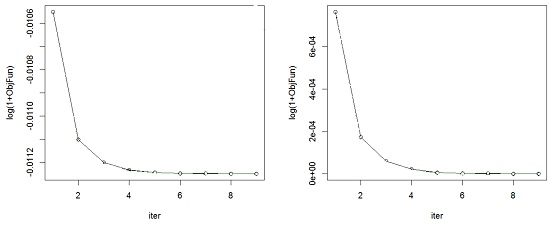
Compactness in part (c) can be replaced by inf-compactness of function and continuity of with respect to its first argument. The convergence of the sequence is an interesting property, since, in general, there is no theoretical guarantee, or it is difficult to prove that the whole sequence converges. It may also continue to fluctuate around a minimum. The decrease of the error criterion between two iterations helps us decide when to stop the iterative procedure.
Proposition 2. Suppose A1 verified, is closed and .- (a)
If AC is verified, then any limit point of is a stationary point of ;
- (b)
If AC is dropped, then any limit point of is a “generalized” stationary point of , i.e., zero belongs to the subgradient of calculated at the limit point.
Proof. We prove . Let be a convergent subsequence of which converges to . First, , because is closed and the subsequence is a sequence of elements of (proved in Proposition 1b).
Let us now show that the subsequence
also converges to
. We simply have:
Since and , we conclude that .
By definition of
, it verifies the infimum in recurrence (11), so that the gradient of the optimized function is zero:
Using the continuity assumptions A1 and AC of the gradients, one can pass to the limit with no problem:
However, the gradient
because (recall that
) for any
which is equal to zero since
. This implies that
.
We prove (b). We use again the definition of the arginf. As the optimized function is not necessarily differentiable at the points of the sequence
, a necessary condition for
to be an infimum is that 0 belongs to the subgradient of the function on
. Since
is assumed to be differentiable, the optimality condition is translated into:
Since
is continuous, then its subgradient is outer semicontinuous (see [
13] Chapter 8, Proposition 7). We use the same arguments presented in (a) to conclude the existence of two subsequences
and
which converge to the same limit
. By definition of outer semicontinuity, and since
, we have:
We want to prove that
. By definition of the (outer) limsup (see [
13] Chapter 4, Definition 1 or Chapter 5B):
In our scenario,
,
,
and
. The continuity of
with respect to both arguments and the fact that the two subsequences
and
converge to the same limit, imply that
. Hence,
. By inclusion (12), we get our result:
This ends the proof. □
The assumption
used in Proposition 2 is not easy to be checked unless one has a close formula of
. The following proposition gives a method to prove such assumption. This method seems simpler, but it is not verified in many mixture models (see
Section 4.2 for a counter Example).
Proposition 3. Assume that A1, A2 and A3 are verified, then . Thus, by Proposition 2 (according to whether AC is verified or not), any limit point of the sequence is a (generalized) stationary point of .
Proof. By contradiction, let us suppose that does not converge to 0. There exists a subsequence such that . Since belongs to the compact set , there exists a convergent subsequence such that . The sequence belongs to the compact set ; therefore, we can extract a further subsequence such that . Besides . Finally since the sequence is convergent, a further subsequence also converges to the same limit . We have proved the existence of a subsequence of such that does not converge to 0 and such that , with .
The real sequence
converges as proved in Proposition 1c. As a result, both sequences
and
converge to the same limit being subsequences of the same convergent sequence. In the proof of Proposition 1, we can deduce the following inequality:
which is also verified for any substitution of
k by
. By passing to the limit on k, we get
. However, the distance-like function
is nonnegative, so that it becomes zero. Using assumption A3,
implies that
. This contradicts the hypothesis that
does not converge to 0.
The second part of the Proposition is a direct result of Proposition 2. □
Corollary 1. Under assumptions of Proposition 3, the set of accumulation points of is a connected compact set. Moreover, if is strictly convex in the neighborhood of a limit point of the sequence , then the whole sequence converges to a local minimum of .
Proof. Since the sequence
is bounded and verifies
, then Theorem 28.1 in [
17] implies that the set of accumulation points of
is a connected compact set. It is not empty since
is compact. The remaining of the proof is a direct result of Theorem 3.3.1 from [
18]. The strict concavity of the objective function around an accumulation point is replaced here by the strict convexity of the estimated divergence. □
Proposition 3 and Corollary 1 describe what we may hope to get of the sequence . Convergence of the whole sequence is bound by a local convexity assumption in the neighborhood of a limit point. Although simple, this assumption remains difficult to be checked since we do not know where might be the limit points. In addition, assumption A3 is very restrictive, and is not verified in mixture models.
Propositions 2 and 3 were developed for the likelihood function in the paper of Tseng [
2]. Similar results for a general class of functions replacing
and
which may not be differentiable (but still continuous) are presented in [
3]. In these results, assumption A3 is essential. Although in [
18] this problem is avoided, their approach demands that the log-likelihood has
limit as
. This is simply not verified for mixture models. We present a similar method to the one in [
18] based on the idea of Tseng [
2] of using the set
which is valid for mixtures. We lose, however, the guarantee of consecutive decrease of the sequence
.
Proposition 4. Assume A1, AC and A2 verified. Any limit point of the sequence is a stationary point of . If AC is dropped, then 0 belongs to the subgradient of calculated at the limit point.
Proof. If converges to, say, , then the result falls simply from Proposition 2.
If does not converge. Since is compact and (proved in Proposition 1), there exists a subsequence such that . Let us take the subsequence . This subsequence does not necessarily converge; it is still contained in the compact , so that we can extract a further subsequence which converges to, say, . Now, the subsequence converges to , because it is a subsequence of . We have proved until now the existence of two convergent subsequences and with a priori different limits. For simplicity and without any loss of generality, we will consider these subsequences to be and , respectively.
Conserving previous notations, suppose that
and
. We use again inequality (13):
By taking the limits of the two parts of the inequality as
k tends to infinity, and using the continuity of the two functions, we have
Recall that under A1-2, the sequence
converges, so that it has the same limit for any subsequence, i.e.,
. We also use the fact that the distance-like function
is non negative to deduce that
. Looking closely at the definition of this divergence (10), we get that if the sum is zero, then each term is also zero since all terms are nonnegative. This means that:
The integrands are nonnegative functions, so they vanish almost everywhere with respect to the measure defined on the space of labels.
The conditional densities
are supposed to be positive (which can be ensured by a suitable choice of the initial point
), i.e.,
Hence,
On the other hand,
ψ is chosen in a way that
iff
. Therefore:
Since
is, by definition, an infimum of
, then the gradient of this function is zero on
. It results that:
Taking the limit on
k, and using the continuity of the derivatives, we get that:
Let us write explicitly the gradient of the second divergence:
We use now the identities (14), and the fact that
, to deduce that:
This entails using (15) that .
Comparing the proved result with the notation considered at the beginning of the proof, we have proved that the limit of the subsequence is a stationary point of the objective function. Therefore, the final step is to deduce the same result on the original convergent subsequence . This is simply due to the fact that is a subsequence of the convergent sequence , hence they have the same limit.
When assumption AC is dropped, similar arguments to those used in the proof of Proposition 2b. are employed. The optimality condition in (11) implies:
Function
is continuous, hence its subgradient is outer semicontinuous and:
By definition of the limsup:
In our scenario,
,
,
and
. We have proved above in this proof that
using only the convergence of
, inequality (13) and the properties of
. Assumption AC was not needed. Hence,
. This proves that
. Finally, using the inclusion (16), we get our result:
which ends the proof. □
The proof of the previous proposition is very similar to the proof of Proposition 2. The key idea is to use the sequence of conditional densities instead of the sequence . According to the application, one may be interested only in Proposition 1 or in Propositions 2–4. If one is interested in the parameters, Propositions 2 to 4 should be used, since we need a stable limit of . If we are only interested in minimizing an error criterion between the estimated distribution and the true one, Proposition 1 should be sufficient.