Entropy Generation on MHD Eyring–Powell Nanofluid through a Permeable Stretching Surface
Abstract
:1. Introduction
2. Mathematical Formulation
3. Physical Quantities of Interest
4. Numerical Method
5. Entropy Generation Analysis
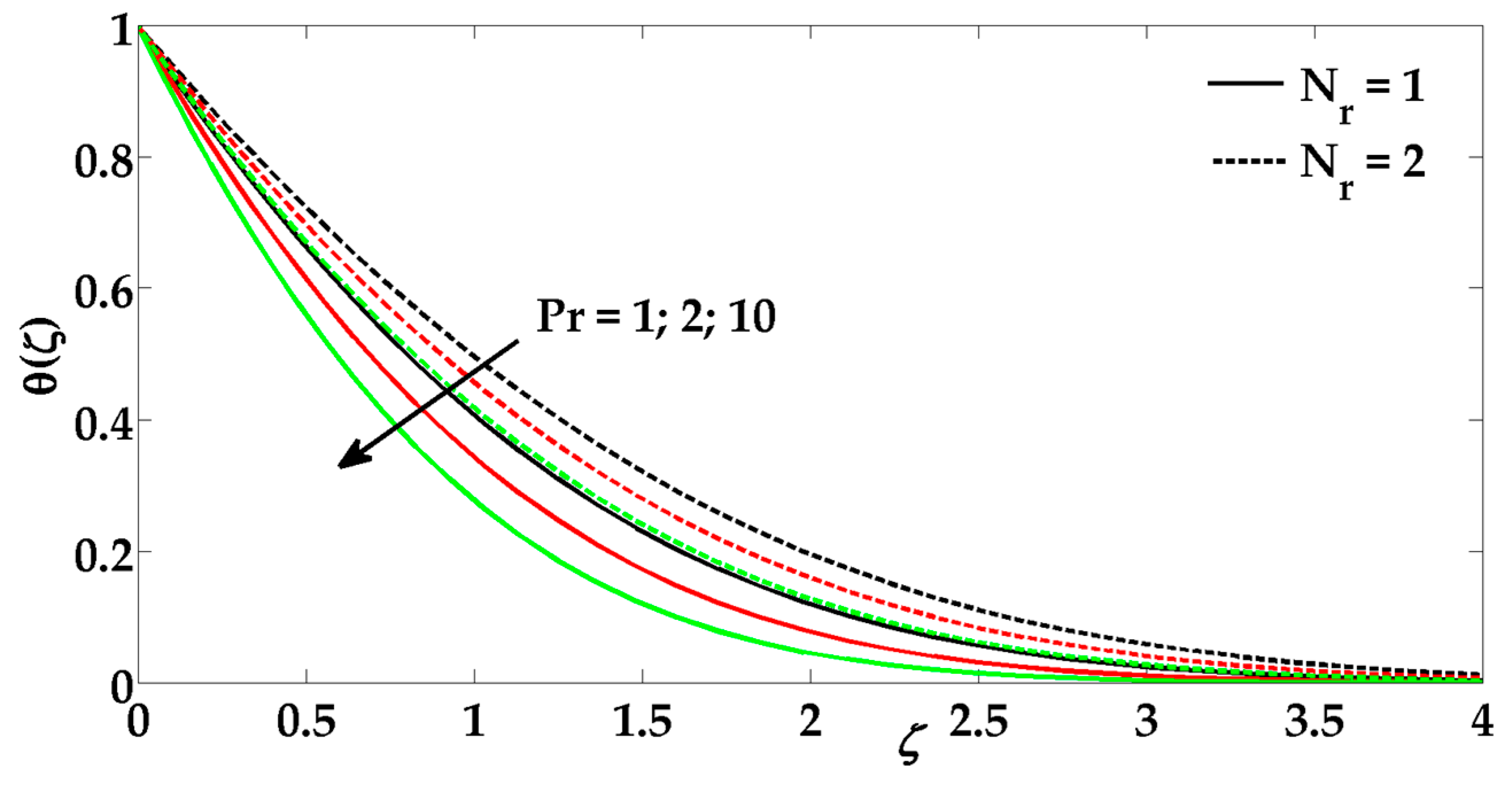
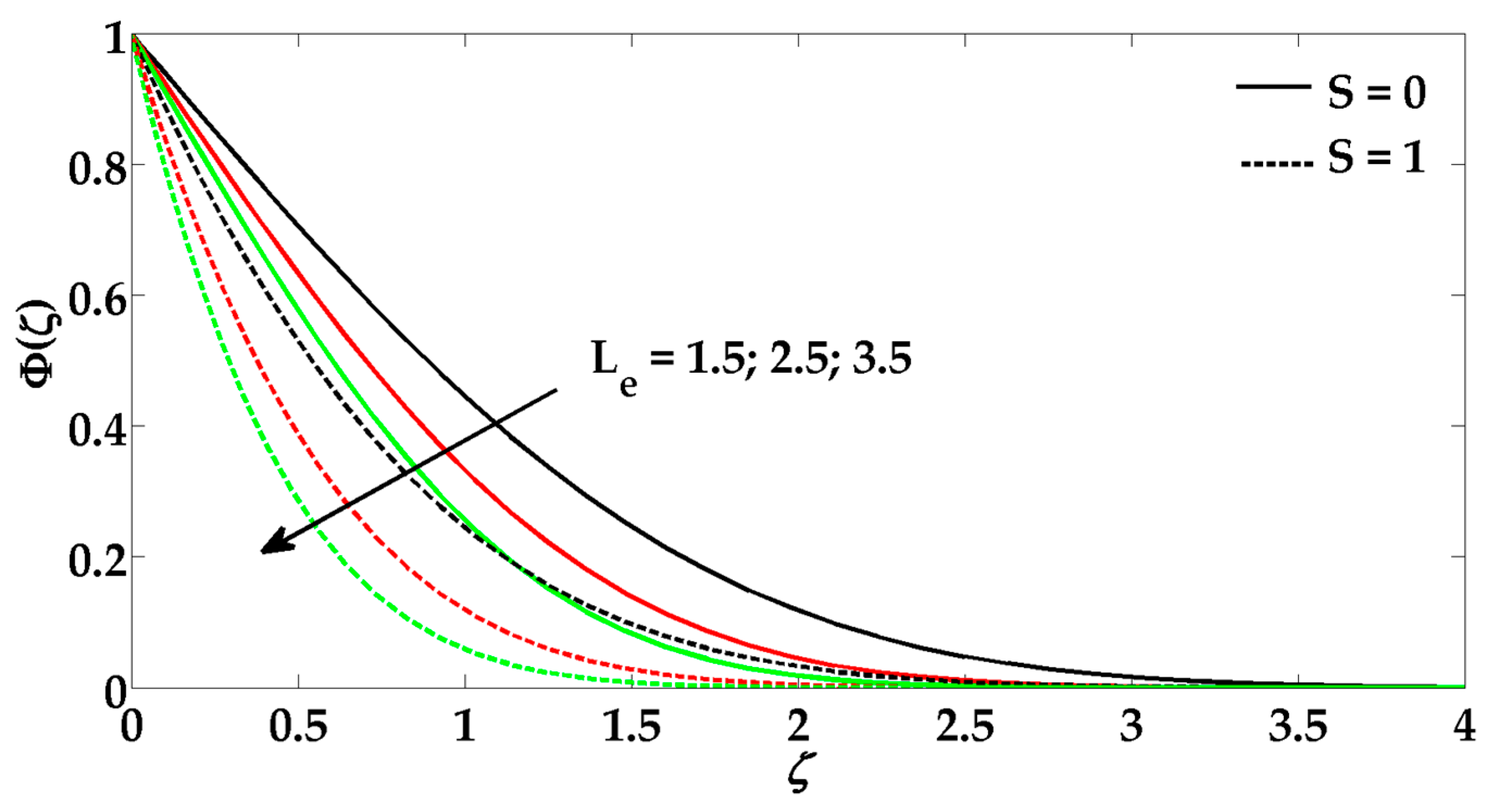
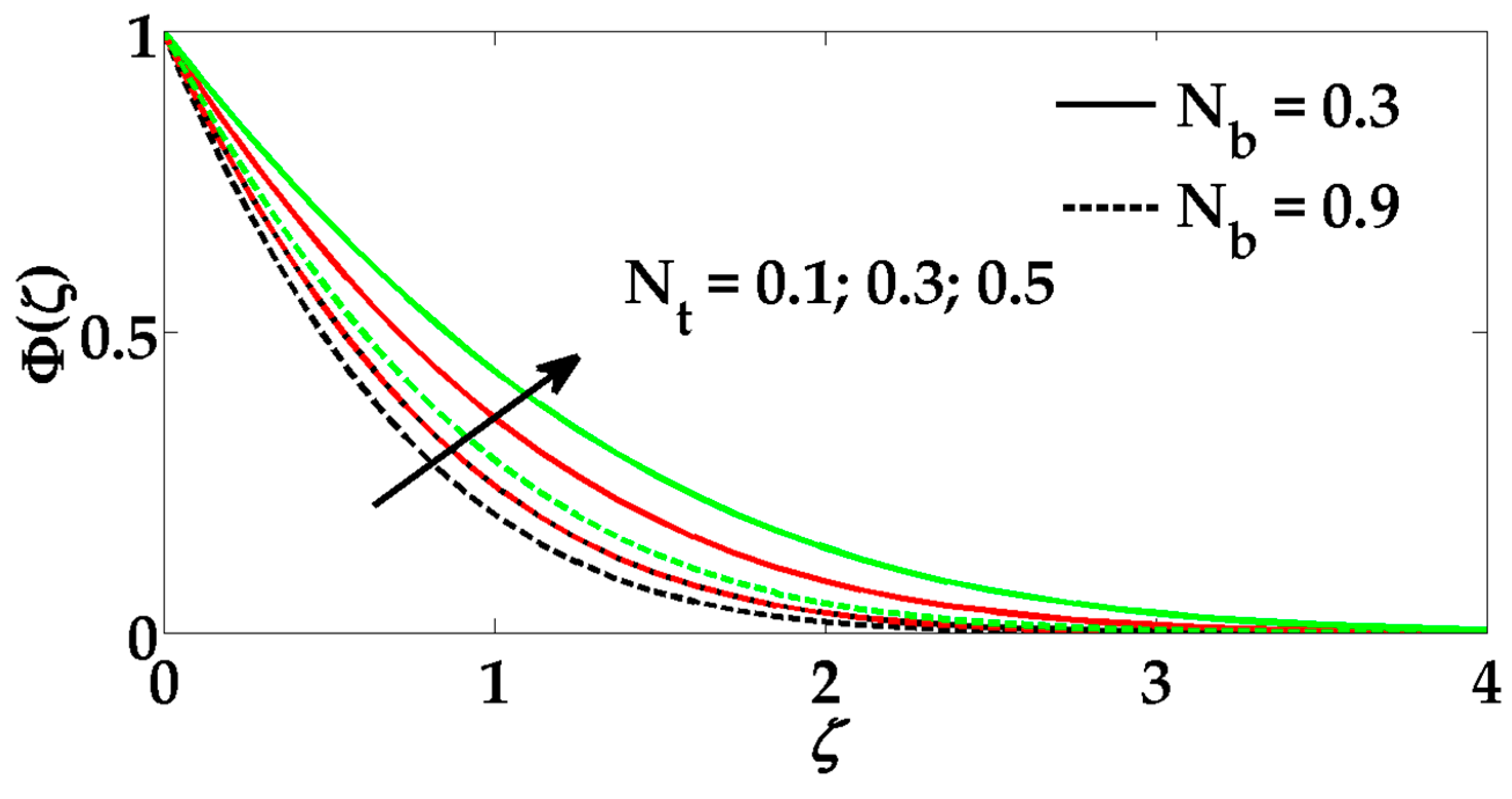
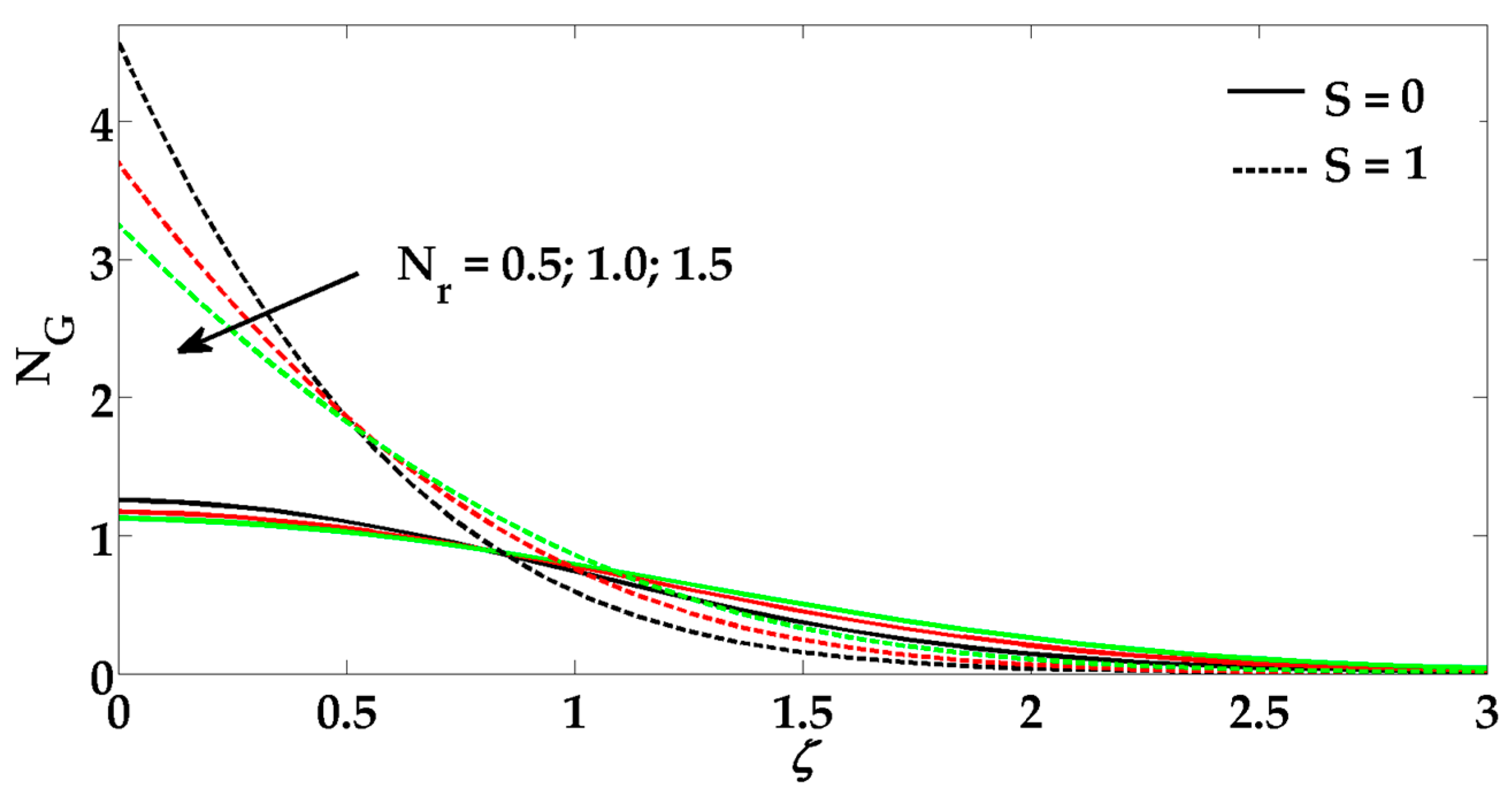
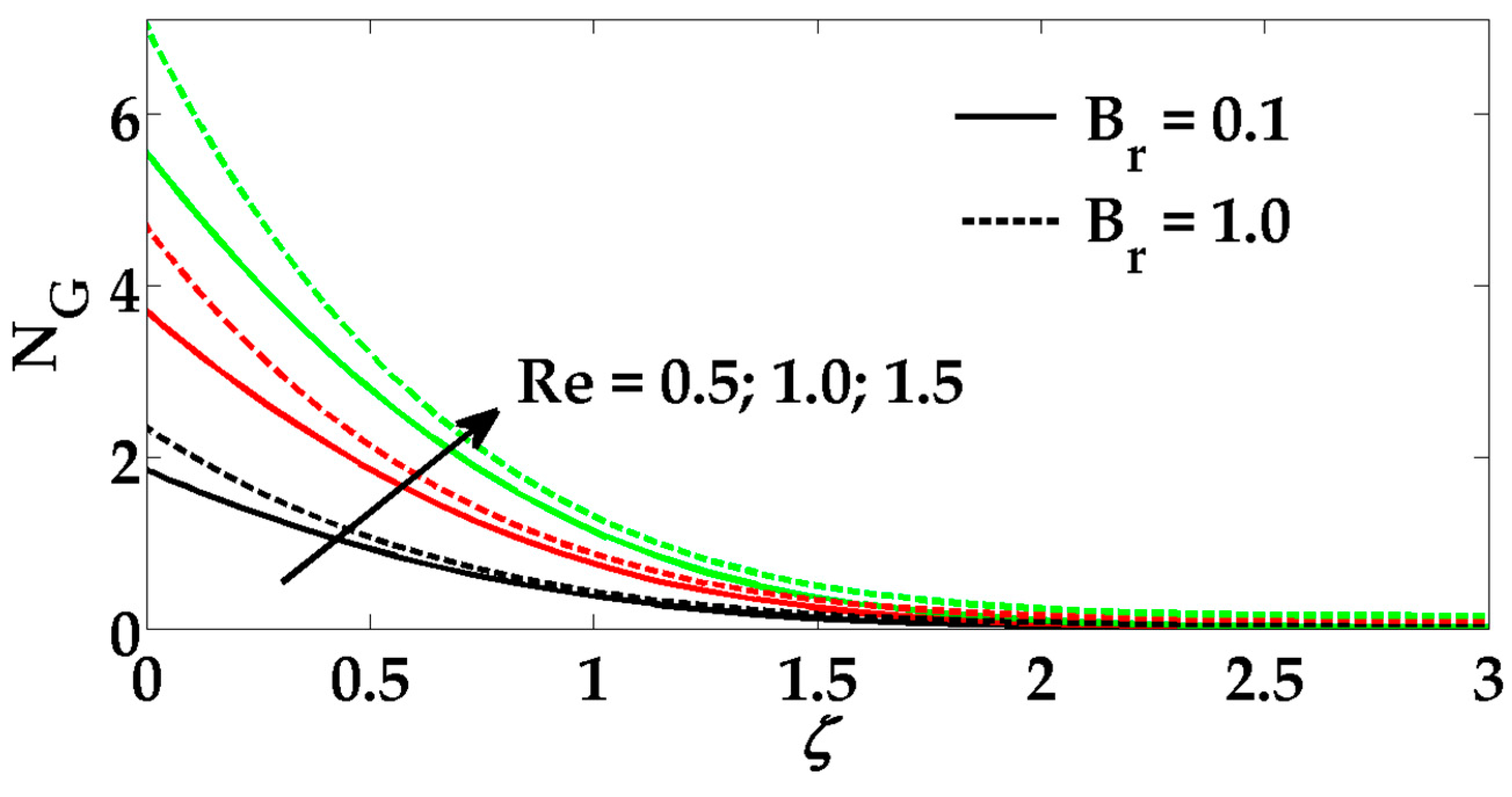
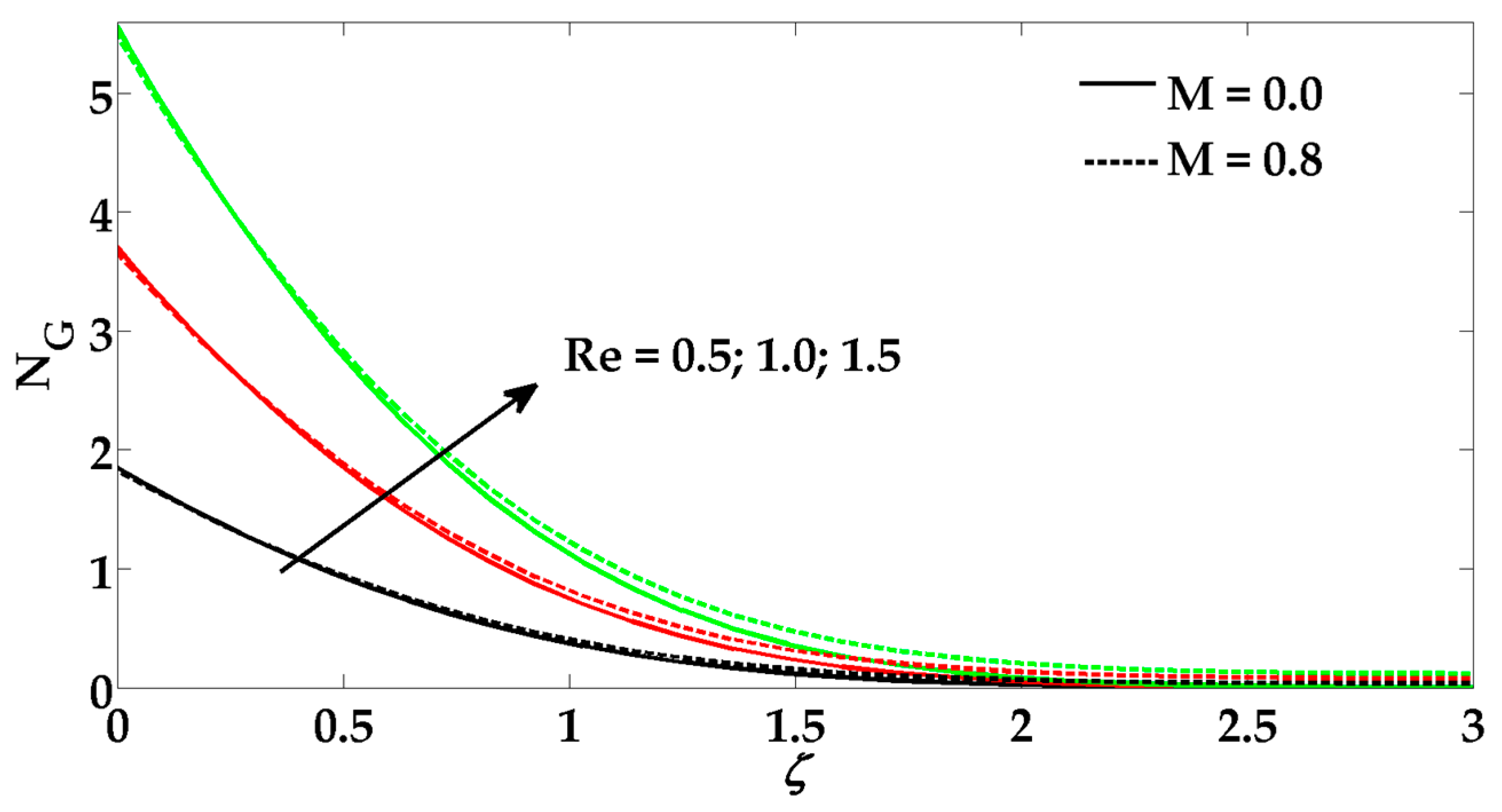
6. Results and Discussion
7. Conclusions
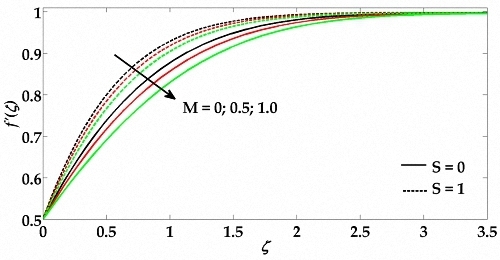
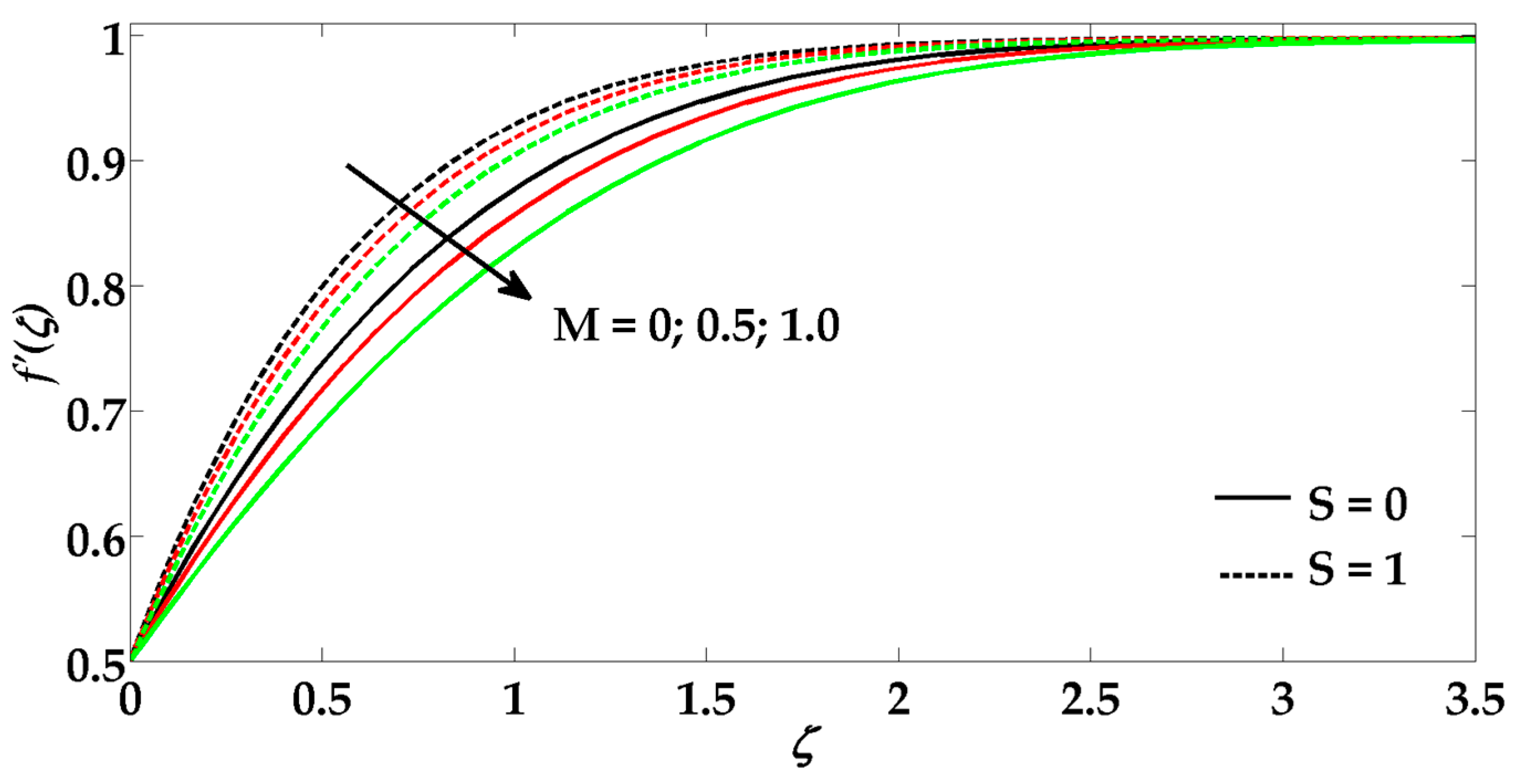
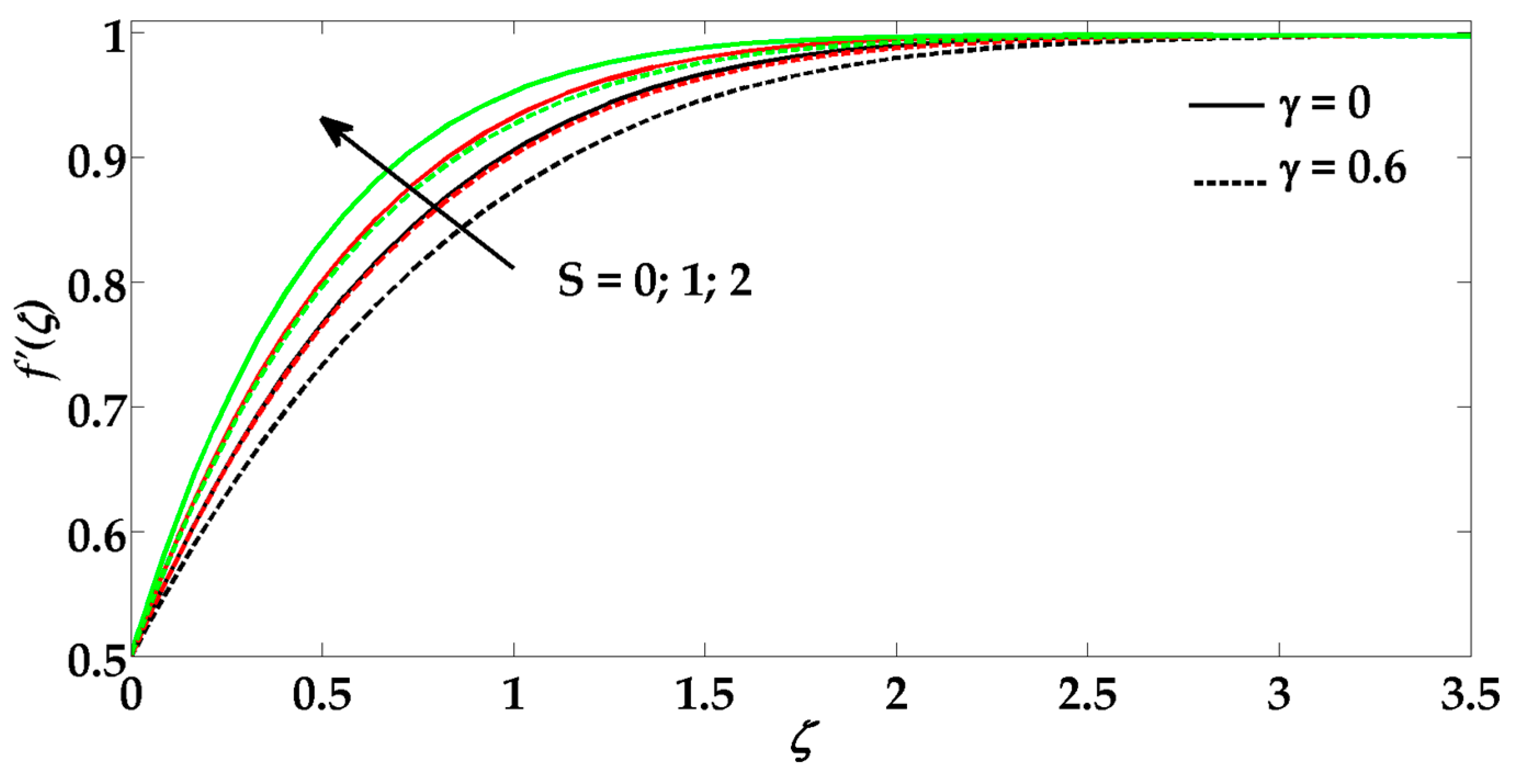
- The velocity of the fluid decreases due to an increment in the fluid parameter and Hartmann number.
- The entropy profile enhances all the physical parameters.
- The temperature profile increases due to an increment in the radiation parameter.
- The nanoparticle concentration increases for large values of the thermophoresis parameter.
- The nanoparticle concentration decreases due to a greater influence of the Lewis number.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Velocity components | |
| Cartesian coordinate | |
| Pressure | |
| Porosity parameter | |
| Reynolds number | |
| Dimensionless entropy number | |
| Time | |
| Prandtl number | |
| Mean absorption coefficient | |
| Suction/injection parameter | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Heat flux | |
| Lewis number | |
| Mass flux | |
| Fluid parameters | |
| Brinkman number | |
| Environmental temperature (K) | |
| Hartman number | |
| Magnetic field | |
| Radiation parameter | |
| Temperature and Concentration | |
| Acceleration due to gravity | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient |
Greek Symbol
| Thermal conductivity of the nano particles | |
| Stretching parameter | |
| Stefan-Boltzmann constant | |
| Viscosity of the fluid (N·s/m2) | |
| Dimensionless constant parameter | |
| Dimensionless concentration difference | |
| Dimensionless temperature difference | |
| Nanoparticle concentration | |
| Temperature profile | |
| Electrical conductivity (S/m) | |
| Stream function | |
| Effective heat capacity of nano particle (J/K) | |
| Nano fluid kinematic viscosity (m2/s) | |
| Fluid parameters |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Laboratory: Argonne, IL, USA, October 1995; pp. 99–106. [Google Scholar]
- Xuan, Y.; Li, Q. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. In MRS Proceedings; Cambridge University Press: Cambridge, UK, 1996; Volume 457. [Google Scholar]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2102–2109. [Google Scholar] [CrossRef]
- Nazar, R.; Jaradat, M.; Arifin, N.; Pop, I. Stagnation-point flow past a shrinking sheet in a nanofluid. Open Phys. 2011, 9, 1195–1202. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayeti, F.; Ganji, D.D.; Rostamiyan, Y. Unsteady boundary-layer flow of nanofluid past a permeable stretching/shrinking sheet with convective heat transfer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H.; Nadeem, S. The combined effects of slip and convective boundary conditions on stagnation-point flow of CNT suspended nanofluid over a stretching sheet. J. Mol. Liq. 2014, 196, 21–25. [Google Scholar] [CrossRef]
- Nadeem, S.; Mehmood, R.; Akbar, N.S. Optimized analytical solution for oblique flow of a Casson-nano fluid with convective boundary conditions. Int. J. Therm. Sci. 2014, 78, 90–100. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.-S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.-S. Entropy Generation on MHD Blood Flow of Nanofluid Due to Peristaltic Waves. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of Entropy Generation in the Flow of Peristaltic Nanofluids in Channels with Compliant Walls. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Phys. A Stat. Mech. Appl. 2015, 417, 273–286. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 2013, 55, 497–510. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Rashidi, M.M. Numerical simulation of Fluid flow over a shrinking porous sheet by Successive linearization method. Alex. Eng. 2016, 55, 51–56. [Google Scholar] [CrossRef]
- Abbas, Z.; Sheikh, M.; Motsa, S.S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy 2016, 95, 12–20. [Google Scholar] [CrossRef]
- Hady, F.M.; Ibrahim, F.S.; Abdel-Gaied, S.M.; Eid, M.R. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 2012, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, S.; Haq, R.U. Effect of thermal radiation for magnetohydrodynamics boundary layer flow of a nanofluid past a stretching sheet with convective boundary conditions. J. Comput. Theor. Nanosci. 2014, 11, 32–40. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganesh, N.V.; Hakeem, A.K.A.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Rostami, B.; Hossain, M.A. Mixed convective heat transfer for MHD viscoelastic fluid flow over a porous wedge with thermal radiation. Adv. Mech. Eng. 2014, 6, 735939. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An analytical treatment for the exact solutions of MHD flow and heat over two–three dimensional deforming bodies. Int. J. Heat Mass Transf. 2015, 90, 781–789. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M. MHD flow of Cattanneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Ganga, B.; Saranya, S.; Vishnu, G.N.; Abdul, H.A. Effects of space and temperature dependent internal heat generation/absorption on MHD flow of a nanofluid over a stretching sheet. J. Hydrodyn. Ser. B 2015, 27, 945–954. [Google Scholar] [CrossRef]
- Akbar, N.S.; Ebaid, A.; Khan, Z.H. Numerical analysis of magnetic field effects on Eyring–Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S. Numerical Simulation of Entropy Generation with Thermal Radiation on MHD Carreau Nanofluid towards a Shrinking Sheet. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]

| 1 | 1 | - | - | - | 1.4998 | - |
| 2 | - | - | - | 1.7638 | - | |
| 10 | - | - | - | 2.0890 | - | |
| - | 2 | - | - | - | 2.1308 | - |
| - | 3 | - | - | - | 2.2947 | - |
| - | 4 | - | - | - | 2.4657 | - |
| - | - | 0.1 | - | - | 2.0890 | 0.6456 |
| - | - | 0.3 | - | - | 1.9087 | 0.9680 |
| - | - | 0.8 | - | - | 1.5922 | 1.1944 |
| - | - | - | 0.2 | - | 1.9936 | 0.8506 |
| - | - | - | 0.4 | - | 1.8325 | 0.6456 |
| - | - | - | 0.7 | - | 1.6444 | 0.4996 |
| - | - | - | - | 1.5 | - | 1.1386 |
| - | - | - | - | 2 | - | 1.4137 |
| - | - | - | - | 3 | - | 1.9450 |
| Present Results | Wang [37] | |
|---|---|---|
| 0 | 1.23258 | 1.23258 |
| 0.1 | 1.14656 | 1.14656 |
| 0.2 | 1.05113 | 1.05113 |
| 1 | 0.00000 | 0.00000 |
| 2 | −1.88730 | −1.88730 |
| 5 | −10.26474 | −10.26474 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S.; Yang, Z. Entropy Generation on MHD Eyring–Powell Nanofluid through a Permeable Stretching Surface. Entropy 2016, 18, 224. https://doi.org/10.3390/e18060224
Bhatti MM, Abbas T, Rashidi MM, Ali ME-S, Yang Z. Entropy Generation on MHD Eyring–Powell Nanofluid through a Permeable Stretching Surface. Entropy. 2016; 18(6):224. https://doi.org/10.3390/e18060224
Chicago/Turabian StyleBhatti, Muhammad Mubashir, Tehseen Abbas, Mohammad Mehdi Rashidi, Mohamed El-Sayed Ali, and Zhigang Yang. 2016. "Entropy Generation on MHD Eyring–Powell Nanofluid through a Permeable Stretching Surface" Entropy 18, no. 6: 224. https://doi.org/10.3390/e18060224
APA StyleBhatti, M. M., Abbas, T., Rashidi, M. M., Ali, M. E.-S., & Yang, Z. (2016). Entropy Generation on MHD Eyring–Powell Nanofluid through a Permeable Stretching Surface. Entropy, 18(6), 224. https://doi.org/10.3390/e18060224