Orthogonal Vector Computations
Abstract
:1. Identifying Quantum Physical Means for Computation
2. Locating Quantum Resources
2.1. State as Context
2.2. Observable as Context
2.3. Probability
2.4. Entanglement
2.5. Evolution as Permutation
2.6. Computational Resources
3. Renditions via Orthogonal Subspaces
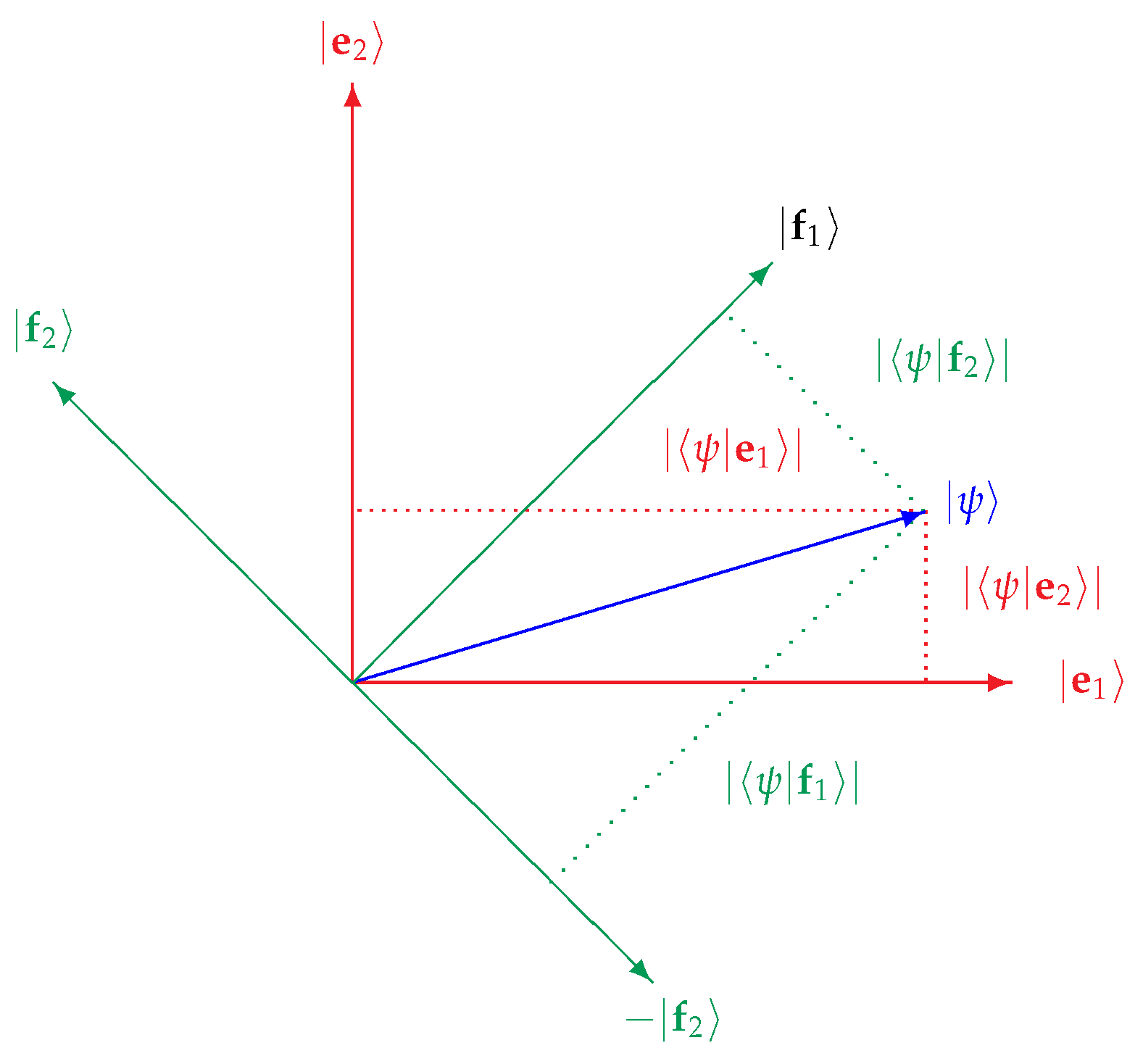
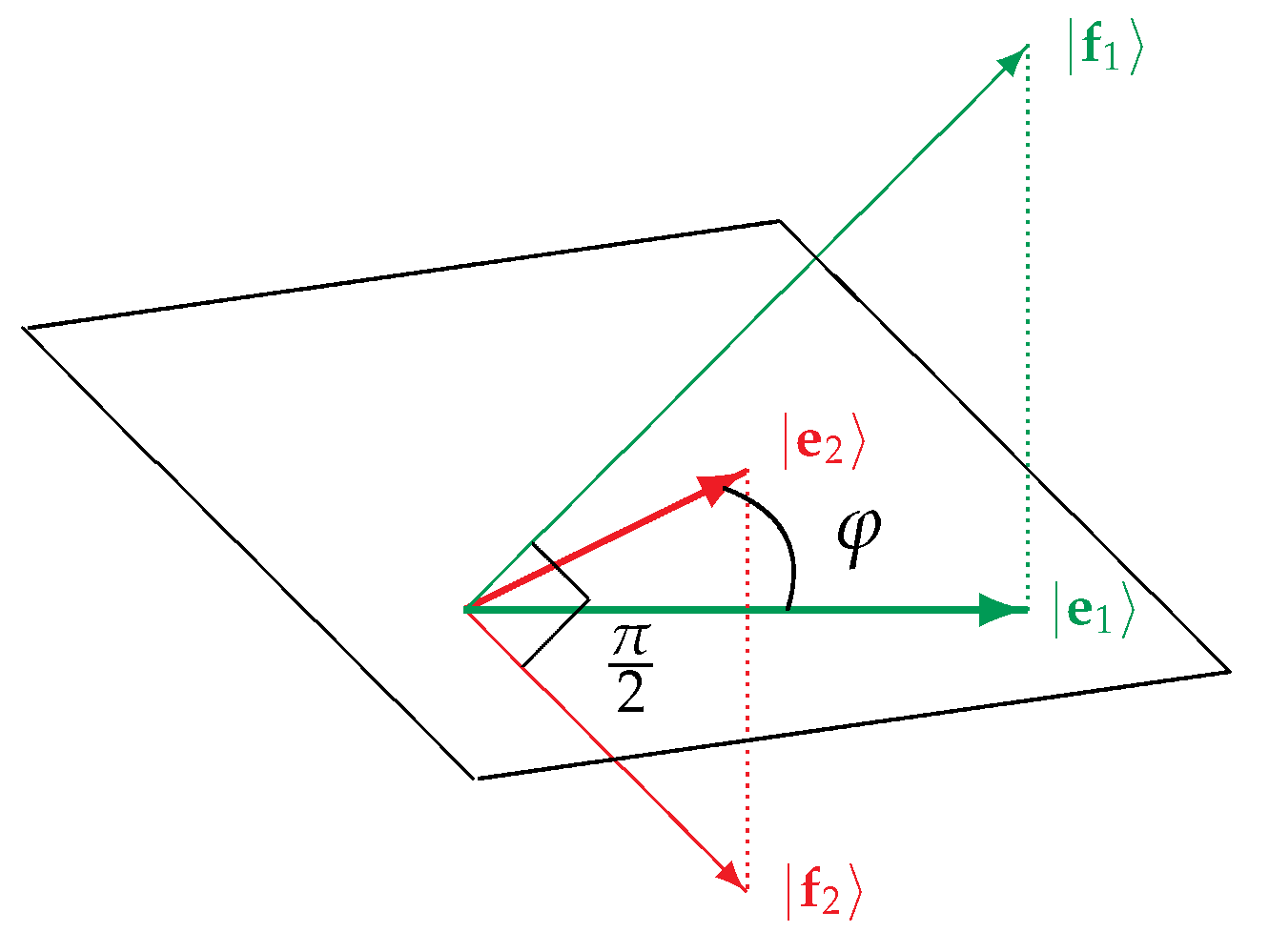
3.1. Example
3.2. Generalized Gram-Schmidt Process
3.3. Counterexample and (In-)Sufficiency
4. Summary
Acknowledgments
Conflicts of Interest
References
- Hermann, A. Frühgeschichte der Quantentheorie (1899-1913); Physik Verlag: Mosbach, Germany, 1969. (In German) [Google Scholar]
- Schrödinger, E. The Interpretation of Quantum Mechanics. Dublin Seminars (1949–1955) and Other Unpublished Essays; Ox Bow Press: Woodbridge, CT, USA, 1995. [Google Scholar]
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 1935, 23, 807–812, 823–828, 844–849. (In German) [Google Scholar] [CrossRef]
- Einstein, A. Ich habe mich sehr gefreut mit Deinen ausführlichen Briefe. Available online: http://alberteinstein.info/vufind1/Record/EAR000024019 (accessed on 21 April 2016). (In German)
- Howard, D. Einstein on locality and separability. Stud. Hist. Philos. Sci. A 1985, 16, 171–201. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Bernstein, E.; Vazirani, U. Quantum complexity theory. In Proceedings of the 25th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 16–18 May 1993; ACM Press: New York, NY, USA, 1993; pp. 11–20. [Google Scholar]
- Bennett, C.H.; Bernstein, E.; Brassard, G.; Vazirani, U. Strengths and weaknesses of quantum computing. SIAM J. Comput. 1997, 26, 1510–1523. [Google Scholar] [CrossRef]
- Fortnow, L. One complexity theorist’s view of quantum computing. Theor. Comput. Sci. 2003, 292, 597–610. [Google Scholar] [CrossRef]
- Castagnoli, G. Highlighting the mechanism of the quantum speedup by time-symmetric and relational quantum mechanics. Found. Phys. 2016, 46, 360–381. [Google Scholar] [CrossRef]
- Svozil, K. Unscrambling the quantum omelette. Int. J. Theor. Phys. 2014, 53, 3648–3657. [Google Scholar] [CrossRef]
- Halmos, P.R. Finite-Dimensional Vector Spaces; Springer: New York, NY, USA, 1974. [Google Scholar]
- Abbott, A.A.; Calude, C.S.; Svozil, K. A variant of the Kochen-Specker theorem localising value indefiniteness. J. Math. Phys. 2015, 56. [Google Scholar] [CrossRef]
- Svozil, K. Quantum information via state partitions and the context translation principle. J. Mod. Opt. 2004, 51, 811–819. [Google Scholar] [CrossRef]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Pitowsky, I. From George Boole to John Bell: The origin of Bell’s inequality. In Bell’s Theorem, Quantum Theory and the Conceptions of the Universe; Kafatos, M., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1989; Volume 37, pp. 37–49. [Google Scholar]
- Mermin, D.N. Quantum Computer Science; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zeilinger, A. Quantum teleportation and the non-locality of information. Philos. Trans. R. Soc. Lond. A 1997, 355, 2401–2404. [Google Scholar] [CrossRef]
- Zeilinger, A. A foundational principle for quantum mechanics. Found. Phys. 1999, 29, 631–643. [Google Scholar] [CrossRef]
- Einstein, A. Quanten-Mechanik und Wirklichkeit. Dialectica 1948, 2, 320–324. (In German) [Google Scholar] [CrossRef]
- Schwinger, J. Unitary operators bases. Proc. Natl. Acad. Sci. USA 1960, 46, 570–579. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.Y.; Wang, L.J.; Mandel, L. Induced coherence and indistinguishability in optical interference. Phys. Rev. Lett. 1991, 67, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Peres, A. Can we undo quantum measurements? Phys. Rev. D 1980, 22, 879–883. [Google Scholar] [CrossRef]
- Scully, M.O.; Drühl, K. Quantum eraser: A proposed photon correlation experiment concerning observation and “delayed choice” in quantum mechanics. Phys. Rev. A 1982, 25, 2208–2213. [Google Scholar] [CrossRef]
- Englert, B.G.; Schwinger, J.; Scully, M.O. Is spin coherence like Humpty-Dumpty? I. Simplified treatment. Found. Phys. 1988, 18, 1045–1056. [Google Scholar] [CrossRef]
- Everett, H., III. “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Wigner, E.P. Remarks on the mind-body question. In The Scientist Speculates; Good, I.J., Ed.; Heinemann and Basic Books: London, UK; New York, NY, USA, 1961; pp. 284–302. [Google Scholar]
- Bell, J.S. Against “measurement”. Phys. World 1990, 3, 33–41. [Google Scholar] [CrossRef]
- Myrvold, W.C. Statistical mechanics and thermodynamics: A Maxwellian view. Stud. Hist. Philos. Sci. B Stud. Hist. Philos. Mod. Phys. 2011, 42, 237–243. [Google Scholar] [CrossRef]
- Jaynes, E.T. Clearing up mysteries—The original goal. In Maximum-Entropy and Bayesian Methods, Proceedings of the 8th Maximum Entropy Workshop, Cambridge, UK, 1–5 August 1988; Skilling, J., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1988; pp. 1–28. [Google Scholar]
- Jaynes, E.T. Probability in Quantum Theory. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Reading, MA, USA, 1990; pp. 381–404. [Google Scholar]
- Galouye, D.F. Simulacron 3; Bantam Books: New York, NY, USA, 1964. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Sipser, M. Limit on the speed of quantum computation in determining parity. Phys. Rev. Lett. 1998, 81, 5442–5444. [Google Scholar] [CrossRef]
- Moore, E.F. Gedanken-experiments on sequential machines. In Automata Studies; Shannon, C.E., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–153. [Google Scholar]
- Svozil, K. Logical equivalence between generalized urn models and finite automata. Int. J. Theor. Phys. 2005, 44, 745–754. [Google Scholar] [CrossRef]
- Donath, N.; Svozil, K. Finding a state among a complete set of orthogonal ones. Phys. Rev. A 2002, 65. [Google Scholar] [CrossRef]
- Svozil, K. Quantum information in base n defined by state partitions. Phys. Rev. A 2002, 66. [Google Scholar] [CrossRef]
- Svozil, K.; Tkadlec, J. On the solution of trivalent decision problems by quantum state identification. Nat. Comput. 2009, 8, 539–546. [Google Scholar] [CrossRef]
- Havlicek, H. Personal communication, 2016. (In German)
- Schläfli, L.; Graf, J.H. Theorie der Vielfachen Kontinuität; Zürcher & Furrer: Zürich, Switzerland, 1901; pp. 134–139. [Google Scholar]
- Hasse, D.; Stachel, H. Almost-orthogonal vector systems. Beitr. Algebra Geom. 1996, 37, 367–381. [Google Scholar]
- Svozil, K. Quantum Queries Associated With Equi-Partitioning of States And Multipartite Relational Encoding Across Space-Time. 2016; arXiv:1601.07102. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svozil, K. Orthogonal Vector Computations. Entropy 2016, 18, 156. https://doi.org/10.3390/e18050156
Svozil K. Orthogonal Vector Computations. Entropy. 2016; 18(5):156. https://doi.org/10.3390/e18050156
Chicago/Turabian StyleSvozil, Karl. 2016. "Orthogonal Vector Computations" Entropy 18, no. 5: 156. https://doi.org/10.3390/e18050156
APA StyleSvozil, K. (2016). Orthogonal Vector Computations. Entropy, 18(5), 156. https://doi.org/10.3390/e18050156





