Analytical Modeling of MHD Flow over a Permeable Rotating Disk in the Presence of Soret and Dufour Effects: Entropy Analysis

Abstract

The main concern of the present article is to study steady magnetohydrodynamics (MHD) flow, heat transfer and entropy generation past a permeable rotating disk using a semi numerical/analytical method named Homotopy Analysis Method (HAM). The results of the present study are compared with numerical quadrature solutions employing a shooting technique with excellent correlation in special cases. The entropy generation equation is derived as a function of velocity, temperature and concentration gradients. Effects of flow physical parameters including magnetic interaction parameter, suction parameter, Prandtl number, Schmidt number, Soret and Dufour number on the fluid velocity, temperature and concentration distributions as well as entropy generation number are analysed and discussed in detail. Results show that increasing the Soret number or decreasing the Dufour number tends to decrease the temperature distribution while the concentration distribution is enhanced. The averaged entropy generation number increases with increasing magnetic interaction parameter, suction parameter, Prandtl number, and Schmidt number.

1. Introduction

Rotating disk flows have received much attention in several industrial and engineering processes. They have feasible applications in many industries, such as rotating machinery, lubrication, oceanography and computer storage devices. Von Karman [1] was, to the best of our knowledge, the first who studied fluid flow due to an infinite rotating disk. He introduced his famous appropriate transformations, resulting in ordinary differential equations, which are a reduced form of the governing partial differential equations.

In several studies, Dufour and Soret effects were assumed to be negligible on heat and mass transfer according to the effects described by Fourier’s and Fick’s laws [2]. These effects are more important when the density differences exist in the flow regime [3]. When heat and mass transfer happen simultaneously in a moving fluid, the energy flux can be generated by temperature gradients as well as composition gradients. The energy flux caused by a composition gradient is named the Dufour or diffusion-thermo effect and also the mass fluxes can be developed by the temperature gradients which are called the Soret or thermal-diffusion effect [4]. In this matter, several studies have been carried out. Das et al. [5] displayed the effect of mass transfer on the free convective flow and heat transfer of a viscous incompressible electrically conducting fluid past a vertical porous plate through a porous medium. Rashidi et al. [6] presented an analytical solution for steady magnetohydrodynamics (MHD) convective and slip flow due to a rotating disk in the presence of viscous dissipation and Ohmic heating. Hayat et al. [7] illustrated thermal-diffusion and diffusion-thermo effects on 2D MHD axisymmetric flow of a second grade fluid in the presence of Joule heating and first order chemical reaction. Osalusi et al. [4] studied Soret and Dufour effects on combined heat and mass transfer of steady hydromagnetic convective and slip flow due to a rotating disk in the presence of viscous dissipation and Ohmic heating numerically using a shooting method. Pal and Talukdar [8] investigated effects of thermal radiation and first-order chemical reaction on unsteady MHD convective flow past a semi-infinite vertical flat plate in the presence of transverse magnetic field under oscillatory suction and heat source in a slip-flow regime. In another study, Turkyilmazoglu and Pop [9] studied heat and mass transfer characteristics of unsteady electrically conducting fluid flow past a suddenly started vertical infinite flat considering Soret and heat source effects.

In recent years, efficiency calculation of heat exchanger systems was restricted to the first law of thermodynamics in many studies. In many industrial systems, various mechanisms that account for irreversibility compete with each other. Thermodynamic optimization has become the concern of several researchers in recent years and is also the condition of the most desirable trade-off between two or more competing irreversibilities [10]. Entropy generation minimization has been comprehensively covered by Bejan [11], specifically in the fields of refrigeration, heat transfer, storage, solar thermal power conversion, and thermal science education. Entropy generation minimization method is employed to optimize the thermal engineering devices for higher energy efficiency. In order to access the best design of thermal systems, one can employ the second law of thermodynamics by minimizing the irreversibility [12,13]. The performance of engineering equipment in the presence of irreversibilities is reduced and the entropy generation function is a measure of the level of available irreversibilities in a process. Since entropy generation is a criterion for measurement of available work destruction of systems, reduction of entropy generation is essential to obtain the optimal design of energy systems [14]. Moreover, entropy generation causes the systems to decrease useful power cycle outputs for a power production device or increase the power input to the cycle for power consumption devices. It is important to emphasize that the second law of thermodynamics is more reliable than the first law of thermodynamics analysis, because of the limitation of the first law efficiency in heat transfer engineering systems [15]. The evaluation of entropy generation is carried out to improve the system performance. In addition, heat transfer, mass transfer, viscous dissipation, finite temperature gradients, etc. can be introduced as the sources of entropy generation [16].

Many researchers have been motivated to conduct applications of the second law of thermodynamics in the design of thermal engineering systems in recent decades. Rashidi et al. [17] investigated analysis of the second law of thermodynamics applied to an electrically conducting incompressible nanofluid flowing over a porous rotating disk. Jafari and Freidoonimehr [18] studied the second law of thermodynamics over a stretching permeable surface in the presence of a uniform vertical magnetic field in a slip nanofluid regime. In another study, Abolbashari et al. [19] used Homotopy Analysis Method (HAM) to study entropy analysis in an unsteady magnetohydrodynamic nanofluid regime adjacent to an accelerating stretching permeable surface. In addition, Abolbashari et al. [20] investigated heat and mass transfer and entropy generation for steady laminar non-Newtonian nanofluid flow induced by a stretching sheet in the presence of velocity slip and convective surface boundary conditions using Optimal HAM. Further, Ellahi et al. [21] studied natural convection boundary layer flow along an inverted cone. They also considered effect of the shape of nanosize particles on entropy generation with base fluid.

Some strongly nonlinear equations used to describe physical systems in the form of mathematical modeling have no exact solutions. Numerical or analytical methods such as Runge–Kutta method [22,23], differential transform method (DTM) [24,25,26] and the present employed analytical method, HAM, can be applied to solve these nonlinear equations. Numerical methods have many disadvantages in comparison with analytical methods. Thus in this article, we apply one of the analytical methods named Homotopy analysis method (HAM) to solve the system of nonlinear differential equations. The HAM was firstly introduced by Liao [27,28,29] to offer a general analytical method for nonlinear problems. Awad [30] presented a simple method for calculating heat transfer from a rotating disk to fluids for a wide range of Prandtl numbers using asymptotic analysis. Recently, HAM was used to solve many nonlinear problems in fluid dynamics and heat transfer [31,32,33,34].

Recently, many researchers have been interested to study MHD and its practical applications [35,36,37,38,39,40,41,42]. The object of this paper is to study the second law of thermodynamics of steady MHD flow over a permeable rotating disk in the presence of Soret and Dufour effects analytically via HAM. The effects of various parameters such as magnetic interaction parameter, suction parameter, Prandtl number, Soret number, Dufour number, and Schmidt number on the fluid velocity, temperature and concentration distributions as well as the averaged entropy generation number are analyzed.

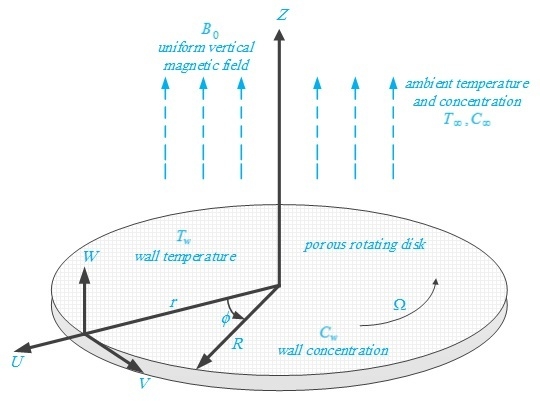
2. Mathematical Formulation

We assume steady, axially symmetric, incompressible flow of an electrically conducting fluid with heat and mass transfer flow past a rotating permeable disk. Consider that the fluid is infinite in extent in the positive z-direction. The fluid is assumed to be Newtonian. The external uniform magnetic field B₀ which is considered unchanged by taking the small magnetic Reynolds number is imposed in the direction normal to the surface of the disk. The induced magnetic field due to motion of the electrically-conducting fluid is negligible. Uniform suction is also applied at the surface of the disk. The flow description and geometrical coordinates are shown in Figure 1. The governing equations, respectively, of continuity, momentum, energy and species diffusion in laminar incompressible flow are given by:

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(1)

$$u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}+\frac{1}{\rho }\frac{\partial P}{\partial r}=\nu \left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{r^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)-\frac{\sigma B_0^2}{\rho }u,$$

(2)

$$u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}=\nu \left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)-\frac{\sigma B_0^2}{\rho }v,$$

(3)

$$u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}+\frac{1}{\rho }\frac{\partial P}{\partial z}=\nu \left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{{\partial }^{2}w}{\partial z^2}\right),$$

(4)

$$u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}=\frac{k}{\rho c_p}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right)+\frac{D{K}_T}{C_s{c}_p}\left(\frac{{\partial }^{2}C}{\partial r^2}+\frac{1}{r}\frac{\partial C}{\partial r}+\frac{{\partial }^{2}C}{\partial z^2}\right),$$

(5)

$$u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}=D\left(\frac{{\partial }^{2}C}{\partial r^2}+\frac{1}{r}\frac{\partial C}{\partial r}+\frac{{\partial }^{2}C}{\partial z^2}\right)+\frac{D{K}_T}{T_m}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right).$$

(6)

By using cylindrical polar coordinates (r, ϕ, z), the disk rotates with constant angular velocity Ω and is placed at z = 0, where z is the vertical axis in the cylindrical coordinate system with r and ϕ as the radial and tangential axes. The components of the flow velocity (u, v, w) are in the directions of increasing (r, ϕ, z), respectively. P is pressure, ρ is the density of the fluid, and T and C are the fluid temperature and concentration, respectively. ν is the kinematic viscosity of the ambient fluid, σ is the electrical conductivity, k is the thermal conductivity, c_p is the specific heat at constant pressure, D is the molecular diffusion coefficient, K_T is the thermal diffusion ratio, C_s is the concentration susceptibility, and T_m is the mean fluid temperature. The appropriate boundary conditions subject to uniform suction w₀ through the disk are:

$$u=0,v=\mathsf{\Omega }r,w=w_0,T=T_w,C=C_w\text{ at }z=0,$$

(7)

$$u\to 0,v\to 0,P\to P_{\infty },T\to T_{\infty },C\to C_{\infty }\text{ at }z\to \infty .$$

(8)

In order to obtain the non-dimensional form of Equations (1)–(6), the following dimensionless variables are introduced as

$$\begin{array}{l}\overline{R}=\frac{r}{L},\overline{Z}=\frac{z}{L},\overline{U}=\frac{u}{\mathsf{\Omega }L},\overline{V}=\frac{v}{\mathsf{\Omega }L},\overline{W}=\frac{w}{\mathsf{\Omega }L},\\ \overline{P}=\frac{p-p_{\infty }}{\rho {\mathsf{\Omega }}^2{L}^2},\overline{\nu }=\frac{\nu }{\mathsf{\Omega }{L}^2},\overline{T}=\frac{T-T_w}{T_{\infty }-T_w},\overline{C}=\frac{C-C_w}{C_{\infty }-C_w},\end{array}$$

(9)

$$\overline{U}=\overline{R}F(\eta ),\overline{V}=\overline{R}G(\eta ),\overline{W}={(\overline{\nu })}^{1/2}H(\eta ),\overline{T}=\theta (\eta ),\overline{C}=\phi (\eta ).$$

(10)

Substituting the dimensionless variables Equations (9) and (10) into Equations (1)–(6), and by introducing a dimensionless normal distance from the disk, $\eta =\overline{Z}{(\overline{\nu })}^{-1/2}$, the following nonlinear ordinary differential equations are obtained:

$$H^{\prime }+2F=0,$$

(11)

$$F^{″}-H{F}^{\prime }-F^2+G^2-MF=0,$$

(12)

$$G^{″}-H{G}^{\prime }-2FG-MG=0,$$

(13)

$$\frac{1}{Pr}{\theta }^{″}-H{\theta }^{\prime }+Du{\phi }^{″}=0,$$

(14)

$$\frac{1}{Sc}{\phi }^{″}-H{\phi }^{\prime }+Sr{\theta }^{″}=0,$$

(15)

where M = σ·B₀²/Ω·ρ is the magnetic interaction parameter, Pr = ν·ρ·c_p/k is the Prandtl number, Sc = ν/D is the Schmidt number, Sr = D·(T_∞ − T_w)·K_T/ν·T_m (C_∞ − C_w) is the Soret number, Du = D·(C_∞ − C_w)·K_T/C_s·c_p·ν·(T_∞ − T_w) is the Dufour number, and F, G, H, θ, and φ are the dimensionless functions of modified dimensionless vertical coordinate η. The transformed boundary conditions are:

$$\begin{array}{l}F(0)=0,G(0)=1,H(0)=W_s,\theta (0)=1,\phi (0)=1,\\ F(\eta )\to 0,G(\eta )\to 0,\theta (\eta )\to 0,\phi (\eta )\to 0,\text{ as }\eta \to \infty ,\end{array}$$

(16)

where Ws = w₀/(ν·Ω)^1/2 is the suction/injection parameter and Ws < 0 shows uniform suction at the disk surface.

3. Entropy Generation Analysis

According to [16,43,44,45], in the presence of axial symmetry and magnetic field and considering the mass transfer effect, the volumetric rate of local entropy generation is defined as

$${\dot{S}}_{gen}^{‴}=\frac{k}{{T_w}^2}{\left[\nabla T\right]}^2+\frac{\mu }{T_w}\mathsf{\Phi }+\frac{1}{T_w}\left[\left(J-QV\right)\cdot \left(E+V\times B\right)\right]+\frac{R_{g}D}{C_w}{\left[\nabla C\right]}^2+\frac{R_{g}D}{T_w}\left[\nabla T\cdot \nabla C\right],$$

(17)

where

$$\left[\nabla T\right]=\left[\frac{\partial T}{\partial r}{\widehat{e}}_r+\frac{1}{r}\frac{\partial T}{\partial \theta }{\widehat{e}}_{\theta }+\frac{\partial T}{\partial z}{\widehat{e}}_z\right],$$

(18)

$$\left[\nabla C\right]=\left[\frac{\partial C}{\partial r}{\widehat{e}}_r+\frac{1}{r}\frac{\partial C}{\partial \theta }{\widehat{e}}_{\theta }+\frac{\partial C}{\partial z}{\widehat{e}}_z\right],$$

(19)

$$\begin{array}{c}\mathsf{\Phi }=2\left[{\left(\frac{\partial u}{\partial r}\right)}^2+\frac{1}{r^2}{\left(\frac{\partial v}{\partial \theta }+u\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]+{\left(\frac{\partial v}{\partial z}+\frac{1}{r}\frac{\partial w}{\partial \theta }\right)}^2\\ +{\left(\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}\right)}^2+{\left[\frac{1}{r}\frac{\partial u}{\partial \theta }+r\frac{\partial }{\partial r}\left(\frac{v}{r}\right)\right]}^2,\end{array}$$

(20)

$$J=\sigma \left(E+V\times B\right).$$

(21)

We assume that the electric force per unit charge E is negligible in comparison with $V\times B,$ in Equations (17) and (21) and we also consider that the electric current J is much greater than QV. Thus, by applying the above assumption and after reduction, Equation (17) can be further simplified as follows

$${\dot{S}}_{gen}^{‴}=\begin{array}{l}\underset{\text{Thermal irreversibility}}{\underbracket{\frac{k}{{T_w}^2}{\left(\frac{\partial T}{\partial z}\right)}^2}}+\underset{\text{Fluid friction irreversibility}}{\underbracket{\frac{\mu }{T_w}\left\{2\left[{\left(\frac{\partial u}{\partial r}\right)}^2+\frac{1}{r^2}{u}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]+{\left(\frac{\partial v}{\partial z}\right)}^2+{\left(\frac{\partial u}{\partial z}\right)}^2+{\left[r\frac{\partial }{\partial r}\left(\frac{v}{r}\right)\right]}^2\right\}}}\hfill \\ +\underset{\text{Magnetic effects}}{\underbracket{\frac{\sigma {{\rm B}}_0{}^2}{T_w}\left(u^2+v^2\right)}}+\underset{\text{Diffusive irreversibility}}{\underbracket{\frac{R_{g}D}{C_w}{\left(\frac{\partial C}{\partial z}\right)}^2+\frac{R_{g}D}{T_w}\left(\frac{\partial T}{\partial z}\right)\left(\frac{\partial C}{\partial z}\right)}}.\hfill \end{array}$$

(22)

The right-hand side of Equation (22) consists of four parts; the first part is local entropy generation due to heat transfer irreversibility, the second part arises due to fluid friction irreversibility, the third part denotes the magnetic effects and entropy generation due to diffusion can be calculated from the fourth part which denotes diffusive irreversibility. It must be noted that the entropy generation due to diffusion is the sum of a cross term with both thermal and concentration gradients and a pure term which involves concentration gradient only. The non-dimensional form of the entropy generation rate is the entropy generation number and indicates the ratio of the actual entropy generation rate $\left({\dot{S}}_{gen}^{‴}\right)$ to the characteristic entropy generation rate $\left({\dot{S}}_0^{‴}\right)$. By using the Von Karman similarity variables given in Equations (9) and (10), the entropy generation number $\left(N_G\right)$ becomes:

$$N_G=\begin{array}{l}\alpha {\theta }^{\prime }{\left(\eta \right)}^2+Br\langle \frac{3}{Re}{H}^{\prime }{\left(\eta \right)}^2+R^2\left\{\left(F^{\prime }{\left(\eta \right)}^2+G^{\prime }{\left(\eta \right)}^2\right)+M\left(F{\left(\eta \right)}^2+G{\left(\eta \right)}^2\right)\right\}\rangle \hfill \\ +\frac{\beta \lambda }{\alpha }{\phi }^{\prime }{\left(\eta \right)}^2+\lambda {\theta }^{\prime }\left(\eta \right){\phi }^{\prime }\left(\eta \right),\hfill \end{array}$$

(23)

where $\alpha =\Delta T/T_w$ is the dimensionless temperature difference, $Br=\mu {\mathsf{\Omega }}^2{L}^2/k\Delta {\rm T}$ is the rotational Brinkman number, $Re=\mathsf{\Omega }{L}^2/\nu$ is the rotational Reynolds number, $\beta =\Delta C/C_w$ is the dimensionless concentration difference, $\lambda =R_{g}D\Delta C/k$ is the diffusive constant parameter, and $N_G={\dot{S}}_{gen}^{‴}/\left(k\mathsf{\Omega }\Delta T/\nu T_w\right)$ is the dimensionless entropy generation rate.

As the Brinkman number (a measure of the effect of viscous dissipation) increases, entropy generation due to viscous and magnetic effects also increases. Increasing the Reynolds number results in a decrease in the effect of fluid friction irreversibility.

The averaged entropy generation number, which is an important measure of total global entropy generation can be evaluated using:

$$N_{G,av}=\frac{1}{\forall }{\displaystyle {\int }_0^m{\displaystyle {\int }_0^{1}2\pi R{N}_{G}dR}d\eta },$$

(24)

where $\forall$ is the volume considered. In order to consider the effects of velocity, thermal and concentration boundary-layers, we calculate the volumetric entropy generation in a large finite domain. Thus, the integration of Equation (24) is obtained in the domain $0\le R\le 1$ and $0\le \eta \le m$; where m is a sufficiently large number.

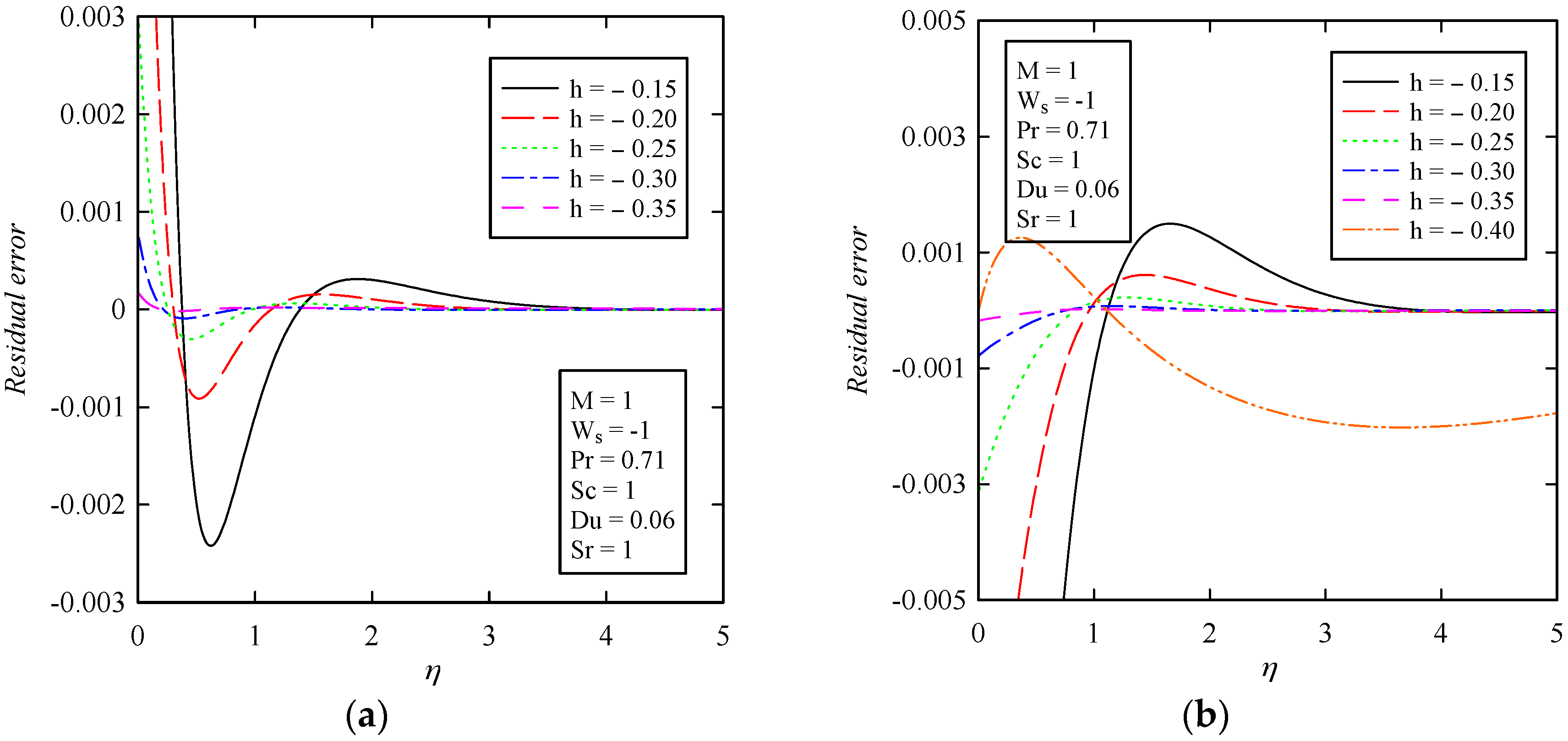
4. HAM Solution

We choose suitable initial approximations, according to the boundary conditions (16) and the rule of solution expression

$$H(0)=W_s,F(0)=0,G(0)=e^{-\eta },\theta (0)=e^{-\eta },\phi (0)=e^{-\eta }.$$

(25)

The auxiliary linear operators ${ℒ}_1(H),{ℒ}_2(F),{ℒ}_3(G),{ℒ}_4(\theta )$ and ${ℒ}_5(\phi )$ are:

$$\begin{array}{l}ℒ(H)=\frac{\partial H}{\partial \eta },ℒ(F)=\frac{{\partial }^{2}F}{\partial {\eta }^2}+\frac{\partial F}{\partial \eta },ℒ(G)=\frac{{\partial }^{2}G}{\partial {\eta }^2}+\frac{\partial G}{\partial \eta },\\ ℒ(\theta )=\frac{{\partial }^2\theta }{\partial {\eta }^2}+\frac{\partial \theta }{\partial \eta },ℒ(\phi )=\frac{{\partial }^2\phi }{\partial {\eta }^2}+\frac{\partial \phi }{\partial \eta },\end{array}$$

(26)

with the following properties

$$\begin{array}{l}{ℒ}_1(c_1)=0,{ℒ}_2(c_2{e}^{-\eta }+c_3)=0,{ℒ}_3(c_4{e}^{-\eta }+c_5)=0,\hfill \\ {ℒ}_4(c_6{e}^{-\eta }+c_7)=0,{ℒ}_5(c_8{e}^{-\eta }+c_9)=0,\hfill \end{array}$$

(27)

where $c_i,i=1-9$, are the arbitrary constants. Nonlinear operators, due to Equations (11)–(15), are introduced as

$${\mathcal{N}}_1\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p)\right]=\frac{\partial \widehat{H}(\eta ;p)}{\partial \eta }+2\widehat{F}(\eta ;p),$$

(28)

$$\begin{array}{ll}{\mathcal{N}}_2\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p),\widehat{G}(\eta ;p)\right]=\hfill & \frac{{\partial }^2\widehat{F}(\eta ;p)}{\partial {\eta }^2}-\widehat{H}(\eta ;p)\frac{\partial \widehat{F}(\eta ;p)}{\partial \eta }\hfill \\ & -\widehat{F}{(\eta ;p)}^2+\widehat{G}{(\eta ;p)}^2-M\widehat{F}(\eta ;p),\hfill \end{array}$$

(29)

$$\begin{array}{ll}{\mathcal{N}}_3\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p),\widehat{G}(\eta ;p)\right]=\hfill & \frac{{\partial }^2\widehat{G}(\eta ;p)}{\partial {\eta }^2}-\widehat{H}(\eta ;p)\frac{\partial \widehat{G}(\eta ;p)}{\partial \eta }\hfill \\ & -2\widehat{G}(\eta ;p)\widehat{F}(\eta ;p)-M\widehat{G}(\eta ;p),\hfill \end{array}$$

(30)

$${\mathcal{N}}_4\left[\widehat{H}(\eta ;p),\widehat{\theta }(\eta ;p),\widehat{\phi }(\eta ;p)\right]=\frac{1}{Pr}\frac{{\partial }^2\widehat{\theta }(\eta ;p)}{\partial {\eta }^2}-\widehat{H}(\eta ;p)\frac{\partial \widehat{\theta }(\eta ;p)}{\partial \eta }+Du\frac{{\partial }^2\widehat{\phi }(\eta ;p)}{\partial {\eta }^2},$$

(31)

$${\mathcal{N}}_5\left[\widehat{H}(\eta ;p),\widehat{\theta }(\eta ;p),\widehat{\phi }(\eta ;p)\right]=\frac{1}{Sc}\frac{{\partial }^2\widehat{\phi }(\eta ;p)}{\partial {\eta }^2}-\widehat{H}(\eta ;p)\frac{\partial \widehat{\phi }(\eta ;p)}{\partial \eta }+Sr\frac{{\partial }^2\widehat{\theta }(\eta ;p)}{\partial {\eta }^2}.$$

(32)

The zero-th order deformation equations are

$$(1-p){ℒ}_1\left[\widehat{H}(\eta ;p)-H_0(\eta )\right]=p\hslash {\mathscr{H}}_H(\eta ){\mathcal{N}}_1\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p)\right],$$

(33)

$$(1-p){ℒ}_2\left[\widehat{F}(\eta ;p)-F_0(\eta )\right]=p\hslash {\mathscr{H}}_F(\eta ){\mathcal{N}}_2\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p),\widehat{G}(\eta ;p)\right],$$

(34)

$$(1-p){ℒ}_3\left[\widehat{G}(\eta ;p)-G_0(\eta )\right]=p\hslash {\mathscr{H}}_G(\eta ){\mathcal{N}}_3\left[\widehat{H}(\eta ;p),\widehat{F}(\eta ;p),\widehat{G}(\eta ;p)\right],$$

(35)

$$(1-p){ℒ}_4\left[\widehat{\theta }(\eta ;p)-{\theta }_0(\eta )\right]=p\hslash {\mathscr{H}}_{\theta }(\eta ){\mathcal{N}}_4\left[\widehat{H}(\eta ;p),\widehat{\theta }(\eta ;p),\widehat{\phi }(\eta ;p)\right],$$

(36)

$$(1-p){ℒ}_5\left[\widehat{\phi }(\eta ;p)-{\phi }_0(\eta )\right]=p\hslash {\mathscr{H}}_{\phi }(\eta ){\mathcal{N}}_5\left[\widehat{H}(\eta ;p),\widehat{\theta }(\eta ;p),\widehat{\phi }(\eta ;p)\right],$$

(37)

where ${\mathscr{H}}_H(\eta ),{\mathscr{H}}_F(\eta ),{\mathscr{H}}_G(\eta ),{\mathscr{H}}_{\theta }(\eta )$, and ${\mathscr{H}}_{\phi }(\eta )$ are the auxiliary functions, which are selected as

$${\mathscr{H}}_H(\eta )={\mathscr{H}}_F(\eta )={\mathscr{H}}_G(\eta )={\mathscr{H}}_{\theta }(\eta )={\mathscr{H}}_{\phi }(\eta )=1,$$

(38)

subject to the boundary conditions

$$\begin{gathered} \widehat{H}(0;p)=W_s,\widehat{F}(0;p)=0,\widehat{G}(0;p)=1,\widehat{\theta }(0;p)=1,\widehat{\phi }(0;p)=1, \\ \widehat{F}(0;\infty )=0,\widehat{G}(0;\infty )=0,\widehat{\theta }(0;\infty )=0,\widehat{\phi }(0;\infty )=0. \end{gathered}$$

(39)

Finally by Taylor's theorem, we obtain

$$\widehat{H}(\eta ;p)=H_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{H}_m(\eta )p^m},$$

(40)

$$\widehat{F}(\eta ;p)=F_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{F}_m(\eta )p^m},$$

(41)

$$\widehat{G}(\eta ;p)=G_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{G}_m(\eta )p^m},$$

(42)

$$\widehat{\theta }(\eta ;p)={\theta }_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\theta }_m(\eta )p^m},$$

(43)

$$\widehat{\phi }(\eta ;p)={\phi }_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\phi }_m(\eta )p^m},$$

(44)

where

$$\begin{array}{c}{H}_m(\eta )={\frac{1}{m!}\frac{{\partial }^m\widehat{H}(\eta ;p)}{\partial p^m}|}_{p=0},F_m(\eta )={\frac{1}{m!}\frac{{\partial }^m\widehat{F}(\eta ;p)}{\partial p^m}|}_{p=0},\\ G_m(\eta )={\frac{1}{m!}\frac{{\partial }^m\widehat{G}(\eta ;p)}{\partial p^m}|}_{p=0},{\theta }_m(\eta )={\frac{1}{m!}\frac{{\partial }^m\widehat{\theta }(\eta ;p)}{\partial p^m}|}_{p=0},\\ {\phi }_m(\eta )={\frac{1}{m!}\frac{{\partial }^m\widehat{\phi }(\eta ;p)}{\partial p^m}|}_{p=0}.\end{array}$$

(45)

Convergence of the series in Equations (40)–(44) strongly depends on the auxiliary parameter $(\hslash )$ [27]. Consider that $\hslash$ is chosen such that the series in Equations (40)–(44) is convergent at p = 1 we have

$$H(\eta )=H_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{H}_m(\eta )},$$

(46)

$$F(\eta )=F_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{F}_m(\eta )},$$

(47)

$$G(\eta )=G_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{G}_m(\eta )},$$

(48)

$$\theta (\eta )={\theta }_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\theta }_m(\eta )},$$

(49)

$$\phi (\eta )={\phi }_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\phi }_m(\eta )}.$$

(50)

To obtain mth-order deformation equations, differentiate Equations (33)–(37) m times with respect to p, divide by m! in p = 0. The results become:

$${ℒ}_1\left[H_m(\eta )-{\mathsf{\chi }}_m{H}_{m-1}(\eta )\right]=\hslash {\mathscr{H}}_H(\eta )R_{1,m}(\eta ),$$

(51)

$${ℒ}_2\left[F_m(\eta )-{\mathsf{\chi }}_m{F}_{m-1}(\eta )\right]=\hslash {\mathscr{H}}_F(\eta )R_{2,m}(\eta ),$$

(52)

$${ℒ}_3\left[G_m(\eta )-{\mathsf{\chi }}_m{G}_{m-1}(\eta )\right]=\hslash {\mathscr{H}}_G(\eta )R_{3,m}(\eta ),$$

(53)

$${ℒ}_4\left[{\theta }_m(\eta )-{\mathsf{\chi }}_m{\theta }_{m-1}(\eta )\right]=\hslash {\mathscr{H}}_{\theta }(\eta )R_{4,m}(\eta ),$$

(54)

$${ℒ}_5\left[{\phi }_m(\eta )-{\mathsf{\chi }}_m{\phi }_{m-1}(\eta )\right]=\hslash {\mathscr{H}}_{\phi }(\eta )R_{5,m}(\eta ),$$

(55)

where

$$R_{1,m}(\eta )=\frac{\partial H_{m-1}(\eta )}{\partial \eta }+2F_{m-1}(\eta ),$$

(56)

$$\begin{array}{ll}{R}_{2,m}(\eta )\hfill & =\frac{{\partial }^2{F}_{m-1}(\eta )}{\partial {\eta }^2}-{\displaystyle \sum _{n=0}^{m-1}\left(H_n(\eta )\frac{\partial F_{m-1-n}(\eta )}{\partial \eta }+F_n(\eta )F_{m-1-n}(\eta )-G_n(\eta )G_{m-1-n}(\eta )\right)}\hfill \\ & -M{F}_{m-1}(\eta ),\hfill \end{array}$$

(57)

$$R_{3,m}(\eta )=\frac{{\partial }^2{G}_{m-1}(\eta )}{\partial {\eta }^2}-{\displaystyle \sum _{n=0}^{m-1}\left(H_n(\eta )\frac{\partial G_{m-1-n}(\eta )}{\partial \eta }+2F_n(\eta )G_{m-1-n}(\eta )\right)}-M{G}_{m-1}(\eta ),$$

(58)

$$R_{4,m}(\eta )=\frac{1}{Pr}\frac{{\partial }^2{\theta }_{m-1}(\eta )}{\partial {\eta }^2}-{\displaystyle \sum _{n=0}^{m-1}\left(H_n(\eta )\frac{\partial {\theta }_{m-1-n}(\eta )}{\partial \eta }\right)}+Du\frac{{\partial }^2{\phi }_{m-1}(\eta )}{\partial {\eta }^2},$$

(59)

$$R_{5,m}(\eta )=\frac{1}{Sc}\frac{{\partial }^2{\phi }_{m-1}(\eta )}{\partial {\eta }^2}-{\displaystyle \sum _{n=0}^{m-1}\left(H_n(\eta )\frac{\partial {\phi }_{m-1-n}(\eta )}{\partial \eta }\right)}+Sr\frac{{\partial }^2{\theta }_{m-1}(\eta )}{\partial {\eta }^2},$$

(60)

and

$${\mathsf{\chi }}_m=\{\begin{array}{ll}0\hfill & m\le 1\hfill \\ 1\hfill & m>1\hfill \end{array},$$

(61)

with respect to the following boundary conditions

$$\begin{array}{l}{H}_m(0)=W_s,F_m(0)=0,G_m(0)=1,{\theta }_m(0)=1,{\phi }_m(0)=1,\\ F_m(\infty )=0,G_m(\infty )=0,{\theta }_m(\infty )=0,{\phi }_m(\infty )=0.\end{array}$$

(62)

The symbolic software MATHEMATICA (version 9.0.1) is used to solve the system of linear equations, Equations (51)–(55) with boundary conditions (62), for m = 1, 2, 3, …

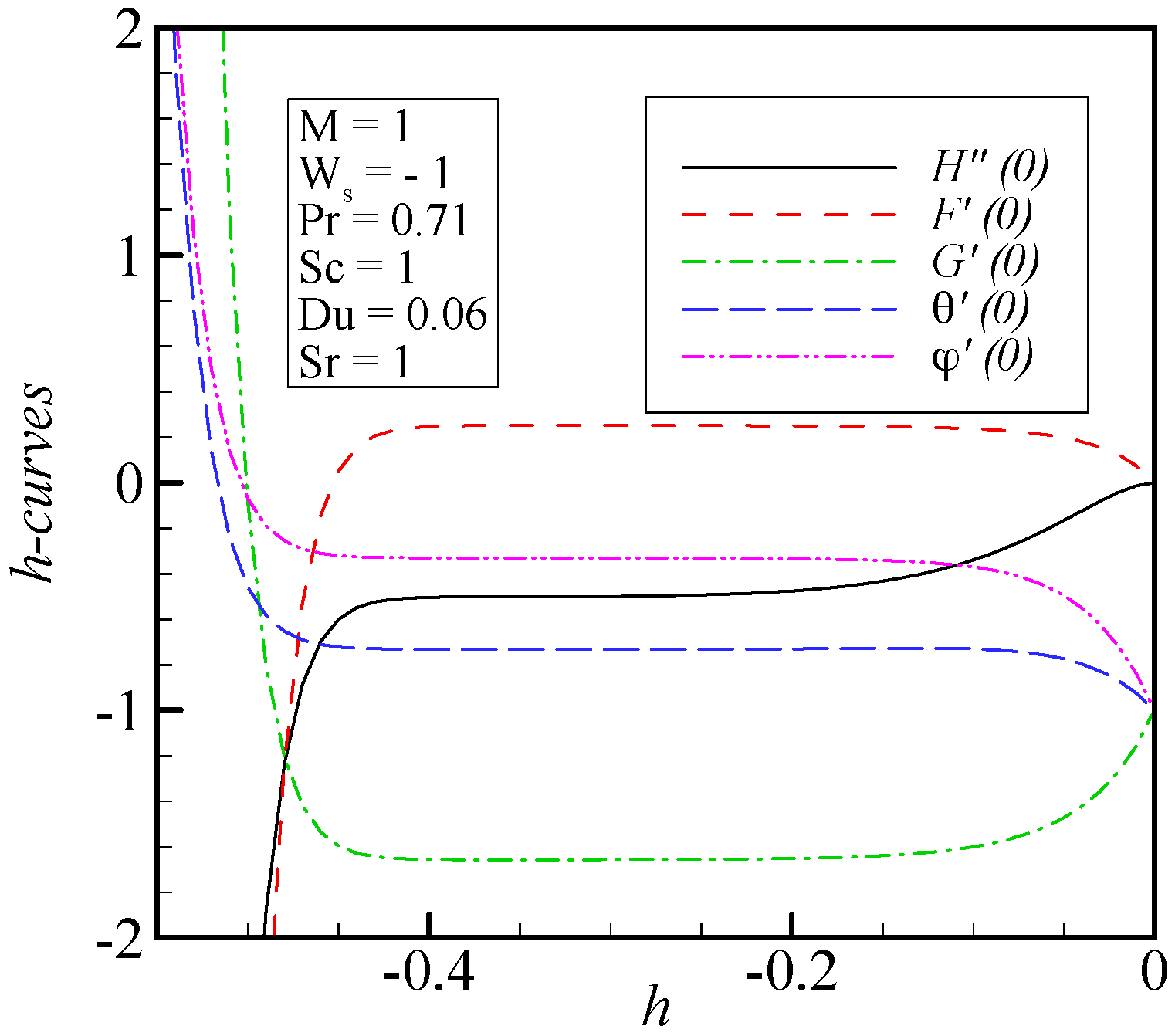
5. Optimal Convergence Control Parameters

Convergence of the series in Equations (40)–(44) forcefully depends on the auxiliary parameter, as mentioned by Liao [27]. It is essential to select an appropriate value of the auxiliary parameter to control and speed up convergence of the approximation series with the assistance of the so-called $\hslash$-curve. Obviously, the valid regions of $\hslash$ correspond to the line segments nearly parallel to the horizontal axis. The $\hslash$-curves of $F^{\prime }(0),G^{\prime }(0),H^{″}(0),{\theta }^{\prime }(0)$ and ${\phi }^{\prime }(0)$ obtained by the 20th order approximation are shown in Figure 2.

The averaged residual errors are defined as:

$$Re{s}_H=\frac{dH\left(\eta \right)}{d\eta }+2F\left(\eta \right),$$

(63)

$$Re{s}_F=\frac{d^{2}F\left(\eta \right)}{d{\eta }^2}-H\left(\eta \right)\frac{dF\left(\eta \right)}{d\eta }-F{\left(\eta \right)}^2+G{\left(\eta \right)}^2-MF\left(\eta \right),$$

(64)

$$Re{s}_G=\frac{d^{2}G\left(\eta \right)}{d{\eta }^2}-H\left(\eta \right)\frac{dG\left(\eta \right)}{d\eta }-2F\left(\eta \right)G\left(\eta \right)-MG\left(\eta \right),$$

(65)

$$Re{s}_{\theta }=\frac{1}{Pr}\frac{d^2\theta \left(\eta \right)}{d{\eta }^2}-H\left(\eta \right)\frac{d\theta \left(\eta \right)}{d\eta }+Du\frac{d^2\phi \left(\eta \right)}{d{\eta }^2},$$

(66)

$$Re{s}_{\phi }=\frac{1}{Sc}\frac{d^2\phi \left(\eta \right)}{d{\eta }^2}-H\left(\eta \right)\frac{d\phi \left(\eta \right)}{d\eta }+Sr\frac{d^2\theta \left(\eta \right)}{d{\eta }^2}.$$

(67)

For example, using the above residual error equations (Equations (64) and (65)), one can obtain the optimum values of auxiliary parameters using the below equations [46,47,48]:

$${\Delta }_{f,m}=\frac{1}{K}{{\displaystyle \sum _{i=0}^K\left[Re{s}_F\left({\displaystyle \sum _{j=0}^m{F}_j\left(i\Delta x\right)}\right)\right]}}^2,$$

(68)

$${\Delta }_{G,m}=\frac{1}{K}{{\displaystyle \sum _{i=0}^K\left[Re{s}_G\left({\displaystyle \sum _{j=0}^m{G}_j\left(i\Delta x\right)}\right)\right]}}^2,$$

(69)

where $\Delta x=10/K$ and $K=20$. For the given order of approximation m, the optimal value of $\hslash$ is given by the minimum values of the ${\Delta }_{F,m}$ and ${\Delta }_{G,m}$ corresponding to nonlinear algebraic equations:

$$\frac{d{\Delta }_{F,m}}{d\hslash }=0,\frac{d{\Delta }_{G,m}}{d\hslash }=0.$$

(70)

In order to check the accuracy of the method and determine the optimal values of $\hslash$, the residual errors displayed in Equations (64) and (65) for the 20th order approximation HAM solutions are presented in Figure 3.

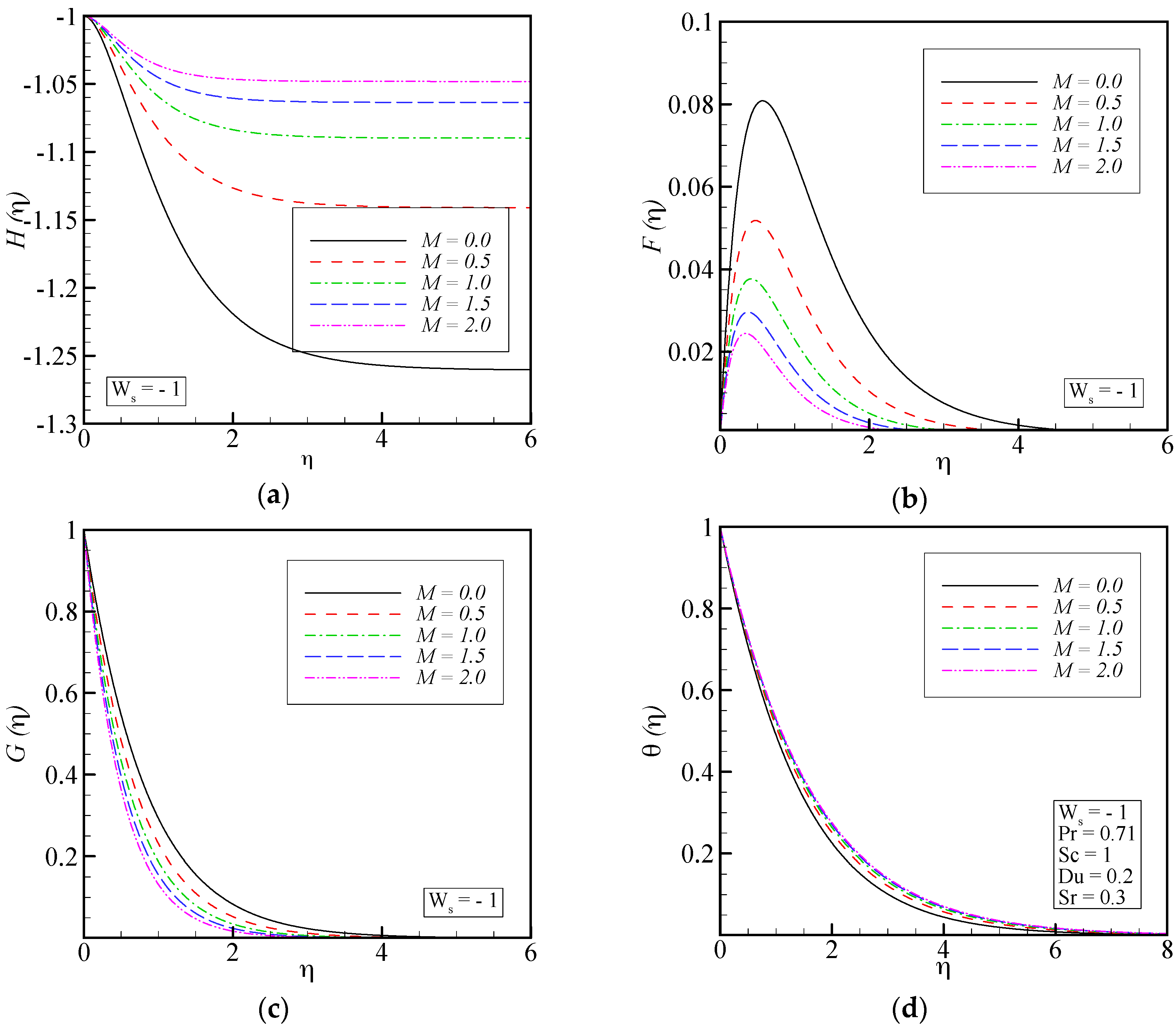
6. Results and Discussion

The nonlinear ordinary differential Equations (11)–(15) subject to boundary conditions (16) have been solved via HAM for some values of the magnetic interaction parameter M, Prandtl number Pr, Schmidt number Sc, Soret number Sr, Dufour number Du, and suction parameter W_s. The values of the physical flow parameters are mentioned in each of the graphs and tables.

Table 1. Numerical values of the radial skin friction coefficient $F^{\prime }(0)$.

M	Ws	Ref. [49]	Ref. [50]	Present
0	0	-	0.510233	0.510186
	−1	-	0.389569	0.389559
	−2	-	0.242421	0.242416
1	0	0.309258	-	0.309237
	−1	0.251044	-	0.251039
	−2	0.188719	-	0.188718
4	0	0.165703	-	0.165701
	−1	0.149016	-	0.149015
	−2	0.129438	-	0.129438

and

Table 2. Numerical values of the tangential skin friction coefficient $-G^{\prime }(0)$.

M	Ws	Ref. [49]	Ref. [50]	Present
0	0	-	0.61592	0.61589
	−1	-	1.17522	1.17523
	−2	-	2.03853	2.03853
1	0	1.06905	-	1.06907
	−1	1.65708	-	1.65709
	−2	2.43136	-	2.43137
4	0	2.01027	-	2.01027
	−1	2.56933	-	2.56933
	−2	3.24134	-	3.24134

illustrate a comparison between our results and those reported by Turkyilmazoglu [49] and Kelson and Desseaux [50] for $F^{\prime }(0)$ and $G^{\prime }(0)$ as well as different values of magnetic interaction parameter and suction parameter. Excellent agreement is observed. The diluting chemical species of most common interest have Schmidt number between 0.1 and 10.0. Thus, we chose Schmidt number 0.22, 0.64, 0.78, and 1, which represent the Schmidt number of helium, ammonia, carbon monoxide, and carbon dioxide, respectively.

The effect of magnetic interaction parameter on the velocity components in radial, tangential and axial directions, temperature distribution as well as concentration profile is presented in Figure 4. Infliction of the vertical magnetic field to the electrically conducting fluid causes a drag-like force named the Lorentz force. This force has the tendency to slow down the flow around the disk at the expense of increasing its temperature and concentration. Thus, as the magnetic field becomes stronger, the velocity profiles in radial, tangential and axial directions decrease and the thermal boundary layer and concentration field increase. It is important to note that as the vertical magnetic field increases, increased resistance on the fluid particles applies, which causes heat to generate in the fluid.

The effect of the suction parameter on all velocity components as well as temperature distribution and concentration profile is illustrated in Figure 5. When suction is applied at the disk surface, the radial, tangential and axial velocity profiles decrease. Applying suction leads to draw the amount of fluid particles into the wall and consequently the velocity boundary layers decrease. In addition, the radial velocity component becomes very small for large values of the suction parameter. The usual decay of temperature and concentration profiles occurs for larger values of the suction parameter.

Figure 6 demonstrates the effect of Prandtl number on the temperature distribution as well as the effect of Schmidt number on the concentration profile. The thermal boundary-layer thickness decreases with increasing Prandtl number. This physically means that the flow with large Prandtl number prevents spreading of heat in the fluid. As the Schmidt number increases, the concentration boundary layer thickness decreases. In other words, molecular diffusion decreases, as Schmidt number increases.

Figure 7 indicates the simultaneous effects of Soret and Dufour number on temperature distribution as well as concentration profile. The Soret effect is a mass flux due to a temperature gradient and the Dufour effect is enthalpy flux due to a concentration gradient and appears in the energy equation. It should be mentioned that Dufour and Soret numbers are arbitrary constants provided that their product remains constant [6,7,51]. Moreover, Du = 0 and Sr = 0 correspond to the condition when thermal diffusion and diffusion thermo effects are of smaller order of magnitude than effects described by Fourier’s and Fick’s laws [7,52]. The thermal boundary layer increases by increasing Dufour number or simultaneously decreasing Soret number. As the Dufour number increases or Soret number decreases, the rate of mass transfer (concentration boundary layer thickness) decreases at the disk.

Figure 8, Figure 9, Figure 10 and Figure 11 display the averaged entropy generation number as a function of suction parameter, Prandtl number, Schmidt number, and Soret and Dufour numbers for a wide range of magnetic interaction parameter. It should be mentioned that the values of α, β and λ are chosen as unity. Figure 8 shows that as the suction through the disk surface increases, the averaged entropy generation number also increases. Moreover, increasing the Prandtl number increases N_{G, av} (Figure 9). It is clear that Schmidt number follows the same trend as Prandtl number. From Figure 10 maximum values of the averaged entropy generation number occur when the values of both Soret and Dufour numbers are maximized simultaneously. Finally, all entropy generation related figures reveal that as the magnetic interaction parameter increases, the averaged entropy generation number also increases.

7. Conclusions

In the current study, a mathematical formulation has been derived for the second law of thermodynamics analysis of MHD fluid flow due to a permeable rotating disk. HAM was used to solve the system of ordinary differential equations. The presented semi numerical/analytical simulations agree closely with previous studies for some special cases. HAM has been shown to be a very strong and efficient technique in determining analytical solutions for nonlinear differential equations. Effects of the six key thermo-physical parameters governing the flow, i.e., magnetic interaction parameter, Prandtl number, Schmidt number, Soret number, Dufour number, and suction parameter on the all dimensionless velocity components, temperature distribution and concentration profile as well as the averaged entropy generation number have been depicted graphically and interpreted in detail. The main results of the present analysis are listed below:

(a)

HAM is shown to demonstrate excellent potential, convergence and accuracy for simulating flow over rotating disk problems.

(b)

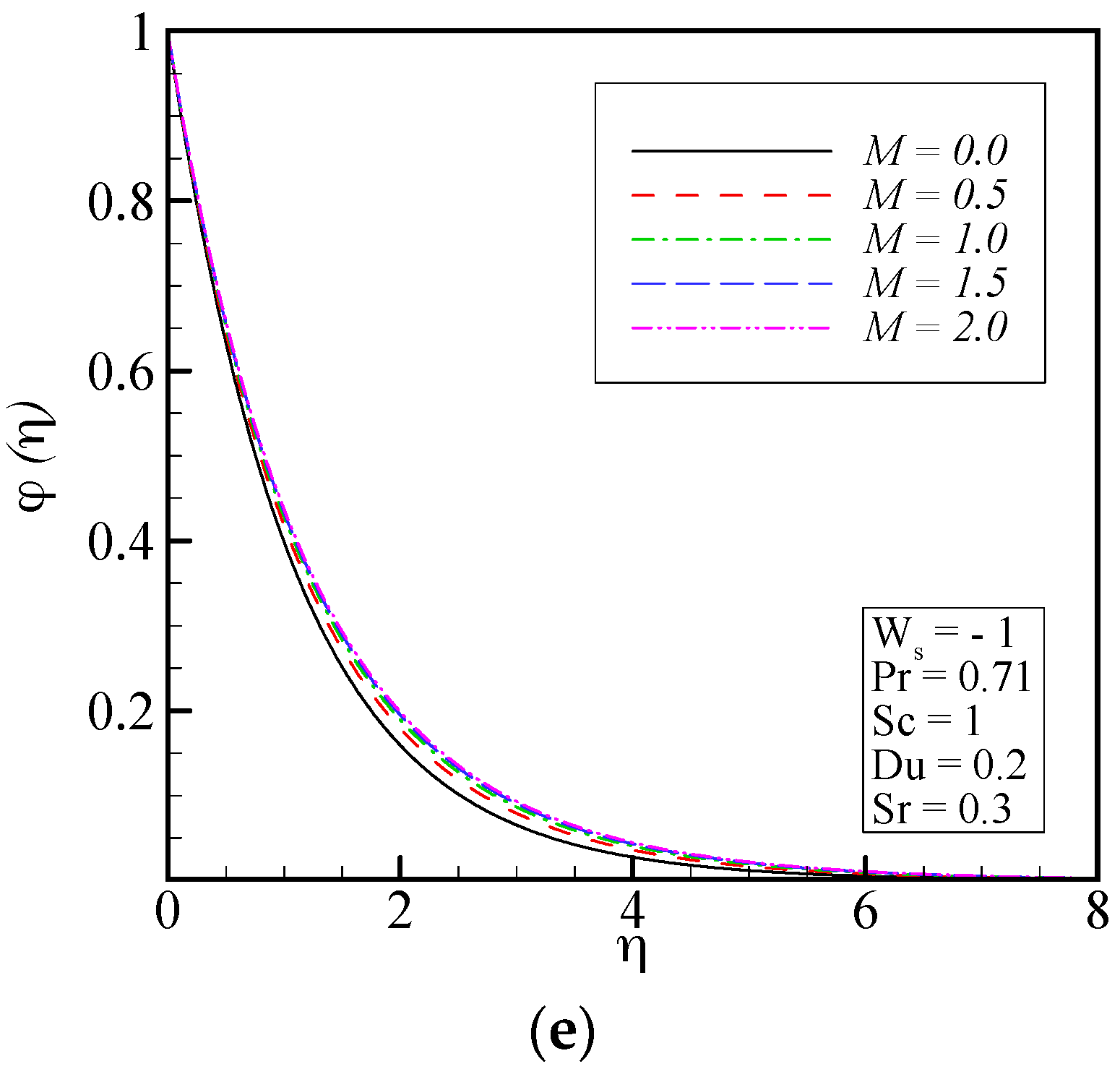
As the magnetic field becomes stronger, the velocity profiles in radial, tangential and axial directions decrease and the thermal boundary layer and concentration field increase.

(c)

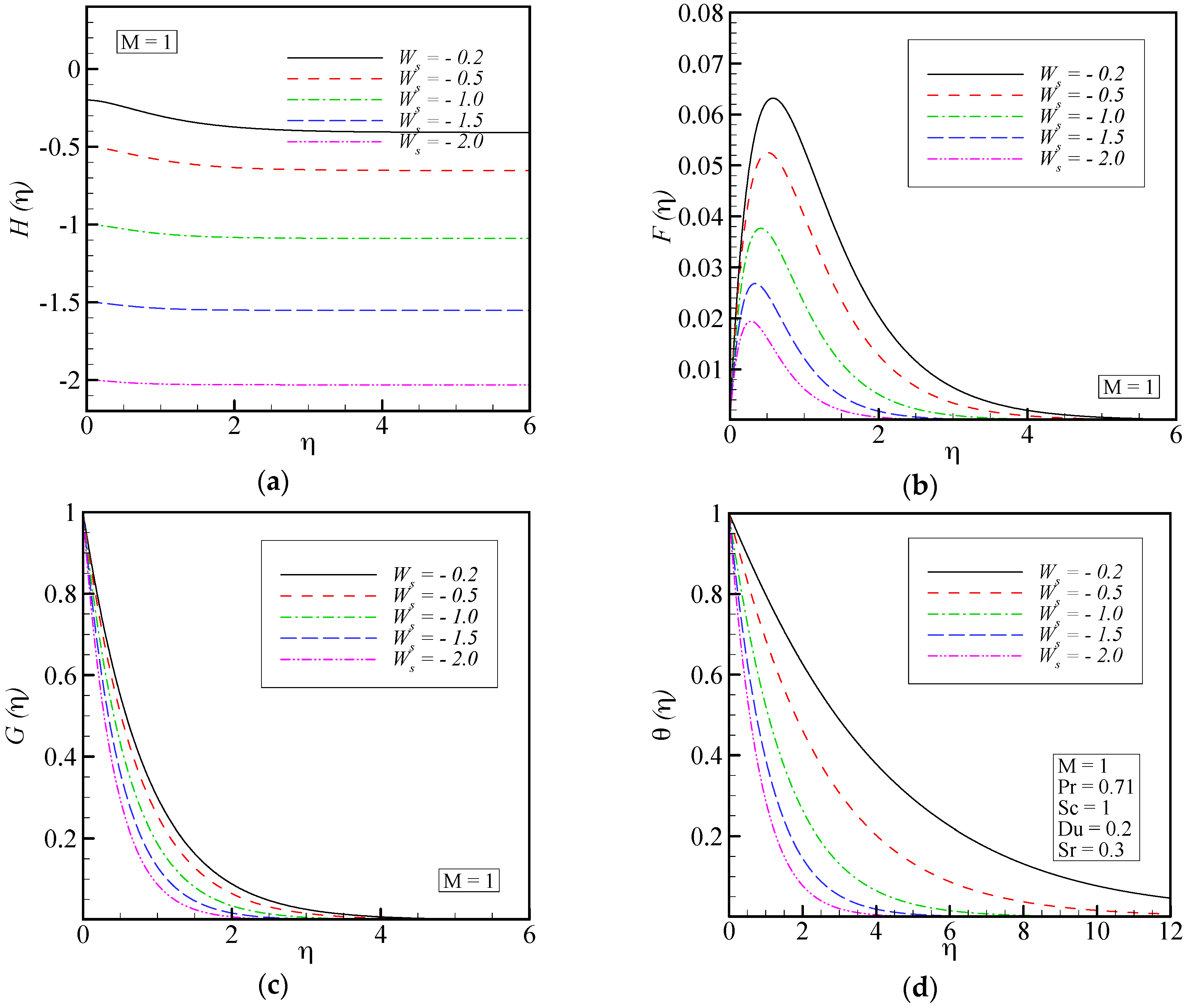
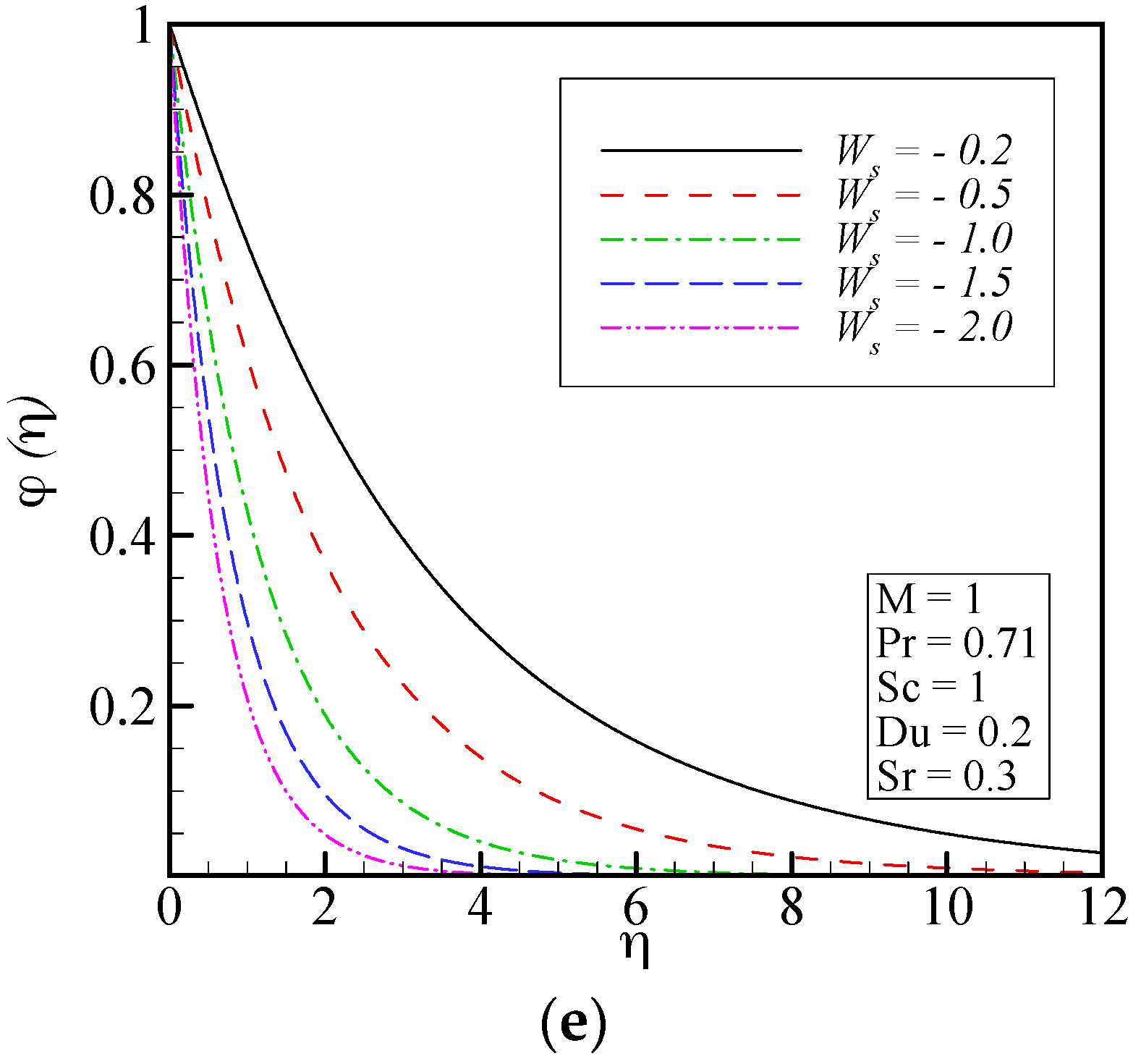
When suction is applied at the disk surface, the radial, tangential and axial velocity profiles decrease. The usual decay of temperature and concentration profiles occurs for larger values of the suction parameter.

(d)

The thermal boundary-layer thickness decreases with increasing Prandtl number. Furthermore, as the Schmidt number increases, the concentration boundary layer thickness decreases.

(e)

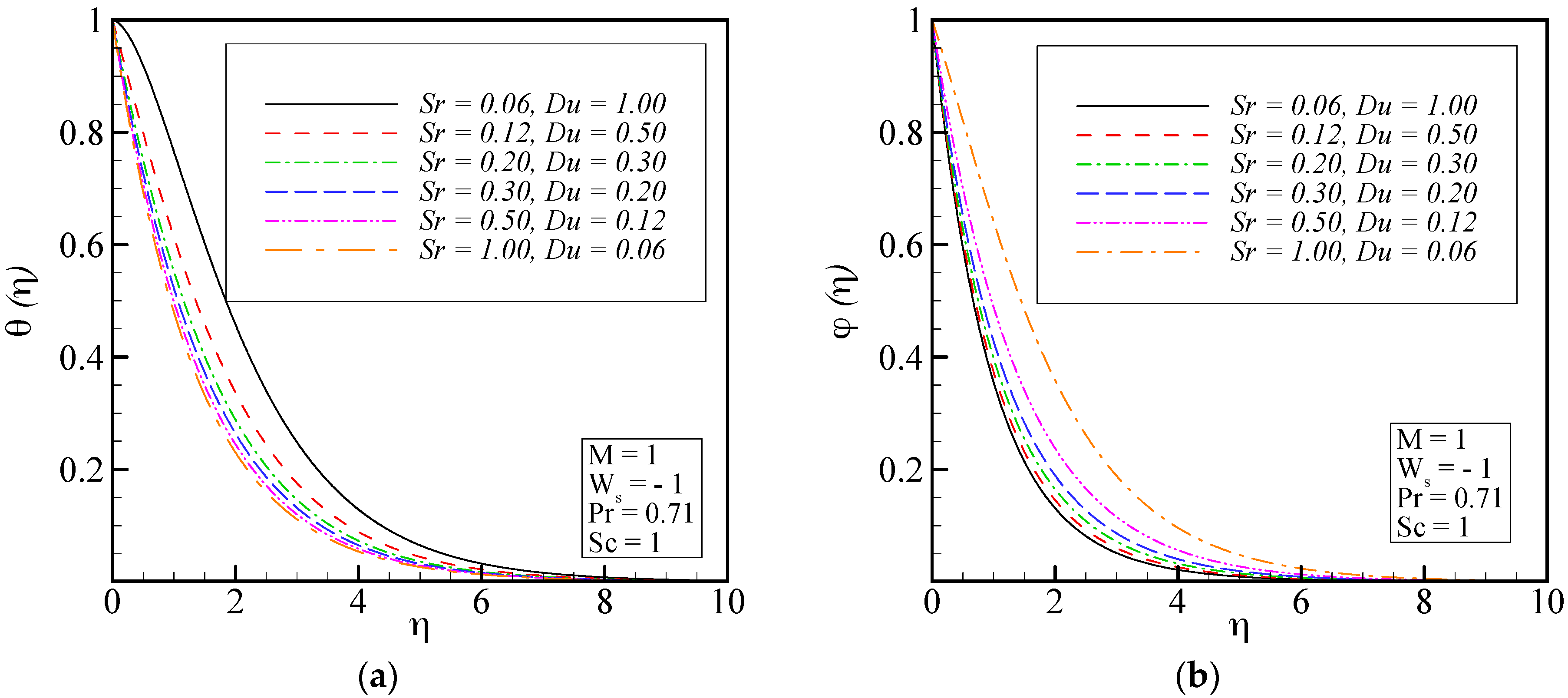
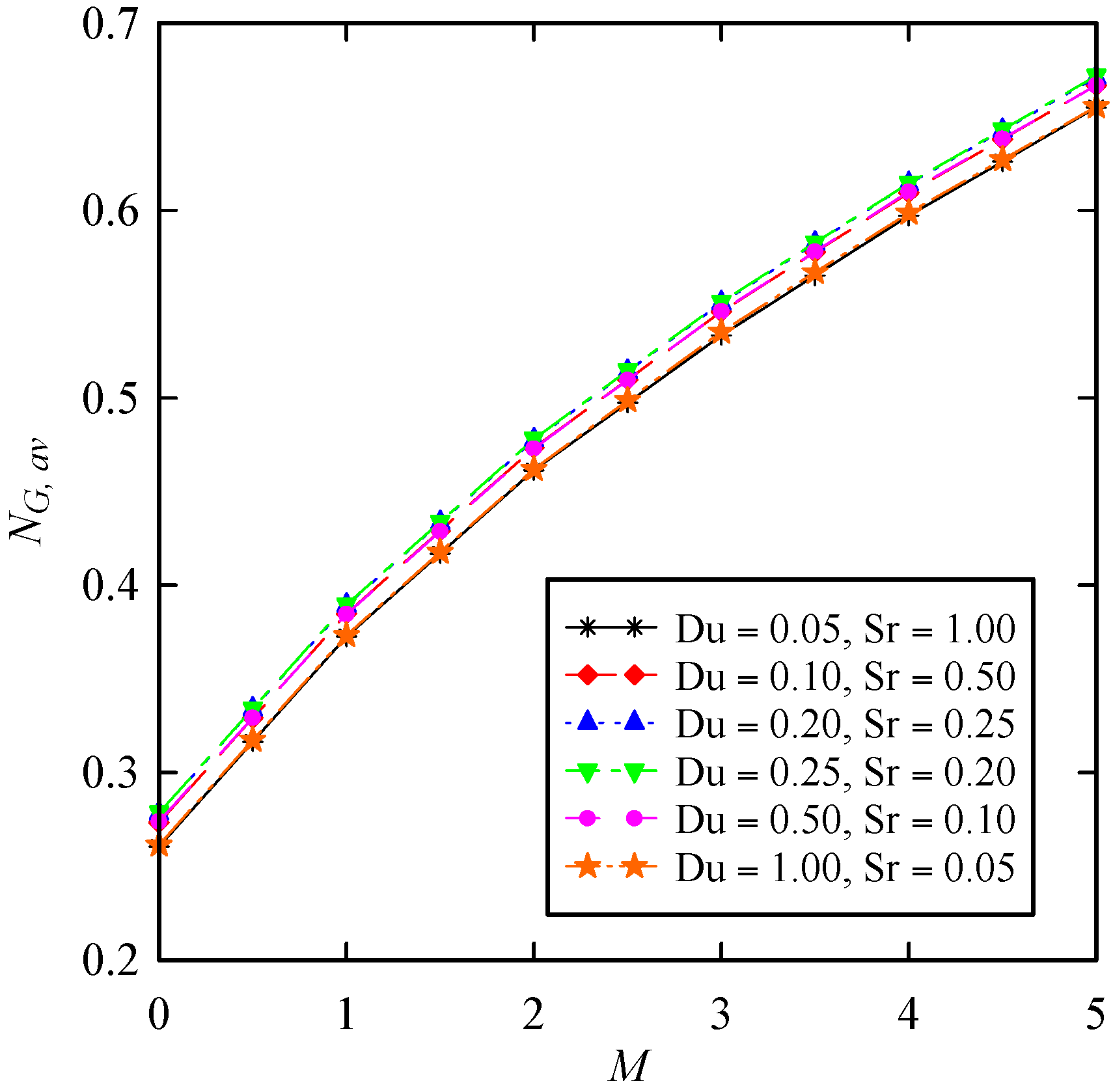
The thermal boundary layer increases by increasing Dufour number or simultaneously decreasing Soret number. As the Dufour number increases or Soret number decreases, the rate of mass transfer (concentration boundary layer thickness) decreases at the disk.

(f)

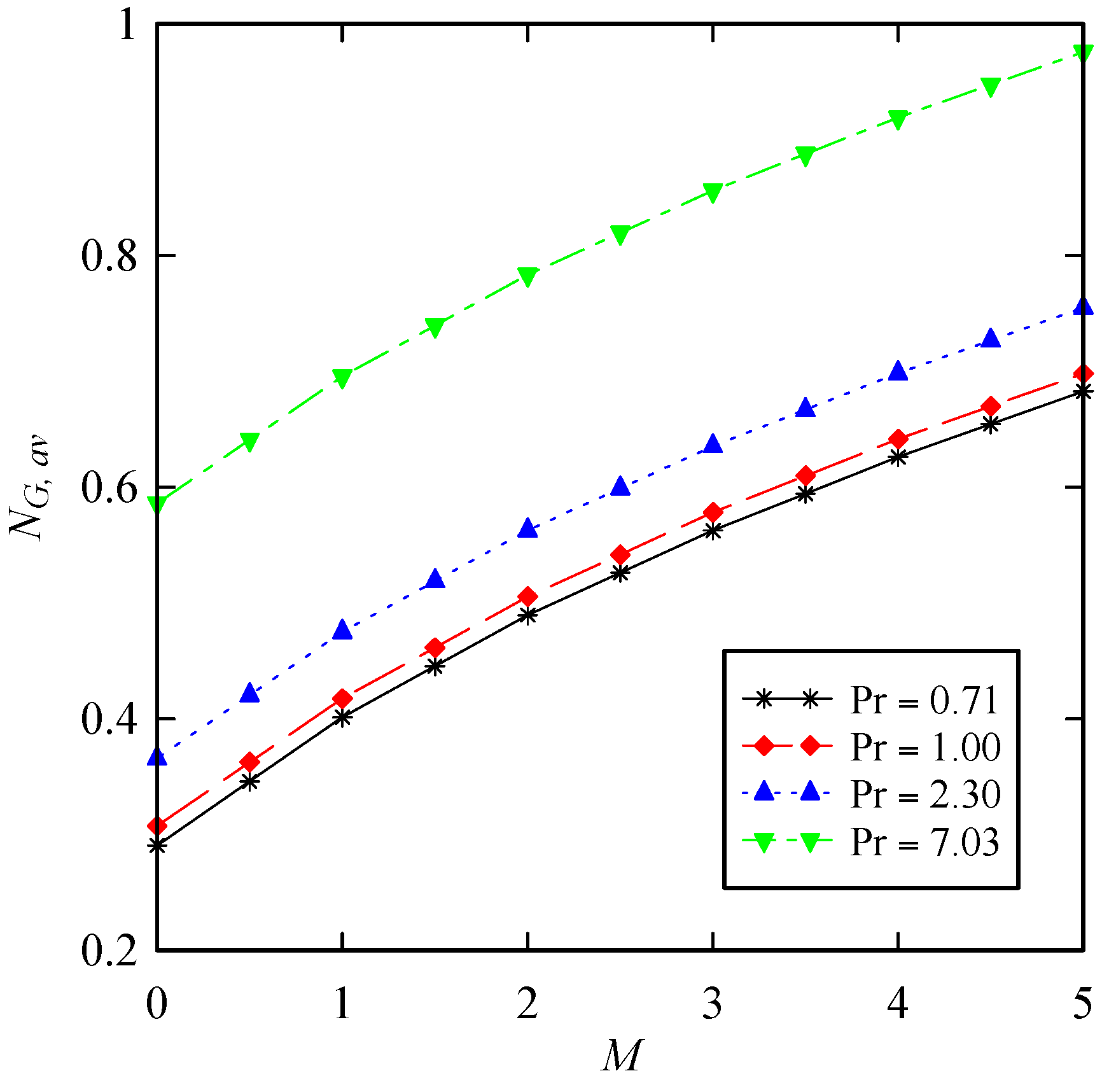
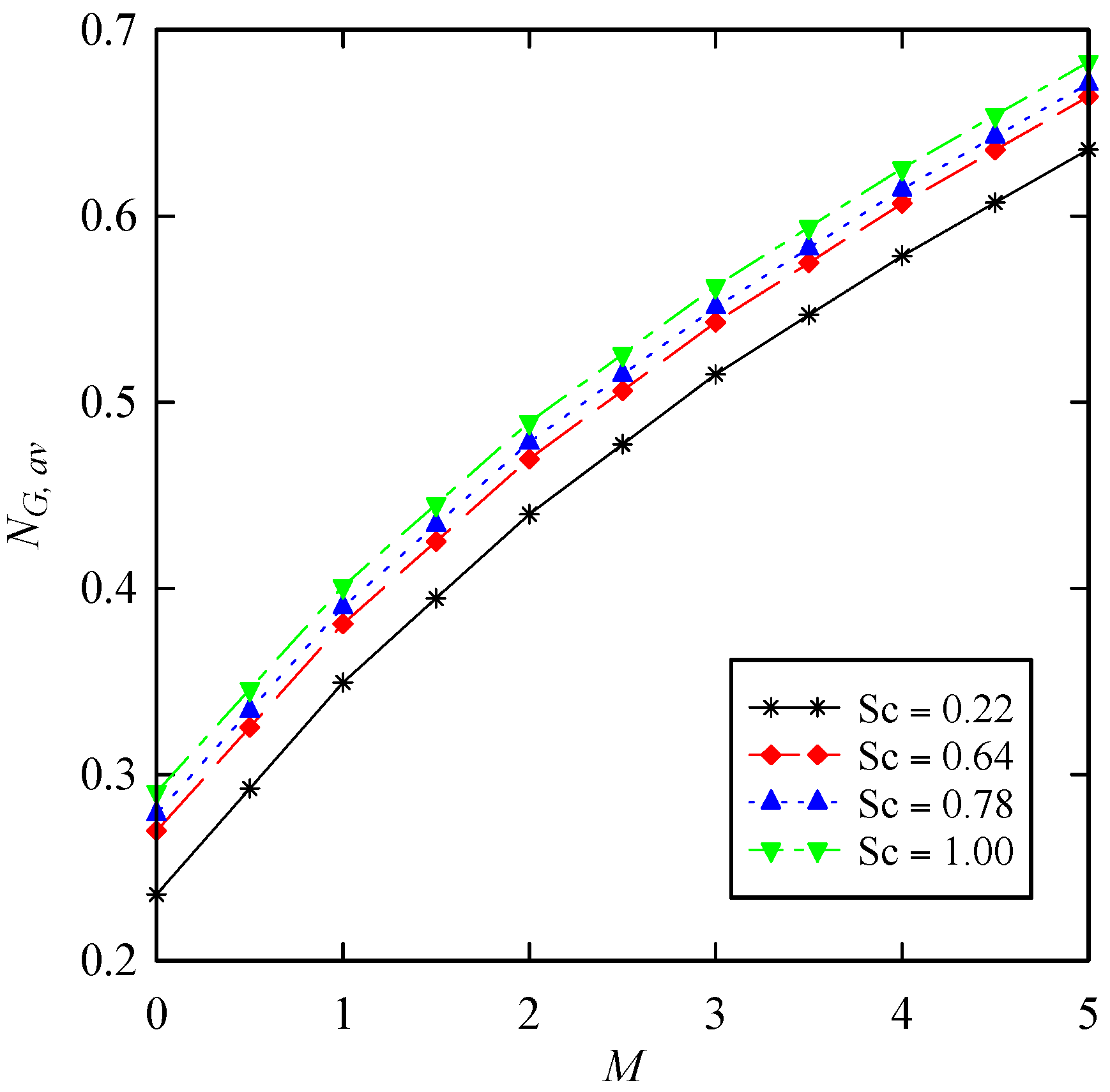
The averaged entropy generation number increases by increasing the magnetic interaction parameter, suction parameter, Prandtl number, and Schmidt number. In addition, the maximum values of averaged entropy generation number occur when the values of both Soret and Dufour numbers are maximized simultaneously.