Abstract
Measurement of the strength of statistical evidence is a primary objective of statistical analysis throughout the biological and social sciences. Various quantities have been proposed as definitions of statistical evidence, notably the likelihood ratio, the Bayes factor and the relative belief ratio. Each of these can be motivated by direct appeal to intuition. However, for an evidence measure to be reliably used for scientific purposes, it must be properly calibrated, so that one “degree” on the measurement scale always refers to the same amount of underlying evidence, and the calibration problem has not been resolved for these familiar evidential statistics. We have developed a methodology for addressing the calibration issue itself, and previously applied this methodology to derive a calibrated evidence measure E in application to a broad class of hypothesis contrasts in the setting of binomial (single-parameter) likelihoods. Here we substantially generalize previous results to include the m-dimensional multinomial (multiple-parameter) likelihood. In the process we further articulate our methodology for addressing the measurement calibration issue, and we show explicitly how the more familiar definitions of statistical evidence are patently not well behaved with respect to the underlying evidence. We also continue to see striking connections between the calculating equations for E and equations from thermodynamics as we move to more complicated forms of the likelihood.
1. Introduction
Measurement of the strength of statistical evidence is, arguably, the primary objective of statistical analysis as applied throughout the biological and social sciences. Various statistics have been proposed as evidence measures, notably the likelihood ratio (LR) or maximum LR (MLR); the Bayes factor (BF); and most recently, the relative belief ratio [1]. Each of these has immediate intuitive appeal. For example, the LR is appealing insofar as it assigns supporting evidence to that hypothesis which assigns higher probability to the observed data, a readily appreciated and appealing property [2,3,4].
In previous work, we have argued that for any evidence measure to be reliably used for scientific purposes, it must be properly calibrated, so that one “degree” on the measurement scale always refers to the same amount of underlying evidence, within and across applications [5,6,7]; and we have begun to develop such a measure. The current paper substantially generalizes previous results, which applied only to the binomial model, to hypothesis contrasts involving the general m-dimensional multinomial likelihood.
At the outset of the project, we defined statistical evidence only very broadly, as a relationship between data and hypotheses in the context of a statistical model. We then posed a measurement question: How do we ensure a meaningfully calibrated mapping between the object of measurement, i.e., the evidence or evidence strength, and the measurement value? Posing the question in this way has led us to develop a novel methodology for addressing it. The current paper is organized so as to make clear the connections between the methodology we are using and a template articulated by the mathematician and physicist Hermann Weyl:
“To a certain degree this scheme is typical for all theoretic knowledge: We begin with some general but vague principle, then find an important case where we can give that notion a concrete precise meaning, and from that case we gradually rise again to generality and if we are lucky we end up with an idea no less universal than the one from which we started. Gone may be much of its emotional appeal, but it has the same or even greater unifying power in the realm of thought and is exact instead of vague.”([8], p. 6, emphasis added)
Following Weyl’s steps, the remainder of the paper is organized as follows: in Section 2 we consider a general but vague notion of statistical evidence. In Section 3 we give that notion a precise (mathematical) meaning, which is, however, demonstrably not general. In particular, the initial mathematical expression for evidence “works” (in a sense to be made explicit below) only for a simple one-sided (composite vs. simple) binomial hypothesis contrast (HC). In Section 4 we generalize the mathematical expression to apply to two-sided composite vs. simple binomial HC, while at the same time extending the formalism to cover m-dimensional multinomial HCs. In Section 5 we generalize one step further, adapting the expression to cover composite vs. composite (nested) HCs in the general multinomial setting. In Section 6 we consider whether the resulting measure of evidence is intrinsically calibrated, drawing on connections with thermodynamics. In the Discussion, we consider the steps that remain in order to render the theory practical and fully general. Section 2 and Section 3 briefly review previously published material [9], although in a somewhat different form in order to make explicit the connections to Weyl’s template and to the new results in Section 4, Section 5 and Section 6.
2. A Vague but General Understanding of Statistical Evidence
We began this project by articulating a set of fundamental characteristics we considered to be inherent in our informal understanding of statistical evidence, in the context of simple coin-tossing experiments. We originally considered a set of n independent tosses of which x land heads, and the evidence that the coin is either biased towards tails or fair. We argued [6,10] that there are general patterns, which we call Basic Behavior Patterns (BBPs), characterizing the relationships among n, x and the evidence that the coin is either biased or fair, which we can agree upon without any formal treatment whatsoever.
We chose the coin-tossing model because it provides a case in which we can elicit relatively naïve intuitions about evidence strength, that is, without appealing to sophisticated knowledge of probability models or formal inference procedures. The BBPs play a role analogous to axioms. However, they are unlike most axiom systems insofar as they are intended to capture in a general but vague way what we mean when we talk about statistical evidence, rather than to impose any particular concrete mathematical requirements on the basis of established statistical theory (e.g., asymptotic convergence; relationship to maximum likelihood estimation; etc.).
In brief, the initial set of BBPs are:
- (i)
- Evidence as a function of changes in x/n for fixed n: If we hold n constant but allow x/n to increase from 0 up to ½, the evidence in favor of bias will at first diminish, and then at some point the evidence will begin to increase, as it shifts to favoring no bias. BBP(i) is illustrated in Figure 1a.
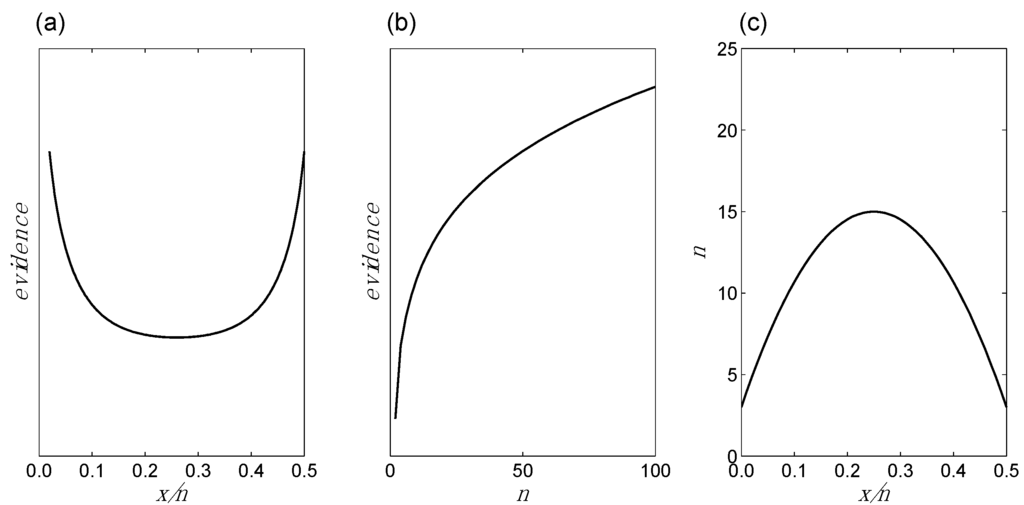 Figure 1. Basic Behavior Patterns (BBPs) for evidence regarding whether a coin toss is fair or biased towards tails: (a) Evidence as a function of changes in x/n for fixed n; (b) evidence as a function of changes in n for fixed x/n; (c) changes in n and x/n for fixed evidence. No calculations are done here and no specific values are assigned to the evidence. Only the basic shapes of the three curves, respectively, are important.
Figure 1. Basic Behavior Patterns (BBPs) for evidence regarding whether a coin toss is fair or biased towards tails: (a) Evidence as a function of changes in x/n for fixed n; (b) evidence as a function of changes in n for fixed x/n; (c) changes in n and x/n for fixed evidence. No calculations are done here and no specific values are assigned to the evidence. Only the basic shapes of the three curves, respectively, are important. - (ii)
- Evidence as a function of changes in n for fixed x/n: For any given value of x/n, the evidence increases as n increases. The evidence may favor bias (e.g., if x/n = 0) or no bias (e.g., if x/n = ½), but in either case it increases with increasing n. Additionally, this increase in the evidence becomes smaller as n increases. For example, five tails in a row increase the evidence for bias by a greater amount if they are preceded by two tails, compared to if they are preceded by 100 tails. BBP(ii) is illustrated in Figure 1b.
- (iii)
- x/n as a function of changes in n (or vice versa) for fixed evidence: It follows from BBPs(i) and BBPs(ii) that in order for the evidence to remain constant, n and x/n must adjust to one another in a compensatory manner. For instance, if x/n increases from 0 to 0.05, in order for the evidence to remain the same, n must increase to compensate; otherwise, the evidence would go down following BBP(i). BBP(iii) is illustrated in Figure 1c.
Note that we have not (yet) attempted to formalize things in any way: There is no probability distribution, no likelihood, no parameterization of the hypotheses. The BBPs characterize evidence in only a very vague manner. However, by the same token, they exhibit a kind of generality: They derive from our general sense of evidence, from what we mean by statistical evidence before we attempt a formal mathematical treatment of the concept.
3. A Precise but Non-general Definition of Statistical Evidence
Can we find a precise mathematical expression that exhibits the BBPs discussed in the previous section? The answer is yes, and the expression is surprisingly simple, although it does not look quite like anything else in the statistical literature.
Let θ = P (coin lands heads), so that our two hypotheses become H1: 0 ≤ θ < ½ vs. H2: θ = ½. Then the likelihood ratio (LR) on given data (n, x) is:
The maximum LR (MLR) is obtained by evaluating Equation (1) at the maximum likelihood estimate (m.l.e.) = x/n, and the area under the LR graph (ALR) is obtained by integrating Equation (1) over the interval [0, ½]. Our first formal definition of evidence, , is:
Figure 2 shows the behavior of , and illustrates that Equation (2) recapitulates the basic patterns of behavior, as shown in Figure 1, which capture our general understanding of evidence.
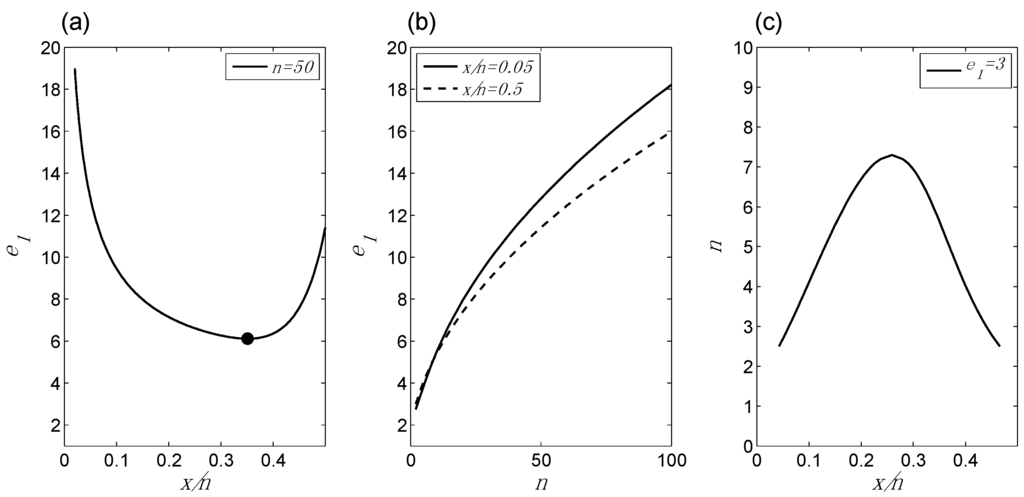
Figure 2.
Behavior of the first evidence measure, e1, in application to the one-sided coin-tossing experiment (coin toss is fair vs. biased towards tails): (a) e1 as a function of changes in x/n for fixed n (the circle at x/n = 0.351 marks the TrP); (b) e1 as a function of changes in n for fixed x/n; (c) changes in n and x/n for fixed e1. This figure, which is based on actual numerical calculations, exhibits the three basic behavior patterns illustrated in Figure 1.
In fact, Equation (2) displays another behavior that we did not predict in advance, but which we might have anticipated. For given n, let the value of x/n at which the evidence shifts from favoring bias to favoring no bias (as shown in Figure 2a) be called the transition point (TrP). As illustrated in Figure 3, the TrP asymptotically approaches x/n = ½ with increasing n.
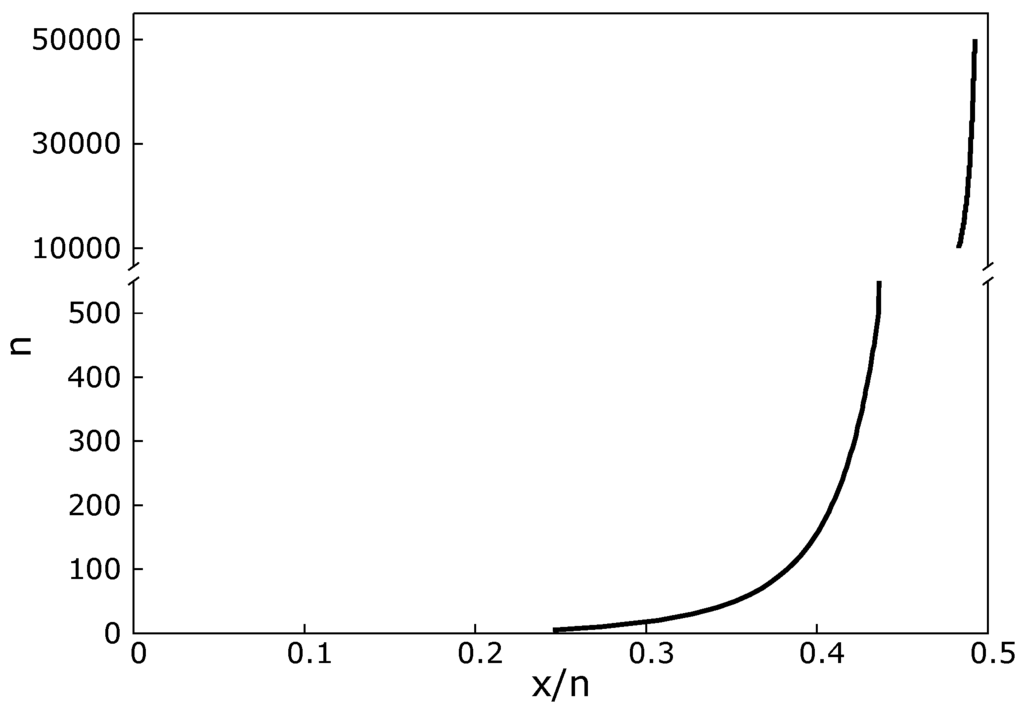
Figure 3.
Behavior of the TrP as a function of n for the one-sided binomial hypothesis contrast, illustrating that the TrP converges from the left toward x/n = ½ as n increases.
The LR itself has been proposed as a definition of statistical evidence by many authors (see, e.g., [2,3,4], and more recently a form of MLR has been proposed as a definition of evidence [11,12] (see also below)). The ALR in this simple model is proportional to the Bayes factor (BF) under a uniform prior, which is often taken as a definition of statistical evidence in Bayesian circles [13,14]; the ALR is also proportional to the relative belief ratio [1].
Arguably both the MLR and the BF (or relative belief ratio) have direct “emotional” (or intuitive) appeal as evidence measures: e.g., the MLR tells us how much more probable are the data on one hypothesis compared to another, which seems on the face of it to be an elegant way to express evidence. However, neither the MLR or the ALR captures the behaviors illustrated in Figure 1, as Figure 4 illustrates. Thus the MLR and the ALR, each of which might appear to be a good candidate evidence measure, both fail to exhibit the basic behaviors of evidence even in this simple setting. On the other hand, the ratio of the two (e1) does capture the set of behaviors we expect of the evidence. This presumably reflects some important underlying relationship between the MLR and the ALR, which to our knowledge has not been previously explored. It also illustrates that the most intuitively appealing mathematical definitions of evidence are not necessarily the best definitions, as they may exhibit behaviors that contradict our general concept of evidence.
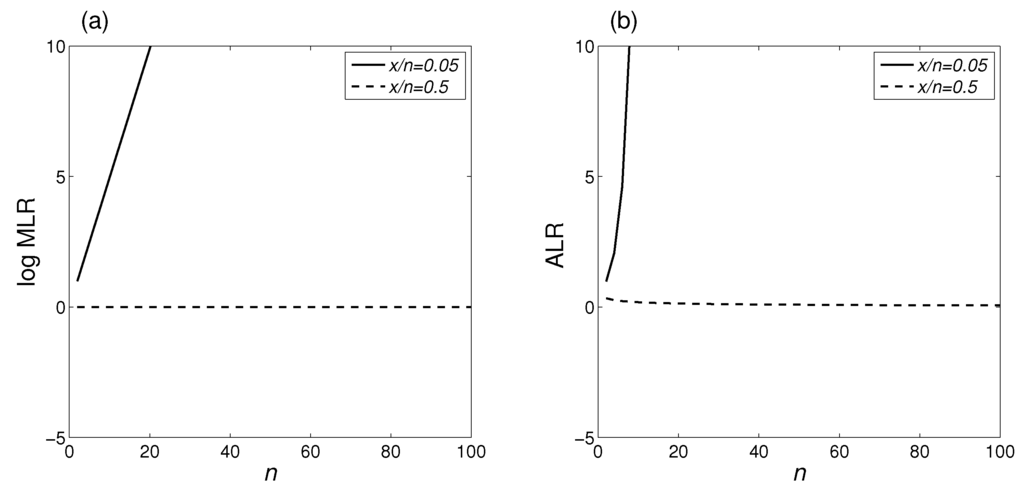
Figure 4.
Behavior of alternative evidence measures as a function of n for fixed x/n, for the one-sided binomial hypothesis contrast: (a) log MLR; (b) log ALR, which is proportional to the Bayes ratio using a uniform prior. Neither statistic exhibits the concave down pattern shown in Figure 1b. The log MLR is either constant (for x/n = 0.5) or linear in n (thus the MLR itself is exponential in n); the log ALR behaves appropriately for x/n = 0.5 (it is < 0 and decaying more slowly as n increases), but for values of x/n supporting “coin is biased” it is slightly concave up.
Equation (2) provides a precise mathematical expression for the evidence that conforms to the BBPs. The equation turns out, however, to be quite specific to the one-sided binomial hypothesis contrast (HC) considered here. For example, as we showed in [9], Equation (2) no longer exhibits the BBPs if we apply it to the only slightly more general case of a two-sided binomial HC, “coin is biased toward either heads or tails” vs. “coin is fair”. Thus e1 appears to satisfy Weyl’s second stage: It is precise, but overly specific. The next question is, how general can we make our definition of evidence while maintaining this level of precision?
We use the lower case “e” for our evidence measure to indicate that at this stage we are only postulating e as an empirical measure, that is, one that exhibits the correct patterns of behavior but is not necessarily on a properly calibrated absolute (context-independent, ratio) scale. This mimics the convention in thermodynamics of using the symbol “t” for empirical temperature, reserving “T” for temperature measured on an absolute scale [15]. We return to the question of calibration below.
Before proceeding, we point out that even the simple one-sided binomial model considered in this section has a practical application in the field of human genetics. One way to find the locations of disease-causing genes is using a technique known as linkage analysis. In the case of what are called “fully informative gametes,” (FIGS) linkage analysis involves a binomial likelihood with data n = the number of FIGS and x = the number of recombinant FIGS (so that n − x is the number of non-recombinant FIGS; a FIG is an offspring of a phase known double backcross mating, which can be definitively classified as either recombinant or non-recombinant). This likelihood is parameterized in terms of the genetic, or recombination, distance θ between two genomic loci, where for biological reasons 0 ≤ θ ≤ ½. Linkage analysis asks the question: Is a given genomic position “linked” to the disease gene or not? Formally, this entails an HC between H1: θ < ½ (“linkage”) and H2: θ = ½ (“no linkage”).
Here we illustrate one difference between the MLR and e1 in application to linkage analysis. Consider two data sets: D1 (n = 50, x = 17), and D2 (n = 85, x = 32). MLR = 13.5 for D1 and 13.8 for D2. Thus we might conclude that both data sets support H1 roughly equally well. (Recall that the MLR can never support H2, but can only indicate varying degrees of support for H1.) For these same data, we obtain e1 = 6.1 and e1 = 7.8, for D1, D2 respectively. However, for D1 the data fall to the left of the TrP, and therefore e1 represents evidence for linkage; whereas for D2, the data fall to the right of the TrP and e1 represents evidence against linkage. If we were to perform linkage analysis using the MLR, we would miss the fact (assuming that e1 is behaving correctly) that one dataset supports linkage but the other doesn’t. This same point applies to the (one-sided) p-value (p-value = 0.016, 0.015 for D1, D2 respectively), and the Bayesian e-value (Ev) of [16,17] (Ev = 0.009, 0.010 for D1, D2). A key feature of e1 is that it represents evidence either in favor of H1 or in favor of H2., depending on the side of the TrP on which the data fall, thereby satisfying BBP(i) (Figure 1a and Figure 2a).
4. First Generalization: From e1 to e2
In [9] we gave a formula for evidence that displayed the BBPs for the two-sided binomial HC “coin is biased in either direction” vs. “coin is fair”. (In [9] this was classified as a Class II(a) HC: composite vs. simple, nested.) Here we extend this formula to the corresponding class of multinomial HCs, with the original binomial Class II(a) as a special case, adapting the notation in the process.
Let n be the number of observations, m be the number of categories, xi be the number of observations in the ith category, and θi be the probability of the ith category. Let θ = (θ1,..,θm) and let x/n = (x1/n,…,xm/n). The multinomial likelihood in m categories can be written as:
where I is the indicator function and is the probability simplex:
Both θi and xi/n satisfy the constraints on the right hand side of Equation (3). We view the simplex as a function of θ when specifying the hypotheses, and as a function of the data x/n when considering the evidence.
In what follows, the mathematics applies to general m, but to illustrate we will focus on the trinomial (“3-sided die”) 2-simplex, which is easily visualized. As shown in Figure 5a, Δ2 is an equilateral triangle with vertices (1, 0, 0), (0, 1, 0) and (0, 0, 1). In general, the point θ = (θ1 = θ2 = … = θm) is called the centroid, which we denote , so that = (⅓, ⅓, ⅓). When viewing the simplex as a function of θ, we also use the shorthand θCENT; when viewed as a function of the data, the centroid similarly occurs at x/n = (⅓, ⅓, ⅓). For any given x/n, the simplex contains six points corresponding to the six possible permuted orders of the data, as shown in Figure 5b. Each of these six points falls into one of six regions, and these regions represent a symmetry group with respect to the likelihood, that is, each point in any one region has a (permuted) homologue in each of the remaining regions corresponding to the same likelihood.
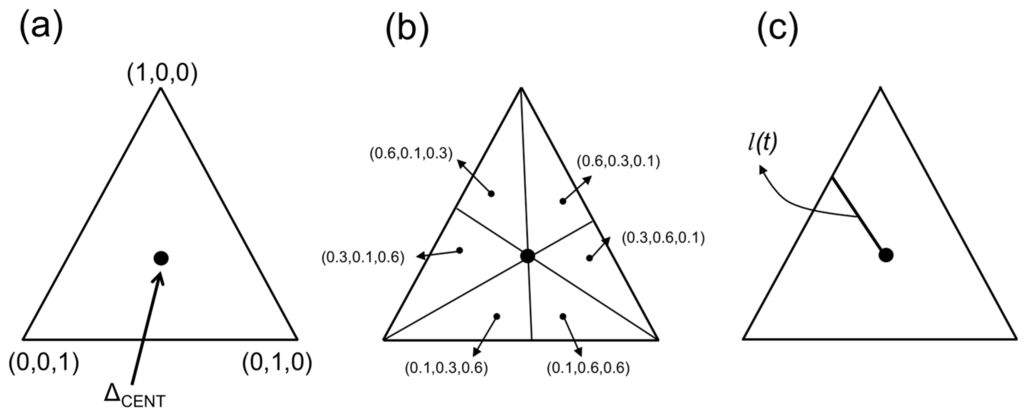
Figure 5.
The trinomial 2-simplex: (a) basic orientation of the simplex in θ = (θ1, θ2, θ3); (b) illustration of permutation symmetry within the simplex; (c) illustration of parameterization of line l used in subsequent figures.
In graphing results as a function of the data, we will use the following convention (illustrated in Figure 5c). Consider a line l running from the centroid to any point on the boundary of the simplex. We parameterize l in terms of the percent Euclidean distance from the centroid, which we refer to as t: e.g., l(t) = l(0.1) represents the point x/n = (x1/n, x2/n, x3/n) along l that is 10% of the distance from the centroid to the boundary. In order to maintain the same orientation as used in the previous binomial graphs, we plot results along a given line l(t) with t running from 1 to 0 (left to right) along the x-axis. Although numerical details vary among different lines, the patterns of all results discussed here apply to all such lines. Hence we can plot results along a particular line without loss of generality.
The natural multinomial generalization of the two-sided binomial HC considered in [9] is H1: vs. H2: . In our current notation, we can rewrite the formula for evidence derived for the binomial in [9], while extending the notation to cover general m-dimensional multinomial HCs, as:
where:
with the numerator evaluated at the m.l.e. = (θ1 = x1/n,..,θm = xm/n) , and:
with the single integral sign standing in for multidimensional integration over the simplex. Equation (6) now becomes the volume under the LR rather than the area under the LR, which is why we switch form “ALR” to “VLR.” In the exponent of Equation (4), d.f. stands for statistical degrees of freedom; b is a constant (See Appendix A for additional details). Note that Equation (2) is the special case of Equation (4) with d.f. = 1 and b = 0. VLR can be easily computed using the multivariate Beta function B, as VLR = mnB(x1+1,…,xm+1).
Figure 6 illustrates the behavior of e2 (Equation (4)), and confirms that e2 continues to exhibit the expected behaviors. These included BBPs(i)–(iii), as described above. In addition, the TrP along any given line l(t) approaches asymptotically, as it did in the original binomial setting.
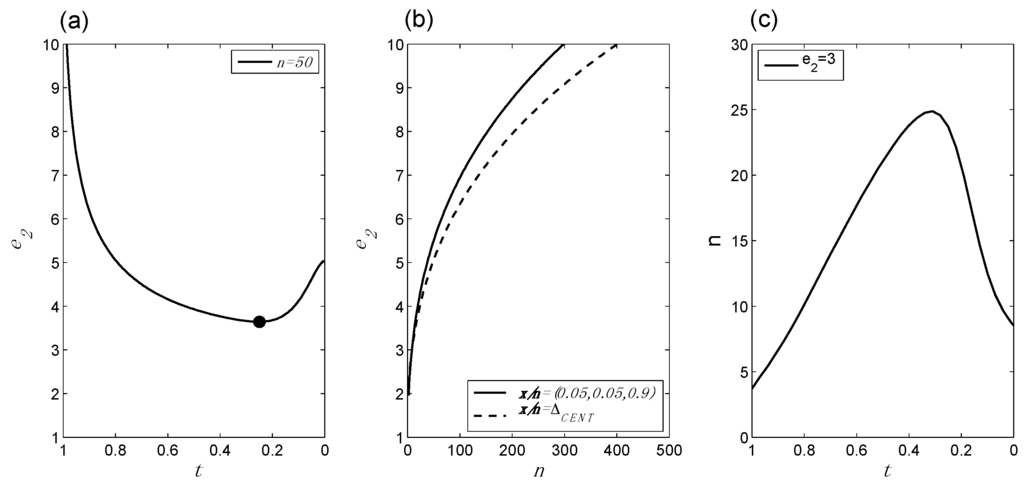
Figure 6.
Behavior of the second evidence measure, e2, in application to the composite vs. simple trinomial HC: (a) e2 as a function of changes in x/n for fixed n, with the TrP indicated by the circle; (b) e2 as a function of changes in n for fixed x/n; (c) changes in n and x/n for fixed e2. e2 continues to exhibit all three basic behavior patterns illustrated in Figure 1 and Figure 2.
We note that the numerator in Equation (4) is defined here as the MLR, whereas previously [9] we used what we called the observed Kullback–Leibler divergence (KLD), defined as the KLD [18] with (for the binomial) used to specify the distribution over which the expectation is taken. As noted in [9], for the binomial HCs considered in that paper, these two quantities are identical; this identity extends to the multinomial extension considered here. Thus which form we use is at present moot. We also argued in [9] that by virtue of this identify, the MLR itself—which is usually interpreted as indicating the evidence—ought instead to be considered as representing the (relative) entropy.
5. Second Generalization: From e2 to e3
We now generalize further to what we previously [9] classified as a Class II(b) HC: composite vs. composite, nested. As before, we consider only the subset of such HCs that maintain basic symmetry around the centroid. (See the Discussion section for further comments.) In particular, consider the set of all lines l(t) extending from the centroid to each point on the boundary of the full Δm−1, and the point tα which is α% of the distance along each such line. For the trinomial, these points form an embedded 2-simplex, which we denote , having the same centroid as Δ2 (Figure 7). Our new HC becomes H1: θ ∈ Δm−1 vs. H2: θ ∈ , for a specified value of α.
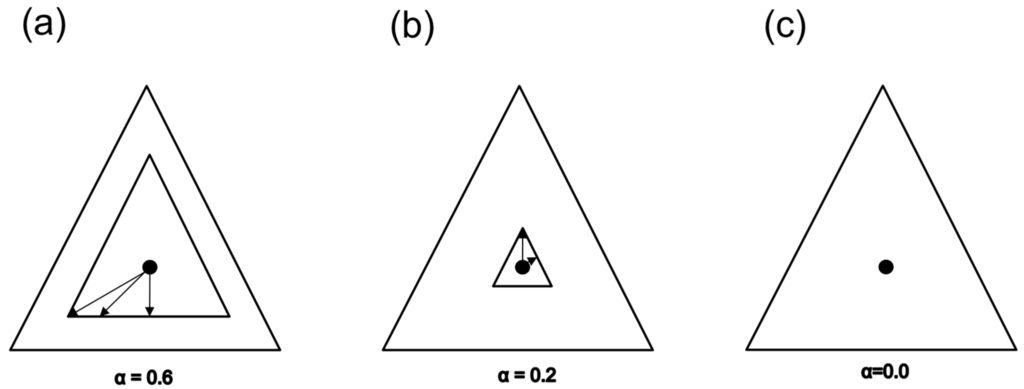
Figure 7.
Illustration of composite vs. composite hypothesis contrast: (a) α = 0.6, (b) α = 0.2, (c) α = 0. As shown, the composite vs. simple HC considered above is the special case α = 0.
In order to extend Equation (4) to the composite vs. composite case, we need to further generalize the notation. Let the maximum likelihood under hypothesis Hi be , indicating that the likelihood is evaluated at the m.l.e. vector under any constraints imposed by Hi. We now extend the calculating formula as follows:
where:
and:
with the single integral sign in (9) again standing in for multi-dimensional integration over θ. V (Equation (9)) is a straightforward generalization of VLR (Equation (6)); the only difference is that in the denominator, rather than fixing θ at the single value stipulated by H2, we use the constrained m.l.e. under H2. S is a generalization of the log of the MLR (Equation (5)); again, the denominator is evaluated at the constrained m.l.e. rather than at a value fixed a priori. Equation (8) has also been called the generalized LR (GLR) and proposed as a definition of statistical evidence for composite vs. composite HCs [11,12]. The reasons for changing from “MLR” to “S” and placing S on the log scale will become clear below. Note that when α = 0, Equation (7) is identical to Equation (4). Thus in moving from e1 to e2 to e3, we are not changing the definition of evidence, but extending it to encompass more general cases.
Figure 8 illustrates that Equation (7) manifests all of the BBPs considered above. The TrP now sits “outside” the H2 (embedded) 2-simplex, converging asymptotically to the boundary of the inner triangle as n increases. This seems a natural extension of the behavior of the TrP in the composite vs. simple case.
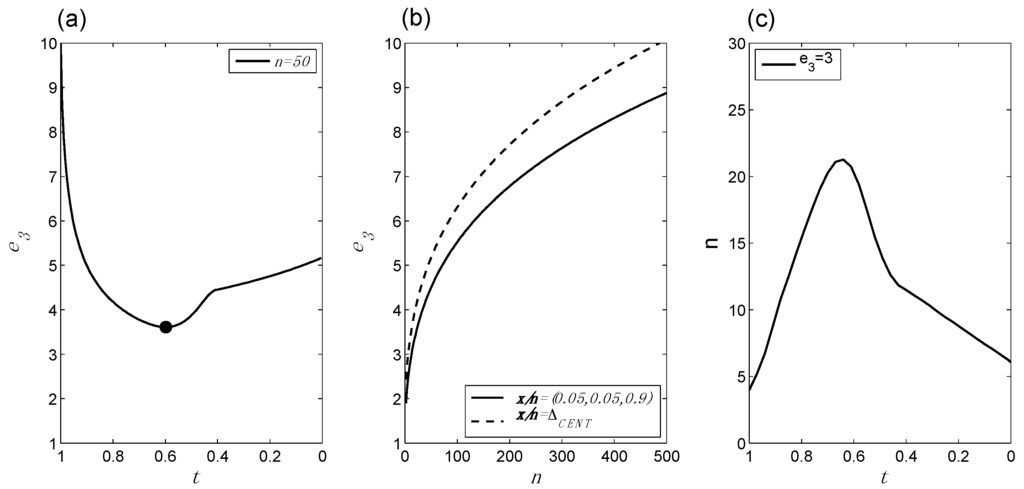
Figure 8.
Behavior of e3 in application to the composite vs. composite trinomial HC, for α = 0.4: (a) e3 as a function of changes in x/n for fixed n, with the TrP indicated by the circle; (b) e3 as a function of changes in n for fixed x/n; (c) changes in n and x/n for fixed e3. e3 continues to exhibit all three basic behavior patterns illustrated in Figure 1, Figure 2 and Figure 6.
In addition, Equation 7 displays some reasonable properties we did not anticipate in advance, in particular with regard to the behavior of the evidence as a function of α. As Figure 9 illustrates, when the data are close to the boundary of the H1 simplex, the evidence for H1 is larger the smaller is α, that is, the more incompatible the data are with H2; when the data are close to the centroid, the evidence for H2 is larger the larger is α, that is, the more incompatible the data are with H1. Again, even unanticipated aspects of the behavior of e3 appear to reflect appropriate behavior for an evidence measure.
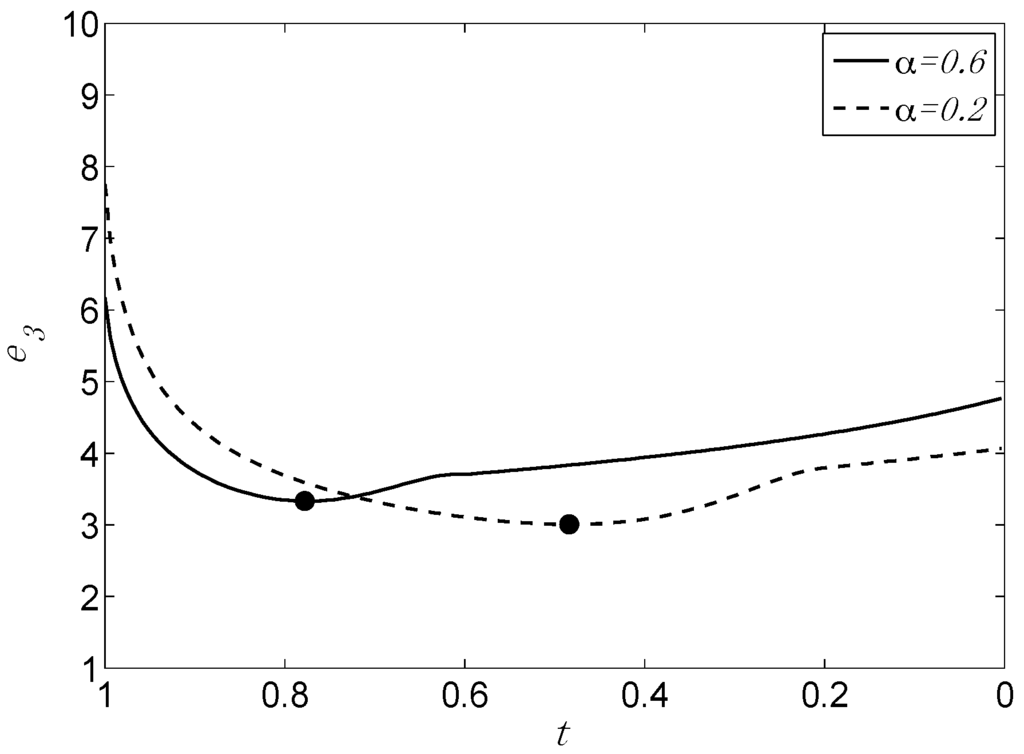
Figure 9.
Behavior of e3 for two different values of α. Of particular note is the relative evidence at x/n near the boundary (t = 1) and near the centroid (t = 0).
To recap to this point: We appear to have successfully discovered a mathematical expression for evidence that is precise, and relatively general, extending at least to multinomial distributions and a broad (though not exhaustive) set of HCs. Equation (7) also almost certainly fits Weyl’s description insofar as it has lost all immediate emotional appeal. Indeed, of the many statisticians and philosophers who have formulated and defended various statistics as evidence measures, none have ever stumbled upon this one as an intuitively appealing candidate. Nevertheless, its behavior appears to do a better job of capturing what we mean by evidence compared to any of the familiar alternatives.
6. Measurement Calibration
As noted above, in using lower case “e” for our measure to this point, we have followed the convention of physics in considering e (whether in the form of e1, e2 or e3) only as an empirical measure, one that exhibits the correct behaviors. But measurement requires more than this, it requires proper calibration, so that a given measurement value always “means the same thing” with respect to the underlying object of measurement, across applications and across the measurement scale. In this section we continue to develop our argument [9,10] that Equation (7)—the most general form of the equation of state thus far—is not merely a good empirical measure of evidence, but also, that it is inherently on a properly calibrated, context-independent ratio scale. From this point forward we therefore refer to Equation (7) using “E”.
Figure 10a illustrates E for a composite vs. simple trinomial HC in a familiar 3-dimensional view, and Figure 10b shows this same HC as a “heat map” imposed on the 2-simplex. As can be seen, E is highest when the data are near the boundaries of the simplex, and lowest along the set of points we now call the transition line (TrL), that is, the set of TrPs, one per line l, that demarcate the transition between “evidence for H1” and “evidence for H2.”
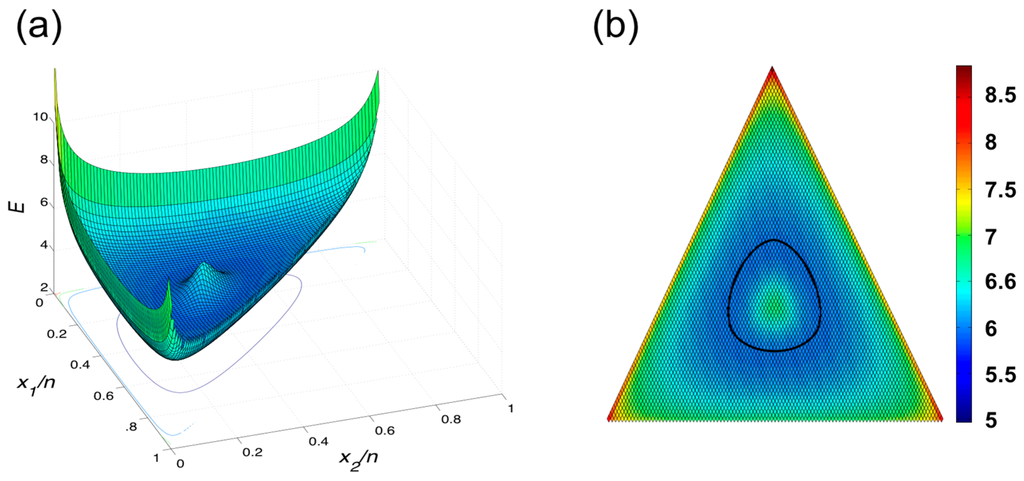
Figure 10.
Behavior of E in application to a composite vs. simple trinomial HC as a function of x/n: (a) ordinary 3D view, (b) representation on the 2-simplex with evidence strength represented by shading. The black line in (b) indicates the TrL, which is the bottom of the trough created in (a) as the evidence shifts (moving from the centroid out) from supporting H2 to supporting H1.
The TrL can be computed by finding the x/n vector along each possible line l that minimizes E; that is, TrL is the set of TrPs comprising the point along each l at which the directional derivative = 0. For the trinomial, the TrPs form a line (TrL), for the quadrinomial they form a plane (TrPL), etc.; Figure 11 illustrates the quadrinomial TrPL. More explicitly, the directional derivative = x/n − becomes the inner product of t and the vector of partial derivatives of E for given data (n, x/n). That is, . The TrP is the value of x/n at which .
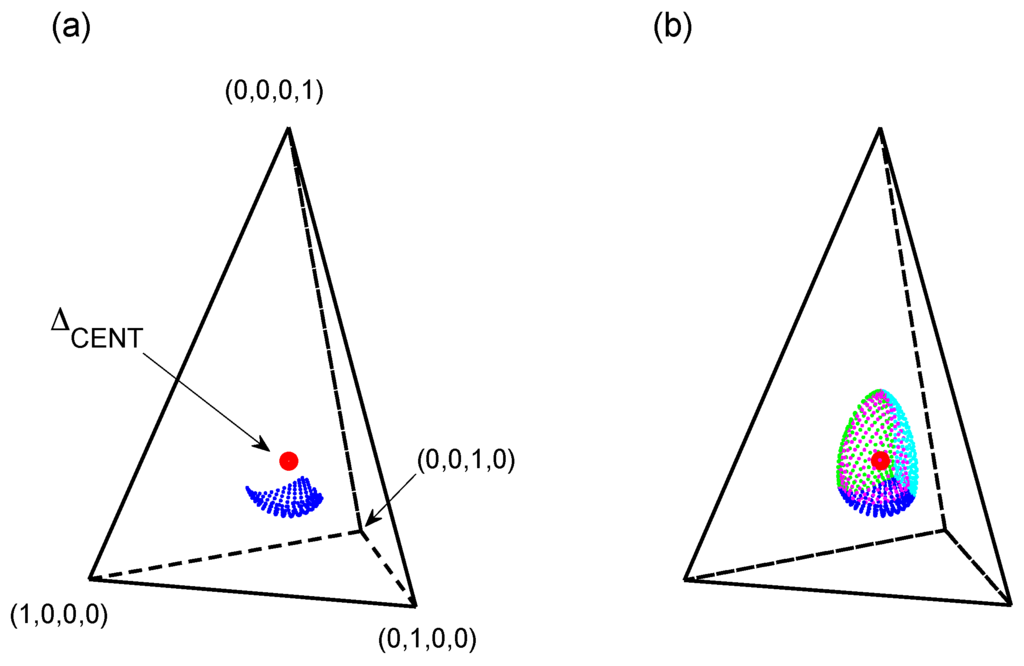
Figure 11.
Illustration of the transition plane (TrPL) for the quadrinomial composite vs. simple HC, H1: vs. H2: θ = (¼, ¼, ¼, ¼). The 3-simplex consists of 4 planes, each of which is defined by 3 of the 4 vertices as labeled in (a). (a) The TrPL along a single plane defined by the vertices (1,0,0,0), (0,1,0,0), and (0,0,1,0); or equivalently, the set of TrPs corresponding to all possible lines l extending from the centroid to that plane. (b) The full TrPL considering all 4 planes, labeled in different colors.
Note that if the directional derivative is positive, x/n supports H1, while if it is negative, x/n supports H2. In practice, it may be useful to show evidence using the sign of the directional derivative to indicate evidence for H2 vs. evidence for H1. (This would be analogous to the convention in physics of showing mechanical work as either positive or negative, to indicate whether the given amount of work is being done by the system or to the system). The (trinomial) TrL separates those data values that constitute evidence for H1 (outside the TrL) from those data values that constitute evidence for H2 (inside the TrL). Note in particular that the TrL is not defined in advance or imposed based on any extraneous considerations, such as error probabilities. Rather, the TrL emerges from the underlying relationships inherent in Equation (7). This is in stark contrast to approaches to evidence measurement based on the MLR or the p-value, in which one specifies a threshold value beyond which the evidence is considered to (sufficiently) favor one hypothesis over the other based on external considerations, such as control of error rates. A natural question to ask, then, is what the TrL itself represents. What features of the system characterize the set of points that constitute the TrL?
We note first that the TrL is a function of n. This follows directly from the behavior noted above for the TrP along any one line l (see Figure 3): as n increases, the TrL converges inwards asymptotically toward the centroid. But for any given n, what do the TrPs along the TrL have in common? Surely we would expect the points that minimize each line l to share some critical characteristic.
For instance, perhaps these points all occur at the same Euclidean distance (Euclid Dist) from the centroid, that is, at a constant value of . Or perhaps the TrPs all correspond to the same MLR, or to the same BF. As Figure 12 shows, none of these suppositions is correct. (The behavior of the MLR along the TrL immediately implies that the p-value obtained from the generalized LR χ2 significance test will also vary along the TrL. Additionally, for the BF the demarcation will depend upon the prior.) The demarcation indicating evidence for or against “die is fair” in our framework is not only conceptually distinct, but also mathematically different from the demarcation in pure likelihood, Bayesian or frequentist settings. Thus there is no obvious relationship between the TrL and readily identifiable quantities that play roles in other approaches to inference.
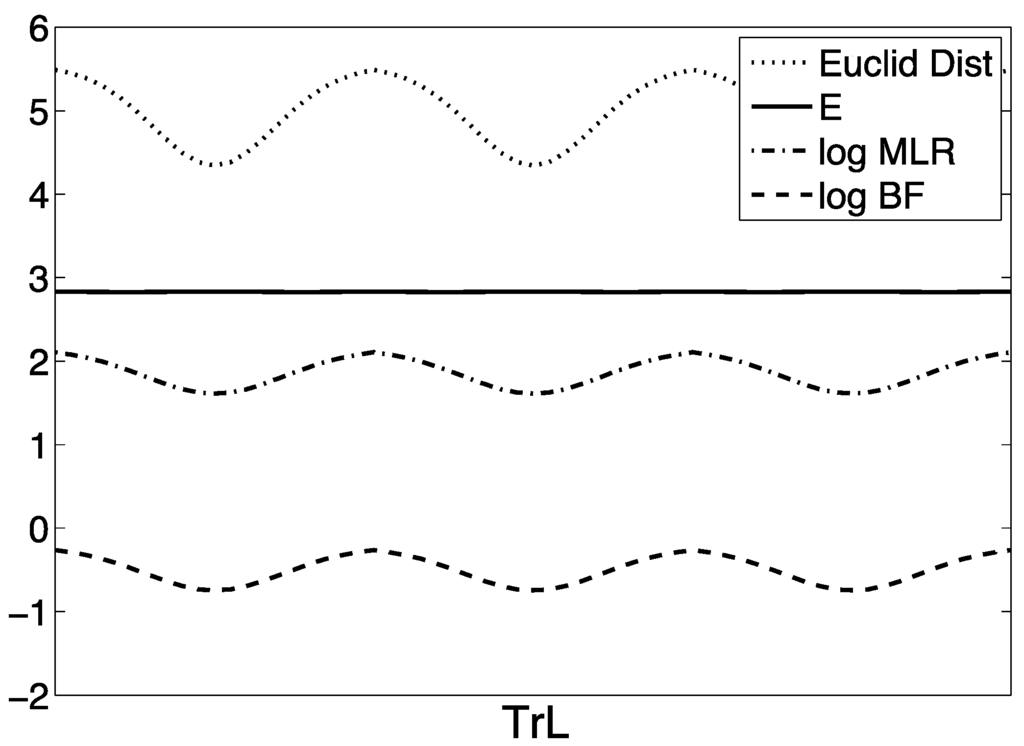
Figure 12.
Various proposed evidence measures plotted along the TrL, traveling from the TrP on the line l which extends to the boundary point x/n = (1, 0, 0) a full 360° around the TrL. Only E is constant along the TrL.
As Figure 12 shows, however, there is one very important quantity that is constant along the TrL: E itself (see Appendix A for additional details.) We can see no obvious analytic feature of the definition of E that guarantees that this would be the case. It appears to again indicate some deep underlying relationship between the maximum log LR (our S) and the volume under the LR (our V). This constancy of E along the TrL is intuitively appealing. It means that for any given n, there is a single value of E that demarcates evidence for one hypothesis vs. the other.
We do not need to stipulate this value in advance based on extraneous considerations, as we would for the LR or the p-value. It is inherent in the calculating equation for E. The fact that E is constant along the TrL supports our previous contention [9,10] that E is in fact intrinsically on a properly calibrated measurement scale. Indeed, we have previously [9] observed formal homologies between the equations of state for calculating the evidence (now in the form of Equations (2) and (7) above) and the ideal gas and Van der Waals equations, respectively, from thermodynamics. In order to explain this homology we have proposed an “information-dynamic” theory, in which evidence is a relationship between different types of information, which are conserved and inter-converted during transformations of the LR graph with new data, under principles strongly resembling the 1st two laws of thermodynamics [19].
The defining equation for E in the underlying theory is:
where S is given by Equation (8) and Q is the amount of evidential information conveyed by new (incoming) data [10,19]. In these terms, the constancy of E along the TrL represents constant dQ/dS, or the incoming evidential information scaled by the change in the entropy. Equation (10) is a formal analogue of the thermodynamic definition of absolute temperature T, dQ = TdS, where Q is heat and S is thermodynamic entropy. Familiar arguments [15] establish that T is on an absolute scale: a given value of T retains the same meaning with respect to the underlying temperature regardless of the circumstances (e.g., regardless of the substance being measured); and T is demonstrably on a ratio scale, in the sense that, e.g., 2 × T represents twice as hot a temperature as T.
dQ = EdS
While the interpretation of the constituent terms differs between Equation (10) as used to define E and the corresponding equation for T, the mathematics is identical. Hence, based on homology and now considering the result that the TrL is an iso-E contour, we continue to hypothesize that E is intrinsically properly calibrated with respect to the underlying evidence.
7. Discussion
We have demonstrated in this paper that the equations we had developed previously for nested binomial HCs can be generalized to apply to nested multinomial HCs involving arbitrarily many categories, with just a few minor adjustments. The resulting quantity E exhibits all of the behaviors of evidence that we set out to capture; it shows considerable coherence beyond these behaviors; and it continues to exhibit striking formal homology with thermodynamic temperature T measured on an absolute scale. Hence our theory as developed to date need not be restricted, as it was previously, to single-parameter likelihoods.
From a mathematical point of view, the connection between evidence and temperature may not be as far fetched as it at first appears. There is of course a sizable literature linking components of statistical inference, information theory and statistical mechanics (see, e.g., [18,20,21,22,23]). But statistical evidence per se plays virtually no role in any of this work; when the term “evidence” is used in this literature it is generally only in passing and without much formal consideration. One thing we have done differently is to take the problem of how to measure evidence on a properly calibrated scale as our starting point.
Additionally, the eminent physicist Callen has proposed a more purely mathematical (rather than physical) cast to the laws of thermodynamics themselves:
“[There is] a notable dissimilarity between thermodynamics and the other branches of classical science….[Thermodynamics] reflects a commonality or universal feature of all laws…[it] is the study of the restrictions on the possible properties of matter that follow from the symmetry properties of the fundamental laws of physics. Thermodynamics inherits its universality…from its symmetry parentage.”([24], pp. 2–3)
Viewing E in terms of the simplex leads naturally to consideration of underlying symmetries. One striking limitation of our results thus far is that E as defined in Equation (7) appears to “work” only for HCs that maintain a certain very basic symmetry around the centroid, including the permutation symmetry described above; when symmetry is violated, E no longer exhibits the correct BBPs. To generalize further, we will almost certainly need to grapple with deeper and more complex forms of symmetry. If we can successfully do so, however, and if the results share a “symmetry parentage” with thermodynamics, then the mathematical connection between the two topics will be clear.
E as defined here is still not sufficiently general to be useful in most statistical applications. Among current limitations, there are two that we are prepared to defend as inherent in the evidence measurement problem. First, E requires a likelihood. This is true of the LR and the BF as well, and, as with those statistics, there may be approximations to E available when a full likelihood is not at hand, e.g., based on pseudo-likelihoods. Second, we have thus far restricted our attention to likelihoods defined over discrete probability spaces. Here we follow [1,3] in stipulating that in scientific applications, all distributions are fundamentally discrete because data are measured only to finite accuracy. Continuous distributions are sometimes useful approximations in such circumstances, but as they add mathematical difficulties with no apparent gain in terms of fundamentals of inference [1], we do not view the restriction to the discrete case as a substantive limitation of the theory. From this perspective, the multinomial provides the most general form of likelihood that we need to consider.
On the other hand, while it may be possible to express many statistical problems in terms of m-dimensional multinomial likelihoods, most interesting scientific problems involve fewer than m parameters, because from a modeling point of view what we seek are useful ways to represent the complex nature of reality in terms of a parsimonious set of explanatory parameters. These “parameterized” multinomials will correspond to HCs involving asymmetries around the centroid, which, as noted above, we have not yet addressed. Additionally, in the current paper we did not address non-nested HCs, as we did for the binomial likelihood in [9]. In fact, the solution for non-nested HCs we proposed previously does not appear to generalize to the multinomial setting, and for this reason we suspect that the simplicity of the binomial 1-simplex obscured a fundamental symmetry issue, which remains to be addressed for non-nested multinomial HCs.
While details remain sketchy, we hypothesize at this point that the three outstanding issues —“parameterized” multinomial HCs, asymmetric HCs, and non-nested HCs—are all connected, and will be resolved only once we achieve a deeper theory of underlying symmetries inherent in information-dynamic systems. This will be the next big challenge in moving the theory forward, which will have to be addressed before we can develop practical and general applications for E.
Acknowledgments
This work was supported by a grant from the W.M. Keck Foundation. We thank Susan E. Hodge and Jayajit Das for helpful discussion.
Author Contributions
Veronica J. Vieland and Sang-Cheol Seok conceived and designed the calculations; Sang-Cheol Seok implemented the calculations; Veronica J. Vieland and Sang-Cheol Seok analyzed the results; Veronica J. Vieland wrote the paper in close consultation with Sang-Cheol Seok. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LR | Likelihood Ratio |
| BF | Bayes Factor |
| MLR | Maximum LR |
| ALR | Area under LR |
| VLR | Volume under LR |
| BBP | Basic Behavior Pattern (for evidence) |
| HC | Hypothesis Contrast |
| TrP | Transition Point |
| TrL | Transition Line |
| TrPL | Transition Plane |
Appendix A. The constants d.f. and b
In [9] we wrote the binomial likelihood as a function of a single parameter θ, and distinguished the (set of) values of θ under H1 and H2, respectively, using subscripts 1, 2 on θ. For what we called Class II (nested, composite vs. simple and composite vs. composite) HCs, we defined d.f. as 1 + [θ1r − θ1l]+ [θ2r − θ2l], where [θir − θil] is the length of the interval on θi under the ith hypothesis (i = 1, 2). (So, e.g., for H1: vs. H2: = ½, this would yield d.f. = 1 + 1 + 0 = 2.) In our current notation, the binomial is expressed as the m = 2 one-simplex, and the length of the interval under H2 is replaced by α as defined above, which defines the length of H2 for the binomial, the area within H2 for the trinomial, etc. For the composite vs. simple HC, we can either continue to consider d.f. as a baseline of 1 + the usual statistical d.f. (m − 1), or we can express d.f. simply as m. For the composite vs. composite HCs considered in this paper, d.f. then becomes m + α.
In [9] we expressed the constant b as a function of (i) V, (ii) the minimum observed Fisher information, (iii) two rate constants and (iv) an additional constant. We noted that the entire derivation of b was somewhat heuristic, although there appeared to be strong constrains on the allowable forms b could take while maintaining the BBPs. Here we greatly simplify the expression for b, while generalizing the notation to include the multinomial case. We then consider the relationship between the current form and the previous version.
We again consider a line l(t), as defined above, from the centroid to a point on the boundary of the simplex. For a composite H2 of size α, the point t = α divides l into two sections: t < α corresponds to data vectors inside the region defined by H2, while t > α corresponds to data vectors outside the H2 region. The point t = α also demarcates a change in the behavior of V (Equation (9)), which decreases moving from t = 0 to t = α, and then increases from t = α to the boundary. Thus the minimum V, VMIN, occurs at the point t = α. (For small n and/or large α, VMIN occurs very slightly outside t = α, but with negligible numerical effects.) We then have:
where g1 follows the curvature of V to make V-b a linearly increasing function of t for t = [0, α] and g2 is a (decreasing) straight line connecting t = α and t = 1 (Figure A1).
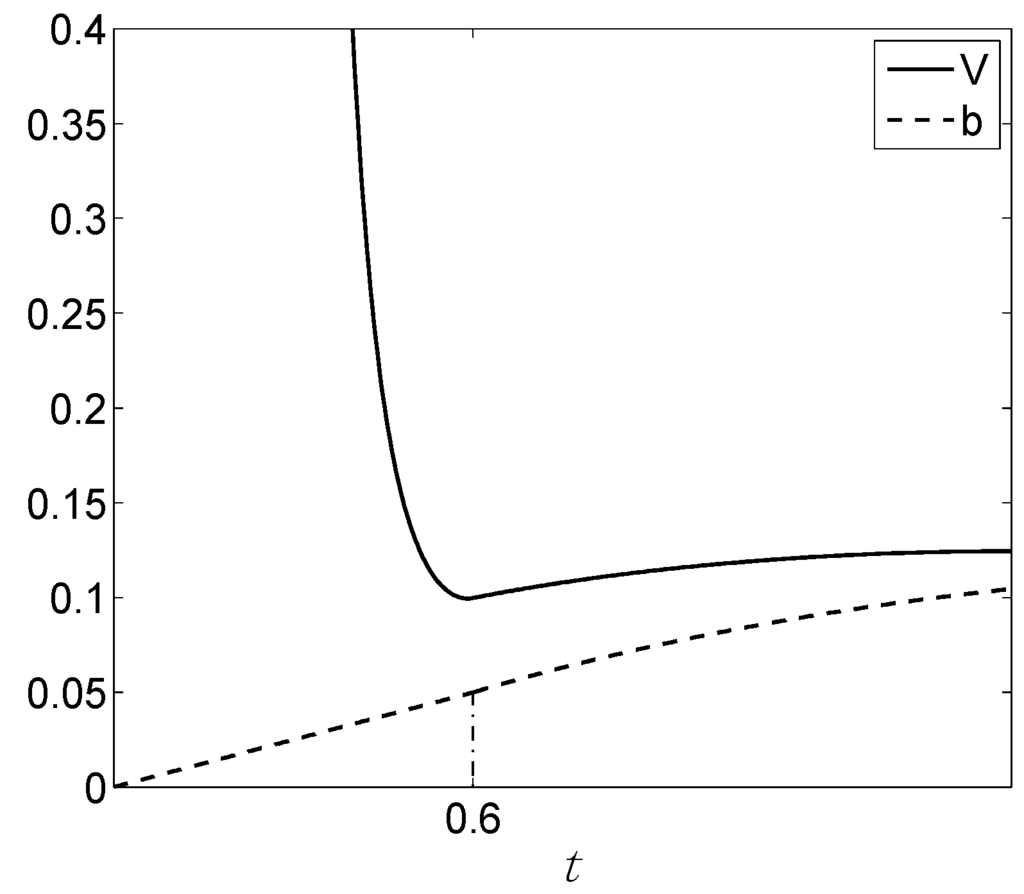
Figure A1.
Illustration of the constant b in relationship to V, for the α = 0.6 composite vs. composite HC (n = 100).
This new formula for b is an improvement over the previous one in four regards. First, it is simpler: in particular, it no longer requires specification of the two rate constants and the additional constant, which is now incorporated into the d.f. Second, it is more general, applying to multinomial HCs and not only binomial HCs. Third, it now makes explicit that b is a function of (i) minimum volume, (ii) d.f., and (iii) the observed value of x/n, or equivalently, the observed value of t. The first two factors have a clear connection to the thermodynamic constant b as it appears in the Van der Waals equation of state, where b “corrects” for minimum volume as a function of physical d.f.; the third factor may also be related to the thermodynamic constant, for systems in which the minimum volume is also a function of the temperature, since the observed value of t also corresponds to how “hot” the system is (that is, the size of E).
Fourth, and perhaps most importantly for us, this revised definition of b yields better behavior than the original b in one key respect, while preserving the BBPs in all other respects. To see this, we first note that E (or e3) as computed from Equation (7), when applied to the binomial composite vs. composite HC, is virtually identical to E as calculated for that same binomial HC in [9], as long as x/n is outside the H2 region, i.e., for t > α. However, when x/n is inside the H2 region (t < α), the new formula for b yields larger values of E (Figure A2). As noted above in connection with Figure 9, when x/n is near the centroid, E in favor of H2 is larger the larger is α, that is, the more incompatible the data are with H1. This seems like the desired behavior. However, we now notice that the original formula for b produced the opposite behavior in the binomial case for x/n close to ½; see Figure 3a in [9]. Thus the new definition of b produces better behavior at least in this one respect.
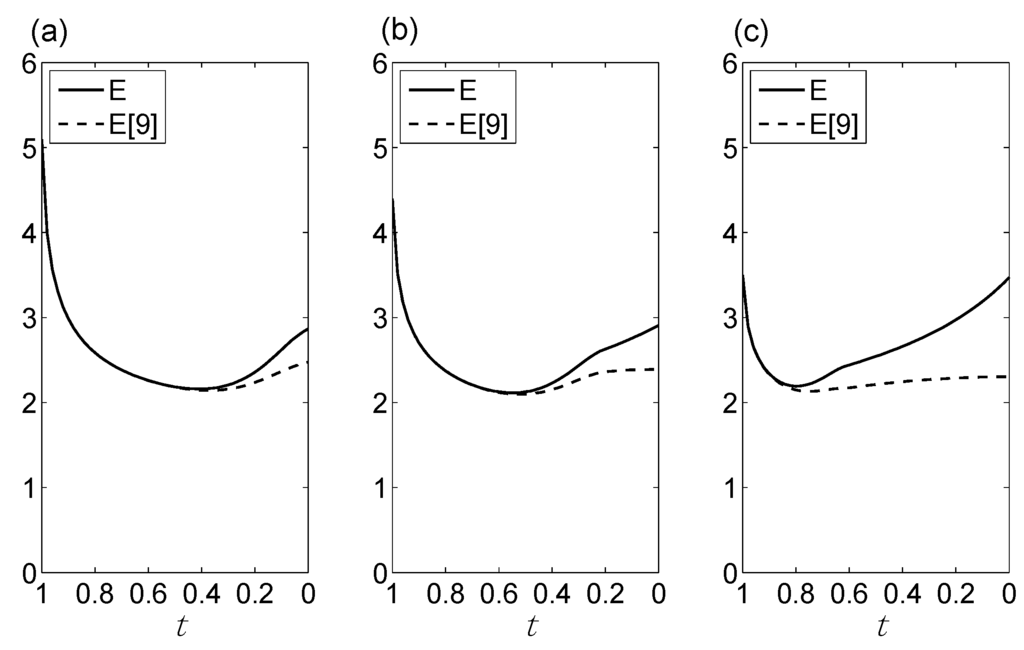
Figure A2.
Comparison of E as computed in [9], denoted “E[9],” using the original version of b, with E as computed from Equation 7, using the revised version of b, in application to the binomial HC H1: vs. H2: , for (a) α = 0.0, (b) α = 0.2, (c) α = 0.6.
While b has been derived “experimentally,” rather than by appeal to any underlying theoretical rationale, nevertheless it is difficult to substantially modify the current formula without disrupting the BBPs. We note, however, a small caveat to the claim above that E is constant along the TrL. In fact, E is not exactly constant for small n, although the deviations are quite small and they decrease as n increases (Table A1).

Table A1.
Deviations of E along the TrL (m = 3) or TrPL (m = 4) as a function of n.
| m = 3 | m = 4 | |||||||
|---|---|---|---|---|---|---|---|---|
| n | Max E | Min E | Diff | Ratio | Max E | Min E | Diff | Ratio |
| 50 | 3.6510 | 3.6449 | 0.0061 | 0.0017 | 4.6245 | 4.6147 | 0.0098 | 0.0021 |
| 100 | 4.4949 | 4.4896 | 0.0053 | 0.0012 | 5.8440 | 5.8342 | 0.0098 | 0.0017 |
| 500 | 7.5096 | 7.5077 | 0.0019 | 0.0003 | 10.4134 | 10.4094 | 0.0040 | 0.0004 |
Notes: Max E = the maximum value of E observed along the TrL (or TrPL); Min E = the minimum observed value along the TrL (or TrPL); Diff = Max E − Min E; Ratio = (Max E − Min E)/Max E.
This may be an inherent property of E for small n, or, it may reflect the fact that the formula for b, which affects the numerical value of E, is still not exactly correct.
References
- Evans, M. Measuring Statistical Evidence Using Relative Belief (Monographs on Statistics and Applied Probability); CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Hacking, I. Logic of Statistical Inference; Cambridge University Press: London, UK, 1965. [Google Scholar]
- Edwards, A. Likelihood; Johns Hopkins University Press: Baltimore, MD, USA, 1992. [Google Scholar]
- Royall, R. Statistical Evidence: A Likelihood Paradigm; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Vieland, V.J. Thermometers: Something for statistical geneticists to think about. Hum. Hered. 2006, 61, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Vieland, V.J. Where’s the Evidence? Hum. Hered. 2011, 71, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Vieland, V.J.; Hodge, S.E. Measurement of Evidence and Evidence of Measurement. Stat. App. Genet. Molec. Biol. 2011, 10. [Google Scholar] [CrossRef]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Vieland, V.J.; Seok, S.-C. Statistical Evidence Measured on a Properly Calibrated Scale across Nested and Non-nested Hypothesis Comparisons. Entropy 2015, 17, 5333–5352. [Google Scholar] [CrossRef]
- Vieland, V.J.; Das, J.; Hodge, S.E.; Seok, S.-C. Measurement of statistical evidence on an absolute scale following thermodynamic principles. Theory Biosci. 2013, 132, 181–194. [Google Scholar] [CrossRef] [PubMed]
- Bickel, D.R. The strength of statistical evidence for composite hypotheses: Inference to the best explanation. Available online: http://biostats.bepress.com/cobra/art71/ (accessed on 24 March 2016).
- Zhang, Z. A law of likelihood for composite hypotheses. Available online: http://arxiv.org/abs/0901.0463 (accessed on 24 March 2016).
- Jeffreys, H. Theory of Probability (The International Series of Monographs on Physics); The Clarendon Press: Oxford, UK, 1939. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Fermi, E. Thermodynamics; Dover Publications: New York, NY, USA, 1956. [Google Scholar]
- Stern, J.M.; Pereira, C.A.D.B. Bayesian epistemic values: Focus on surprise, measure probability! Logic J. IGPL 2014, 22, 236–254. [Google Scholar] [CrossRef]
- Borges, W.; Stern, J. The rules of logic composition for the bayesian epistemic e-values. Logic J. IGPL 2007, 15, 401–420. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover Publications: Mineola, NY, USA, 1968. [Google Scholar]
- Vieland, V.J. Evidence, temperature, and the laws of thermodynamics. Hum. Hered. 2014, 78, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Duncan, T.L.; Semura, J.S. The deep physics behind the second law: Information and energy as independent forms of bookkeeping. Entropy 2004, 6, 21–29. [Google Scholar] [CrossRef]
- Caticha, A. Relative Entropy and Inductive Inference. Available online: http://arxiv.org/abs/physics/0311093 (accessed on 24 March 2016).
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).