For the subsequent quantitative analyses of the impact of emission mitigation on economic growth, it is convenient to introduce the new concept of “conventional output”.
3.2.1. “Polluted” Growth Equation
We assume that at some time
the economic consequences of emission mitigation become relevant for society. Then, conventional output
becomes interesting, besides total output. For its computation, the following growth equation is proposed:
are pollution-modified output elasticities, which replace the
in Equation (
7):
with the technology multipliers
These general output elasticities allow to model, in principle, how different technologies of abating the various types and magnitudes
of pollution reduce the output elasticities for total output to the ones for conventional output. If the pollution-modified output elasticities do not satisfy the integrability conditions (
9),
is not a state function [
36]. Then, the integral of the rhs of Equation (
20) from
to
would not be path independent and its evaluation would require methods that are beyond the scope of this article. Therefore, at present, we only consider scenarios for which it is not unreasonable to assume that all factors and their output elasticities are affected by emission mitigation in the same way, and that one simple number
is sufficient to represent the net, output-elasticity-reducing effect of the three products
in Equation (
21). Then,
In such scenarios, the production function for the conventional output at the time
will remain to be twice differentiable, satisfying the three differential Equations (
9). However, linear homogeneity and the resulting Equations (
10) and (
11) no longer hold for
.
We insert the pollution-reduced output elasticies Equation (
23) into the “polluted” growth Equation (
20), and integrate it for a fixed time
t between an initial point
to a final point
, where the output is
.
At the time of interest
,
, and the path integral that corresponds to the integral in Equation (
14) becomes
. It is equal to the integral of the lhs of Equation (
20), which is
. From that, the production function for the conventional output at time
results to be
The total output
Y at
, which
includes the goods and services dedicated to pollution abatement, and which results from Equation (
15), is given by Equation (
16) at
:
3.2.2. Thermoeconomic Energy and Cost Optimization
We assume that at the time , society realizes that the best action to avoid all sorts of pollution is reducing energy conversion. There is the austerity option, i.e., reduce the demand for energy services. In addition, there is the efficiency option, i.e., use energy more efficiently at unchanged energy services. Let us analyze the latter option.
Energy conservation via heat-exchanger networks, heat pumps and cogeneration of heat and electricity may fit into a scenario where Equation (
24) holds, because these emission-mitigating technologies consist of components such as metal tubes and plates, ceramics and plastics, valves and switches, meters for the flow of masses and electricity, cables, pipes, compressors, steam and gas turbines, combustion engines and electric motors, and technical services, which all have been part of total output of a highly industrialized country for quite some time. It may not be too crude an approximation to assume that the amount of capital, labor, and energy required for their production is just a certain part of the mix of production factors needed for the generation of the total output.
Based on static exergy-enthalpy demand profiles for process heat and electricity of the Netherlands, (west) Germany, Japan, and the USA in the 1970s/1980s, thermoeconomic analyzes of the potentials and cost of energy optimization have been performed. The focus has been on the thermodynamic
limits to energy optimization. This allowed simplifications of the general model of waste heat recovery that made it computable within the Revised Simplex Algorithm [
37].
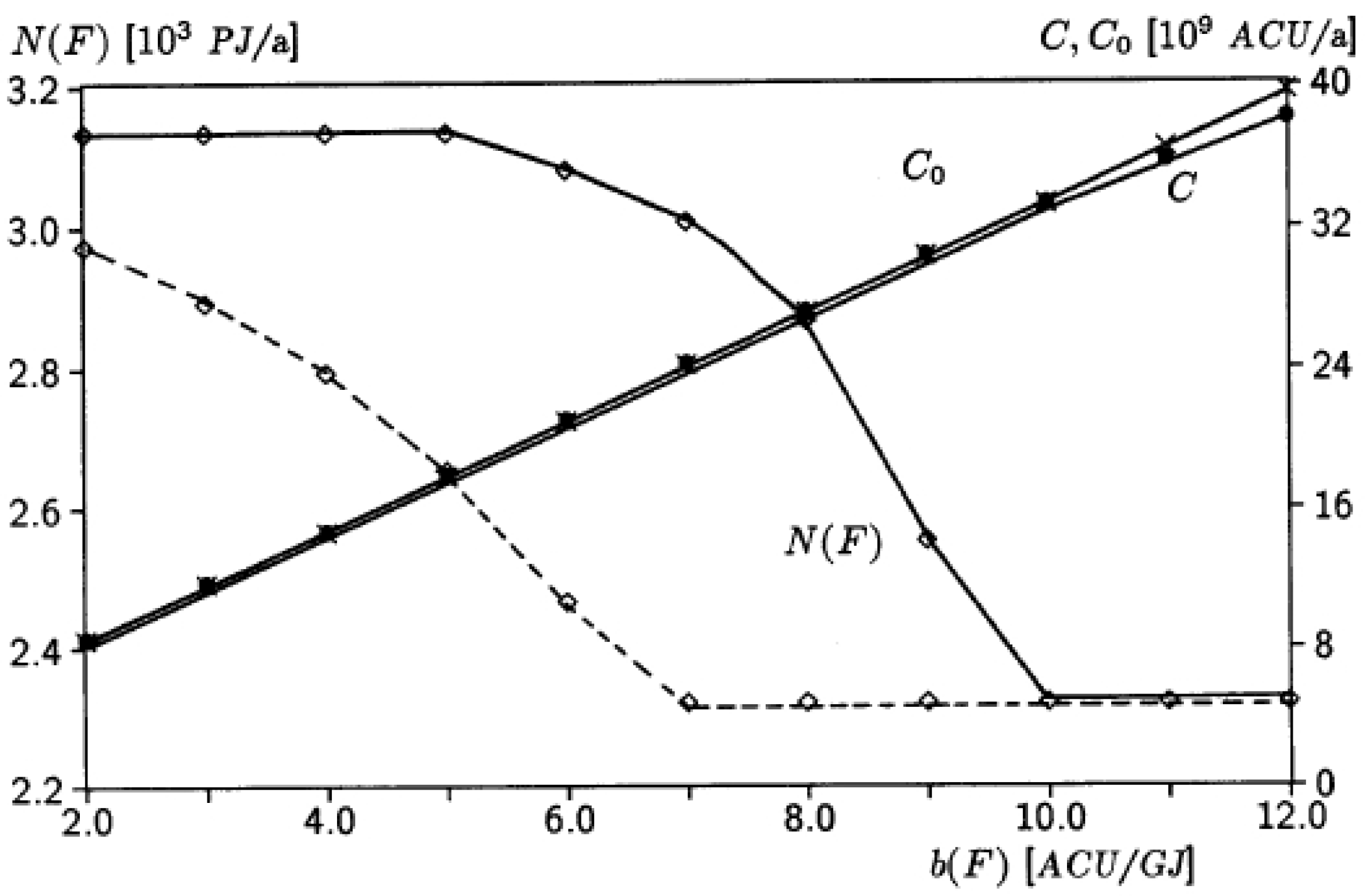
Figure 1 shows the result of energy optimization subject to upper cost limits for (west) Germany [
37]. For the sake of simplicity, only one type of primary energy, called fuel
F, has been considered.
is the number of units of fuel that are anually required to meet the
fixed demand for energy services, as it is represented by the enthalpy-exergy demand profile. The associated annual cost, which is
C with energy-conservation devices and
without, includes costs of investment, maintenance, and fuel. The optimized annual demand for primary energy,
, begins to decrease, when, at increasing fuel cost
, total cost
C can be reduced by reducing energy consumption via energy conservation.
If the upper cost limit
must not be exceeded,
reaches its minimum at
10 ACU/GJ in
Figure 1 [
38]. (If 10-percent subsidies are possible, so that the upper cost limit is
, the fuel-price increase that is necessary to exhaust the savings potential stops at 7 ACU/GJ.) For more details, like the specific costs of fuel burners and of the energy-conservation devices that partly replace them, annuities, and energy transportation distances, see [
37].
Let us assume that in the idealized world of energy conservation, represented by the solid curve in
Figure 1, there is an enlightened society in which the political leaders, public opinion, and the common man all agree that maximum energy conservation is
the thing that should be done first to fight pollution, and that one should begin with the optimization scheme of
Figure 1. In order to stimulate such a transformation of the energy system, the fuel price is quintupled by energy taxation [
1,
39] from
= 2 ACU/GJ to
10 ACU/GJ at
[
40]. Then, the amount of primary energy required to satisfy the fixed demand for energy services will be reduced from its maximum at
PJ per year, at a total system cost of
ACU per year, to its minimum at
PJ per year, with the total system cost at
ACU per year.
Thus, the full annual additional cost of capital, labor, and energy required for providing unchanged energy services at maximum energy conservation via heat exchanger networks (ex), heat pumps (hp) and cogeneration (cog) is
An energy tax that, as assumed, quintuples the fuel price generates substantial revenues for the state treasury [
41,
42,
43]. It may benefit society as a whole, if it is used to finance the systems of social security so that the taxes and levies on labor may be reduced signficantly. However, there are people who are afraid that tax increases whatsoever are venom for the economy and strangulate economic growth. They would reason that the loss of conventional output in our fuel-taxation and energy-conservation scenario [
44] is given by the cost difference in Equation (
26), and that it will have consequences for later times, too. Then, in this pessimistic view, the conventional output at
would be
Inserting
from Equation (
24) and
from Equation (
25) into Equation (
27), dividing by
, using [
45]
, and taking the logarithm yields the equation for the (output-elasticities-reducing) constant
as
Its numerical value
follows from
, computed according to Equation (
15) for known
at
, and Equation (
26).
The annuity method distributes the cost of the energy-conversion technologies to a number of years
. On the other hand, the system has become more energy efficient. An admittedly crude model assumption is that interest rates, maintenance costs, fuel price increase, and annuities can be chosen in such a way that the difference between the gains from energy conservation and the annual losses
are such that one obtains conventional output for times
(wthin the time span restricted by the annuity method) by replacing
in Equation (
24) with
. Thus, the production function for conventional output, when pollution abatement is practiced via energy conservation stimulated by energy taxation, is
with the number
given by Equation (
28).
Just to give an idea of how one might actually compute this number, we assume that
is the year 1986 and that the annual cost
in Equation (
26) would have been imposed on the (west) German sector “Industries” by triggering energy conservation via energy taxation as described above. (In reality, this did not happen. Rather, the substantial German worries about the forest-killing emissions of SO
and NO
led to legislation in the mid-1980s that very successfully enforced desulphurization and denitrification of the flue gases of power stations, and the catalytic converter for cars as well.)
The empirical output of the sector “Industries” of the Federal Republic of Germany in 1986 was about
, see [
1], p. 264. This corresponds to
, if, in a rough approximation, one assumes that
. This output is well reproduced by the LinEx function
[
10], and we use its number for
in Equation (
28). Thus,
is the relative reduction of conventional output. Furthermore, observing Equations (
15)–(
18),
in Equation (
28) is obtained by computing the logarithm
. Although the technology constants
a and
c have somewhat varied in response to the oil-price shocks 1973–1981, we approximate
by the output of the German Sector “Industries” in the base year 1960. This output is
DM
, according to [
1], p. 264. Then
. With this and Equation (
30), one gets
as the multiplier of the output elasticities. Thus, the reduction of output elasticities in the first, pessimistic scenario, which charges the full cost increase to energy conservation, is nearly 10%.
A second, more optimistic scenario for the same energy system is based on the trade-off between primary energy consumption and total cost at
fixed fuel price
. Figure 4 of [
37] shows the trade-off curves that correspond to
= 4 ACU/GJ and
= 8 ACU/GJ. The trade-off curves are computed by optimizing a linearly weighted, two-component objective function, where the weights of the components “required fuel
” and “cost
C ” vary between 0 and 1. At
= 4 ACU/GJ the quantity of fuel,
, that is necessary to satisfy the fixed demand for energy services, reaches its minimum of
PJ/year at a cost increase of 30%, or, in absolute numbers,
If, at the given fuel price
= 4 ACU/GJ, society decides to exhaust its energy conservation potential, and establishes rules that make all its members pay for it as in the pessimistic scenario, then
takes the place of
in Equations (
30) and (
28), and instead of Equation (
30) and Equation (
31) one has
and
Here, the reductions of conventional output and of the output elasticities are just 1% and 2%, respectively. The corresponding conventional output at times
is given by Equation (
29), with
being replaced by
.
3.2.3. Nuclear Exit, CO Abatement, and Photovoltaics Implementation
Valuation judgements, and uncertainties about the influence of present decisions on future developments, are crucial problems in economics. This does not only show in the two scenarios of energy conservation discussed above, but also in the question: “What are the appropriate energy carriers for the future?”
After the 2011 Fukushima catastrophe, when the tsunami that followed the 11 March earthquake destroyed insufficiently protected emergency generators of the Fukushima Daiichi power plants, causing the core meltdowns of three nuclear reactors and the explosion of a fourth one, Germans decided that nuclear power were too risky for them. The law of 2010, that had considerably extended the operation time of German nuclear reactors in order to reduce CO emissions, was revoked, eight nuclear power plants were shut down right away, and the last of the remaining nine ones is sheduled to cease operation in 2022. Since then, the majority of German citizens and politicians are convinced that renewable energies are the only acceptable non-fossil energies.
This is not the place to enter into the discussions of the precipitous German nuclear-exit decision and the chaotic energy policy thereafter. In the present article, the German priority for renewable energies only motivates considering scenarios of nuclear exit and aspired CO-emission mitigation by the massive introduction of photovoltaics (PV) into the German energy system.
Before doing that, it is useful to have a look at the life-cycle CO emissions from important energy carriers and their energy-conversion technologies.
The estimates of the life-cycle CO
emissions of photovoltaics in
Table 1 take into account that by the year 2014 Chinese PV cells have conquered roughly two thirds of the world market, and of the German market as well, and that CO
emissions of PV production are in China about twice as large as in Germany [
46].
Table 2 reports German primary energy consumption after reunification, and
Table 3 shows the shares of the principal energy carriers. The decrease in primary energy consumption between 1991 and 2012 is partly due to the shift of production from east Germany to the energetically more efficient west German factories, and to improved thermal housing insulation as well, and partly it is due to the long-term trend in many highly industrialized countries to outsource the production of energy-intensive goods to developing countries and concentrate on high-tech, high-priced goods and services instead.
Table 4 indicates the shares of PV and other renewables in German electricity generation. Electricity generation requires roughly 16% of German primary energy. In 2014, renewables contributed about 28% to it. By then, the share of photovoltaics had increased to 1% in primary energy consumption and to roughly 6% in electricity generation (Source: Bundesumweltamt).
Specific CO
emissions of gross electricity generation in Germany since 1991 are shown in
Table 5. They include only the emissions from the direct combustion of fossil fuels. There are two indicators:
gives the CO
emissions in grams per kWh of electricity
generated in Germany, and
gives these emissions in grams per kWh of electricity
consumed in Germany. Thus, if less electricity is consumed than generated in Germany,
is larger than
. In 2014, Germany paid about 30 million Euros to neighboring countries for accepting surplus electricity from fluctuating wind power and photovoltaics. The surplus has to be accepted by the grid because of the legal obligations from the German Renewable Energy Law (GREL). Since 2011, the specific CO
emissions in
Table 5 no longer decrease. The increase of the specific CO
emissions after 2010 is due to the substitution of lignite power plants for nuclear power plants. The specific life-cycle emissions from photovoltaics,
Table 1, are not included in
Table 5.
By the end of 2014, total German electricity-generation
capacity was about 194 GW. Forty-five percent of that was renewables: 20% solar, 18% wind, whose capacities sum up to 74 GW, and 7% others. (Source: Bundesministerium für Wirtschaft und Energie, “Zahlen und Fakten”).
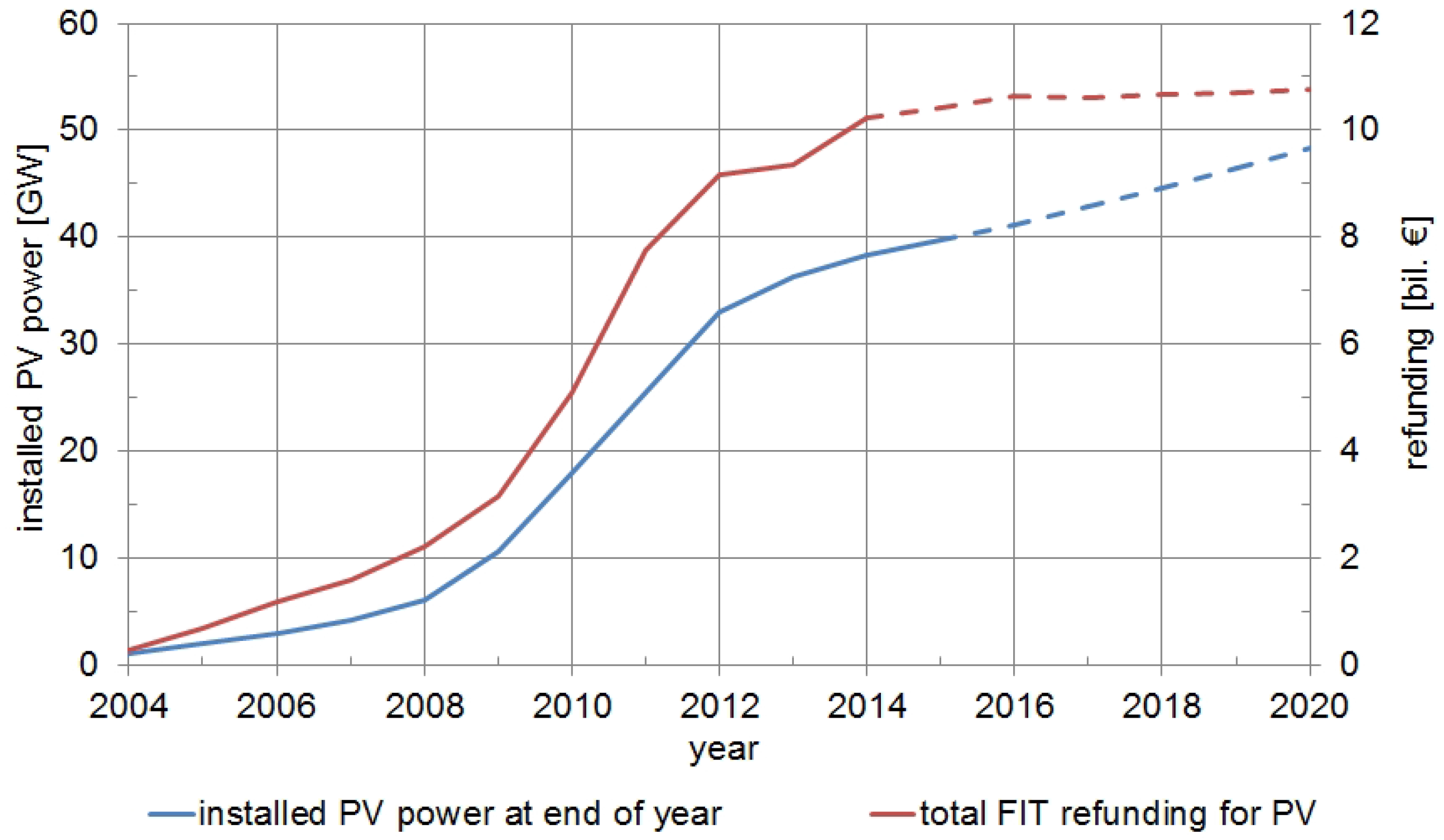
Figure 2 shows the growth of the installed capacity of photovoltaic electricity generation and the annual payments (“refunding”) handed out to the PV-electricity producers according to the provisions of the (often reformed and rather complicated) German feed-in tariff (FIT) system, established by the GREL, which obliges (essentially private) consumers to subsidize the producers of renewable energies. It led to an average PV refunding of 32 ct/kWh in 2013 [
51]; (ct = Eurocent) [
52].
There have been lively debates on the cost of the renewables. Especially, people do not like the surcharge due to the GREL on their electricity bills, and many argue that industry should pay its share, too. There is no way of even trying to cut a clear path through the jungle of arguments on (i) hidden and open subsidies for fossil and nuclear fuels, on the one hand, and renewables, on the other hand, (ii) the external costs of energy carriers and their conversion technologies, including the problem of discounting future damages [
1,
53], and (iii) the comparison and valuation of risks. Rather, let us play with the above-mentioned numbers concerning specific CO
emissions, Watts, Joules, and Euros in the two scenarios (A and B) that lead to the results in
Table 6.
The refunding on the right ordinate of
Figure 2, annually paid to the (mostly decentralized) providers of PV electricity by the consumers, correspondingly reduces the latter’s (debt-free) consumption of goods and services from the traditional basket [
54]. It represents the loss in Equation (
19), with
only for
, and
refunding.
In order to avoid runaway PV subsidies, a legal barrier of 52 GW on photovoltaics capacity has been introduced recently, despite strong opposition from PV lobbyists. Once it will have been reached, the annual payments to the providers of PV power are expected to not exceed 10–11 billion Euros [
51]. Without that limitation, and assuming a linear extrapolation of the 2010 refunding gradient in
Figure 2, the annual PV subsidies
would increase by roughly 2 billion Euros per year.
Let us consider two scenarios of PV implementation and the resulting reduction of conventional output. They begin with the year 2011 in
Table 6. Scenario A is with the legal barrier on PV capacity, and Scenario B is without. The total German output is given by the GDP in
Table 7. For the scenario years after 2014, numbers are used that result from the 2014 output and its growth with the average of the 2012–2014 growth rates, which is roughly 0.9%. Thus, the assumed GDP of the year 2014+
n in
Table 6 is
Table 3,
Table 4 and
Table 5 show the success of German energy policy on emission mitigation after 11 March 2011. Right now, this policy does not support enthusiasm, even if one takes into account that after 2022, when the last German nuclear reactor will have ceased operation—and if German energy policy will not perform another U-turn—it will prevent further growth of nuclear waste, which emits ionizing particles and photons. It is a matter of risk-perception and -valuation, whether or not one considers the losses of conventional GDP in
Table 6 as an acceptable PV share of the price for the still ongoing shake-up of the German energy system.
Thus, the relative loss of conventional GDP in 2014 would be about 0.4% in scenario A and 0.5% in scenario B. In 2018, the losses would be 0.4% and 0.8%. Of course, recessions would increase the percentages of the losses.