Rényi Divergences, Bures Geometry and Quantum Statistical Thermodynamics

Abstract

The Bures geometry of quantum statistical thermodynamics at thermal equilibrium is investigated by introducing the connections between the Bures angle and the Rényi 1/2-divergence. Fundamental relations concerning free energy, moments of work, and distance are established.

1. Introduction

Galileo once said “philosophy is written in the language of mathematics and the characters are triangles, circles and other figures” [1]. Since then, natural philosophy and geometry evolved side by side, leading groundbreaking perceptions of the foundations of today’s modern science. A particular example was introduced by Gibbs [2,3], who successfully described the theory of thermodynamics by using convex geometry in which the coordinates of this special phase space are nothing but the elements of classical thermodynamics. While the Gibbsian interpretation has been successful for the understanding of the relations among the thermodynamical entities, it lacks the basic notion of a geometry: the distance. The latter constitutes the fundamental motivation for Weinhold’s geometry [4], where an axiomatic algorithm leads a scalar product, and thus induces a Riemannian metric into the convex Gibbsian state space. Later, Ruppeiner proposed that any instrument of a geometry that describes a thermodynamical state of a system should lead to physically meaningful results [5]. To that end, the Riemannian scalar curvature of an embedded metric has been related with the thermodynamical criticality [6], and the theory has been applied to many classical and quantum mechanical systems [7].

It is quite logical to search for abstract relations among geometry and thermodynamical processes, since that is what we are familiar with in the “macro-world”. In particular, the proportionality of the work done by a physical system during a transformation to the distance between start and end points provides strong motivation for the subject matter. Here, we explore if a similar relation exists within the theory of equilibrium quantum statistics. We do not over-complexify our strategy and indigenise the Descartian rule of thumb [8]: any problem in geometry can be reduced to that of a problem of finding the lengths (the distances) of straight lines (between any given points). We show that the latter idea indeed leads to new insights concerning quantum statistical thermodynamics if we measure the distance between two arbitrary quantum thermal states relative to an “unbiased” reference state.

Such a reference state must be unique and must have well-defined geometrical and physical interpretations. To that end, we make all our calculations with respect to the maximally mixed state (the maximum entropy state from a thermodynamical point of view), and it lies in the geometrical center of state space of density operators [9]. We use the elements of the well-known Bures geometry of the space of density operators [9,10]; i.e., we use the elements of the geometry of quantum statistical ensembles and search for physically meaningful relations concerning thermodynamics. The Bures distance has already been considered in quantum statistical mechanics [11], non equilibrium thermodynamics [12,13], and quantum phase transitions [14,15,16]. Very recently, it has also been shown to be a useful tool for determining the inner friction during thermodynamical processes [17].

While one can assume a more abstract mathematical path that may end up with similar expressions as found in this contribution, we bring another player to the game that clarifies the thermodynamical connections. We first show the relation between the Bures distance with the Rényi α-divergences [18,19] for a specific value of $\alpha =1/2$. The Rényi divergences are shown to be the generalisations of the quantum entropies from which the measures of quantum information can be recovered [19]. Statistical thermodynamics based on Rényi divergences has also been discussed in the literature [20,21,22] under strict constraints—i.e., maximizing the divergence itself with the assumption of a fixed internal energy and considering quasi-static isothermal processes with general interest in systems that are far from equilibrium. Second, the divergences have already played critical roles in the search for the laws of quantum thermodynamics [23,24,25]. Finally, as we shall see here, the choice of $\alpha =1/2$ directly relates the curved geometry of space of the density operators to the quantum entropies, and it has the physical meaning of being the measure of maximal conditional entropy between the statistical ensembles under consideration [19].

Equipped with the Rényi divergence, we first establish fundamental identities among distance and occupation probabilities of a given quantum thermal state. Later on, we use same identities to further develop our approach to unearth the implicit connections between distance, free energy, and work distribution during thermal transformations that occur between equilibrium quantum states.

This paper is organized as follows. In Section 2, we introduce the necessary elements of Bures geometry, Rényi divergences, and their relations. In Section 3, we present our results. We conclude in Section 4.

2. The Space of Density Operators

A complex $N\times N$ matrix ρ acting on a Hilbert space $\mathbb{H}$ of dimension N is called a density matrix if it is positive semi-definite ($⟨\psi |\rho |\psi ⟩\ge 0 \forall |\psi ⟩\in \mathbb{H}$), Hermitian ($\rho ={\rho }^{†}$), and normalized ($\text{tr}\rho =1$). The set of density matrices, $\mathbb{D}$, is the intersection of the space of all positive operators $\mathbb{P}$ with a hyperplane parallel to the linear subspace of traceless operators [9]. $\mathbb{D}$ is a convex set, and the maximally mixed state

$${\rho }_{\ast }=\frac{1}{N}{\mathbf{1}}_N,$$

(1)

lies at its centre with ${\mathbf{1}}_N$ being the $N\times N$ identity operator.

2.1. The Bures Geometry

There exists a family of monotone metrics [9] that can be used to measure the geometrical (statistical) distance between any given two density operators ρ, $\sigma \in \mathbb{D}$. Among all of these measures, the minimal one is given by the Bures distance [10]

$$D_B(\rho ,\sigma )=\text{tr}\rho +\text{tr}\sigma -2F(\rho ,\sigma ),$$

(2)

where $F(\rho ,\sigma )=\text{tr}\sqrt{\sqrt{\sigma }\rho \sqrt{\sigma }}$ is Uhlmann’s root fidelity [26]. The Bures distance measures the length of the curve between ρ and σ within the set of all positive operators $\mathbb{P}$, while the length of the curve within $\mathbb{D}$ is measured by the Bures angle [26,27,28]

$$cos{d}_B(\rho ,\sigma )=F(\rho ,\sigma ),0\le d_B\le \frac{\pi }{2}.$$

(3)

There is a Riemannian metric—the Bures metric—associated with the distances (2) and (3). First, we recall that, due to the positivity property, any density operator $\rho \in \mathbb{D}$ acting on $\mathbb{H}$ can be written as $\rho =K{K}^{†}$, where $K:=\sqrt{\rho }U$, with U being a unitary operator. We can search for a curve $\rho (\tau )$ within $\mathbb{D}$ by imposing that the amplitudes remain parallel

$${\dot{K}}^{†}K=K^{†}\dot{K},$$

(4)

where $\dot{K}$ denotes the differentiation of K with respect to the arbitrary parametrization τ. The condition (4) is satisfied if $\dot{K}=GK$ [29], where G is a Hermitian matrix. It follows that

$$d\rho =G\rho +\rho G.$$

(5)

The Bures metric $d{s}_B^2$ is then defined as

$$d{s}_B^2=\frac{1}{2}\text{tr}Gd\rho .$$

(6)

If the density operator is strictly positive $\rho >0$, the matrix G is uniquely determined. Note that, although there are some methods to determine the Bures metric exactly [11], it is generally very difficult to compute, and an exact form of this metric will not be needed in the current contribution.

The elements of the Bures geometry have been used in the context of quantum statistics in the literature. In particular, the Bures metric (and the distances that belong to it) have proven to be useful tools for the characterisation of quantum criticality and quantum phase transitions [14,15,16] and thermodynamics of topological insulators at finite temperature [30]. The Bures distance has also been proven to be a lower bound for the estimation of the energy–time uncertainty [31,32]. Another neat example was provided by Twamley [11], where the Bures distance between two squeezed thermal states was evaluated, and the curvature of the corresponding Bures metric was suggested as a measure to optimize detection statistics. More resent studies revealed the deeper connections between the quantum thermodynamical processes and the Bures geometry. Specifically, it has been shown that the quantum irreversible work [12,13] as well as the quantum inner friction [17] are bounded from below by the Bures angle.

Here, we look at the picture from a different perspective. We shall calculate the distance between two equilibrium quantum thermal states with respect to the maximally-mixed state. It turns out that this relative distance can be written in terms of the difference between the corresponding free energies, leading to fundamental relations between work, distance, and efficiency. First, however, we should equip ourselves with the Rényi divergences to clarify the statistical connections.

2.2. The Rényi α-Divergences

The quantum Rényi α-divergences [19] are the generalizations of the family of Rényi entropies [18] from which the measures of quantum information can be recovered. Moreover, the Rényi divergences admit a central role in so-called generalized quantum second laws of thermodynamics [23,24], as well as laws of quantum coherence that enters thermodynamical processes [25]. In their most general form, for two given density operators ρ, $\sigma \in \mathbb{D}$, the α-divergences are defined as [19,33,34]

$$S_{\alpha }(\rho ||\sigma )=\left\{\begin{array}{cc}\frac{1}{\alpha -1}ln\text{tr}{\rho }^{\alpha }{\sigma }^{1-\alpha },\hfill & \alpha \in [0,1).\hfill \\ \frac{1}{\alpha -1}ln\text{tr}{({\sigma }^{1-\alpha /2\alpha }\rho {\sigma }^{1-\alpha /2\alpha })}^{\alpha },\hfill & \alpha >1.\hfill \end{array}\right.$$

(7)

Here, we remain in the domain of equilibrium statistical thermodynamics at finite temperature, and to do so, we shall only deal with a single preferred value of $\alpha =1/2$. Physically, it corresponds the maximum conditional entropy between the states ρ and σ [19], and the divergence reads

$$S_{1/2}(\rho ||\sigma )=-2ln\text{tr}\sqrt{\rho }\sqrt{\sigma }.$$

(8)

It is easy to see that the argument of the logarithm on the right hand side of Equation (8) is nothing but the root fidelity $F(\rho ,\sigma )$ for two commuting operators ρ, $\sigma \in \mathbb{D}$. Thus, a natural relation between the entropy function and the Bures geometry is constructed to give

$$S_{1/2}(\rho ||\sigma )=-ln{cos}^2{d}_B(\rho ,\sigma ),[\rho ,\sigma ]=0,0\le d_B\le \frac{\pi }{2}.$$

(9)

Note that here we follow Reference [34] for the definition of Rényi divergences (7). In Reference [19], divergences presented as $d_{\alpha }\equiv [1/(\alpha -1)]ln\text{tr}{\rho }^{\alpha }{\sigma }^{1-\alpha }$ for $\alpha \in (0,1)\cap (1,2]$ and $d_{\alpha }^{\prime }\equiv [1/(\alpha -1)]ln\text{tr}{({\sigma }^{(1-\alpha )/(2\alpha )}\rho {\sigma }^{(1-\alpha )/(2\alpha )})}^{\alpha }$ for $\alpha \in [1/2,1)\cap (1,\infty )$. The authors did notice the relation $d_{1/2}^{\prime }=-2lnF(\rho ,\sigma )$, but also write $d_{1/2}^{\prime }\ne d_{1/2}$. Here, we state indeed $d_{1/2}^{\prime }=d_{1/2}$ if $[\rho ,\sigma ]=0$. What is more, the commutativity condition provides consistency to our theory, due to the fact that we shall only deal with thermal states in the energy eigenbasis where they are diagonal. In this case, the Bures angle (3) and the Bures distance (2) are equivalent to the classical Bhattacharyya and Hellinger statistical distances [9], respectively. The latter connections signify the statistical significance of the divergence $S_{1/2}(\rho ||\sigma )$.

The relation (8) will be the starting point of our interpretation of equilibrium geometric thermodynamics in the next section with the final ingredient of a suitable reference point (1).

3. Results

Here, we present our contributions to the geometric interpretations of quantum statistical thermodynamics. We shall start with fundamental relations among equilibrium fluctuations, Rényi divergences, and Bures angle. Afterwards, we shall provide a relation concerning the distance between two equilibrium quantum states and the change in the corresponding free energies. We finalize this section by providing a relation between work, distance, and Carnot efficiency.

3.1. Fundamental Relations

Let ${\rho }_{th}$ be a thermal state of quantum mechanical system acting on a N-dimensional Hilbert space and described by the Hamiltonian $\mathrm{H}$ at finite equilibrium temperature $\beta =1/k_{B}T$, with $k_B$ being the Boltzmann constant. We have

$${\rho }_{th}={\displaystyle \sum _{i=1}^N}{p}_i|{\psi }_i⟩⟨{\psi }_i|,$$

(10)

where $p_i=e^{-\beta E_i}/Z$ are the occupation probabilities, $|{\psi }_i⟩$ and $E_i$ are the eigenvectors and the corresponding eigenvalues of the Hamiltonian $\mathrm{H}$ that satisfy the eigenvalue equation $\mathrm{H}|{\psi }_i⟩=E_i|{\psi }_i⟩$, and $Z=\text{tr}{e}^{-\beta \mathrm{H}}$ is the partition function.

The Rényi divergence of ${\rho }_{th}$ with respect to the maximally mixed state ${\rho }_{\ast }$ becomes

$$S({\rho }_{th}||{\rho }_{\ast })=-2lnF({\rho }_{th},{\rho }_{\ast })=-2ln\frac{1}{\sqrt{N}}{\displaystyle \sum _{i=1}^N}{p}_i^{1/2},$$

(11)

where we set $S_{1/2}(\rho ||\sigma )\equiv S(\rho ||\sigma )$ for the sake of simplicity. We obtain

$${\displaystyle \sum _{i=1}^N}{p}_i^{1/2}=\sqrt{N}{e}^{-S({\rho }_{th}||{\rho }_{\ast })/2}.$$

(12)

The first immediate consequence of Equation (12) is that since $p_i\le p_i^{1/2} \forall i$, we have ${\sum }_i{p}_i^{1/2}\ge 1$, and thus $lnN\ge S({\rho }_{th}||{\rho }_{\ast })$, as expected.

We continue by taking the square of both sides of the fundamental Equation (12) to obtain

$$1+2{\displaystyle \sum _{i<j}^N}{p}_i^{1/2}{p}_j^{1/2}=N{e}^{-S({\rho }_{th}||{\rho }_{\ast })}.$$

(13)

Inspired by the Wootter’s statistical distance [35], we may introduce a distinguishability measure between the energy eigenstates of the system that is given by

$$cos{d}_W={\displaystyle \sum _{i<j}^N}{p}_i^{1/2}{p}_j^{1/2},$$

(14)

which is a function of fidelity through Equation (11).

Finally, using Equations (9) and (14), we arrive at the relation

$${cos}^2{d}_B=\frac{1+2cos{d}_W}{N}.$$

(15)

The strict positivity of $cos{d}_W$ requires $0\le d_B<\pi /2$, which leads $(N-1)/2\ge cos{d}_W>0$.

3.2. Geometry, Entropy, and the Thermodynamical Free Energy

We start by rewriting Equation (11) as

$$S({\rho }_{th}||{\rho }_{\ast })=lnN+lnZ-2ln{Z}^{\prime },$$

(16)

where $Z={\sum }_n{e}^{-\beta E_n}$ and $Z^{\prime }={\sum }_n{e}^{-\beta E_n/2}$. Let ${\rho }^{(1)}$ and ${\rho }^{(2)}$ be two distinct thermal states of a given quantum system corresponding to different temperatures $T_1$ and $T_2$ with $T_2>T_1$. We have

$$\begin{array}{ccc}\hfill -k_B{T}_{1}S({\rho }^{(1)}||{\rho }_{\ast })& =& -k_B{T}_{1}lnN+{\Omega }_1-{\Omega }_1^{\prime },\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill -k_B{T}_{2}S({\rho }^{(2)}||{\rho }_{\ast })& =& -k_B{T}_{2}lnN+{\Omega }_2-{\Omega }_2^{\prime },\hfill \end{array}$$

(18)

where ${\Omega }_i=-k_B{T}_{i}ln{Z}_i$ and ${\Omega }_i^{\prime }=-k_B(2T_i)ln{Z}_i^{\prime }$, and $i=1,2$ are the thermodynamical potentials. By subtracting Equation (18) from Equation (17), we obtain

$$k_B{T}_{2}S({\rho }^{(2)}||{\rho }_{\ast })-k_B{T}_{1}S({\rho }^{(1)}||{\rho }_{\ast })=ln\left[\frac{{({cos}^2{d}_B({\rho }^{(2)},{\rho }_{\ast }))}^{k_B{T}_2}}{{({cos}^2{d}_B({\rho }^{(1)},{\rho }_{\ast }))}^{k_B{T}_1}}\right]=-\Delta \Omega +\Delta {\Omega }^{\prime }+k_B\Delta TlnN,$$

(19)

where $\Delta x=x_2-x_1$, and we use Equation (9). Thus, any transformation between ${\rho }^{(1)}$ and ${\rho }^{(2)}$ that changes the thermodynamical free energy can equivalently be understood as the change in the relative position with respect to the maximum entropy state in the state space of density operators.

Our result, Equation (19), is a general one in the sense that we do not restrict ourselves with systems that are described by certain types of Hamiltonians. Secondly, all the other coordinates that can be included in the theory are encoded to the free energy and to the distance function through density operator formalism. One can of course apply the geometrical properties of the distance function to Equation (19) to obtain a pool of equalities and inequalities, though this is not a prime motivation of or an immediate issue for the current contribution.

However, one rogue element $Z^{\prime }={\sum }_n{e}^{-\beta E_n/2}$ remains without a satisfactory physical interpretation. To make its contribution to the theory more explicit, we take the square of $Z^{\prime }$ to obtain

$$Z^{\prime 2}=Z(1+2cos{d}_W)=NZ{cos}^2{d}_B.$$

(20)

If we take the natural logarithm of both sides of Equation (20), we obtain Equation (16).

To acquire a better understanding of $Z^{\prime }$ and the corresponding free energy ${\Omega }^{\prime }$, let us first recall the quantum relative entropy $D(\rho ||\sigma ):=\text{tr}(\rho ln\rho -\rho ln\sigma )$ defined for all $\rho ,\sigma$ acting on a Hilbert space of dimension N becomes

$$D({\rho }_{th}||{\rho }_{\ast })=lnN-lnZ-\beta U,$$

(21)

for an arbitrary thermal state ${\rho }_{th}=e^{-\beta \mathrm{H}}/Z$ with $U:=\text{tr}({\rho }_{th}\mathrm{H})$ being the internal energy. By obtaining the expression for $lnZ$ from Equation (21) and by using Equation (16), we find

$${\Omega }^{\prime }=\frac{1}{\beta }D({\rho }_{th}||{\rho }_{\ast })+U+k_{B}TS({\rho }_{th}||{\rho }_{\ast })-2k_{B}TlnN.$$

(22)

If we now consider ${\rho }^{(1)}$ and ${\rho }^{(2)}$ as the two distinct thermal states of a given quantum system corresponding to different temperatures $T_1$ and $T_2$ with $T_2>T_1$ like before and calculate $\Delta {\Omega }^{\prime }$, Equation (19) gives

$$-\Delta \Omega +\Delta U=\frac{1}{{\beta }^{(1)}}D({\rho }^{(1)}||{\rho }_{\ast })-\frac{1}{{\beta }^{(2)}}D({\rho }^{(2)}||{\rho }_{\ast })+k_B\Delta TlnN,$$

(23)

which is trivial in the sense that we do not require the knowledge of Equation (19) to obtain it, though the inverse statement is not true. That is, by starting from Equation (23), one cannot obtain Equation (19) without the knowledge of the potential ${\Omega }^{\prime }$ (22). A final straightforward calculation also yields $-\Delta \Omega +\Delta U=k_B{T}_{2}S({\rho }^{(2)})-k_B{T}_{1}S({\rho }^{(1)})$, with $S(\rho ):=-\text{tr}\rho ln\rho$ being the von Neumann entropy as the equivalent form of Equation (23); i.e., we recover the conventional thermodynamics.

We complete this section by noting that

$$p_i=\frac{N{e}^{-\beta E_i}}{Z^{\prime 2}}{e}^{-S({\rho }_{th}||{\rho }_{\ast })}$$

(24)

for a given thermal state ${\rho }_{th}$. It follows that

$$ln{p}_i=lnN-\beta E_i-S({\rho }_{th}||{\rho }_{\ast })-2ln{Z}^{\prime },$$

(25)

and thus,

$$T{S}_{th}-k_{B}TS({\rho }_{th}||{\rho }_{\ast })=U+2k_{B}Tln{Z}^{\prime }-k_{B}TlnN,$$

(26)

where we write $S_{th}:=-k_B{\sum }_i{p}_{i}ln{p}_i$ as the usual thermodynamical entropy. Now,

$$ln{Z}^{\prime }=ln{\displaystyle \sum _{i=1}^N}{e}^{-\beta E_i/2}=ln{\displaystyle \sum _{i=1}^N}{p}_i\left(\frac{1}{p_i}{e}^{-\beta E_i/2}\right)\le {\displaystyle \sum _{i=1}^N}{p}_{i}ln\left(\frac{1}{p_i}{e}^{-\beta E_i/2}\right),$$

(27)

by using Jensen’s inequality. Therefore, we obtain

$$2k_{B}Tln{Z}^{\prime }\le 2T{S}_{th}-U.$$

(28)

It is easy to see that the above inequality constitutes a first law for the auxiliary potential ${\Omega }^{\prime }$, as it can equivalently be written as ${\Omega }^{\prime }\ge U-2T{S}_{th}$. Finally, we combine Equations (26) and (28) to give

$$S_{th}\ge k_B\left(lnN-S({\rho }_{th}||{\rho }_{\ast })\right).$$

(29)

The presented geometric bound to the equilibrium entropy $S_{th}$ can more easily be obtained via an application of Jensen’s inequality to our fundamental Equation (12) at the expense of the knowledge gained from Equations (24)–(28).

3.3. Work and Distance

Before we proceed, let us define $S_R^{(i)}=S({\rho }^{(i)}||{\rho }_{\ast })$ and ${\Delta }_{T}x:=k_B{T}_2{x}^{(2)}-k_B{T}_1{x}^{(1)}$ for the sake of clarity. It follows from Equation (19) that

$$-\Delta \Omega ={\Delta }_T{S}_R-k_B\Delta TlnN-\Delta {\Omega }^{\prime }\ge W,$$

(30)

where $W\ge 0$ is the positive work done by the system during the transformation. Rearranging the terms such that $W+\Delta {\Omega }^{\prime }\le {\Delta }_T{S}_R-k_B\Delta TlnN$ and due to the fact that ${\Delta }_T{S}_R-k_B\Delta TlnN\le 0$ and $W\ge 0$, we obtain

$$W\ge {\Delta }_T{S}_R-k_B\Delta TlnN,$$

(31)

or equivalently,

$$\begin{array}{}(32)& \hfill \frac{{\eta }_c}{1-{\eta }_c}& \ge & \frac{{\Delta }_T{S}_R-W}{k_B{T}_{1}lnN},\hfill (33)& \hfill {\eta }_c& \ge & \frac{{\Delta }_T{S}_R-W}{k_B{T}_{2}lnN},\hfill \end{array}$$

where ${\eta }_c:=1-(T_1/T_2)$ is the Carnot efficiency.

A more general relation between the moments of work and distance can be obtained as follows. We recall that

$$S({\rho }_{th}||{\rho }_{\ast })=lnN+lnZ-2ln{Z}^{\prime }=lnN-lnZ+ln\left(\frac{Z^2}{Z^{\prime 2}}\right).$$

(34)

By expanding the last term $ln(Z^2/Z^{\prime 2})$ up to its first order, we write

$$\begin{array}{ccc}\hfill k_{B}TS({\rho }_{th}||{\rho }_{\ast })& \sim & k_{B}TlnN+\Omega +\frac{k_{B}T}{N}{e}^{-\beta \Omega }{e}^{S({\rho }_{th}||{\rho }_{\ast })}-k_{B}T,\hfill \\ & \sim & k_{B}TlnN+\Omega +\frac{k_{B}T}{N}{e}^{S({\rho }_{th}||{\rho }_{\ast })}(1-\beta \Omega )-k_{B}T,\hfill \end{array}$$

(35)

where T is the equilibrium temperature of the system. By rearranging the terms and solving for the potential Ω, we obtain

$${\Omega }^{(1)}\sim k_{B}T\frac{S({\rho }_{th}||{\rho }_{\ast })-\frac{1}{N}{e}^{S({\rho }_{th}||{\rho }_{\ast })}-lnN+1}{1-\frac{1}{N}{e}^{S({\rho }_{th}||{\rho }_{\ast })}}$$

(36)

as the first order approximation to the free energy. Similarly, the contribution of the second order term from the expansion of $ln(Z^2/Z^{\prime 2})$ leads

$${\Omega }^{(2)}\sim k_{B}T\frac{S({\rho }_{th}||{\rho }_{\ast })-\frac{2}{N}{e}^{S({\rho }_{th}||{\rho }_{\ast })}+\frac{1}{2N^2}{e}^{2S({\rho }_{th}||{\rho }_{\ast })}-lnN+\frac{3}{2}}{1-\frac{2}{N}{e}^{S({\rho }_{th}||{\rho }_{\ast })}+\frac{1}{N^2}{e}^{2S({\rho }_{th}||{\rho }_{\ast })}}.$$

(37)

It is easy to recognize the pattern

$$1-\frac{1}{N}{e}^x+\frac{1}{N^2}{e}^{2x}-\dots \sim {\left(1+g\frac{e^x}{N}\right)}^{-1/2},$$

(38)

with g being a constant. Thus, we obtain

$$\Omega \sim k_{B}T\left[\sqrt{1+g\frac{e^{S({\rho }_{th}||{\rho }_{\ast })}}{N}}\left(S({\rho }_{th}||{\rho }_{\ast })-lnN+\frac{1}{2}\right)+1\right]$$

(39)

as the approximate geometric description of the thermodynamical free energy.

As before, let ${\rho }^{(1)}$ and ${\rho }^{(2)}$ be two distinct thermal states of a given quantum system corresponding to different temperatures $T_1$ and $T_2$, with $T_2>T_1$. Let us define

$$h^{(i)}:=\sqrt{1+g\frac{e^{S_R^{(i)}}}{N}}\left(S_R^{(i)}-lnN+\frac{1}{2}\right),$$

(40)

where $i=1,2$. Thus, for any thermodynamical transformation ${\rho }^{(1)}\to {\rho }^{(2)}$, the change in the free energy reads

$$-\Delta \Omega \sim -{\Delta }_{T}h-k_B\Delta T.$$

(41)

Moreover, in terms of the Carnot efficiency, we obtain

$${\eta }_c\sim \frac{1}{k_B{T}_2}(\Delta \Omega -{\Delta }_{T}h).$$

(42)

For our final touch, we use the Jarzynski equality [36] to write

$$\frac{{\eta }_c}{1-{\eta }_c}\sim -\frac{1}{k_B{T}_1}{\Delta }_{T}h-ln⟨exp\frac{-W}{k_B{T}_1}⟩,$$

(43)

where $⟨,⟩$ denotes the average over an ensemble of measurements performed on the work W. We read the Equation (43) as: during a thermodynamical transformation between two quantum thermal states, maximum work can be extracted with maximum efficiency by optimizing the difference of the relative distances of each state with respect to the maximum entropy state, while keeping all the other parameters (forces) constant.

Equation (43) can be particularly useful for the investigations of systems that undergo quantum phase transitions (QPTs), as the Bures distance and the moments of work considered to be witnesses of QPTs, separately [14,15,16,37]. This connection requires further calculations that are out of the context of this work, and can be the topic of another contribution.

3.4. Examples

We are now ready to complete our analysis with some numerical examples. To that end, we consider two fundamental quantum systems—quantum harmonic oscillator and an ensemble of spin 1/2 particles, described by the Hamiltonians ($\hslash =1$) ${\mathrm{H}}_{ho}={\omega }_f{\widehat{a}}^{†}\widehat{a}$ and ${\mathrm{H}}_s={\omega }_a{\widehat{S}}_z$, respectively. Here, ${\widehat{a}}^{†}$$(\widehat{a})$ and ${\widehat{S}}_z=(1/2){\sum }_k{\widehat{\sigma }}_z^k$ are the bosonic creation (annihilation) and collective spin operators, and we denote resonance frequencies with ${\omega }_f$ and ${\omega }_a$, respectively.

We assume that both systems are in thermal equilibrium at temperature $T_i/\omega =0.1$ ($k_B=\hslash =1$, ${\omega }_f={\omega }_a=\omega$). We calculate the change in thermodynamical free energy ($-\Delta \Omega =T_{f}ln{Z}_f-T_{i}ln{Z}_i$) with respect to final temperature $T_f$, and compare it with the numerical data obtained from Equations (19) and (41), where we set $g=\pi$ for both systems.

In Figure 1a, we show the free energy change in quantum harmonic oscillator for $N=100$. Equation (19) is in perfect agreement with the exact results. Our approximated result (Equation (41)) agrees well within the temperature regime, except for a small anomaly occurring in the low temperatures, as shown in the inset. We numerically verified that for even higher dimensions (i.e., $N>100$), the offset minimalizes.

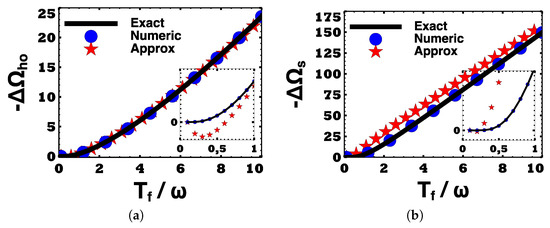
Figure 1. Free energy changes for (a) quantum harmonic oscillator with $N=100$ and (b) an ensemble of $n_s=25$ ($N=2^{n_s}$) spin-$1/2$ particles with respect to the scaled temperature $T/\omega$. Black-solid line represents the exact results obtained via calculating $-\Delta \Omega =T_{f}ln{Z}_f-T_{i}ln{Z}_i$, while blue-circles and red-stars represents the data obtained from Equations (19) and (41) with $g=\pi$, respectively. All the other parameters are as explained in the text.

Figure 1b depicts the change in free energy for an ensemble of $n_s=25$ ($N=2^{n_s}$) spin-$1/2$ atoms. As in the bosonic case, Equation (19) is in perfect agreement with the analytical results. At this point, we also note that Equation (19) gives precise results for a single two-level system, as well. The approximation diverges greater than that of our calculation for the bosonic case in the temperature regime under consideration.

To test the exact bounds on positive work done by a system (i.e., Equation (32)), we consider generalized quantum Rabi model ($\hslash =1$)

$$\widehat{H}=\frac{\omega }{2}{\widehat{\sigma }}_z+ϵ{\widehat{\sigma }}_x+\omega {\widehat{a}}^{†}\widehat{a}+g{\widehat{\sigma }}_x(\widehat{a}+{\widehat{a}}^{†})$$

(44)

as a hybrid spin–boson quantum Otto engine. The model has already been considered in the literature, and we refer to Reference [38] for details. Here, ω is the resonance frequency of the system, g is the strength of atom–field coupling, and ϵ is a small coefficient which breaks the $Z_2$ symmetry of the model. We assume that the engine operates between the temperatures $T_1=0.05$ and $T_2\in \{0.2,0.25\}$ (scaled with $\hslash \omega /{\kappa }_B$) with the corresponding frequencies of ${\omega }_1=\omega$ and ${\omega }_2=2\omega$, and we set $ϵ=0.005\omega$.

Let us define $\zeta :={\eta }_c/(1-{\eta }_c)$ and $\kappa :=({\Delta }_T{S}_R-W)/(T_{1}lnN)$, with $N=n_{boson}{n}_{spin}=30\times 2=60$. It follows that we have ${\zeta }_1=3$ and ${\zeta }_2=4$ for $T_2=0.2$ and $T_2=0.25$, respectively. Figure 2 shows our typical results for κ with respect to $g/\omega$ with the verification of analytical results.

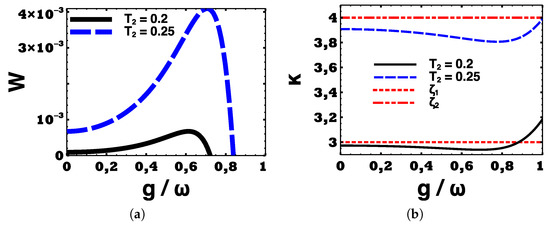
Figure 2. (a) Extracted work from Rabi system as a quantum Otto engine for $T_2=0.2$ (black-solid) and $T_2=0.25$ (blue-dashed); (b) The change in the parameter $\kappa =({\Delta }_T{S}_R-W)/(T_{1}lnN)$ for $T_2=0.2$ (black-solid) and $T_2=0.25$ (blue-dashed). Corresponding upper bounds ${\zeta }_1=3$ and ${\zeta }_2=4$ are flagged with red-dotted and red dot–dot–dashed lines. The x-axis is the scaled interaction strength $g/\omega$ in both figures. All the other parameters are as explained in the text.

4. Concluding Remarks

All of our results concerning geometry and quantum statistics follow from the distance between two quantum equilibrium states. They are not explicit in the conventional theory, and require relative measurements with respect to the maximally mixed state to surface out.

The use of density operator formalism in the construction of geometry and statistical thermodynamics led to a general, system, and process independent theory. Furthermore, all of the relations rise as functions of the occupation probabilities, instead of the thermal entropy, $S_{th}$, itself. The latter—as a fundamental requirement for statistical explorations of physical systems within the quantum mechanical framework—brings consistency to the theory.

Finally, the leading results concerning the ties among efficiency, distance, work, and its moments—as being established in equilibrium—present new angles to the emerging field of thermal quantum machines. They simply suggest distance optimization procedures to have robust work harvesting with maximum possible efficiency. Another particular implication is that our results combine and verify separate discussions on the detection of QPTs via either Bures geometry [14,15,16] or the moments of work [37]. Indeed, as their difference is bounded by or equalised to a universal constant, if one of them can detect a physical phenomena, the detection with the same event by other is inevitable.