Quantum Thermodynamics with Degenerate Eigenstate Coherences
Abstract
:1. Introduction
2. General Formalism
2.1. Microscopic Derivation of Lindblad Master Equations
2.2. Average Thermodynamics
2.3. Fluctuating Thermodynamics
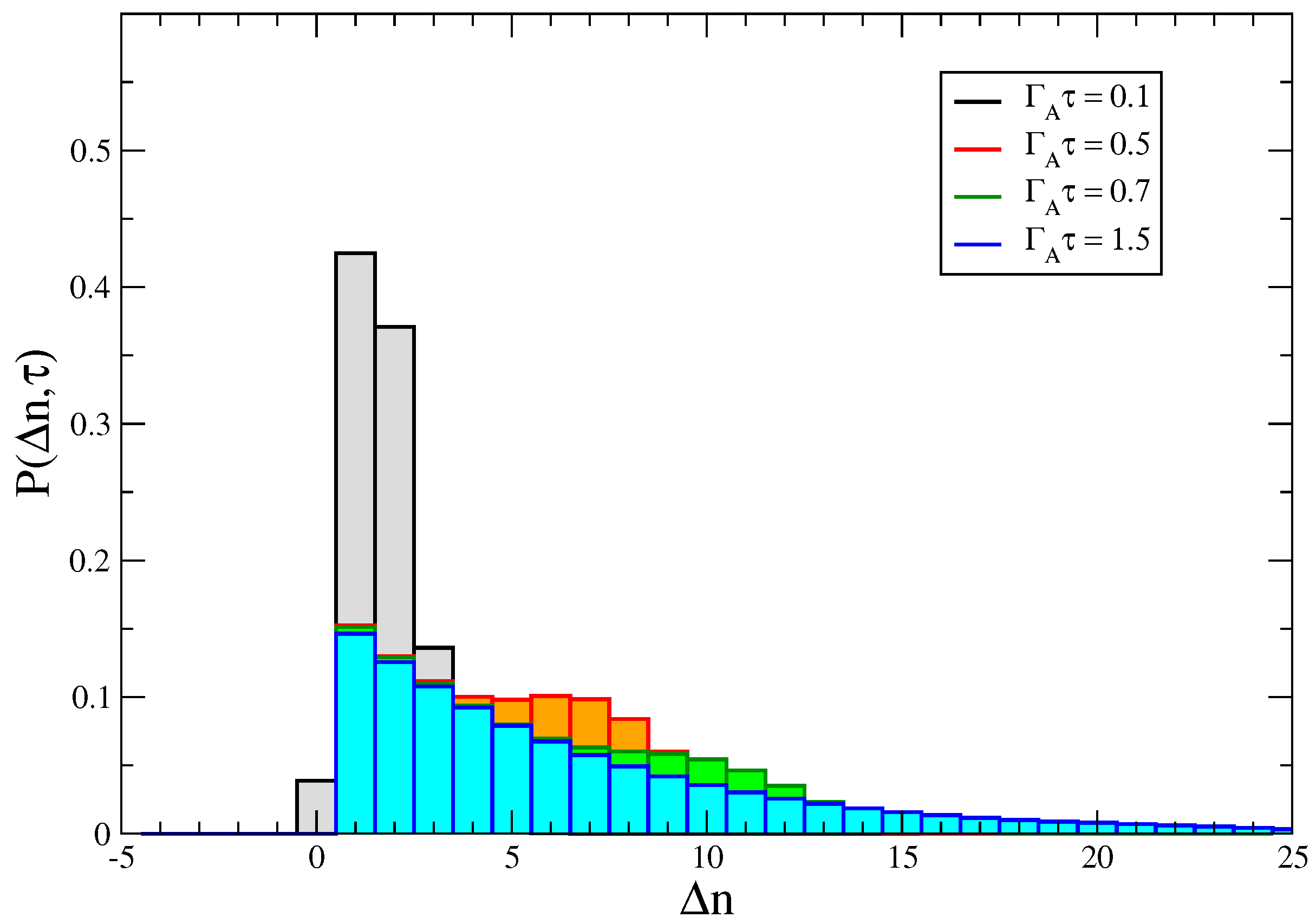
2.3.1. Counting Statistics
2.3.2. Finite-Time Fluctuation Theorem
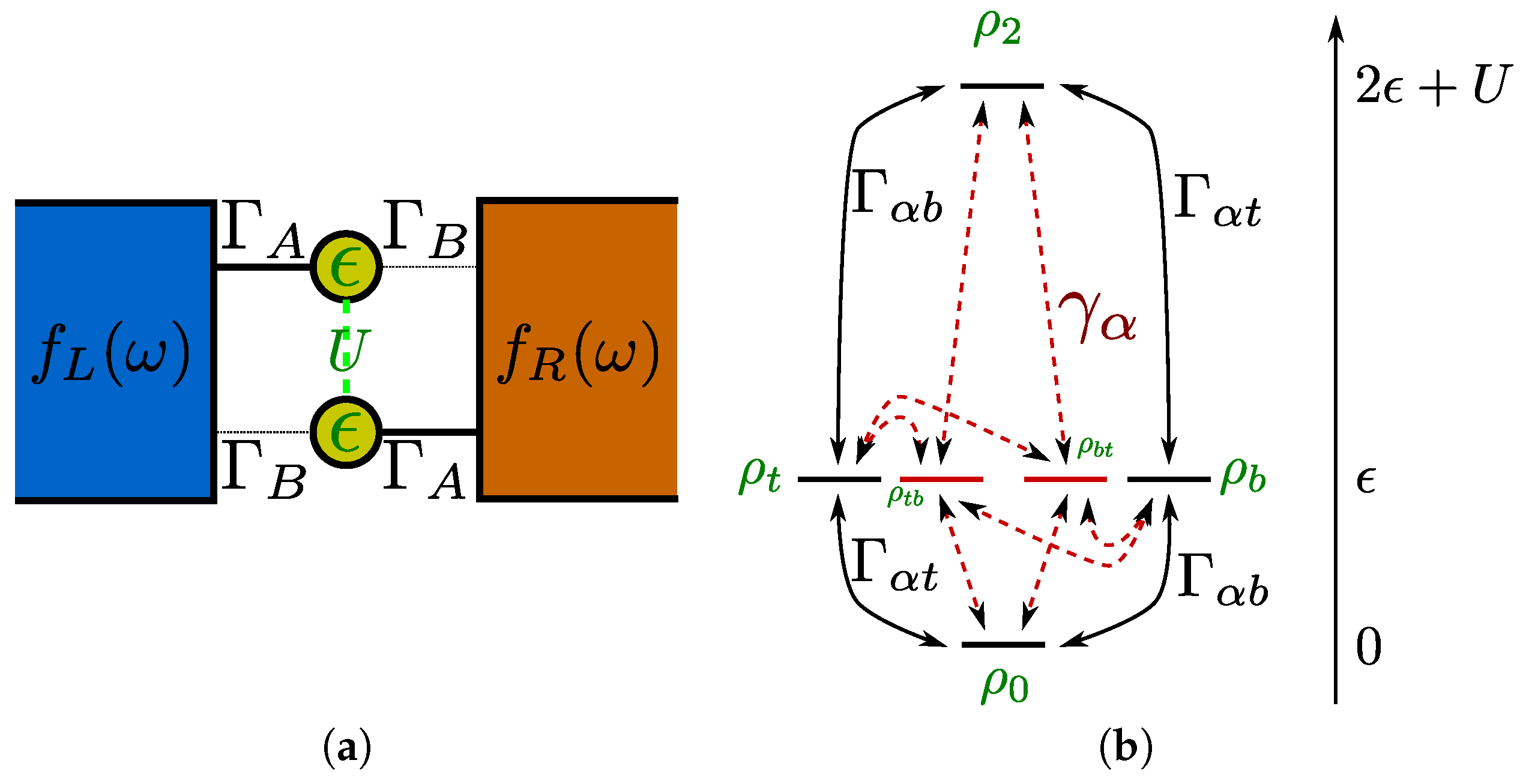
3. Degenerate Single Quantum Dot Circuit
3.1. Model
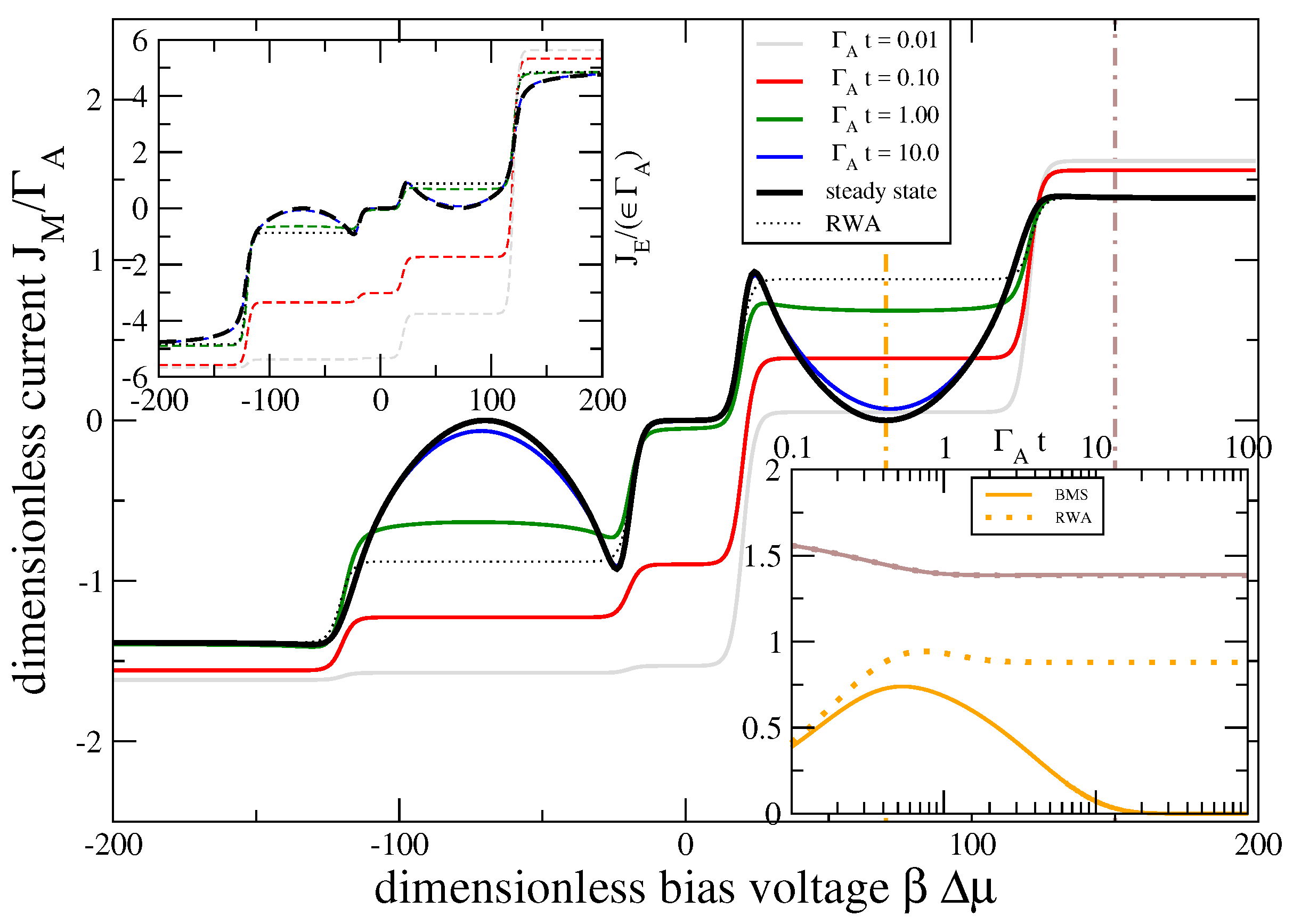
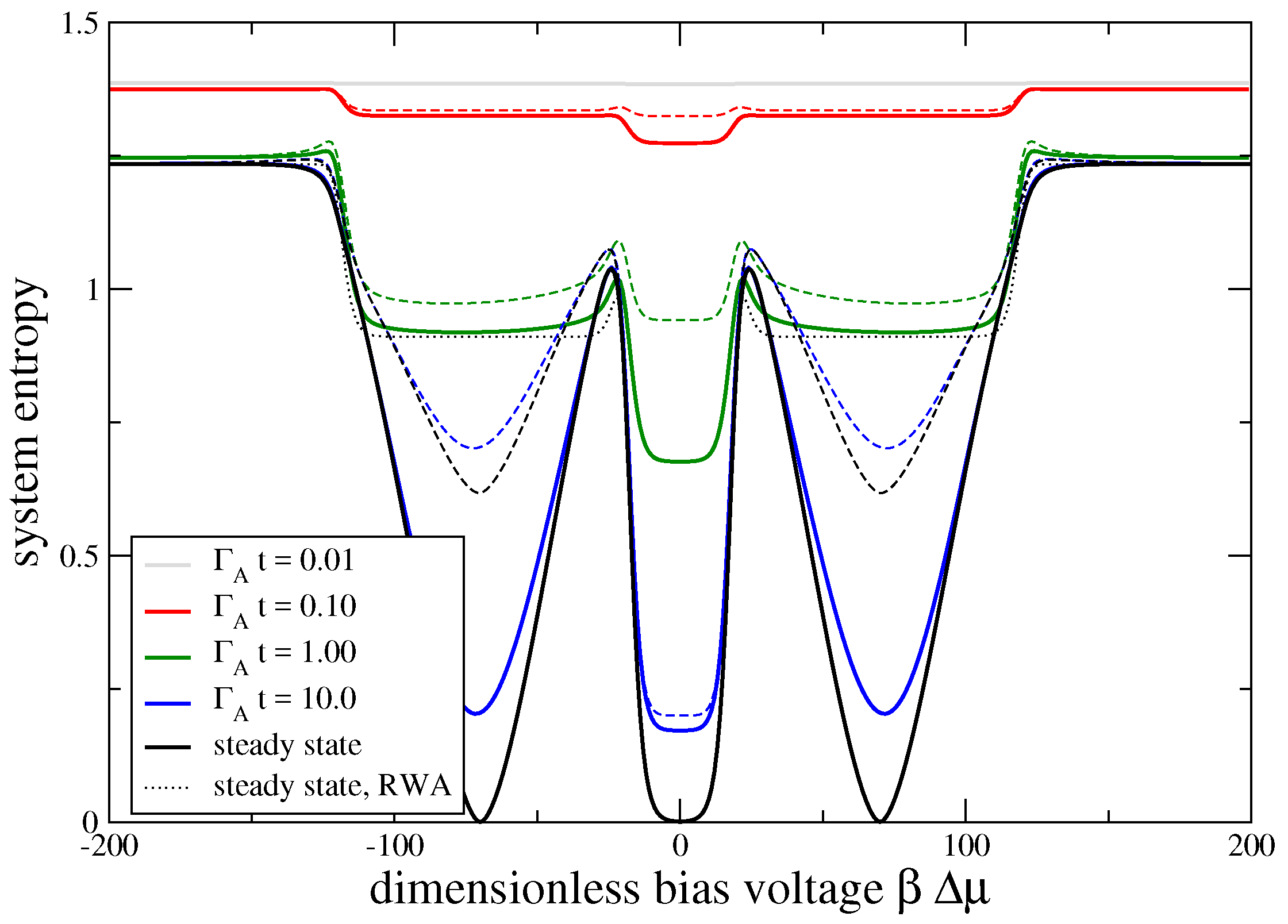
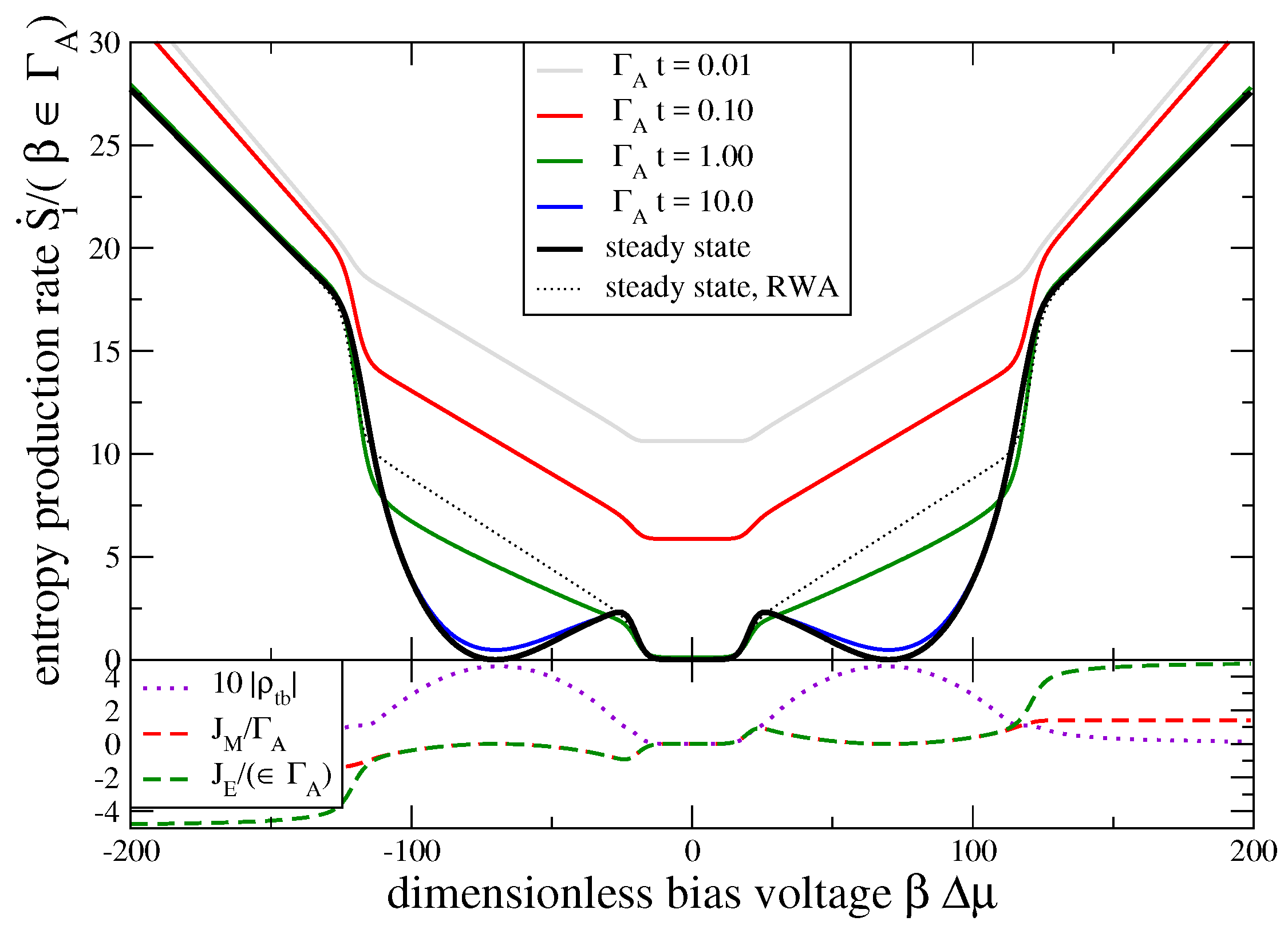
3.2. Model Thermodynamics
3.3. Statistics and Fluctuation Theorem
4. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. KMS Condition with Chemical Potentials
Appendix B. Positivity of Entropy Production
Appendix C. Details for the Specific Model
Appendix C.1. Reservoir Correlation Functions
Appendix C.2. Liouvillian
Appendix C.3. Wide-Band Limit
Appendix C.4. Current Suppression Point
References
- Fujisawa, T.; Hayashi, T.; Tomita, R.; Hirayama, Y. Bidirectional counting of single electrons. Science 2006, 312, 1634–1636. [Google Scholar] [CrossRef] [PubMed]
- Gustavsson, S.; Leturcq, R.; Studer, M.; Shorubalko, I.; Ihn, T.; Ensslin, K.; Driscoll, D.C.; Gossard, A.C. Electron counting in quantum dots. Surf. Sci. Rep. 2009, 64, 191–232. [Google Scholar] [CrossRef]
- Küng, B.; Rössler, C.; Beck, M.; Marthaler, M.; Golubev, D.S.; Utsumi, Y.; Ihn, T.; Ensslin, K. Irreversibility on the level of single-electron tunneling. Phys. Rev. X 2012, 2, 011001. [Google Scholar] [CrossRef]
- Saira, O.-P.; Yoon, Y.; Tanttu, T.; Möttönen, M.; Averin, D.V.; Pekola, J.P. Test of the Jarzynski and Crooks fluctuation relations in an electronic system. Phys. Rev. Lett. 2012, 109, 180601. [Google Scholar] [CrossRef] [PubMed]
- Liebisch, T.C.; Reinhard, A.; Berman, P.R.; Raithel, G. Atom counting statistics in ensembles of interacting Rydberg atoms. Phys. Rev. Lett. 2005, 95, 253002. [Google Scholar] [CrossRef] [PubMed]
- Malossi, N.; Valado, M.M.; Scotto, S.; Huillery, P.; Pillet, P.; Ciampini, D.; Arimondo, E.; Morsch, O. Full counting statistics and phase diagram of a dissipative Rydberg gas. Phys. Rev. Lett. 2014, 113, 023006. [Google Scholar] [CrossRef] [PubMed]
- Krinner, S.; Stadler, D.; Husmann, D.; Brantut, J.-P.; Esslinger, T. Observation of quantized conductance in neutral matter. Nature 2015, 517, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Pekola, J.P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 2015, 11, 118–123. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Spohn, H.; Lebowitz, J.L. Irreversible Thermodynamics for Quantum Systems Weakly Coupled to Thermal Reservoirs; John Wiley & Sons: New York, NY, USA, 2007; pp. 109–142. [Google Scholar]
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Niedenzu, W.; Kurizki, G. Thermodynamics of quantum systems under dynamical control. Adv. Atom. Mol. Opt. Phys. 2015, 64, 329. [Google Scholar]
- Spohn, H. Kinetic equations from Hamiltonian dynamics: Markovian limits. Rev. Mod. Phys. 1980, 52, 569. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Gardiner, C.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 56. [Google Scholar]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Harbola, U.; Esposito, M.; Mukamel, S. Quantum master equation for electron transport through quantum dots and single molecules. Phys. Rev. B 2006, 74, 235309. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Van den Broeck, C.; Esposito, M. Ensemble and trajectory thermodynamics: A brief introduction. Physica A 2015, 418, 6–16. [Google Scholar] [CrossRef]
- Esposito, M. Stochastic thermodynamics under coarse graining. Phys. Rev. E 2012, 85, 041125. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Harbola, U.; Mukamel, S. Entropy fluctuation theorems in driven open systems: Application to electron counting statistics. Phys. Rev. E 2007, 76, 031132. [Google Scholar] [CrossRef] [PubMed]
- Harbola, U.; Esposito, M.; Mukamel, S. Statistics and fluctuation theorem for boson and fermion transport through mesoscopic junctions. Phys. Rev. B 2007, 76, 085408. [Google Scholar] [CrossRef]
- Cuetara, G.B.; Esposito, M.; Gaspard, P. Fluctuation theorems for capacitively coupled electronic currents. Phys. Rev. B 2011, 84, 165114. [Google Scholar] [CrossRef]
- Correa, L.A.; Palao, J.P.; Adesso, G.; Alonso, D. Performance bound for quantum absorption refrigerators. Phys. Rev. E 2013, 87, 042131. [Google Scholar] [CrossRef] [PubMed]
- Krause, T.; Brandes, T.; Esposito, M.; Schaller, G. Thermodynamics of the polaron master equation at finite bias. J. Chem. Phys. 2015, 142, 134106. [Google Scholar] [CrossRef] [PubMed]
- Cuetara, G.B.; Esposito, M. Double quantum dot coupled to a quantum point contact: A stochastic thermodynamics approach. New J. Phys. 2015, 17, 095005. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625. [Google Scholar] [CrossRef]
- Cuetara, G.B.; Engel, A.; Esposito, M. Quantum thermodynamics of rapidly driven systems. New J. Phys. 2015, 17, 055002. [Google Scholar] [CrossRef]
- Uzdin, R.; Levy, A.; Kosloff, R. Equivalence of quantum heat machines, and quantum-thermodynamic signatures. Phys. Rev. X 2015, 5, 031044. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Thermodynamics of quantum-jump-conditioned feedback control. Phys. Rev. E 2013, 88, 062107. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Niedenzu, W.; Brumer, P.; Kurizki, G. Power enhancement of heat engines via correlated thermalization in a three-level “working fluid”. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Niedenzu, W.; Gelbwaser-Klimovsky, D.; Kurizki, G. Performance limits of multilevel and multipartite quantum heat machines. Phys. Rev. E 2015, 92, 042123. [Google Scholar] [CrossRef] [PubMed]
- Cuetara, G.B.; Esposito, M.; Imparato, A. Exact fluctuation theorem without ensemble quantities. Phys. Rev. E 2014, 89, 052119. [Google Scholar] [CrossRef] [PubMed]
- Braun, M.; König, J.; Martinek, J. Theory of transport through quantum-dot spin valves in the weak-coupling regime. Phys. Rev. B 2004, 70, 195345. [Google Scholar] [CrossRef]
- Darau, D.; Begemann, G.; Donarini, A.; Grifoni, M. Interference effects on the transport characteristics of a benzene single-electron transistor. Phys. Rev. B 2009, 79, 235404. [Google Scholar] [CrossRef]
- Schultz, M.G.; von Oppen, F. Quantum transport through nanostructures in the singular-coupling limit. Phys. Rev. B 2009, 80, 033302. [Google Scholar] [CrossRef]
- Schaller, G.; Kießlich, G.; Brandes, T. Transport statistics of interacting double dot systems: Coherent and non-Markovian effects. Phys. Rev. B 2009, 80, 245107. [Google Scholar] [CrossRef]
- Schultz, M.G. Quantum transport through single-molecule junctions with orbital degeneracies. Phys. Rev. B 2010, 82, 155408. [Google Scholar] [CrossRef]
- Nilsson, H.; Karlström, O.; Larsson, M.; Caroff, P.; Pedersen, J.; Samuelson, L.; Wacker, A.; Wernersson, L.-E.; Xu, H. Correlation-induced conductance suppression at level degeneracy in a quantum dot. Phys. Rev. Lett. 2010, 104, 186804. [Google Scholar] [CrossRef] [PubMed]
- Karlström, O.; Pedersen, J.; Samuelsson, P.; Wacker, A. Canyon of current suppression in an interacting two-level quantum dot. Phys. Rev. B 2011, 83, 205412. [Google Scholar] [CrossRef]
- Lidar, D.A.; Bihary, Z.; Whaley, K.B. From completely positive maps to the quantum Markovian semigroup master equation. Chem. Phys. 2001, 268, 35–53. [Google Scholar] [CrossRef]
- Schaller, G.; Brandes, T. Preservation of positivity by dynamical coarse-graining. Phys. Rev. A 2008, 78, 022106. [Google Scholar] [CrossRef]
- Schaller, G. Open Quantum Systems Far from Equilibrium; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 881. [Google Scholar]
- Schaller, G. Quantum equilibration under constraints and transport balance. Phys. Rev. E 2011, 83, 031111. [Google Scholar] [CrossRef] [PubMed]
- Spohn, H. Entropy production for quantum dynamical semigroups. J. Math. Phys. 1978, 19, 1227–1230. [Google Scholar] [CrossRef]
- Silaev, M.; Heikkilä, T.T.; Virtanen, P. Lindblad-equation approach for the full counting statistics of work and heat in driven quantum systems. Phys. Rev. E 2014, 90, 022103. [Google Scholar] [CrossRef] [PubMed]
- Braig, S.; Brouwer, P. Rate equations for coulomb blockade with ferromagnetic leads. Phys. Rev. B 2005, 71, 195324. [Google Scholar] [CrossRef]
- Jordan, A.N.; Sukhorukov, E.V. Transport statistics of bistable systems. Phys. Rev. Lett. 2004, 93, 260604. [Google Scholar] [CrossRef] [PubMed]
- Schaller, G.; Kießlich, G.; Brandes, T. Counting statistics in multistable systems. Phys. Rev. B 2010, 81, 205305. [Google Scholar] [CrossRef]
- Lindblad, G. Completely positive maps and entropy inequalities. Commun. Math. Phys. 1975, 40, 147–151. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulnes Cuetara, G.; Esposito, M.; Schaller, G. Quantum Thermodynamics with Degenerate Eigenstate Coherences. Entropy 2016, 18, 447. https://doi.org/10.3390/e18120447
Bulnes Cuetara G, Esposito M, Schaller G. Quantum Thermodynamics with Degenerate Eigenstate Coherences. Entropy. 2016; 18(12):447. https://doi.org/10.3390/e18120447
Chicago/Turabian StyleBulnes Cuetara, Gregory, Massimiliano Esposito, and Gernot Schaller. 2016. "Quantum Thermodynamics with Degenerate Eigenstate Coherences" Entropy 18, no. 12: 447. https://doi.org/10.3390/e18120447
APA StyleBulnes Cuetara, G., Esposito, M., & Schaller, G. (2016). Quantum Thermodynamics with Degenerate Eigenstate Coherences. Entropy, 18(12), 447. https://doi.org/10.3390/e18120447




