Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals
Abstract
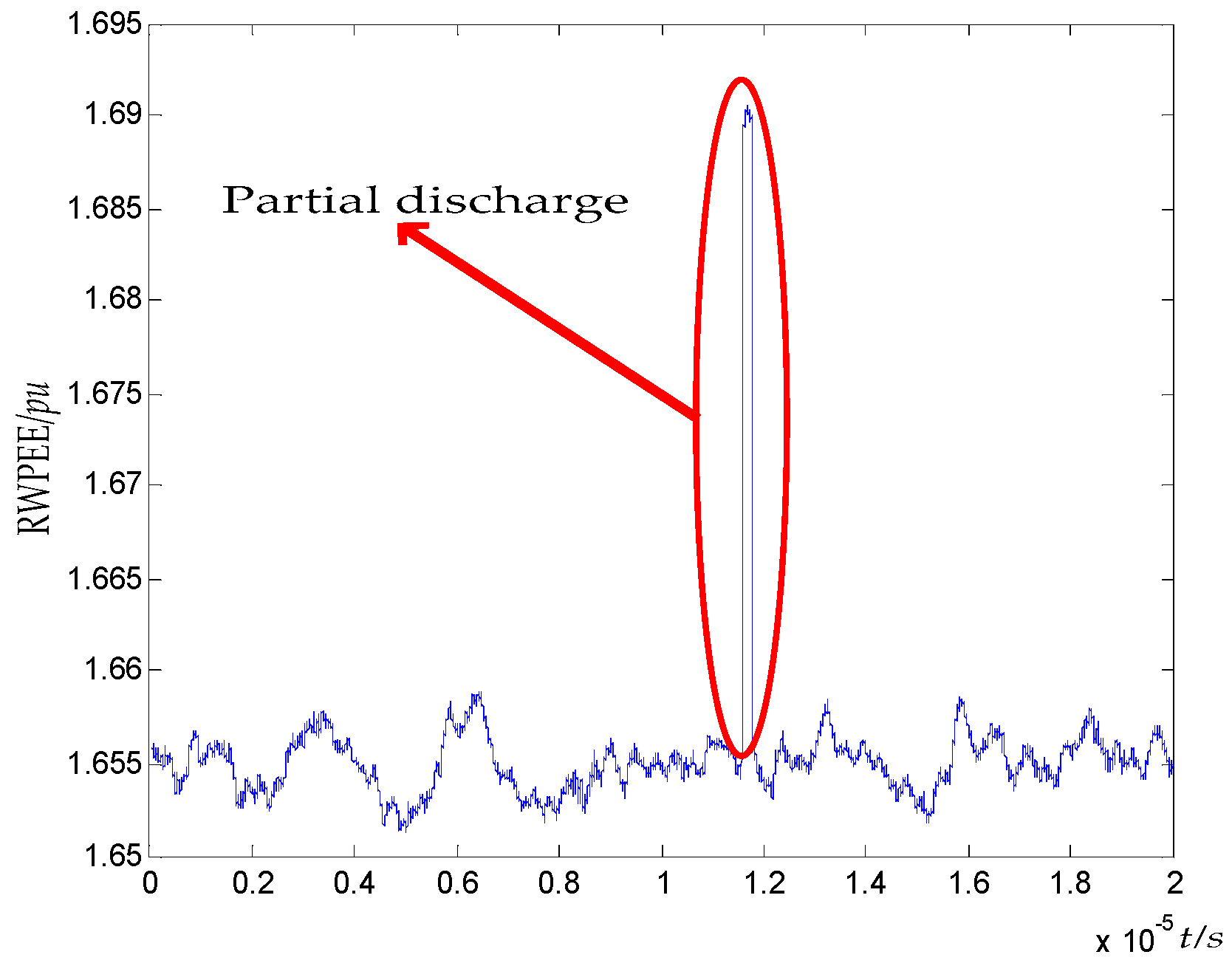
:1. Introduction
2. Application of SWE and SWPE in a Power System
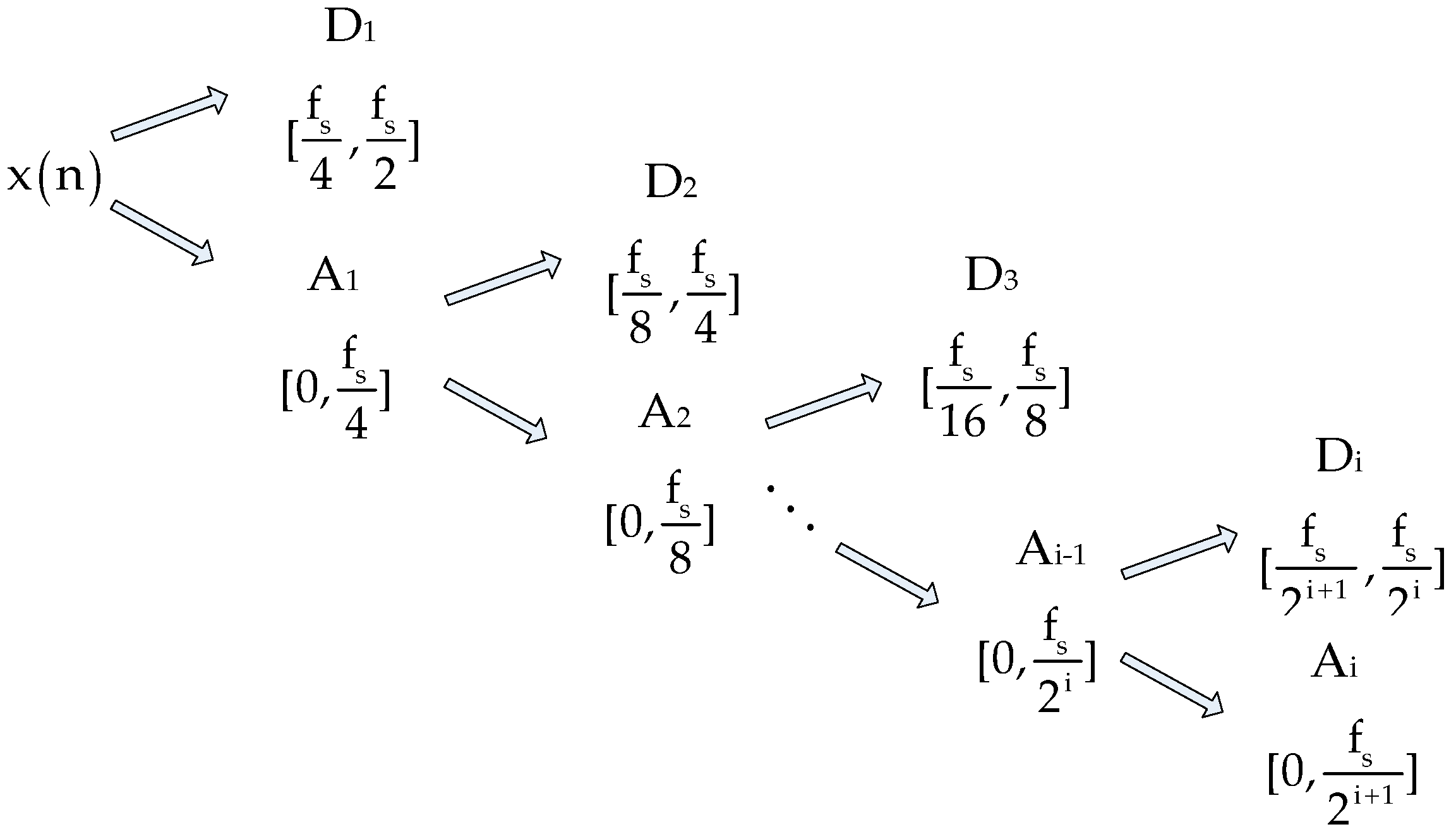
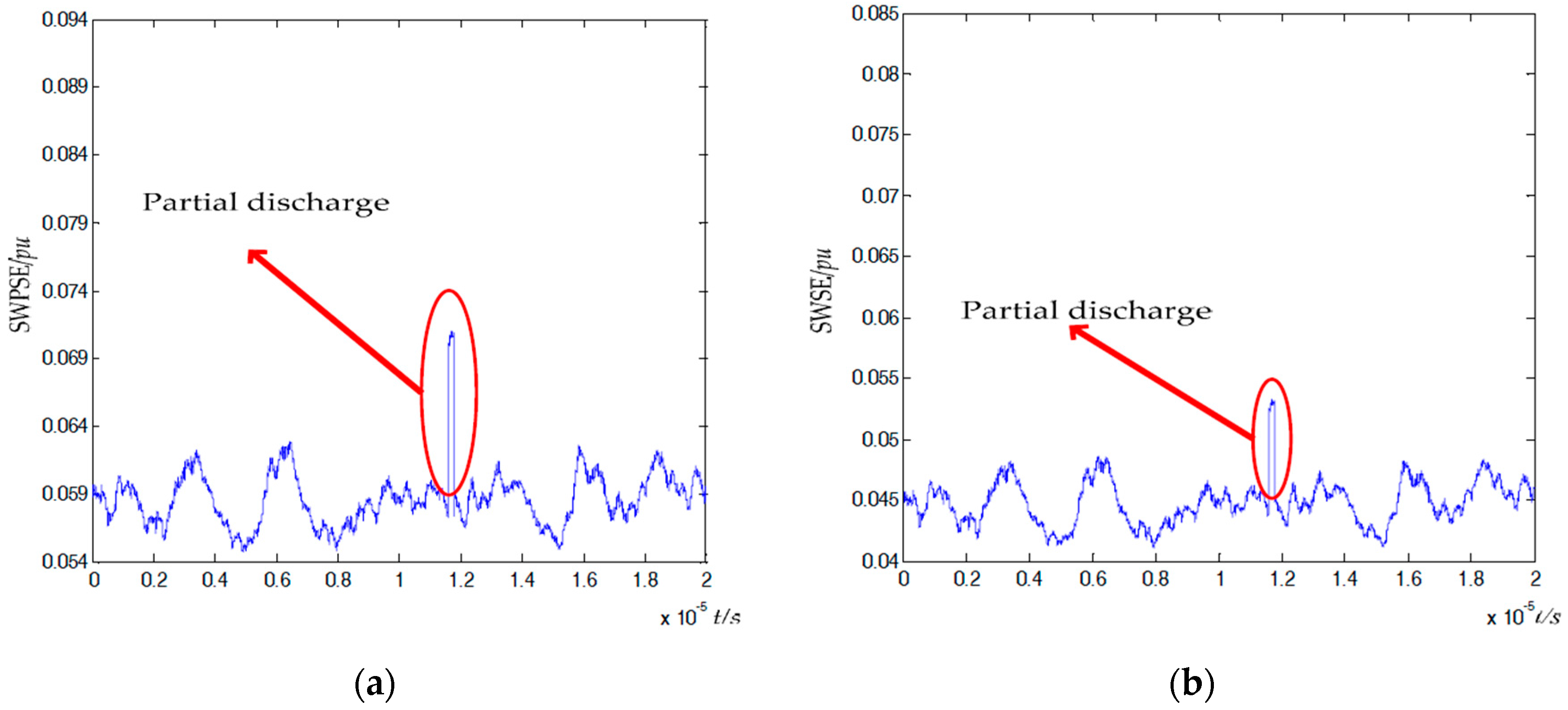
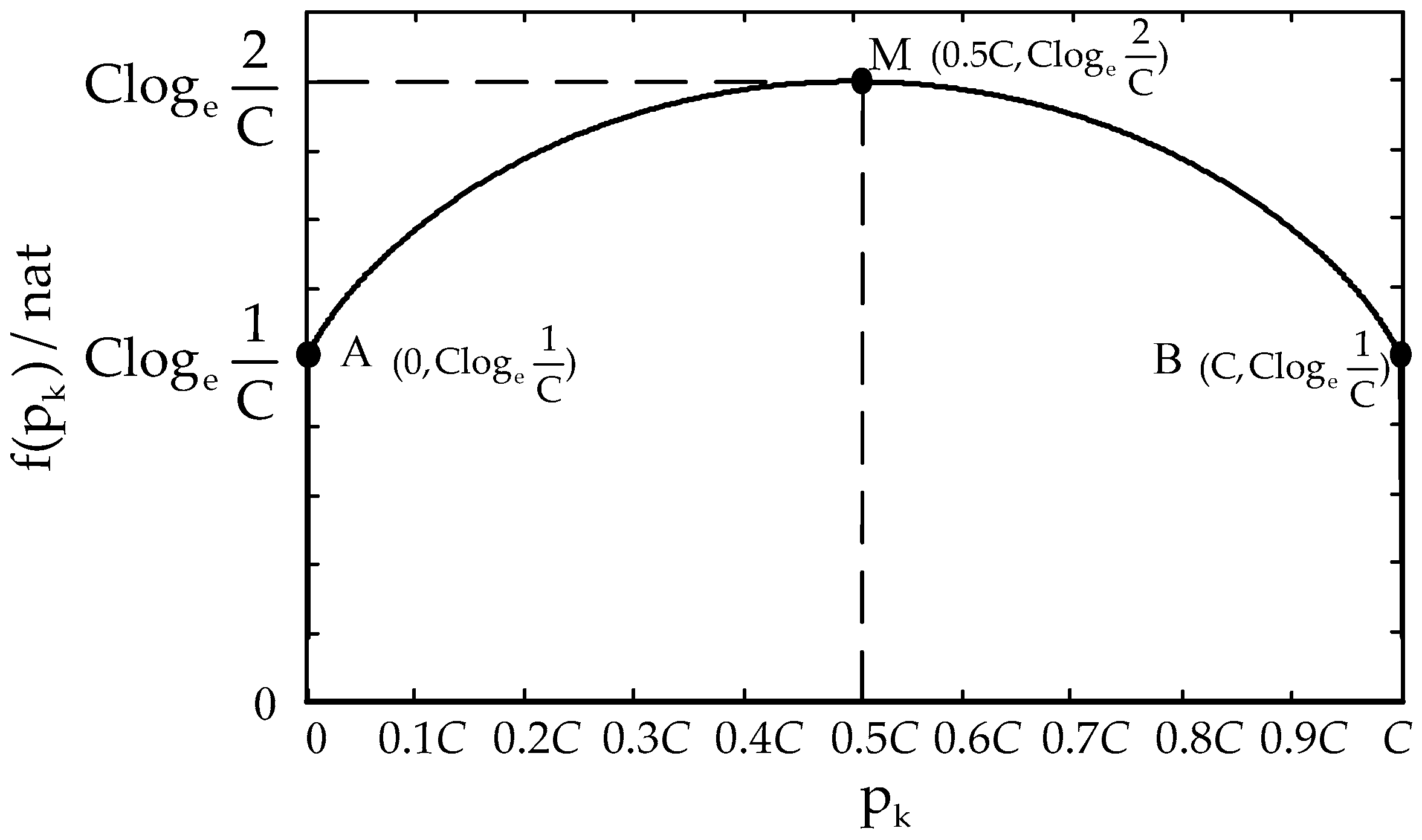
2.1. Application of SWE in a Power System
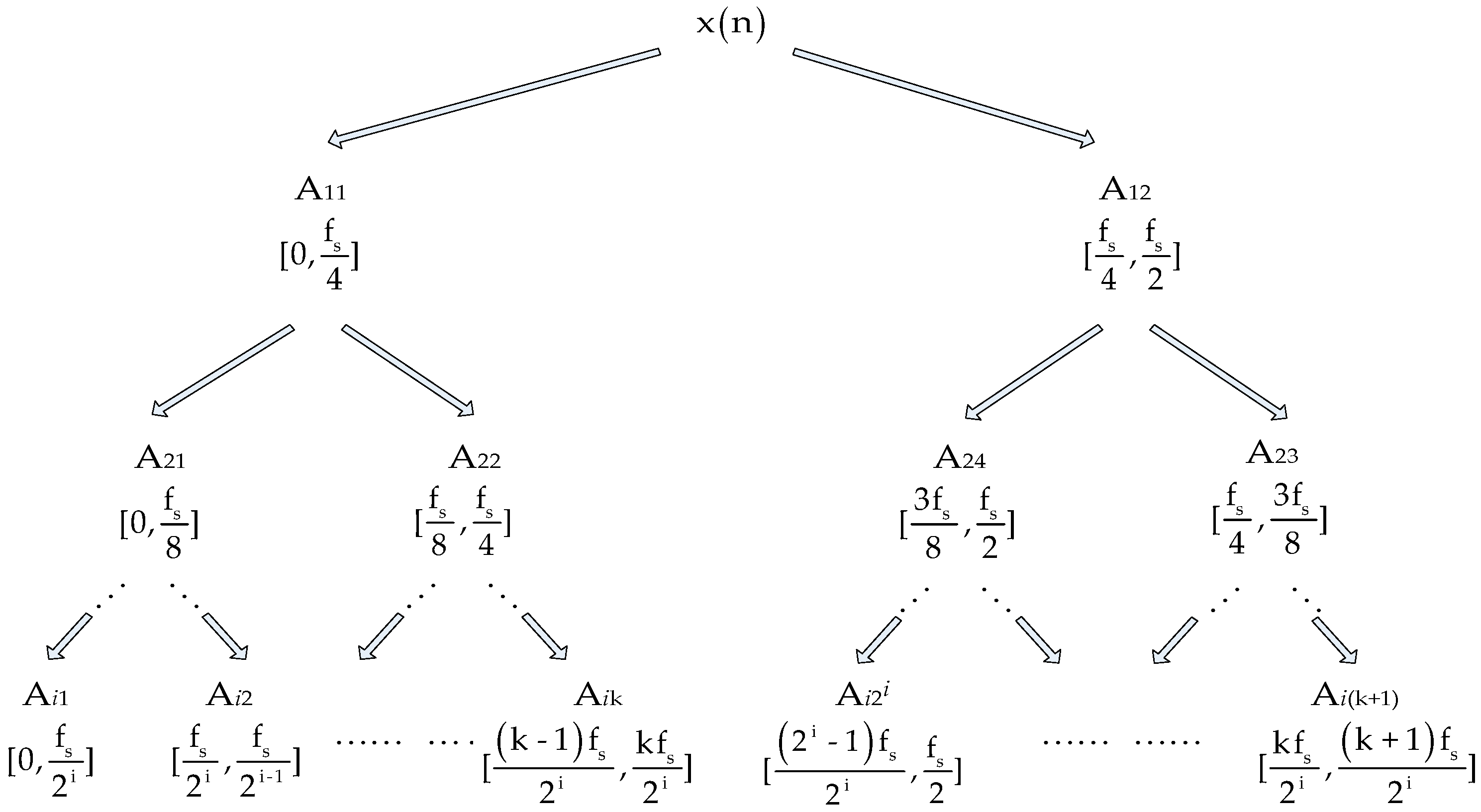
2.2. Application of SWPE in a Power System
2.3. Problems Existed in SWE and SWPE in a Power System
- When the measured signal is more complex and contains a lot of random signals, there is the severe energy leakage and frequency aliasing in the wavelet coefficients (or reconstructed signals) with increasing of the wavelet decomposition scale [32]. So, the complexity and feature of signal can not be accurately expressed when the adjacent wavelet coefficients (or reconstructed signals) are taken as basic data to participate in the calculation of SWE and SWPE.
- When most signal components concentrate in the high frequency band, due to the roughness of wavelet decomposition in the high frequency band, the high frequency components of similar frequency will be in the same scale and calculation accuracy of SWE is directly reduced.
- For feature extraction of different transient signals, the studies, about the relationship between different entropy statistical properties and the signal feature, are still in the initial stage, which needs theoretical basis to support the transient signal extraction.
- For the different transient signals, sampling frequency of signals and wavelet decomposition scale exert influence on the accuracy and speed of feature extraction, but there has been no relevant research lately.
3. Comparison of Feature Extraction Accuracy and Wavelet Aliasing Effect on SWE and SWPE
3.1. Comparison in Accuracy of Feature Extraction for SWE and SWPE
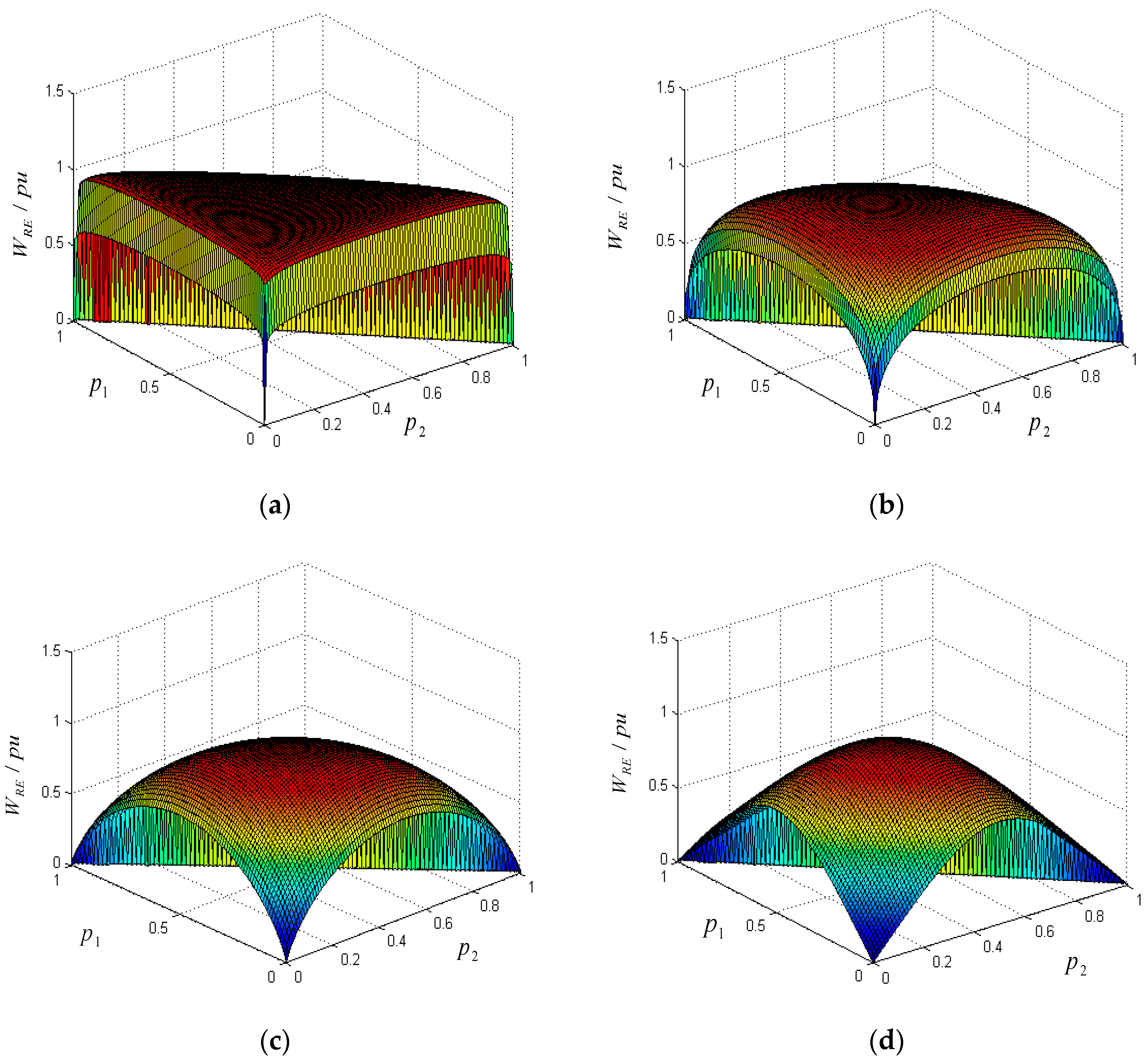
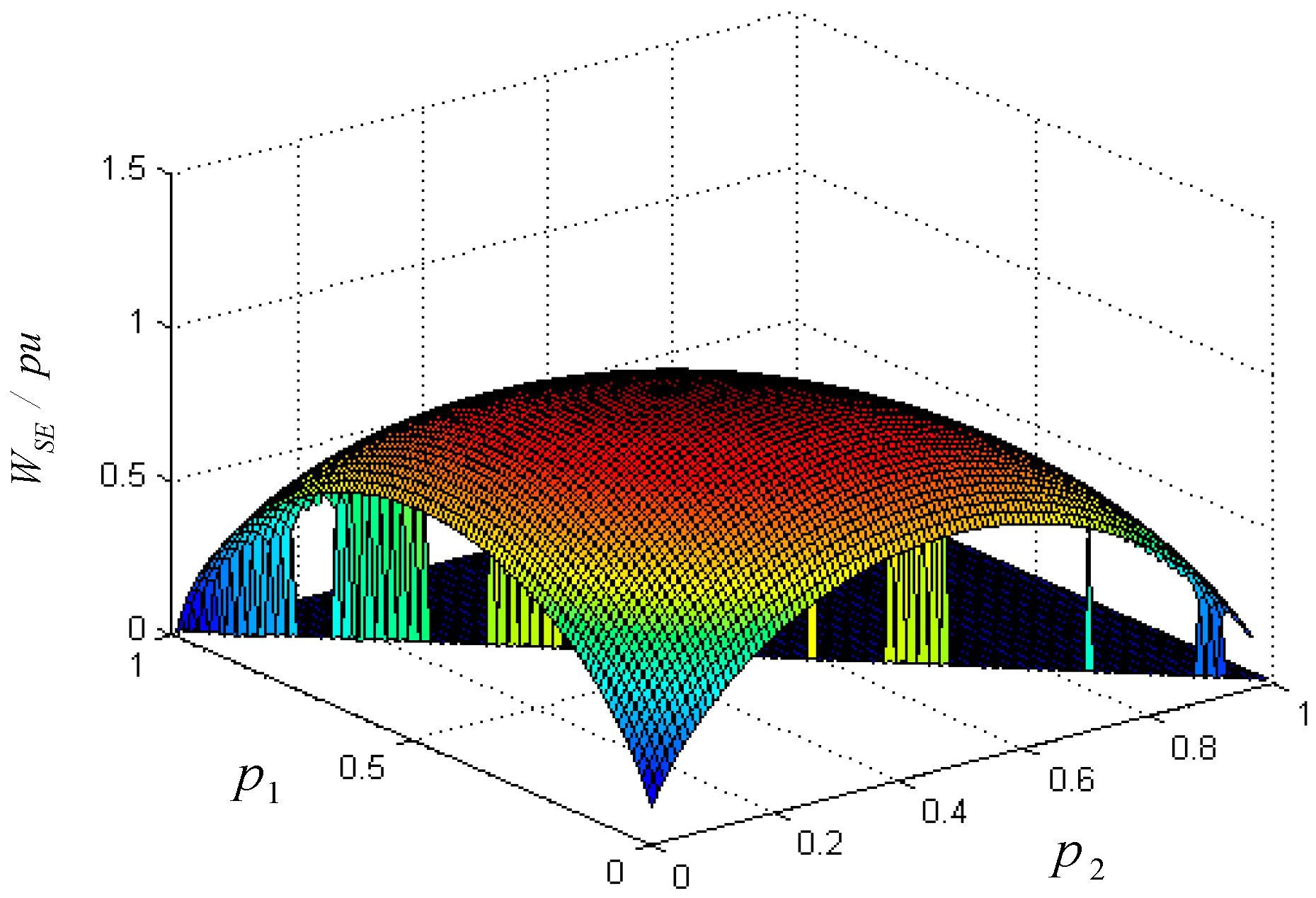
3.2. Wavelet Aliasing Effect on SWE and SWPE
4. Conclusions
- Basic theory about analysis and operation mechanism of transient signals based on wavelet and different entropy should be deeply studied and improved. For the negative influence of wavelet aliasing on SWE and SWPE, selecting different entropy of various statistical properties, optimizing the parameter of entropy, adjusting sampling frequency and selecting different orthogonal wavelet bases should be considered to reduce the effect of wavelet aliasing on accuracy of feature extraction.
- When SWE and SWPE are applied to relay protection, there are some difficulties such as high sampling rate, complex calculation, etc. So, engineering applications put forward higher requirements for the ability of real time application. The further researches should focus on the optimizing algorithm structure and the improving operation speed of SWE and SWPE.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.K.; Li, H.Y.; Wang, Y.J.; Xie, R.H.; Liu, X.B. A novel approach to extracting casing status features using data mining. Entropy 2014, 16, 389–404. [Google Scholar] [CrossRef]
- Luo, G.M.; He, Z.Y.; Lin, S. Discussion on using discrepancy among wavelet relative entropy values to recognize transient signals in power transmission line. Power Syst. Technol. 2008, 32, 47–51. [Google Scholar]
- El-Zonlcoly, A.M.; Desoulci, H. Wavelet entropy based algorithm for fault detection and classification in FACTS compensated transmission line. Int. J. Electr. Power 2011, 33, 1368–1374. [Google Scholar] [CrossRef]
- Dehghani, M.; Khooban, M.H.; Nilcnam, T. Fast fault detection and classification based on a combination of wavelet singular entropy theory and fuzzy logic in distribution lines in the presence of distributed generations. Int. J. Electr. Power 2016, 78, 455–462. [Google Scholar] [CrossRef]
- Fu, L.; He, Z.; Qian, Q. Feature extraction of fault transient and fault type determination for transmission ehv lines. Proc. CSEE 2010, 30, 100–106. [Google Scholar]
- Zhou, L.; Xia, X.; Wan, Y.; Zhang, H.; Lei, P. Harmonic detection based wavelet transform. Trans. China Electrotech. Soc. 2006, 21, 67–74. [Google Scholar]
- Zhang, B.; Sun, J. A power quality analysis method based on mallat algorithm and fast fourier transform. Power Syst. Technol. 2007, 31, 35–40. [Google Scholar]
- He, Z.; Fu, L.; Lin, S.; Bo, Z. Fault detection and classification in EHV transmission line based on wavelet singular entropy. IEEE Trans. Power Deliv. 2010, 25, 2156–2163. [Google Scholar] [CrossRef]
- Lin, S.; Gao, S.; He, Z.Y.; Deng, Y.J. A pilot directional protection for HVDC transmission line based on relative entropy of wavelet energy. Entropy 2015, 17, 5257–5273. [Google Scholar] [CrossRef]
- Samui, A.; Samantaray, S.R. Wavelet Singular Entropy-Based Islanding Detection in Distributed Generation. IEEE Trans. Power Deliv. 2013, 28, 411–418. [Google Scholar] [CrossRef]
- PiotrKowski, R.; Castro, E.; Gallego, A. Wavelet power, entropy and bispectrum applied to AE signals fordamage identification and evaluation of corroded galvanized steel. Mech. Syst. Signal Process. 2009, 23, 432–445. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, Q.; Cui, Y.; Zhang, Q. A new detection approach of transient disturbances combining wavelet packet and Tsallis entropy. Neurocomputing 2014, 142, 393–407. [Google Scholar] [CrossRef]
- He, Z.Y.; Qian, Q.Q. Multi-resolution entropy and its application in EHV transmission line fault detection. Electr. Power Autom. Equip. 2001, 21, 9–12. [Google Scholar]
- He, Z.Y.; Liu, Z.G.; Qian, Q.Q. Study on wavelet entropy theory and adaptability of its application in power system. Power Syst. Technol. 2004, 28, 17–21. [Google Scholar]
- He, Z.Y.; Cai, Y.M.; Qian, Q.Q. A study of wavelet entropy theory and its application in electric power system fault detection. Proc. CSEE 2005, 25, 38–43. [Google Scholar]
- Luo, G.; Zhang, D.; Tseng, K.J.; He, J. Impulsive noise reduction for transient Earth voltage-based partial discharge using Wavelet-entropy. IET Sci. Meas. Technol. 2016, 10, 69–76. [Google Scholar] [CrossRef]
- El Safty, S.; El-Zonlcoly, A. Applying wavelet entropy principle in fault classification. Electr. Power Energy Syst. 2009, 31, 604–607. [Google Scholar] [CrossRef]
- Dubey, R.; Samantara, S.R. Wavelet singular entropy-based symmetrical fault-detection and out-of-step protection during power swing. IET Gener. Transm. Distrib. 2013, 7, 1123–1134. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.P.; Zheng, Z.H. Application of wavelet singular entropy theory in transient protection and accelerated trip of transmission line protection. Autom. Electr. Power Syst. 2009, 33, 79–83. [Google Scholar]
- Jia, Y.; He, Z.Y.; Zhao, J.J. A method to identify voltage sag sources in distribution network based on wavelet entropy and probability neural network. Power Syst. Technol. 2009, 33, 63–69. [Google Scholar]
- Li, D.H.; Wang, B.; Ma, Y.X. Grounding fault detection based on wavelet entropy and neural network for loop net of DC system. Electr. Power Autom. Equip. 2008, 28, 51–54. [Google Scholar]
- Wang, Y.S.; Tan, Z.Y.; Liu, X.M. Fault type recognition for distribution network based on wavelet singular entropy and support vector machine. Power Syst. Prot. Control 2011, 39, 16–20. [Google Scholar]
- Li, G.Y.; Wang, H.L.; Zhao, M. Short-time power quality disturbances identification based on improved wavelet energy entropy and SVM. Trans. China Electrotech. Soc. 2009, 24, 161–167. [Google Scholar]
- Yu, N.H.; Li, C.J.; Yang, J.; Cai, M.; Dong, B.; Gong, L.Y.; Ma, Y.Y. Operating state feature extraction based on wavelet-packet time entropy for distribution network. Electr. Power Autom. Equip. 2014, 34, 64–71. [Google Scholar]
- Liu, Q.; Chang, Y.; Xu, Y.; Hao, W. Fault position identification for series compensated transmission lines with sssc based on improved wavelet packet entropy. Autom. Electr. Power Syst. 2011, 35, 65–70. [Google Scholar]
- Sun, L.J.; Hu, X.G.; Ji, Y.C. Fault diagnosis for high voltage circuit breakers with improved characteristic entropy of wavelet packet. Proc. CSEE 2007, 27, 103–108. [Google Scholar]
- Zhang, J.; Wang, X.G.; Li, Z.L. Application of neural network based on wavelet packet-energy entropy in power system fault diagnosis. Power Syst. Technol. 2006, 30, 72–80. [Google Scholar]
- Liu, Z.G.; Cui, Y.; Li, W.H. Combined power quality disturbances recognition using wavelet packet entropies and S-transform. Entropy 2015, 17, 5811–5828. [Google Scholar] [CrossRef]
- Huang, N.T.; Chen, H.J.; Zhang, S.X.; Cai, G.W.; Li, W.G.; Xu, D.G.; Fang, L.H. Mechanical fault diagnosis of high voltage circuit breakers based on wavelet time-frequency entropy and one-class support vector machine. Entropy 2016, 18, 1–17. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Wei, W.; Wu, L.L. Motor mechanical fault diagnosis based on wavelet packet, Shannon entropy, SVM and GA. Electr. Power Autom. Equip. 2010, 30, 87–91. [Google Scholar]
- Chen, W.; Xie, B.; Long, Z.; Cui, L.; Li, Y.; Zhou, Q.; Chen, X. Stage identification in air-gap discharge of oil-impregnated paper insulation based on wavelet packet energy entropy. Proc. CSEE 2016, 36, 563–569. [Google Scholar]
- Chen, J.K.; Li, H.Y.; Yang, S.Y.; Kou, B.Q. Application of wavelet packet singularity entropy and PSD in power harmonics detection. Trans. China Electrotech. Soc. 2010, 25, 193–199. [Google Scholar]
- Chen, J.K.; Dou, Y.H.; Wang, Z.H.; Li, G.Q. A novel method for PD feature extraction of power cable with renyi entropy. Entropy 2015, 17, 7698–7712. [Google Scholar] [CrossRef]
- Chen, J.K.; Li, G.Q. Tsallis wavelet entropy and its application in power signal analysis. Entropy 2014, 16, 3009–3025. [Google Scholar] [CrossRef]
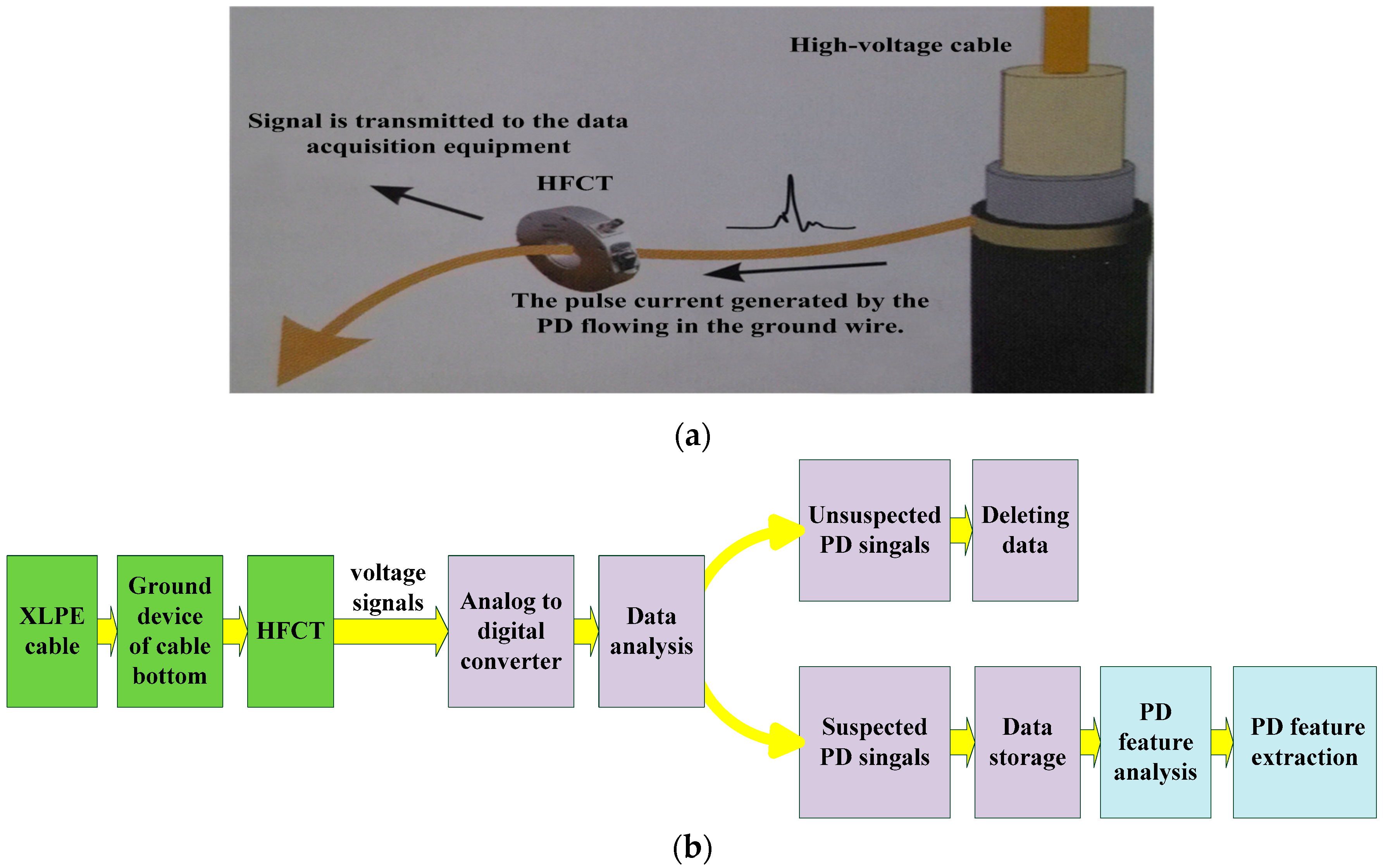


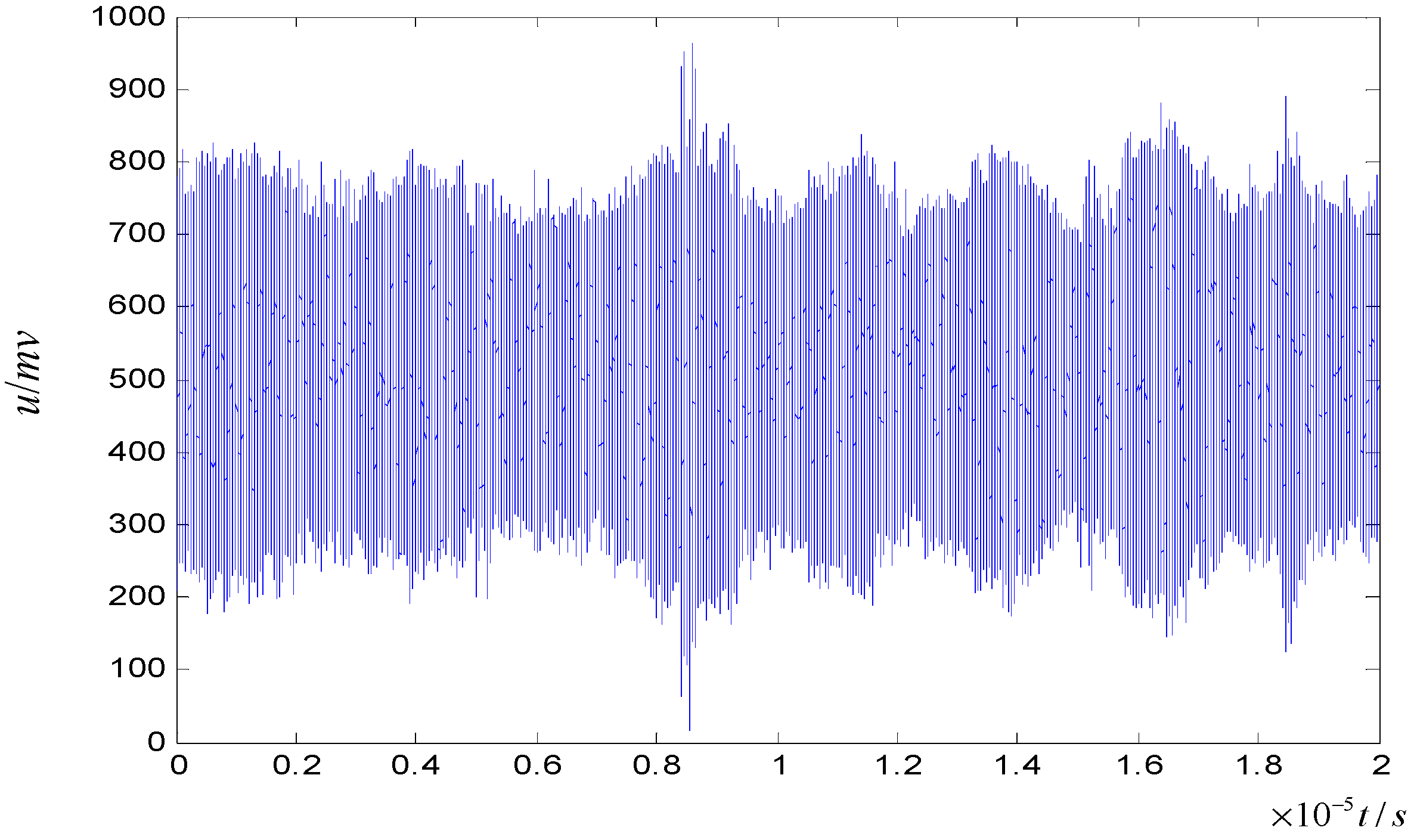
| Model | Cable Core | Cross-Sectional Area | Insulation Layer | Metal Sheath | The Voltage Rating |
|---|---|---|---|---|---|
| YJLW03 | Coppersplicing wire | 800 mm² | XLPE | Aluminum | 127 kV/220 kV |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Dou, Y.; Li, Y.; Li, J. Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals. Entropy 2016, 18, 437. https://doi.org/10.3390/e18120437
Chen J, Dou Y, Li Y, Li J. Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals. Entropy. 2016; 18(12):437. https://doi.org/10.3390/e18120437
Chicago/Turabian StyleChen, Jikai, Yanhui Dou, Yang Li, and Jiang Li. 2016. "Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals" Entropy 18, no. 12: 437. https://doi.org/10.3390/e18120437
APA StyleChen, J., Dou, Y., Li, Y., & Li, J. (2016). Application of Shannon Wavelet Entropy and Shannon Wavelet Packet Entropy in Analysis of Power System Transient Signals. Entropy, 18(12), 437. https://doi.org/10.3390/e18120437





