Symplectic Entropy as a Novel Measure for Complex Systems
Abstract
:1. Introduction
2. Materials and Methods
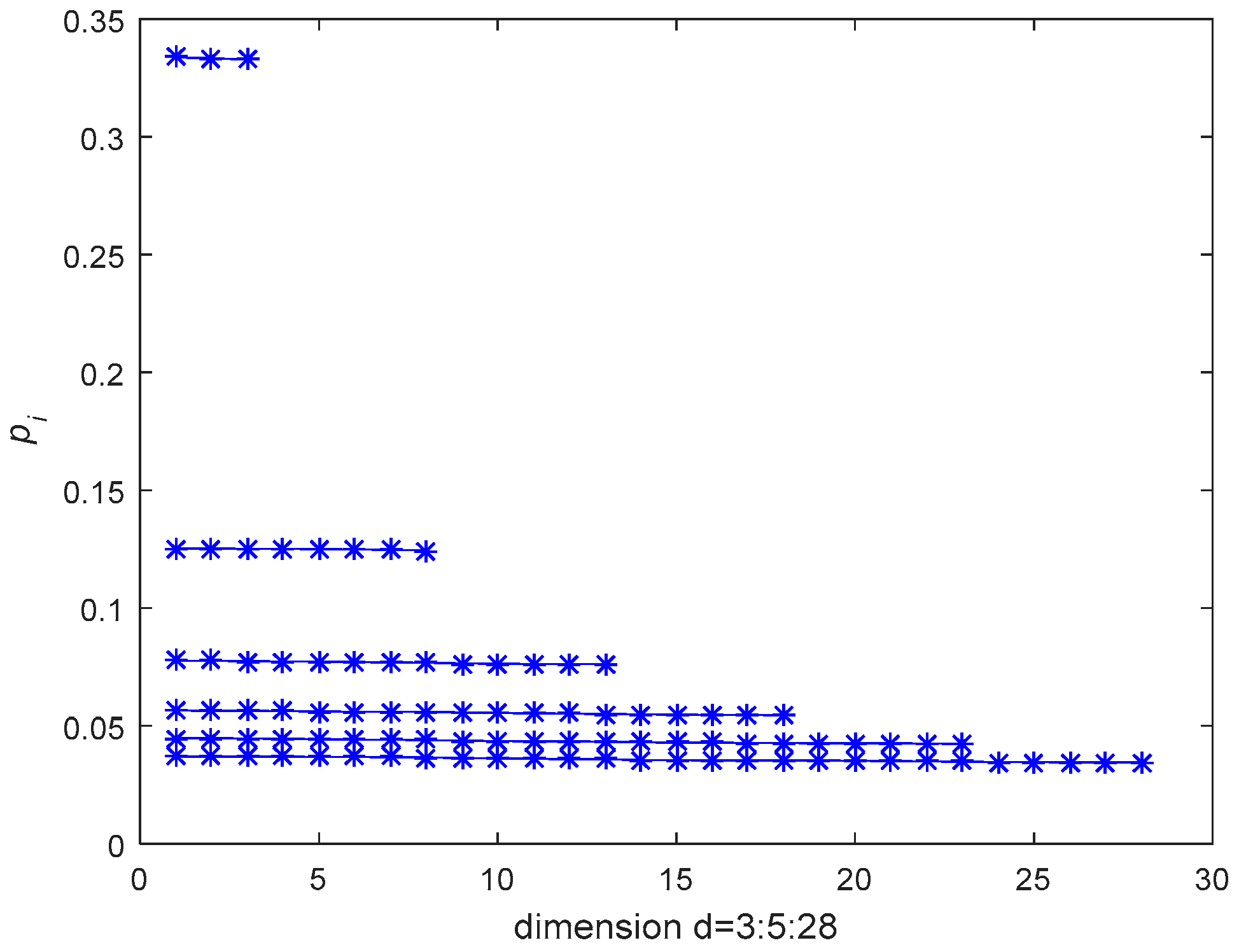
2.1. Symplectic Entropy
2.2. Materials
2.2.1. Synthetic Time Series
- Lorenz chaotic system:
- Rössler chaotic system:
- Van der Pol chaotic system:
2.2.2. Real Time Series
2.2.3. Surrogate Data and Null Hypothesis
3. Results
3.1. Applicantion to Synthetic Time Series
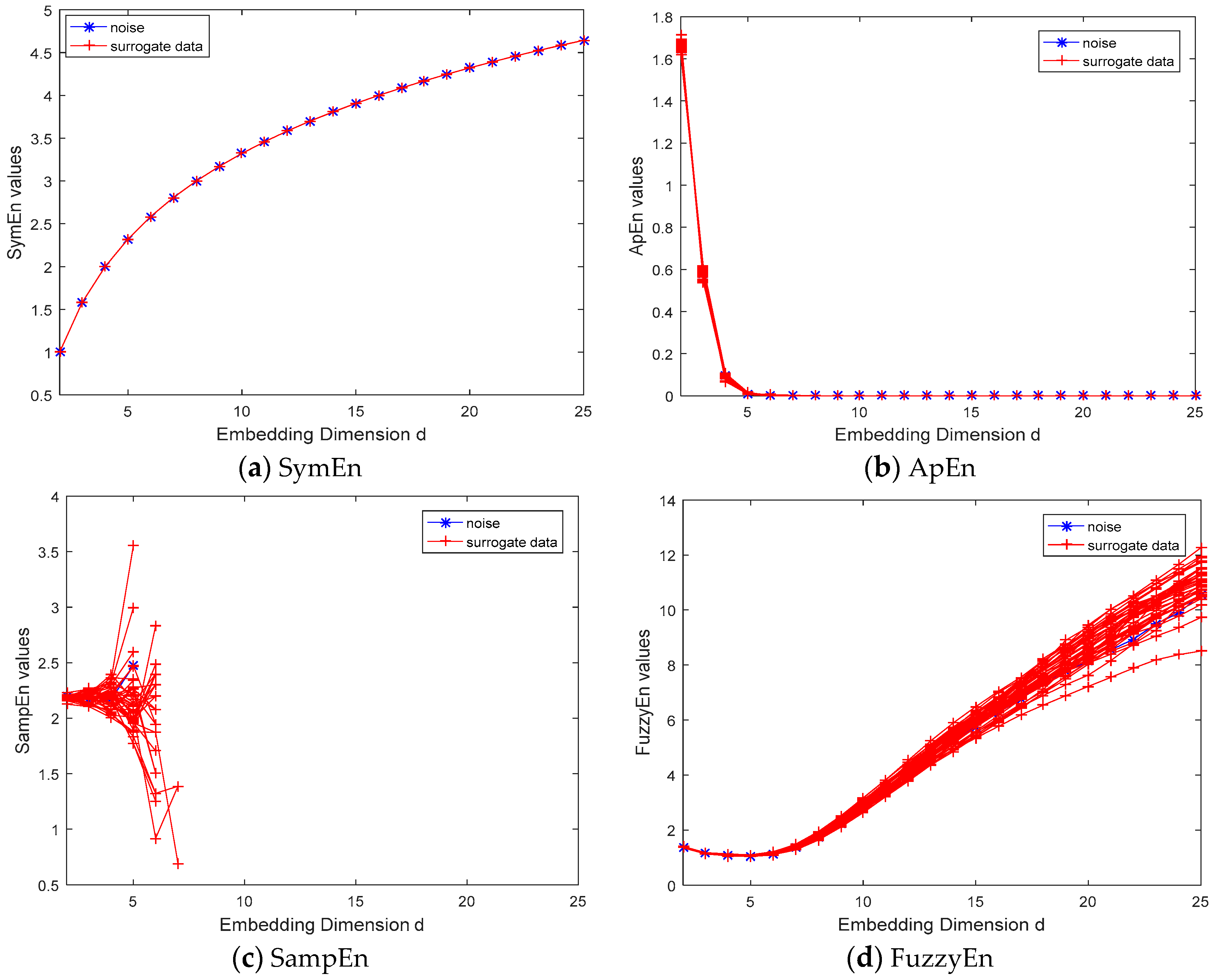
3.1.1. Tests on Gaussian White Noise Process
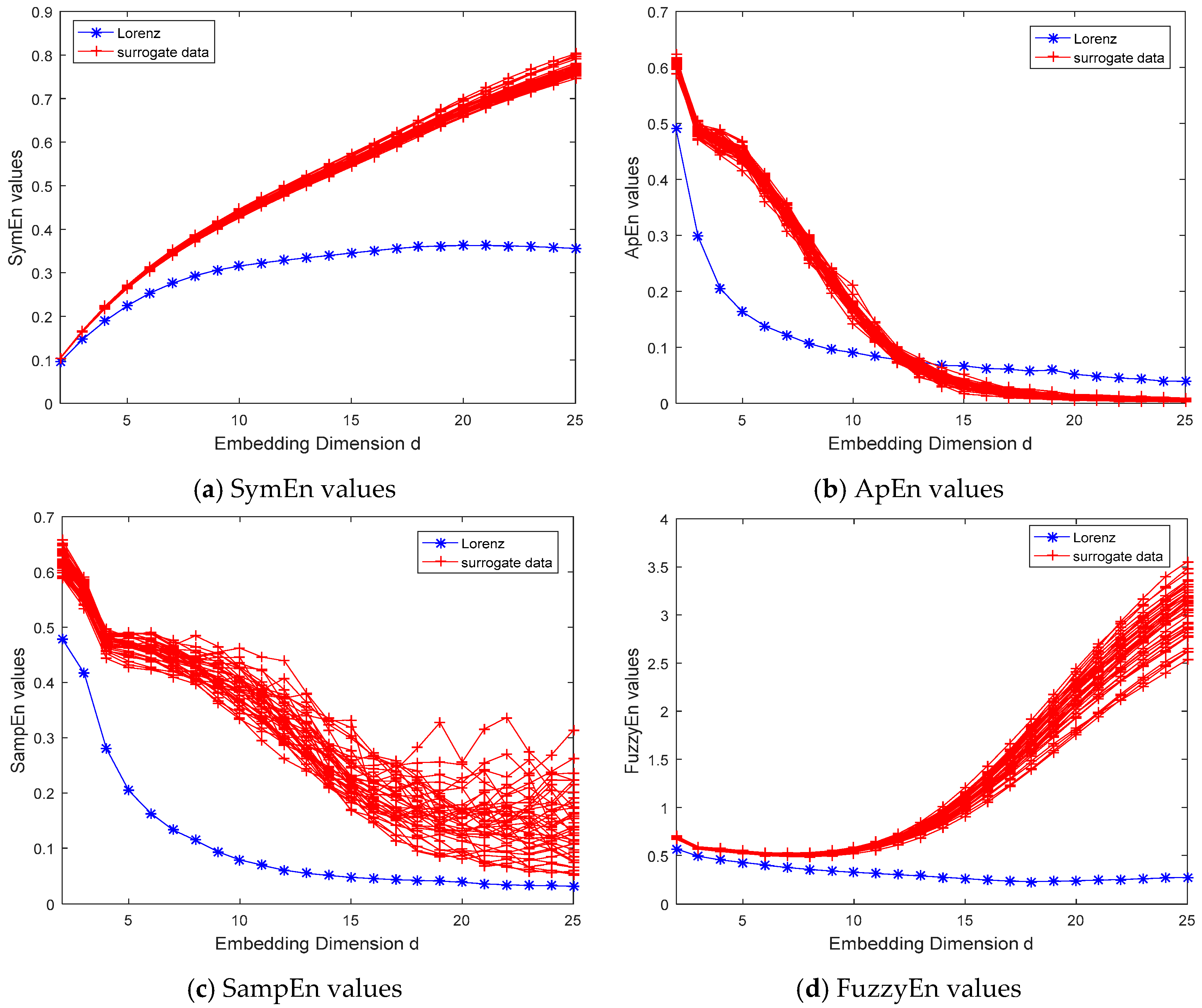
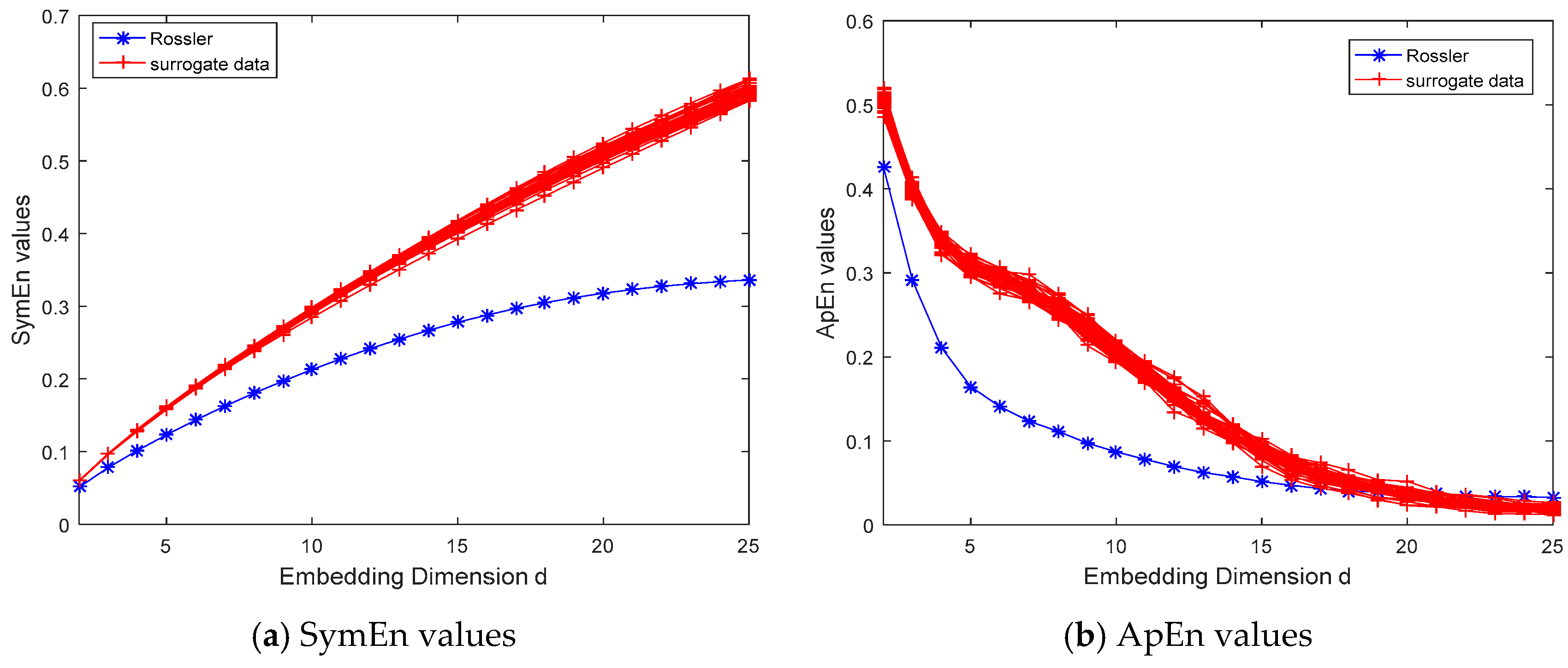
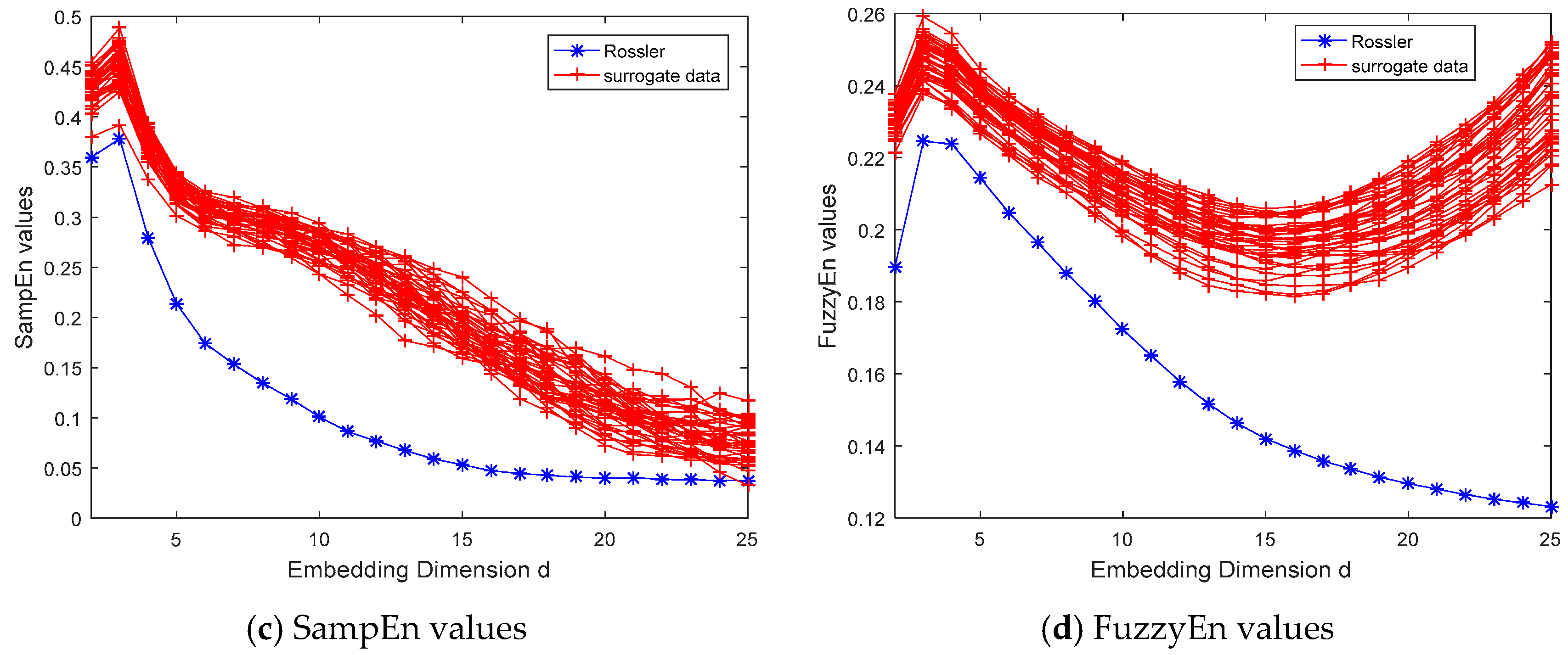
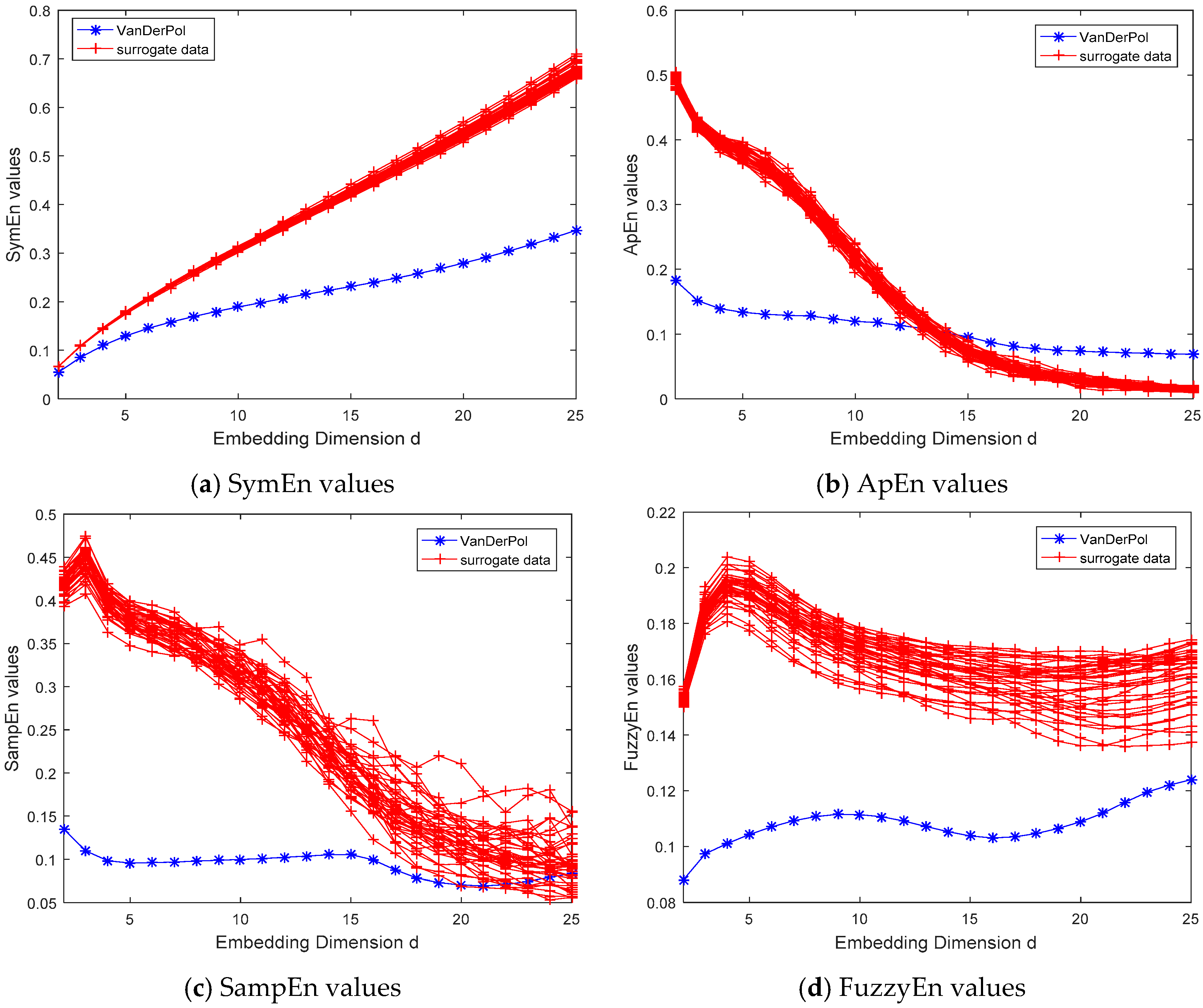
3.1.2. Tests on Chaotic Dynamical Systems
3.2. Application to Real Time Series
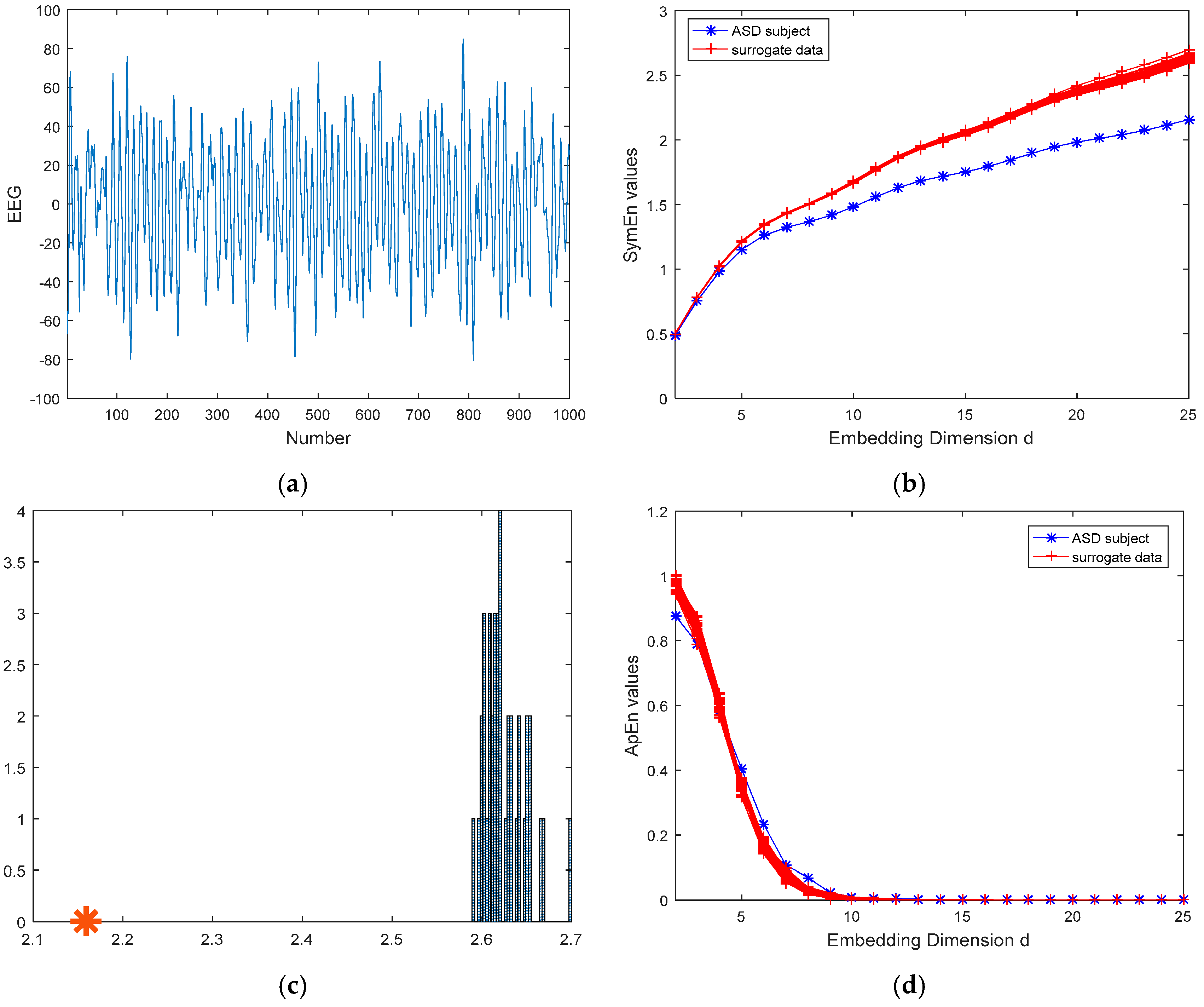
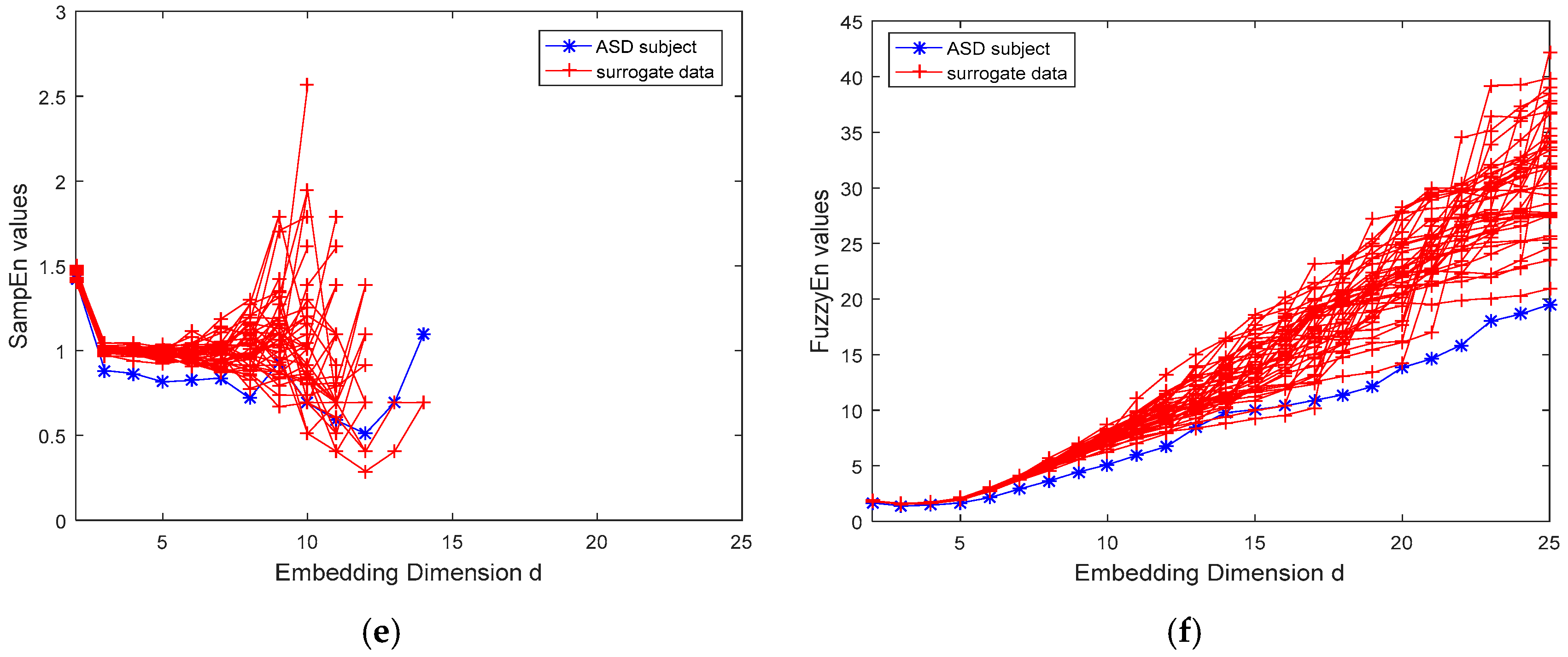
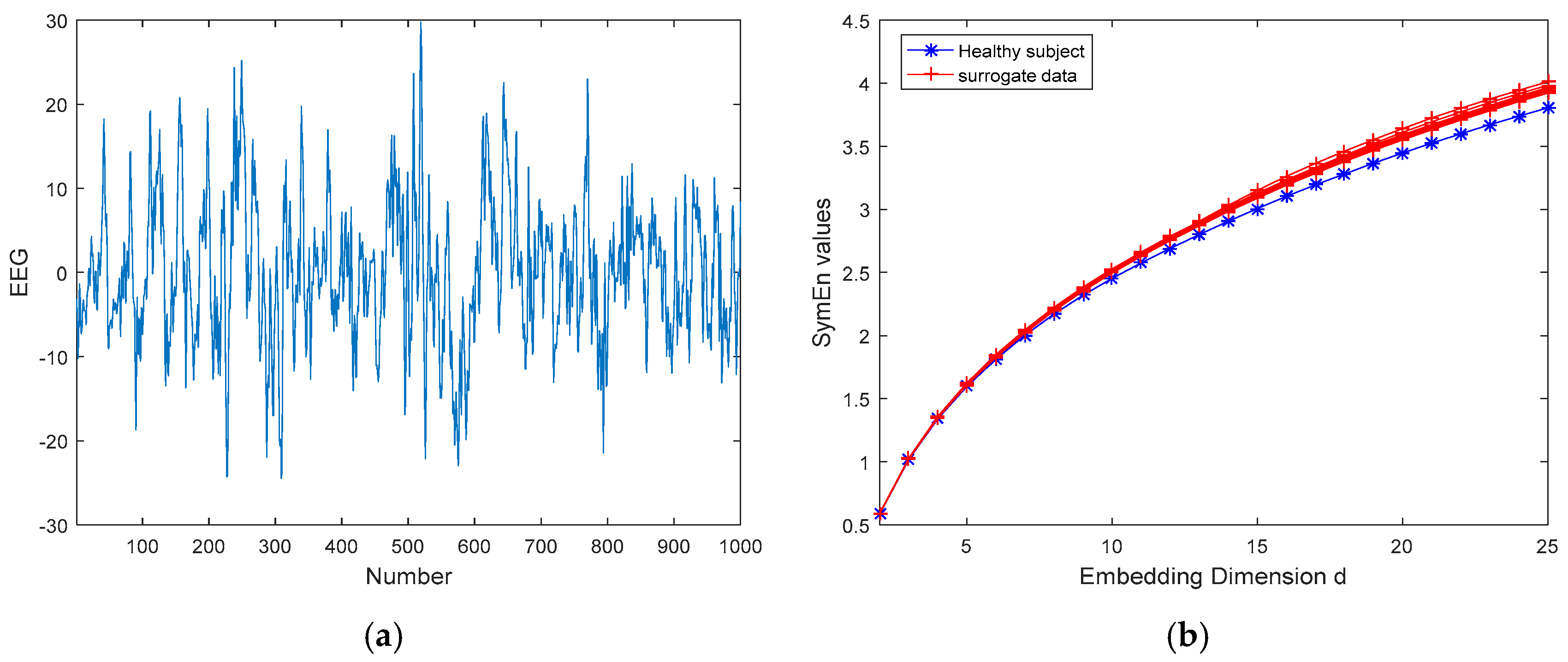
3.2.1. The EEG for ASD and Healthy Subjects
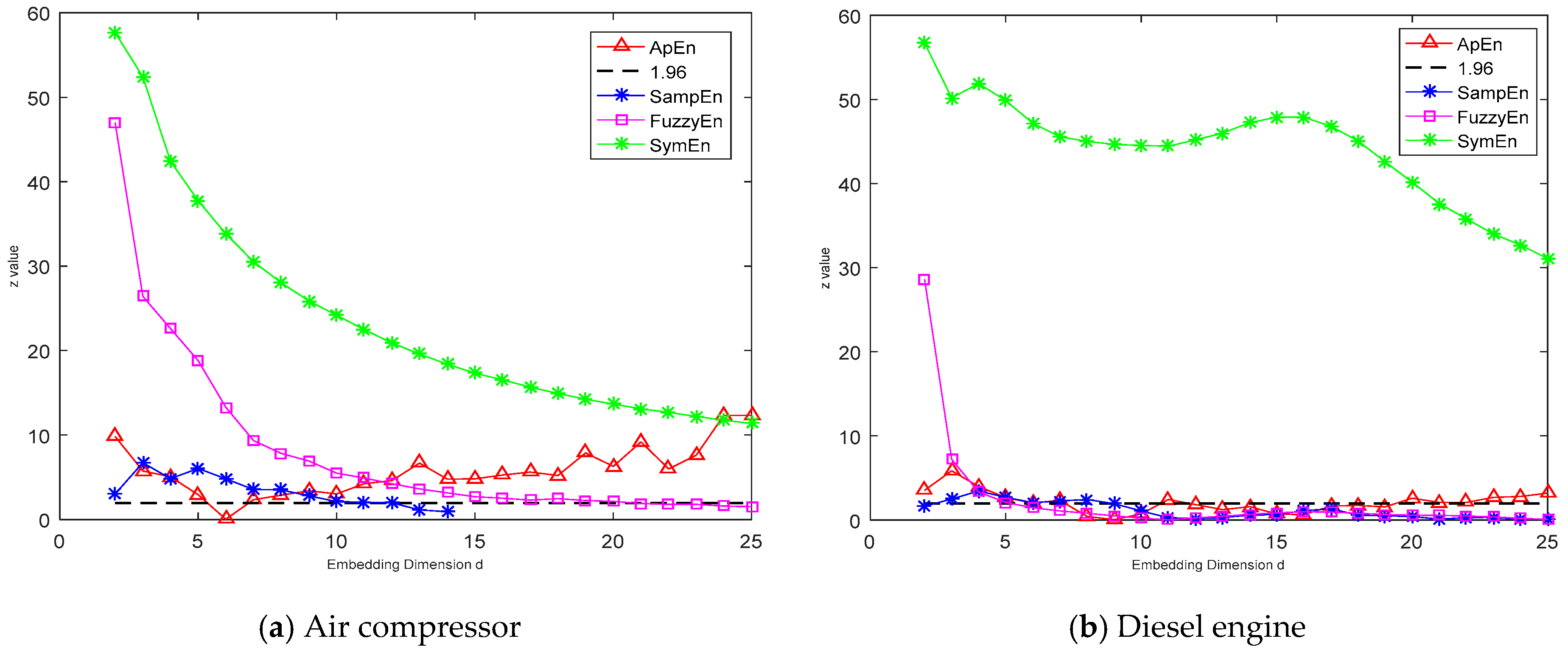
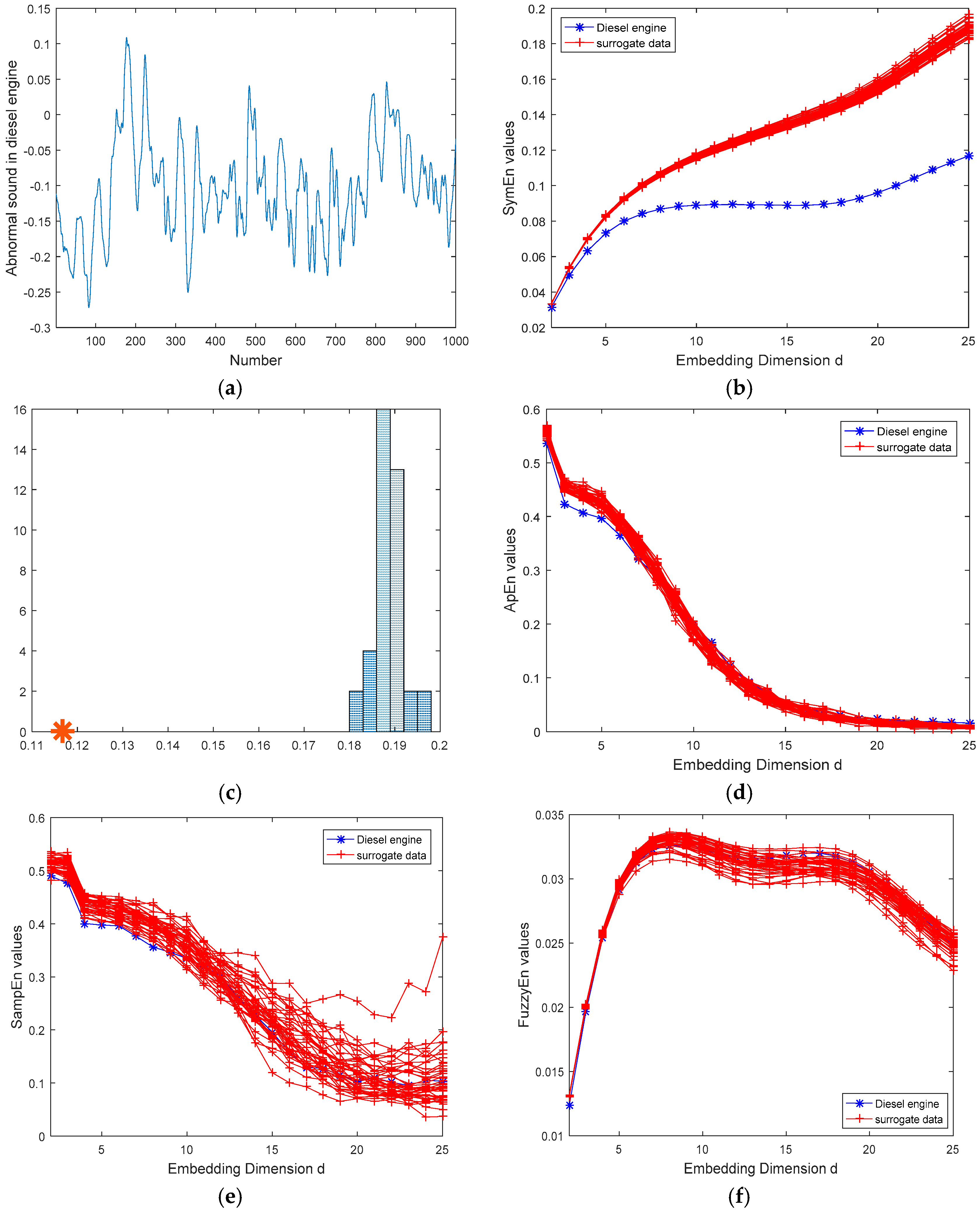
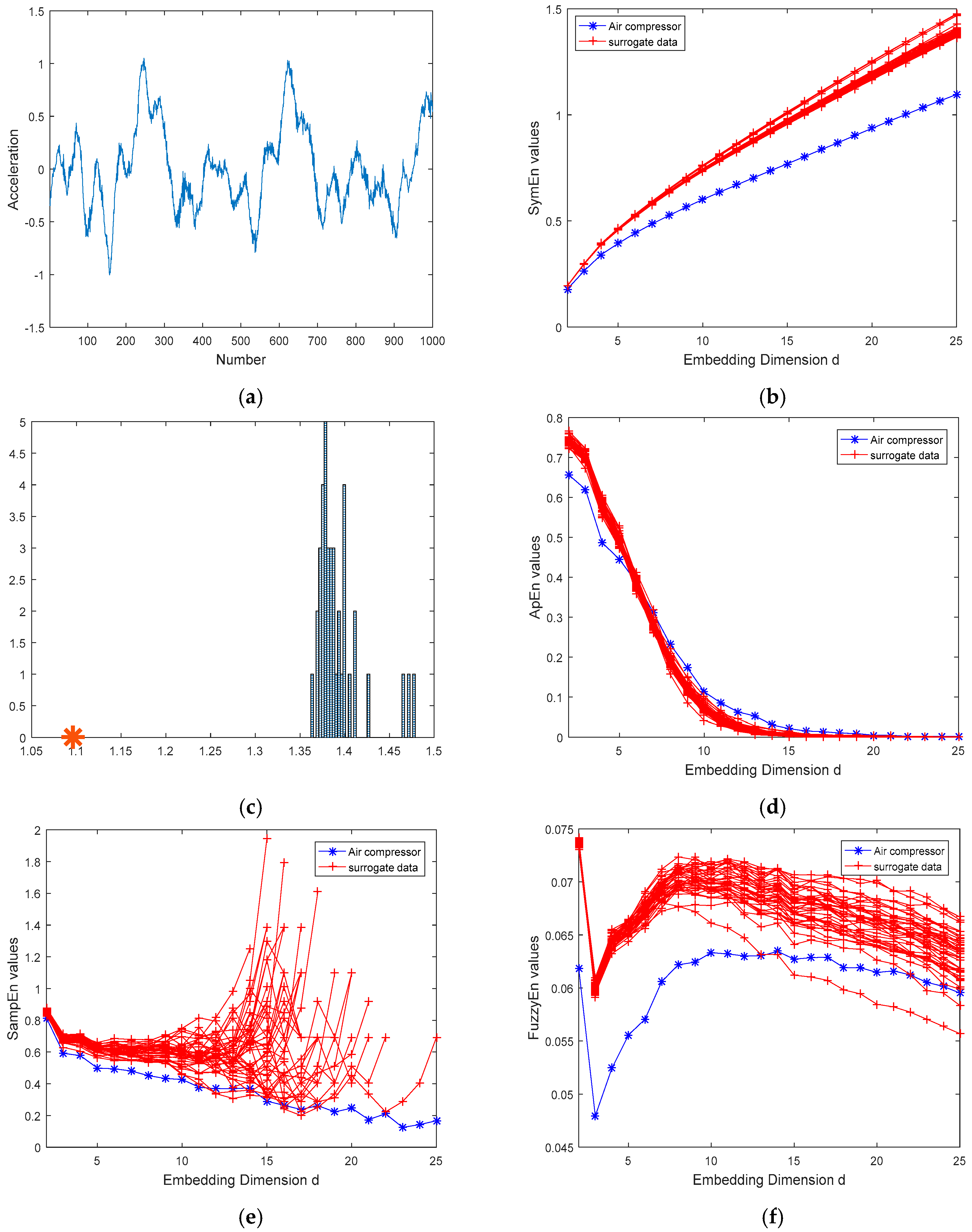
3.2.2. The Time Series for Diesel Engine and Air Compressor
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Consolini, G.; Tozzi, R.; De Michelis, P. Complexity in the sunspot cycle. Astron. Astrophys. 2009, 506, 1381–1391. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W. Complexity measures of brain wave dynamics. Cogn. Neurodyn. 2011, 5, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Dokos, S.; Sivakumar, B.; Mengersen, K. Symplectic geometry spectrum regression for prediction of noisy time series. Phys. Rev. E 2016, 93, 052217. [Google Scholar] [CrossRef] [PubMed]
- Lei, M.; Wang, Z.H.; Feng, Z.J. A method of embedding dimension estimation based on symplectic geometry. Phys. Lett. A 2002, 303, 179–189. [Google Scholar] [CrossRef]
- Nazimuddin, A.K.M.; Hasan, M.R. Applications of Riemannian geometry comparing with symplectic geometry. Ann. Pure Appl. Math. 2014, 6, 170–177. [Google Scholar]
- Hou, X.H.; Deng, Z.C.; Zhou, J.X. Symplectic analysis for the wave propagation properties of conventional and auxetic cellular structures. Int. J. Numer. Anal. Model. 2011, 2, 298–314. [Google Scholar]
- Hong, S.; Kim, Y.; Park, Y.; Rothe, K.D. Symplectic embedding and Hamilton–Jacobi analysis of proca model. Mod. Phys. Lett. A 2002, 17, 435–451. [Google Scholar] [CrossRef]
- Gao, Q.; Tan, S.J.; Zhang, H.W.; Zhong, W.X. Symplectic algorithms based on the principle of least action and generating functions. Int. J. Numer. Methods Eng. 2012, 89, 438–508. [Google Scholar] [CrossRef]
- Lim, C.W.; Xu, X.S. Symplectic elasticity: Theory and applications. Appl. Mech. Rev. 2010, 63, 050802. [Google Scholar] [CrossRef]
- Torres, D.M. Nonlinear symplectic grassmannians and Hamiltonian actions in prequantum line bundles. Int. J. Geom. Methods Mod. Phys. 2012, 9, 1250001. [Google Scholar] [CrossRef]
- Feng, K. On Difference Schemes and Symplectic Geometry. In Proceedings of the 1984 Beijing Symposium Differential Geometry and Differential Equations, Beijing, China, 13–17 August 1984.
- Lei, M.; Meng, G. Symplectic principal component analysis: A new method for time series analysis. Math. Probl. Eng. 2011, 2011, 793429. [Google Scholar] [CrossRef]
- Van Loan, C. A symplectic method for approximating all the eigenvalues of a Hamiltonian matrix. Linear Algebra Appl. 1984, 61, 233–251. [Google Scholar] [CrossRef]
- Benner, P.; Faβbender, H. An implicitly restarted symplectic Lanczos method for the Hamiltonian eigenvalue problem. Linear Algebra Appl. 1997, 263, 75–111. [Google Scholar] [CrossRef]
- Salam, A.; Al-Aidarous, E.; EI Farouk, A. Optimal symplectic householder transformations for SR decomposition. Linear Algebra Appl. 2008, 429, 1334–1353. [Google Scholar] [CrossRef]
- Salam, A.; EI Farouk, A.; Al-Aidarous, E. Symplectic Householder transformations for a QR-like decomposition, a geometric and algebraic approaches. J. Comput. Appl. Math. 2008, 214, 533–548. [Google Scholar] [CrossRef]
- Salam, A. On theoretical and numerical aspects of symplectic Gram–Schmidt-like algorithms. Numer. Algorithms 2005, 39, 237–242. [Google Scholar] [CrossRef]
- Zhong, W.X. The inverse iteration method for the eigenproblem of large symplectic matrices. Comput. Struct. Mech. Appl. 1992, 9, 227–238. [Google Scholar]
- Zhong, W.X.; Williams, F.W.; Leung, A.Y.T. Symplectic analsyis for periodical electro-magnetic waveguides. J. Sound Vib. 2003, 267, 227–244. [Google Scholar] [CrossRef]
- Zhong, W. Plane elasticity problem in strip domain and Hamiltonian system. J. Dalian Univ. Technol. 1991, 31, 373–384. (In Chinese) [Google Scholar]
- Yao, W.; Zhong, W.; Lim, C.W. Symplectic Elasticity; World Scientific: Singapore, 2009. [Google Scholar]
- Lü, C.F.; Lim, C.W.; Yao, W.A. A new analytic symplectic elasticity approach for beams resting on Pasternak elastic foundations. J. Mech. Mater. Struct. 2009, 4, 1741–1754. [Google Scholar] [CrossRef]
- Zhong, W.X. Duality System in Applied Mechanics and Optimal Control; Kluwer Academic: Boston, FL, USA, 2004. [Google Scholar]
- Zhao, L.; Chen, W.Q. Symplectic Analysis of Plane Problems of Functionally Graded Piezoelectric Materials. Mech. Mater. 2009, 41, 1330–1339. [Google Scholar] [CrossRef]
- Lim, C.W.; Yao, W.A.; Cui, S. Benchmarks of analytical symplectic solutions for bending of cornersupported rectangular thin plates. IES J. Part A Civ. Struct. Eng. 2008, 1, 106–115. [Google Scholar] [CrossRef]
- Batista, M. Discussion of ‘Benchmark symplectic solutions for bending of corner-supported rectangular thin plates’ by C.W. Lim, W.A. Yao and S. Cui. IES J. Part A Civ. Struct. Eng. 2010, 3, 70. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.-S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Lei, M.; Meng, G. A Noise Reduction Method for Continuous Chaotic Systems Based on Symplectic Geometry. J. Vib. Eng. Technol. 2015, 3, 13–24. [Google Scholar]
- Niu, X.; Qu, F.; Wang, N. Evaluating Sprinters’ Surface EMG Signals Based on EMD and Symplectic Geometry. J. Ocean Univ. Qingdao 2005, 35, 125–129. (In Chinese) [Google Scholar]
- Xie, H.; Wang, Z.; Huang, H. Identification determinism in time series based on symplectic geometry spectra. Phys. Lett. A 2005, 342, 156–161. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Guzmán-Vargas, L.; Ramírez-Rojas, A.; Angulo-Brown, F. Multiscale entropy analysis of electroseismic time series. Nat. Hazards Earth Syst. Sci. 2008, 8, 855–860. [Google Scholar] [CrossRef]
- Hino, H.; Wakayama, K.; Murata, N. Entropy-based sliced inverse regression. Comput. Stat. Data Anal. 2013, 67, 105–114. [Google Scholar] [CrossRef]
- Elton, R.J.; Vasuki, P.; Mohanalin, J. Voice Activity Detection Using Fuzzy Entropy and Support Vector Machine. Entropy 2016, 18, 298. [Google Scholar] [CrossRef]
- Xie, H.; Guo, J.; Zheng, Y. Using the modified sample entropy to detect determinism. Phys. Lett. A 2010, 374, 3926–3931. [Google Scholar] [CrossRef]
- Kanner, L. Autistic disturbances of affective contact. Nerv. Child 1943, 2, 217–250. [Google Scholar]
- Theiler, J.; Prichard, D. Constrained-realization Monte-Carlo method for hypothesis testing. Physica D 1996, 94, 221–235. [Google Scholar] [CrossRef]
- Lei, M.; Meng, G.; Fan, J.; Wade, J.; Bian, D.; Sarkar, N. Nonlinear analysis of electroencephalograms of healthy people during driving test based on symplectic principal component analysis method. In Proceedings of the 2014 24th Annual International Conference of Society for Chaos Theory in Psychology & Life Sciences, Milwaukee, WI, USA, 31 July–2 August 2014; p. 10.
- Lei, M.; Meng, G.; Zhang, W.M.; Sarkar, N. Sample entropy of electroencephalogram for children with autism based on virtual driving game. Acta Phys. Sin. 2016, 65, 108701. [Google Scholar]
- Rens, J.; Clark, R.E.; Howe, D. Vibration analysis and control of reciprocating air-compressors. Int. J. Appl. Electromagn. Mech. 2001, 15, 155–162. [Google Scholar]
- Ning, D.; Sun, C.; Gong, Y.; Zhang, Z.; Hou, J. Extraction of fault component from abnormal sound in diesel engines using acoustic signals. Mech. Syst. Signal Process. 2016, 75, 544–555. [Google Scholar]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B. Testing for nonlinearity in time series: The method of surrogate data. Physica D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Lei, M.; Wang, Z.; Feng, Z. Detecting nonlinearity of action surface EMG signal. Phys. Lett. A 2001, 290, 297–303. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Discrimination power of measures for nonlinearity in a time series. Phys. Rev. E 1997, 55, 5443–5447. [Google Scholar] [CrossRef]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal patterns, entropy, and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Muñoz, M.; Moreno, F.; Bermal, N.; Arroyo, J.; Paniagua, L. Engine diagnosis method based on vibration and acoustic emission energy. Insight 2012, 54, 149–154. [Google Scholar]
- Kugiumtzis, D. On the reliability of the surrogate data test for nonlinearity in the analysis of noisy time series. Int. J. Bifurc. Chaos 2001, 11, 1881–1896. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; Meng, G.; Zhang, W.; Wade, J.; Sarkar, N. Symplectic Entropy as a Novel Measure for Complex Systems. Entropy 2016, 18, 412. https://doi.org/10.3390/e18110412
Lei M, Meng G, Zhang W, Wade J, Sarkar N. Symplectic Entropy as a Novel Measure for Complex Systems. Entropy. 2016; 18(11):412. https://doi.org/10.3390/e18110412
Chicago/Turabian StyleLei, Min, Guang Meng, Wenming Zhang, Joshua Wade, and Nilanjan Sarkar. 2016. "Symplectic Entropy as a Novel Measure for Complex Systems" Entropy 18, no. 11: 412. https://doi.org/10.3390/e18110412
APA StyleLei, M., Meng, G., Zhang, W., Wade, J., & Sarkar, N. (2016). Symplectic Entropy as a Novel Measure for Complex Systems. Entropy, 18(11), 412. https://doi.org/10.3390/e18110412