Abstract
Application of the phenomenon of self-organization for the development of wear resistant materials has been reviewed. For this purpose the term of self-organization and dissipative structures as applied to tribology have been discussed. The applications of this phenomenon have been shown in order to develop new wear resistant- and antifriction materials. Specific examples have been shown for the application of the self-organization phenomenon and the generation of dissipative structures for the formation of tribotechnical materials with enhanced wear resistance for current collecting materials and antifriction materials of bearings.
1. Introduction
Over the past several years there have been many scientific publications regarding the application of nonequilibrium thermodynamics and the theory of self-organization in tribology, for instance [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Normally articles on nonequilibrium thermodynamics as applied to friction are divided into two types. One type of articles is typified by the detailed description of the theory without any practical recommendations and without any possibility of its practical application. The second type of articles is characterized by the detailed description of relevant experiments mentioning that the results of such experiments correspond to nonequilibrium thermodynamics. What is common with these two types of articles is lack of recommendations for the application of nonequilibrium thermodynamics, for instance, for the development of wear resistant materials, as well as their lack of explanations as to what the authors believe self-organization means. For example, in [1] it is declared that the phenomenon of self-organization exists in tribosystems, and it is concluded that surface energy is one of the most important parameters in self-organization of tribosystems. However, the authors of [1] fail to define what self-organization actually means. In [9] nonequilibrium stationary distribution of work performed by external forces over a mesoscopic system with multiple degrees of freedom is reviewed. The recommendations for applying the results achieved are not presented in [9]. In [10] it is proposed to use the second law of thermodynamics in order to determine the tribosystem’s degradation (accumulation of defects and damages). The degradation is determined by growth in entropy, while production of entropy is determined by the velocity of accumulation of damages. However, the article does not review the phenomenon of self-organization which results in deceleration of the degradation. In [2] it is emphasized that self-organization leads to the reduction in friction force and intensity of wear, and that to proceed with self-organization, the tribosystem is required to lose thermodynamic stability. However, in [2] there is not a single definition of self-organization. In [3], based on the results of testing various lubricants, the authors chose a lubricant which ensured the lowest wear intensity. This action of the lubricant is associated with self-organization. However, Barszcz et al. [3] does not explain what self-organization means and how this phenomenon relates with the reduction of intensity of wear. The authors in [6] correlate self-organization with the change in friction ratio without explaining what self-organization actually means. Nosonovsky et al. [15,16,17] suggested to use the phenomenon of self-organization in tribology, in particular, in order to form biosimilar tribotechnical materials. Self-organization is determined as formation of order in nonequilibrium conditions. The authors of this description offered the same definition for dissipative structures in [18]. Despite the correctness of this definition, it is not clear as to how it may be used in order to develop new materials.
The authors have been developing new wear-resistant materials, using the results of the use of non-equilibrium thermodynamics and the theory of self-organization to tribology more than 30 years. The article presents some of the results of our work in this area. This article attempts to describe the phenomenon of self-organization in order to apply the same for the development of new tribotechnical materials. The article will show the examples of formation of such materials.
2. The Physical Meaning of the Self-Organization Phenomenon as Applied to Friction
In [19] self-organization was defined as a process of formation of dissipative structures. Therefore this section discusses the notion of dissipative structures. The term “dissipative structures” was conceived by Prigogine [20], who presented dissipative structures as consisting of big fluctuations using the example of a fluid’s flow velocity profile. At a deviation from equilibrium fluctuations are not stable around the equilibrium state [18,20]. Formation of fluctuations is accompanied by a growth of free energy or negative production of entropy. After this, the system returns to the state with less free energy. In the tribosystem, thermodynamic equilibrium may only be achieved where there is no friction. In a steady-state with linear dependency of thermodynamic flows on thermodynamic forces production of entropy—according to Prigogine’s theorem—is minimal. The terms of Prigogine’s theorem can only be achieved under relatively mild friction conditions, i.e., at a low sliding speed, low clamping force, etc. The stationary state of a tribosystem in which Prigogine’s theorem applies can be considered as thermodynamically stable. The increase in sliding speed, pressing force or other parameter of friction leads to the removal of the tribosystem from equilibrium. A curve which describes such a state in a phase space depending on the changing parameter is called a thermodynamic branch. If removing of tribosystem from equilibrium is accompanied by the action of the Prigogine’s theorem, the states on the thermodynamic branch are thermodynamically stable. However, after a certain critical value of the parameter, the system’s state can become unstable. Any negligibly small perturbation can then deviate the system from a thermodynamic branch (a catastrophe).
Thermodynamic stability of a nonequilibrium state is determined by the following condition [18]:
where δ—fluctuation; Xn, Jn—thermodynamic forces and flows, correspondingly; S—entropy; t—time. The sum in the right hand side of Equation (1) is called excessive production of the entropy. The values δXn and δJn are fluctuations of the corresponding flows and forces in steady-state conditions.
In [21] it is shown that as the number of interacting thermodynamic flows increases the probability of a loss of thermodynamic stability of the tribosystem increases. Hence, the probability of self-organization grows. Taking into account only pair interactions of n flows with each other the probability (P) is:
If inequality is apparent at the beginning of the disturbance (1), this condition is stable. However, during certain processes or under the influence of various processes, one can get a negative contribution leading to excessive production of entropy which grows as the disturbance grows. In this case this condition can become unstable (positive production of entropy is a sufficient but not mandatory condition of instability). Only after going through instability can the self-organization process begin.
The new regime which is installed in the system can correspond to the orderly condition, i.e., it can have entropy which is lower than the chaotic condition one. In this case bifurcation takes place at the critical point (emergence of a new parameter at the critical value for solving the equation). As a result, a new branch of solutions emerges. Prigogine proposed naming such ordered configurations, which emerge outside of the scope of stability of the thermodynamic branch, dissipative structures [20]. The choice of solution by the system which emerges in the bifurcation point, i.e., the process of formation of dissipative structures, is called as self-organization. Just as any fluctuation dissipative structures are generated spontaneously and in a surge mode. This means that the relevant physical-chemical process characterizing dissipative structures starts as an avalanche. This corresponds to a catastrophe on a thermodynamic branch.
A great number of publications have been devoted to the theory, experiments, and description of such structures. This is why here we will not describe any specific structures, but will rather refer to certain general results.
Only nonlinear equations can have more than one solution. Therefore bifurcations—and henceemergence of dissipative structures—can only take place in a system in which the processes are governed by nonlinear laws.
The analysis of the known processes of self-organization, for example, during the formation of Benar cells [18] or Turing structures [22], shows that the formation of dissipative structures is only possible as a result of interaction of two or more processes. The analysis of stability condition validates this (1). In [23] it is shown that the loss of stability of tribosystem is impossible when accounting for one process only. Entropy of an equilibrium condition is maximal. If one excludes the factors supporting nonequilibrium condition, then such system will transit to an equilibrium condition. Such a spontaneous transition will feature positive entropy production. Thus, other factors being equal, the entropy of a nonequilibrium condition of the system is less than the entropy of its equilibrium condition. This is true for the formation of dissipative structures. The process of self-organization (formation of dissipative structures) is abrupt, not gradual, therefore the boundary conditions and the flow of entropy are not changed. Hence, as the entropy is reduced so should the production of entropy. This corresponds to the assertion in [19] that after formation of dissipative structures in the system, production of the entropy is lower than under the same conditions but without self-organization. Production of entropy is reduced due to intensive processes characterized by the increase of free energy, i.e., negative affinity. Such processes feature negative production of entropy. This does not contradict the second law of thermodynamics as the overall production of entropy remains positive.
Reduction of production of entropy does not always mean the formation of dissipative structures. For instance, during the formation of a gradient of temperatures in a mixture of two gases the diffusion can take place towards increasing the gradient of concentration. At the same time, the entropy will reduce [20]. Such a thermodiffusion is a result of linear processes: the variance of concentrations is proportional to the variance of temperatures. The variance of concentrations is formed gradually from the mixture, not as a surge, which is the case of self-organization. Besides, during diffusion molecules move regardless of each other, i.e., the process of diffusion is chaotic in this sense. Thus, thermodiffusion is not a self-organization process.
So, why is self-organization interesting for friction processes? According to de Donder [24], any change in the entropy in an open nonequilibrium system consists of the flow of entropy (interface with a medium) and the production of entropy (processes inside the system) [23]:
At the same time, the flow of entropy of one body under friction consists of flows of the entropy relating with exchange between energy and substance:
where: —flow of the entropy relating with exchange of heat; —flow of the entropy relating with the flow of substance from a medium into the body under friction; —flow of the entropy relating with wear of the body under friction.
The negative sign before the flow of entropy relating with wear means that the substances leave the body under friction with their own entropy.
Production of the entropy of one body under friction consists of a part connected with dissipation of energy during heat transfer and deformation, and the part relating with physical and chemical processes that take place in the surface layers, . Thus, production of the entropy in (3) equals:
In this case (3) will look as follows:
In a steady-state condition ():
Entropy is an additive value therefore, other factors being equal, the greater the value of , the higher the intensity of wear. Based on Equation (7) it can be concluded that, other factors being equal, the intensity of wear is reduced as the production of entropy decreases.
It was earlier mentioned that during self-organization production of entropy is reduced, hence the intensity of wear is also reduced. Due to this, the phenomenon of self-organization represents interest to tribology. It should be noted that during a self-organization the process with negative entropy production appears as an avalanche. Part of the energy of friction is spent on the processes with negative entropy production Thus, during self-organization, part of the friction energy that could be spent on wear, is spent on the passage of the process with negative entropy production contributing to a reduction of the wear rate. Avalanche-like appearance of such a process leads to a finite value of negative entropy production, the positive part of the production of entropy does not change in this case. If the process with negative entropy production would gradually appear, then at the same time it has increased the positive part of entropy production. Other things being equal, entropy production and the rate of wear at the same time would always be greater than an avalanche-like occurrence. This also differs the self-organization from a gradual process, for example increasing the break-contact area under running-in.
Despite the fact that during self-organization the intensity of wear decreases, not every case of the decrease of intensity of wear can be attributed to self-organization. For instance, the decrease of intensity of wear takes place during a “mechanical” run-in process where an area of contact is increased and the pressure in that contact is reduced. Such “mechanical” run-in process is characterized by gradual reduction in the intensity of wear. In case of self-organization the intensity of wear is reduced in an abrupt fashion.
The difference between a gradual and abrupt (self-organization) decrease in the intensity of wear is shown using the example of different types of schematic dependencies of wear and wear rate of the friction distance on Figure 1. Figure 1 shows typical dependencies of wear and the intensity of wear of the friction distance without self-organization (Figure 1a,b) and with self-organization (Figure 1c,d).
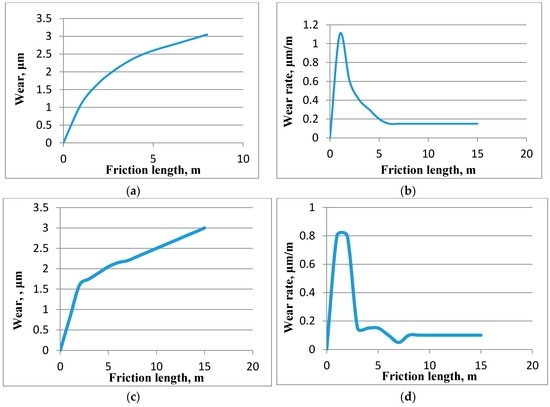
Figure 1.
Typical dependencies of wear and intensity of wear during run-in period; (a,b) without self-organization; (c,d) with self-organization.
In the case where there is no self-organization, the wear (Figure 1a) and reduction of the intensity of wear (Figure 1b) are shown by smooth and gradual curves. In the case where there is self-organization, the wear is shown as a broken curve (Figure 1c). Reduction in the intensity of wear in the case where there is self-organization is abrupt (Figure 1d) in the breaking point of the wear curve.
For dependencies shown in Figure 1a,b, the increase of the contact area, reduction of pressure and intensity of wear take place due to the wear and plastic deformation in a gradual manner. At the same time, no new physical and chemical processes emerge. For dependencies shown in Figure 1c,d, the break on the wear curve (Figure 1c) is caused by the emergence of a new physical and chemical process which, prior to that could only be an unstable fluctuation. This process is accompanied by negative production of the entropy. The abrupt reduction of intensity of wear in Figure 1d points to an avalanche-like emergence of a physical-chemical process with negative entropy production. This process is dissipative structures. Such real broken dependences are described, for example, for cutting tool [25,26]. In [25,26] and in Figure 1c,d friction conditions allow passage of self-organization, i.e., the thermodynamic stability of the tribosystem may be lost under these conditions. The loss of thermodynamic stability, therefore, and self-organization are stochastic processes (due to the fact that compliance with the conditions of Lyapunov’s theorem) is necessary but not sufficient) [20]. Thus, for tribosystems [25,26] (Figure 1c,d) the only possibility to lose thermodynamic stability appears. Therefore, in spite of compliance with the necessary conditions of stability loss from the beginning of friction, self-organization (the breaking in the curves) occurs after a sliding distance has been traveled. That is not self-organization since the beginning of friction (Figure 1c,d) shows that on the dependence of the wear (wear rate) on the friction parameter in [25,26]—a cutting rate bifurcation is possible. One branch after the bifurcation point (thermodynamic)—a characteristic dependence before the inflection point (Figure 1c,d). The second branch (dissipative structures) is a characteristic dependence after the inflection point (Figure 1c,d). An example of physical-chemical process with negative entropy production is precipitation of tin from a solid solution based on copper during the friction of a tin-lead bronze as described in [27]. This precipitation of tin from a solid solution based on copper contradicts the equilibrium phase diagram of Cu-Sn. Hence this is not a spontaneous process which is characterized by the negative production of entropy. The friction does not directly initiate precipitation of tin from this solid solution. The friction in this case directly initiates deformation, wear, heating, heat conductivity, etc. Precipitation of tin from the solid solution may be the result of the interaction of these processes. Importantly, precipitation of tin from a solid solution is a probabilistic process, i.e., it may or may not take place under the same conditions (clamping force). If tin is not precipitated the scoring load would amount to 980 N, while in the case of the precipitation of tin it would amount to 1441 N. Thus, bifurcation appears to depend on the friction coefficient of the load. The listed characteristics suggest that the process of the precipitation of tin from a solid solution is a dissipative structure. Despite the fact that instability invariably precedes to self-organization, the reverse assertion is not always true.
On the basis of classical works by Prigogine and our experience in research of self-organization during friction the characteristics of self-organization in this case are formulated below:
- Self-organization can only take place after the tribosystem loses its thermodynamic stability in a nonlinear zone. Various mathematical models of stability loss that are not strictly linear cases are summarized in [23,28,29,30]. As a result we obtain conditions of loss of thermodynamic stability of the tribosystem with current collection, recommendations on alloying of coating for the cutting tool by relatively heavy elements to reduce seizure, recommendations to alloy coating of the cutting tool with relatively light elements to reduce the wear rate at friction without seizure.
- In the case of self-organization, a spontaneous, avalanche-like stable and consistent unprompted process emerges abruptly (a process with the negative production of entropy is a process which moves in the direction of increasing free energy). In this process a considerable amount of friction energy was consumed that previously would be spent for wear, so the self-organization usually leads to an abrupt decrease in wear rate. Abruptness can be explained using the Figure 1d and Figure 2. The formation of dissipative structures is accompanied by a sharp decrease in wear rate (Figure 1d and Figure 2 of the “dissipative structures” curve). Curve “dissipative structures” (Figure 2) has the highest value (at the bifurcation point), and the lowest value of the wear rate. In the experiments, we were not able to fix the intermediate value of wear rate between the upper and lower value decreasing an increment of the argument (electric current density). With a decrease in increment of the argument, we recorded the highest (at the bifurcation point) or the lowest value of the wear rate. Perhaps the presence of such a “forbidden zone” can serve as a primary criterion of abruptness in the formation of dissipative structures. During running in (Figure 1b) at increasing of the contact area intermediate values between the highest and lowest value of the wear rate can be fixed with a decreasing in the increment of the argument (time).
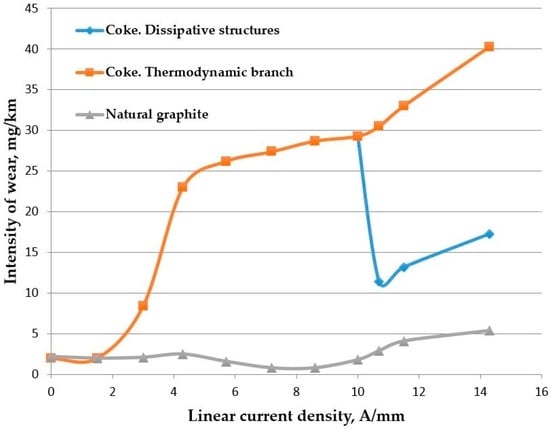 Figure 2. Dependency of intensity of wear of current collecting materials based on charred coal and natural graphite on the density of current.
Figure 2. Dependency of intensity of wear of current collecting materials based on charred coal and natural graphite on the density of current. - The process (2) is not initiated directly by friction.
- A nonspontaneous process initiated directly by friction is for example, a wear, deformation, heating or heat conductivity.
- A process (2) is a result of interaction of the flows of other processes (5).
- In the case of self-organization, the production of entropy is reduced as compared with the same condition but without self-organization, consequently, the wear rate decreases abruptly when self-organization is observed.
- Self-organization is a probabilistic process (a consequence of the fact that the conditions of Lyapunov theorem are necessary but not sufficient). This can lead to a bifurcation in the dependence of the wear rate on friction parameters.
- Process of type (2) is a dissipative structure.
- Stability of a process (2) is expressed by the preservation (invariability) of the production of entropy in a certain range of changes of external conditions. Because of compliance with this condition analytical expression for the lubricating effect of the electric current is derived [23].
- The more complex system, i.e., the more processes initiated in it can take place, the softer the conditions of the self-organization process (the probability of loss of thermodynamic stability by the system is increased). Early manifestation of self-organization results in reduced wear. Development of the more complex tribosystem can be accomplished through increasing of the amounts of alloying elements in the friction materials.
The following definitions are put forth:
- (1)
- Self-organization is a process of formation of dissipative structures.
- (2)
- Dissipative structures are a stable, nonspontaneous process with negative production of entropy, which is not initiated directly by friction, which does not exist before self-organization (except for fluctuations), which reduces the overall production of entropy as compared with the same condition without dissipative structures, and which is a result of interaction of dissipative (spontaneous) processes.
- (3)
- Thus, the physical meaning of self-organization is the following: the portion of energy of friction, which could be spent before self-organizing has started could lead to the wear rate increase. Once the self-organization has initiated the energy is consumed by another process. This reduces the wear rate.
3. Examples of Practical Application of the Phenomena of Self-Organization in Friction
Based on the definition and attributes of self-organization it may be concluded that in order to reduce the intensity of wear it is necessary to perform at least one of the following three actions:
- -
- Shifting self-organization of the tribosystem to softer conditions of friction;
- -
- Intensification of nonspontaneous processes which characterize dissipative structures;
- -
- Increasing complexity of the tribosystem, for example, by way of complicating the alloying process.
The intensity of wear normally grows as any friction parameter becomes more stringent. It can also grow constantly over time or during the run-in period. Therefore a shift in self-organization towards softer friction conditions results in the reduction of integral wear. As an example, let’s use a tribosystem with a current collecting material, a sliding electric contact of the current collecting material—a contact wire of an electrified rail transport. The interacting materials are a copper contact wire and carbon current collecting materials based on charred coal. In [31] the possibility of nonspontaneous chemical reactions on the surface of copper during friction is shown:
4Cu + CO2 = C + 2Cu2O
2Cu + CO2 = C + 2CuO
The reactions (8) and (9) are typified by negative affinity in the range of temperatures from 298 K to 2000 K (Table 1).

Table 1.
Affinity of the reactions (8) and (9) [26].
In [32] it is shown that the reactions (8) and (9) can serve as the mechanism of self-organization in a sliding electrical contact. Figure 2 shows the dependencies of the intensity of wear of a carbon current collecting material on the density of electric current. The bifurcation point is shown, out of which develops a thermodynamic branch, as well as the branch of dissipative structures. The experimental procedure and tests described in [30].
Two samples of current collecting material slide on a ring of copper wire of 600 mm diameter. The width of the wire is 6 mm, and the rotational speed of the ring is 200 rotations/min. Between the sample and the wire an electric current is formed. Wear of the current collecting materials was determined by their decrease in weight. Wear of the wire was determined by the change in the diameter of the wire.
In [30], based on studies of the friction surfaces of sliding electrical contacts specific to different areas of dependence Figure 2 indirectly confirmed the reactions (8) and (9) on the curve “dissipative structures”.
The main nonspontaneous stage of the reactions (8) and (9) is the decompounding of СО2 which is adsorbed on copper into oxygen and carbon. In [33] it is emphasized that in the presence of natural graphite the temperature of the start of the decomposition of the CO2 reaction is reduced.
This is why a current collective material based on natural graphite has been manufactured. The dependency of intensity of wear of this material on the density of electric current is shown in Figure 2, which suggests that before the bifurcation point, the intensity of wear of the current collecting material based on charred coal was approximately 30 times higher than the intensity of wear of the current collecting material based on natural graphite. After the bifurcation point this variance can grow and in the case of the formation of dissipative structures it can decrease sharply. It needs to be understood that hardness of the material based on charred coal is twice as high as the hardness of the material based on natural graphite. Thus it has become possible to significantly reduce the integral wear of the current collecting material by shifting self-organization to the relatively softer conditions of friction.
The second option for reducing the intensity of wear is intensification of nonspontaneous processes in dissipative structures. As applied to sliding electric contacts this implies an increase of velocity of the reactions (8) and (9). Increasing the reactions’ velocity enables an increase of absolute value at the negative part of the production of entropy and to reduce the overall production of entropy in Equation (7). In order to increase the reactions’ velocity it is proposed to use a catalyst [34]. This should result in a reduction of the wear intensity.
According to [35,36,37,38] the simplest catalyst of the CO2 decomposition reaction may be iron. The mixture of the current collecting material based on charred coal has been infused with three types of powders: steel powder, iron powder, and coppered iron powder. The experimental procedure and tests were described in [30].
Figure 3 shows dependencies of wear of the copper counterbody at the current density of 10.7 A/mm, which corresponded to the “dissipative structures” of the curve in Figure 2. Figure 3 suggests that the coppered iron powder has little influence on the intensity of wear, the steel powder reduces the intensity of wear by about half, while the iron powder reduces the intensity of wear by at least ten-fold. The wear rate of the collector material behaved similarly. Thus, the use of a catalyst for accelerating the processes with negative entropy production leads to a decrease in wear rate. There are tribosystems in which you need to increase the intensity of wear, for example, when machining parts. It was demonstrated [39] on a purposeful use of a catalyst accelerating the processes of positive entropy production for the grinding of artificial diamonds was demonstrated.
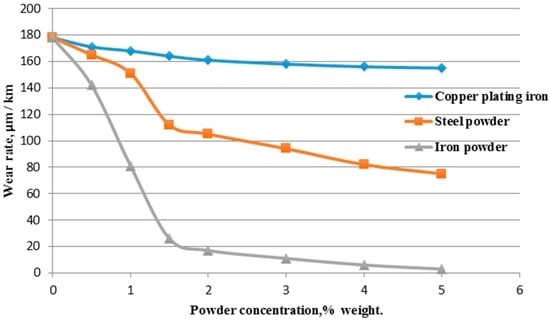
Figure 3.
Dependency of wear of a copper overhead contact on the content of various catalyst powders in current collecting materials based on charred coal at current density of 10.7 A/mm.
Increase of complexity of the content of materials under friction in order to increase the probability of self-organization is exemplified by the development of new antifriction aluminum alloys. Conventional antifriction aluminum alloys contain 2–4 alloying elements, for instance, the alloys Al—20% Sn—1% Cu or Al—10% Sn—2% Pb—1% Cu [40]. During the development of new antifriction alloys 7–9 alloying elements have been used simultaneously. The chemical compositions of antifriction bronze, the known aluminum alloy AlSn20, and the new antifriction alloy are shown in Table 2.

Table 2.
Chemical composition of alloys for friction tests.
Tests were carried out according to the procedure described in [27]. The tests were conducted on a friction machine in a “shoe-and-roller” design. The oil was kept in a special bath where the lower part of a rotating steel roller was permanently dipped. The shoe was made of aluminium alloys. The corner radius of the working surfaces was 20 mm; the shoe’s length was 10 mm. The counter-body was shaped like a roller and manufactured from steel 1045. The rollers were 40 mm in diameter and 10 mm wide. The working surface of the rollers was polished before testing. The rotation speed of the rollers was 500 rpm.
The intensity of wear of the alloys and the steel counter-body has been shown in Figure 4 and Figure 5, respectively. As a result of the complication of alloying, the intensity of wear of the new antifriction alloy has been reduced approximately 1.5 times, while the intensity of wear of the steel counterbody has been reduced approximately six times. Besides, it has been possible to reduce the contents of tin in the aluminum alloy by half. The breaks are marked with abrupt changes in the coefficient of friction on the dependence of the friction coefficient on load of new anti-friction aluminum alloys [41]. The best anti-friction alloy has six sections of reduced friction coefficients corresponding to the time of formation of new secondary structures. The ability of multi-component alloy to adapt to changing frictional conditions is related, in our opinion to high probability of loss of thermodynamic stability in accordance with Equation (2). Therefore, multicomponent alloys have a high ability to self-organize. This results in improved tribological properties in comparison with the alloys with less complex alloying.
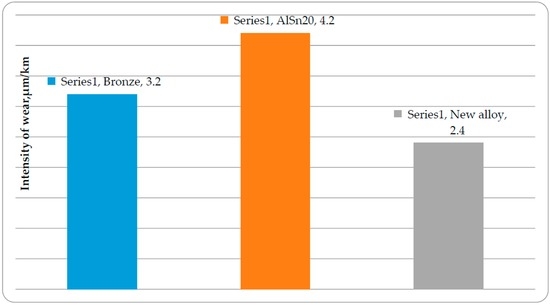
Figure 4.
Intensities of wear of antifriction aluminum alloys and bronze.
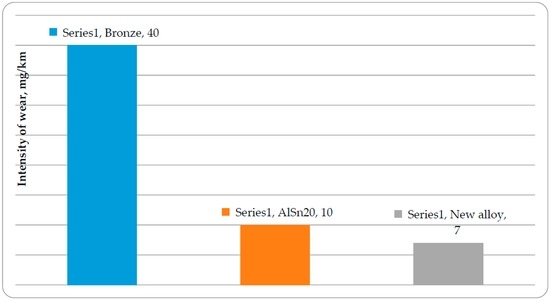
Figure 5.
Intensities of wear of a steel counter-body when operating together with antifriction aluminum alloys and bronze.
4. Conclusions
The properties, attributes, and definition of self-organization during friction have been shown and presented. The examples of developments of new wear resistant- and antifriction materials have been shown, along with the application of the phenomenon of self-organization. Self-organization and formation of dissipative structures leads to lower wear rate.
A self-organization shift under relatively mild friction conditions reduces wear. This is shown in the examples of the application of a natural graphite for sliding electrical contacts, and by the complexity of the alloying of antifriction alloys for bearings.
Intensification of physical and chemical processes with negative entropy production on the friction surfaces reduces the wear rate. This is illustrated by the use of a catalyst for sliding electrical contacts. Intensification of physical and chemical processes with positive entropy production on the friction surfaces increases the wear rate. This is illustrated by the use of a catalyst in artificial diamond machining.
The increase of the probability of loss of thermodynamic stability through the complexity of alloying allows one to increase the ability of anti-friction alloys to self-organize and improve their tribological properties.
Acknowledgments
The Ministry of Education of the Russian Federation supported this work by contract No. 14.577.21.0199, a unique identifier of contract RFMEFI57715X0199.
Author Contributions
Iosif Gershman performed theoretical modeling and wrote the paper, Eugeniy I. Gershman and Alexander E. Mironov performed experimental work, German S. Fox-Rabinovich and Stephen C. Veldhuis participated in writing and editing of the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yurov, V.M.; Kubich, V.I. Some questions of self-organization tribological systems containing thin layers of grease. Eurasian Phys. Tech. J. 2015, 12, 23–27. [Google Scholar]
- Nosonovsky, M. Self-organization at the frictional interface for green tribology. Philos. Trans. R. Soc. A 2010, 368, 4755–4774. [Google Scholar] [CrossRef] [PubMed]
- Barszcz, M.; Paszeczko, M.; Lenik, K. Self-organization of friction surface of Fe-Mn-C-B coating with increased resistance to abrasion. Arch. Metall. Mater. 2015, 60, 2651–2656. [Google Scholar]
- Hirai, Y.; Yabu, H.; Kaido, M.; Suzuki, A.; Shimomura, M. Learning from Nature; Relationship between Surface Microstructures and Tribology. J. Surf. Finish. Soc. Jpn. 2013, 64, 38–41. [Google Scholar] [CrossRef]
- Mortazavi, V. Modeling of Instabilities and Self-Organization at the Frictional Interface. Ph.D. Thesis, University of Wisconsin-Milwaukee, Milwaukee, WI, USA, 2014. [Google Scholar]
- Menezes, P.L.; Kailas, S.V.; Lovell, M.R. Self-organization and friction during sliding. In Proceedings of the ASME/STLE 2012 International Joint Tribology Conference IJTC2012, Denver, CO, USA, 7–10 October 2012.
- Zypman, F.R.; Ferrante, J.; Jansen, M.; Scanlon, K.; Abel, P. Evidence of self-organized criticality in dry sliding friction. J. Phys. Condens. Matter 2003, 15. [Google Scholar] [CrossRef]
- Hou, Z.G.; Zhao, J.; Xu, L.Q.; Guo, Z. The Friction Coefficient and Self-Organization Feature on Rake Face when Turning Hardened Steel with Coating Tools. Adv. Mater. Res. 2010, 97–101, 1871–1874. [Google Scholar] [CrossRef]
- Gomez-Solano, J.R.; July, C.; Mehl, J.; Bechinger, C. Non-equilibrium work distribution for interacting colloidal particles under friction. New J. Phys. 2015, 17. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. A 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear―A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef]
- Banjac, M.; Vencl, A.; Otović, S. Friction and Wear Processes—Thermodynamic Approach. Tribol. Ind. 2014, 36, 341–347. [Google Scholar]
- Abdel-Aal, H.A. Thermodynamic modeling of wearm. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3622–3636. [Google Scholar]
- Bryant, M.D. Entropy and dissipative processes of friction and wear. FME Trans. 2009, 37, 55–60. [Google Scholar]
- Nosonovsky, M. Entropy in tribology: In the search for applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Mortazavi, V. Friction-Induced Vibrations and Self-Organization: Mechanics and Non-Equilibrium Thermodynamics of Sliding Contact; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Nosonovsky, M.; Bhushan, B. Thermodynamics of surface degradation, self-organization and self-healing for biomimetic surfaces. Philos. Trans. R. Soc. A 2009, 367, 1607–1627. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics from Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Klimontovich, Yu.L. Introduction in Physics of Open Systems; Janus-K: Moscow, Russia, 2002. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; John Wiley & Sons: Hoboken, NJ, USA, 1971. [Google Scholar]
- Fox-Rabinovich, G.S.; Gershman, I.S.; Yamamoto, K.; Biсsa, A.; Veldhuis, S.C.; Beake, B.D.; Kovalev, A.I. Self-Organization During Friction in Complex Surface Engineered Tribosystems. Entropy 2010, 12, 275–288. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Gershman, I.S.; Bushe, N.A. Elements of Thermodynamics and Self-Organization during Friction. In Self-Organization during Friction: Advanced Surface Engineered Materials and Systems Designed; Taylor & Francis: Abingdon-on-Thames, UK, 2006; Chapter 2; pp. 13–58. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; John Wiley & Sons: Hoboken, NJ, USA, 1962. [Google Scholar]
- Fox-Rabinovich, G.S.; Weatherly, G.C.; Dodonov, A.I.; Kovalev, A.I.; Shuster, L.S.; Veldhuis, S.C.; Dosbaeva, G.K.; Wainstein, D.L.; Migranov, M.S. Nano-crystalline filtered arc deposited (FAD) TiAlN PVD coatings for high-speed machining applications. Surf. Coat. Technol. 2004, 177–178, 800–811. [Google Scholar] [CrossRef]
- Fox-Rabinovich, G.S.; Yamamoto, K.; Kovalev, A.I. Synergetic Alloying of Self-Adaptive Wear-Resistant Coatings. In Self-Organization during Friction: Advanced Surface Engineered Materials and Systems Designed; Taylor & Francis: Abingdon-on-Thames, UK, 2006; Chapter 10; pp. 297–334. [Google Scholar]
- Gershman, I.S.; Mironov, A.E.; Gershman, E.I.; Fox-Rabinovich, G.S.; Veldhuis, S.C. Self-Organization during Friction of Slide Bearing Antifriction Materials. Entropy 2015, 17, 7967–7978. [Google Scholar] [CrossRef]
- Fox-Rabinovich, G.S.; Kovalev, A.I.; Endrino, J.L.; Veldhuis, S.C.; Shuster, L.S.; Gershman, I.S. Surface-Engineered Tool Materials for High Performance Machining. In Self-Organization during Friction: Advanced Surface Engineered Materials and Systems Designed; Taylor & Francis: Abingdon-on-Thames, UK, 2006; Chapter 9; pp. 232–296. [Google Scholar]
- Fox-Rabinovich, G.S.; Gershman, I.S.; Kovalev, A.I.; Yamamoto, K. Development of the Ternary and Higher-Ordered Protective or Wear-Resistant Materials and Coatings for High-Temperature Applications and Thermodynamics-Based Principles of their Synergetic Alloying. In Self-Organization during Friction: Advanced Surface Engineered Materials and Systems Designed; Taylor & Francis: Abingdon-on-Thames, UK, 2006; Chapter 11; pp. 336–380. [Google Scholar]
- Gershman, I.S. Formation of Secondary Structures and Self-Organization Process of Tribosystems during Friction with the Collection of Electric Current. In Self-Organization during Friction: Advanced Surface Engineered Materials and Systems Designed; Taylor & Francis: Abingdon-on-Thames, UK, 2006; Chapter 8; pp. 197–227. [Google Scholar]
- Heinicke, G. Tribochemistry; Academie Werlag: Berlin, Germany, 1984. [Google Scholar]
- Bushe, N.A.; Gershman, J.S.; Mironov, A.E. Processes of Self-Organizing of Tribosystem at Friction with Current Collection and without Current Collection. In Proceedings of the 2nd World Tribology Congress, Vienna, Austria, 3–7 September 2001; pp. 68–76.
- Fialkov, A.S. Carbon: The Interlayer Compounds and Composites on Its Basis; Aspect Press: London, UK, 1997. [Google Scholar]
- Gershman, I.S.; Gershman, E.I. Catalytic Effect during Friction. J. Frict. Wear 2011, 32, 431–436. [Google Scholar] [CrossRef]
- Lu, Y.; Xue, J.Z.; Shen, S.K. Activation of CH4, CO2 and Their Reactions over Co Catalyst Studied Using a Pulsed-Flow Micro-Reactor. React. Kinet. Catal. Lett. 1998, 62, 365–371. [Google Scholar] [CrossRef]
- Eremin, A.V.; Ziborov, V.S.; Shumova, V.V.; Voiki, D.; Roth, P. Formation of O (1D) Atoms in Thermal Decomposition of CO2. Kinet. Catal. 1997, 38, 1–7. [Google Scholar]
- Sakakini, B.H.; Tabatabaei, J.; Watson, M.J.; Waugh, K.C. Structural Changes of the Cu Surface of a Cu/ZnO/Al2O3 Catalyst, Resulting from Oxidation and Reduction, Probed by CO Infrared Spectroscopy. J. Mol. Catal. A Chem. 2000, 162, 297–306. [Google Scholar] [CrossRef]
- Ehrensberger, K.; Palumbo, R.; Larson, C.; Steinfeld, A. Production of Carbon from Carbon Dioxide with Iron Oxides and High-Temperature. Ind. Eng. Chem. Res. 1997, 36, 645–648. [Google Scholar] [CrossRef]
- Ashkinazi, E.E.; Ral’chenko, V.G.; Frolov, V.D.; Basov, A.A.; Konov, V.I.; Gershman, I.S. Friction of CVD diamond on intermetallide. J. Frict. Wear 2008, 29, 277–281. [Google Scholar] [CrossRef]
- Mironov, A.E.; Gershman, I.S.; Ovechkin, A.V.; Gershman, E.I. The Interrelation of the Run-In Ability of Bronzes and Aluminum Based Antifriction Alloys with Their Mechanical Properties and Degree of Alloying. J. Frict. Wear 2016, 37, 23–26. [Google Scholar] [CrossRef]
- Mironov, A.E.; Gershman, I.S.; Ovechkin, A.V.; Gershman, E.I. Comparison of Scoring Resistance of New Antifriction Aluminum Alloys and Tradition al Antifriction Bronze. J. Frict. Wear 2015, 36, 257–261. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).