Multiscale Entropy Analysis on Human Operating Behavior
Abstract
:1. Introduction
2. Methods and Data Description
- A moving-averaging procedure, also known as the coarse-gained procedure, denoted as:where is the original time series, and represents the moving-averaged time series at time scale .
- The computation of sample entropy for the moving-averaged time series at time scale :
3. Results and Anlysis
3.1. MMSE Analysis on the Three Groups
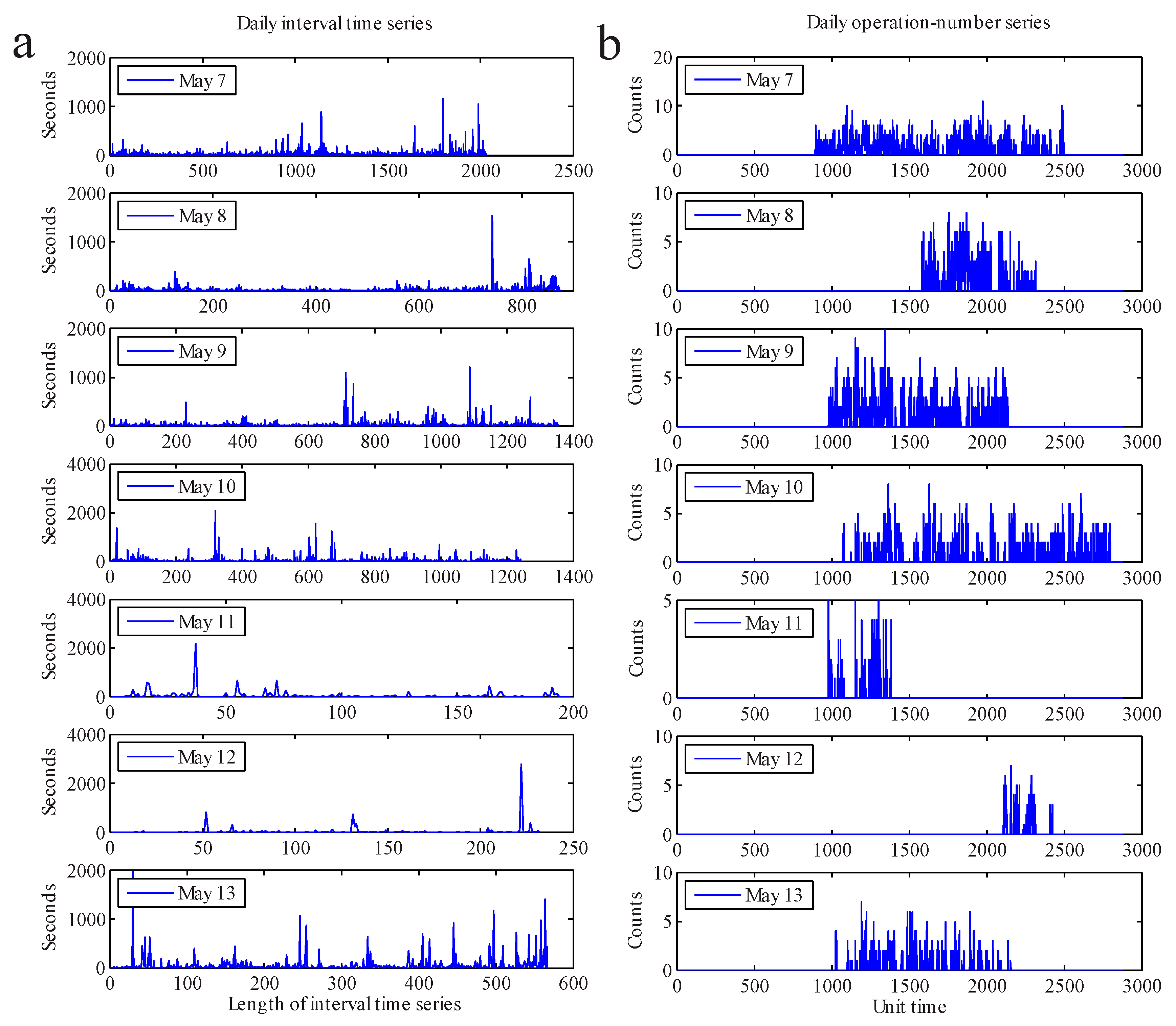
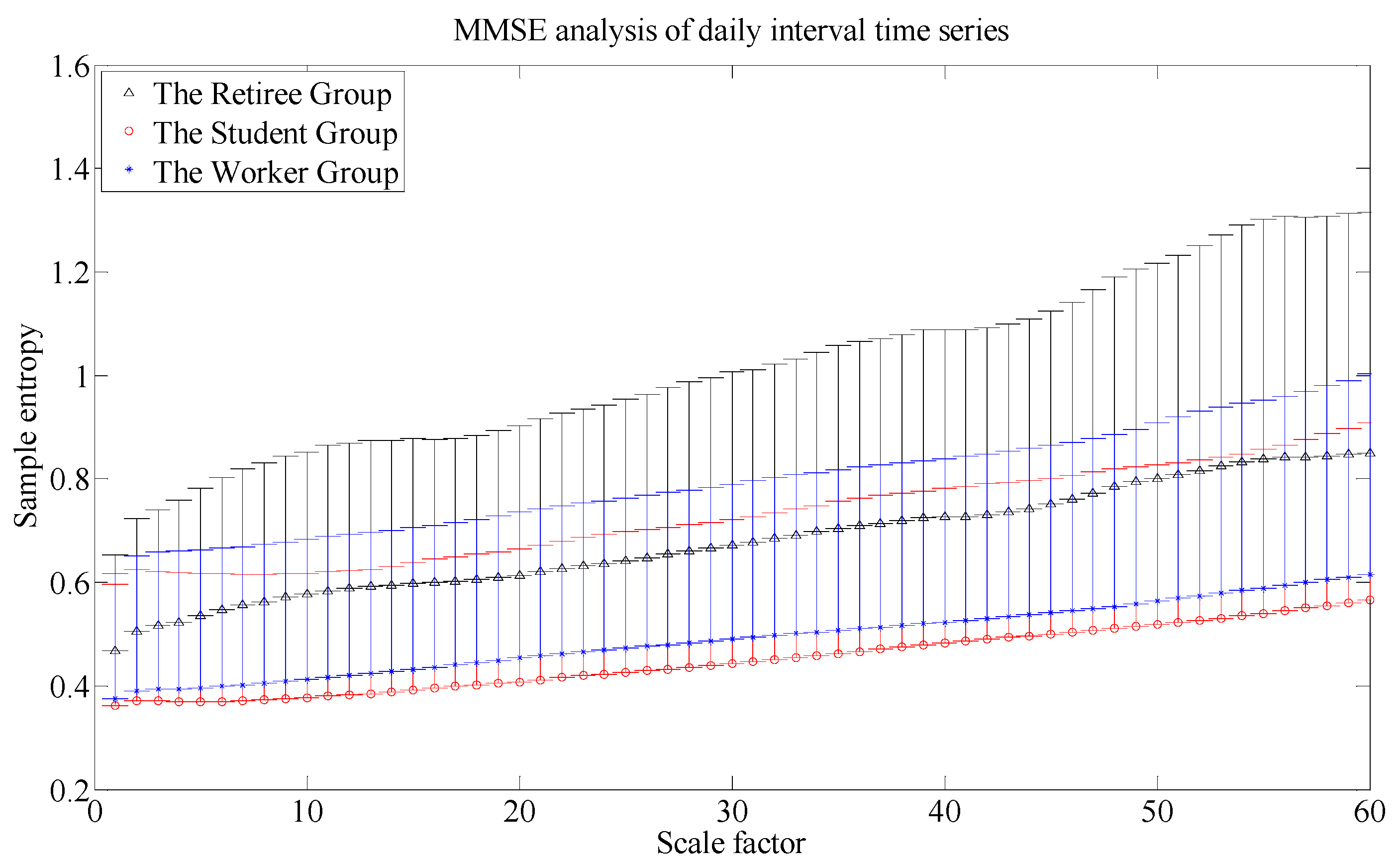
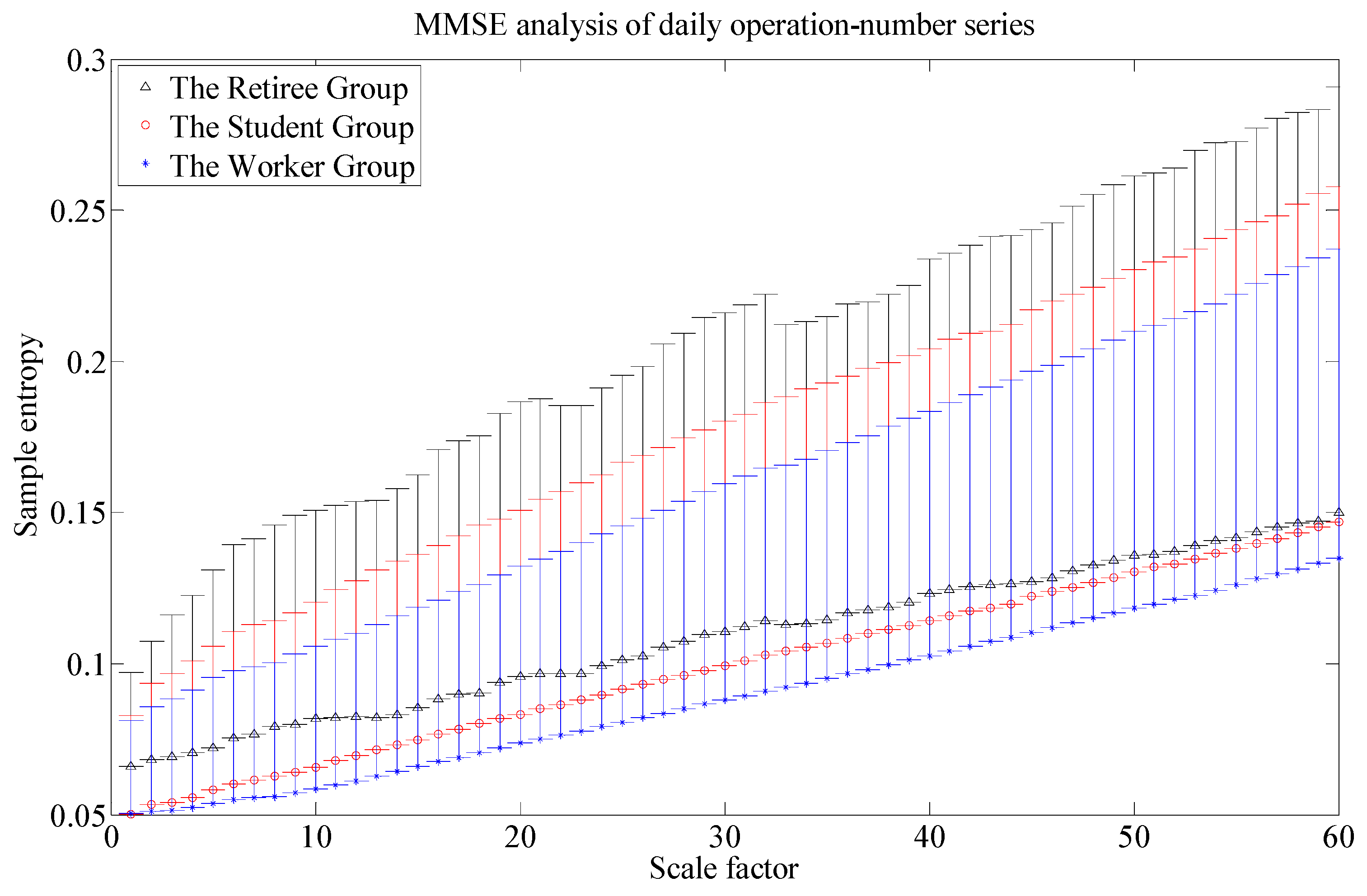
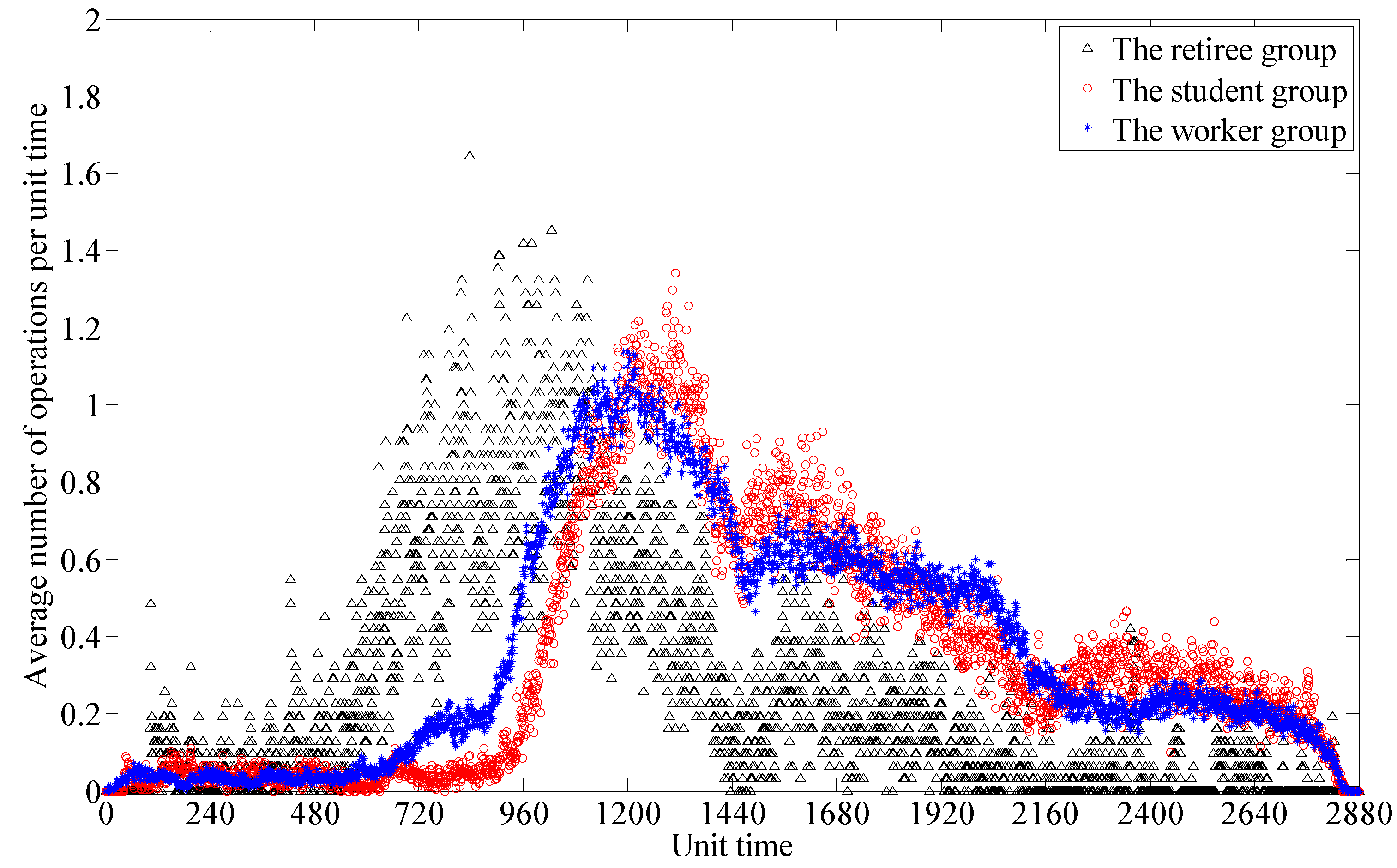
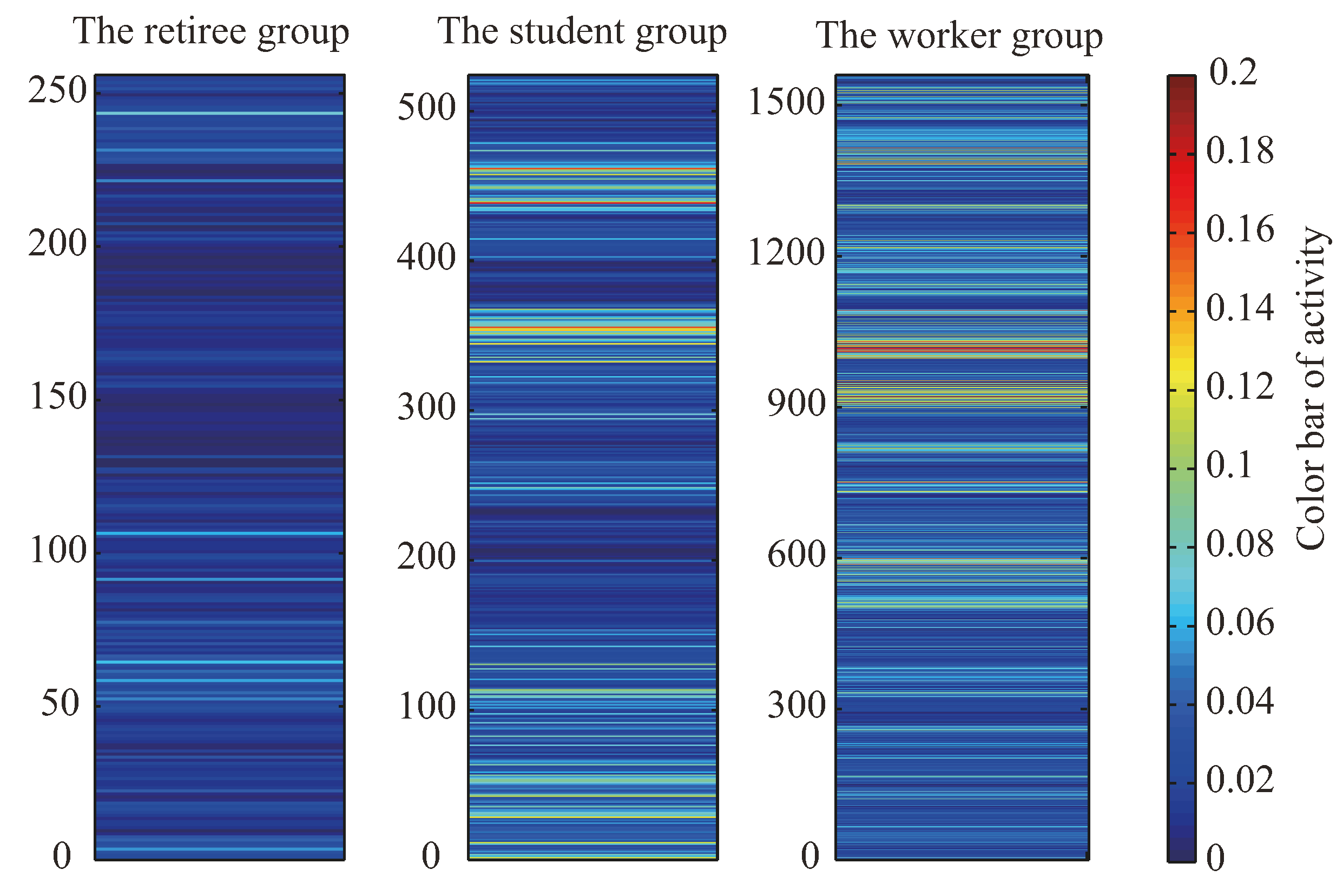
3.2. The Activity Analysis on the Three Groups
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barabasi, A.L. The origin of bursts and heavy tails in human dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, J.G.; Barabási, A.L. Human dynamics: Darwin and Einstein correspondence patterns. Nature 2005, 437, 1251. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, A.; Oliveira, J.G.; Dezsö, Z.; Goh, K.-I.; Kondor, I.; Barabási, A.-L. Modeling bursts and heavy tails in human dynamics. Phys. Rev. E 2006, 73, 036127. [Google Scholar] [CrossRef] [PubMed]
- Ratkiewicz, J.; Fortunato, S.; Flammini, A.; Flammini, A.; Vespignani, A. Characterizing and modeling the dynamics of online popularity. Phys. Rev. Lett. 2010, 105, 158701. [Google Scholar] [CrossRef] [PubMed]
- Karsai, M.; Kaski, K.; Barabási, A.L.; Kertész, J. Universal features of correlated bursty behaviour. Sci. Rep. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.Q.; Xie, W.J.; Li, M.X.; Podobnik, B.; Zhou, W.X.; Stanley, H.E. Calling patterns in human communication dynamics. Proc. Natl. Acad. Sci. USA 2013, 110, 1600–1605. [Google Scholar] [CrossRef] [PubMed]
- Radicchi, F. Human activity in the web. Phys. Rev. E 2009, 80, 026118. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.D.; Cai, S.M.; Huang, J.; Fu, Y.; Zhou, T. Scaling behavior of online human activity. EPL Europhys. Lett. 2012, 100, 48004. [Google Scholar] [CrossRef]
- Pan, J.; Hu, H.; Liu, Y. Human behavior during Flash Crowd in web surfing. Physica A 2014, 413, 212–219. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- McIntosh, A.R.; Kovacevic, N.; Itier, R.J. Increased brain signal variability accompanies lower behavioral variability in development. PLoS Comput. Biol. 2008, 4, e1000106. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wei, Q.; Fan, S.Z.; Lu, C.W.; Lin, T.Y.; Abbod, M.F.; Shieh, J.S. Adaptive computation of multiscale entropy and its application in EEG signals for monitoring depth of anesthesia during surgery. Entropy 2012, 14, 978–992. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Humeau, A.; Mahé, G.; Chapeau-Blondeau, F.; Rousseau, D.; Abraham, P. Multiscale analysis of microvascular blood flow: A multiscale entropy study of laser Doppler flowmetry time series. IEEE Trans. Biomed. Eng. 2011, 58, 2970–2973. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Govindan, R.B.; Wilson, J.D.; Eswaran, H.; Lowery, C.L.; Preißl, H. Revisiting sample entropy analysis. Physica A 2007, 376, 158–164. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- China Internet Data Platform, 2012. Available online: http://www.datatang.com/data/43910 (accessed on 9 December 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Hu, H.; Liu, X.; Hu, Y. Multiscale Entropy Analysis on Human Operating Behavior. Entropy 2016, 18, 3. https://doi.org/10.3390/e18010003
Pan J, Hu H, Liu X, Hu Y. Multiscale Entropy Analysis on Human Operating Behavior. Entropy. 2016; 18(1):3. https://doi.org/10.3390/e18010003
Chicago/Turabian StylePan, Junshan, Hanping Hu, Xiang Liu, and Yong Hu. 2016. "Multiscale Entropy Analysis on Human Operating Behavior" Entropy 18, no. 1: 3. https://doi.org/10.3390/e18010003
APA StylePan, J., Hu, H., Liu, X., & Hu, Y. (2016). Multiscale Entropy Analysis on Human Operating Behavior. Entropy, 18(1), 3. https://doi.org/10.3390/e18010003




