Hot Spots and Persistence of Nitrate in Aquifers Across Scales
Abstract
:1. Introduction
2. Methodology
2.1. Entropy
2.2. Normalized Risk Index
2.3. Hurst Exponent
- Compute the mean .
- Detrend the series by subtracting mean for .
- Calculate the summation of all detrended series for .
- Rescale the range, by dividing the range by the standard deviation.
- Calculate the mean of the rescaled range for all sub-series of length ; .
- Finally, the value of the Hurst exponent is obtained using an ordinary least square regression with as the independent variable and as the dependent variable. The gradient of the fit is the estimate of the Hurst exponent.
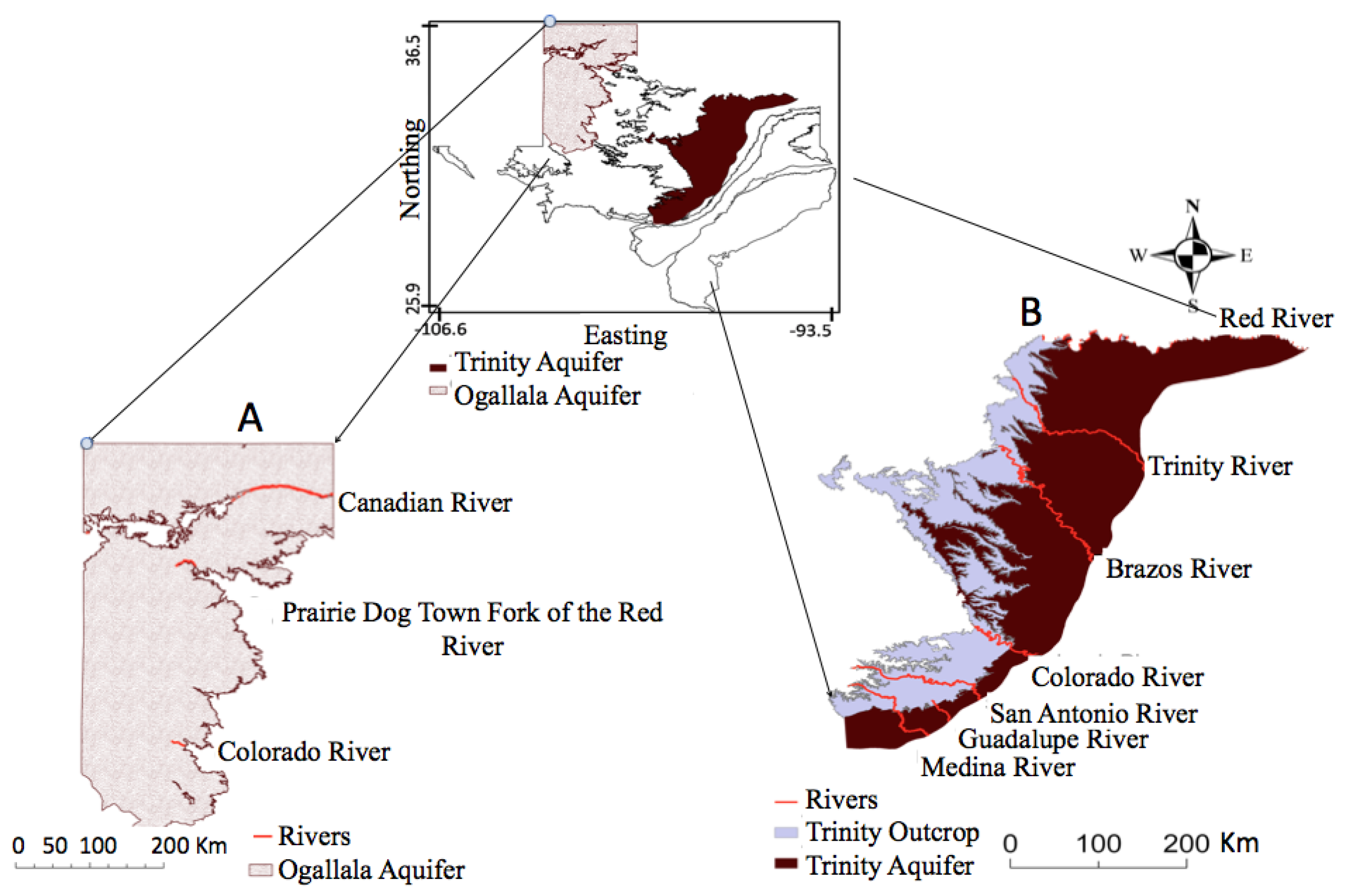
3. Study Site
3.1. Ogallala Aquifer
3.2. The Trinity Aquifer
4. Data Analysis
5. Results and Discussion
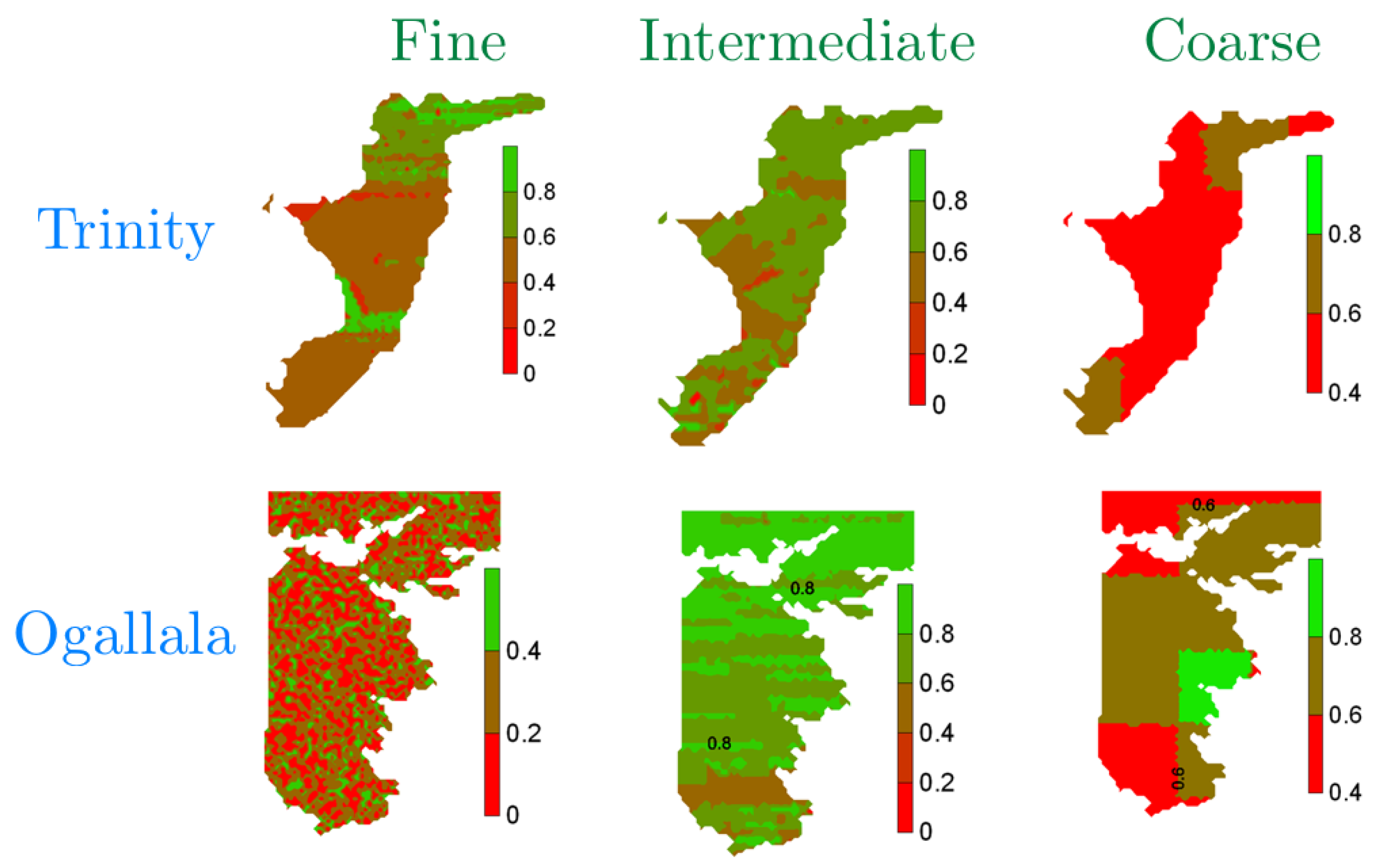
5.1. Trend and Persistence of Nitrate-N across Scales
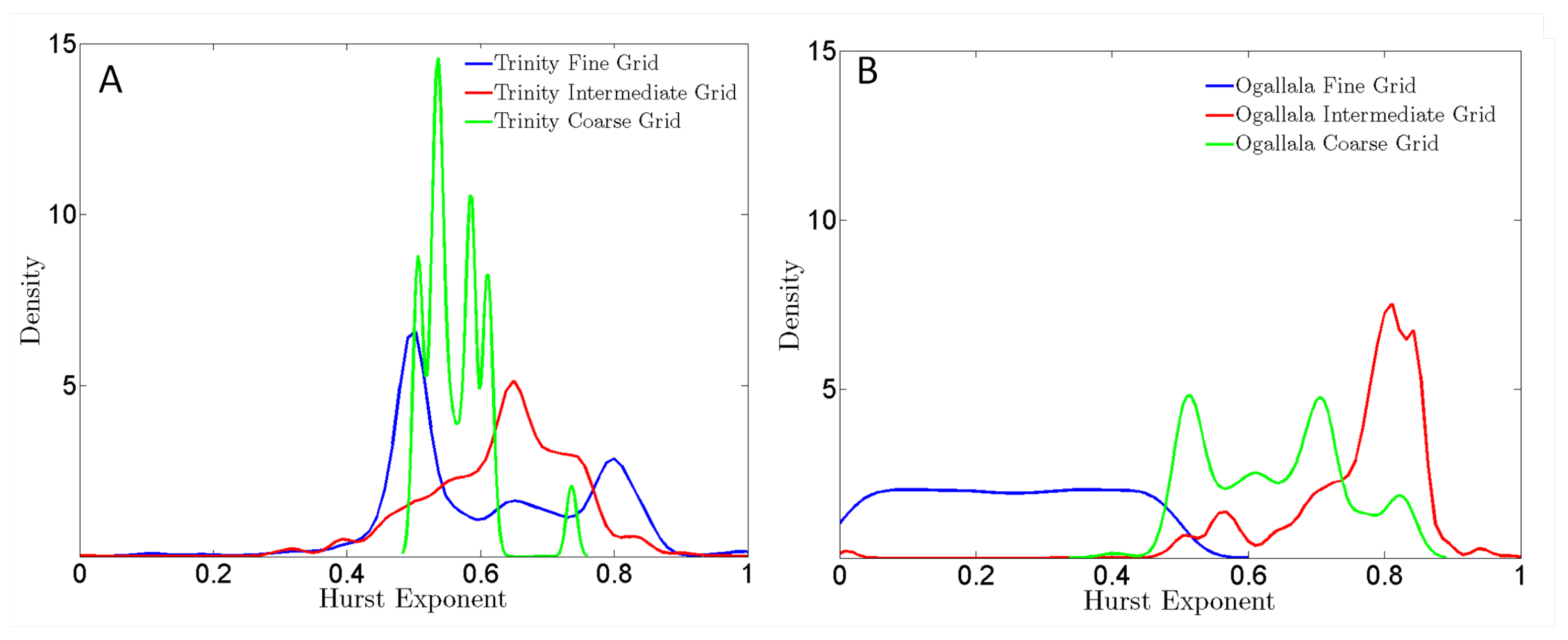
5.2. Temporal Variability of Nitrate-N
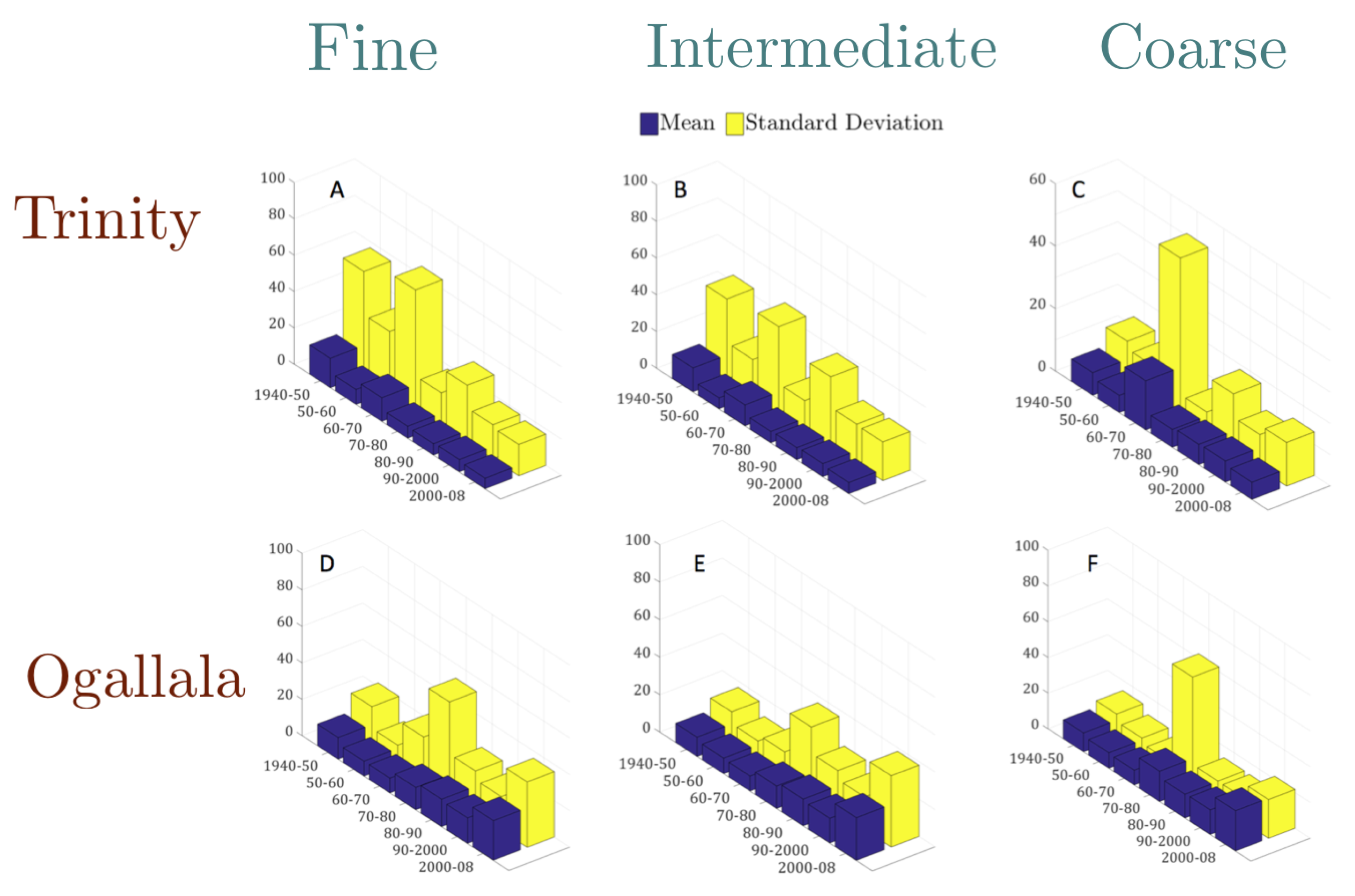
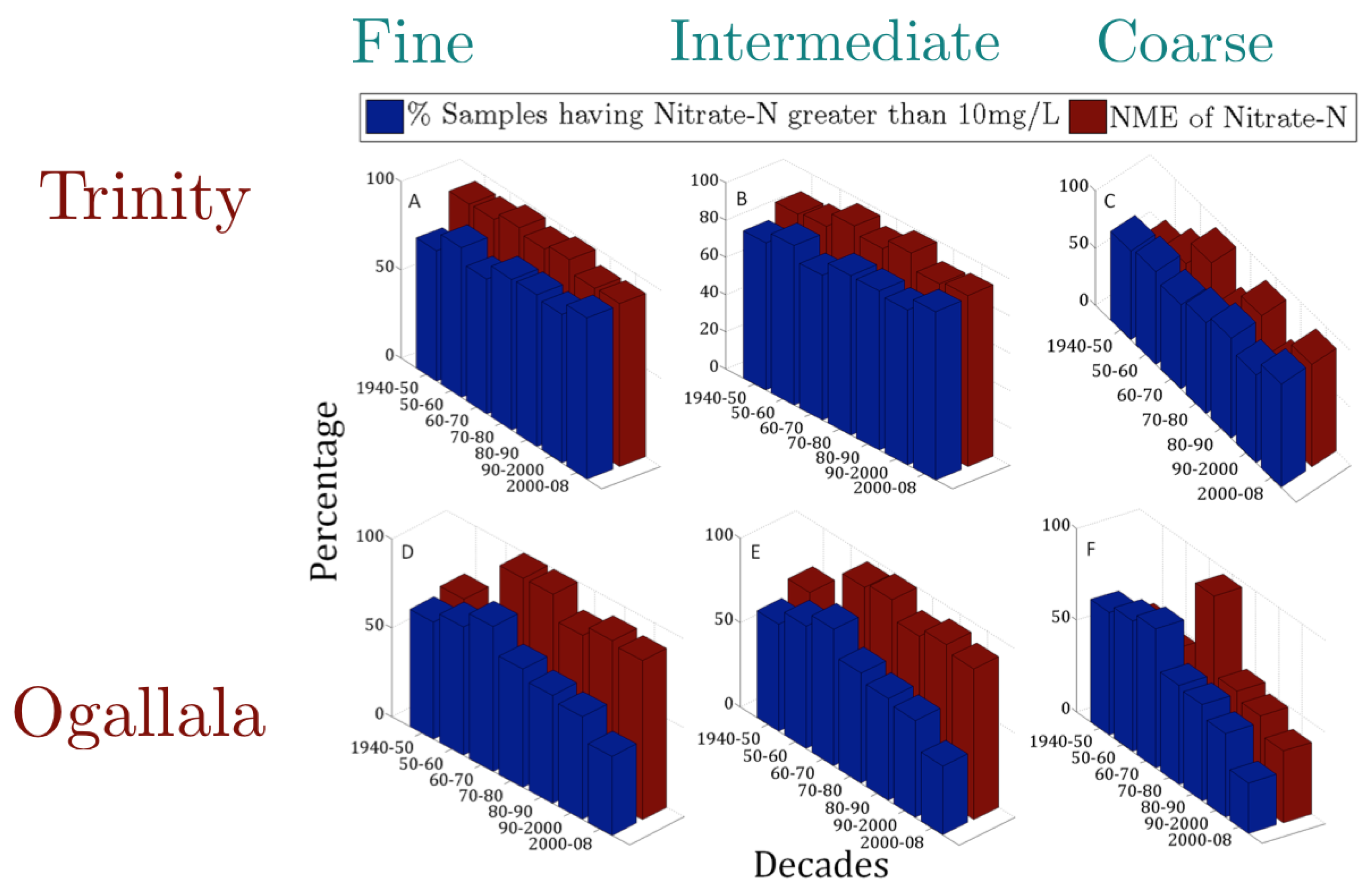
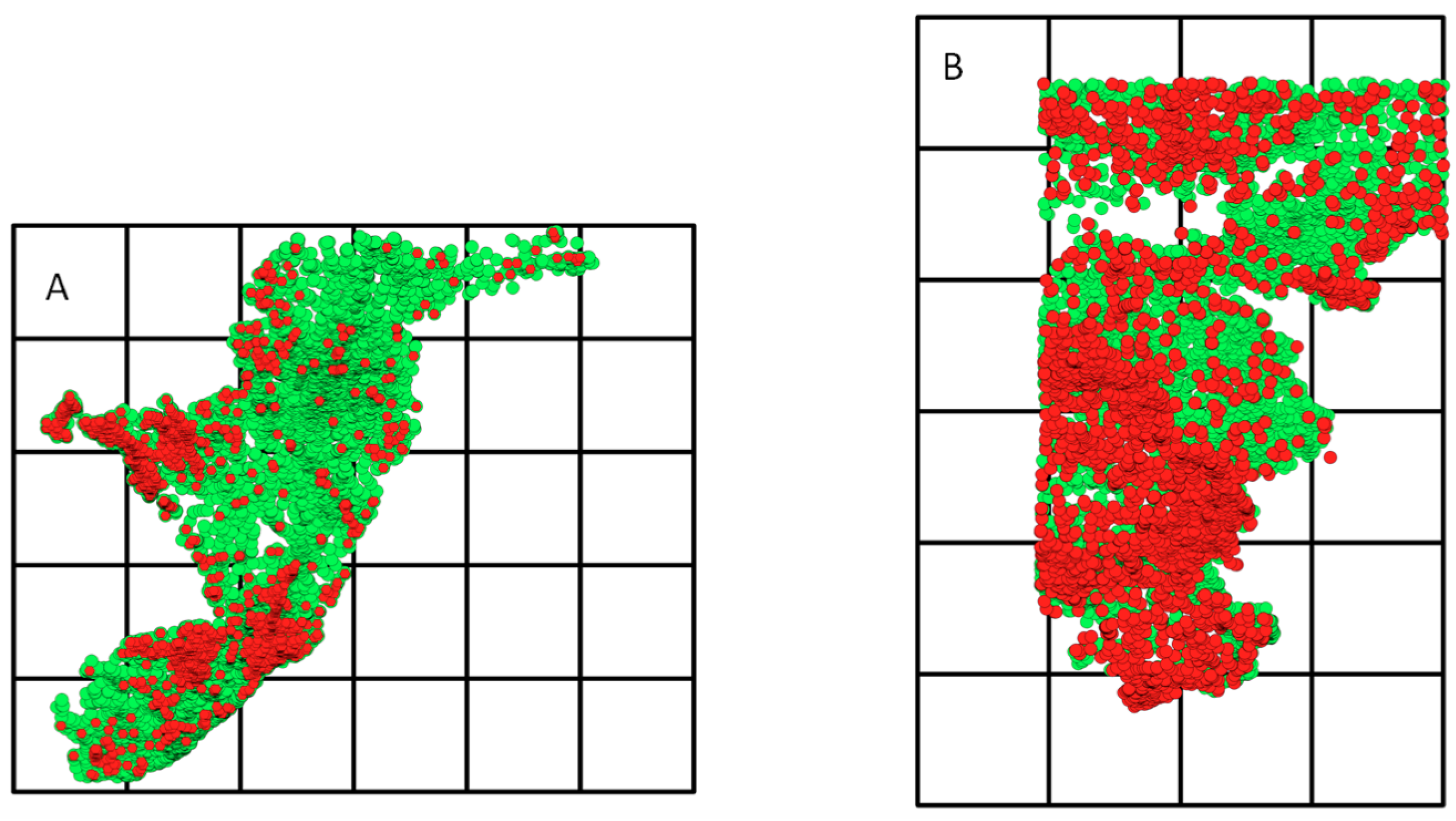
5.3. Hot Spots of Nitrate-N
| Aquifers | Grid | Normalized Risk Index (%) |
|---|---|---|
| Ogallala | Fine | 67.8 |
| Intermediate | 64.2 | |
| Coarse | 39.1 | |
| Trinity | Fine | 75.3 |
| Intermediate | 61.3 | |
| Coarse | 40.9 |
6. An Application: Designing Monitoring Strategies
| Aquifers | Sampling Strategy | |
|---|---|---|
| Ogallala | Base case | 89.3 |
| Removing one alternate sample | 89.3 | |
| Removing two alternate samples | 63.8 | |
| Removing 10% (randomly) | 88.7 | |
| Removing 20% (randomly) | 88.7 | |
| Removing 50% (randomly) | 85.2 | |
| Removing 75% (randomly) | 60.0 | |
| Trinity | Base case | 92.4 |
| Removing one alternate sample | 92.2 | |
| Removing two alternate samples | 91.9 | |
| Removing 10% (randomly) | 91.7 | |
| Removing 20% (randomly) | 91.7 | |
| Removing 50% (randomly) | 91.9 | |
| Removing 75% (randomly) | 90.4 |
7. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [PubMed]
- Hudak, P. Regional trends in nitrate content of Texas groundwater. J. Hydrol. 2000, 228, 37–47. [Google Scholar] [CrossRef]
- Brender, J.; Olive, J.; Felkner, M.; Suarez, L.; Hendricks, K.; Marckwardt, W. Intake of nitrates and nitrites and birth defects in offspring. Epidemiology 2004, 15. [Google Scholar] [CrossRef]
- Brender, J.D.; Weyer, P.J.; Romitti, P.A.; Mohanty, B.P.; Shinde, M.U.; Vuong, A.M.; Sharkey, J.R.; Dwivedi, D.; Horel, S.A.; Kantamneni, J.; et al. Prenatal nitrate intake from drinking water and selected birth defects in offspring of participants in the National Birth Defects Prevention Study. Environ. Health Perspect. 2013, 121, 1083–1089. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, J.O.; Govoni, M. Inorganic nitrate is a possible source for systemic generation of nitric oxide. Free Radical Biol. Med. 2004, 37, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Showers, W.J.; Genna, B.; McDade, T.; Bolich, R.; Fountain, J.C. Nitrate contamination in groundwater on an urbanized dairy farm. Environ. Sci. Technol. 2008, 42, 4683–4688. [Google Scholar] [CrossRef] [PubMed]
- McMahon, P.B.; Böhlke, J.; Kauffman, L.J.; Kipp, K.L.; Landon, M.; Crandall, C.A.; Burow, K.R.; Brown, C.J. Source and transport controls on the movement of nitrate to public supply wells in selected principal aquifers of the United States. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Williams, A.; Johnson, J.; Lund, L.; Kabala, Z. Spatial and temporal variations in nitrate contamination of a rural aquifer, California. J. Environ. Qual. 1998, 27, 1147–1157. [Google Scholar] [CrossRef]
- Spalding, R.F.; Exner, M.E. Occurrence of nitrate in groundwater—A review. J. Environ. Qual. 1993, 22, 392–402. [Google Scholar] [CrossRef]
- Harter, T.; Davis, H.; Mathews, M.C.; Meyer, R.D. Shallow groundwater quality on dairy farms with irrigated forage crops. J. Contam. Hydrol. 2002, 55, 287–315. [Google Scholar] [CrossRef]
- Gormly, J.R.; Spalding, R.F. Sources and Concentrations of Nitrate-Nitrogen in Ground Water of the Central Platte Region, Nebraskaa. Groundwater 1979, 17, 291–301. [Google Scholar] [CrossRef]
- Keeney, D.; Olson, R.A. Sources of nitrate to ground water. Crit. Rev. Environ. Sci. Technol. 1986, 16, 257–304. [Google Scholar] [CrossRef]
- Domagalski, J.L.; Ator, S.; Coupe, R.; McCarthy, K.; Lampe, D.; Sandstrom, M.; Baker, N. Comparative study of transport processes of nitrogen, phosphorus, and herbicides to streams in five agricultural basins, USA. J. Environ. Qual. 2008, 37, 1158–1169. [Google Scholar] [CrossRef] [PubMed]
- Green, C.T.; Böhlke, J.K.; Bekins, B.A.; Phillips, S.P. Mixing effects on apparent reaction rates and isotope fractionation during denitrification in a heterogeneous aquifer. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Nolan, B.T.; Hitt, K.J.; Ruddy, B.C. Probability of nitrate contamination of recently recharged groundwaters in the conterminous United States. Environ. Sci. Technol. 2002, 36, 2138–2145. [Google Scholar] [CrossRef] [PubMed]
- Wick, K.; Heumesser, C.; Schmid, E. Groundwater nitrate contamination: Factors and indicators. J. Environ. Manag. 2012, 111, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Boumans, L.; Fraters, B.; van Drecht, G. Nitrate in the upper groundwater of “De Marke” and other farms. NJAS-Wageningen J. Life Sci. 2001, 49, 163–177. [Google Scholar] [CrossRef]
- Elmi, A.A.; Madramootoo, C.; Egeh, M.; Liu, A.; Hamel, C. Environmental and agronomic implications of water table and nitrogen fertilization management. J. Environ. Qual. 2002, 31, 1858–1867. [Google Scholar] [CrossRef] [PubMed]
- Fraters, D.; Boumans, L.J.; van Drecht, G.; de Haan, T.; Wim, D. Nitrogen monitoring in groundwater in the sandy regions of the Netherlands. Environ. Pollut. 1998, 102, 479–485. [Google Scholar] [CrossRef]
- Salo, T.; Turtola, E. Nitrogen balance as an indicator of nitrogen leaching in Finland. Agric. Ecosyst. Environ. 2006, 113, 98–107. [Google Scholar] [CrossRef]
- Pabich, W.J.; Valiela, I.; Hemond, H.F. Relationship between DOC concentration and vadose zone thickness and depth below water table in groundwater of Cape Cod, USA. Biogeochemistry 2001, 55, 247–268. [Google Scholar] [CrossRef]
- Arora, B.; Mohanty, B.P.; McGuire, J.T.; Cozzarelli, I.M. Temporal dynamics of biogeochemical processes at the Norman Landfill site. Water Resour. Res. 2013, 49, 6909–6926. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Follett, R.F. Nitrogen in the Environment; Elsevier: San Diego, CA, USA, 2008. [Google Scholar]
- Assaf, H.; Saadeh, M. Geostatistical assessment of groundwater nitrate contamination with reflection on DRASTIC vulnerability assessment: The case of the Upper Litani Basin, Lebanon. Water Resour. Manag. 2009, 23, 775–796. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal evolution of groundwater composition in an alluvial aquifer (Pisuerga River, Spain) by principal component analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Mogheir, Y.; de Lima, J.; Singh, V. Characterizing the spatial variability of groundwater quality using the entropy theory: I. Synthetic data. Hydrol. Processes 2004, 18, 2165–2179. [Google Scholar] [CrossRef]
- Husain, T. Hydrologic Uncertainty Measure and Network Design. J. Am. Water Resour. Assoc. 1989, 25, 527–534. [Google Scholar] [CrossRef]
- Bueso, M.; Angulo, J.; Cruz-Sanjulian, J.; García-Aróstegui, J. Optimal spatial sampling design in a multivariate framework. Math. Geol. 1999, 31, 507–525. [Google Scholar] [CrossRef]
- Mariethoz, G.; Renard, P.; Froidevaux, R. Integrating collocated auxiliary parameters in geostatistical simulations using joint probability distributions and probability aggregation. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Dwivedi, D.; Mohanty, B.P.; Lesikar, B.J. Estimating Escherichia coliloads in streams based on various physical, chemical, and biological factors. Water Resour. Res. 2013, 49, 2896–2906. [Google Scholar] [CrossRef] [PubMed]
- Chapman, T.G. Entropy as a measure of hydrologic data uncertainty and model performance. J. Hydrol. 1986, 85, 111–126. [Google Scholar] [CrossRef]
- Mishra, A.K.; Özger, M.; Singh, V.P. An entropy-based investigation into the variability of precipitation. J. Hydrol. 2009, 370, 139–154. [Google Scholar] [CrossRef]
- Singh, V.P.; Marini, G.; Fontana, N. Derivation of 2D power-law velocity distribution using entropy theory. Entropy 2013, 15, 1221–1231. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Eng. 1951, 116, 770–808. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM Sigmobile Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L 2 theory. Probab. Theory Relat. Fields 1981, 57, 453–476. [Google Scholar]
- Maritan, A.; Rinaldo, A.; Rigon, R.; Giacometti, A.; Rodríguez-Iturbe, I. Scaling laws for river networks. Phys. Rev. E 1996, 53. [Google Scholar] [CrossRef]
- Bak, P.; Paczuski, M.; Shubik, M. Price variations in a stock market with many agents. Phys. A Stat. Mech. Appl. 1997, 246, 430–453. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.K.; Stanley, H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. 2002, 99, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Szolgayová, E.; Laaha, G.; Blöschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Processes 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–798. [Google Scholar] [CrossRef]
- Montanari, A.; Rosso, R.; Taqqu, M.S. Some long-run properties of rainfall records in Italy. J. Geophys. Res. 1996, 101, 29431–29438. [Google Scholar] [CrossRef]
- Sakalauskienė, G. The Hurst phenomenon in hydrology. Environ. Res. Eng. Manag. 2003, 3, 16–20. [Google Scholar]
- Ground Water Atlas of the United States, Oklahoma, Texas, HA 730-E. Available online: http://pubs.usgs.gov/ha/ha730/ch_e/E-text8.html (accessed on 1 May 2015).
- McCarthy, J.F.; Zachara, J.M. Subsurface transport of contaminants. Environ. Sci. Technol. 1989, 23, 496–502. [Google Scholar] [CrossRef]
- Texas Water Development Board. Available online: http://www.twdb.state.tx.us (accessed on 1 May 2015).
- Toth, J. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Al-Zabet, T. Evaluation of aquifer vulnerability to contamination potential using the DRASTIC method. Environ. Geol. 2002, 43, 203–208. [Google Scholar]
- Scott, J. Computerized Stratified Random Site-Selection Approaches for Design of a Ground-Water-Quality Sampling Network; Technical Report; Department of the Interior, US Geological Survey: Oklahoma City, OK, USA, 1990. [Google Scholar]
- Monitoring-Well Network and Sampling Design for Ground-Water Quality, Wind River Indian Reservation, Wyoming. Available online: http://pubs.usgs.gov/sir/2005/5027/ (accessed on 1 May 2015).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dwivedi, D.; Mohanty, B.P. Hot Spots and Persistence of Nitrate in Aquifers Across Scales. Entropy 2016, 18, 25. https://doi.org/10.3390/e18010025
Dwivedi D, Mohanty BP. Hot Spots and Persistence of Nitrate in Aquifers Across Scales. Entropy. 2016; 18(1):25. https://doi.org/10.3390/e18010025
Chicago/Turabian StyleDwivedi, Dipankar, and Binayak P. Mohanty. 2016. "Hot Spots and Persistence of Nitrate in Aquifers Across Scales" Entropy 18, no. 1: 25. https://doi.org/10.3390/e18010025
APA StyleDwivedi, D., & Mohanty, B. P. (2016). Hot Spots and Persistence of Nitrate in Aquifers Across Scales. Entropy, 18(1), 25. https://doi.org/10.3390/e18010025





