Abstract
In this paper, we investigate efficient estimation of differential entropy for multivariate random variables. We propose bias correction for the nearest neighbor estimator, which yields more accurate results in higher dimensions. In order to demonstrate the accuracy of the improvement, we calculated the corrected estimator for several families of random variables. For multivariate distributions, we considered the case of independent marginals and the dependence structure between the marginal distributions described by Gaussian copula. The presented solution may be particularly useful for high dimensional data, like those analyzed in the systems biology field. To illustrate such an application, we exploit differential entropy to define the robustness of biochemical kinetic models.
1. Introduction
Determining an entropy of random variable has been broadly studied since the nineteenth century. Originally, the entropy concept crystallized in thermodynamics and quantum mechanics [1,2]. In information theory, the entropy was introduced by Claude Shannon [3] in 1948 for random variables with a discrete probability space. A natural extension of a discrete entropy is a differential entropy [4] defined for a continuous random variable with probability density function (pdf) by:
It is worth mentioning that both notions, although analogous, have different properties, e.g., differential entropy is not necessarily non-negative.
The notion of entropy has many applications in various research fields. As an example, we mention here the emerging field of systems biology. It combines knowledge from various disciplines, including molecular biology, engineering, mathematics and physics, to model and analyze cellular processes. One of the challenging tasks in systems biology is to study interactions of regulatory, signaling and metabolism processes by means of biochemical kinetic models [5]. To check the robustness of such models, adequate sensitivity analysis procedures have to be applied.
Efficient entropy estimation is crucial for sensitivity analysis methods based on the mutual information of random variable measurements. An interesting approach for multi-variables system has been proposed recently by Lüdtke et al. [6]. However, it is based on a discrete entropy estimator and requires a computationally-inefficient variable discretization procedure. Having this concerns in mind, we propose here a more efficient k-nn differential entropy estimator, which can be used to calculate sensitivity indices in lieu of its discrete equivalent. Its application to sensitivity analysis for the model of the p53-Mdm2 feedback loop is presented in Section 5. In our approach, there is no need for variable discretization, and more importantly, an improved entropy estimator can be successfully used for highly multidimensional variables.
The estimation of differential entropy from the sample is an important problem with many applications; consequently, many methods have been proposed. Furthermore, several estimators based on the k-nn approach were analyzed, and their mathematical properties were investigated; see the discussion in the next section. We would like to emphasize that our main motivation here was very practical. Therefore, we focused on efficient implementation and bias correction for the well-established k-nn estimator with already proven consistency. The theory justifying our bias correction algorithm is based on the consistency analysis by Kozachnko and Leonenko [7]. Moreover, we performed extensive simulations for random samples from many multidimensional distributions recognized as most adequate in systems biology models.
Our improved k-nn entropy estimator explores the idea of correcting the density function evaluation near the boundary of random variable support. This smart idea has been proposed previously in [8] for several distributions. However, the novelty and usefulness of our approach lies in efficient bias correction of the classical k-nn estimator, which is applicable for any data sample (i.e., the a priori knowledge of the underlying distribution is not required).
2. k-nn Estimators of Differential Entropy
There are several approaches to entropy estimation from data samples; some are based on random variable discretization by partitioning [9], while others aim to estimate the probability mass according to the pdf [8,10]. The most efficient methods for probability mass estimation are based on k-th nearest neighbor (k-nn) estimation. The first k-nn approach to entropy estimation is dated to 1987 with the entropy estimator provided by Kozachenko and Leonenko [7] together with the proof of convergence. In this section, we recall definition and main properties of the k-nn entropy estimator by Kozachenko and Leonenko and we compare it to other approaches proposed in the literature.
Denote by for i.i.d. samples of continuous random variable . Let be the d-dimensional distance of point to its nearest neighbor in the sample and be the volume of a d-dimensional unit ball. The estimator is defined for d-dimensional distributions as follows [7]:
white where is the Euler–Mascheroni constant.
For completeness, we recall here the further study conducted by Kraskov et al. [11], who proposed a variant of the entropy estimator for the k-th nearest neighbor:
where is the d-dimensional distance of point to its k-th nearest neighbor in the sample and is the digamma function with and .
Notice that for , the Kraskov estimator given by Equation (2) performs almost equally to the Kozachenko–Leonenko estimator defined in Equation (1) with only a small unnoticeable difference stemming from:
According to analyses presented by Kozachenko et al. (1987) and Kraskov et al. (2004) in [7,11], k-nn estimators defined by Equations (1) and (2) converge in probability towards the real entropy value with increasing sample size:
Both estimators were shown to be consistent, i.e., asymptotically unbiased with the variance vanishing as the sample size increases. Moreover, for one-dimensional random variables, the estimator can be considered unbiased, even for a relatively small sample size, whereas the increase of dimension results in significant estimator bias even for a moderate sample size; see the exemplary case in Figure 1. The proof presented in [7] of the Kozachenko–Leonenko estimator in Equation (1) requires the following condition on the pdf for the asymptotic unbiasedness of the estimator:
and for the estimator consistency:
where denote a metric in and the expectations are over independent variables x and y.
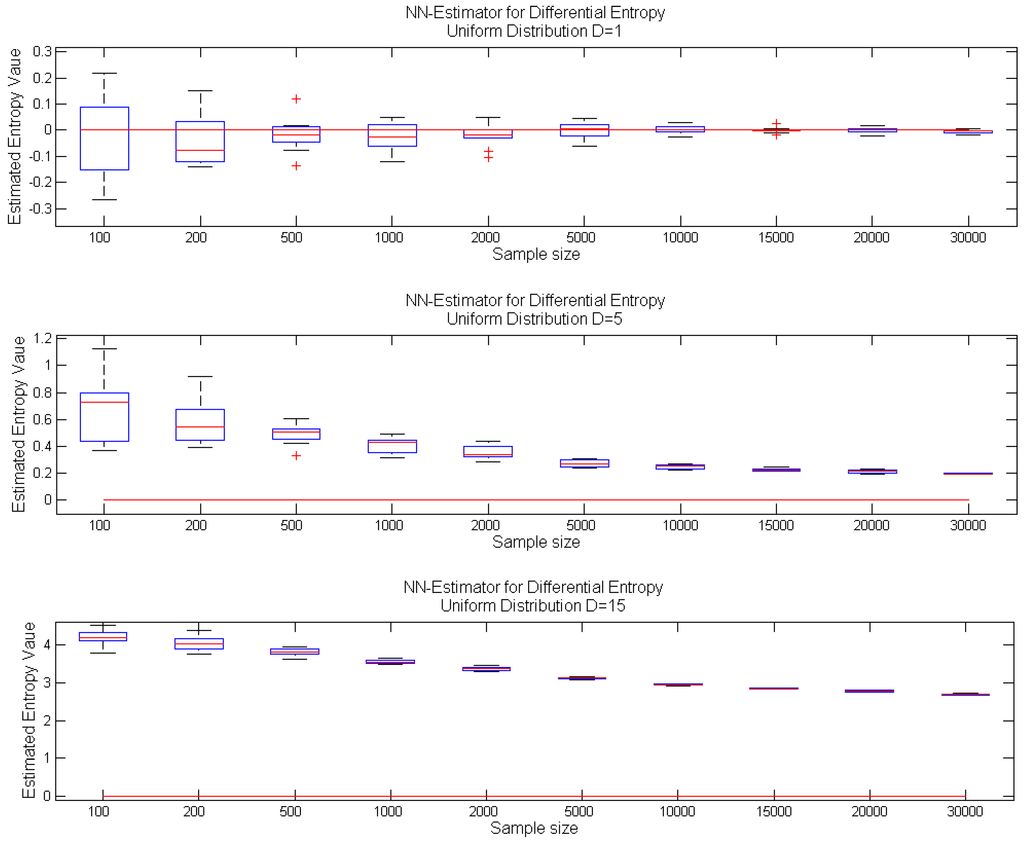
Figure 1.
Performance of the k-nn estimator Equation (1) for increasing sample size: box-plots of estimated entropy values for samples from a uniform distribution: on interval [0,1] (top); on hypercube (center); on hypercube (bottom); with real entropy value denoted by the red line.
Pérez-Cruz (2008) in [12] requires a somehow weaker assumption that the pdf must exist, i.e., the probability measure must be absolutely continuous. Consequently, the almost sure convergence of the entropy estimator is stated by the author.
The k-nn estimator for the related notion of Shannon entropy was proposed by Leonenko et al. (2008) in [13]. It can be shown that it is equivalent to those defined by Equation (2) with component replaced by . Similarly, the Shannon entropy estimator presented by Penrose et al. (2013) in [14] can be expressed by Equation (1) with the component replaced by . Both estimators were proven to be convergent to the real entropy value in with some restrictions for density . Namely, in [13], the pdf must be bounded, and for some . The boundness condition has been relaxed in [15] to an unbounded pdf with additional constraint ; white while in [14], the pdf must be bounded or the pdf must be defined on with
It is worth mentioning that also, estimators for the Kullback–Leibler divergence were proposed and analyzed by Pérez-Cruz and Wang in [12,16]. Nevertheless, these estimators were based on the same idea of probability mass estimation by the distance to the k-nn in a sample; consequently, when used for estimating mutual information (cf. Definition 2), they suffer from the same problems as the above-mentioned entropy estimators.
A slightly different concept based on order statistics generalized to Voronoi regions in multiple dimensions was explored by Miller [17] to estimate the differential entropy and applied in [18] for independent component analysis. Unfortunately, the complexity of calculating the volume of Voronoi regions appears to be exponential in the dimension, and therefore, the method does not seem to be promising for our applications.
3. Bias Correction of the k-nn Entropy Estimator
In higher dimensions, k-nn estimators for many important distributions converge slowly and with noticeable bias; cf. Figure 1. Moreover, the entropy value is often overestimated; see Figure 1 for a d-dimensional uniform distribution and Appendix Figure A1 for a d-dimensional distribution with independent marginals sampled from an exponential distribution. On the other hand, for some distributions, like multivariate Gaussian ones, the estimator performs well, even in higher dimensions; cf. Appendix Figure A1 (top panel). As argued in [8], the overestimation problem affects random variables with bounded support. Before giving the description of our bias correction procedure, we briefly present the density mass estimation problem.
Recall that the k-nn estimation for continuous random variables requires probability mass estimation in small neighborhoods of sampled points. Consequently, when the sample points are located densely near the boundary of a given distribution, the calculations might be overestimated, as the samples’ neighborhoods might exceed the boundary of random variable support.
Therefore, the entropy estimator bias stems from overestimation of the pdf that occurs when the sample point is located near the boundaries of a random variable support. The curse of dimensionality implies that the boundary area increases with the variable dimension. Thus, in higher dimensions, neighborhoods of sampled points more frequently exceed the boundaries of a variable support.
Here, we focus on correcting the bias of the k-nn estimator. We restrict our further analysis to the Kozachenko and Leonenko estimator in Equation (1), but our procedure may be easily adapted to reduce the bias of the estimator defined by Equation (2) and other estimators discussed in the previous section. The precise reason for the biased performance of the k-nn entropy estimator may be exposed by analyzing the proof of its convergence [7].
Let be a set of independent random samples of a variable with probability density function . Let be a metric in with a neighborhood of radius r centered at point x defined by:
Then, the volume of the neighborhood is equal to , where is the unit ball volume according to the metric ρ.
For differential entropy estimation, the probability mass of a random variable X in a point is estimated using the following Lebesgue theorem with a small volume neighborhoods centered at sampled points .
Theorem 1 (Lebesgue). Let ; then, for almost all and open balls with radius :
By analyzing the proof of convergence of the k-nn estimator (see the Appendix), we noticed that the application of Lebesgue’s theorem for distributions with support can introduce a systematic error to the estimated value. The formal analysis reduces to a quotation of the main steps of the proof of convergence. The key point of the proof in which the systematic error is to be noticed is presented in Equation (B1) in the Appendix. The bias stems from the relatively slow convergence with the sample size to the exponent of the averaged pdf within neighborhoods of vanishing volumes that can exceed variable support.
To illustrate this issue, let us consider the exemplary case of the uniform distribution X on d-dimensional unit cube . Every point in a cube is equally probable and the pdf for points and for points outside the the cube. Lebesgue’s theorem applied for X states:
and it introduces the following estimation error for points x near the boundaries, i.e., with neighborhood partially outside the cube :
where . Our correction to the entropy estimator is based on the logarithm of the proportions of neighborhood volumes inside the support of X to the volume of the whole neighborhood :
Finally, for defined by Equation (1), the corrected entropy estimator is defined as follows:
To ensure the efficient implementation of our approach, we use the maximum metric in :
for points and . In this metric, the neighborhoods are d-dimensional hypercubes, and the unit ball volume equals .
The support boundaries are estimated based on the sample and are determined simply as the leftmost and the rightmost values for each dimension. Determined boundary values (in an amount of at most ) are removed from the sample in the preprocessing phase, before entropy estimation.
Algorithm 1 presents the pseudocode of the corrected k-nn entropy estimator. The bias correction presented on the uniform example can be applied for any multivariate distribution. However, due to the source of bias, our correction is much more efficient for random variables with bounded support. Therefore, in the next section, we focus on the usefulness of Algorithm 1 for multidimensional uniform and beta distributions with both independent and dependent marginals. The exemplary dependency structure is modeled by a Gaussian copula.
The issue of estimator convergence for a one-dimensional variable has been analyzed by van der Meulen and Tsybakov [19], and the bias was proven to be of order , where n is the sample size.
Furthermore, the bounded support of a random variable as a source of k-nn estimator bias was already identified in papers by Sricharan et al. [8,20]. The authors estimated the bias using Taylor expansion of pdf , as:
where , under the assumption that p is two-times continuously differentiable and is bounded away from zero. Compare also further work by Sricharan et al. [21,22].
It should be emphasized that the usefulness of analytical bias estimations is limited to variables with known pdf . In contrast to previous approaches, we did not aim at proving asymptotic bounds for differential entropy estimator bias. Instead, we propose the efficient heuristic procedure for bias correction. Moreover, in the applications, e.g., in systems biology, we have no a priori knowledge about the probability distributions of a random sample. The analytical bounds as in Equation (7) is of limited value without knowledge of pdf. To compare our bias correction procedure (Algorithm 1) to the estimation given by Equation (7), we calculated both corrections for a d-dimensional uniform distribution (see Figure 2). It occurred that compared to our method , the Equation (7) significantly underestimates the bias for higher dimensions.


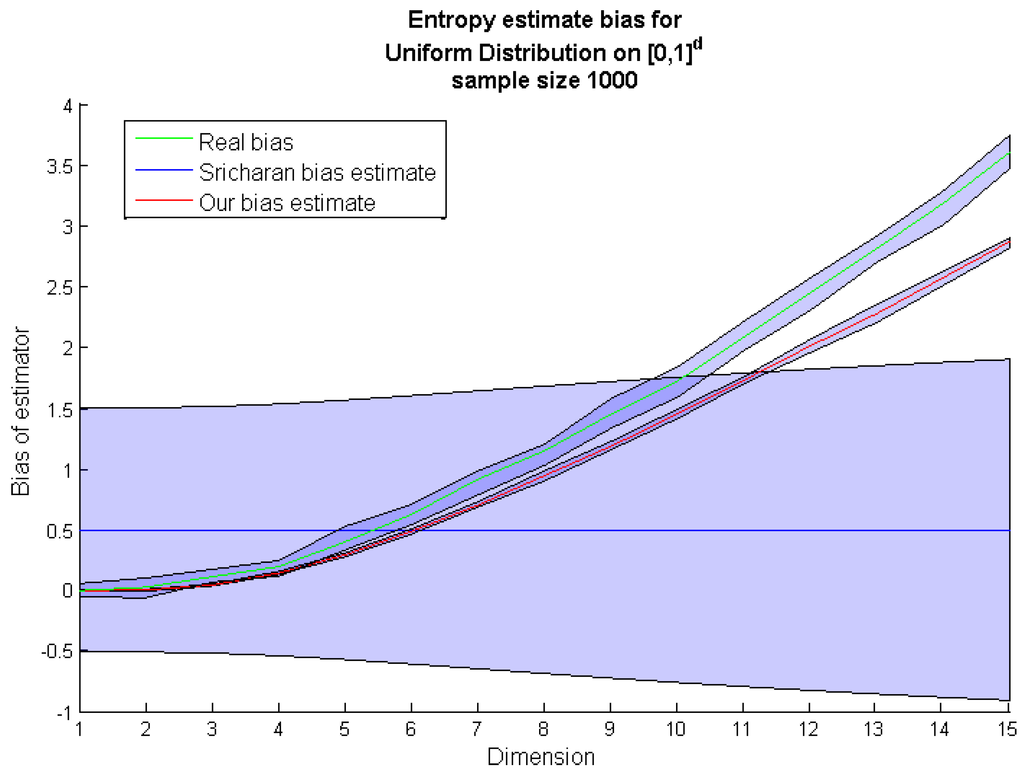
Figure 2.
Comparison of the k-nn entropy bias estimate by Sricharan et al. [8] (blue line) with the real bias based on the k-nn entropy estimation from sampled points (green line) and the k-nn entropy bias estimate obtained by our method (red line).
4. k-nn Estimator Performance for Different Distributions
As argued above, the heavy bias for the k-nn differential entropy estimator characterizes multidimensional distributions supported on a bounded interval. If the sampled points appear frequently near interval boundaries, the probability mass determined with the use of the Lebesgue’s theorem is overestimated, due to the fact that the radius of an estimated neighborhood exceeds the distribution support. The reason for bias of sample based k-nn density estimators can be found in [8].
For the highly multivariate variables, improved estimator defined in Equation (6) performed significantly better with much smaller bias than the original k-nn estimator in Equation (1). Here, we demonstrate the efficiency of the proposed correction for two families of marginal distributions defined on the [0,1] interval: uniform and Beta. To study the estimator behavior, we sampled random points from multivariate distributions with both correlated and independent marginals.
4.1. Independent Marginals Case
Novel bias correction yields spectacular improvement of estimator accuracy for a multidimensional uniform distribution on unit hypercube (i.e., a multivariate distribution with independent uniform marginals on interval [0,1]). Analogous outcomes were achieved for multidimensional distributions with independent beta marginals (with supports on interval [0,1]); see Figure 3. Notice that the application of our bias correction is necessary, as comparable results could not be obtained by the increase of sample size; cf. Figure 4.
For completeness, we also tested the performance of estimator correction for multidimensional distributions with independent marginals that have unbounded support, e.g., Gaussian distribution, and one side bounded support, e.g., exponential distribution; see Appendix Figure A1. For a multivariate Gaussian distribution, the correction slightly underestimates the real value, but not significantly, especially for a bigger sample size. While for a multivariate distribution with independent exponential marginals, the corrected estimator introduces a small improvement; cf. Figure A2 in the Appendix.
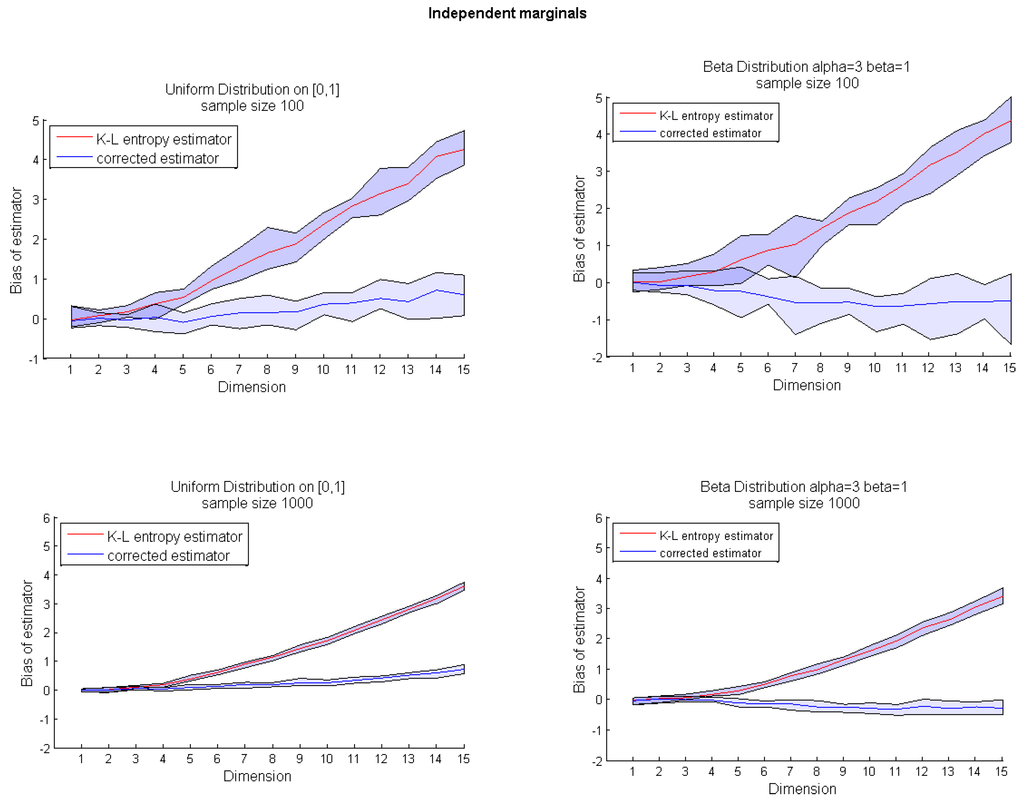
Figure 3.
Bias of the entropy estimator for growing dimensions for original k-nn entropy estimator in Equation (1) (red) and corrected entropy estimator in Equation (6) (blue) for multivariate random variables with independent marginals sampled from a uniform distribution on interval [0,1] (left); and from the Beta(3,1) distribution (right); for two different sample sizes (top and bottom).
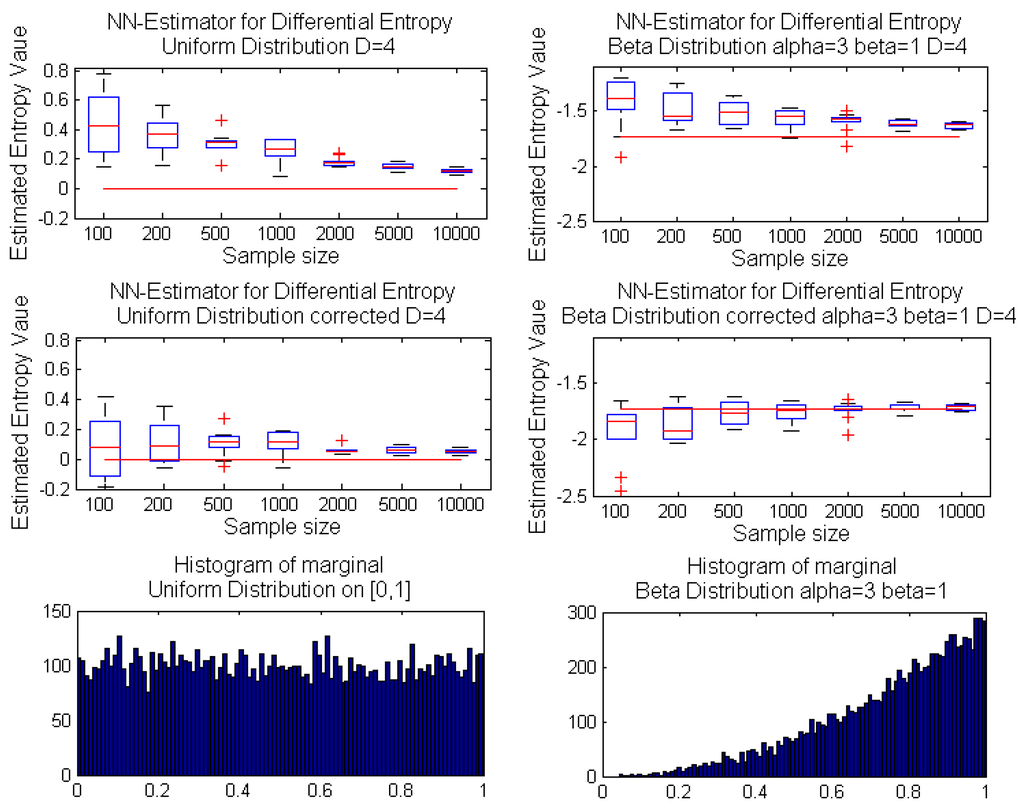
Figure 4.
Box plots for the growing sample size of estimated entropy values with k-nn entropy estimator in Equation (1) (top); and corrected entropy estimator in Equation (6) (center); for four-dimensional random variables with independent marginals sampled from a uniform distribution on interval [0,1] (left); and the Beta(3,1) distribution (right); w.r.t. the real entropy value denoted by the red line. The bottom panels demonstrate the histograms of marginal distributions.
4.2. Dependent Marginals Case
We aim here to test the accuracy of the corrected k-nn estimator for samples from multidimensional distributions with dependent marginals. The exemplary structure of dependency is provided by the Gaussian copula:
where is a joint cumulative distribution function of the multivariate Gaussian distribution with mean vector zero and the covariance matrix equal to the correlation matrix Σ, and is the inverse cumulative distribution function of the standard normal distribution. See Figure A3 in the Appendix for a copula probability density function and a copula function in the two-dimensional case.
The dependent marginals case is much more realistic in many applications, e.g., for sensitivity analysis in systems biology. We decided that the dependency structure between marginal distributions by means of an appropriate copula is flexible enough to model various dependencies between model parameters. Moreover, the controlled dependence structure allows one to calculate the real estimated entropy value and to estimate the bias of an estimator [23]. It occurred that in the case of dependent variables, the accuracy gained by the corrected estimator is as significant as in the case of independent marginals. Improvement of the k-nn estimator was tested for samples from multivariate distributions with marginals supported on a bounded interval, i.e., uniformly distributed on interval [0,1] and non-uniformly distributed on interval [0,1] (beta marginals); cf. Figure 5 and Figure 6.
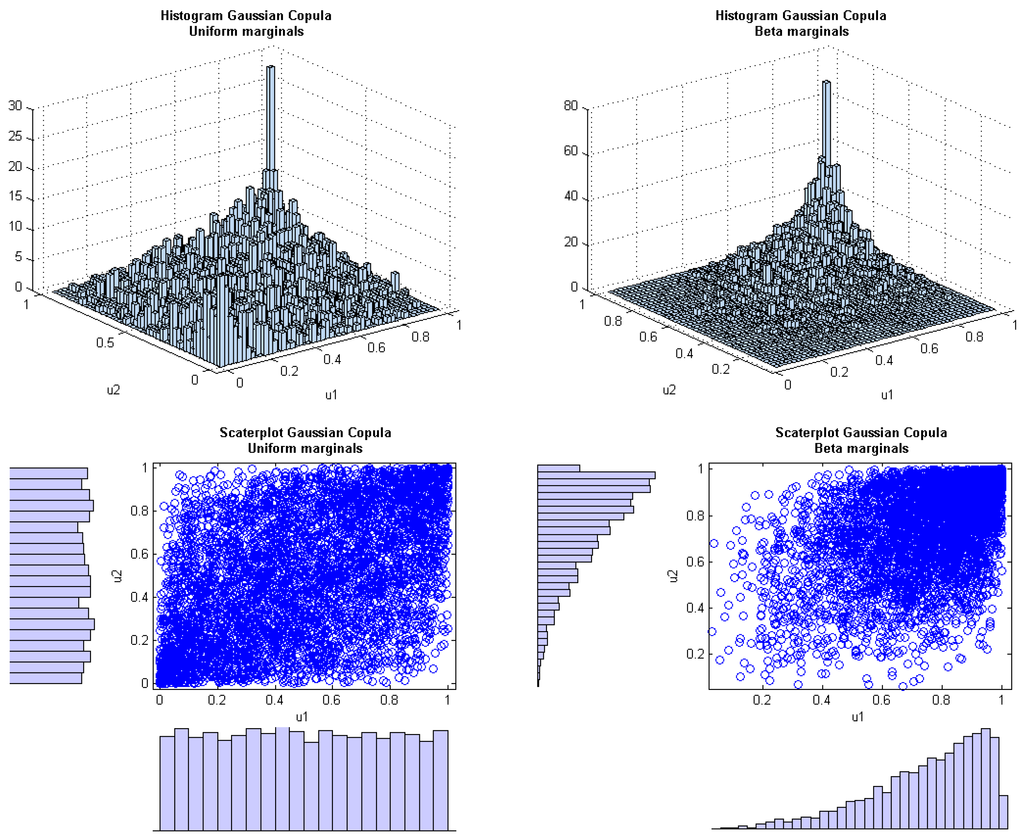
Figure 5.
Bivariate distributions with a Gaussian copula dependence structure with correlation coefficient and marginals sampled from a uniform distribution on interval [0,1] (left); vs. marginals sampled from the Beta(3,1) distribution (right).
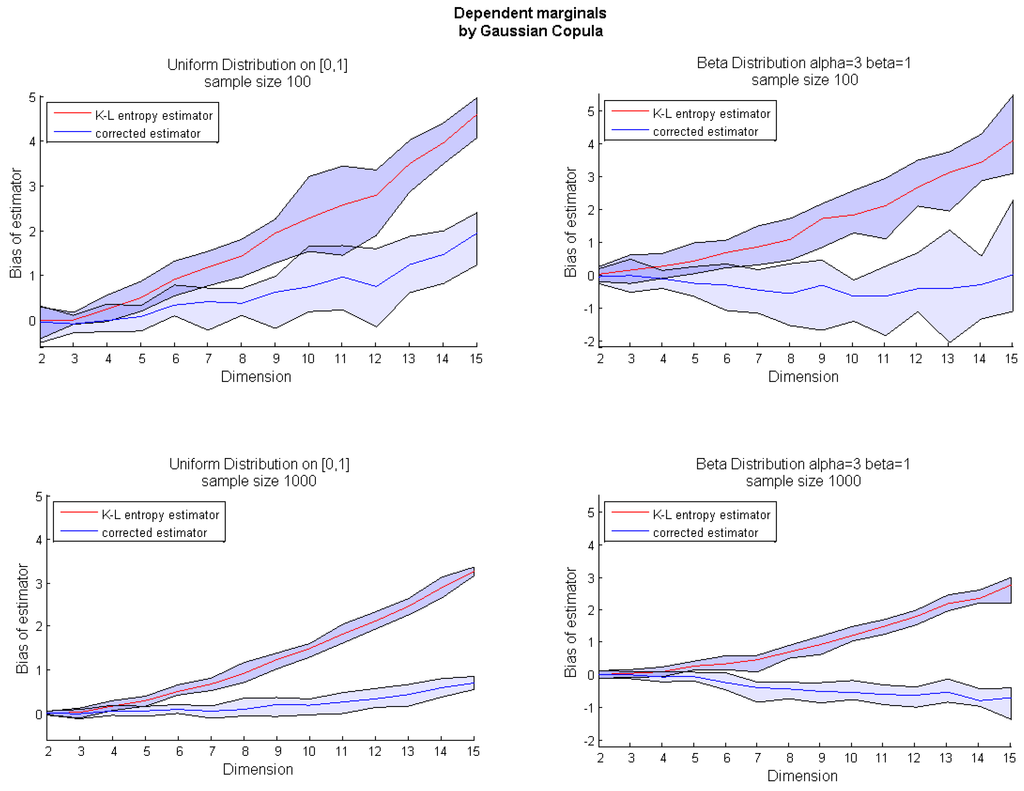
Figure 6.
Bias of the entropy estimator for growing dimensions for original k-nn entropy estimator in Equation (1) (red) and corrected entropy estimator in Equation (6) (blue) for multivariate random variables with dependent marginals sampled from a uniform distribution on interval [0,1] (left); and the Beta(3,1) distribution (right); for two different sample sizes (top-bottom). The dependence structure is given by the Gaussian copula with correlation coefficients among marginals .
5. Sensitivity Indices Based on the k-nn Entropy Estimator
Efficient entropy estimation is crucial in many applications, especially in sensitivity analysis based on mutual information [6]. Particularly, in systems biology, aiming to formally describe complex natural phenomena, an in-depth sensitivity analysis is required to better understand the modeled system behavior. Although, the method proposed by Lüdtke et al. [6] provides an approach to sensitivity analysis for multi-variables system, it is based on entropy estimation requiring variable discretization and, consequently is computationally inefficient. Moreover, it may provide biased or inadequate results for continuous random variables.
Therefore, here, we propose to modify the approach from [6] by applying our corrected k-nn differential entropy estimation with no need for variable discretization. The main concept in sensitivity analysis, taken from information theory, is mutual information (MI) between random variables. Mutual information indicates the amount of shared information between two random variables, i.e., input variable (parameter or explanatory variable) and output variable (explained variable). When used for samples of parameters and samples of corresponding model response, estimated MI can indicate the sensitivity of a model to the parameters.
Definition 2. The mutual information between continuous random variables and is defined by:
where is the joint distribution of X and Y and , and are probability density functions.
Definition 3. The conditional entropy of a random variable given random variable is defined as:
where and are respectively the joint and the conditional probabilities densities functions of variables X and Y.
There exist the following analogies between the information theoretic measures and set theory operations (see Figure B1 in the Appendix):
Inspired by [6], we redefine sensitivity indices for parameters (considered as continuous random variables) using the notion of differential entropy:
| information theory | set theory |
Definition 4. white Assume that are the parameters of the model and Y is the model output, then single sensitivity indices are defined as:
white Analogously, group sensitivity indices for pairs of parameters are defined as:
Clearly, Definition 4 can be extended for any subset of parameters.
The sensitivity indices reflect the impact of parameters on the model output. It may happen that the group sensitivity index for a pair of parameters had a high value, indicating the significant influence of these parameters, while two single sensitivity indices for these two parameters had a low value. We interpret such a case as the opposite (negative) interaction between this pair of parameters. To quantify such interactions, we use the following notion:
Definition 5. If are parameters of the model and Y is model output, then interactions indices within a pair of parameters are defined by:
An analogous definition of interactions was introduced by McGill in [24] for discrete random variables. The following corollary expresses the interaction indices by the group sensitivity indices; see also the Venn diagrams depicted in Figure B1 in the Appendix.
Corollary 6. Interaction index within the pair of parameters and can be expressed as the sum of single sensitivity indices of parameter and parameter to the output variable Y minus the group sensitivity index for a pair of parameters:
5.1. Case Study: Model of the p53-Mdm2 Feedback Loop
To validate the new approach to the global sensitivity analysis based on the entropy measure, we tested the method on a well-known and widely-studied example of the negative feedback loop of the p53 protein and Mdm2 ligase.
Tumor suppressor p53 protein, also known as TP53 transcription protein 53, is a transcription factor determining the fate of a cell in the case of DNA damage; p53 indirectly, via activation of the transcription of the encoding p21 gene, can block the cell cycle to repair DNA or activate a process of programmed cell death, called apoptosis. The main regulator of the concentration of p53 protein is ligase Mdm2/Hdm2 (double minute 2 mouse/human double minute 2), which, through ubiquitination, leads to degradation of p53 in the proteasome. In more than half of the cases of human cancers, p53 is inactivated or absent, which allows the mutated tumor cells to replicate and determines their immortality. Consequently, this protein is under investigation due to its property of leading to self-destruction of cancer cells, which could be successfully used as therapy in many types of cancer [25]. The modelled system (Figure 7 left panel) can be formally described with the use of ordinary differential equations (ODE) as follows:
where the variables of the modeled system correspond to the concentration of species p53, mRna Mdm2 and Mdm2, respectively. The initial values of the variables are given by species concentrations at starting time point :
| p53 protein; | |
| Mdm2 ligase; | |
| mRna Mdm2 precursor of Mdm2 ligase. |
The parameters of the model denoted by correspond to reaction rates with the following base values and their biological interpretations:
| p53 production; | Mdm2 transcription; | ||
| Mdm2-dependent p53 degradation; | Mdm2 degradation; | ||
| p53-dependent Mdm2 production; | independent p53 degradation; | ||
| p53 threshold for degradation by Mdm2. |
To investigate the sensitivity of the model to the parameter changes, the parameters () were perturbed around the base value according to Gamma distributions:
with shape parameters and and mean values equal to parameter base values . The negative regulation of p53 protein by Mdm2 ligase results in an oscillatory behavior in time (see Figure 7 right panel). A parameter responsible for negative regulation is Mdm2-dependent p53 degradation rate denoted by .
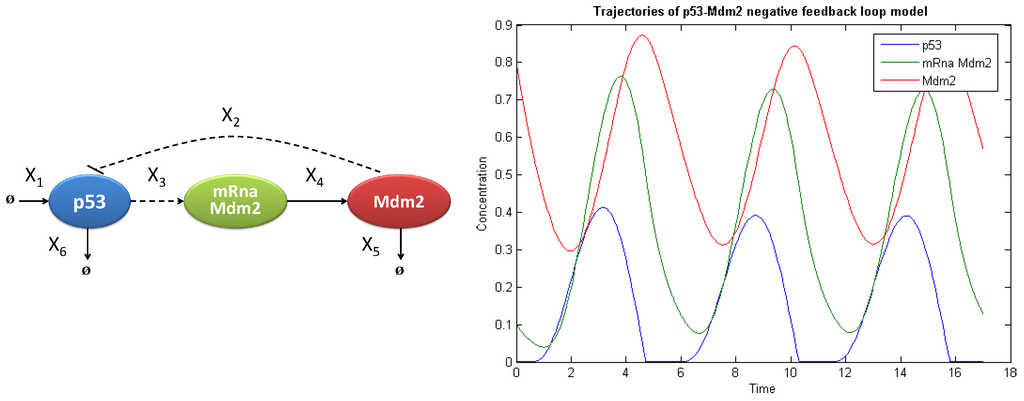
Figure 7.
Graphical scheme of the modelled system (left); and the oscillatory behavior for the considered parameters values (right).
Different possible system trajectories resulting from the perturbation of parameters are depicted in Figure B2 in the Appendix. It is worth noting that oscillatory behavior is sensitive to specific parameter values.
The output of the model Y is a three-dimensional variable with components denoting the species concentration that are averaged with respect to time:
To interpret novel sensitivity indices based on differential entropy, we compared them to standard local sensitivity indices, which are partial derivatives of model output w.r.t. the parameters of interest. As illustrated by the heat maps in Figure 8, both methods indicated the model inflow and outflow parameters ( and , respectively) as crucial for the systems’ behavior. Interestingly, the standard method (LSA) did not capture the parameter responsible for the negative feedback loop, whereas the method based on mutual information showed high sensitivity to the parameter crucial for the oscillatory behavior of the model.
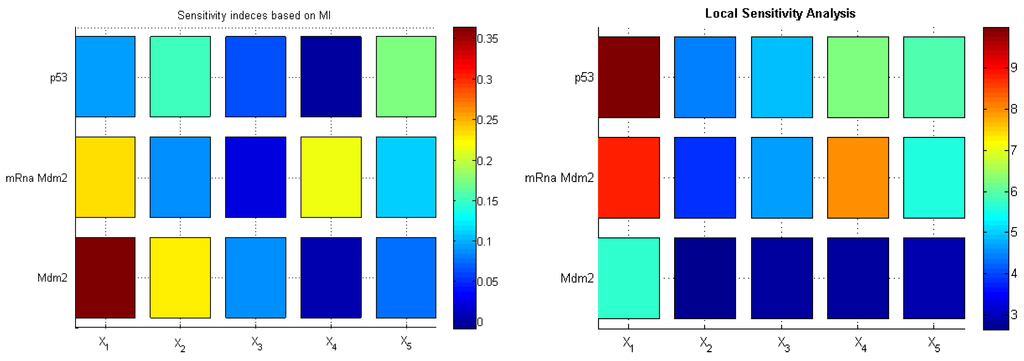
Figure 8.
Sensitivity indices based on mutual information (MI) (left); local sensitivity analysis based on derivatives of variables w.r.t. parameters averaged in time (right).
The global sensitivity analysis aims at identifying the influence of some group of parameters on the system behavior. There exist several well-established approaches to this task, like the Sobol method or multi-parameter sensitivity analysis; see, e.g., [26]. However, determining the nature of mutual interactions as compatible or opposite seems a novelty, which was made possible thanks to defining the interaction indices.
In our case study, we determined the pair of parameters (model inflow) and (negative feedback) to have the highest sensitivity index among all pairs of parameters. Moreover, these parameters play the opposite roles in the model, which was illustrated as a negative interaction index for this pair of parameters. Analogously, parameters and responsible for Mdm2 transcription and degradation have a negative interaction and high common impact on the model behavior; see Figure 9.
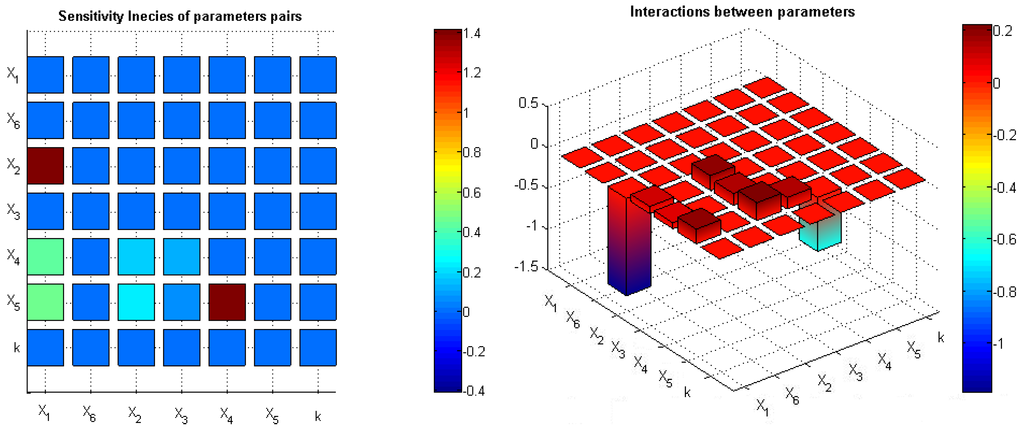
Figure 9.
Sensitivity indices for pairs of parameters (left); interactions within pairs of parameters, respectively, for the model output (right).
6. Conclusions
In this work, we study the issue of efficient estimation of the differential entropy. By analyzing the proof of convergence of the estimator proposed in [7], we designed the efficient bias correction procedure that can by applied to any data sample (no a priori knowledge of the probability density function is required).
The source of systematic bias that impairs all existing sample based k-nn estimators has been identified previously in [8]. The problem affects all distributions defined on a finite support, and due to the curse of dimensionality, the bias increases for multivariate distributions.
We have compared the bias correction proposed by Sricharan et al. [8] to our procedure, which has been exhaustively tested for many families of distributions. It turned out that the correction spectacularly proposed in this paper improves the accuracy of the estimator in tested multivariate distributions (we illustrated the accuracy gain for multivariate uniform and beta distributions with both independent and dependent marginals). It is worth mentioning that, in the case of the distribution with support bounded at one side (e.g., exponential), the proposed amendment is relatively small. The correction does not introduce improvement for a multivariate Gaussian distribution with unbounded support. However, for the latter family of distributions, the original estimator bias is not observed.
Summarizing, our results can be successfully used in many applications, the most prominent for us being the sensitivity analysis for kinetic biochemical models, where one often assumes parameters (e.g., reaction rates or initial conditions) originate from distributions with bounded support. The applicability of an efficient entropy estimator for sensitivity analysis has been presented on the model of the p53-Mdm2 feedback loop.
Acknowledgments
This work was supported by the Polish NCNGrant No. UMO-2014/12/W/ST5/00592, as well as by the Biocentrum-Ochota project POIG02.03.00-00-003/09 and by the European Union from resources of the European Social Fund, Project POKL.04.01.01-00-051/10-00, “Information technologies: Research and their interdisciplinary application”.
Author Contributions
Agata Charzyńska developed the algorithm for bias correction. Anna Gambin supervised the study. Agata Charzyńska and Anna Gambin wrote the manuscript and reviewed and approved the final version.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. Performance of the Corrected k-nn Estimator
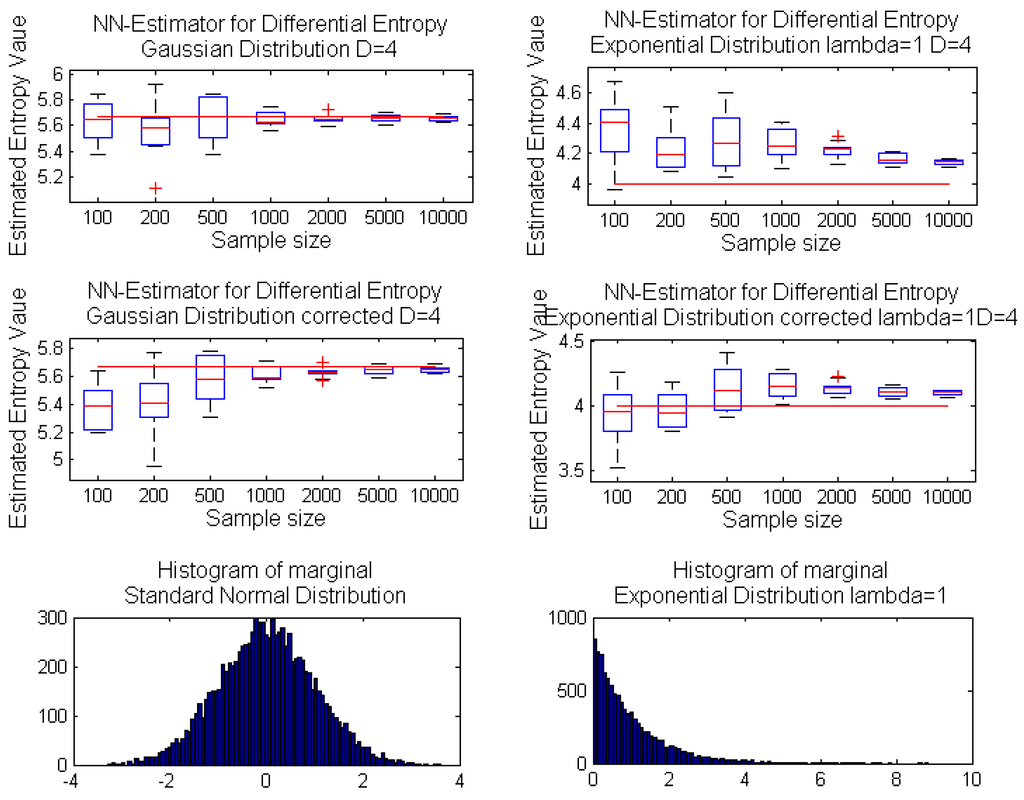
Figure A1.
Box plots for the growing sample size of estimated entropy values with k-nn entropy estimator Equation (1) (top); and corrected entropy estimator Equation (6) (middle); for four-dimensional random variables with independent marginals sampled from a standard normal distribution (left); and an Exponential(1) distribution (right); w.r.t. the real entropy value denoted by the red line. The bottom panels demonstrate the histograms of the marginal distributions.
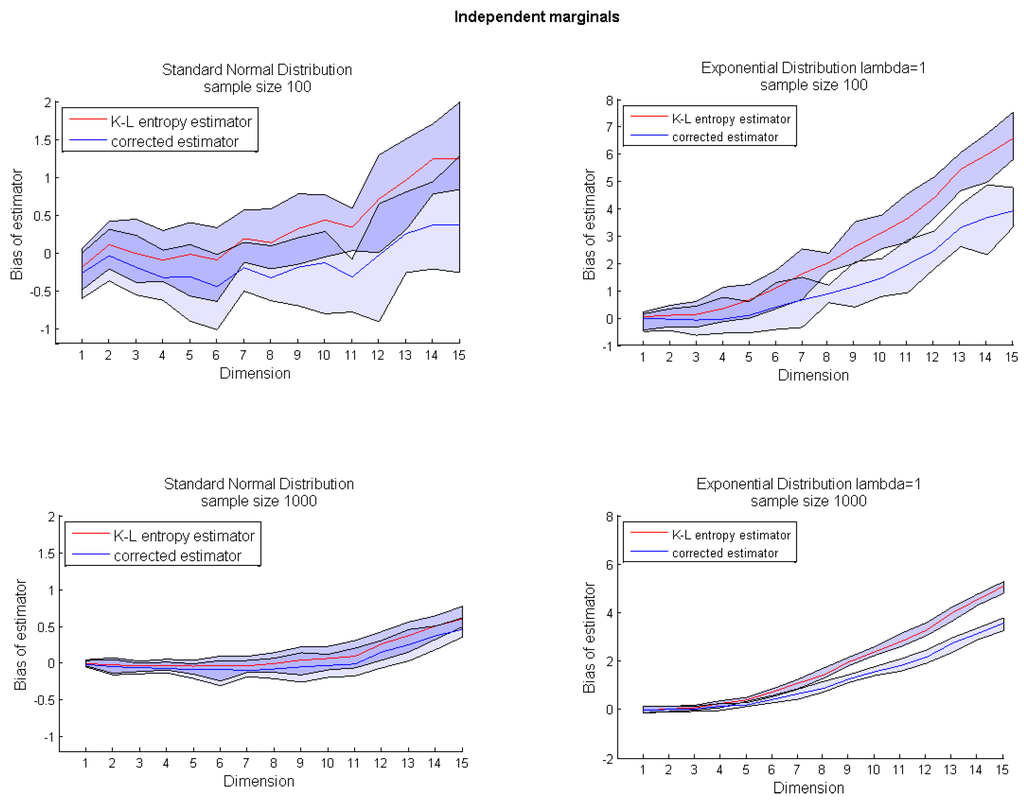
Figure A2.
The bias of the entropy estimator for growing dimensions for original k-nn entropy estimator in Equation (1) (red), and corrected entropy estimator in Equation (6) (blue) for multivariate random variables with independent marginals sampled from a standard normal distribution (left); and an Exponential(1) distribution (right); for two different sample sizes (top-bottom).
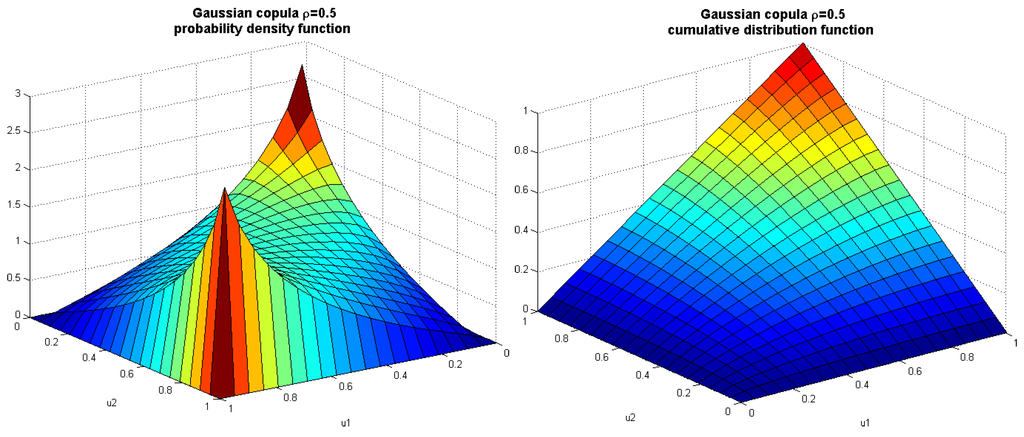
Figure A3.
Gaussian copula probability density function for two marginal variables with correlation coefficient (left); and a two-dimensional copula function with correlation coefficient (right).
B. Sketch of the Proof of k-nn Estimator Convergence [7]
Let us define variables:
based on sampled points , where denotes the distance to the nearest neighbor within sampled points. Consequently, are i.i.d. random variables, and the entropy estimator given by the Equation (1) equals:
For each point x, the cumulative distribution function (cdf) of a random variable conditioned on equals:
where is a small random radius determining the neighborhood of sampled point . The volume of neighborhood tends to zero with increasing sample size n. The application of the white Lebesgue’s theorem, yields:
The expectation of the logarithm of the limiting random variable with the cdf:
and the pdf:
equals:
Finally:
and the arithmetical average over samples gives the estimate of the expectation. Passing to the limit under the integral is justified in detail in [7]. To ensure the asymptotic unbiasedness of the estimator, the assumption stated in the Equation (3) must be met, and for the estimator consistency, the assumption from the Equation (4) is required. This finishes the proof of convergence for the k-nn entropy estimator.
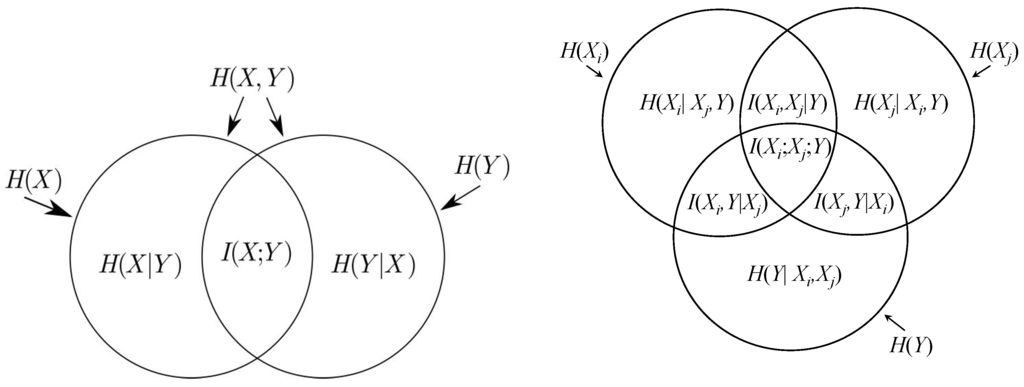
Figure B1.
Venn diagrams for information theoretic measures, including interactions between pairs of parameters.
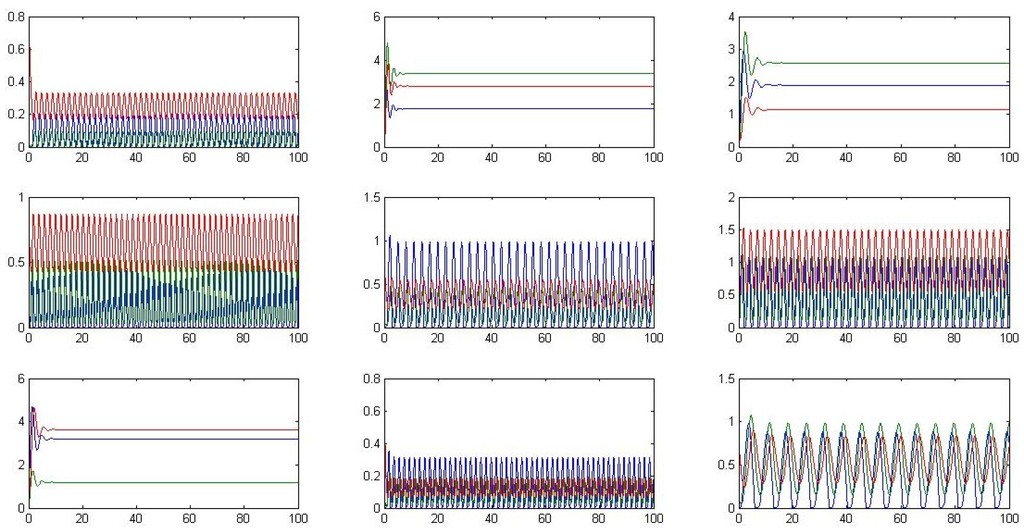
Figure B2.
Possible trajectories of the p53-Mdm2 negative feedback loop with perturbed parameters. The vertical axis denotes time; the horizontal axis denotes species concentration. The blue line corresponds to the p53 protein concentration; the green line corresponds to the mRna Mdm2 concentration; and the red line corresponds to the Mdm2 ligase concentration.
References
- Clausius, R. On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff’s Annalen der Physick 1850, LXXIX. [Google Scholar]
- Maxwell, J.C. Theory of Heat; Longmans, Green and Co.: London, UK, 1871. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lazo, A.; Rathie, P. On the entropy of continuous probability distributions. IEEE Trans. Inf. Theory 1978, 24, 120–122. [Google Scholar] [CrossRef]
- Westerhoff, H.V.; Palsson, B.O. The evolution of molecular biology into systems biology. Nat. Biotechnol. 2004, 22, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Lüdtke, N.; Panzeri, S.; Brown, M.; Broomhead, D.; Knowles, J.; Montemurro, M.A.; Kell, D. Information-theoretic sensitivity analysis: A general method for credit assignment in complex networks. J. R. Soc. Interface 2008, 5, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Kozachenko, L.; Leonenko, N. Sample Estimate of the Entropy of a Random Vector. Probl. Peredachi Inf. 1987, 23, 9–16. [Google Scholar]
- Sricharan, K.; Raich, R.; Hero, A.O. Boundary Compensated k-NN Graphs. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, Kittila, Finland, 29 August– 1 September 2010.
- Dorval, A. Probability distributions of the logarithm of inter-spike intervals yield accurate entropy estimates from small datasets. J. Neurosci. Methods 2008, 173, 129–139. [Google Scholar] [CrossRef] [PubMed]
- Raykar, V.C. Probability Density Function Estimation by different Methods; Report for Course assignment 1 of ENEE 739Q SPRING; University of Maryland: College Park, MD, USA, 2002. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Cruz, F. Estimation of Information Theoretic Measures for Continuous Random Variables. In Proceedings of the Advances in Neural Information Processing Systems 21 (NIPS 2008), Vancouver, BC, Canada, 2008; p. 1260.
- white Leonenko, N.; Pronzato, L.; Savani, V. A class of Rényi information estimators for multidimensional densities. Ann. Statist. 2008, 36, 2153–2182. [Google Scholar] [CrossRef]
- white Penrose, M.D.; Yukich, J.E. Limit theory for point processes in manifolds. Ann. Appl. Probab. 2013, 23, 2161–2211. [Google Scholar] [CrossRef]
- Leonenko, N.; Pronzato, L. Correction: A class of Rényi information estimators for multidimensional densities. Ann. Statist. 2010, 38, 3837–3838. [Google Scholar] [CrossRef]
- white Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k -nearest-neighbor distances. IEEE Trans. Inform. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- white Miller, E.G. A new class of entropy estimators for multidimensional densities. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP ’03), HongKong, China, 6–10 April 2003.
- Learned-Miller, E.G. Hyperspacings and the estimation of information theoretic quantities; University of Massachusetts-Amherst Technical Report: Amherst, MA, USA, 2004. [Google Scholar]
- Van der Meulen, E.C.; Tsybakov, A.B. Root-n consistent estimators of entropy for densities with unbounded support. Scand. J. Stat. 1996, 23, 75–83. [Google Scholar]
- Sricharan, K.; Raich, R.; Hero, A. Optimized intrinsic dimension estimation. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 5418–5421.
- Sricharan, K.; Raich, R.; Hero, A. Estimation of nonlinear functionals of densities with confidence. IEEE Trans. Inform. Theory 2012, 58, 4135–4159. [Google Scholar] [CrossRef]
- Sricharan, K.; Wei, D.; Hero, A. Ensemble estimators for multivariate entropy estimation. IEEE Trans. Inform. Theory 2013, 59, 4374–4388. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Sun, Z. Mutual Information is Copula Entropy. Available online: http://arxiv.org/abs/0808.0845v1 (accessed on 23 December 2015).
- white McGill, W.J. Multivariate information transmission. Psychometrika 2006, 19, 97–116. [Google Scholar] [CrossRef]
- Geva-Zatorsky, N.; Rosenfeld, N.; Itzkovitz, S.; Milo, R.; Sigal, A.; Dekel, E.; Yarnitzky, T.; Liron, Y.; Polak, P.; Lahav, G.; et al. Oscillations and variability in the p53 system. Mol. Syst. Biol. 2006, 2. [Google Scholar] [CrossRef] [PubMed]
- Charzyńska, A.; Nałȩcz, A.; Rybiński, M.; Gambin, A. Sensitivity analysis of mathematical models of signalling pathways. BioTechnol. J. Biotechnol. Comput. Biol. Bionanotechnol. 2012, 93, 291–308. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).