Heat Transfer and Pressure Drop Characteristics in Straight Microchannel of Printed Circuit Heat Exchangers
Abstract
:1. Introduction
2. Experimental Setup and Data
2.1. Microchannel PCHE
2.2. Experimental Setup
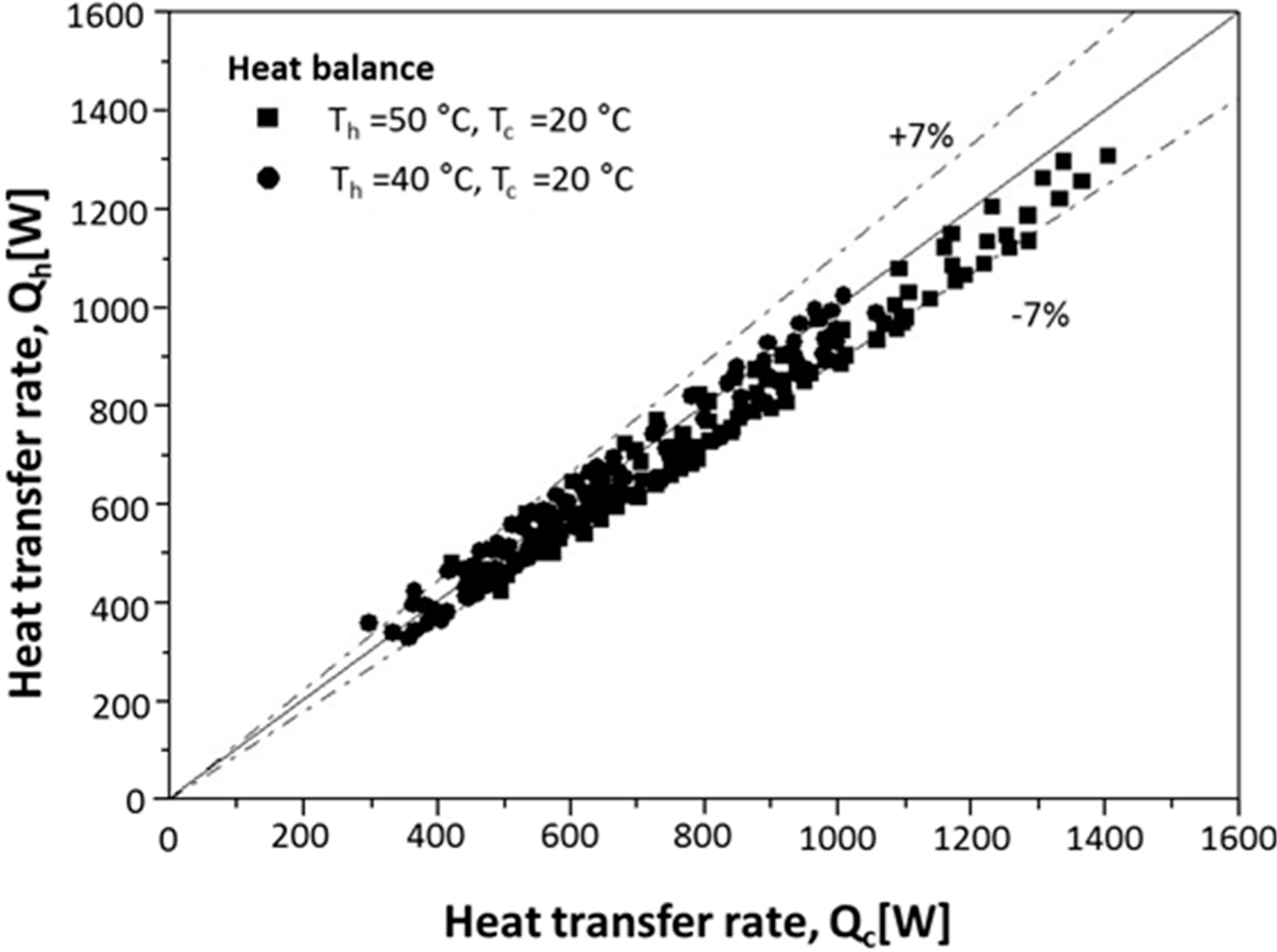
2.3. Experimental Conditions and Results Analysis
3. Experimental Results and Discussion
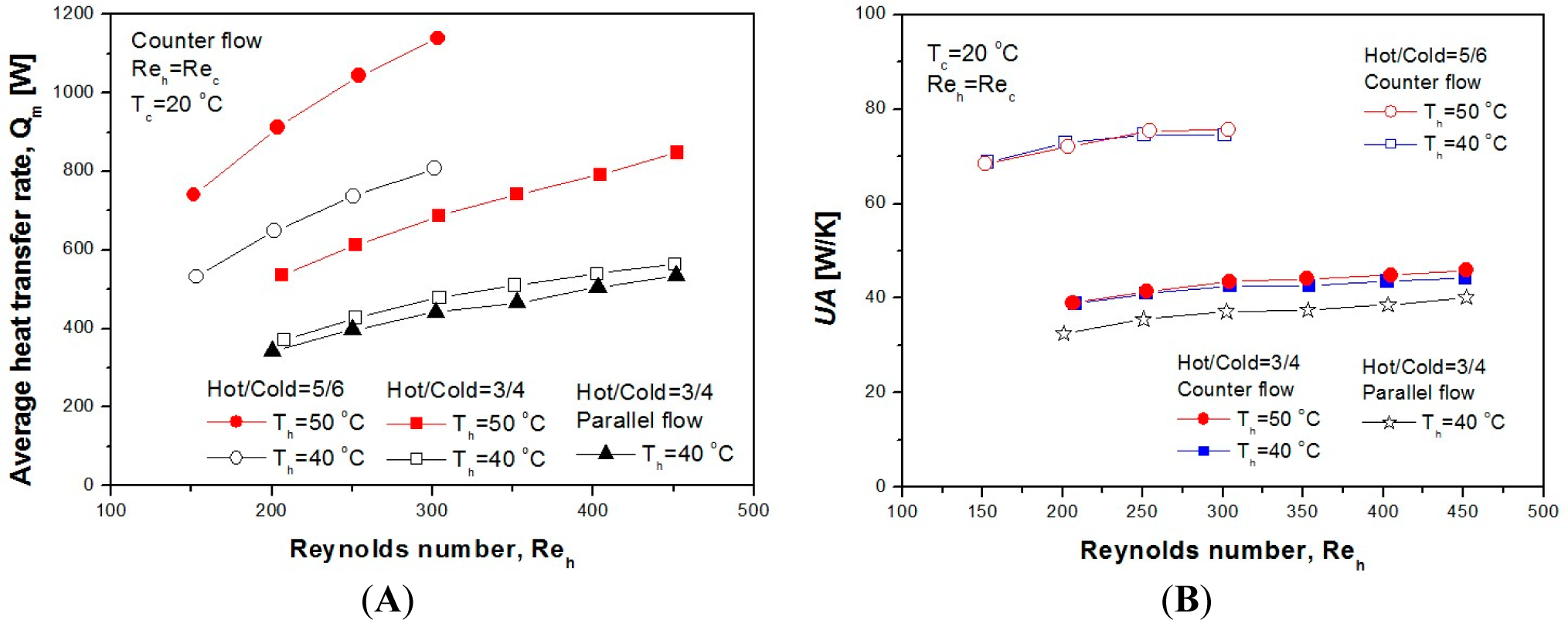
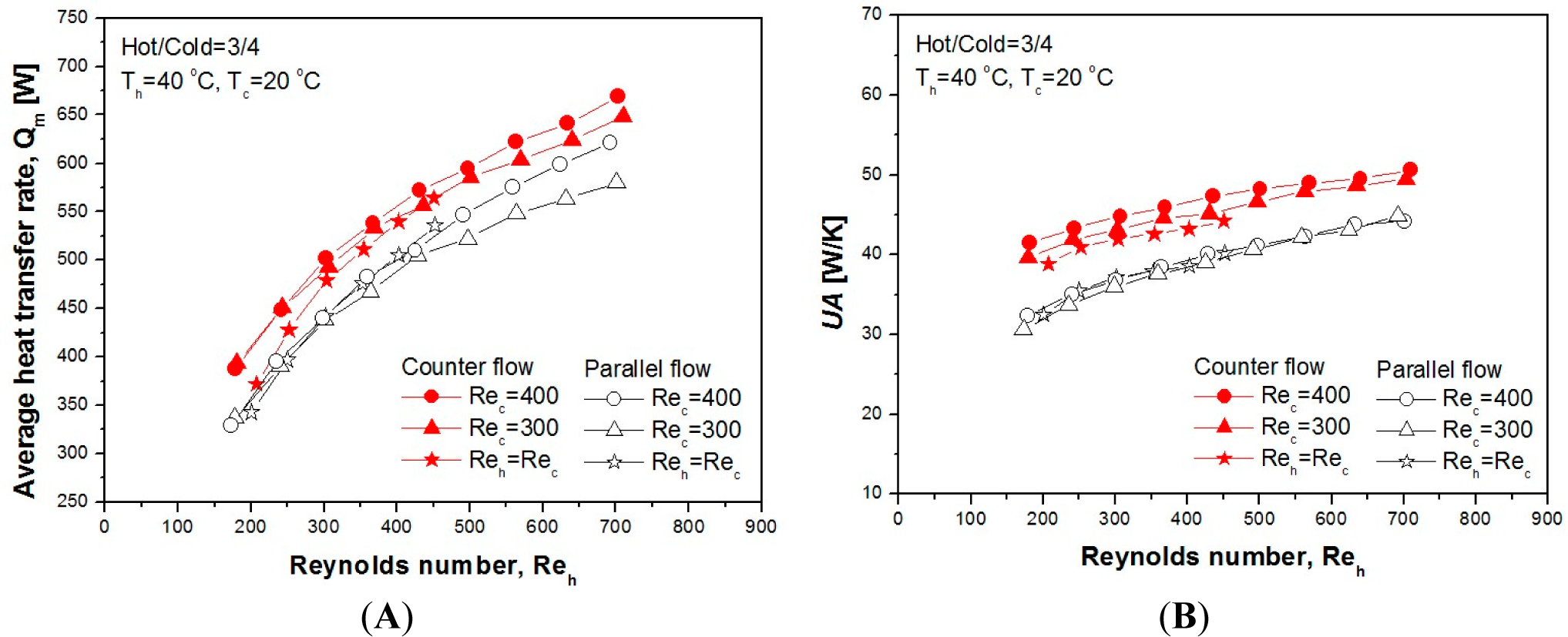
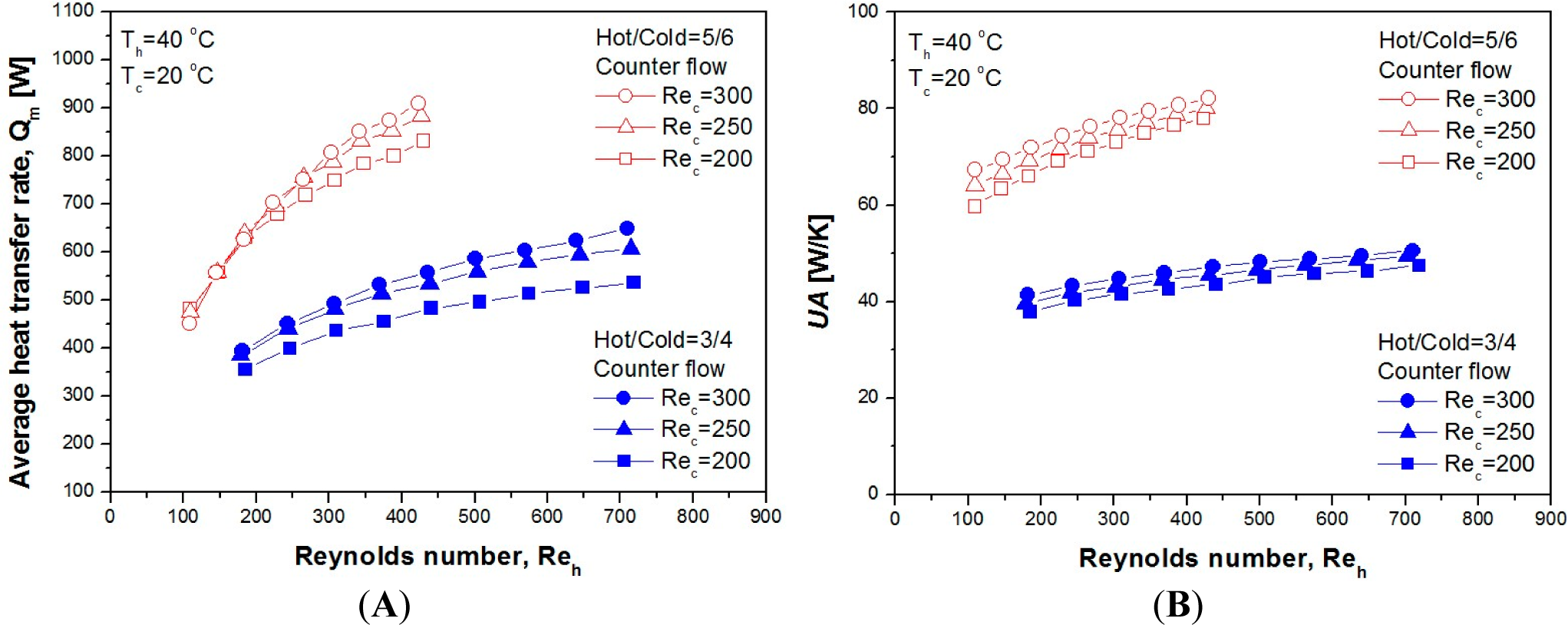
3.1. Heat Transfer Characteristics
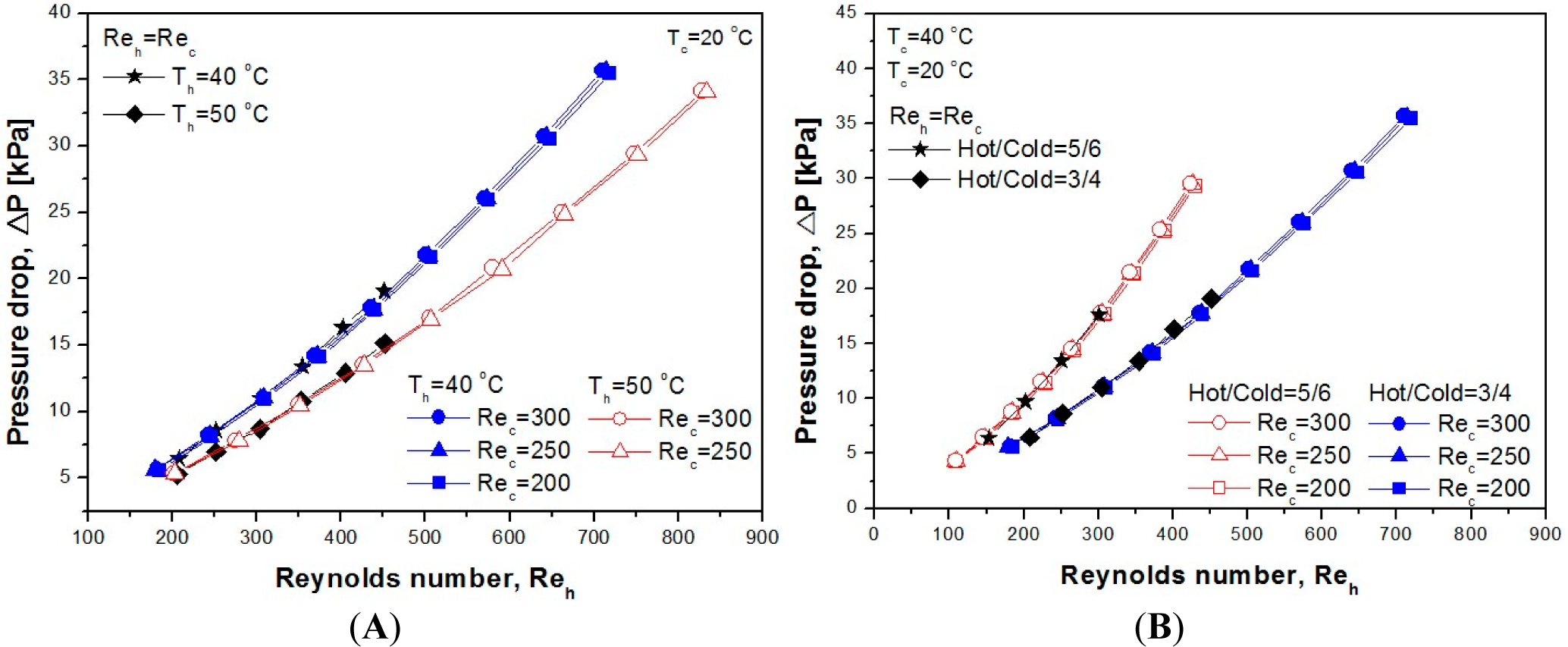
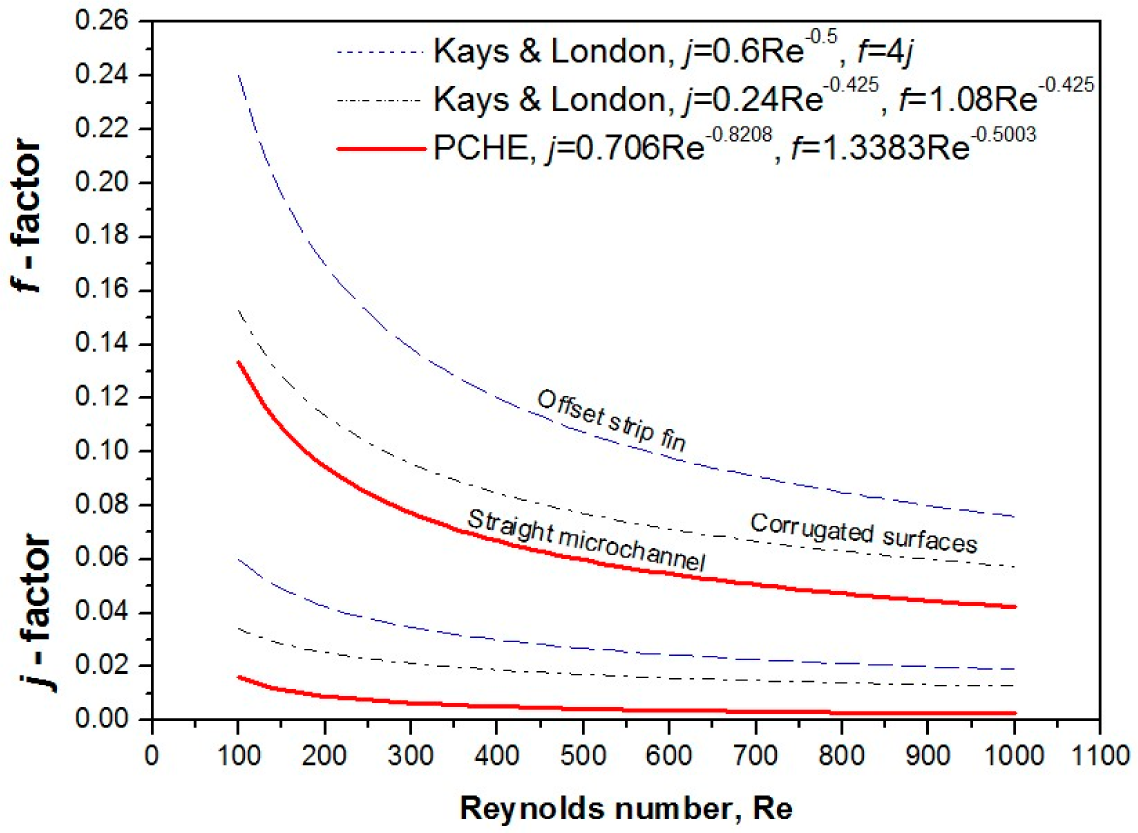
3.2. Pressure Drop Characteristics
4. Conclusions
- The average heat transfer rate of the counterflow PCHE is about 6.8, and the UA of the heat transfer performance is excellent to the extent of approximately 10%–15%.
- As the Reynolds number of the hot and cold sides increases and the inlet temperature increases, the average heat transfer rate also increases. This increase was the general performance characteristic of the heat exchanger according to the increase of the flow rate.
- As the Reynolds number of the hot and cold sides increases, the pressure drop increases. If the inlet temperature of the hot side is constant, the pressure drop according to the change of Reynolds number of the cold side shows equal results.
- The heat transfer performance is not affected by the change in the inlet temperature of the hot side, but if the inlet temperature is high at the time of the pressure drop, which shows a slight pressure drop.
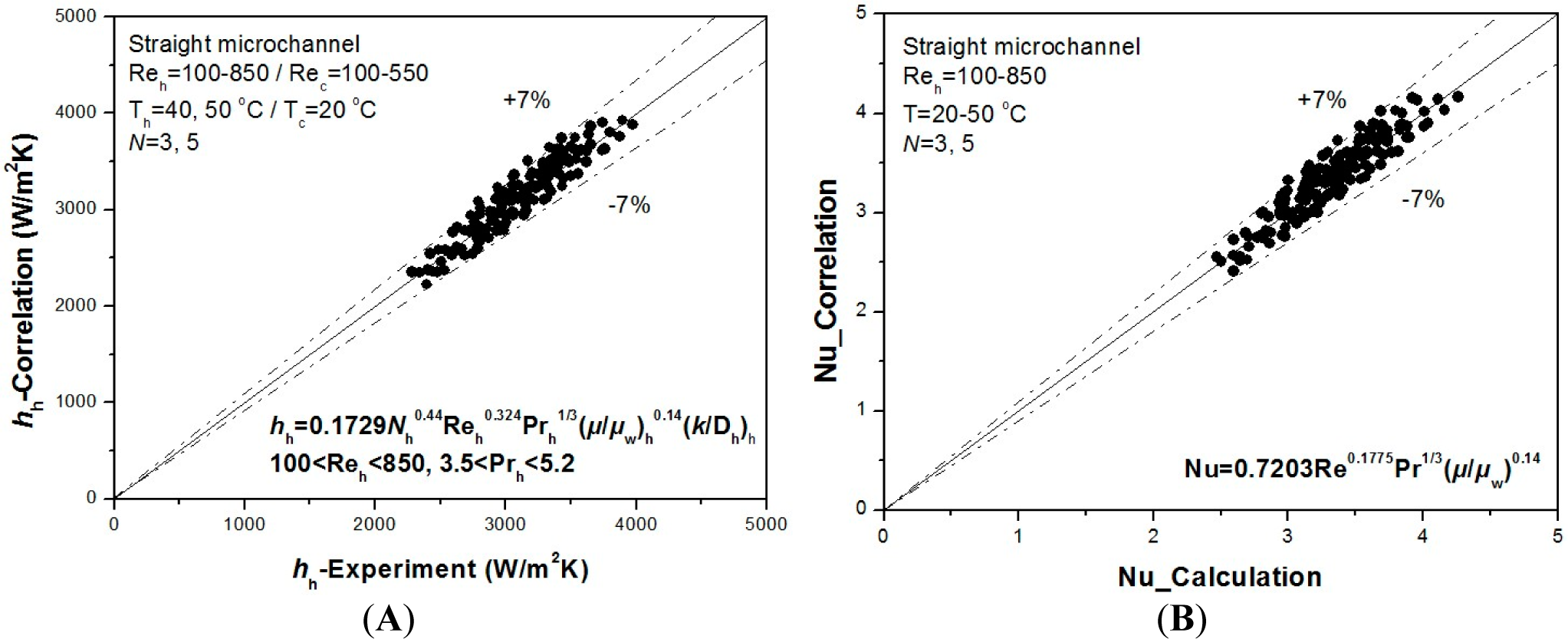
- The heat transfer coefficient correlations of the hot and cold sides using the modified Wilson plot method are proposed. The Reynolds number range of these correlations is 100–850.
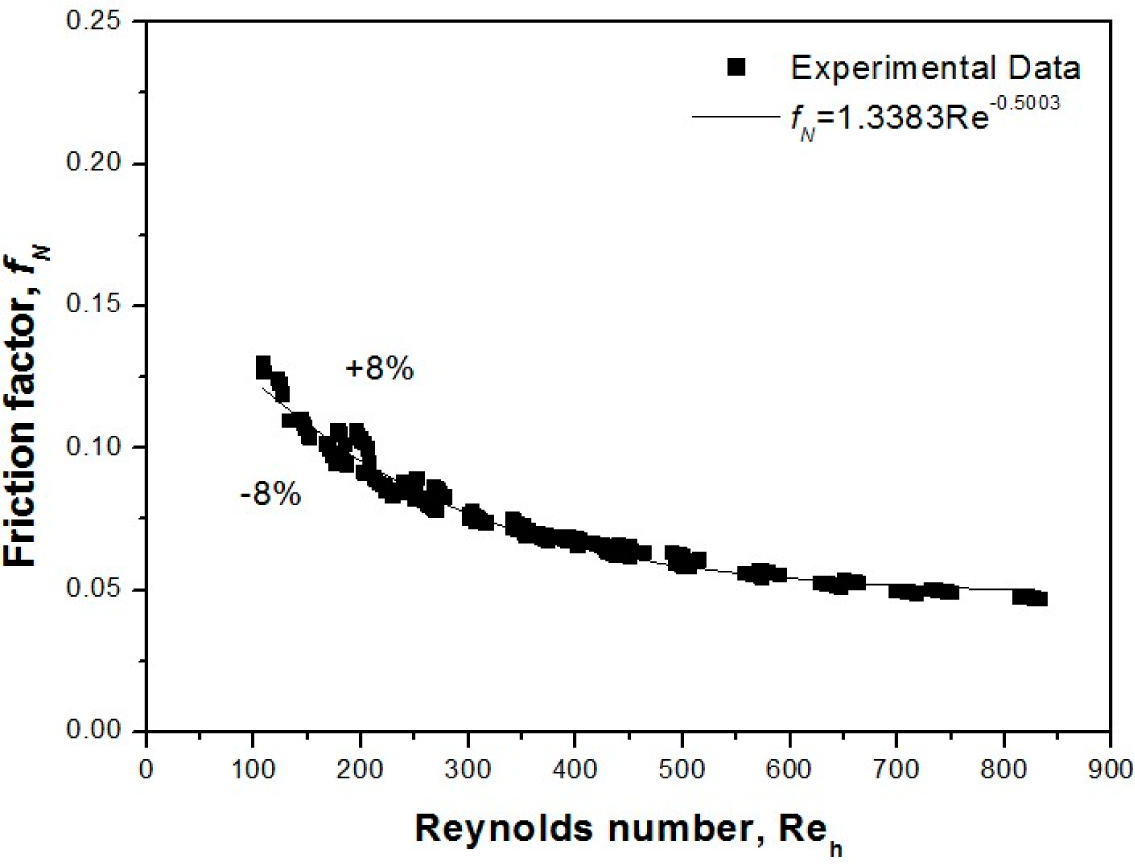
- The friction factor fN was calculated using the pressure drop results. The application scope is the same as above. It is expected that the experimental results obtained in this study will be usable as the basis for future performance experimental data.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Ac | Minimum free flow area (mm)2 |
| As | Total effective heat transfer area (mm)2 |
| B | Bias error |
| Cp | Specific heat (J/kg·K) |
| Dh | Hydraulic diameter (mm) |
| f | Friction factor |
| G | Core mass velocity (kg/m2·s) |
| Gp | Fluid mass velocity in the port (kg/m2·s) |
| H | Thickness of metal sheet (mm) |
| j | Colburn j-factor |
| L | Length of metal sheet (mm) |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Re | Reynolds number |
| UA | Heat transfer performance (W/K) |
| h | Heat transfer coefficient (W/m2·K) |
| k | Thermal conductivity (W/m·K) |
| N | Stacked number of metal sheet |
| ΔP | Pressure drop (kPa) |
| Q | Heat transfer rate (W) |
| ΔTLMTD | Log mean temperature difference (K) |
| W | Width of metal sheet (mm) |
| Greek Symbols | |
|---|---|
| ρ | Fluid density (kg/m3) |
| µ | Dynamic viscosity (N·s/m2) |
| Π | Uncertainty |
| Subscripts | |
|---|---|
| c | Cold |
| i | Inlet |
| o | Outlet |
| h | Hot |
| m | Mean |
References
- Kim, Y.H. Heat Transfer and Fluid Flow Characteristics on Printed Circuit Heat Exchangers with Microchannel Configurations. Ph.D. Thesis, Korea University, Seoul, Korea, 2009. [Google Scholar]
- Johnston, A.M.; Levy, W.; Rumbold, S.O. Application of PCHE technology within heterogeneous catalytic reactors. Proceedings of the American Institute of Chemical Engineers (AIChE) Annual Meeting, Reno, NV, USA, 4–9 November 2001.
- Gromoll, B. Micro cooling systems for high density packaging. Revue Générale de Thermique 1998, 37, 781–789. [Google Scholar]
- Kwon, O.K.; Choi, M.J.; Choi, Y.J. Heat transfer and pressure drop characteristics in zigzag channel angles of printed circuit heat exchangers. Korean J. Air-Cond. Refrig. Eng 2009, 21, 475–482. [Google Scholar]
- Nikitin, K.; Kato, Y.; Ngo, N. Printed circuit heat exchanger thermal-hydraulic performance in supercritical CO2 experimental loop. Int. J. Refrig 2006, 29, 807–814. [Google Scholar]
- Peng, X.F.; Peterson, G.P. Convective heat transfer and flow friction for water flow in microchannel structures. Int. J. Heat Mass Transf 1995, 39, 2599–2608. [Google Scholar]
- Lee, J.; Mudawar, I. Assessment of the effectiveness of nanofluids for single-phase and two-phase heat transfer in micro-channels. Int. J. Heat Mass Transf 2007, 50, 452–463. [Google Scholar]
- Qu, W.; Mudawar, I. Experimental and numerical study of pressure drop and heat transfer in a single-phase micro-channel heat sink. Int. J. Heat Mass Trans 2002, 45, 2549–2565. [Google Scholar]
- Shen, S.; Xu, J.L.; Zhou, J.J.; Chen, Y. Flow and heat transfer in microchannels with rough wall surface. Energy Convers. Manag 2006, 47, 1311–1325. [Google Scholar]
- Rachkovskij, D.A.; Kussul, E.M.; Talayev, S.A. Heat exchange in short microtubes and micro heat exchangers with low hydraulic losses. Micro. Technol 1998, 4, 151–158. [Google Scholar]
- Kang, S.W.; Tsen, S.C. Analysis of effectiveness and pressure drop in micro cross-flow heat exchanger. Appl. Therm. Eng 2007, 5–6, 877–885. [Google Scholar]
- Ngo, L.; Katoa, Y.; Nikitina, K.; Tsuzukia, N. New printed circuit heat exchanger with S-shaped fins for hot water supplier. Exp. Therm. Fluid Sci 2006, 30, 811–819. [Google Scholar]
- Tsuzuki, N.; Kato, Y.; Ishizuka, T. High performance printed circuit heat exchanger. Appl. Therm. Eng 2007, 30, 1702–1707. [Google Scholar]
- Ma, T.; Zeng, M.; Luo, T. Numerical study on thermo-hydraulic performance of an offset-bubble primary surface channels. Appl. Therm. Eng 2013, 61, 44–52. [Google Scholar]
- Ma, T.; Xin, F.; Li, L. Effect of fin-endwall fillet on thermal hydraulic performance of airfoil printed circuit heat exchanger. Appl. Therm. Eng 2015. [Google Scholar] [CrossRef]
- Ma, T.; Li, L.; Xu, X.; Chen, Y.; Wang, Q. Study on local thermal-hydraulic performance and optimization of zigzag-type printed circuit heat exchanger at high temperature. Energy Convers. Manag 2015. [Google Scholar] [CrossRef]
- Baek, S.W.; Lee, C.K.; Jeong, S.K. Effect of flow maldistribution and axial conduction on compact microchannel heat exchanger. Cryogenics 2014, 60, 49–61. [Google Scholar]
- Bartel, N.; Chen, M.; Utgikar, V.P. Comparative analysis of compact heat exchangers for application as the intermediate heat exchanger for advanced nuclear reactors. Ann. Nucl. Energy 2015, 81, 143–149. [Google Scholar]
- Figley, J.; Sun, X.; Mylavarapu, S.K. Numerical study on thermal hydraulic performance of a Printed Circuit Heat Exchanger. Prog. Nucl. Energy 2013, 68, 89–96. [Google Scholar]
- Kim, T.H.; Kwon, J.G.; Yoon, S.H. Numerical analysis of air-foil shaped fin performance in printed circuit heat exchanger in a supercritical carbon dioxide power cycle. Nucl. Eng. Des 2015, 288, 110–118. [Google Scholar]
- Koo, G.W.; Lee, S.M.; Kim, K.Y. Shape optimization of inlet part of a printed circuit heat exchanger using surrogate modeling. Appl. Therm. Eng 2014, 72, 90–96. [Google Scholar]
- Mylavarapu, S.K.; Sun, X.; Glosup, R.E. Thermal hydraulic performance testing of printed circuit heat exchangers in a high-temperature helium test facility. Appl. Therm. Eng 2014, 65, 605–614. [Google Scholar]
- Xu, X.; Ma, T.; Li, L. Optimization of fin arrangement and channel configuration in an airfoil fin PCHE for supercritical CO2 cycle. Appl. Therm. Eng 2014, 70, 867–875. [Google Scholar]
- Yoon, S.H.; NO, H.C.; Kang, G.B. Assessment of straight, zigzag, S-shape, and airfoil PCHEs for intermediate heat exchangers of HTGRs and SFRs. Nucl. Eng. Des 2014, 270, 334–343. [Google Scholar]
- Yoon, S.J.; Sabharwall, P.; Kim, E.S. Numerical study on crossflow printed circuit heat exchanger for advanced small modular reactors. Int. J. Heat Mass Transf 2014, 70, 250–263. [Google Scholar]
- Jeong, C.H.; Kim, H.R.; Ha, M.Y. Numerical investigation of thermal enhancement of plate fin type heat exchanger with creases and holes in construction machinery. Appl. Therm. Eng 2014, 62, 529–544. [Google Scholar]
- Kim, I.H.; Sun, X. CFD study and PCHE design for secondary heat exchangers with FLiNaK-Helium for SmAHTR. Int. J. Nucl. Eng. Des 2014, 270, 325–333. [Google Scholar]
- Kim, I.H.; NO, H.C. Thermal hydraulic performance analysis of a printed circuit heat exchanger using a helium-water test loop and numerical simulations. Appl. Therm. Eng 2011, 31, 4064–4073. [Google Scholar]
- Kim, I.H.; NO, H.C. Thermal-hydraulic physical models for a Printed Circuit Heat Exchanger covering He, He-CO2 mixture, and water fluids using experimental data and CFD. Exp. Therm. Fluid Sci 2013, 48, 213–221. [Google Scholar]
- Cowell, T.A. A general method for the comparison compact heat transfer surfaces. J. Heat Transf. ASME 1990, 112, 288–294. [Google Scholar]
- Shah, R.K. Assessment of modified Wilson plot techniques for obtaining heat exchanger design data. Heat Transf 1990, 5, 51–56. [Google Scholar]
- Kays, W.M.; London, A.L. Compact Heat Exchangers, 2nd ed; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- ANSI/ASME PTC 19.1, Measuring Uncertainty; The American Society of Mechanical Engineers: New York, NY, USA, 1998.
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertain of NIST Measurement Results; NIST Technical Note 1297; NIST: Gaithersburg, MD, USA, 1994. [Google Scholar]
- Wilson, E.E. A basis for rational design of heat transfer apparatus. J. Heat Transf. ASME 1915, 37, 47–82. [Google Scholar]
- Manglik, R.M.; Bergles, A.E. Heat Transfer Enhancement of Intube Flows in Process Heat Exchangers by Means of Twisted-tape Inserts; Report No. HTL-18; Heat Transfer Laboratory, Rensselaer Polytechnic Institute: Troy, NY, USA, 1991. [Google Scholar]
- Hesselgreaves, J.E. Compact Heat Exchangers; Pergamon: Edinburgh, UK, 2001. [Google Scholar]


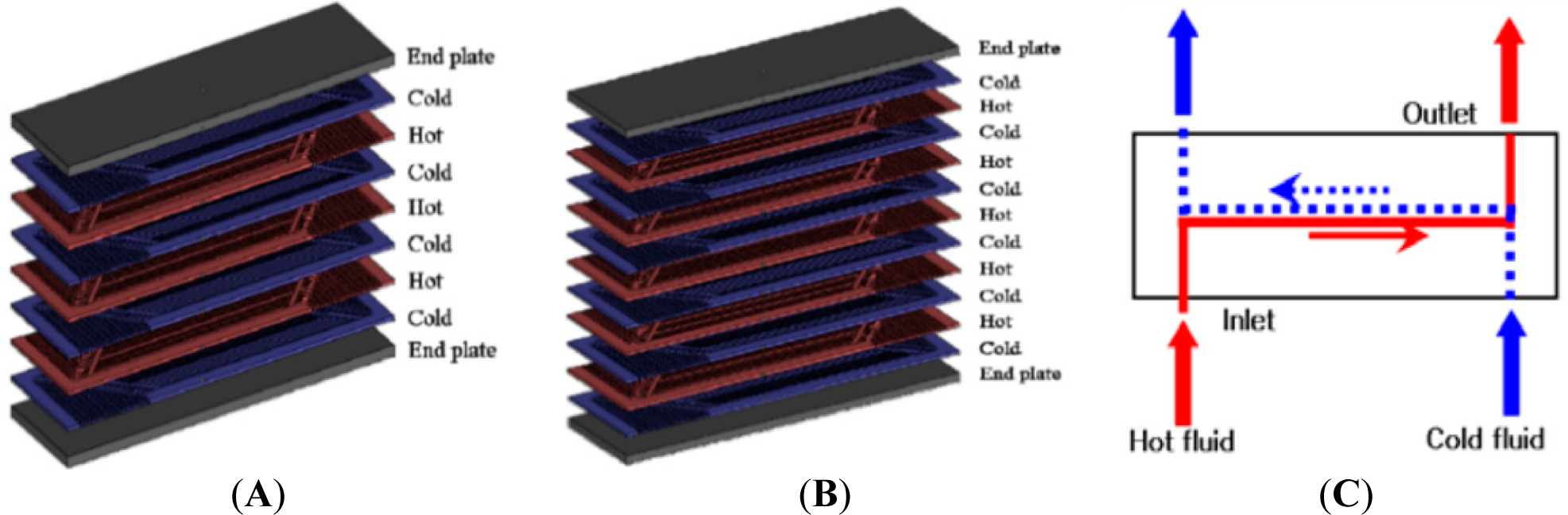




| Metal-plate material | SUS304L | |
|---|---|---|
| Dimensions of PCHE (W × L × H), mm | 141 × 40 × 16 | |
| Dimensions of plates (W × L × H), mm | 141 × 40 × 1 | |
| Dimensions of end plates (W × L × H), mm | 141 | |
| Number of plates | Hot side | 3, 5 |
| Cold side | 4, 6 | |
| Number of channels per plate | 22 | |
| Channel width | 800 μm | |
| Land (solid) width | 600 μm | |
| Channel height | 600 μm | |
| Parameters | Uncertainty (%) |
|---|---|
| Temperature, T | 0.6 |
| Pressure drop, ΔP | 0.92 |
| Flow rate of hot side, | 1.19 |
| Flow rate of cold side, | 0.94 |
| Averaged heat transfer rate, Qm | 1.19 |
| Reynolds number of hot side | 3.13 |
| Reynolds number of cold side | 3.29 |
| Heat transfer coefficient of hot side | 7.36 |
| Heat transfer coefficient of cold side | 7.31 |
| Friction factor, f | 5.8 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.-W.; Kim, Y.-H.; Kim, D.; Choi, Y.-D.; Lee, K.-J. Heat Transfer and Pressure Drop Characteristics in Straight Microchannel of Printed Circuit Heat Exchangers. Entropy 2015, 17, 3438-3457. https://doi.org/10.3390/e17053438
Seo J-W, Kim Y-H, Kim D, Choi Y-D, Lee K-J. Heat Transfer and Pressure Drop Characteristics in Straight Microchannel of Printed Circuit Heat Exchangers. Entropy. 2015; 17(5):3438-3457. https://doi.org/10.3390/e17053438
Chicago/Turabian StyleSeo, Jang-Won, Yoon-Ho Kim, Dongseon Kim, Young-Don Choi, and Kyu-Jung Lee. 2015. "Heat Transfer and Pressure Drop Characteristics in Straight Microchannel of Printed Circuit Heat Exchangers" Entropy 17, no. 5: 3438-3457. https://doi.org/10.3390/e17053438
APA StyleSeo, J.-W., Kim, Y.-H., Kim, D., Choi, Y.-D., & Lee, K.-J. (2015). Heat Transfer and Pressure Drop Characteristics in Straight Microchannel of Printed Circuit Heat Exchangers. Entropy, 17(5), 3438-3457. https://doi.org/10.3390/e17053438





