Exact Solutions of Non-Linear Lattice Equations by an Improved Exp-Function Method
Abstract
:1. Introduction
2. Generalized Exp-Function Method for Non-Linear Lattice Equations
3. Theorem and Improvement
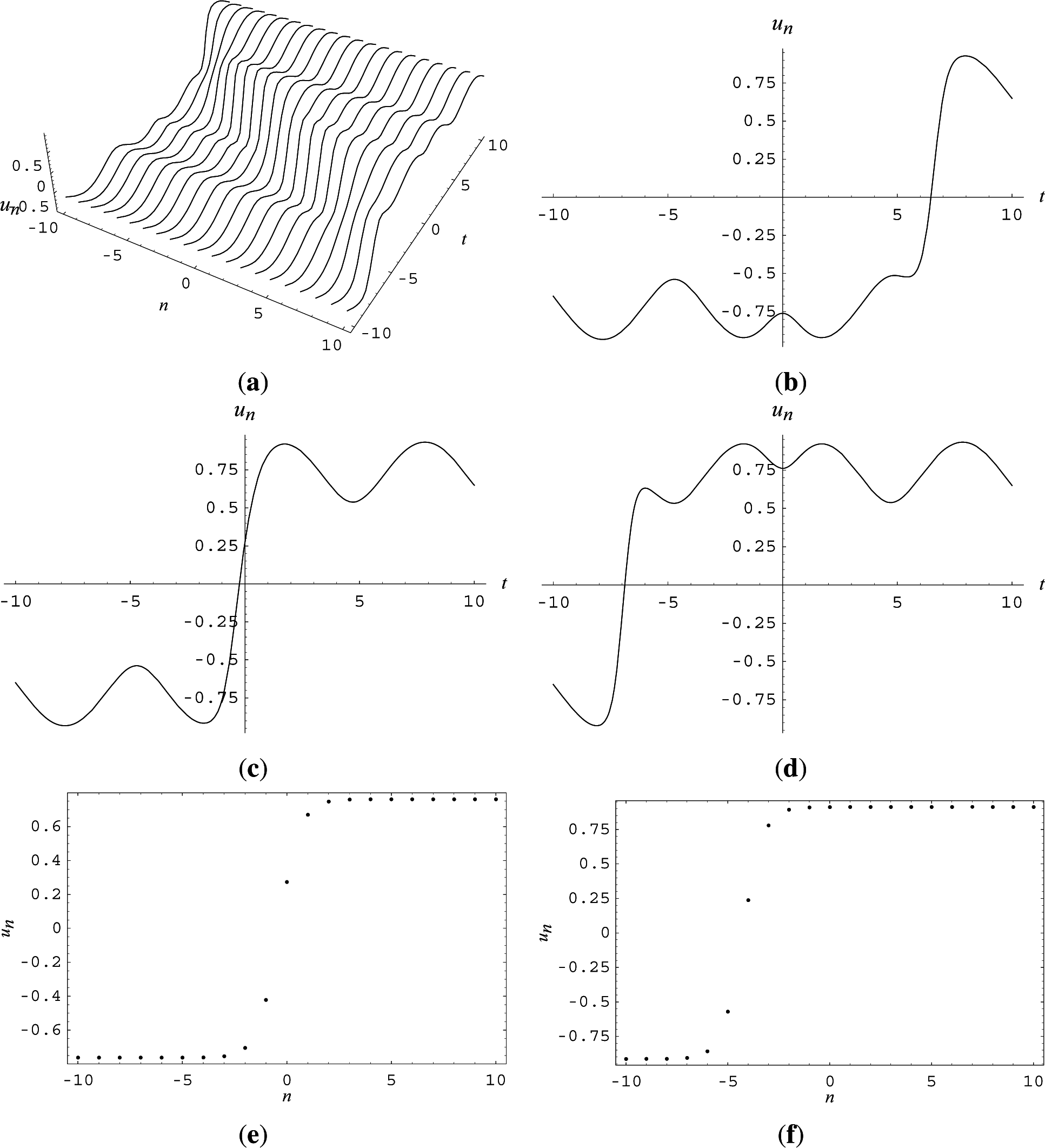
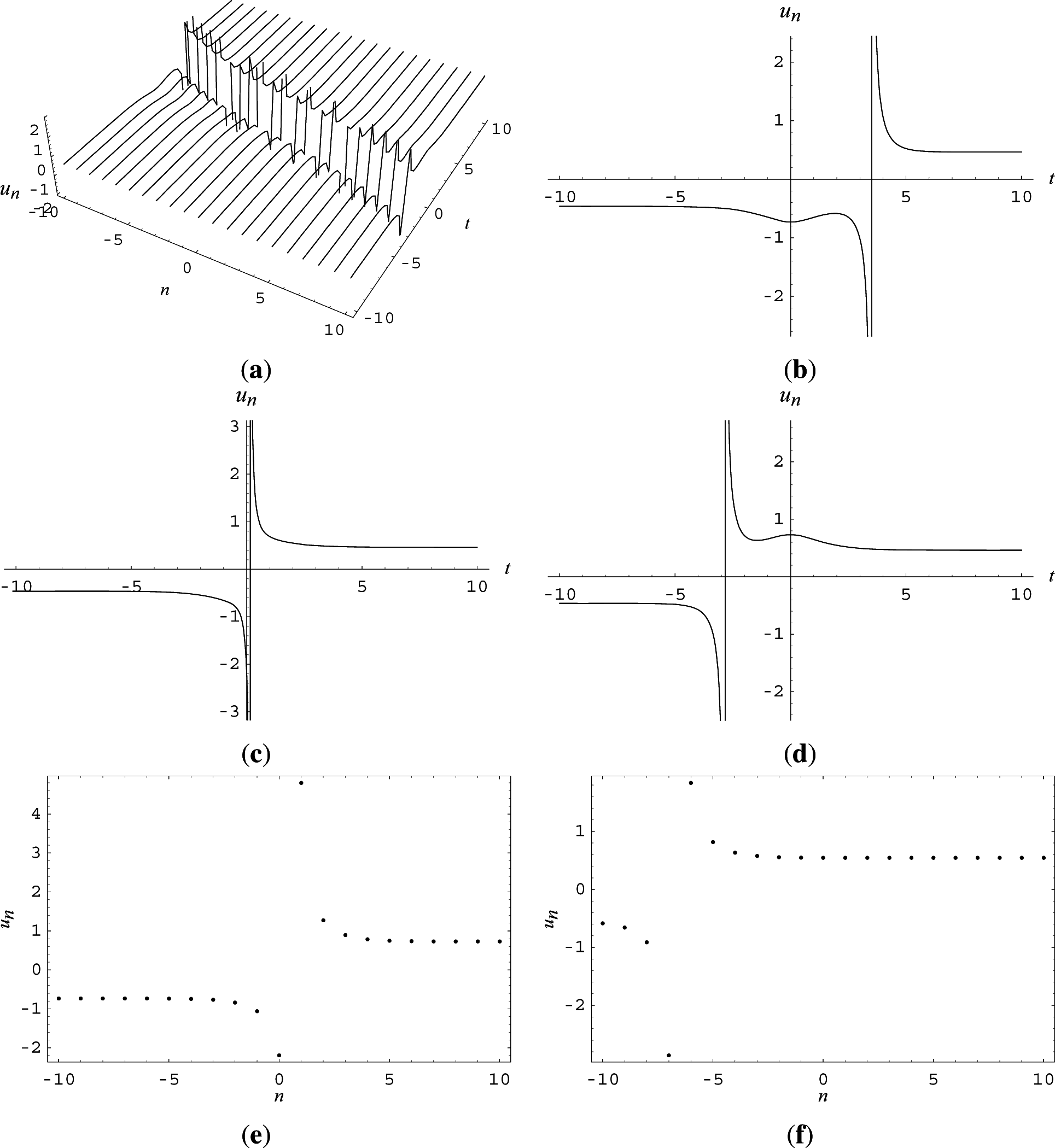
4. Application
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fermi, E.; Pasta, J.; Ulam, S. Collected Papers of Enrico Fermi II; University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Toda, M. Theory of Nonlinear Lattics, 2nd ed; Springer: Berlin, Germany, 1989. [Google Scholar]
- Garder, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 1965, 19, 1095–1097. [Google Scholar]
- Miurs, M.R. Bäcklund Transformation; Springer: Berlin, Germany, 1978. [Google Scholar]
- Hirota, R. Exact solution of the Korteweg–de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar]
- Wang, M.L. Exact solutions for a compound KdV-Burgers equation. Phys. Lett. A. 1996, 213, 279–287. [Google Scholar]
- Malfliet, M. Solitary wave solutions ofnonlinear wave equations. Am. J. Phys. 1992, 60, 650–654. [Google Scholar]
- Liu, S.K.; Fu, Z.T.; Liu, S.D.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar]
- Abdel-Salam, E.A-B.; Al-Muhiameed, Z.I.A. Exotic localized structures based on the symmetrical lucas function of the (2+1)-dimensional generalized Nizhnik–Novikov–Veselov system. Turk. J. Phys. 2011, 35, 241–256. [Google Scholar]
- Tabatabaei, K.; Celik, E.; Tabatabaei, R. The differential transform method for solving heat-like and wave-like equations with variable coeffcients. Turk. J. Phys. 2012, 36, 87–98. [Google Scholar]
- Fan, E.G. Travelling wave solutions in terms of special functions for nonlinear coupled evolution systems. Phys. Lett. A 2002, 300, 243–249. [Google Scholar]
- Fan, E.G. An algebraic method for finding a series of exact solutions to integrable and nonintegrable nonlinear evolution equations. J. Phys. A: Math. Gen. 2003, 36, 7009–7026. [Google Scholar]
- Dai, C.Q.; Wang, Y.Y.; Tian, Q.; Zhang, J.F. The management and containment of self-similar rogue waves in the inhomogeneous nonlinear Schrödinger equation. Ann. Phys. 2012, 327, 512–521. [Google Scholar]
- Dolapci, I.T.; Yildirim, A. Some exact solutions to the generalized Korteweg–de Vries equation and the system of shallow water wave equations. Nonlinear Anal. Model. Control. 2013, 18, 27–36. [Google Scholar]
- He, J.H. Asymptotic methods for solitary solutions and compactons. Abstr. Appl. Anal. 2012, 2012, 916793, 130pages. [Google Scholar]
- Dai, C.Q.; Wang, X.G.; Zhou, G.Q. Stable light-bullet solutions in the harmonic and parity-time-symmetric potentials. Phys. Rev. A 2014, 89, 013834. [Google Scholar]
- Dai, C.Q.; Zhu, H.P. Superposed Kuznetsov–Ma solitons in a two-dimensional graded-index grating waveguide. J. Opt. Soc. Am. B 2013, 30, 3291–3297. [Google Scholar]
- Liu, Y.; Gao, Y.T.; Sun, Z.Y.; Yu, X. Multi-soliton solutions of the forced variable-coefficient extended Korteweg–de Vries equation arisen in fluid dynamics of internal solitary vaves. Nonlinear Dyn. 2011, 66, 575–587. [Google Scholar]
- Zhang, S.; Cai, B. Multi-soliton solutions of a variable-coefficient KdV hierarchy. Nonlinear Dyn. 2014, 78, 1593–1600. [Google Scholar]
- He, J.H.; Wu, X. H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals. 2006, 30, 700–708. [Google Scholar]
- He, J.H.; Abdou, M.A. New periodic solutions for nonlinear evolution equations using Exp-function method. Chaos Solitons Fractals 2006, 34, 1421–1429. [Google Scholar]
- He, J.H.; Zhang, L.N. Generalized solitary solution and compacton-like solution of the Jaulent–Miodek equations using the Exp-function method. Phys. Lett. A 2008, 372, 1044–1047. [Google Scholar]
- Ebaid, A. Exact solitary wave solutions for some nonlinear evolution equations via Exp-function method. Phys. Lett. A 2007, 365, 213–219. [Google Scholar]
- Zhang, S. Exp-function method for solving Maccari’s system. Phys. Lett. A 2007, 371, 65–71. [Google Scholar]
- Zhang, S. Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365, 448–453. [Google Scholar]
- Zhang, S. Exp-function method for constructing explicit and exact solutions of a lattice equation. Appl. Math. Comput. 2008, 199, 242–249. [Google Scholar]
- Dai, C.Q.; Zhang, J.F. Application of He’s exp-function method to the stochastic mKdV equation. Int. J. Nonlinear Sci. Num. Simul. 2009, 10, 675–680. [Google Scholar]
- Marinakis, V. The exp-function method and n-soliton solutions. Z. Naturforsch. A 2008, 63, 653–656. [Google Scholar]
- Zhang, S. Application of Exp-function method to high-dimensional nonlinear evolution equation. Chaos Solitons Fractals 2008, 38, 270–276. [Google Scholar]
- Ebaid, A. Generalization of He’s exp-function method and new exact solutions for Burgers equation. Z. Naturforsch. A 2009, 64, 604–608. [Google Scholar]
- Ebaid, A. Exact solutions for the generalized Klein–Gordon equation via a transformation and Exp-function method and comparison with Adomian’s method. J. Comput. Appl. Math. 2009, 223, 278–290. [Google Scholar]
- Mohyud-Din, S.T.; Khan, Y.; Faraz, N.; Yildirim, A. Exp-function method for solitary and periodic solutions of Fitzhugh–Nagumo equation. Int. J. Numer. Methods H 2012, 22, 335–341. [Google Scholar]
- Bekir, A.; Aksoy, E. Exact solutions of extended shallow water wave equations by exp-function method. Int. J. Numer. Method. H 2013, 23, 305–319. [Google Scholar]
- Chai, Y.Z.; Jia, T.T.; Hao, H.Q.; Zhang, J.W. Exp-function method for a generalized mKdV equation. Discrete Dyn. Nat. Soc. 2014, 2014, 153974. [Google Scholar]
- He, J.H. Exp-function method for fractional differential equations. Int. J. Nonlinear Sci. Num. Simul. 2013, 14, 363–366. [Google Scholar]
- Yan, L.M. Generalized exp-function method for non-linear space-time fractional differential equations. Therm. Sci. 2014, 18, 1573–1576. [Google Scholar]
- Malik, S.A.; Qureshi, I.M.; Amir, M.; Malik, AN; Haq, I. Numerical solution to generalized Burgers’–Fisher equation using exp-function method hybridized with heuristic computation. PLoS ONE 2015, 10, 1–15. [Google Scholar]
- Kudryashov, N.A.; Loguinova, N.B. Be careful with the Exp-function method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1881–1890. [Google Scholar]
- Aslan, I.; Marinakis, V. Some remarks on exp-function method and its applications. Commun. Theor. Phys. 2011, 56, 397–403. [Google Scholar]
- Aslan, I. Some remarks on exp-function method and its applications-a supplement. Commun. Theor. Phys. 2013, 60, 521–525. [Google Scholar]
- Edaid, A. An improvement on the Exp-function method when balancing the highest order linear and nonlinear terms. J. Math. Anal. Appl. 2012, 392, 1–5. [Google Scholar]
- Zhang, S.; Zhou, Y.Y. Kink-type solutions of the mKdV lattice equation with an arbitrary function. Adv. Mater. Res. 2014, 989–994, 1716–1719. [Google Scholar]
- Zhang, S.; Zhang, H.Q. Discrete Jacobi elliptic function expansion method for nonlinear differential-difference equations. Phys. Scr. 2009, 80, 045002. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, J.; Zhou, Y. Exact Solutions of Non-Linear Lattice Equations by an Improved Exp-Function Method. Entropy 2015, 17, 3182-3193. https://doi.org/10.3390/e17053182
Zhang S, Li J, Zhou Y. Exact Solutions of Non-Linear Lattice Equations by an Improved Exp-Function Method. Entropy. 2015; 17(5):3182-3193. https://doi.org/10.3390/e17053182
Chicago/Turabian StyleZhang, Sheng, Jiahong Li, and Yingying Zhou. 2015. "Exact Solutions of Non-Linear Lattice Equations by an Improved Exp-Function Method" Entropy 17, no. 5: 3182-3193. https://doi.org/10.3390/e17053182
APA StyleZhang, S., Li, J., & Zhou, Y. (2015). Exact Solutions of Non-Linear Lattice Equations by an Improved Exp-Function Method. Entropy, 17(5), 3182-3193. https://doi.org/10.3390/e17053182




