Abstract
Spin dynamics on networks allows us to understand how a global consensus emerges out of individual opinions. Here, we are interested in the effect of heterogeneity in the initial geographic distribution of a competing opinion on the competitiveness of its own opinion. Accordingly, in this work, we studied the effect of spatial heterogeneity on the majority rule dynamics using a three-state spin model, in which one state is neutral. Monte Carlo simulations were performed on square lattices divided into square blocks (cells). Accordingly, one competing opinion was distributed uniformly among cells, whereas the spatial distribution of the rival opinion was varied from the uniform to heterogeneous, with the median-to-mean ratio in the range from 1 to 0. When the size of discussion group is odd, the uncommitted agents disappear completely after Ttr = 3.30 ± 0.05 update cycles, and then the system evolves in a two-state regime with complementary spatial distributions of two competing opinions. Even so, the initial heterogeneity in the spatial distribution of one of the competing opinions causes a decrease of this opinion competitiveness. That is, the opinion with initially heterogeneous spatial distribution has less probability to win, than the opinion with the initially uniform spatial distribution, even when the initial concentrations of both opinions are equal. We found that although the time to consensus TC >> Ttr, the opinion’s recession rate is determined during the first 3.3 update cycles. On the other hand, we found that the initial heterogeneity of the opinion spatial distribution assists the formation of quasi-stable regions, in which this opinion is dominant. The results of Monte Carlo simulations are discussed with regard to the electoral competition of political parties.
1. Introduction
Nowadays, it is recognized that many features of collective behavior of large social systems are almost independent of the attributes of individuals and details of social interactions [1]. This gives rise to the use of spin models for modeling opinion dynamics in complex social systems [1–5]. In general, a spin model consists of N spins located on the network nodes. Each node can adopt any of two or more admissible spin states defined in the model. The system evolution is governed by an updating rule and is strongly dependent on the network topology, connectivity, heterogeneity, etc. [6–10]. In this regard, the introduction of a neutral state can also have a considerable impact on the spin dynamics [11–15]. Furthermore, heterogeneities in the initial spatial distributions of non-zero spins also affect the system dynamics [16]. In the context of opinion dynamics, spin states can be associated with competing opinions and uncommitted attitudes.
A wide class of opinion dynamics models is based on the majority rule, according to which a chosen group of nodes (agents) adopt the state of the local majority. In the classic two-state Galam model [17], a variable number of groups of arbitrary size are formed simultaneously, and then, the majority rule is simultaneously applied to each group. Further, the majority rule model was modified such that only a single group of a fixed size G is updated at each time step [18–20]. If a sampling is random and G is odd, the two-state majority rule system tends to a consensus [18]. Because of the lack of detailed balance, majority rule models do not conserve the average magnetization. Consequently, the probability to reach a specific consensus in a majority rule model has a nontrivial initial state dependence [19,20]. The effect of spatial heterogeneity of rival opinions on the opinion dynamics has been studied in [16], using the dominant influence rule model with random noise. It was found that the spatial heterogeneity reduces the opinion’s competitiveness defined as the probability to win the competition. However, the use of a log-logistic distribution, random nose, and a new updating rule in the model studied in [16] introduces too many parameters that govern the opinion dynamics.
In this paper, we address the effect of heterogeneity in the initial geographic distribution of competing opinion on its own competitiveness in the classic majority rule system. The rest of the paper is structured as follows: in Section 2 we introduce the model to study the effect of spatial heterogeneity and provide the details of the Monte Carlo simulations. Section 3 is devoted to the results of numerical simulations and their discussion in the context of electoral competition. The main conclusions are outlined in Section 4.
2. Model and Details of Numerical Simulations
In order to model interactions among social agents, it is necessary to define the environment in which these interactions take place. In this regard, the paradigm of spatial social network equipped with a metric allows us to understand how relationships among agents (individuals, groups, or communities) affect the attributes and behaviors of themselves and other agents [21]. Many social networks are embedded in geographical space with nodes tied to geographic places and links representing connections between the places. However, generally, network links are not necessarily embedded in space. Examples include electoral networks in which each voter is linked to a specific polling station, but it can also interact with voters linked to other polling stations. Although the majority of voters have relatively small degrees, a small number of agents may have large degrees. Furthermore, there are groups of voters which are highly connected within themselves but loosely connected to other groups. Consequently, the structure of electoral network is very complex. Nonetheless, some features of electoral dynamics can be simulated on networks with relatively simple structures or even square lattices [11–20]. This enables us to study how the factors, which have been chosen as the important ones for a phenomenon under study, influence the outcome, while avoiding the possible effects of other attributes.
2.1. Spatial Distributions of Competing Opinions
Geographic distribution of competing opinions can be visualized, for example, in the distribution of party members, or in the records of electoral voting. In order to study the effect of geographic heterogeneity on the opinion competitiveness, one needs to quantify the heterogeneities of spatial distributions. For this purpose, the spatial network can be divided into blocks (cells) allowing to construct the spatial (geographic) distributions of rival opinions. In the case of voter networks, these cells can be associated either with pooling stations, or with electoral districts. In this regard, it is pertinent to note that in the two-state spin models, the spatial distributions of opposite spins are strongly coupled and so the spatial heterogeneity of negative spin distribution is intimately related to the spatial heterogeneity of the positive spin distribution. In a three-state model, non-zero spins can be distributed among cells by random sampling without replacement, such that there is no correlation between spatial distributions of opposite spins, if the third (neutral) state is prevalent.
So, let us consider a voter network with N nodes divided into K cell of different sizes nj, where j specifies the spatial (geographic) position of the cell (j = 1, 2, …, K). Per definition
. Let us assign the spin s = 1 to N1 nodes and spin s = −1 to N−1 nodes, whereas the rest N0 = (N − N1 − N−1) nodes remain in the neutral state with spin s = 0. A natural measure of heterogeneity in the spatial spin distribution is the entropy of the distribution defined as:
where the normalized occupation probability is equal to:
while Nsj is the number of spins s in the cell j with nj nodes, psj = Nsj/nj is the “concentration” of spin s in the cell j, and ps = Ns / N is the overall concentration of spin s on the whole network. Notice that, per definition, p1 + p−1 + p0 =1. In the case of random uniform distribution
and so Ss = ln K, whereas inhomogeneous spatial distributions are characterized by Ss < ln K.
It should be pointed out that the entropy of distribution is not the only possible measure of heterogeneity in the spatial distribution of spin. One can also use appropriate functions of different moments of the probability density function, or, in some cases, the ratio of the mean to median of the spatial distribution [16]. The last is the measure of the degree of spatial concentration of the spin distribution among cells.
2.2. Details of Monte Carlo Simulations
In order to diminish the number of model parameters, in this work we used the square lattices of size N divided on K square cells of the same size n = N / K. Specifically, we used square lattices with N = 1600, 2500, 3600, and 4900 nodes divided into K = N/100 square cells (districts) with 100 nodes each (see Figure 1) and periodic boundary conditions.

Figure 1.
Spatial distributions of positive (black), negative (white), and zero (gray) spins on lattice of size 50× 50 : (a) Initial spatial distributions with M1 = M−1 = 10 and (b) the corresponding distribution of spins at the transition from the three- to two-state regime of majority rule dynamics. (c) Initial spatial distributions with M−1 = 5 < M1 =10 and (d) the corresponding distribution of spins at the transition from the three- to two-state regime of the majority rule dynamics.
Each node of lattice i ∈ [1, N] can be in one of the three admissible states with si = 1, −1, or 0. In the voter network, the adepts of rival opinions (parties) can be associated with non-zero spins (s =1 or −1), whereas the nodes with spin s = 0 can be associated with uncommitted voters. In order to avoid correlations between initial spatial distributions of the opposite spins, in all simulations performed in this work, the positive spins were initially assigned to 10 randomly chosen nodes in each of N cells, such that p1j (t = 0) = p1(t = 0) = 0.1 and
. Afterward, the negative spin was assigned to M−1 randomly chosen nodes (0 ≤ M−1 ≤10) in each of k randomly selected districts, whereas N/10 − kM−1 negative spins were uniformly distributed among the rest K − k districts. Accordingly, the rest 0.8N nodes are initially in the state with s = 0 (see Figure 1a,c).
Specifically, we used k = 0.5⌈K⌉, where ⌈K⌉ denotes the smallest integer not less than K. Therefore, it is a straightforward matter to deduce that
, whereas the occupation probabilities (2) of negative spins are equal to:
where H−1 = M−1 / m−1 is the ratio of the distribution’s median (M−1) to its mean (m−1). Therefore, S1 = ln K, whereas the entropy (1) of the negative spin distribution (3) is an univalued function of the heterogeneity index H−1, as it is shown in Figure 2.
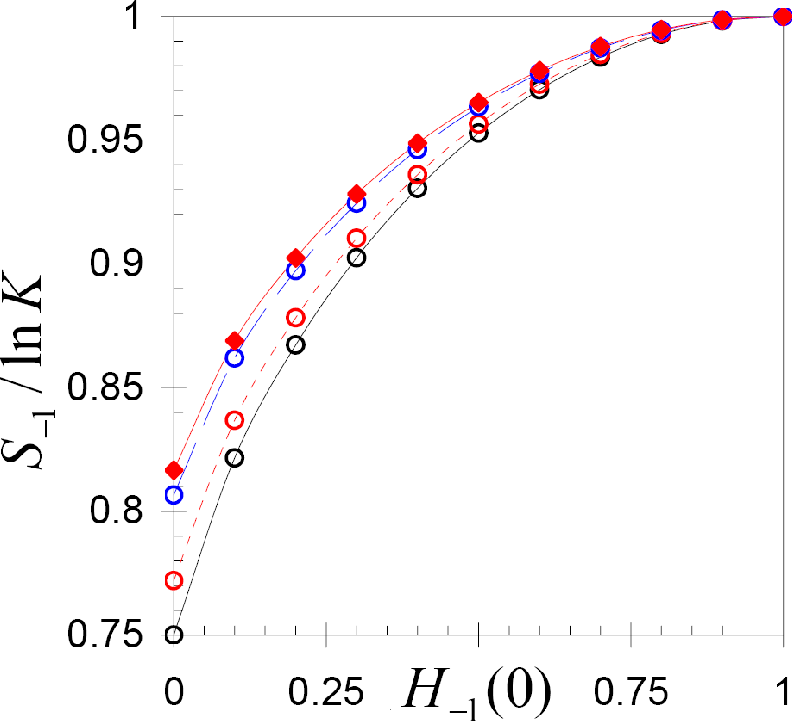
Figure 2.
The normalized entropy S−1 / ln K of the initial spatial distribution of negative spins on square lattices of different size, versus the heterogeneity index H−1. From the bottom to top: N = 1600, 2500, 3600, and 4900.
Once the initial spin states of all nodes are defined, the system evolves according to the local majority rule as follows. In each update step (t =1,2,3,…), all nodes of a randomly chosen group of size G either adopt the state with spin:
or conserve their state, if s(t) = 0. Simulations of the two-state majority rule model on square lattices performed in [20] suggest that the size of the discussion group does not have qualitative effects on the spin dynamics. Hence, in this work, the discussion group of size G = 5 was defied as the von Neumann neighborhoods which can be located in the same or different cells. Thus, in each step a node with its neighborhoods was selected by random sampling with replacement, without any reference to cells. Consequently, not all nodes are necessary updated during the cycle of N updates. In this work, at least 106 simulations were performed with each initial spin distribution on lattice of size N = 2500. Additionally, the Monte Carlo simulations were performed for some initial spin distributions on lattices of other sizes.
It is a straightforward matter to understand, that neutral states will disappear necessarily, after a sufficient number of updates; and subsequently, the system will involve in a two-state majority rule regime. Hence, the consensus will be necessarily reached. Accordingly, the quantities that we focus on are: (1) the number of updating steps until, getting to the last state with the spin zero has been disappeared (ttr); (2) the system magnetization Δp(t) = p1 − p−1 ; (3) the entropy (1) at the transition from the three- to two-state regime; (4) the time to consensus (TC = tC / N); and (5) the consensus probabilities P1 and P−1 =1− P1.
3. Results and Discussion
The main aim of this study is to reveal how the initial heterogeneity of the spatial distribution of competing opinion affects the opinion’s own competitiveness. Therefore, the key question to be answered by Monte Carlo simulations is: How does the initial heterogeneity in the spatial distribution of the opposite spins (rival opinions) affect the majority rule dynamics when the size of the discussion group is odd? Accordingly, the three issues that we address in this work are:
- What happens with the three-state regime during the majority rule system evolution? How does the number of update steps needed to disappear all the neutral state (ttr) depend on the lattice size and the initial distributions of opposite spins? Does the system have a non-zero magnetization at the transition from the three- to two-state regime? If yes, how does the magnetization depend on the initial heterogeneity in the spatial distributions of the opposite spins? How are the opposite spins distributed among cells once the last neutral state has disappeared?
- How does the heterogeneous system to consensus in the two-state regime? How does the heterogeneity in the initial spatial distributions affect the time to consensus TC in the different scenarios of evolution?
- How does the heterogeneity in the initial spatial distribution of one of two rival opinions affect its own probability to win the competition?
First of all, we found that the time to transition from the three to two -state regime increases linearly, with respect to the number of nodes N and it is independent of the initial spatial distributions of non-zero spins. This means that our majority rule model evolves in the three-state regime during only the first Ttr = ttr / N = 3.30 ± 0.05 cycles of N updates, independently of the lattice size and heterogeneity in the initial spatial distributions of the rival opinions. Furthermore, we found that the magnetization at the transition from the three- to two-state regime Δptr = p1(ttr) − p−1(ttr) increases as the heterogeneity of the negative spin distribution increases, even when the initial magnetization of the system was zero (Δp0 = p1(0) − p−1(0) = 0). Specifically, we found that the data of numerical simulations are best fitted by the following relationship:
where ΔH0 = H1(0) − H−1(0), while a = 0.17 and β = 1.47 ± 0.07 are the fitting constants (see Figure 3a). Likewise, we found that the heterogeneities of spin distributions at the transition from the three-state to the two-state regime are characterized by entropies S1(ttr) ≥ S−1(ttr) and heterogeneity indexes H1(ttr) ≥ H−1(ttr), where the equalities are achieved only if H−1(0) =1 (see Figure 3b). It is pertinent to point out that these results were reproduced on lattices of different sizes.
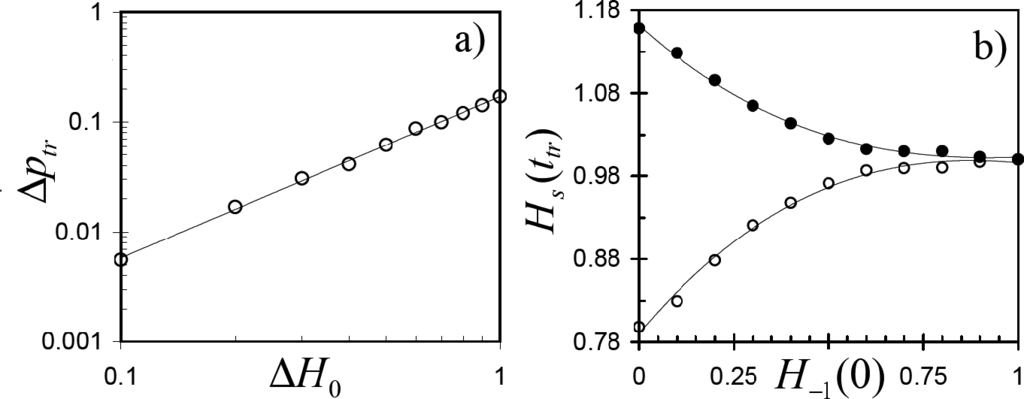
Figure 3.
(a) System magnetization at the transition from the three- to two-state regime Δptr versus ΔH0; straight line—data fitting with Equation (5). (b) Heterogeneity indexes of spin distribution at the transition from the three- to two-state regime versus the heterogeneity index at t = 0 for positive (full circles) and negative (circles) spins: data are averaged over 106 realizations on lattice of size N = 2500; curves—data fittings to eye guide.
Therefore, although the evolution of our three-state system in the two-state is governed by the same updating rule as in the classic two-state majority rule model studied in [18–20], the spatial distributions of the competing states after ttr = (3.30 ± 0.05)N updates in the three-state regime (see Figure 1d) differ from the spin distributions after 3.3N updates in the classic two-state majority rule model. The last is similar to the spin distributions after t0 updates in the three-state system with H−1(0) = H1(0) =1 (see Figure 1b).
After all the neutral states have disappeared, there are two different scenarios of three-state system evolution in the two-state majority rule regime, similar to those observed in [18–20] for the two-state majority rule model. Specifically, in most realizations, one opinion quickly becomes dominant and eventually wins after TC = tC / N cycles of updates. In the remaining realizations, the system reaches a long-living non-consensus configuration associated with segregation of alternative states (opinions), into two or more nearly straight stripes (see Figure 5 in [20]). These stripes are ultimately unstable and so consensus is always reached, albeit very slowly. The authors of [20] have suggested two ways of automatic detection of stripe configurations. One is based on the analysis of correlation functions for two spins that are located a distance
apart (stripe state arises if the correlation function in the direction(s) parallel to the stripe is greater than a threshold value about 0.5). Alternatively, all realizations with tC > tS were counted as reaching a coherent state [20]. Specifically, in simulations on lattices of size N = 2500 with G = 3 it was found that tS = 600 [20]. Both methods lead to essentially the same results. In this work, we confirm this result in the case of G = 3 and found that in the case of discussion group size G = 5; all realizations with tCS > 210 updates are characterized by the stripe configurations. In this way, we found that in the case of uniform initial distributions of both positive and negative spins (that is H−1(0) = H1(0) =1) non-consensus long-living configurations (stripes) are formed with probability PS = 30% ± 3%, as this is in the case of the two-state majority rule model [20], as well as in the zero-temperature evolution of the Ising model with Glauber kinetics [22,23]. We also found that the characteristic time to consensus in systems with long-living stripes scales with the system size as:
in agreement with the scaling reported in [20] for the two-state majority rule model.
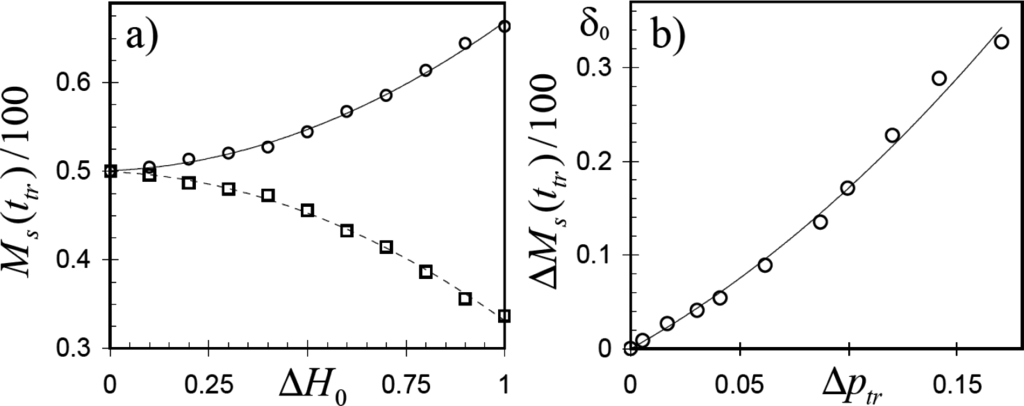
Figure 5.
(a) Normalized medians Ms (t0)/100 of spin distributions versus ΔH0 (circles and squares correspond to positive and negative spin distributions, respectively). (b) Normalized difference ΔMs (ttr)/100 versus Δptr. Data are averaged over 106 realizations on lattices of different sizes; curve in panel (b)—data fitting with Equation (9).
At the same time, we noted that when the initial spin states in the two-state majority rule model are randomly distributed with equal densities, then the probability to reach a coherent non-consensus state is approximately PS = 33% and quickly decreases as the difference between initial spin densities Δp(0) increases (see Figures 8 and 9 from [20]). Controversially, in our simulations we found that the probability to form a non-consensus coherent state increases with the increase of ΔH0 (see Figure 4a) as:
notwithstanding that Δptr is also the increasing function of ΔH0 (see Figure 3a). Accordingly, although the increase of PS with increase of Δptr is rater small, the tendency PS = 0.4 − 0.023ln(Δptr) clearly differs from the quick decrease of PS as the initial magnetization Δp0 increases in the two-state majority rule model (see Figure 4a). This unexpected reverse behavior of PS can be associated with the characteristic spatial heterogeneity of the opposite spin distributions at the starting of the two-state regime in the three-state majority rule model (see Figure 3a). This means that the effect of heterogeneity in the spin spatial distributions at the transition point exceeds the effect of magnetization at this point.
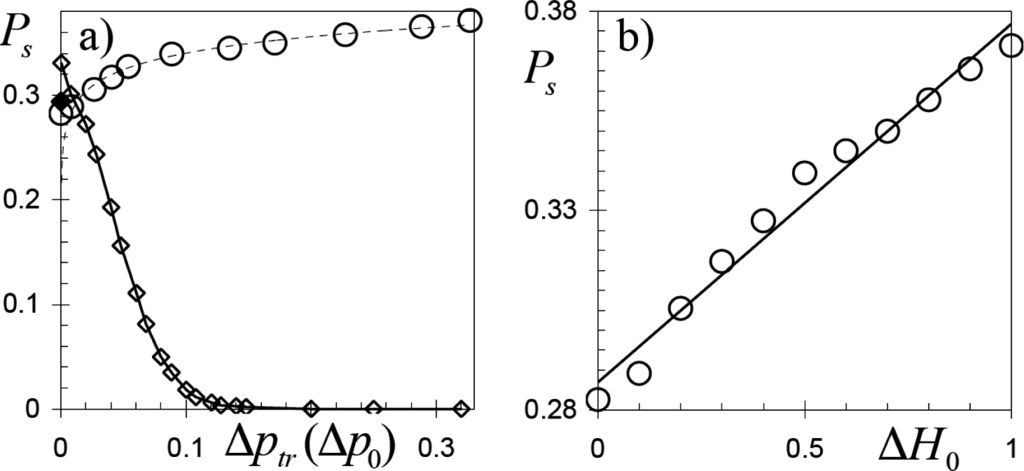
Figure 4.
Probability of non-consensus coherent configurations (stripes) PS versus: (a) Δptr (three-state model) and Δp0 (two-state model). Circles and full rhomb—data of Monte Carlo simulations in this work on the lattice of size N = 2500; rhombi—data from Figure 9 of [20] obtained by simulations of the two-state majority rule model on lattice of size N = 2500 and (b) ΔH0.
For realizations without long-living coherent configurations, we found that a consensus is reached after:
cycles of updates, where the scaling exponent α =1.24 ± 0.06 is independent of ΔH0 and consistent with the value α = 1.24 found in the numerical simulations of the two-state majority rule model on square lattices with G = 3 [20]. Furthermore, we found that the mean time to consensus is an almost independent of ΔH0, despite the observation that Δptr increases with increase of ΔH0 (see Figure 3a). This suggests, that the effect of magnetization Δptr > 0 is compensated by the effect of heterogeneity in spatial distributions of spins at ttr, which is characterized by S1(ttr) ≥ S−1(ttr). In this regard, we found that the medians of spin distributions at the transition from the three- to two-state regime Ms(ttr) are monotonic functions of ΔH0 (see Figure 5a), such that their difference ΔMtr = M1(ttr) − M−1(ttr) can be well fitted by following empirical equation:
where b1 = 1.8 and b2 = 15 are fitting constants (see Figure 5b). At the same time, we found that the probabilities to reach the consensus in positive (P1) or negative (P−1) spin state, both are linear functions of ΔH0, such that:
where the fitting constant is found to be g = 0.81± 0.04 (see Figure 6a). Notice that from Equations (5) and (10) it follows that:
where c = g / a1/β (see Figure 6b). So, the decrease of opinion competitiveness due to the heterogeneity in the initial spatial distribution is yet determined by the system evolution in the three-state regime during the first 3.3 update cycles.
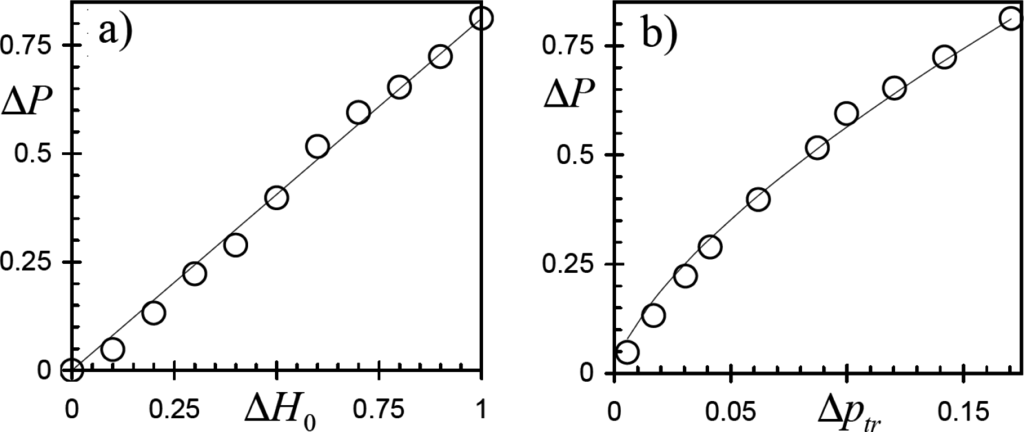
Figure 6.
The difference of exit probabilities ΔP versus: (a) ΔH0 and (b) Δp0 for the tree-state MR dynamics without long-living non-consensus configurations. Circles - data of numerical simulations averaged over 105 realizations; curves—data fittings with Equations (10) and (11) in panels (a) and (b), respectively.
Elections provide a precise global measurement of the state of the electorate’s opinions and so constitute an ideal playground for application of the statistical physics tools to model the opinion dynamics. In this background, the decrease of p−1(to) and probability to win (P−1) as the heterogeneity in the initial spatial distribution of party adepts increases explains the well known fact that the “electoral strength” of political party depends not only on the number of party members, but also on their distribution among the electoral districts (see [24]). Specifically, a spatial concentration of party members unfavorable affects its global electoral performance. This is consistent with empirical observations [25].
On the other hand, although the concentration of party members in a few districts leads to decrease the possibility to win (see Figure 6a), it aids the formation of stable regions in which the party is dominant (see Figure 4a), as this is actually observed in Mexico (see [25]). An interesting issue on the minority survival was discussed in [26]. Specifically, the authors of [26] have pointed out that a minority cluster tends to have biased estimates of the relative popularity of opinions in the society as a whole.
4. Conclusions
Summarizing, heterogeneity in the initial geographic distribution of a competing opinion leads to decrease of its own competitiveness. This illustrates the empiric observation that the electoral strength of party tends to increase as the spatial distribution of party adepts becomes more homogeneous. One of the striking findings of this study is that the competitiveness decrease rate is determined during the first 3.3 update cycles of system evolution in the three-state regime, whereas the total time to consensus TC >> Ttr is independent of the initial geographic distributions of rival opinions.
On the other hand, the concentration of party adepts in a few districts assists the formation of stable regions of this party dominance, even when the cells of the adept’s concentration were not initially connected. Moreover, we found that the effect of heterogeneity in spatial distributions of spins at the transition point exceeds the effect of magnetization at this point, such that the probability to form the coherent state increases as the magnetization at the transition point increases. Such unexpected behavior can be associated with a peculiar spatial distribution of rival opinions at the starting point of the two-state regime in the three-state majority rule model and requires further analysis.
In a more general context of spin dynamics, the findings of this work provide an insight into majority rule dynamics of three-state spatially embedded networks that may be useful to understand some general features in evolution of a wide variety of physical, biological, and social systems. In this regard, the empirical relations found in this work may be useful for further insight. There are, of course, many other possible factors which could be included into our model to make it more realistic.
Acknowledgments
This work was supported by the Electoral Institute of the Federal District, Mexico (IEDF).
PACS Codes: 89.65.-s; 87.23.Ge; 02.50.-r
Author Contributions
Alexander S. Balankin designed the study, interpreted the results, and drafted the manuscript. Miguel Ángel Martínez Cruz, Felipe Gayosso Martínez, and Claudia L. Martínez-González designed the model, developed the software, analyzed the data, and interpreted the results. Leobardo Morales Ruiz and Julián Patiño Ortiz performed numerical simulations, analyzed the data, and interpreted the results. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Galam, S. Sociophysics: A Physicist’s Modeling of Psycho-Political Phenomena; Springer: New York, NY, USA, 2012. [Google Scholar]
- Galam, S. Application of statistical physics to politics. Physica A 1999, 274, 132–139. [Google Scholar]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar]
- Xiong, X.; Liu, Y.; Zhu, J. Competition of Dynamic Self-Confidence and Inhomogeneous Individual Influence in Voter Models. Entropy 2013, 15, 5292–5304. [Google Scholar]
- Li, P.-P.; Zheng, D.-F.; Hui, P.M. Dynamics of opinion formation in a small-world network. Phys. Rev. E 2006, 73, 056128. [Google Scholar]
- Lambiotte, R.; Ausloos, M.; Hołyst, J.A. Majority model on a network with communities. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef]
- Crokidakis, N.; Forgerini, F.L. Consequence of reputation in the Sznajd consensus model. Phys. Lett. A 2010, 374, 3380–3383. [Google Scholar]
- Fernández-Gracia, J.; Castelló, X.; Eguíluz, V.M.; San Miguel, M. Dynamics of link states in complex networks: The case of a majority rule. Phys. Rev. E 2012, 86, 066113. [Google Scholar]
- Bagnoli, F.; Rechtman, R. Topological bifurcations in a model society of reasonable contrarians. Phys. Rev. E 2013, 88, 062914. [Google Scholar]
- Galam, S. Local dynamics vs. social mechanisms: A unifying frame. Europhys. Lett. 2005, 70, 705–711. [Google Scholar]
- De la Lama, M.S.; Szendro, I.G.; Iglesias, J.R.; Wio, H.S. Van Kampen’s expansion approach in an opinion formation model. Eur. Phys. J. B 2006, 51, 435–442. [Google Scholar]
- Biswas, S.; Chatterjee, A.; Senc, P. Disorder induced phase transition in kinetic models of opinion dynamics. Physica A 2012, 391, 3257–3265. [Google Scholar]
- Crokidakis, N.; Anteneodo, C. Role of conviction in nonequilibrium models of opinion formation. Phys. Rev. E 2012, 86, 061127. [Google Scholar]
- Crokidakis, N. Role of noise and agents’ convictions on opinion spreading in a three-state voter-like model. J. Stat. Mech. 2013, 2013. [Google Scholar] [CrossRef]
- Balankin, A.S.; Martínez, M.Á.; Trejo, A. Effect of initial concentration and spatial heterogeneity of active agent distribution on opinion dynamics. Physica A 2011, 390, 3876–3887. [Google Scholar]
- Galam, S. Majority rule, hierarchical structures and democratic totalitarism: A statistical approach. J. Math. Psychol. 1986, 30, 426–434. [Google Scholar]
- Krapivsky, P.L.; Redner, S. Dynamics of majority rule in two-state interacting spin systems. Phys. Rev. Lett. 2003, 90, 238701. [Google Scholar]
- Mobilia, M.; Redner, S. Majority versus minority dynamics: Phase transition in an interacting two-state spin system. Phys. Rev. E 2003, 68, 046106. [Google Scholar]
- Chen, P.; Redner, S. Majority rule dynamics in finite dimensions. Phys. Rev. E 2005, 71, 036101. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar]
- Spirin, V.; Krapivsky, P.L.; Redner, S. Fate of zero-temperature Ising ferromagnets. Phys. Rev. E 2001, 63, 036118. [Google Scholar]
- Spirin, V.; Krapivsky, P.L.; Redner, S. Freezing in Ising ferromagnets. Phys. Rev. E 2002, 65, 016119. [Google Scholar]
- Gudgin, G.; Taylor, P.J. Electoral Bias and the Distribution of Party Voters. Trans. Inst. Br. Geogr. 1974, 63, 53–74. [Google Scholar]
- Martínez-Cruz, M.A.; Balankin, A.S.; Morales, O.; Samayoa, D.; García, E.I. Análisis fractal de elecciones federales 1991–2003. Cientifíca. 2006, 10, 175–183. [Google Scholar]
- Nowak, A.; Vallacher, R.R. Toward Computational Social Psychology: Cellular Automata and Neutral Network Models of Interpersonal Dynamics. In Connectionist Models of Social Reasoning and Social Behavior, 2nd ed; Reed, S.J., Miller, L.S., Eds.; Lawrence Erlboum Accociation: Hillsdale, NJ, USA, 2013; pp. 277–311. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).