Entropy and Recurrence Measures of a Financial Dynamic System by an Interacting Voter System
Abstract
:1. Introduction
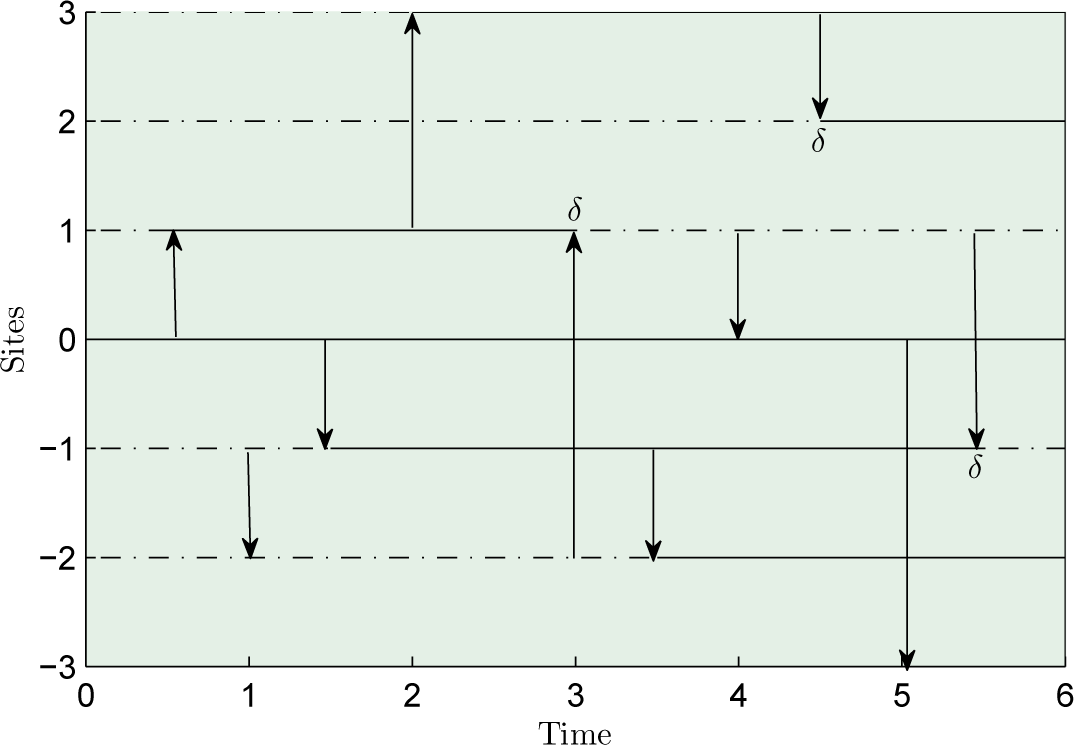
2. Price Process Modeling by a Finite-Range Voter System
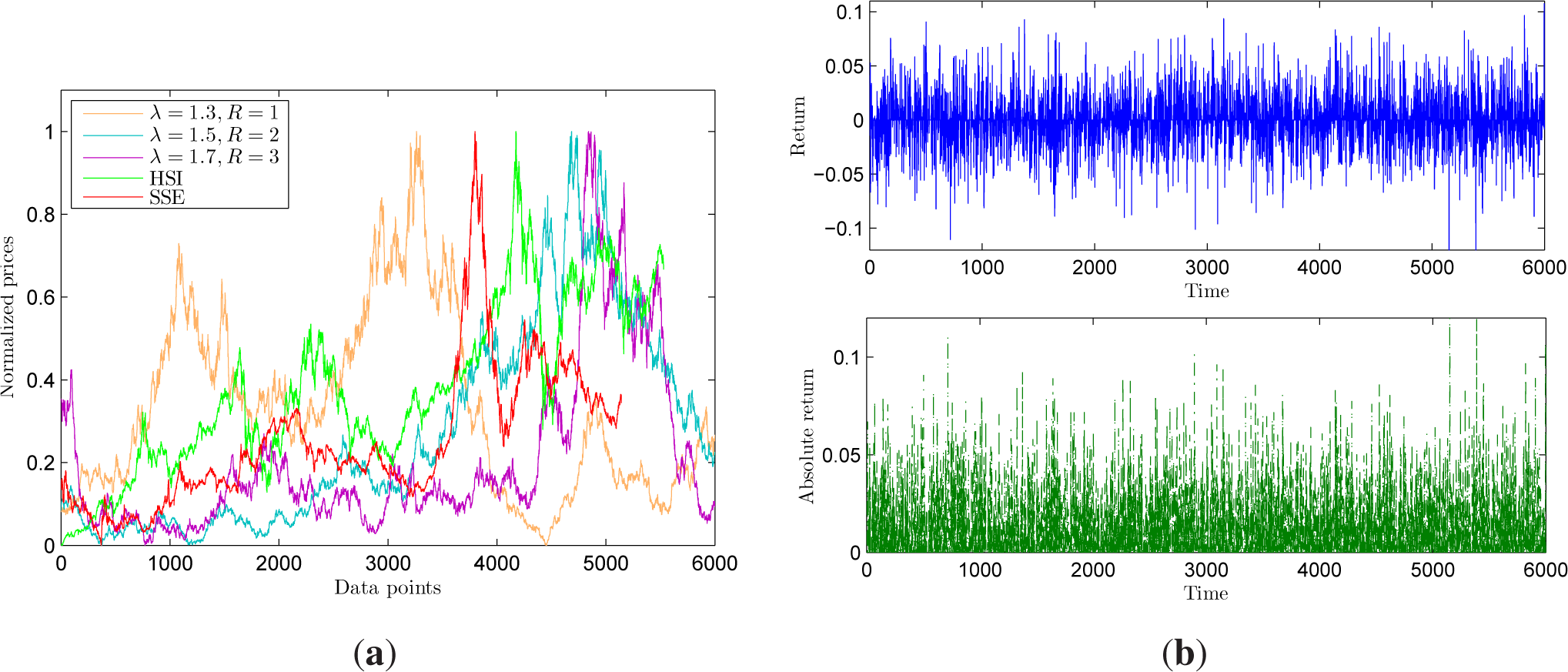
3. Comparison Empirical Analysis of Complexity Behaviors
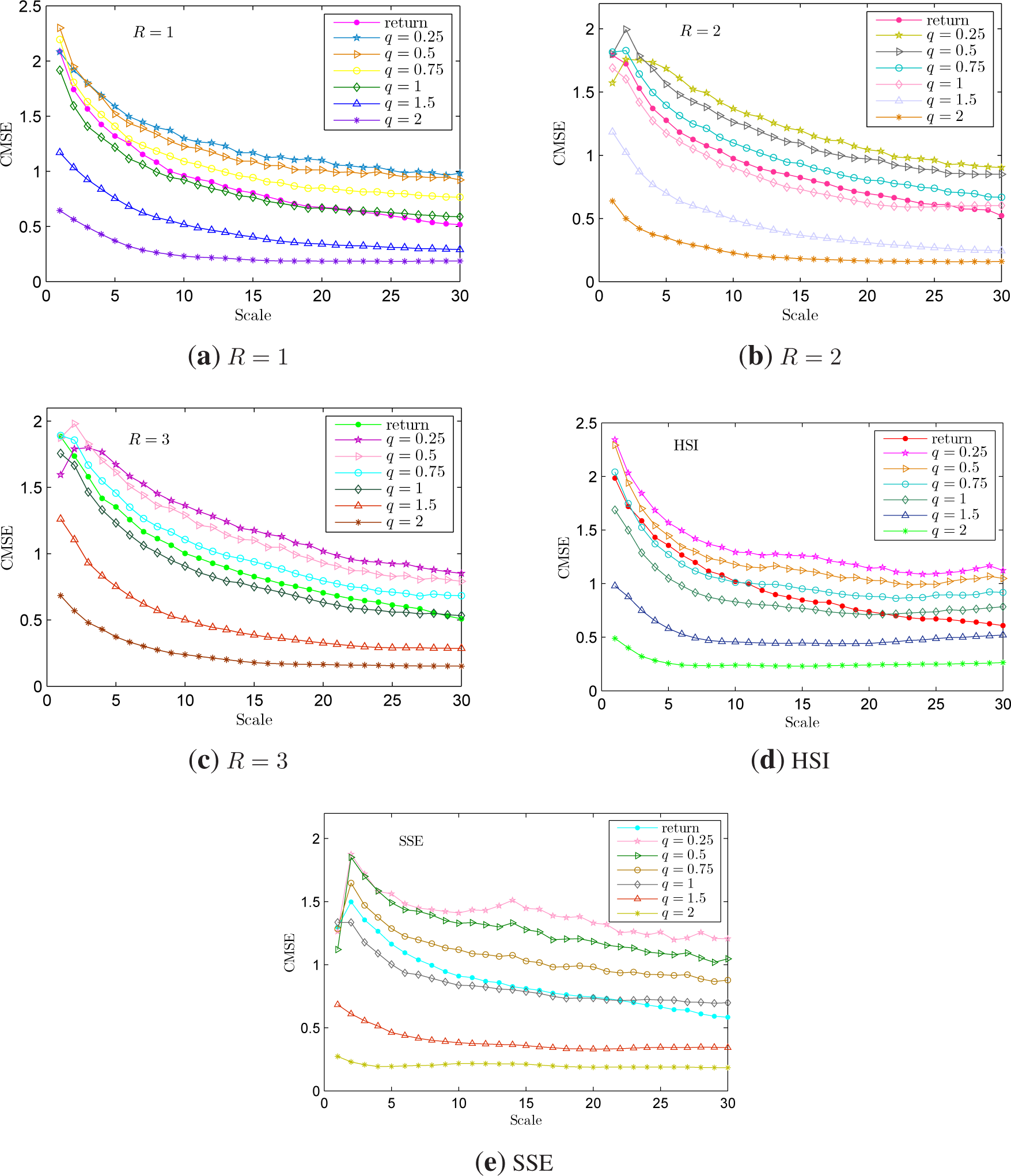
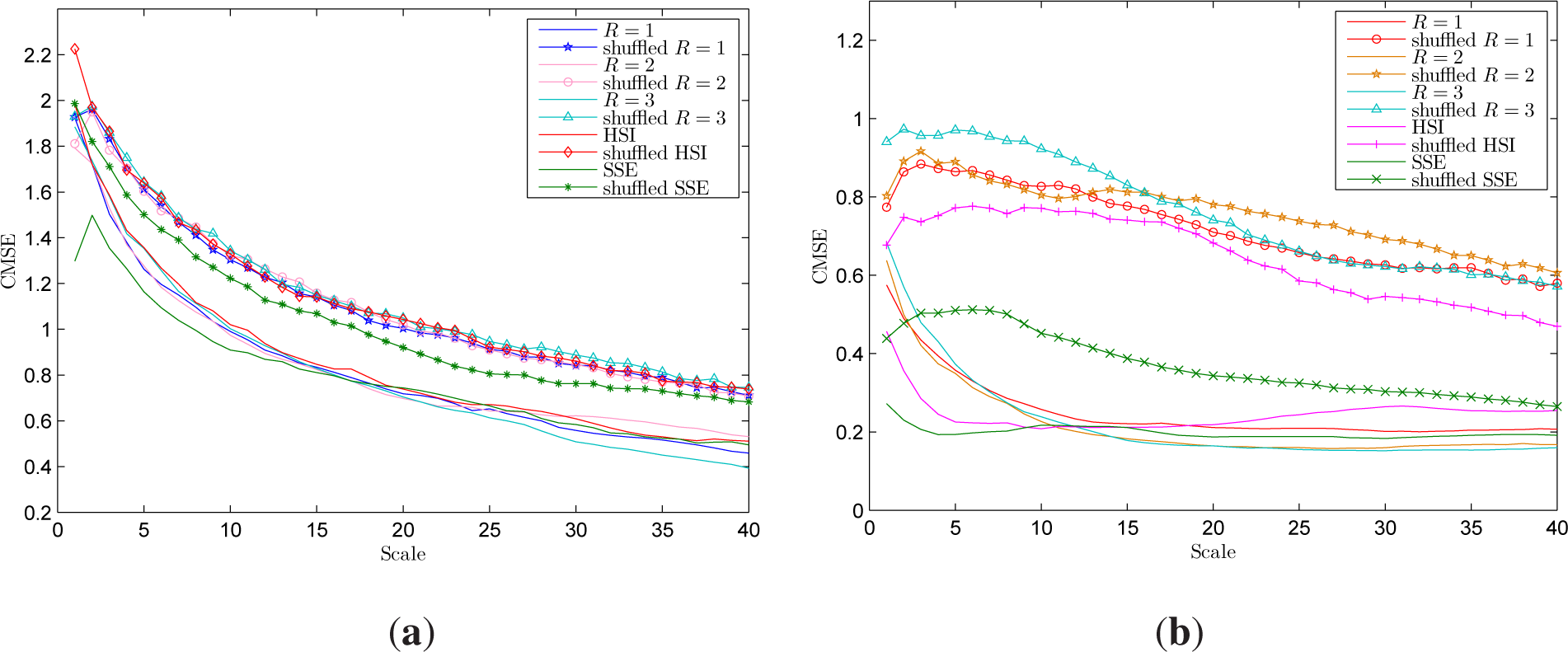
3.1. Composite Multiscale Entropy Analysis
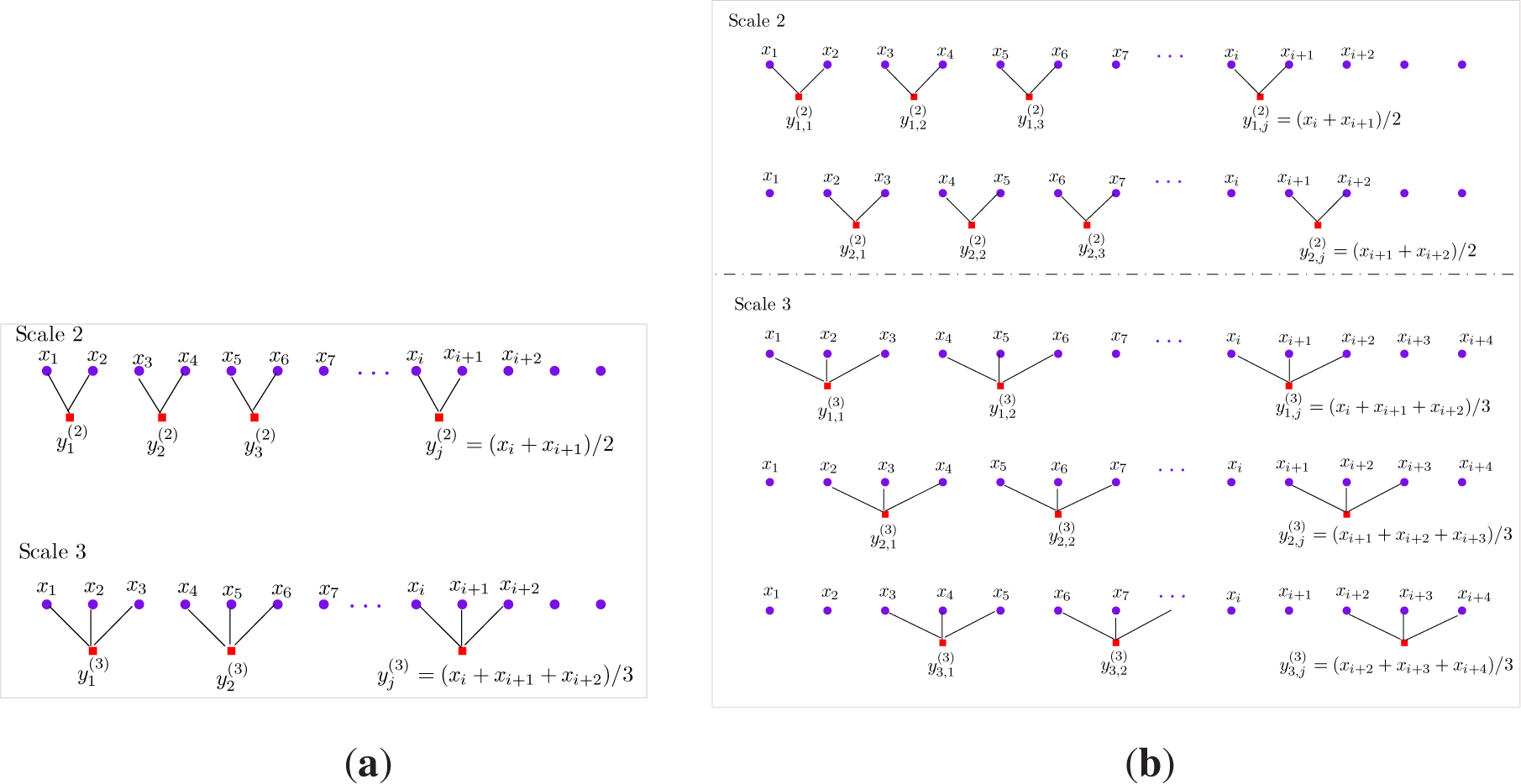
- For an one-dimensional time series x = {x1, x2, ⋯, xN}, consecutive coarse-grained time series are constructed by averaging a successively increasing number of points within non-overlapping windows. Unlike the MSE algorithm in which each of the coarse-grained time series {y(τ)} is computed as , the k-th coarse-grained time series in the CMSE method for a scale factor τ, is defined as:Note that for τ = 1, the coarse-grained time series is simply the original time series. Figure 3 shows a schematic illustration of the coarse-graining procedure for both MSE (a) and CMSE (b) with τ = 2 and τ = 3, respectively, from which a clear difference between these two methods can be seen.
- The entropy measure, the sample entropy (SampEn), is calculated for each coarse-grained time series and then plotted as a function of the scale factor. SampEn quantifies the regularity or predictability of a time series, which is defined as the negative logarithm of the conditional probability that a point that repeats itself within a tolerance of ϵ in an m-dimensional phase space will repeat itself in an m + 1-dimensional phase space:where C(m, ϵ) is the number of repeating points in the m-dimensional phase space, repeating is defined as points closer than ϵ in a Euclidean sense to the examined points; for details, see [35–37,47]. Finally, the CMSE value is defined as the means of the sample entropies of all coarse-grained time series, that is:while the MSE is computed by only using the first coarse-grained time series i.e., .
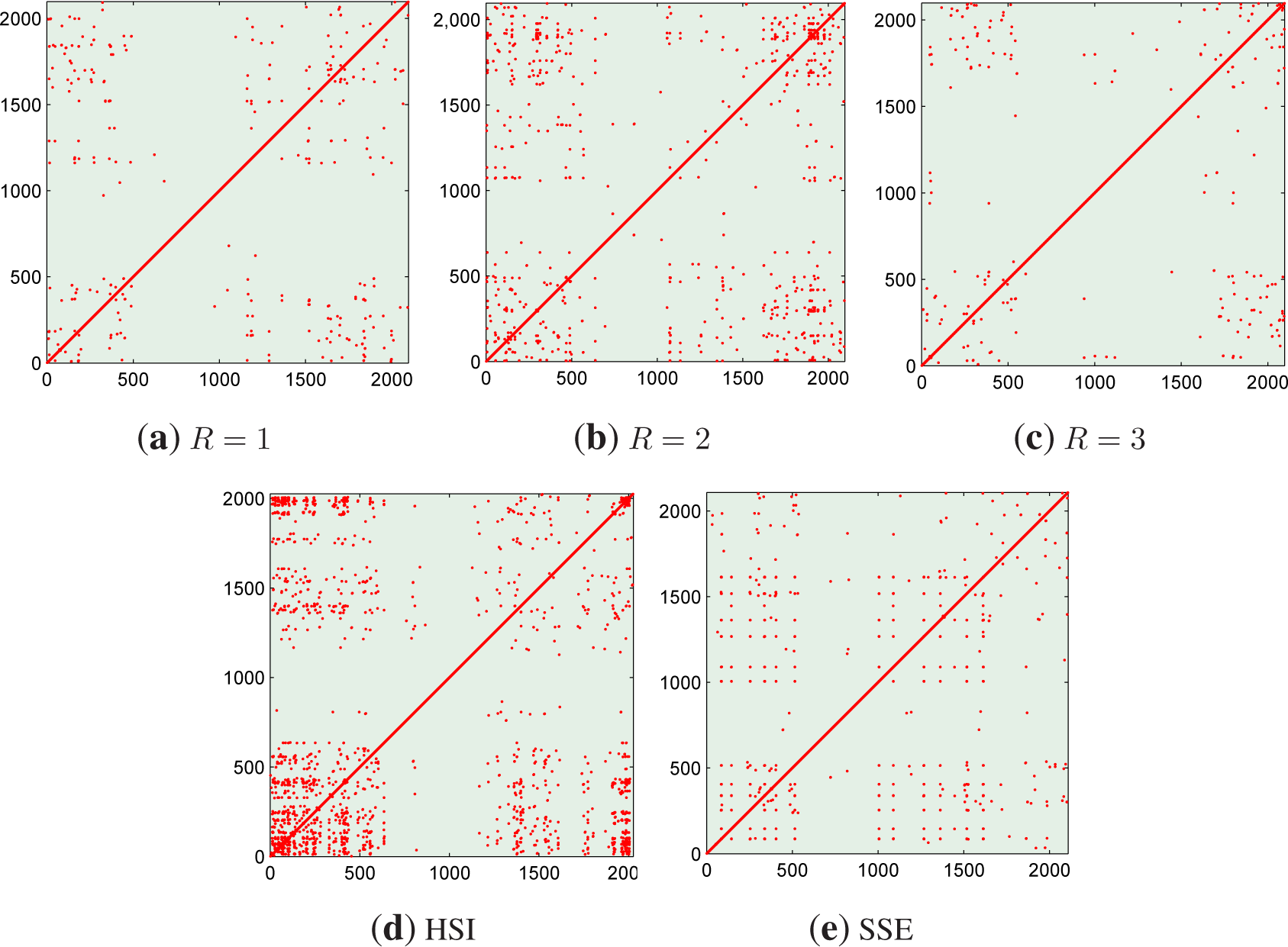
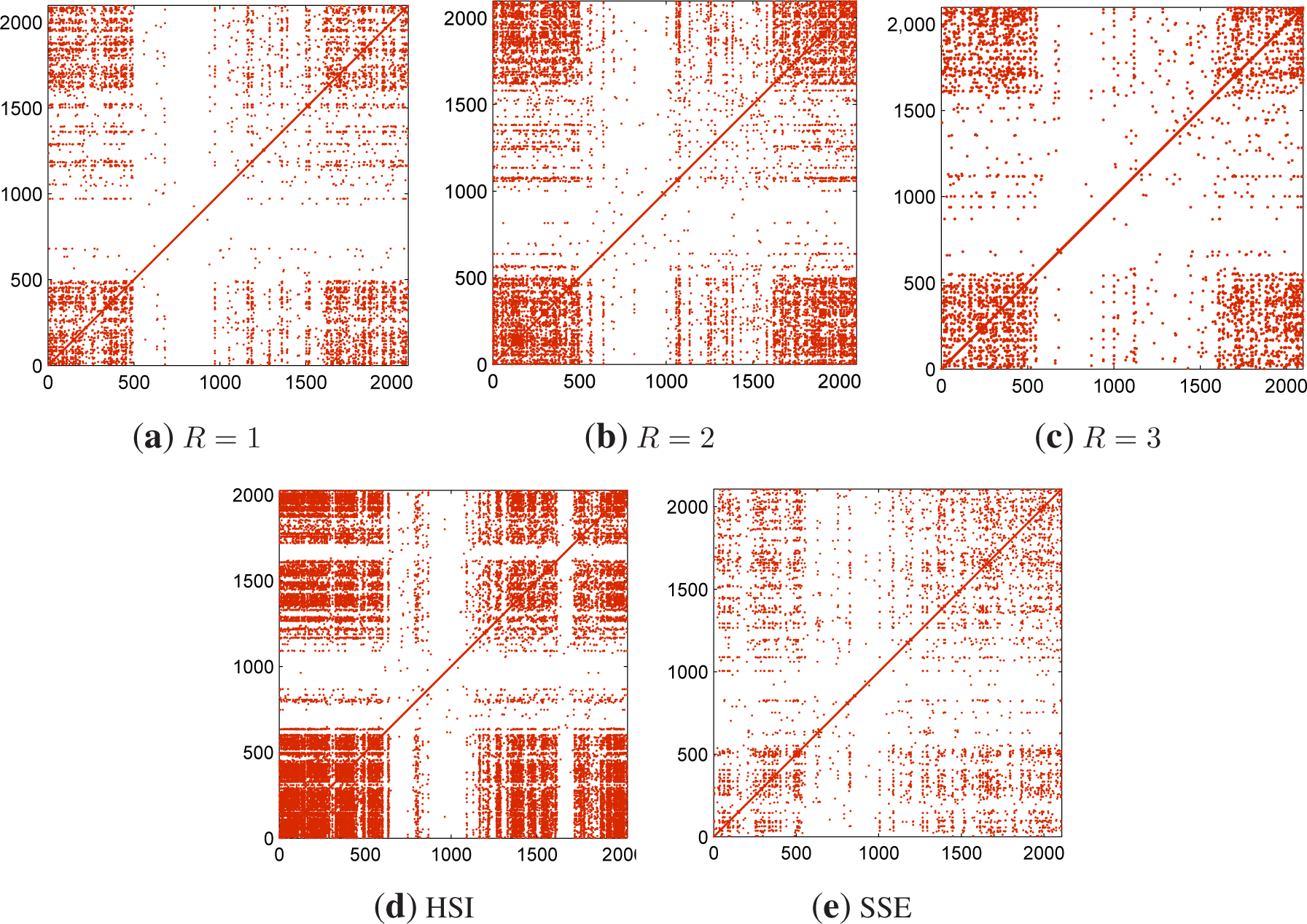
3.2. Recurrence Plot and Recurrence Quantification Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Calvet, L.E.; Fisher, A.J. Multifractal Volatility: Theory, Forecasting, and Pricing; Academic Press: Waltham, MA, USA, 2008. [Google Scholar]
- Chakraborti, A.; Toke, I.M.; Patriarca, M.; Aberget, F. Econophysics review: I. Empirical facts. Quant. Financ 2011, 11, 991–1012. [Google Scholar]
- Gabaix, X.; Gopicrishnan, P.; Plerou, V.; Stanley, H.E. Understanding the cubic and half-cubic laws of financial fluctuations. Physica A 2003, 324, 1–5. [Google Scholar]
- Guo, Y.L.; Wang, J. Simulation and statistical analysis of market return fluctuation by Zipf method. Math. Probl. Eng 2011, 2011, 253523. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Liao, Z.; Wang, J. Forecasting model of global stock index by stochastic time effective neural network. Expert Syst. Appl 2010, 37, 834–841. [Google Scholar]
- Lux, T. Financial Power Laws: Empirical Evidence, Models and Mechanisms; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Mandelbrot, B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risks; Springer: Berlin/Heidelberg, Germany and New York, NY, USA, 1997. [Google Scholar]
- Stanley, H.E.; Gabaix, X.; Gopikrishnan, P.; Plerou, V. Economic fluctuations and statistical physics: The puzzle of large fluctuations. Nonlinear Dyn 2006, 44, 329–340. [Google Scholar]
- Cheng, W.Y.; Wang, J. Dependence phenomenon analysis of the stock market. Europhys. Lett 2013, 102. [Google Scholar] [CrossRef]
- Cont, R.; Bouchaud, J.P. Herd behavior and aggregate fluctuation in financial markets. Macroecon. Dyn 2000, 4, 170–196. [Google Scholar]
- Fang, W.; Wang, J. Statistical properties and multifractal behaviors of market returns by Ising dynamic systems. Int. J. Mod. Phys. C 2012, 23. [Google Scholar] [CrossRef]
- Krause, S.M.; Bottcher, P.; Bornholdt, S. Mean-field-like behavior of the generalized voter-model-class kinetic Ising model. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature 1999, 397, 498–500. [Google Scholar]
- Ross, S.M. An Introduction to Mathematical Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Samanidou, E.; Zschischang, E.; Stauffer, D.; Lux, T. Agent-based models of financial markets. Rep. Prog. Phys 2007, 70, 409–450. [Google Scholar]
- Stauffer, D.; Penna, T.J.P. Crossover in the Cont-Bouchaud percolation model for market fluctuation. Physica A 1998, 256, 284–290. [Google Scholar]
- Mills, T.C. The Econometric Modeling of Financial Time Series; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Niu, H.L.; Wang, J. Volatility clustering and long memory of financial time series and financial price model. Digit. Signal Process 2013, 23, 489–498. [Google Scholar]
- Wang, F.; Wang, J. Statistical analysis and forecasting of return interval for SSE and model by lattice percolation system and neural network. Comput. Ind. Eng 2012, 62, 198–205. [Google Scholar]
- Wang, J.; Wang, Q.Y.; Shao, J.G. Fluctuations of stock price model by statistical physics systems. Math. Comput. Model 2010, 51, 431–440. [Google Scholar]
- Wang, T.S.; Wang, J.; Zhang, J.H.; Fang, W. Voter interacting systems applied to Chinese stock markets. Math. Comput. Simul 2011, 81, 2492–2506. [Google Scholar]
- Xiao, D.; Wang, J. Modeling stock price dynamics by continuum percolation system and relevant complex systems analysis. Physica A 2012, 291, 4827–4838. [Google Scholar]
- Yu, Y.; Wang, J. Lattice-oriented percolation system applied to volatility behavior of stock market. J. Appl. Stat 2012, 39, 785–797. [Google Scholar]
- Zhang, J.H.; Wang, J. Modeling and simulation of the market fluctuations by the finite range contact systems. Simul. Model. Pract. Theory 2010, 18, 910–925. [Google Scholar]
- Zhang, J.H.; Wang, J.; Shao, J.G. Finite-range contact process on the market return intervals distributions. Adv. Complex Syst 2010, 13, 643–657. [Google Scholar]
- Zivot, E.; Wang, J.H. Modeling Financial Time Series with S-PLUS; Springer: New York, NY, USA, 2006. [Google Scholar]
- Staufffer, D.; Sornette, D. Self-organized percolation models for stock market fluctuations. Physica A 1999, 271, 496–506. [Google Scholar]
- Chen, M.F. From Markov Chains to Non-Equilibrium Particle Systems; World Scientific: Singapore, Singapore, 1992. [Google Scholar]
- Durrett, D. Lecture Notes on Particle Systems and Percolation; Wadsworth & Brooks: California, CA, USA, 1998. [Google Scholar]
- Liggett, T.M. Interacting Particle Systems; Springer: New York, NY, USA, 1985. [Google Scholar]
- Liggett, T.M. Stochastic Interacting Systems: Contact, Voter and Exclusion Processes; Springer: Heidelberg, Germany, 1999. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Mutltiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef]
- Cirugeda-Roldan, E.; Cuesta-Frau, D.; Miro-Martinez, P.; Oltra-Crespo, S. Comparative Study of Entropy Sensitivity to Missing Biosignal Data. Entropy 2014, 16, 5901–5918. [Google Scholar]
- Martina, E.; Rodriguez, E.; Perez, R.E.; Ramirez, J.A. Multiscale entropy analysis of crude oil price dynamics. Energy Econ 2011, 33, 936–947. [Google Scholar]
- Vargas, L.G.; Rojas, A.R.; Brown, F.A. Multiscale entropy analysis of electroseismic time series. Nat. Hazards Earth Syst. Sci 2008, 8, 855–860. [Google Scholar]
- Wu, S.D.; Wu, C.W.; Liu, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar]
- Hsieh, D.A. Chaos and nonlinear dynamics: Application to financial markets. J. Financ 1991, 46, 1839–1877. [Google Scholar]
- Frauch, J.B.; Contreras, D.; Lleso, L.T. Assessing nonlinear structures in real exchange rates using recurrence plot strategies. Physica D 2002, 171, 249–264. [Google Scholar]
- Guhathakurta, K.; Bhattacharya, B.; Chowdhury, A.R. Using recurrence plot analysis to distinguish between endogenous and exogenous stock market crashes. Physica A 2010, 389, 1984–1882. [Google Scholar]
- Aparicio, T.; Pozo, E.F.; Saura, D. Detecting determinism using recurrence quantification analysis: Three test procedures. J. Econ. Behav. Organ 2008, 65, 768–787. [Google Scholar]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep 2007, 438, 237–329. [Google Scholar]
- Rolski, T.; Schmidt, V.; Schmidli, H.; Teugels, J. Stochastic Processes for Insurance and Finance; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Lamberton, D.; Lapeyre, B. Introduction to Stochastic Calculus Applied to Finance; Chapman and Hall/CRC: London, UK, 2000. [Google Scholar]
- Gaylord, R.; Wellin, P. Computer Simulations with Mathematica: Explorations in the Physical, Biological and Social Science; Springer: New York, NY, USA, 1995. [Google Scholar]
- Zheng, Z. Matlab Programming and the Applications; China Railway Publishing House: Beijing, China, 2003. [Google Scholar]
- Dionisio, A.; Menezes, R.; Mendes, D.A. Entropy-Based Independence Test. Nonlinear Dyn 2006, 44, 351–357. [Google Scholar]
- Frazer, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar]
- Ilinski, K. Physics of Finance: Gauge Modeling in Non-equilibrium Pricing; Wiley: New York, NY, USA, 2001. [Google Scholar]
| data | return | q = 0.25 | q = 0.5 | q = 0.75 | q = 1 | q = 1.5 | q = 2 |
|---|---|---|---|---|---|---|---|
| {λ = 1.3, R = 1} | 0.52026 | 0.63220 | 0.74669 | 0.81593 | 0.85684 | 0.88665 | 0.87644 |
| {λ = 1.5, R = 2} | 0.51066 | 0.65271 | 0.68973 | 0.76012 | 0.80596 | 0.84566 | 0.84251 |
| {λ = 1.7, R = 3} | 0.44587 | 0.63266 | 0.74921 | 0.82767 | 0.87982 | 0.92975 | 0.93350 |
| HSI | 0.52570 | 0.85341 | 0.88780 | 0.89769 | 0.89280 | 0.85217 | 0.79179 |
| SSE | 0.52271 | 0.72742 | 0.79722 | 0.81659 | 0.81297 | 0.76844 | 0.70621 |
| Data | RR (h = 0.02, 0.04) | DET (h = 0.02, 0.04) | Lmean (h = 0.02, 0.04) | |||
|---|---|---|---|---|---|---|
| R = 1 | 0.0005 | 0.0027 | 0.9044 | 0.6649 | 46.7234 | 3.6071 |
| R = 2 | 0.0007 | 0.0046 | 0.8373 | 0.6817 | 15.6688 | 3.2662 |
| R = 3 | 0.0005 | 0.0018 | 0.9336 | 0.6779 | 51.0233 | 4.5073 |
| HSI | 0.0010 | 0.0163 | 0.7685 | 0.7793 | 7.2597 | 3.5210 |
| SSE | 0.0006 | 0.0021 | 0.8503 | 0.5994 | 20.4435 | 3.9045 |
| Data | LENT (h = 0.02, 0.04) | LAM (h = 0.02, 0.04) | TT (h = 0.02, 0.04) | |||
|---|---|---|---|---|---|---|
| R = 1 | 0.3921 | 1.1084 | 0.0049 | 0.0671 | 2.0000 | 2.3217 |
| R = 2 | 0.7699 | 1.2140 | 0.0095 | 0.0989 | 2.3333 | 2.4383 |
| R = 3 | 0.7629 | 1.1562 | 0.0000 | 0.0449 | 0.0000 | 2.6015 |
| HSI | 1.1184 | 1.6163 | 0.0072 | 0.2814 | 2.0000 | 2.8932 |
| SSE | 0.4499 | 0.8834 | 0.1154 | 0.1334 | 2.3116 | 2.6532 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.-L.; Wang, J. Entropy and Recurrence Measures of a Financial Dynamic System by an Interacting Voter System. Entropy 2015, 17, 2590-2605. https://doi.org/10.3390/e17052590
Niu H-L, Wang J. Entropy and Recurrence Measures of a Financial Dynamic System by an Interacting Voter System. Entropy. 2015; 17(5):2590-2605. https://doi.org/10.3390/e17052590
Chicago/Turabian StyleNiu, Hong-Li, and Jun Wang. 2015. "Entropy and Recurrence Measures of a Financial Dynamic System by an Interacting Voter System" Entropy 17, no. 5: 2590-2605. https://doi.org/10.3390/e17052590
APA StyleNiu, H.-L., & Wang, J. (2015). Entropy and Recurrence Measures of a Financial Dynamic System by an Interacting Voter System. Entropy, 17(5), 2590-2605. https://doi.org/10.3390/e17052590





