Thermodynamic Analysis of a Waste Heat Driven Vuilleumier Cycle Heat Pump
Abstract
:1. Introduction
2. VM Cycle Heat Pump
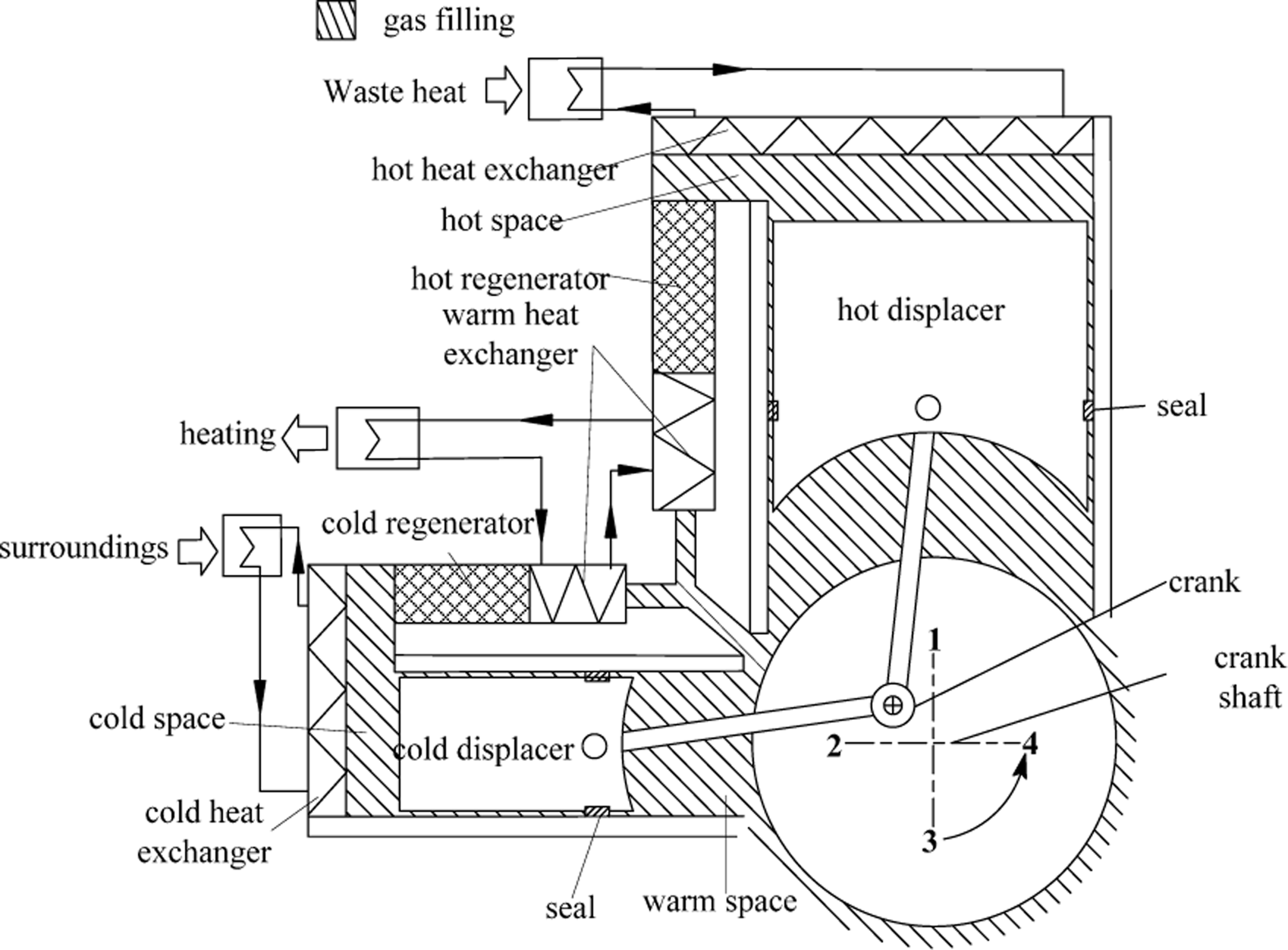
2.1. Configuration
2.2. Working Process
- Process 1–2: the crankcase rotates counterclockwise, making the crankshaft push the hot displacer to the bottom of the hot space, while the cold displacer moves to the top of the cold space. During this process, the hot space volume increases, and the cold space volume decreases. As the hot displacer moves to the bottom, the working fluid from the warm space is heated to close to the hot space temperature (Th) by filling materials when going through the hot regenerator, and then the working fluid goes into the hot space. The working fluid in the cold space is pushed by the cold displacer to the warm space, where it is heated to near the warm space temperature (Ta) by the filling material in the cold regenerator. Both the temperature and the pressure of the VM cycle heat pump increase rapidly. Output heat is supplied by the warm heat exchanger in the warm space.
- Process 2–3: the crank moves from left to the bottom. The hot displacer still goes to the bottom of hot space. Meanwhile the cold displacer leaves the top to the bottom of cold space. The volumes of both are increasing. During this process, the working fluid in the warm space is cooled to nearly the cold space temperature (Tc) by the filling material in the cold regenerator, and then enters the cold space. Gas in the hot space absorbs heat from high temperature waste heat through the hot heat exchanger, while the cold space is absorbing heat from the low temperature surroundings using the cold heat exchanger.
- Process 3–4: the crank rotates from bottom to right. The hot displacer leaves the bottom of the hot space to the top, and the cold displacer keeps moving to the bottom of the cold space. The hot space volume decreases, while the cold space volume keeps increasing. During this process, the working fluid in the hot space is pushed into the warm space by the hot displacer and cooled to nearly the warm space temperature (Ta) by the filling materials when crossing the hot regenerator. The gas temperature decreases, and the pressure also drops.
- Process 4–1: the crank moves from right to the top. The hot displacer moves to the top of the hot space, and the cold displacer leaves the bottom to the top of cold space. The hot space volume decreases to nearly 0, and the cold space volume decreases continuously. During this process, gas in the hot space is cooled to nearly the warm space temperature (Ta) by the filling in the hot regenerator, then goes into warm space, with the pressure drop. A part of the gas in the cold space is heated to nearly the warm space temperature by the filling in the cold regenerator when it passes through the cold heat exchanger, and then returns to the warm space.
3. Thermodynamic Analysis
- Processes occurring in all spaces are isothermal, i.e. the temperature of the compression or the expansion process is stable.
- No losses occur in all the processes within the cycle, which means there is no heat transfer or flow resistance.
- The working fluid is considered as ideal gas.
3.1. Working Fluid
3.2. Calculation Parameters
3.3. Equations for the Energy and Exergy Analyses
3.4. Calculation Results
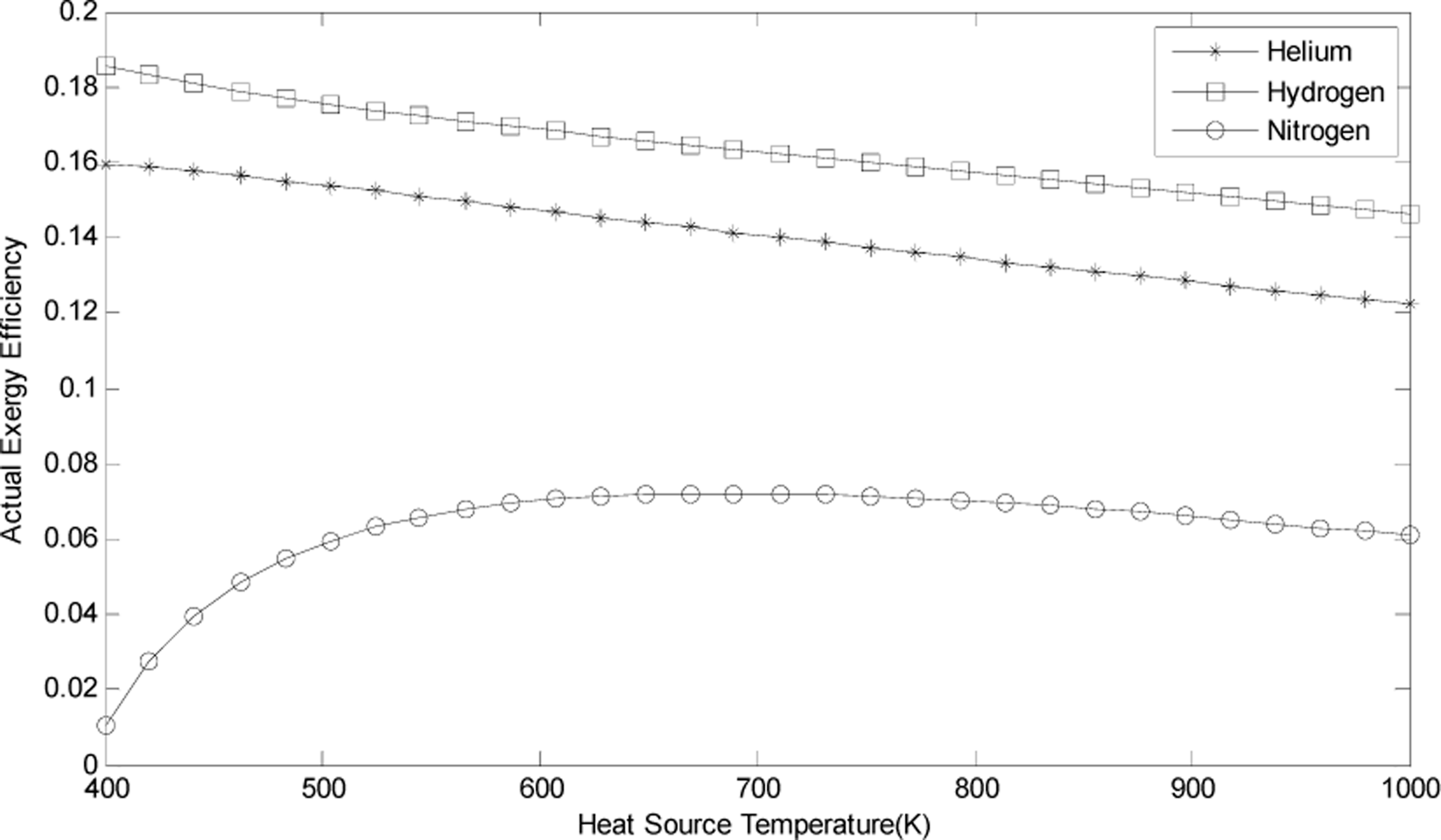
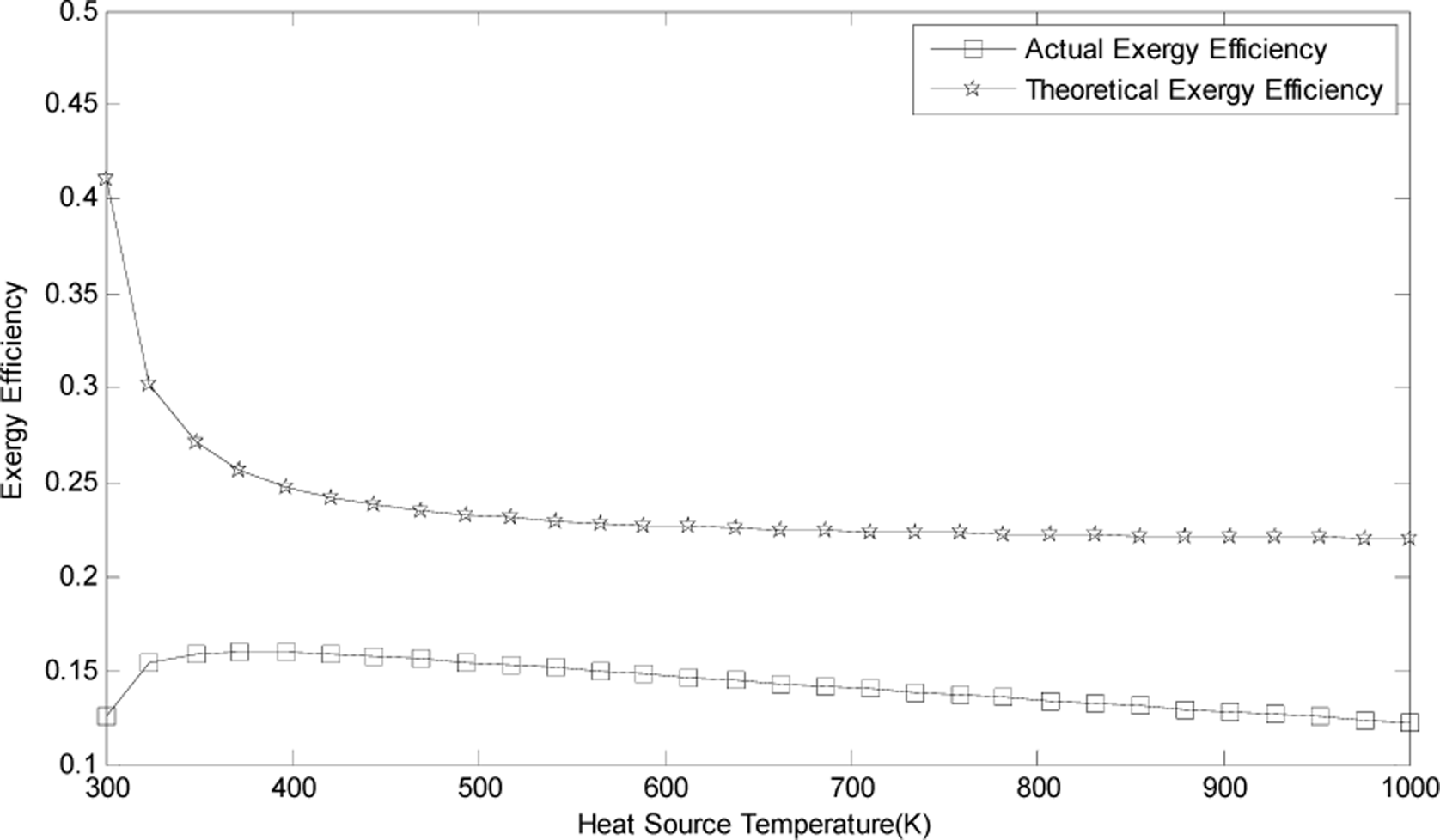
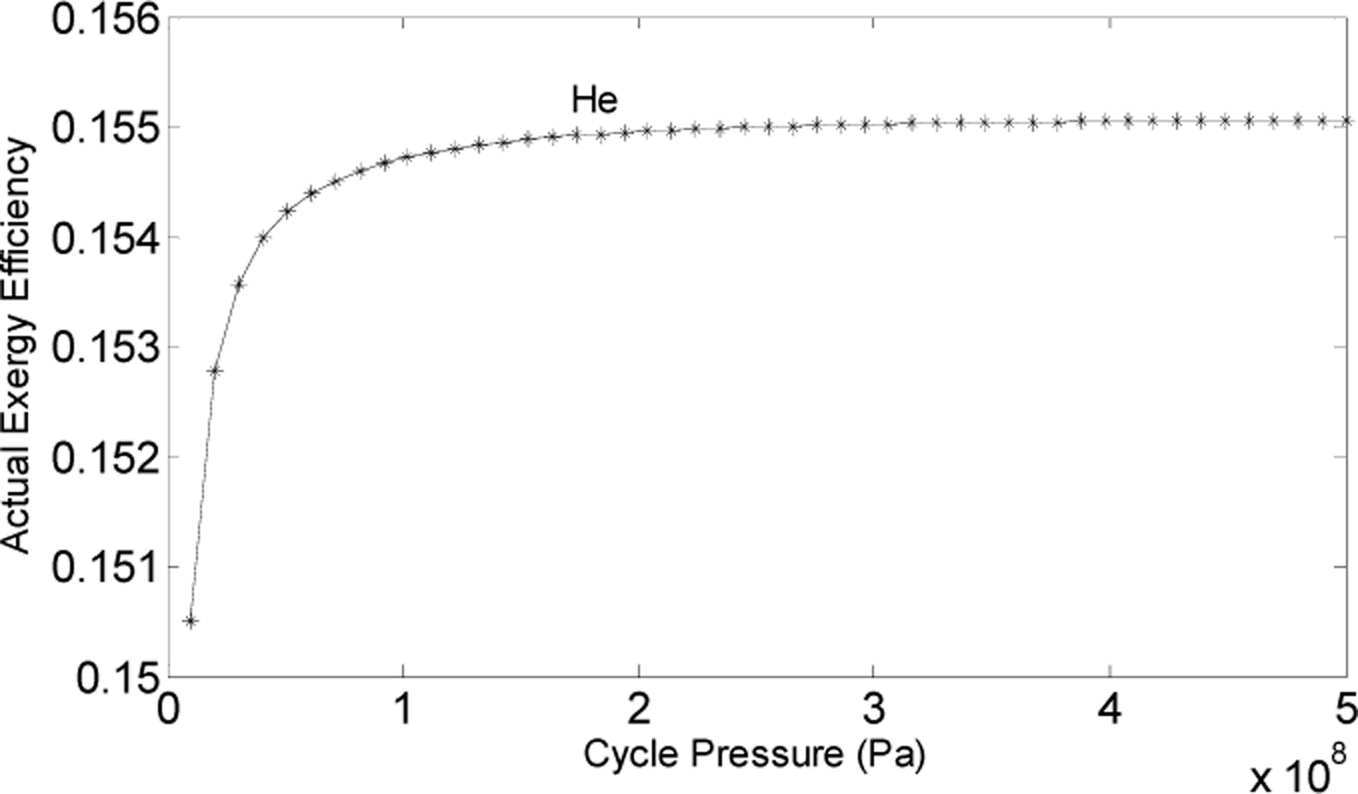
3.5. The Influence of Parameters on Exergy Efficiency
4. Conclusions
- According to the calculation results, the theoretical and actual exergy efficiency are 0.23 and 0.15, separately. Reheat losses and flow friction losses account for almost 83% of the total loss.
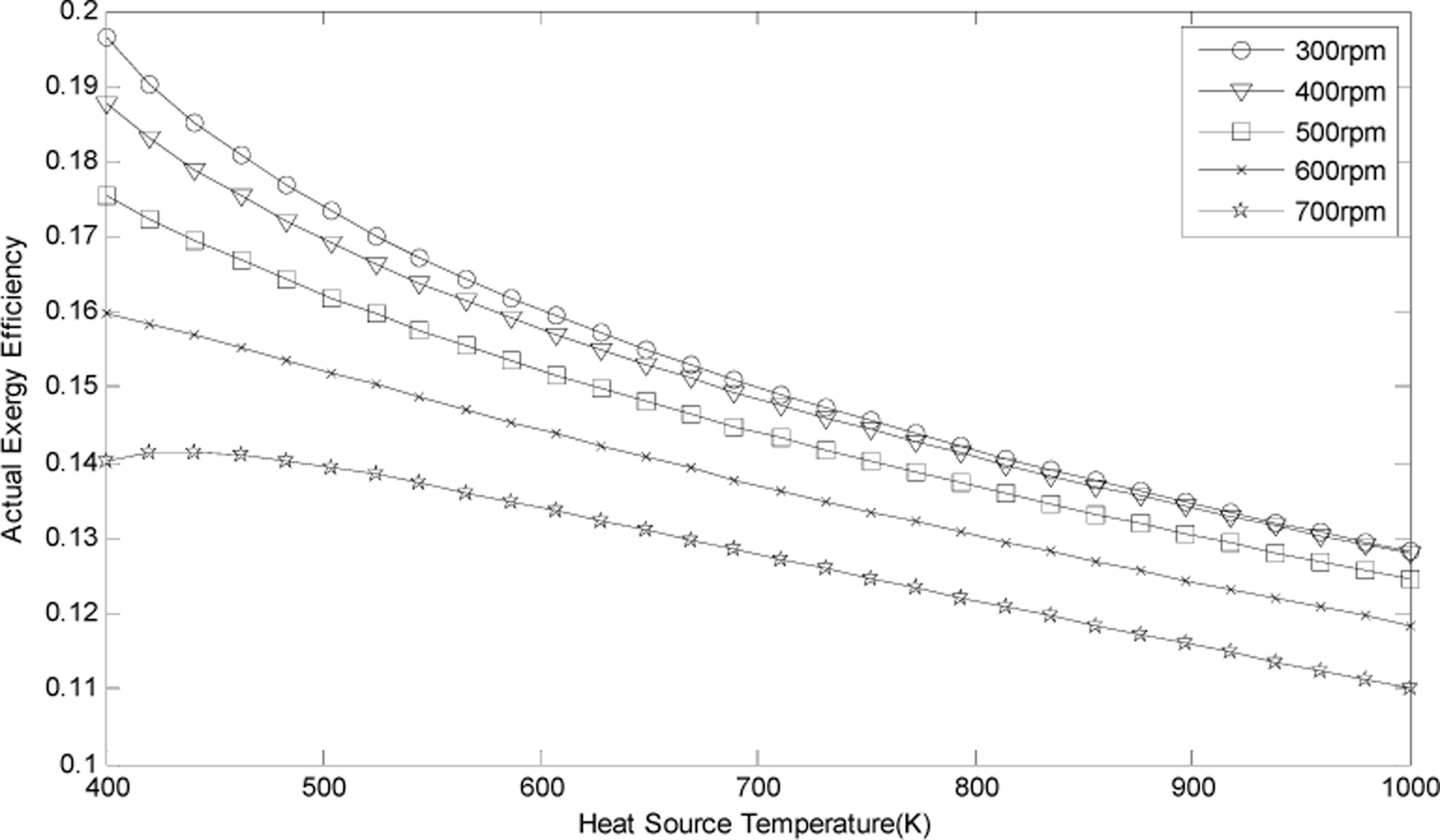
- As the temperature of waste heat increases, the theoretical exergy efficiency decreases, while the actual one first increases then decreases, reaching a maximum at the point of 370K. Low temperature waste heat under 600K temperature is more suitable as the driving heat source of a VM cycle heat pump.
- The cycle pressure and speed also have great influence on the exergy efficiency. The selected cycle pressure should be higher than 100MPa, and 200–300rpm is optimum for speed.
Acknowledgments
Nomenclature
| D | Diameter (m) |
| Z | Stroke (m) |
| Φ | Volume phase angle (°) |
| L | Length (m) |
| δ | Clearance (m) |
| T | Temperature (K) |
| P | Pressure (Pa) |
| n | Rotational speed (rpm) |
| ω | Volume ratio |
| He | Helium |
| R | Universal gas constant (JK−1mol−1) |
| CP | Specific heat (Jkg−1K−1) |
| V | Volume (m3) |
| τ | Temperature ratio |
| Q | Heat quality (W) |
| θ | Pressure phase angle (°) |
| ψ | Porosity |
| D | Diameter (m) |
| A | Area (m2) |
| a | Specific heat transfer area (m2) |
| COP | Coefficient of performance |
| r | Hydraulic radius (m) |
| ρ | Density (kgm−3) |
| M | Mass flux (kgs−1) |
| ΔP | Pressure drop (Pa) |
| Fs | Correction factor |
| Δ | Heat loss (W) |
| Zp | Gas compressibility factor |
| COPex | Exergy efficiency |
| Subscripts | |
|---|---|
| co | Cold space |
| h | Hot space |
| a | Warm space |
| R | Regenerator |
| av | Average |
| max | Maximum |
| min | Minimum |
| m | Material |
| f | Flow |
| sh | Shuttle |
| p | Pumping |
| i | Ideal |
| e | Effective |
Author Contributions
Conflicts of Interest
References
- Grossman, P.Z.; Energy, Shocks. Crises and the Policy Process: A Review of Theory and Application. Energy Policy. 2015, 8, 56–69. [Google Scholar]
- Skouloudis, A.N.; Kassomenos, P. Combining Environment and Health Information Systems for the Assessment of Atmospheric Pollution on Human Health. Sci. Total Environ. 2014, 488–489, 362–368. [Google Scholar]
- Semkov, K.; Mooney, E.; Connolly, M.; Adley, C. Efficiency Improvement through Waste Heat Reduction. Appl. Therm. Eng. 2014, 70, 716–722. [Google Scholar]
- National Data. Available online: http://data.stats.gov.cn/workspace/index;jsessionid=0E028DD36CE5EEC4B0FDC6EB60547493?m=hgnd accessed on 13 March 2015.
- Dong, L.; Huang, H.; Kobayashi, N. Development of an all-in-one Type Adsorption Heat Pump for Heating Application. Int. J. Chem. React. Eng. 2011, 9, 18–24. [Google Scholar]
- Xie, Y.B.; Deng, X.D.; Zhao, J.H. Fuzzy Comprehensive Evaluation of System Performance for Vuilleumier Cycle Heat Pump Driven by Solar, Geo-thermal and Biomass Energy. Appl. Power Energy Technol. 2014, 8, 1080–1083. [Google Scholar]
- Vuilleumier, R. Method and Apparatus for Including Heat Change. U.S. Patent 1, 275, 507 1918. [Google Scholar]
- Bian, S. Cryogenic Refrigerator; China Machine Press: Beijing, China, 1990; pp. 56–57. [Google Scholar]
- ASHRAE, Engine-driven heating and cooling equipment. In ASHRAE Systems and Equipment Handbook; Machinery Industry Press: Beijing, China, 1981; pp. 54–65.
- Wu, Y. Refrigeration and Cryogenic Technology Principle; High Education Press: Beijing, China, 2007; pp. 26–33. [Google Scholar]
- Li, X. Refrigeration Principle and Equipment; Machinery Industry Press: Beijing, China, 2006; p. 39. [Google Scholar]
- Wang, R.; Ding, G.; Wu, J. Refrigeration Principles and Techniques; Science Press: Beijing, China, 2005; pp. 15–28. [Google Scholar]
- Rule, T.T.; Qvale, E.B. Steady-Stale Operation of the Idealized Vuilleumier Refrigerator. Adv. Cryog. Eng. 1969, 14, 343–352. [Google Scholar]
- White, R. Vuilleumier Cycle Cryogenic Refrigeration; Technical Report AFFDL-TR-76-17; Air Force Wright Aeronautical Laboratories, Wright-Patterson Air Force Base: Dayton, OH, USA, 1976. [Google Scholar]
- Carlsen, H. Development of a Gas Fired Vuilleumier Heat Pump for Residential Heating. Proceedings of the Intersociety Energy Conversion Engineering Conference, Washington, D.C., WA, USA, 6–11 August 1989; IEEE: New York, NY, USA, 1989; pp. 2257–2263. [Google Scholar]
- Carlsen, H. Development of a New 20 kW Gas Fired Heat Pump Based on the Vuilleumier Cycle. Proceedings of the 25th Intersociety Energy Conversion Engineering Conference, Reno, NV, USA, 12–17 August 1990; IEEE: New York, NY, USA, 1990; pp. 233–238. [Google Scholar]
- Kuhl, H.-D.; Schulz, S.; Thomas, B.; Carlsen, H. Conversion of a Crank-driven Vuilleumier Heat Pump into a Free Piston Machine. Proceedings of the Intersociety Energy Conversion Engineering Conference, Atlanta, GA, USA, 8–13 August 1993.
- Pfeffer, T.; Kuehl, H.-D.; Schulz, S.; Walther, C. Development and Experimental Investigation of New Concepts for Regenerators of Regenerative Gas Cycles-exemplary for Vuilleumier heat Pumps. Eng. Res. 2000, 65, 257–272. [Google Scholar]
- Lee, G.T.; Kang, B.H.; Yoo, H. Effects of Geometric Configuration on the Cooling Performance of a Vuilleumier Cycle Heat Pump. Proceedings of the Energy Conversion Engineering Conference, Washington, D.C., WA, USA, 11–16 August 1996; IEEE: New York, NY, USA, 1996; pp. 781–786. [Google Scholar]
- Finkelstein, T. Isothermal Sinusoidal Analysis of Balanced Compound Vuilleumier Heat Pumps. Proceedings of the Intersociety Energy Conversion Engineering Conference, San Diego, CA, USA, 3–7 August 1992.
- Sekiya, H.; Yamashita, I. Multisimulation Model for Stirling and Vuilleumier Cycle Machines. JSME Int. J. Ser. B Fluids Therm. Eng. 1993, 36, 383–390. [Google Scholar]
- Sekiya, H.; Kobayashi, K.; Fukuda, E. Numerical Analysis and Experimental Investigation of a Free Piston Vuilleumier Cycle Heat Pump. Proceedings of the 29th Intersociety Energy Conversion Engineering Conference, Washington, D.C., WA, USA, 7–11 August 1994.
- Kawajiri, K.; Honda, T.; Sugimoto, T. Study of Free Piston Vuilleumier Heat Pump (Performance Characteristics of Prototype Machine at Forced Vibration). Trans. Jpn Soc. Mech. Eng. Ser. B 1996, 62, 2430–2437. [Google Scholar]
- Xie, Y.B.; Wang, S.H.; Li, B.; Liu, Y. Influences of Binary Mixtures on the Regenerator of VM Cycle Heat Pump. Appl. Mech. Mater. 2011, 52–54, 249–254. [Google Scholar]
- Rios, P.A.; Smith, J.L., Jr. An Analysis of Stirling Cycle Refrigerator. Adv. Cryog. Eng. 1969, 14, 332–342. [Google Scholar]
- Ozcan, H.; Dincer, I. Thermodynamic Analysis of a Solar Driven Tri-generation System for Building Applications. In Progress in Exergy, Energy, and the Environment; Springer International Publishing: New York, NY, USA, 2014; pp. 169–180. [Google Scholar]

| Parameter | Symbol | Value |
|---|---|---|
| Working fluid | He | — |
| Universal gas constant | R | 8.314 J/(K·mol) |
| Specific heat | CP | 5.187×103J/(kg·K) |
| Thermal conductivity | λ | 0.306W/(m·K) |
| Parameter | Symbolor Instruction | Value |
|---|---|---|
| Cylinder bore | Dco | 0.0699 m |
| Stroke | Z | 0.0312 m |
| Space phase angle | Φ | 90° |
| Displacer length | L | 0.04359 m |
| Displacer radial clearance | δ | 0.00015 m |
| Regenerator diameter | DR | 0.0226 m |
| Regenerator length | LR | 0.0226 m |
| Regenerator material | Stainless steel wire | — |
| Hot space temperature | Th | 553 K |
| Warm space temperature | Ta | 338 K |
| Cold space temperature | Tco | 263 K |
| Surrounding temperature | T0 | 273 K |
| Average temperature | 408 K | |
| Average pressure | Pav | 10.0×106 Pa |
| Drive system | Single crank, Double-acting pistons drive | — |
| Rotational speed | n | 600 rpm = 10 Hz |
| Volume ratio | ω | 10 |
| Item | Symbol | Value |
|---|---|---|
| Stroke volume of cold space | Vco | 119.73×10−6 m3 |
| Temperature ratio | τ | 2.1 |
| Pressure phase angle | θ | 85.8° |
| Temperature ratio at cold side | τco | 1.3 |
| Temperature ratio at hot side | τh | 0.6 |
| Pressure factor | 0.2 | |
| Pressure ratio | Pmax/Pmin | 1.5 |
| Maximum pressure | Pmax | 12.4×106 Pa |
| Minimum pressure | Pmin | 8.1×106 Pa |
| Theoretical cooling of cold space | Qco | 4020.1 W |
| Theoretical heat consumption of hot space | Qh | 2948.7 W |
| Theoretical heat rejection of warm space | Qa | 6968.8 W |
| Theoretical exergy efficiency | COPex,i | 0.23 |
| Subject | Symbol | Value |
|---|---|---|
| Reheat loss | ΔQR | 1317.9 W |
| Flow friction loss | ΔQf | 1196.6 W |
| Shuttle loss | ΔQsh | 322.4 W |
| Pumping loss | ΔQp | 0.8 W |
| Wall heat conduction loss | ΔQdw | 6.7 W |
| Filling heat conduction loss | ΔQdm | 1.7 W |
| Heat conduction loss | ΔQd | 8.4 W |
| Leakage loss | ΔQl | 201.0 W |
| Total loss | ΔQ | 3046.9 W |
| Actual cooling | Qco,ac | 1497.3 W |
| Actual heat rejection | Qa,ac | 4769.1 W |
| Actual heat consumption | Qh,ac | 3271.8 W |
| Actual exergy efficiency | COPex,e | 0.15 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Sun, X. Thermodynamic Analysis of a Waste Heat Driven Vuilleumier Cycle Heat Pump. Entropy 2015, 17, 1452-1465. https://doi.org/10.3390/e17031452
Xie Y, Sun X. Thermodynamic Analysis of a Waste Heat Driven Vuilleumier Cycle Heat Pump. Entropy. 2015; 17(3):1452-1465. https://doi.org/10.3390/e17031452
Chicago/Turabian StyleXie, Yingbai, and Xuejie Sun. 2015. "Thermodynamic Analysis of a Waste Heat Driven Vuilleumier Cycle Heat Pump" Entropy 17, no. 3: 1452-1465. https://doi.org/10.3390/e17031452
APA StyleXie, Y., & Sun, X. (2015). Thermodynamic Analysis of a Waste Heat Driven Vuilleumier Cycle Heat Pump. Entropy, 17(3), 1452-1465. https://doi.org/10.3390/e17031452





