1. Introduction
Quantitative measures of graph complexity based on Shannon entropy have been studied extensively since the late 1950s (see Dehmer and Mowshowitz [
1] for an overview). Dehmer, Mowshowitz and Shi [
2] introduced a new measure of this type defined by a vertex decomposition associated with partial Hosoya polynomials. This paper explores the properties of this new measure (called Hosoya entropy) and relates it to existing measures of graph complexity, see [
1,
3–
6].
Entropy-based measures have been used successfully to distinguish between classes of chemical compounds (see, for example, [
3]). Of particular interest is the measure associated with the vertex partition given by the orbits of the automorphism group of a graph. This measure of complexity, capturing the symmetry structure of a graph, marked the start of investigations into graph complexity using Shannon entropy (see [
5]). Computation of this measure requires knowledge of the orbits of the automorphism group, which of course can be determined by constructing the group. Automorphisms (or symmetries) figure prominently in chemical applications, such as interpretation of Nuclear Magnetic Resonance and Infrared spectra as noted by Bohanec and Perdih [
7], who present an improved algorithm for constructing the automorphism group. Other contributions, appearing in the chemical literature, to the challenging problem of finding efficient algorithms for constructing automorphisms, the entire group, or orbits of the group, include the work of Balasubramanian [
8] (concerned with edge weighted graphs), Ivanov [
9] (finding the symmetries that preserve Euclidean distance as a subgroup of the automorphism group), and Figueras [
10] (determining equivalence classes of atoms as orbits of the automorphism group). Studies of this kind form part of the broad concern with characterizing structural complexity addressed by the current paper. It should be noted that graph entropy measures have been applied in many different fields besides chemistry. For example, such measures have been used for characterizing structural patterns in software [
11], for analyzing ontologies represented as networks [
12], and for classifying biological networks [
13].
Given the importance of symmetry in studies of structural complexity, why bother with yet another graph entropy measure? Any partition of the vertices of a graph can be used to define such a measure, and the number partitions of a set of n elements is given by the Bell number B(n). The Bell numbers B0 to B10 range from 1 to 115, 975. Compared to the number of possibilities, it is clear that negligibly few entropy-based measures have been defined and studied so far. Thus, we contend that Hosoya entropy is a welcome addition to the small list inasmuch as it captures important structural features of a graph that have yet to be investigated from the perspective of complexity.
The
Hosoya Polynomial H(
G,
x) [
14] captures distance information about an undirected, connected graph. Its
k-th coefficient is the number of pairs of vertices at distance
k from each other. The first derivative of the Hosoya polynomial evaluted at
x = 1 gives the Wiener index [
15] (
i.e., the sum of the distances beween all pairs of vertices) of a graph. More formally, let
G = (
V,
E) be an undirected, connected graph with vertex set
V and edge set
E where
V = {
v1, …,
vn}. Suppose further that
d =
d(
G) is the diameter of
G (
i.e., the maximum distance between any pair of vertices in G), and that
d(
G,
k) is the number of pairs of vertices in
G at distance k from each other. Then
.
Our main concern here is with
partial Hosoya polynomials [
2,
16] (also called
partial Wiener polynomials [
17]. Let
d(
u,
v) denote the distance between
u and
v in
G. Then the partial Hosoya polynomial with respect to vertex
v is given by
. These partial polynomials can be used in constructing the entire Hosoya polynomial, which has been done in special cases (e.g., [
18]). We use these polynomials here to obtain a decomposition of the vertices. Two vertices
u and
v are said to be
Hosoya-equivalent or H-equivalent if they have the same partial Hosoya polynomial,
i.e., the number of vertices at distance
i is the same for both
u and
v for all
i between 1 and the diameter of
G. Clearly, the family of sets of H-equivalent vertices constitutes a partition of the vertices.
Let
G = (
V,
E) be a connected, undirected graph, and
h the number of sets of H-equivalent vertices in
G. If
ni is the cardinality of the i-th set of H-equivalent vertices for 1 ≤
i ≤
h, the Hosoya entropy (or H-entropy) of
G (introduced in [
19]) is given by
The H-equivalence partition can be found from the distance matrix D(G) = (dij), 1 ≤ i, j ≤ n of a connected graph G with n vertices, where dij is the distance (or length of a shortest path) between vertices vi and vj. Thus, the respective numbers of elements in the i-th row equal to r for 1 ≤ r ≤ d are the coefficients of the partial Hosoya polynomial of vi. We will refer to these numbers, listed by distance, as the Hosoya profile or H-profile of vi. So, two vertices with the same H-profile, as found from the distance matrix, are H-equivalent.
Bonchev [
3] defines a related entropy-based measure using the distance matrix. Let
nk be the number of entries in
D(
G) equal to
k (0 ≤
k ≤
d). The measure in question is then the entropy of the finite probability scheme given by the
d + 1 probabilities
. This measure is quite different from Hosoya entropy. Yet another related measure defined by Bonchev uses what he calls the Hosoya decomposition of a graph [
3]. This decomposition is given by the family of matchings of orders zero through the maximum order
max. Once again a finite probability scheme is constructed with elements
nk/
N where
nk is the number of matchings of order
k (0 ≤
k ≤
max) and
N is the total number of matchings. The entropy of this scheme is called the information index on the Hosoya graph decomposition. This measure too is quite different from what we call Hosoya entropy.
A very small example, namely P4 (a path with 3 edges), illustrates the differences between these measures. The finite probability scheme for Bonchev’s measure based on the distance matrix is
. The scheme for the measure based on matchings is
. Finally, the scheme for Hosoya entropy is
.
In the sequel we will explore basic properties of Hosoya entropy and relate it to the classical measure of graph complexity.
2. Elementary Properties
The value of H(G) for a graph G with n vertices is between 0 and log(n). The minimum is achieved when all the vertices are H-equivalent; the maximum is reached when no two vertices of G are H-equivalent. Complete graphs and cycles have H-entropy 0. Another class of graphs with 0 H-entropy is given in the following theorem.
Theorem 1. If G is a connected, r-regular graph with h ≤ 2, then H(G) = 0.
Proof. If its diameter is 1, G must be complete and thus has H-entropy 0. Suppose the diameter of G is 2. Since G is r-regular, the i − th row of its distance matrix consists of r 1′s and n − 1 − r 2′s, with a 0 in the i − th column, for 1 ≤ i ≤ n. So, all the rows of the distance matrix are permutations of each other, and hence the vertices are all H-equivalent. □
Corollary 1. If G is a regular, complete bigraph, H(G) = 0.
Proof. Since G is complete bipartite, its diameter is at most 2, and given that it is regular, G satisfies the conditions of the theorem. □
Note that every vertex in a graph with 0 H-entropy has the same eccentricity and the radius of the graph coincides with the diameter.
Regular graphs of degree > n/2 also have 0 H-entropy.
Theorem 2. If G is a connected, regular graph of degree > n/2, H(G) = 0.
Proof. Consider the product of any row of the distance matrix D(G) with any of its columns. Since G is regular of degree > n/2 each row (and column) of D(G) consists of at least n/2 1′s, and by the pigeon hole principle there must me at least one pair of 1′s in a common position which means the product must be positive. Thus, D2 > 0 which means the diameter of G is at most 2, and by the previous theorem, H(G) = 0. □
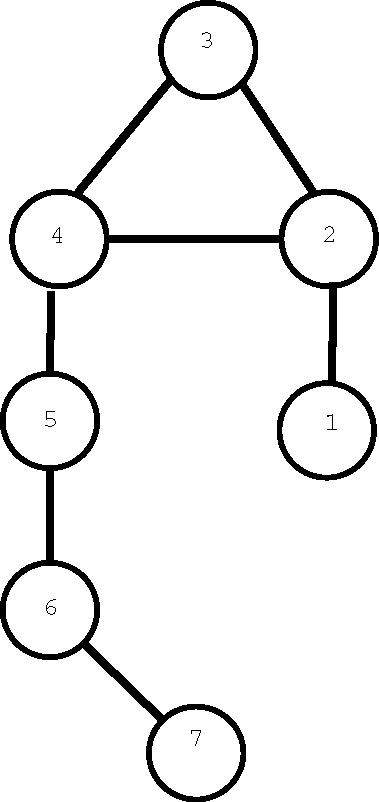
Graphs with H-entropy log(n) are more difficult to characterize. The following figure shows the smallest graph with maximum H-entropy. Adding a vertex and joining it to 7 produces a graph on eight vertices with H-entropy log(8). Continuing in this way (adding a new vertex and joining it to the one with the highest label) we can generate an infinite class of graphs with maximum H-entropy.
We will see in Section 3 that if no pair of vertices in a connected graph are H-equivalent, the graph must have a trivial automorphism group. However, the converse is not true, so maximum H-entropy graphs form a subset of graphs with trivial group.
In general, H-entropy depends on the structure rather than the size of a graph. Cycles and complete graphs of every order have H-entropy 0. On the other hand, the H-entropy of path graphs increases monotonically with the number of vertices.
The distance matrix of a connected graph can be used to investigate the likelihood of particular values of H-entropy. This follows from the fact that two vertices are H-equivalent if the rows representing them in the distance matrix are permutations of each other. Repetitions are allowed in these permutations, since in general several elements in a given row may have the same numerical value. To illustrate, consider the problem of estimating the likelihood of zero H-entropy, i.e., the case in which all the vertices are H-equivalent and thus all the rows of the distance matrix are permutations of each other. Apart from the constraints of graph structure, the configuration of a row in D(G) depends on two parameters, namely, the number n of vertices and the diameter d of G - there are n elements in the row and they vary between 1 and d, apart from a single 0. So, excluding 0 the number of possible rows R is given by R = d!S(n, d) where S(n, d) denotes a Stirling number of the second kind. d!S(n, d) is the number of ways of placing the n distinct row indices into d different containers representing the distinct elements 1, 2, …, d with no container empty. Ignoring graph structure, choosing each of n rows independently gives a probability of (Rn)−1 for all n rows to be permutations of each other. Admittedly this value is far smaller than the actual probability since not all the permutations are consistent with the structural constraints of the graph. However, this approach provides a useful framework for investigating the problem.
3. Hosoya Entropy and Information Content
The information content
I(
G) of a graph
G, a measure introduced in the late 1950’s (see [
1] for a review), applies the Shannon entropy function to a finite probability scheme associated with the orbits of the automorphism group of a graph. This measure applies to directed and undirected, disconnected as well as connected graphs. The relationship between
I(
G) and
H(
G) derives from the fact that two vertices of a connected graph are H-equivalent if they are similar.
Theorem 3. Let G be a connected graph with automorphism group Aut(T). If vertices u and v of G are similar (i.e., belong to the same orbit of Aut(T)), they are H-equivalent.
Proof. Suppose u and v are similar, and let S(x) denote the Hosoya profile of vertex x. Let ki be an element of S(u), i.e, ki denotes the number of vertices at distance i from u, where 1 ≤ i ≤ h and h is the diameter of G. If S(u) ≠ S(v), then there is a ki ∈ S(u) such that ki ∉ S(v). Let
be the vertices whose distance from u is i. Then there is a path of length i from u to one of the wj that does not correspond to any path of length i from v, contradicting the similarity of u and v. □
The theorem allows for obtaining bounds on H(G) for several classes of graphs, and is useful for determining Aut(G) since vertices with different H-profiles cannot be similar.
Corollary 2. (1) If Aut(G) is transitive, then H(G) = 0.
(2) Let G + K denote the join of graphs G and K. Then H(G + K) ≤ I(G + K) and H(nG) ≤ I(G), where nG denotes the join of n disjoint copies of G.
(3) Let G × K and G ⊗ K denote the cartesian and wreath products, respectively, of G and K. Then H(G × K) ≤ I(G × K) and H(G ⊗ K) ≤ I(G ⊗ K)
Proof. (1) If Aut(G) is transitive, all the vertices of G are H-equivalent.
(2) The partition of V (G + K) given by H-equivalence must, according to the Theorem be coarser than the partition associated with Aut(G + K), i.e., blocks in the Hosoya partition may be unions of orbits of Aut(G). The second part of the statement follows from the fact that H(nG) ≤ I(nG) = I(G).
(3) As in the case of joins, the blocks in the partitions associated with the cartesian and wreath products may also be unions of orbits, thus resulting in H-entropy at most that of information content. □
Unlike the information content measure for which
, the H-entropy of
(assuming
G complement is connected), is not the same as
H(
G). For example, the graph
G in
Figure 1 has
H(
G) =
log(7) = 2.807 but
. More generally, for
n ≥ 7 a regular
n-vertex graph of degree smaller than
with identity group, might have H-entropy close to
log(
n) but the complement (if connected) would have H-entropy 0. This is a consequence of Theorem 2.3.
Theorem 4. There exist connected graphs with zero H-entropy whose automorphism groups are not transitive.
Proof. Let
G be a regular
n-vertex graph of degree 3 for which
Aut(
G) is not transitive. Such exists by a well known theorem of Frucht [
20]. If
n ≥ 7, the complement of
G (which has the same automorphism group as
G) is regular of degree >
, and by Theorem 2.2,
. □
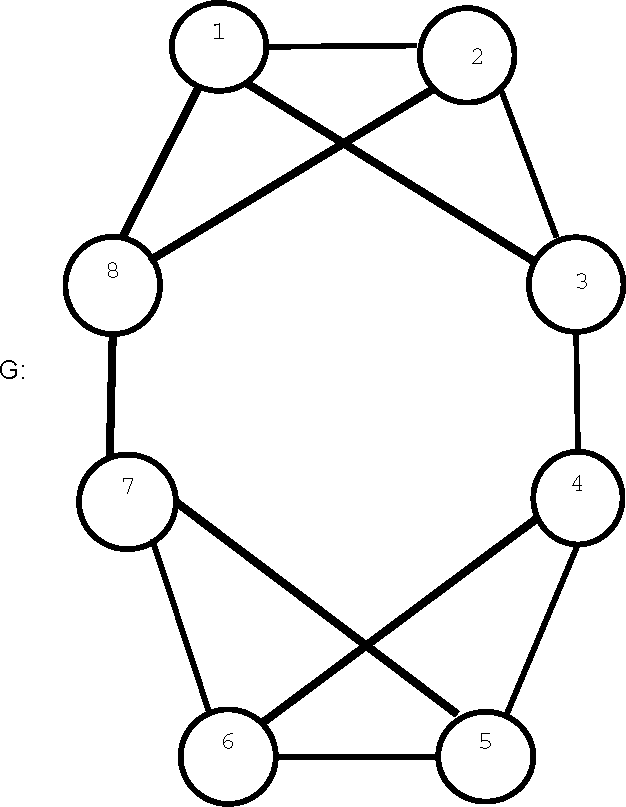
The automorphism group of graph
G in
Figure 2 has two orbits consisting of vertices 1, 2, 5, 6 and 3, 4, 7, 8, respectively, and these orbits have different H-profiles, so that the
H(
G) = 1. However,
, with the same group and orbit structure as G has H-entropy 0.
4. Hosoya Entropy of Trees
The H-entropy of some simple classes of trees is summarized in the following theorem.
Theorem 5. (1) Let Pn denote the path on n vertices, and let k ≥ 1. (a) H(Pn) = log(k), if n = 2k, (b), if n = 2k + 1.
(2) Let Sn denote the star for n ≥ 3. Then.
Proof. (1) The H-equivalence partition of the vertices Pn is the same as the orbit structure of its automorphism group. For n = 2k there are k equivalence classes of size 2; for n = 2k + 1 there are k equivalence classes of size 2 and one of size 1.
(2) The star Sn also enjoys the same H-equivalence partition as its orbit structure, namely one class of size n − 1 and one of size 1. □
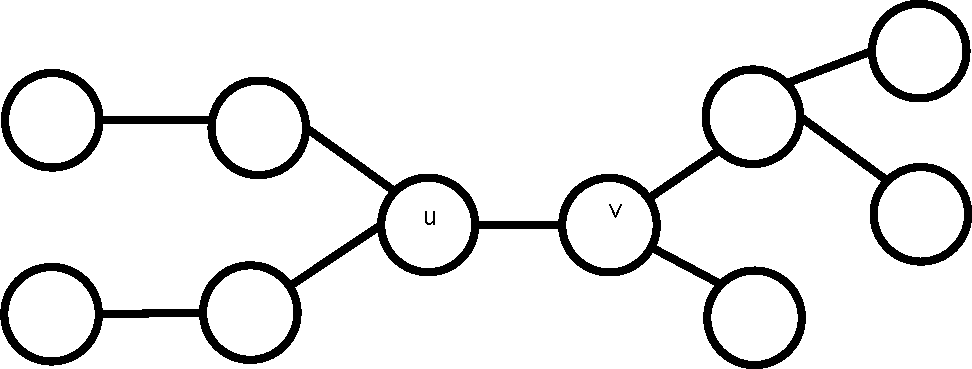
One might think that in the special case of trees, H-equivalence of vertices would imply similarity, but this is not true as shown by the counterexample in
Figure 3.
The tree in the figure is the smallest such counterexample. To show this we define the level (≥ 1) of a vertex v in a tree T as the maximum distance of any vertex from v. The demonstration is divided into cases according to the level of the two similar vertices. If both are level one, T must be K2. For level two, there are two subcases: both vertices are of degree one or two. Level three subdivides into three subcases: both vertices being of degree one, two, or three. For level greater than three, it is immediately evident that T must have at least ten vertices. In all the cases, it is obvious that either the two vertices cannot be H-equivalent or T has at least ten vertices.
This example can be extended to a tree representing a simple hydrocarbon with 10 vertices of degree 4 (carbon atoms) and 22 vertices of degree 1 (hydrogen atoms) in which two of the carbon vertices have the same Hosoya profile but are not similar. Compounds like this for which the Hosoya entropy differs from automorphism based entropy may have useful chemical properties.
Rootings of a tree at each of two similar vertices facilitates investigation of the relationship between H-equivalence and orbits.
Theorem 6. Vertices u and v in a tree T are similar if and only if the trees Tu and Tv rooted at u and v respectively are isomorphic.
Proof. Suppose the rootings of
T,
Tu and
Tv rooted at
u and
v, respectively, are isomorphic, and that
ϕ is the isomorphism mapping
Tu onto
Tv. Clearly,
u and
v are similar since
ϕ can be seen as automorphism of
T taking u to
v. Conversely, let
u and
v be similar vertices of
T, and suppose
σ ∈ Aut(
T) such that
σ(
u) =
v. Without loss of generality we can assume that
σ(
u) =
v, since
T is a tree [
21]. For any vertices
x,
y in
T let [
x,
y] denote the unique path in
T between
x and
y. Now,
σ[
u,
x] = [
σ(
u),
σ(
x)] = [
v,
y] where
σ(
x) =
y. Let
x ≠
u be a vertex of
Tu. Consider the path [
u,
x] in
Tu. We have
σ[
u,
x] = [
σ(
u),
σ(
x)] = [
v,
y]. Note that [
v,
y] is a path in
Tv. Since every edge in
Tu is on a path from
u, and every edge in
Tv is on a path from
v, then every edge ab in
Tu corresponds to the edge
σ(
a)
σ(
b) in
Tv, showing the two rootings to be isomorphic, which concludes the proof. □
5. Conclusion
This paper has initiated an investigation of Hosoya entropy, a newly defined measure of graph complexity, related to a growing list of measures dating back to the 1950s [
1,
3–
6]. This measure may be of special interest in distinguishing chemical molecules. We have shown that similarity of vertices is a sufficient, but not necessary, condition for H-equivalence, and demonstrated the utility of the distance matrix of a graph in determining such equivalence. We plan to explore further the use of Hosoya entropy in quantitative measurement of similarity. Finding a necessary condition for H-equivalence for graphs in general and for trees in particular present challenging open problem. Characterizing graphs with minimum and maximum H-entropy also remains an open problem.