1. Introduction
Probabilistic conditional knowledge bases containing conditionals of the form (
B|A)[
d] with the reading “
if A, then B with probability d” are a powerful means for knowledge representation and reasoning when uncertainty is involved [
1,
2]. If
A and
B are propositional formulas over a propositional alphabet Σ, possible worlds correspond to elementary conjunctions over Σ, where an elementary conjunction is a conjunction containing every element of Σ exactly once, either in non-negated or in negated form. A possible worlds semantics is given by probability distributions over the set of possible worlds, and a probability distribution
P satisfies (
B|A)[
d] if for the conditional probability
the relation
P (
B|A) =
d holds. For a knowledge base
consisting of a set of propositional conditionals,
P is a model of
if
P satisfies each conditional in
. The principle of maximum entropy (ME principle) is a well-established concept for choosing the uniquely determined model of
having maximum entropy. This model is the most unbiased model of
in the sense that it completes the knowledge given by
inductively but adds as little additional information as possible [
3–
9].
While for a set of propositional conditionals there is a general agreement about its ME model, the situation changes when the conditionals are built over a relational first-order language. As an illustration, consider the following example.
Example 1 (Elephant Keeper).
The elephant keeper example, adapted from [
10,
11],
models the relationships among elephants in a zoo and their keepers. Elephants usually like their keepers, except for keeper Fred. However, elephant Clyde gets along with everyone, and therefore he also likes Fred. The knowledge base EK consists of the following conditionals: Conditional ek1 models statistical knowledge about the general relationship between elephants and their keepers, whereas conditional ek2 represents knowledge about the exceptional keeper Fred and his relationship to elephants in general. Conditional ek3 models the subjective belief about the relationship between the elephant Clyde and keeper Fred. From a common sense point of view, the knowledge base EK makes perfect sense: conditional ek2 is an exception from ek1, and ek3 is an exception from ek2.
When trying to extend the ME principle from the propositional case to such a relational setting, a central question is how to interpret the free variables occurring in a conditional. For instance, note that a straightforward complete grounding of EK yields a grounded knowledge base that can be viewed as a propositional knowledge base. However, this grounded knowledge is inconsistent since it contains both (likes(clyde, fred)|elephant(clyde), keeper(fred))[0.9] and (likes(clyde, fred)|elephant(clyde), keeper(fred))[0.05], and no probability distribution P can satisfy both P (likes(clyde, fred)|elephant(clyde), keeper(fred)) = 0.9 and P (likes(clyde, fred)|elephant(clyde), keeper(fred)) = 0.05.
Thus, when extending the ME principle to the relational case with free variables as in
EK, the exact role of the variables has to be specified. There are various approaches dealing with a combination of probabilities with a first-order language (e.g., [
12,
13]); a comparison and evaluation of some approaches is given [
14]). In the following, we focus on two semantics that both employ the principle of maximum entropy for probabilistic relational conditionals, the
aggregation semantics [
15] proposed by Kern-Isberner and the logic FO-PCL [
16] elaborated by Fisseler. While both approaches are related in the sense that they refer to a set of constants when interpreting the variables in the conditionals, there is also a major difference. FO-PCL requires all groundings of a conditional to have the same probability
d given in the conditional, and in general, FO-PCL needs to restrict the possible instantiations for the variables occurring in a conditional by providing constraint formulas like
U ≠
V or
U ≠
a in order to avoid inconsistencies. On the other hand, under aggregation semantics the grounded instances may have distinct probabilities as long as they aggregate to the given probability
d, and aggregation semantics is defined only for conditionals without constraint formulas.
In this paper, a logical framework PCI extending aggregation semantics to conditionals with instantiation restrictions and also providing a grounding semantics is proposed. From a knowledge representation point of view, this provides greater flexibility, e.g., when expressing knowledge about individuals known to be exceptional with respect to some relationship. We show that both the aggregation semantics of [
15] and the semantics of FO-PCL [
16] come out as special cases of PCI, thereby also helping to clarify the relationship between the two approaches. Moreover, we investigate the ME models under PCI-grounding and PCI-aggregating semantics, which are different in general, and we give a condition on knowledge bases ensuring that both ME semantics coincide.
This paper is a revised and extended version of [
17] and is organized as follows. In Section 2, we very briefly recall the background of FO-PCL and aggregation semantics. In Section 3, the logic framework PCI is developed and two alternative satisfaction relations for grounding and aggregating semantics are defined for PCI by extending the corresponding notions of [
15,
16]. In Section 4, the maximum entropy principle is employed with respect to these satisfaction relations; we show that the resulting semantics coincide for knowledge bases that are
parametrically uniform [
11,
16]. In Section 5, we present and discuss ME distributions for some concrete knowledge bases both under PCI-grounding and PCI-aggregating semantics, and point out their differences and common features, covering in particular the groundings of the given conditionals. Finally, in Section 6 we conclude and point out further work.
2. Background: FO-PCL and Aggregation Semantics
As already pointed out in Section 1, simply grounding a relational knowledge base
easily leads to inconsistency. Therefore, the logic FO-PCL [
11,
16] employs instantiation restrictions for the free variables of a conditional. An FO-PCL conditional has additionally a constraint formula determining the
admissible instantiations of free variables, and the grounding semantics of FO-PCL requires that all admissible ground instances of a conditional
c must have the probability given by
c.
Example 2 (Elephant Keeper with instantiation restrictions).
In FO-PCL, adding K ≠ fred to conditional ek1 and E ≠ clyde to conditional ek2 in EK yields the knowledge base ′EK with: Note that, e.g., the ground instance (
likes(
clyde, fred)
|elephant(
clyde),
keeper(
fred))[0.05]
of conditional ek′2 is not admissible, and that the set of admissible ground instances of ′EK is indeed consistent under probabilistic semantics for propositional knowledge bases as considered, e.g., in [
8,
18].
Thus, under FO-PCL semantics, ′EK is consistent, where a probability distribution P satisfies an FO-PCL conditional r, denoted by
, iff all admissible ground instances of r have the probability specified by r.
In contrast, the aggregation semantics, as given in [
15], does not consider instantiation restrictions, since its satisfaction relation (in this paper denoted by
to indicate
no instantiation
restriction), is less strict with respect to probabilities of ground instances:
(
B|A)[
d] iff the quotient of the sum of all probabilities
P (
Bi ∧
Ai) and the sum of
P (
Ai) is
d, where (
B1|A1)
,…, (
Bn|An) are the ground instances of (
B|A). In this way, the aggregation semantics is capable of balancing the probabilities of ground instances, resulting in greater flexibility and higher tolerance with respect to consistency issues. Provided that there are enough individuals so that the corresponding aggregation over all probabilities is possible, the knowledge base
EK that is inconsistent under FO-PCL semantics is consistent under aggregation semantics.
3. PCI Logic
The logical framework PCI (
probabilistic
conditionals with
instantiation restrictions) uses probabilistic conditionals with and without instantiation restrictions and provides different options for a satisfaction relation. The syntax of PCI given in [
19] uses the syntax of FO-PCL [
11,
16]. In the following, we will precisely state the formal relationship among
,
, and the satisfaction relations offered by PCI.
As FO-PCL, PCI uses function-free, sorted signatures of the form Σ = (
, mathvariant='script'
, Pred). In a PCI-signature Σ = (
,
, Pred),
= {s1,…, sk} is a set of sort names or just sorts. The set
is a finite set of constants symbols where each d ∈ has a unique sort s ∈. With
we denote the set of all constants having sort s; thus
is a set being the union of (disjoint) sets of sorted constant symbols. Pred is a set of predicate symbols, each having a particular number of arguments. If p ∈ Pred is a predicate taking n arguments, each argument position i must be filled with a constant or variable of a specific sort si. Thus, each p ∈ Pred comes with an arity of the form s1 ×…× sn ∈ indicating the required sorts for the arguments. Variables
also have a unique sort, and all formulas and variable substitutions must obey the obvious sort restrictions. In the following, we will adopt the unique names assumption, i.e., different constants denote different elements. The set of all terms is defined as
. Let Σ be the set of quantifier-free first-order formulas defined over Σ and
in the usual way.
Definition 1 (Instantiation Restriction). An instantiation restriction is a conjunction of inequality atoms of the form t1 ≠ t2 with t1, t2 ∈ TermΣ. The set of all instantiation restriction is denoted by CΣ.
Since an instantiation restriction may be a conjunction of inequality atoms, we can express that a conditional has multiple restrictions, e.g., by stating E ≠ clyde ∧ K ≠ fred.
Definition 2 (q-, p-, r-Conditional).
Let A, B ∈ Σ be quantifier-free first-order formulas over Σ
and.
(B|A) is called a qualitative conditional (or just q-conditional). Note that A is the antecedence and B the consequence of the qualitative conditional. The set of all qualitative conditionals over Σ is denoted by (Σ|Σ).
Let (B|A) ∈ (Σ|Σ) be a qualitative conditional and let d ∈ [0, 1] be a real value. Here (B|A)[d] is called a probabilistic conditional (or just p-conditional) with probability d. The set of all probabilistic conditionals over Σ is denoted by (Σ|Σ)prob.
Let (B|A)[d] ∈ (Σ|Σ)prob be a probabilistic conditional and let C ∈ CΣ be an instantiation restriction. In addition, 〈(B|A)[d], C〉 is called an instantiation restricted conditional (or just r-conditional). The set of all instantiation restricted conditionals over Σ is denoted by.
Instantiation restricted qualitative conditionals are defined analogously. If it is clear from the context, we may omit qualitative, probabilistic, and instantiation restricted and just use the term conditional.
Definition 3 (PCI knowledge base). A pair (Σ, ) consisting of a PCI signature and a set of instantiation restricted conditionals = {r1,…, rm} with ri ∈
is called a PCI knowledge base.
For an instantiation restricted conditional r = 〈(B|A)[d], Ci, ΘΣ(r) denotes the set of all ground substitutions with respect to the variables in r. A ground substitution θ ∈ ΘΣ(r) is applied to the formulas A, B and C in the usual way, i.e., each variable is replaced by a certain constant according to the mapping θ = {v1/c1,…, vl/cl} with vi ∈
, ci ∈
, 1 ≤ i ≤ l. Therefore, θ(A), θ(B), and θ(C) are ground formulas and we have θ((B|A)) := (θ(B)|θ(A)).
Given a ground substitution θ over the variables occurring in an instantiation restriction C ∈, the evaluation of C under θ, denoted by
, yields true iff θ(t1) and θ(t2) are different constants for all t1 ≠ t2 ∈ C.
Definition 4 (Admissible Ground Substitutions and Instances).
Let Σ = (
,
,
Pred)
be a many-sorted signature and let r = 〈(
B|A)[
d],
C〉 ∈
be an instantiation restricted conditional. The set of admissible ground substitutions
of r is defined as The set of admissible ground instances
of r is defined as In the following, when we talk about the ground instances of a conditional, we will always refer to its admissible ground instances.
As for an FO-PCL knowledge base [
11], for a PCI knowledge base (Σ,
) we define the
Herbrand base (
) as the set of all ground atoms in all
gndΣ(
ri) with
ri ∈ . Every subset
ω ⊆
(
) is a
Herbrand interpretation, defining a logical semantics for
. The set Ω
Σ := {
ω | ω ⊆
(
)} denotes the set of all Herbrand interpretations. Herbrand interpretations are also called
possible worlds.
Definition 5 (PCI Interpretation).
The probabilistic semantics of (Σ,
) is a possible worlds semantics [
12]
where the ground atoms in (
)
are binary random variables. A PCI interpretation
P of a knowledge base (Σ,
) is thus a probability distribution P : Ω
Σ → [0, 1].
The set of all probability distributions over Ω
Σ is denoted by or just by.
The PCI framework offers two different satisfaction relations:
is based on grounding as in FO-PCL, and
extends aggregation semantics to r-conditionals.
Definition 6 (PCI Satisfaction Relations).
Let P ∈ and let 〈(
B|A)[
d],
C〉 ∈
be an r-conditional with.
The two PCI satisfaction relations andare defined by:We say that P satisfies 〈(
B|A)[
d],
C〉
under PCI-grounding semantics
.
Correspondingly, P satisfies 〈(
B|A)[
d],
C〉
under PCI-aggregation semantics
.
As usual, the satisfaction relations
with ★ ∈ {△, ⊛} are extended to a set of conditionals
by defining
The following proposition states that PCI properly captures both the instantiation-based semantics
|=
fopcl of FO-PCL [
11] and the aggregation semantics
of [
15] (cf. Section 2).
Proposition 1 (PCI captures FO-PCL and aggregation semantics [
19]).
Let 〈(
B|
A)[
d];
C〉
be an r-conditional and let (
B|
A)[
d]
be a p-conditional, respectively. Then the following holds: 4. PCI Logic and Maximum Entropy Semantics
If a knowledge base
is consistent, there are usually many different models satisfying
. The principle of maximum entropy chooses the unique distribution that has maximum entropy among all distributions satisfying a knowledge base
[
5,
8]. Applying this principle to the PCI satisfaction relations
and
yields
with ★ being △ or ⊛, and where
is the
entropy of a probability distribution
P.
Example 3 (Misanthrope).
The knowledge base MI = {
R1,
R2},
adapted from [
11],
models friendship relations within a group of people with one exceptional member, a misanthrope. In general, if a person V likes another person U, then it is very likely that U likes V, too. However, there is one person, the misanthrope, who generally does not like other people:Within the PCI framework, consider MI together with constants and the corresponding ME distributions ME△(
MI)
and ME⊛(
MI)
under PCI-grounding and PCI-aggregation semantics, respectively.
Under ME△(MI), all six ground conditionals emerging from R1 have probability 0.9, for instance, ME△(MI)(likes(a, b) | likes(b, a)) = 0.9.
On the other hand, for the distribution ME⊛(MI), we have ME⊛(MI) (likes(a, b) | likes(b, a)) = 0.46016768 and ME⊛(MI)(likes(a, c) | likes(c, a)) = 0.46016768, while the other four ground conditionals resulting from R1 have probability 0.96674480.
Example 3 shows that in general the ME model under PCI-grounding semantics of a knowledge base
differs from its ME model under PCI-aggregation semantics. However, if
is
parametrically uniform [
11,
16], the situation changes. Parametric uniformity of a knowledge base
is introduced in [
11] and refers to the fact that the ME distribution under FO-PCL (or PCI-grounding) semantics satisfying a set of
m ground conditionals can be represented by a set of just
m optimization parameters. A relational knowledge base
is parametrically uniform iff for every conditional
r ∈ ,
all ground instances of
r have the
same optimization parameter (see [
11,
16] for details). For instance, the knowledge base
′
EK from Example 2 is parametrically uniform, while the knowledge base
MI from Example 3 is not parametrically uniform. Thus, if
is parametrically uniform, just
one optimization parameter for each conditional
r ∈ instead of one optimization parameter for
each ground instance of r has to be computed; this can be exploited when computing the ME distribution [
17]. In [
20], a set of transformation rules is developed that transforms any consistent knowledge base
into a knowledge base
′ such that
and
′ have the same ME model under grounding semantics and
′ is parametrically uniform.
Using the PCI framework providing both grounding and aggregating semantics for conditionals with instantiation restrictions, the ME models for PCI-grounding and PCI-aggregation semantics coincide if is parametrically uniform.
Proposition 2 ([
19]).
Let be a PCI knowledge base. If is parametrically uniform, then ME△(
) =
ME⊛(
).
Thus, while in general ME△() ≠ ME⊛(R), parametric uniformity of ensures that ME△() = ME⊛().
5. Computation and Comparison of Maximum Entropy Distributions
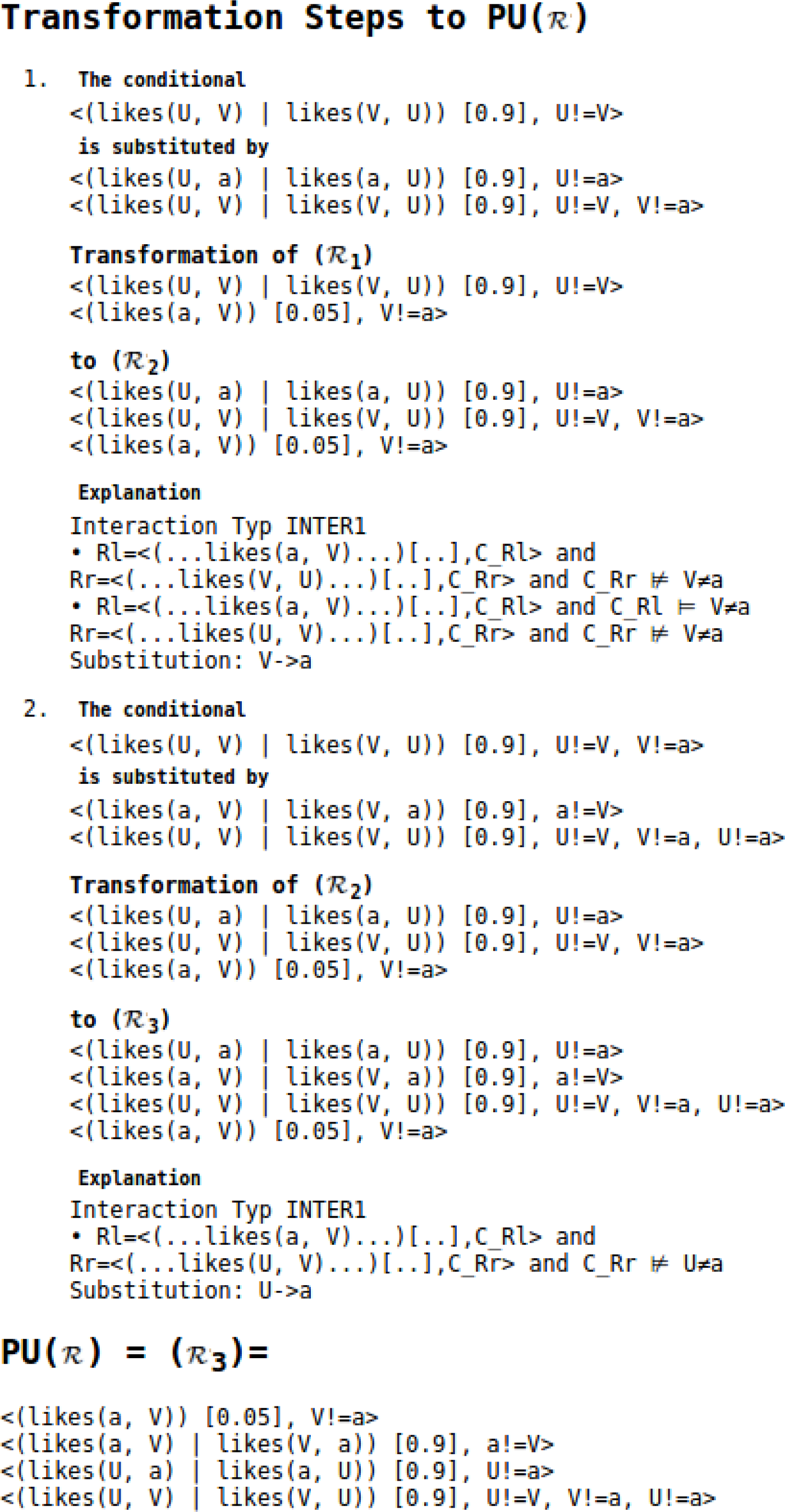
In Example 3 we already presented some concrete probability values for ME distributions. We will now look into more details of the ME distributions obtained from both PCI-grounding and PCI-aggregation semantics. In particular, we will illustrate how the ME distribution for PCI-grounding and PCI-aggregation semantics evolve when transforming a knowledge base that is not parametrically uniform into a knowledge base that is parametrically uniform.
5.2. Maximum Entropy Distributions for Grounding and Aggregation Semantics
Using KREATOR we computed the ME distributions for the three knowledge bases
1,
2, and
3 involved in the
transformation of
MI for both PCI-grounding and PCI-aggregation semantics. For all admissible ground instances of the conditionals occurring in
1,
2 and
3, we computed their probability under the ME distributions for PCI-grounding and PCI-aggregation semantics. The results are shown in
Table 2, using the abbreviation
l(
x, y) for
likes(
x, y).
There are three pairwise different ME distributions (i.e., ME⊛(1), ME⊛(2), ME⊛(3)) under PCI-aggregation semantics for the three pairwise different knowledge bases 1, 2, 3. On the other hand ME△(1) = ME△(2) = ME△(3) = ME⊛( 3) holds since the
transformation process does not change the maximum entropy model under PCI-grounding semantics and because 3 is parametrically uniform.
It is interesting to note that for the ground instances originating from R1 there are two distinct probabilities under ME⊛(1), three probabilities under ME⊛(2), and as implied by Proposition 2 one probability under ME⊛(3). In all cases, PCI-aggregation semantics ensures that the distinct probabilities aggregate to the probability stated in the corresponding conditionals.
For the comparison of PCI-grounding and PCI-aggregation, it is also interesting to compare their ME behavior with respect to queries that are not instances of a conditional given in the knowledge base. For example, for
likes(
b, c) we observe
and for
likes(
b, a) we get
for PCI-aggregation semantics, while
holds for
i ∈ {1, 2, 3} under PCI-grounding semantics.
6. Conclusions and Further Work
In this paper, we considered maximum entropy based semantics for relational probabilistic conditionals. FO-PCL [
16] employs a grounding semantics and uses instantiation restrictions for the free variables occurring in a conditional, requiring all admissible instances of a conditional to have the given probability. Aggregating semantics [
15] defines probabilistic satisfaction by interpreting the intended probability of a conditional with free variables only as a guideline for the probabilities of its instances that aggregate to the conditional’s given probability, while the actual probabilities for grounded instances may differ.
While the original definition of aggregation semantics [
15] considered only conditionals without constraints representing instantiation restrictions, we developed the framework PCI extending aggregation semantics so that instantiation restrictions can also be taken into account, but without giving up the flexibility of aggregating over distinct probabilities. In comparison with [
15], under PCI-aggregation semantics one can restrict the set of groundings of a conditional over which aggregating with respect to a conditional takes place by providing a corresponding constraint formula for the conditional. From a knowledge representation point of view, this can be useful in various situations, for instance when we talk about a particular relationship among individuals while already knowing that a specific individual like Clyde is an exception with respect to the given relationship.
Note that PCI captures both grounding semantics and aggregating semantics without instantiation restrictions as special cases. For the case that a knowledge base is parametrically uniform, PCI-grounding and PCI-aggregation semantics coincide when employing the maximum entropy principle, while for a knowledge base that is not parametrically uniform the two ME semantics induce different models in general. We illustrated the differences and common features of both semantics on a concrete knowledge base, using the KREATOR environment for computing the ME models and answering queries with respect to these distributions. We expect that observations of this kind will support the discussion of both formal and common sense properties of probabilistic first-order inference in general and inference according to the principle of maximum entropy in a first-order setting in particular.