Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory
Abstract
:1. Introduction
2. Classical Probabilities
3. Quantum Probabilities
3.1. Elementary Tests in Quantum Mechanics
3.2. von Neumann’s Axioms
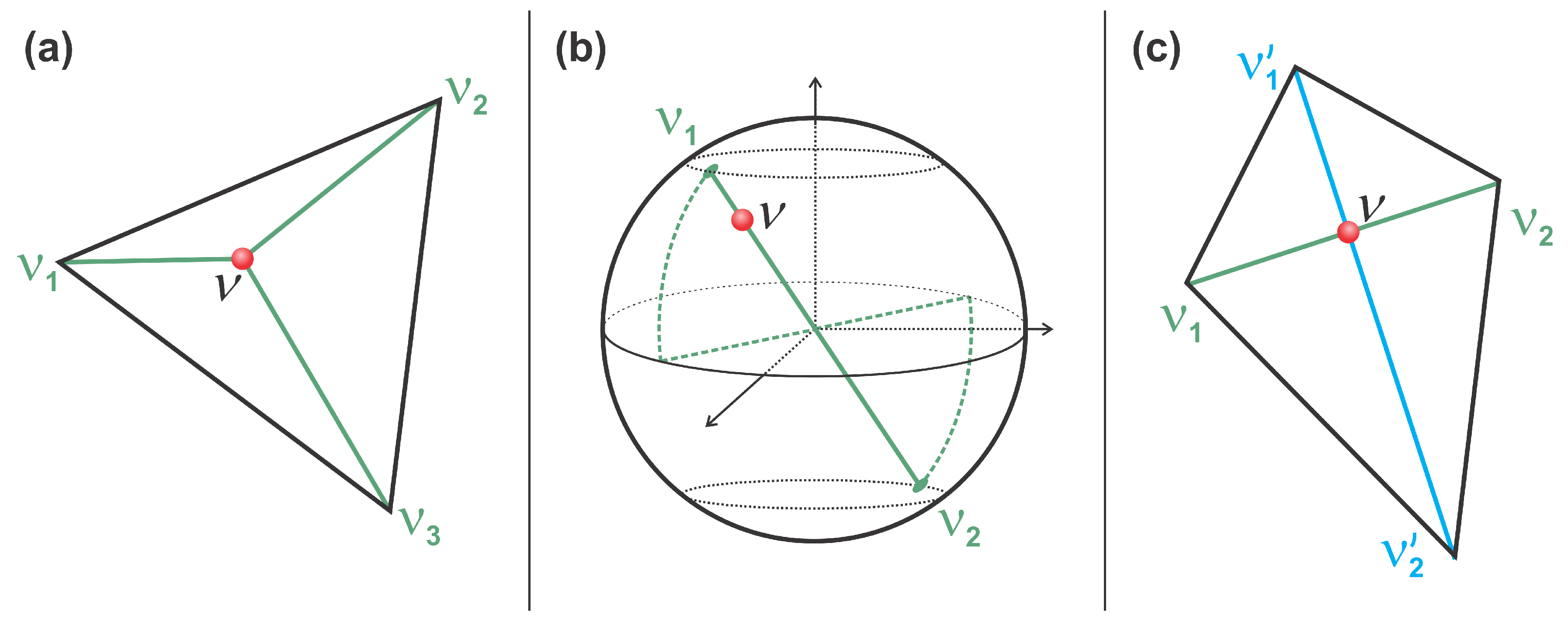
3.3. Quantum Correlations
4. Generalized Setting
4.1. Non-Kolmogorovian Information Theory and Contextuality
- R.T. Cox [72,73] showed that if a rational agent is confronted with a Boolean algebra representing empirical events, then any function measuring his degree of belief of the occurrence of any event must be equivalent to a classical probability calculus. In [112], it is shown that if a rational agent is confronted with a non-distributive algebra of physical events, then the consistent probabilities must be those of Equation (9).
- In a similar way, in the Cox approach (see [59] and the references therein), it is shown that Shannon’s entropy:is the most natural information measure for an agent confronted with a Boolean algebra of events. In other words, when only one empirical context is involved and the probabilities are measures defined in a Boolean algebra, such as those of Equation (1), then Shannon’s measure is a natural choice. In the quantum case, the probability distribution must be replaced by a state represented as a density matrix ρ. Now, as explained above, we have a classical probability distribution for each empirical context. This implies that the information measure has to be modified in such a way that Shannon’s measure is obtained when the quantum measure is restricted to a Boolean subalgebra of . As is well known, the von Neumann entropy:does the job. These ideas can be made more precise, both from the formal and the operational points of view. Indeed, in [59], it is shown that, if the Boolean algebra is replaced by a non-Boolean one (such as or more general ones), then the von Neumann and measurement entropies must be used (we refer the reader to [59] for the details of the derivation). In other words: if the event algebras are non-Boolean, then probabilities will be non-Kolmogorovian, and then, the information measures will depart from Shannon’s entropy and more general classical ones (we will discuss the specific form of this departure in Section 5).
4.2. Communication and Correlations in the Generalized Setting
5. Generalized Entropies and Majorization
5.1. Entropies and Majorization in Classical and Quantum Theories
5.2. Entropies and Majorization in General Probabilistic Theories
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bub, J. Quantum mechanics is about quantum information. Found. Phys. 2005, 35, 541–560. [Google Scholar] [CrossRef]
- Popescu, S. Nonlocality beyond quantum mechanics. Nat. Phys. 2014, 10, 264–270. [Google Scholar] [CrossRef]
- Amaral, B.; Cunha, M.T.; Cabello, A. Exclusivity principle forbids sets of correlations larger than the quantum set. Phys. Rev. A 2014, 89, 030101. [Google Scholar] [CrossRef]
- Cabello, A. Exclusivity principle and the quantum bound of the Bell inequality. Phys. Rev. A 2014, 90. [Google Scholar] [CrossRef]
- Clifton, R.; Bub, J.; Halvorson, H. Characterizing quantum theory in terms of information-theoretic constraints. Found. Phys. 2003, 33, 1561–1591. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1935; Volume 31, pp. 555–563. [Google Scholar]
- Schrödinger, E. Probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 1936, 32, 446–452. [Google Scholar] [CrossRef]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277–4281. [Google Scholar] [CrossRef] [PubMed]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2001, 88. [Google Scholar] [CrossRef]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ludwig, G. Foundations of Quantum Mechanics I; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Ludwig, G. Foundations of Quantum Mechanics II; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Varadarajan, V.S. Geometry of Quantum Theory; Springer: Berlin, Germany; Heidelberg, Germany, 1965. [Google Scholar]
- Varadarajan, V.S. Geometry of Quantum Theory: Volume 2: Quantum Theory of Covariant Systems; Van Nostrand Reinhold Company: New York, NY, USA, 1970. [Google Scholar]
- Mielnik, B. Geometry of quantum states. Commun. Math. Phys. 1968, 9, 55–80. [Google Scholar] [CrossRef]
- Mielnik, B. Theory of filters. Commun. Math. Phys. 1969, 15, 1–46. [Google Scholar] [CrossRef]
- Mielnik, B. Generalized quantum mechanics. Commun. Math. Phys. 1974, 37, 221–256. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Geometrization of quantum mechanics. Commun. Math. Phys. 1979, 65, 189–201. [Google Scholar] [CrossRef]
- Birkhoff, G.; von Neumann, J. The logic of quantum mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Dalla Chiara, M.L.; Giuntini, R.; Greechie, R. Reasoning in Quantum Theory: Sharp and Unsharp Quantum Logics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 22. [Google Scholar]
- Rédei, M. Quantum Logic in Algebraic Approach; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Beltrametti, E.G.; Cassinelli, G. The Logic of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2010; Volume 15. [Google Scholar]
- Svozil, K. Quantum Logic; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Engesser, K.; Gabbay, D.M.; Lehmann, D. Handbook of Quantum Logic and Quantum Structures: Quantum Structures; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Jauch, J.M. Foundations of Quantum Theory; Addison-Wesley Educational Publishers Inc.: Boston, MA, USA, 1968. [Google Scholar]
- Piron, C. On the Foundations of Quantum Physics; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Diederik, A. The one and the many: towards a unification of the quantum and the classical description of one and many physical entities. PhD thesis, Free University of Brussels, Brussels, Belgium, 1981. [Google Scholar]
- Kalmbach, G. Orthomodular Lattices; Academic Press: Waltham, MA, USA, 1983; Volume 18. [Google Scholar]
- Kalmbach, G. Measures and Hilbert Lattices; World Scientific: Singapore, Singapore, 1986. [Google Scholar]
- Dvurecenskij, A.; Pulmannová, S. New Trends in Quantum Structures; Kluwer Academic Publisher: Dordrecht, 2000. [Google Scholar]
- Yngvason, J. The role of type III factors in quantum field theory. Rep. Math. Phys. 2005, 55, 135–147. [Google Scholar] [CrossRef]
- Murray, F.J.; von Neumann, J. On rings of operators. Ann. Math. 1936, 37, 116–229. [Google Scholar] [CrossRef]
- Murray, F.J.; von Neumann, J. On rings of operators. II. Trans. Am. Math. Soc. 1937, 41, 208–248. [Google Scholar] [CrossRef]
- Von Neumann, J. On rings of operators. III. Ann. Math. 1940, 41, 94–161. [Google Scholar] [CrossRef]
- Von Neumann, J.; Murray, F.J. On rings of operators IV. Ann. Math. 1943, 44, 716–808. [Google Scholar] [CrossRef]
- Von Neumann, J. Zur algebra der funktionaloperationen und theorie der normalen operatoren. Math. Ann. 1930, 102, 370–427. [Google Scholar] [CrossRef]
- Halvorson, H.; Müger, M. Algebraic Quantum Field Theory. In Philosophy of Physics; Butterfield, J.B., Earman, J.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 731–922. [Google Scholar]
- Rédei, M.; Summers, S.J. Quantum probability theory. Stud. Hist. Philos. Sci. B 2007, 38, 390–417. [Google Scholar] [CrossRef]
- Rédei, M. Some historical and philosophical aspects of quantum probability theory and its interpretation. In Probabilities, Laws, and Structures; Springer: Berlin/ Heidelberg, Germany, 2012; pp. 497–506. [Google Scholar]
- Rédei, M. The Birkhoff-von Neumann Concept of quantum Logic. In Handbook of Quantum Logic and Quantum Structures; Engesser, K., Gabbay, D., Lehmann, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 1–22. [Google Scholar]
- Bratteli, O.; Robinson, D.W. Operator Algebras and Quantum Statistical Mechanics: Volumes 1 and 2; Springer: Berlin, Germany; Heidelberg, Germany, 2012. [Google Scholar]
- Beltrametti, E.; Bugajski, S.; Varadarajan, V. Extensions of convexity models. J. Math. Phys. 2000, 41, 2500–2514. [Google Scholar] [CrossRef]
- Wilce, A. Quantum logic and probability theory. The Stanford Encyclopedia of Philosophy (Winter 2013 Edition). Zalta, E.N., Ed.; Available online: http://plato.stanford.edu/archives/win2013/entries/qt-quantlog/ (accessed on 26 October 2015).
- Barnum, H.; Wilce, A. Information processing in convex operational theories. Electron. Notes Theor. Comput. Sci. 2011, 270, 3–15. [Google Scholar] [CrossRef]
- Barnum, H.; Duncan, R.; Wilce, A. Symmetry, compact closure and dagger compactness for categories of convex operational models. J. Philos. Log. 2013, 42, 501–523. [Google Scholar] [CrossRef]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Generalized no-broadcasting theorem. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef]
- Barnum, H.; Dahlsten, O.C.; Leifer, M.; Toner, B. Nonclassicality without entanglement enables bit commitment. In Proceedings of the IEEE Information Theory Workshop, Porto, Portugal, 5–9 May 2008; pp. 386–390.
- Short, A.J.; Wehner, S. Entropy in general physical theories. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Barrett, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75. [Google Scholar] [CrossRef]
- Perinotti, P. Discord and nonclassicality in probabilistic theories. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Barnum, H.; Barrett, J.; Leifer, M.; Wilce, A. Teleportation in general probabilistic theories. In Mathematical Foundations of Information Flow; Proceedings of Symposia in Applied Mathematics; Abramsky, S., Milsove, M., Eds.; American Mathematical Society: Providence, RI, 2012; Volume 71, pp. 25–48. [Google Scholar]
- Holik, F.; Massri, C.; Plastino, A. Generalizing Entanglement via Informational Invariance for Arbitrary Statistical Theories. SOP Trans. Thoer. Phys. 2014, 1, 138–153. [Google Scholar] [CrossRef]
- Mackey, G. The Mathematical Foundations Of Quantum Mechanics; W.A. Benjamin, Inc: New York, NY, USA, 1963. [Google Scholar]
- Davies, E.B.; Lewis, J.T. An operational approach to quantum probability. Commun. Math. Phys. 1970, 17, 239–260. [Google Scholar] [CrossRef]
- Srinivas, M. Foundations of a quantum probability theory. Commun. Math. Phys. 1975, 16, 1672–1685. [Google Scholar] [CrossRef]
- Gudder, S.P. Stochastic Methods in Quantum Mechanics. In Series in Probability and Applied Mathematics; Bharucha, A.T., Ed.; Dover Publications: Mineola, NY, USA, 1979. [Google Scholar]
- Holik, F.; Plastino, A. Quantum Mechanics: A New Turn in Probability Theory. In Contemporary Research in Quantum Systems; Zoheir, E., Ed.; Nova Publishers: New York, NY, USA, 2014. [Google Scholar]
- Holik, F.; Plastino, A.; Sáenz, M. Natural information measures in Cox’ approach for contextual probabilistic theories. Quant. Inform. Process. 2015. submitted. [Google Scholar]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Holevo, A. Statistical Structure of Quantum Theory; Springer: Berlin, Germany; Heidelberg, Germany, 2001; Volume 67. [Google Scholar]
- Ingarden, R.S. Quantum information theory. Rep. Math. Phys. 1976, 10, 43–72. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Statistical Laboratory of the University of California, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Barnum, H.; Barrett, J.; Clark, L.O.; Leifer, M.; Spekkens, R.; Stepanik, N.; Wilce, A.; Wilke, R. Entropy and information causality in general probabilistic theories. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Hein, C.A. Entropy in operational statistics and quantum logic. Found. Phys. 1979, 9, 751–786. [Google Scholar] [CrossRef]
- Salicru, M.; Menendez, M.; Morales, D.; Pardo, L. Asymptotic distribution of (h, φ)-entropies. Commun. Stat. Theory Methods 1993, 22, 2015–2031. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Zozor, S.; Holik, F.; Portesi, M.; Lamberti, P.W. A family of generalized quantum entropies: Definition and properties. 2015; arXiv:1506.02090. [Google Scholar]
- Kolmogorov, A.N. Foundations of the Theory of Probability; Chelsea Publishing Company: New York, NY, USA, 1956. [Google Scholar]
- Rocchi, P. Janus-Faced Probability; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Cox, R.T. Algebra of Probable Inference; The Johns Hopkins Press: Baltimore, MD, USA, 1961. [Google Scholar]
- Cox, R.T. Probability, frequency and reasonable expectation. Am. J. Phys. 1946, 14, 1–13. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- De Finetti, B. Teoria Della Probabilita; Einaudi: Torino, Italy, 1970. [Google Scholar]
- Holik, F.; Massri, C.; Plastino, A.; Zuberman, L. On the lattice structure of probability spaces in quantum mechanics. Int. J. Theor. Phys. 2013, 52, 1836–1876. [Google Scholar] [CrossRef]
- Busch, P.; Kiukas, J.; Lahti, P. On the notion of coexistence in quantum mechanics. Math. Slovaca 2010, 60, 665–680. [Google Scholar] [CrossRef]
- Heinonen, T. Imprecise Measurements in Quantum Mechanics. PhD. Thesis, University of Turku, Finland, 2005. [Google Scholar]
- Ma, Z.; Zhu, S. Topologies on quantum effects. Rep. Math. Phys. 2009, 64, 429–439. [Google Scholar] [CrossRef]
- Foulis, D.J.; Gudder, S.P. Observables, calibration, and effect algebras. Found. Phys. 2001, 31, 1515–1544. [Google Scholar] [CrossRef]
- Cattaneo, G.; Gudder, S. Algebraic structures arising in axiomatic unsharp quantum physics. Found. Phys. 1999, 29, 1607–1637. [Google Scholar] [CrossRef]
- Busch, P.; Lahti, P.J.; Mittelstaedt, P. The Quantum Theory of Measurement; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Foulis, D.J.; Bennett, M.K. Effect algebras and unsharp quantum logics. Found. Phys. 1994, 24, 1331–1352. [Google Scholar] [CrossRef]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Raggio, G.A. A remark on Bell’s inequality and decomposable normal states. Lett. Math. Phys. 1988, 15, 27–29. [Google Scholar] [CrossRef]
- Earman, J. Some Puzzles and Unresolved Issues About Quantum Entanglement. Erkenntnis 2014, 80, 303–337. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34. [Google Scholar] [CrossRef]
- Hayashi, M. Quantum Information; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Datta, A. A condition for the nullity of quantum discord. 2010; arXiv:1003.5256. [Google Scholar]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Wittmann, B.; Ramelow, S.; Steinlechner, F.; Langford, N.K.; Brunner, N.; Wiseman, H.M.; Ursin, R.; Zeilinger, A. Loophole-free Einstein-Podolsky-Rosen experiment via quantum steering. New J. Phys. 2012, 14. [Google Scholar] [CrossRef]
- Branciard, C.; Cavalcanti, E.G.; Walborn, S.P.; Scarani, V.; Wiseman, H.M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Smith, D.H.; Gillett, G.; de Almeida, M.P.; Branciard, C.; Fedrizzi, A.; Weinhold, T.J.; Lita, A.; Calkins, B.; Gerrits, T.; Wiseman, H.M.; et al. Conclusive quantum steering with superconducting transition-edge sensors. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Reid, M. Monogamy inequalities for the Einstein-Podolsky-Rosen paradox and quantum steering. Phys. Rev. A 2013, 88. [Google Scholar] [CrossRef]
- Jevtic, S.; Pusey, M.; Jennings, D.; Rudolph, T. Quantum steering ellipsoids. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef]
- Aerts, D.; Daubechies, I. A characterization of subsystems in physics. Lett. Math. Phys. 1979, 3, 11–17. [Google Scholar] [CrossRef]
- Aerts, D.; Daubechies, I. A mathematical condition for a sublattice of a propositional system to represent a physical subsystem, with a physical interpretation. Lett. Math. Phys. 1979, 3, 19–27. [Google Scholar] [CrossRef]
- Holik, F.; Plastino, A. Quantal effects and MaxEnt. J. Math. Phys. 2012, 53. [Google Scholar] [CrossRef]
- Holik, F.; Massri, C.; Plastino, A. The introduction of symmetry constraints within MaxEnt Jaynes’s methodology. 2014; arXiv:1501.00074. [Google Scholar]
- De Barros, J. Decision Making for Inconsistent Expert Judgments Using Negative Probabilities. In Quantum Interaction; Atmanspacher, H., Haven, E., Kitto, K., Raine, D., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8369, pp. 257–269. [Google Scholar]
- Bueno-Soler, J.; Carnielli, W. May be and may be not: Paraconsistent probabilities from the LFI viewpoint. CLE e-Prints 2015, 15. Available online: http://www.cle.unicamp.br/e-prints/vol_15,n_2,2015.html (accessed on 26 October 2015). [Google Scholar]
- Holik, F. Logic, Geometry and Probability Theory. SOP Trans. Thoer. Phys. 2014, 1, 128–137. [Google Scholar] [CrossRef]
- De Barros, J.A.; Oas, G. Some Examples of Contextuality in Physics: Implications to Quantum Cognition. In Contextuality from Quantum Physics to Psychology; Dzhafarov, E., Zhang, R., Jordan, S.M., Eds.; World Scientific: Singapore, Singapore, 2015. [Google Scholar]
- De Barros, J.A.; Dzhafarov, E.N.; Kujala, J.V.; Oas, G. Measuring observable quantum contextuality. 2014; arXiv:1406.3088. [Google Scholar]
- Cabello, A. Proposal for revealing quantum nonlocality via local contextuality. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef]
- Renes, J.M. The physics of quantum information: Complementarity, uncertainty, and entanglement. Int. J. Quantum Inf. 2013, 11. [Google Scholar] [CrossRef]
- Bub, J. Quantum computation from a quantum logical perspective. Quant. Inform. Process. 2007, 7, 281–296. [Google Scholar]
- Navara, M.; Rogalewicz, V. The pasting constructions for orthomodular posets. Math. Nachr. 1991, 154, 157–168. [Google Scholar] [CrossRef]
- Garner, A.J.; Dahlsten, O.C.; Nakata, Y.; Murao, M.; Vedral, V. A framework for phase and interference in generalized probabilistic theories. New J. Phys. 2013, 15, 093044. [Google Scholar] [CrossRef]
- Brukner, U.; Zeilinger, A. Information Invariance and Quantum Probabilities. Found. Phys. 2009, 39, 677–689. [Google Scholar] [CrossRef]
- Holik, F.; Sáenz, M.; Plastino, A. A discussion on the origin of quantum probabilities. Ann. Phys. 2014, 340, 293–310. [Google Scholar] [CrossRef]
- Lombardi, O.; Holik, F.; Vanni, L. What is Shannon information? Synthese 2015. [Google Scholar] [CrossRef]
- Schumacher, B. Quantum coding. Phys. Rev. A 1995, 51. [Google Scholar] [CrossRef]
- Lombardi, O.; Holik, F.; Vanni, L. What is quantum information? 2014. Available online: http://philsci-archive.pitt.edu/11159/ (accessed on 26 October 2015).
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Barnum, H.; Knill, E.; Ortiz, G.; Viola, L. Generalizations of entanglement based on coherent states and convex sets. Phys. Rev. A 2003, 68. [Google Scholar] [CrossRef]
- Barnum, H.; Knill, E.; Ortiz, G.; Somma, R.; Viola, L. A subsystem-independent generalization of entanglement. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Barnum, H.; Ortiz, G.; Somma, R.; Viola, L. A generalization of entanglement to convex operational theories: Entanglement relative to a subspace of observables. Int. J. Theor. Phys. 2005, 44, 2127–2145. [Google Scholar] [CrossRef] [Green Version]
- Viola, L.; Barnum, H. Entanglement and subsystems, entanglement beyond subsystems, and all that. In Philosophy of Quantum Information and Entanglement; Bokulich, A., Jaeger, G., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 16–43. [Google Scholar]
- Somma, R.; Ortiz, G.; Barnum, H.; Knill, E.; Viola, L. Nature and measure of entanglement in quantum phase transitions. Phys. Rev. A 2004, 70. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Marzolino, U. Sub-shot-noise quantum metrology with entangled identical particles. Ann. Phys. 2010, 325, 924–935. [Google Scholar] [CrossRef]
- Balachandran, A.; Govindarajan, T.; de Queiroz, A.R.; Reyes-Lega, A. Entanglement and Particle Identity: A Unifying Approach. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Balachandran, A.; Govindarajan, T.; de Queiroz, A.R.; Reyes-Lega, A. Algebraic approach to entanglement and entropy. Phys. Rev. A 2013, 88. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84. [Google Scholar] [CrossRef]
- Csiszàr, I. Information-Type Distance Measure and Indirect Observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Marshall, A.W.; Olkin, I.; Arnold, B. Inequalities: Theory of Majorization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zozor, S.; Bosyk, G.M.; Portesi, M. General entropy-like uncertainty relations in finite dimensions. J. Phys. A Math. Theor. 2014, 47. [Google Scholar] [CrossRef]
- Von Neumann, J. Thermodynamik quantenmechanischer Gesamtheiten. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1927, 1927, 273–291. [Google Scholar]
- Barnum, H.; Barrett, J.; Krumm, M.; Mueller, M.P. Entropy, majorization and thermodynamics in general probabilistic theories. 2015; arXiv:1508.03107v1. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holik, F.; Bosyk, G.M.; Bellomo, G. Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory. Entropy 2015, 17, 7349-7373. https://doi.org/10.3390/e17117349
Holik F, Bosyk GM, Bellomo G. Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory. Entropy. 2015; 17(11):7349-7373. https://doi.org/10.3390/e17117349
Chicago/Turabian StyleHolik, Federico, Gustavo M. Bosyk, and Guido Bellomo. 2015. "Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory" Entropy 17, no. 11: 7349-7373. https://doi.org/10.3390/e17117349
APA StyleHolik, F., Bosyk, G. M., & Bellomo, G. (2015). Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory. Entropy, 17(11), 7349-7373. https://doi.org/10.3390/e17117349





