Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine
Abstract
:1. Introduction
| Category | Characteristics |
|---|---|
| White Tea | wilted and unoxidized |
| Yellow tea | unwilted and unoxidized, with sweltering |
| Green tea | unwilted and unoxidized |
| Oolong tea | wilted, bruised, and partially oxidized |
| Black tea | wilted and fully oxidized |
| Post-fermented tea | fermented green tea |
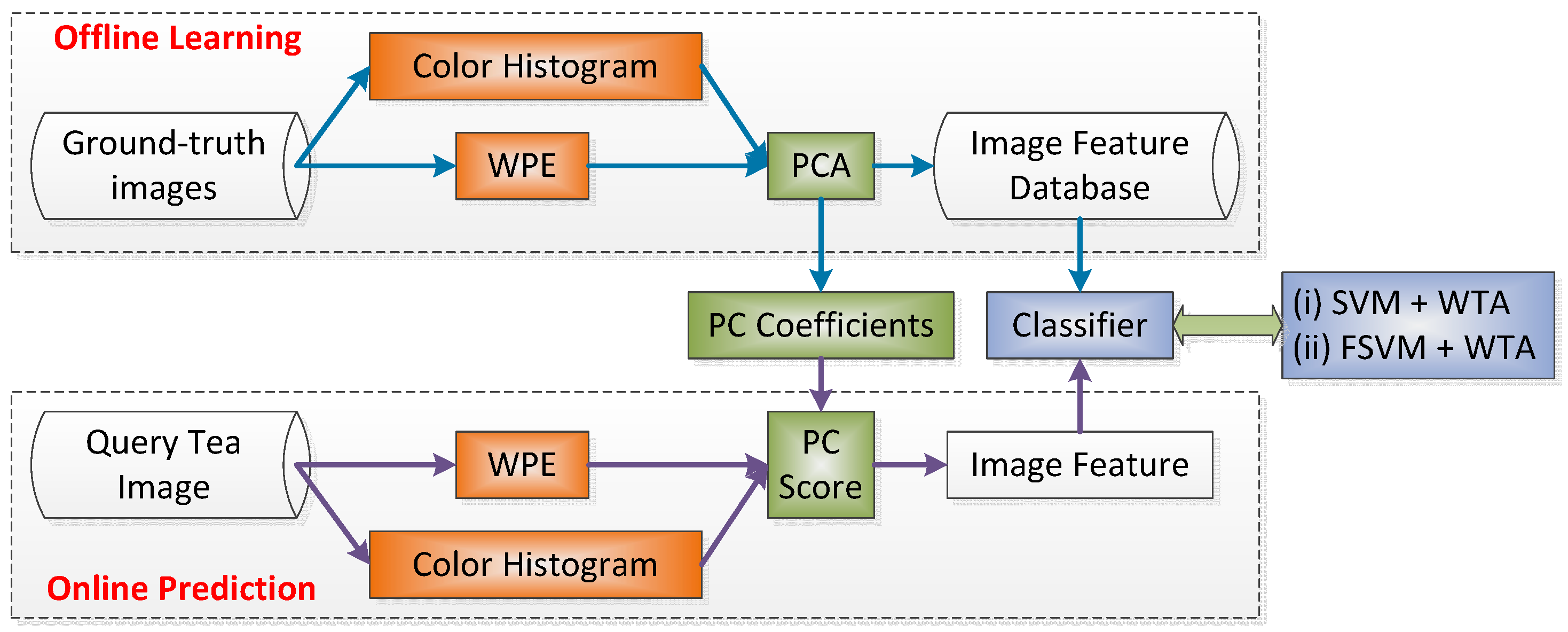
2. Proposed Method
2.1. Tea Preparation
| Category | Number | Origins |
|---|---|---|
| Green tea | 100 | Henan; Guizhou; Jiangxi; Anhui; Zhejiang; Jiangsu |
| Black tea | 100 | Yunan; Hunan; Hubei; Fujian |
| Oolong tea | 100 | Fujian; Guangdong |
2.2. Image Acquiring
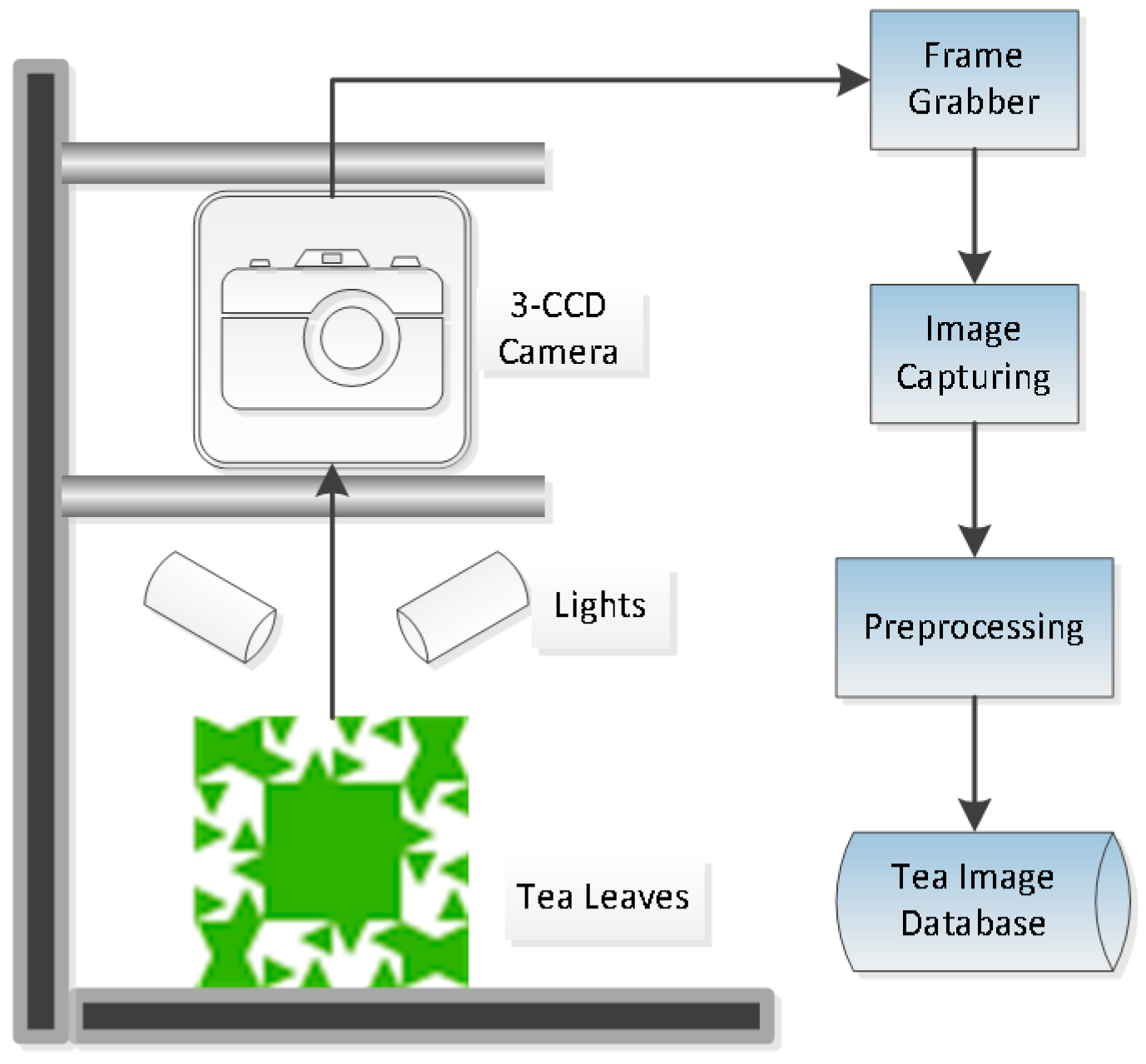
2.3. Feature Processing
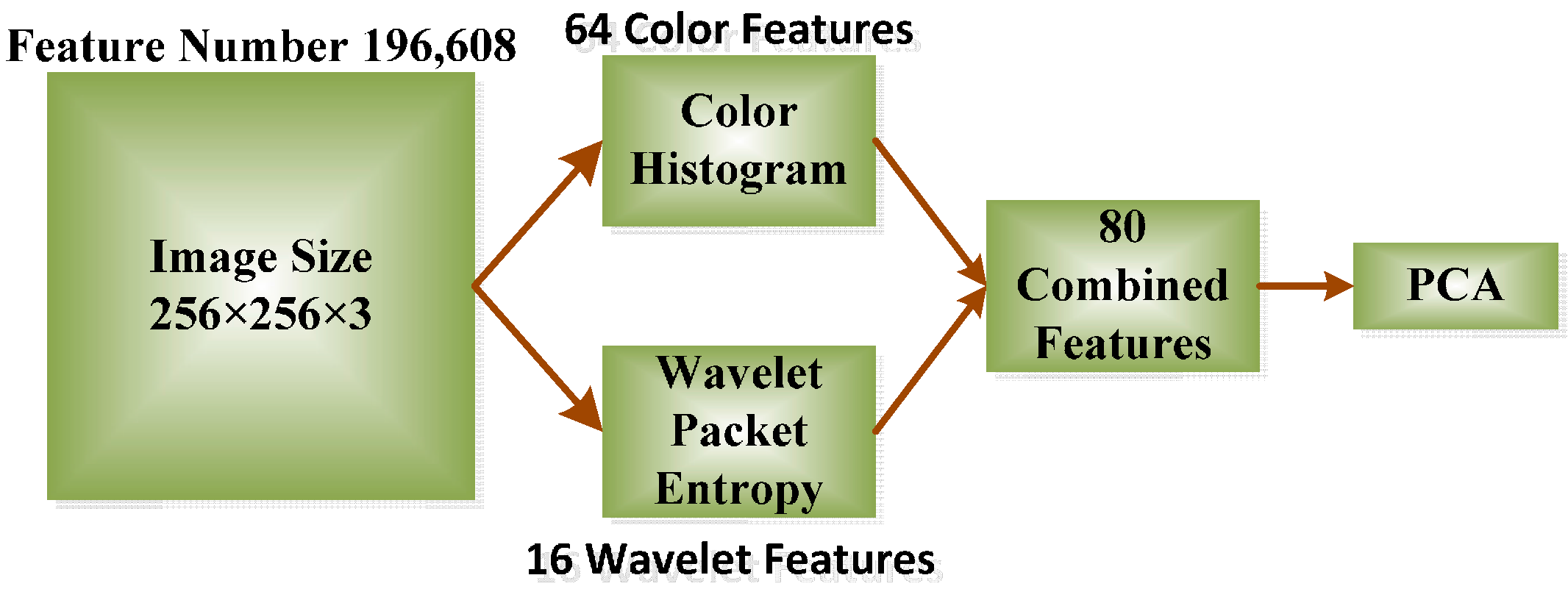
2.3.1. Color Histogram
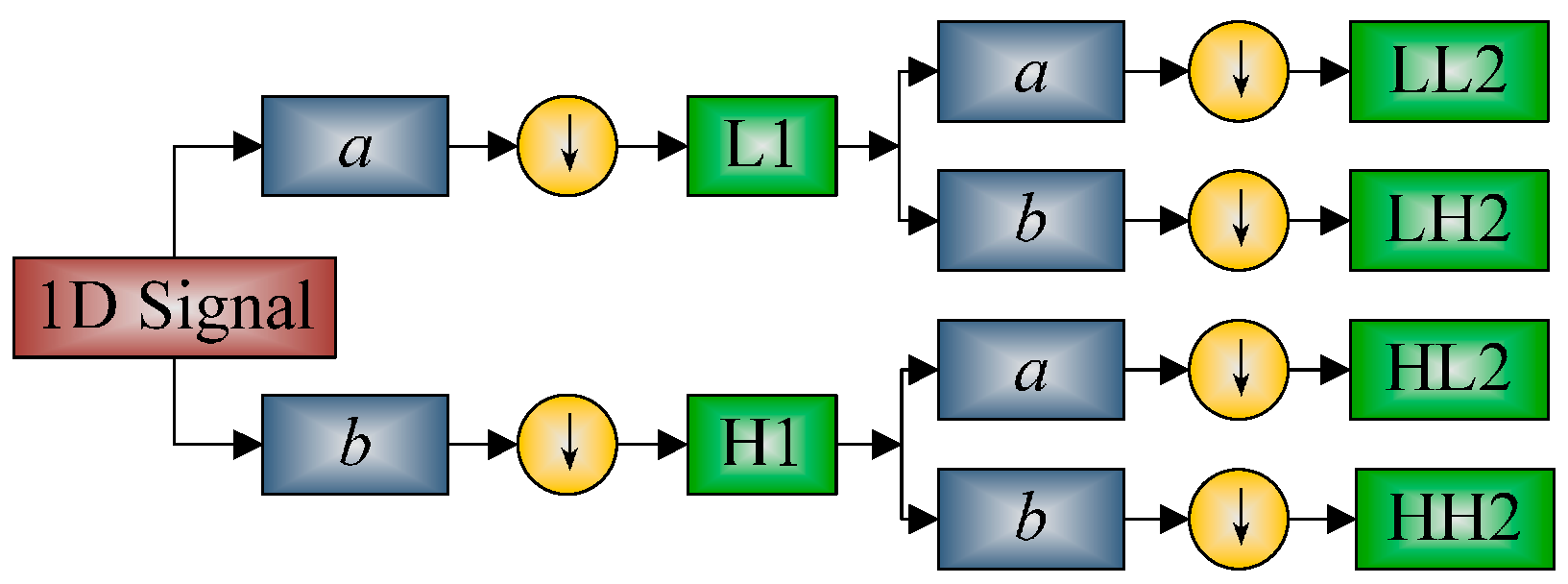
2.3.2. Discrete Wavelet Packet Transform
2.3.3. Shannon Entropy
| Pseudocode of WPE | |
|---|---|
| Step A | Input Image. Read the 2D Image. |
| Step B | 1D-DWPT. Pass the image through low-pass and high-pass filters and perform downsampling along x-axis and y-axis in sequence. Obtain four subbands. |
| Step C | 2D-DWPT. For the four subbands obtained in 1D-DWPT, we continually implement 1D-DWPT to each subband, and finally obtained 16 subbands. |
| Step D | WPE. Extract Shannon entropy from the 16 subbands obtained by 2D-DWPT, and output the final feature vector of 16 elements. |
2.3.4. Principal Component Analysis
2.4. Classification
2.4.1. Support Vector Machine
2.4.2. Fuzzy SVM
2.4.3. Fuzzy Membership Function
2.4.4. Multiclass Technique
2.5. Statistical Setting
3. Results and Discussions
3.1. Feature Extraction
| Green | Oolong | Black | |
|---|---|---|---|
| Sample Image |  |  |  |
| Color Histogram |  |  |  |
| Discrete Wavelet Transform (DWT) |  |  |  |
| Discrete Wavelet Packet Transform (DWPT) |  |  |  |
3.2. PCA Result
| # of PC | 1 | 2 | 3 | 4 | 5 |
| Variance Explained | 93.91% | 99.08% | 99.49% | 99.78% | 99.90% |

3.3. Classification Performance Comparison
| Existing Approaches | |||||||
| # of Original Features | # of Reduced Features | Classifier | Green Tea | Oolong Tea | Black Tea | Overall | Rank |
| 8 metal features | 8 | BP-ANN [10] | N/A | N/A | N/A | 95% | 6 |
| 3735 spectrum features | 5 | SVM [12] | 90% | 100% | 95% | 95% | 6 |
| 12 color + 12 texture features | 11 | LDA [17] | 96.7% | 92.3% | 98.5% | 95.8% | 5 |
| 2 color + 6 shape features | 8 | GNN [18] | 95.8% | 94.4% | 97.9% | 96.0% | 4 |
| 64 CH + 7 texture + 8 shape features | 14 | FSCABC-FNN [21] | 98.1% | 97.7% | 96.4% | 97.4% | 2 |
| Proposed Approaches | |||||||
| 64 CH + 16 WPE features | 5 | SVM + WTA | 95.7% | 98.1% | 97.9% | 97.23% | 3 |
| 64 CH + 16 WPE features | 5 | FSVM + WTA | 96.2% | 98.8% | 98.3% | 97.77% | 1 |
3.4. Optimal Wavelet
| Wavelet | Recall Rate |
|---|---|
| db1 | 96.37% |
| db2 | 96.60% |
| db3 | 96.57% |
| bior2.2 | 96.53% |
| bior3.3 | 97.10% |
| bior4.4 | 97.77% |

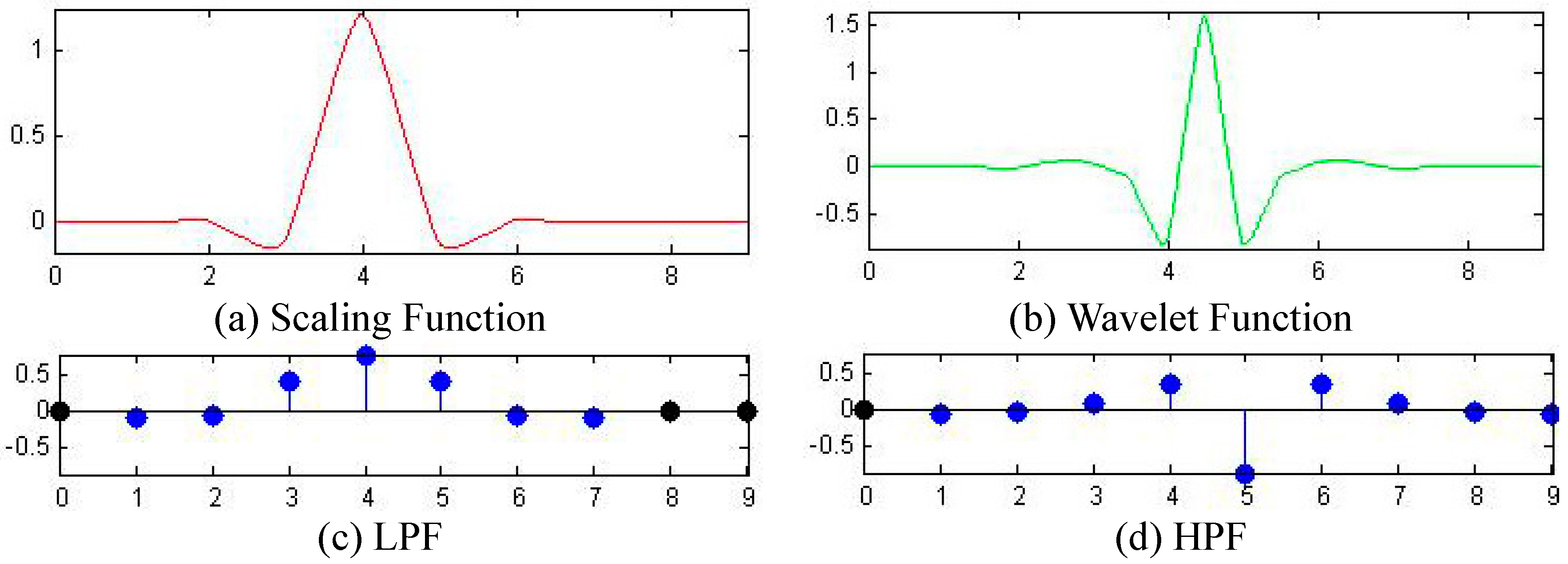
3.5. Further Discussion of Methods
4. Conclusion
Acknowledgment
Author Contributions
Abbreviation
| (A)(BP)(F)NN | (Artificial) (Back-propagation) (Feed-forward) neural network |
| (D)W(P)T | (Discrete) wavelet (packet) transform |
| (FSC)ABC | (Fitness-scaled Chaotic) Artificial bee colony |
| (F)SVM | (Fuzzy) support vector machine |
| (L)(H)PF | (Low-) (High-) Pass Filter |
| CCD | charge-coupled device |
| CH | Color Histogram |
| FMF | Fuzzy membership function |
| GNN | Genetic neural-network |
| LDA | Linear discriminant analysis |
| NIR | Near-infrared |
| SCV | Stratified cross validation |
| SE | Shannon entropy |
| WPE | Wavelet packet entropy |
| WTA | Winner-Takes-All |
Conflicts of Interest
References
- Yang, C.S.; Landau, J.M. Effects of tea consumption on nutrition and health. J. Nutr. 2000, 130, 2409–2412. [Google Scholar] [PubMed]
- Lim, H.J.; Shim, S.B.; Jee, S.W.; Lee, S.H.; Lim, C.J.; Hong, J.T.; Sheen, Y.Y.; Hwang, D.Y. Green tea catechin leads to global improvement among Alzheimer’s disease-related phenotypes in NSE/hAPP-C105 Tg mice. J. Nutr. Biochem. 2013, 24, 1302–1313. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.; Li, S.X. Dose-response meta-analysis on coffee, tea and caffeine consumption with risk of Parkinson’s disease. Geriatr. Gerontol. Int. 2014, 14, 430–439. [Google Scholar] [CrossRef] [PubMed]
- Sironi, E.; Colombo, L.; Lompo, A.; Messa, M.; Bonanomi, M.; Regonesi, M.E.; Salmona, M.; Airoldi, C. Natural compounds against neurodegenerative diseases: Molecular characterization of the interaction of catechins from Green Tea with Aβ1-42, PrP106–126, and Ataxin-3 Oligomers. Chem. Eur. J. 2014, 20, 13793–13800. [Google Scholar] [CrossRef]
- Bøhn, S.K.; Croft, K.D.; Burrows, S.; Puddey, I.B.; Mulder, T.P.J.; Fuchs, D.; Woodman, R.J.; Hodgson, J.M. Effects of black tea on body composition and metabolic outcomes related to cardiovascular disease risk: A randomized controlled trial. Food Funct. 2014, 5, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Hajiaghaalipour, F.; Kanthimathi, M.S.; Sanusi, J.; Rajarajeswaran, J. White tea (Camellia sinensis) inhibits proliferation of the colon cancer cell line, HT-29, activates caspases and protects DNA of normal cells against oxidative damage. Food Chem. 2015, 169, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Ch Yiannakopoulou, E. Green Tea catechins: Proposed mechanisms of action in breast cancer focusing on the interplay between survival and apoptosis. Anti-Cancer Agents Medicinal. Chem. 2014, 14, 290–295. [Google Scholar] [CrossRef]
- Wang, L.F.; Zhang, X.W.; Liu, J.; Shen, L.; Li, Z.Q. Tea consumption and lung cancer risk: A meta-analysis of case-control and cohort studies. Nutrition 2014, 30, 1122–1127. [Google Scholar] [CrossRef] [PubMed]
- Horanni, R.; Engelhardt, U.H. Determination of amino acids in white, green, black, oolong, pu-erh teas and tea products. J. Food Compos. Anal. 2013, 31, 94–100. [Google Scholar] [CrossRef]
- Herrador, M.A.; González, A.G. Pattern recognition procedures for differentiation of green, black and oolong teas according to their metal content from inductively coupled plasma atomic emission spectrometry. Talanta 2001, 53, 1249–1257. [Google Scholar] [CrossRef]
- Zhao, J.W.; Chen, Q.S.; Huang, X.Y.; Fang, C.H. Qualitative identification of tea categories by near infrared spectroscopy and support vector machine. J. Pharm. Biomed Anal. 2006, 41, 1198–1204. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.S.; Zhao, J.W.; Fang, C.H.; Wang, D.M. Feasibility study on identification of green, black and oolong teas using near-infrared reflectance spectroscopy based on support vector machine (SVM). Spectrochim. Acta A Mol. Biomol. Spectrosc. 2007, 66, 568–574. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Chen, X.J.; He, Y. Application of multispectral image texture to discriminating tea categories based on DCT and LS-SVM. Spectrosc. Spectr. Anal. 2009, 29, 1382–1385. [Google Scholar]
- Chen, Q.S.; Liu, A.P.; Zhao, J.W.; Ouyang, Q. Classification of tea category using a portable electronic nose based on an odor imaging sensor array. J. Pharm. Biomed. Anal. 2013, 84, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Liang, Y.Z.; Bin, J.; Zhang, Z.M.; Huang, J.H.; Shu, R.X.; Yang, K. Classification of green and black teas by PCA and SVM analysis of cyclic voltammetric signals from metallic oxide-modified electrode. Food Anal. Method 2014, 7, 472–480. [Google Scholar] [CrossRef]
- Borah, S.; Hines, E.L.; Bhuyan, M. Wavelet transform based image texture analysis for size estimation applied to the sorting of tea granules. J. Food Eng. 2007, 79, 629–639. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, J.; Cai, J. Identification of tea varieties using computer vision. Trans. ASABE 2008, 51, 623–628. [Google Scholar] [CrossRef]
- Jian, W.; Xian, Y.Z.; Shi, P.D. Identification and grading of tea using computer vision. Appl. Eng. Agric. 2010, 26, 639–645. [Google Scholar] [CrossRef]
- Gill, G.S.; Kumar, A.; Agarwal, R. Monitoring and grading of tea by computer vision —A review. J. Food Eng. 2011, 106, 13–19. [Google Scholar] [CrossRef]
- Laddi, A.; Sharma, S.; Kumar, A.; Kapur, P. Classification of tea grains based upon image texture feature analysis under different illumination conditions. J. Food Eng. 2013, 115, 226–231. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Ji, G.L.; Phillips, P. Fruit classification using computer vision and feedforward neural network. J. Food Eng. 2014, 143, 167–177. [Google Scholar] [CrossRef]
- Cattani, C. Fractional calculus and Shannon wavelet. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Ji, G.L.; Dong, Z.C. Exponential wavelet iterative shrinkage thresholding algorithm with random shift for compressed sensing magnetic resonance imaging. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 116–117. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. Computational analysis of the model describing HIV infection of CD4(+)T cells. Biomed Res. Int. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.-H.; Chou, L.-S.; Chiu, H.-L. Gap-type a-Si TFTs for front light sensing application. J. Disp. Technol. 2011, 7, 679–683. [Google Scholar] [CrossRef]
- De Almeida, V.E.; da Costa, G.B.; Fernandes, D.D.S.; Diniz, P.H.G.D.; Brandão, D.; de Medeiros, A.C.D.; Véras, G. Using color histograms and SPA-LDA to classify bacteria. Anal. Bioanal. Chem. 2014, 406, 5989–5995. [Google Scholar] [CrossRef] [PubMed]
- Cattani, C. Harmonic wavelet approximation of random, fractal and high frequency signals. Telecommun. Syst. 2010, 43, 207–217. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Phillips, P.; Dong, Z.C.; Ji, G.L.; Yang, J.Q. Detection of Alzheimer’s disease and mild cognitive impairment based on structural volumetric MR images using 3D-DWT and WTA-KSVM trained by PSOTVAC. Biomed. Signal Process. Control 2015, 21, 58–73. [Google Scholar] [CrossRef]
- Fang, L.T.; Wu, L.N.; Zhang, Y.D. A novel demodulation system based on continuous wavelet transform. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S.; Wu, L. A novel method for magnetic resonance brain image classification based on adaptive chaotic PSO. Prog. Electromagn. Res. 2010, 109, 325–343. [Google Scholar] [CrossRef]
- Abdon, A. Numerical analysis of time fractional three dimensional difussion equation. Therm. Sci. 2015, 19, 7–12. [Google Scholar]
- Cattani, C.; Pierro, G.; Altieri, G. Entropy and multifractality for the myeloma multiple TET 2 gene. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Sun, P.; Phillips, P. Pathological brain detection based on wavelet entropy and Hu moment invariants. Bio-Med. Mater. Eng. 2015, 26, 1283–1290. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.-B.; Ge, J.; Lin, Y.; Ye, F. Radar emitter signal recognition based on multi-scale wavelet entropy and feature weighting. J. Cent. South Univ. 2014, 21, 4254–4260. [Google Scholar] [CrossRef]
- Moshrefi, R.; Mahjani, M.G.; Jafarian, M. Application of wavelet entropy in analysis of electrochemical noise for corrosion type identification. Electrochem. Commun. 2014, 48, 49–51. [Google Scholar] [CrossRef]
- Yang, Y.H.; Li, X.L.; Liu, X.Z.; Chen, X.B. Wavelet kernel entropy component analysis with application to industrial process monitoring. Neurocomputing 2015, 147, 395–402. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Phillips, P.; Ji, G.L. Binary PSO with mutation operator for feature selection using decision tree applied to spam detection. Knowl.-Based Syst. 2014, 64, 22–31. [Google Scholar] [CrossRef]
- Wang, S.H.; Zhang, Y.D.; Dong, Z.C.; Du, S.D.; Ji, G.L.; Yan, J.; Yang, J.Q.; Wang, Q.; Feng, C.M.; Phillips, P. Feed-forward neural network optimized by hybridization of PSO and ABC for abnormal brain detection. Int. J. Imaging Syst. Techn. 2015, 25, 153–164. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Dong, Z.C.; Wang, S.H.; Ji, G.L.; Yang, J.Q. Preclinical diagnosis of magnetic resonance (MR) brain images via discrete wavelet packet transform with tsallis entropy and generalized eigenvalue proximal support vector machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Dong, Z.C.; Liu, A.J.; Wang, S.H.; Ji, G.L.; Zhang, Z.; Yang, J.Q. Magnetic resonance brain image classification via stationary wavelet transform and generalized eigenvalue proximal support vector machine. J. Med. Imaging Health Inform. 2015, 5, 1395–1403. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Dong, Z.C. Classification of alzheimer disease based on structural magnetic resonance imaging by kernel support vector machine decision tree. Prog. Electromagn. Res. 2014, 144, 171–184. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Ji, G.L.; Dong, Z.C. An MR brain images classifier system via particle swarm optimization and kernel support vector machine. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-F.; Wang, S.-D. Fuzzy support vector machines. Neural Netw. IEEE Trans. 2002, 13, 464–471. [Google Scholar]
- Xian, G.-M. An identification method of malignant and benign liver tumors from ultrasonography based on GLCM texture features and fuzzy SVM. Expert Syst. Appl. 2010, 37, 6737–6741. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Dong, Z.C.; Phillips, P.; Wang, S.H.; Ji, G.L.; Yang, J.Q. Exponential wavelet iterative shrinkage thresholding algorithm for compressed sensing magnetic resonance imaging. Inform. Sci. 2015, 322, 115–132. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, S.; Tetarway, S.; Sinha, R.K. Support vector machine and fuzzy C-mean clustering-based comparative evaluation of changes in motor cortex electroencephalogram under chronic alcoholism. Med. Biol. Eng. Comput. 2015, 53, 609–622. [Google Scholar] [CrossRef] [PubMed]
- Abe, S. Fuzzy support vector machines for multilabel classification. Pattern Recognit. 2015, 48, 2110–2117. [Google Scholar] [CrossRef]
- Manthalkar, R.; Biswas, P.K.; Chatterji, B.N. Rotation and scale invariant texture features using discrete wavelet packet transform. Pattern Recognit. Lett. 2003, 24, 2455–2462. [Google Scholar] [CrossRef]
- Prabhakar, B.; Reddy, M.R. HVS scheme for DICOM image compression: Design and comparative performance evaluation. Eur. J. Radiol. 2007, 63, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A.; Alkahtani, B.S.T. Analysis of the Keller–Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar] [CrossRef]
- Yang, X.-J.; Srivastava, H.M.; He, J.-H.; Baleanu, D. Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A 2013, 377, 1696–1700. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Khan, Y.; Mohyud-Din, S.T. Local fractional variational iteration method for diffusion and wave equations on cantor sets. Romanian. J. Phys. 2014, 59, 36–48. [Google Scholar]
- Zhang, Y.D.; Dong, Z.C.; Phillips, P.; Wang, S.H.; Ji, G.L.; Yang, J.Q.; Yuan, T.-F. Detection of subjects and brain regions related to Alzheimer’s disease using 3D MRI scans based on eigenbrain and machine learning. Front. Comput. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Dong, Z.C.; Ji, G.L.; Wang, S.H. Effect of spider-web-plot in MR brain image classification. Pattern Recognit. Lett. 2015, 62, 14–16. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Dong, Z.C.; Phillips, P.; Ji, G.L.; Yang, J.Q. Pathological brain detection in magnetic resonance imaging scanning by wavelet entropy and hybridization of biogeography-based optimization and particle swarm optimization. Prog. Electromagn. Res. 2015, 152, 41–58. [Google Scholar]
- Wang, S.H.; Zhang, Y.D.; Ji, G.L.; Yang, J.Q.; Wu, J.G.; Wei, L. Fruit classification by wavelet-entropy and feedforward neural network trained by fitness-scaled chaotic ABC and biogeography-based optimization. Entropy 2015, 17, 5711–5728. [Google Scholar] [CrossRef]
- Yuan, T.-F.; Hou, G.L. The effects of stress on glutamatergic transmission in the brain. Mol. Neurobiol. 2015, 51, 1139–1143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Wang, S.H. Detection of Alzheimer’s disease by displacement field and machine learning. PeerJ. 2015, 3. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ma, J.; Feng, Q.; Luo, L.; Chen, W.; Shi, P. Nonlocal Prior Bayesian Tomographic Reconstruction. J. Math. Imag. Vis. 2008, 30, 133–146. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.; Pickwell-MacPherson, E. Frequency-wavelet domain deconvolution for terahertz reflection imaging and spectroscopy. Optic. Express 2010, 18, 1177–1190. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chen, W.; Yin, X.; Ye, X.; Bao, X.; Luo, L.; Feng, Q.; Li, Y. Improving Low-dose Abdominal CT Images by Weighted Intensity Averaging over Large-scale Neighborhoods. Eur. J. Radiol. 2011, 80, e42–e49. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A. On the stability and convergence of the time-fractional variable order telegraph equation. J. Comput. Phys. 2015, 293, 104–114. [Google Scholar] [CrossRef]
- Atangana, A. Convergence and stability analysis of a novel iteration method for fractional biological population equation. Neural Comput. Appl. 2014, 25, 1021–1030. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yang, X.; Zhang, Y.; Phillips, P.; Yang, J.; Yuan, T.-F. Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine. Entropy 2015, 17, 6663-6682. https://doi.org/10.3390/e17106663
Wang S, Yang X, Zhang Y, Phillips P, Yang J, Yuan T-F. Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine. Entropy. 2015; 17(10):6663-6682. https://doi.org/10.3390/e17106663
Chicago/Turabian StyleWang, Shuihua, Xiaojun Yang, Yudong Zhang, Preetha Phillips, Jianfei Yang, and Ti-Fei Yuan. 2015. "Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine" Entropy 17, no. 10: 6663-6682. https://doi.org/10.3390/e17106663
APA StyleWang, S., Yang, X., Zhang, Y., Phillips, P., Yang, J., & Yuan, T.-F. (2015). Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine. Entropy, 17(10), 6663-6682. https://doi.org/10.3390/e17106663








