1. Introduction
In the past few years, finite-time control issues have become a hot topic due to their wide applications in practical engineering, such as switched systems [
1–
3], Markovian jump systems [
4,
5], singular systems [
6],
etc. For real industrial systems, it is usually required that the values of the system states should not exceed some given level in a certain time interval, avoiding the saturations of the sensors or damages to the equipments caused by the excitation of nonlinear dynamics [
7]. On the other hand, it is always necessary to observe some transient properties of the industrial systems such as overshoot, settlement time,
etc. [
8].
As for the finite-time control, there are mainly two kinds of issues, including finite-time boundedness (FTB) and finite-time stability (FTS). Given constraints on the initial values and the energy of disturbance inputs, a system is called FTB if its states remain under a given value over a fixed time interval [
9]. While FTS [
10] can be viewed as a special case of FTB where no disturbances are considered. In particular, recently the issue concerning input to output finite-time stability (IO-FTS) has also been investigated based on Differential/Difference LMIs [
11], where necessary and sufficient conditions are achieved. Though IO-FTS is a more general type, we think the research on FTB is the basis of IO-FTS study and can be applied (if achieved) to it by introducing the IO-FTS concept. Hence this paper deals with the FTB as a primary issue.
Note that both of FTB and FTS deal with the short-time performances over a finite time interval, which is the key difference from the Lyapunov stability where the asymptotical behaviors over a infinite time interval are investigated. Though the asymptotical performances are usually sufficient for the industrial operations, the aforementioned situations make it necessary to pay close attention to FTB and FTS problems.
At present, topics about hybrid and stochastic systems also raise interest; for instance, lead-following consensus of multi-agent systems [
12], synchronization of complex networks based on entropy measures [
13,
14]. As a typical type of hybrid and stochastic system, Markovian jump systems are largely employed to describe the practical industrial processes with random mode changes due to such as failures of the components, abrupt environment changes, variations of the operation point,
etc. [
15–
17]. The mode change is ruled by a Markov chain subject to certain mode-to-mode transition probabilities. In addition, recently many interesting results concerning the finite-time control of Markovian jump systems have been achieved. For instance, in [
18], FTB is investigated for a class of singular time-delayed neural networks with Markovian jumps. Authors of [
19] make a research on the
H∞ finite-time control for Markovian jump systems. Further, subject to average dwell time and partially known transition probabilities,
H∞ filtering is studied to obtain the FTB performance for Markovian jump systems in [
20].
Furthermore, due to finite speeds of the information transmission, time-delays always exist which are the resource of poor control performances and even system instabilities. Therefore it is more reasonable to add the delay terms into the controlled systems. In addition, disturbances in the environment also have a bad effect on the control performance. To minimize or reduce the effect of the external disturbance on the controlled system, it is popular to introduce the
H∞ control concept [
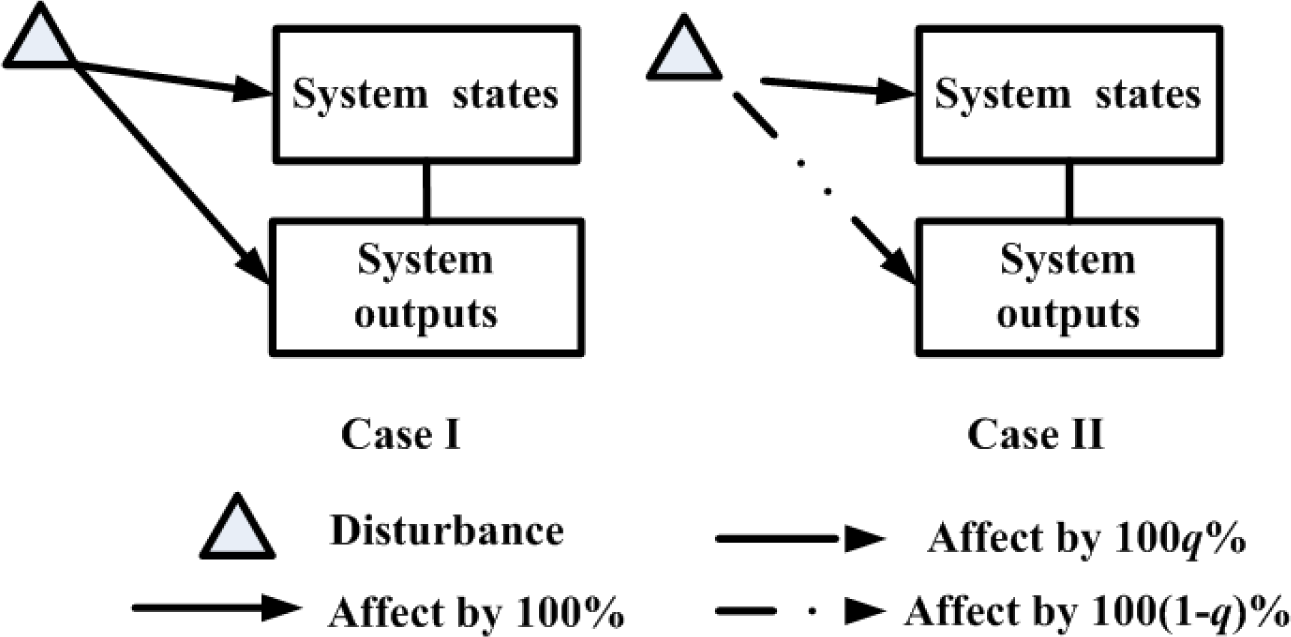
21]. However, to the best of our knowledge, in most of the literatures it is usually assumed that the disturbance is incorporated into both the system states and the outputs with the same influence degree of 100%, which actually is not accurate enough to reflect the real system due to the case where the disturbance affects the system states and outputs with different percentages of the total degrees, respectively. In particular, as is shown in
Figure 1, the disturbance enters both the system states and system outputs. Here two cases are considered. In Case I, the disturbance affects the system states and system outputs by 100%. While in Case II, the disturbance enters the system states and system outputs by 100
q% and 100(1
−q)%, respectively, where
q is called the distribution ratio (0 ≤
q ≤ 1), and 100
q% and100(1
−q)% refer to the disturbance influence degree. In this paper, this work will be carried out as one of the few attempts.
Motivated by aforementioned facts,
H∞ finite-time control for discrete delayed nonlinear systems with Markovian jumps and disturbances of probabilistic distributions is addressed in this paper. Firstly, referring to the model in [
22] which is the interconnection of a linear dynamic system and a static nonlinear operator, a new set of equations are established to describe the discrete-time delayed nonlinear system with Markovian jumps. By introducing the Bernoulli distribution and Binomial distribution sequences, the disturbance distributed into the system states and outputs by different influence degrees is incorporated into the model system. Then by employing the Lyapunov functions and state feedback control method, some new criteria are derived such that the robust
H∞ finite-time control performances are achieved for all possible Markovian jumps and disturbances of probabilistic distributions. Finally an example is provided to validate the developed control laws.
The contributions of this paper mainly lie in three aspects: (i) establish a more general model which helps extend the results into more nonlinear systems; (ii) attenuate the effect of the disturbance on the output with a prescribed level; (iii) model the disturbance influence degree between the system states and the outputs such that the effect of disturbances subject to certain probabilistic distribution on the control performance is investigated.
The rest of this paper is organized as follows. Problem formulations and preliminaries are given in Section 2. Section 3 presents the main results of the robust H∞ finite-time controller design. In Section 4, an illustrative example is demonstrated to verify the effectiveness of the proposed control approaches. Finally, some conclusions are drawn in Section 5.
Notations: The superscript “T” stands for matrix transposition. l2[0,∞) is the space of square integrable vector functions over [0, ∞). ℜn denotes n dimensional Euclidean space, and ℜn×m is the set of all n×m real matrices. I denotes identity matrix of appropriate orders. * denotes the symmetric parts. diag{…} stands for a block-diagonal matrix. ||x|| denotes the Euclid norm of vector x. The notation X > Y, where X and Y are matrices of the same dimensions, means that the matrix X−Y is positive definite. Pr{⋅} denotes the occurrence probability of event “⋅”. Pr{A|B} represents the occurrence probability of event A on condition B. E{⋅} stands for the mathematical expectation of event “⋅”. If X ∈ ℜp and Y ∈ ℜq, C(X;Y) denotes the space of all continuous functions mapping ℜp → ℜq. N0 represents the set of nonnegative integers.
2. Problem Formulations and Preliminaries
Based on the model [
22], we establish the following new sets of equations with Markovian jumps:
with the initial condition function
x(
k) =
ρ(
k)
∀k ∈ [−τ,0], where
x(
k) ∈ ℜ
n is the system state,
u(
k) ∈ ℜ
m is the control input,
w(
k) ∈ ℜ
s is the external disturbance which belongs to
l2[0, ∞). ξ ∈ ℜ
L is the input of the nonlinear function ϕ, ϕ ∈
C(ℜ
L; ℜ
L) is the nonlinear function satisfying ϕ (0) = 0,
L ∈
N0 is the number of nonlinear functions.
A(
rk) ∈ ℜ
n×n,
Ad(
rk) ∈ ℜ
n×n,
Bp(
rk) ∈ ℜ
n×L,
Bu(
rk) ∈ ℜ
m,
Bw(
rk) ∈ ℜ
n×s,
Cq(
rk) ∈ ℜ
L×n,
Cqd(
rk) ∈ ℜ
L×n,
Dp(
rk) ∈ ℜ
L×L,
Du(
rk) ∈ ℜ
L×m, and
Dw (
rk) ∈ ℜ
L×s are mode-dependent matrices where
r(
k) denotes the discrete-time Markov chain taking values from a finite set
V = {1,2, ⋯,
s} with the mode-to-mode transition probabilities as follows:
where 0 ≤
μij ≤ 1,
.
For a better representation, here we denote Q(rk) as Qi ∀rk = i, i ∈ V, i.e., A(rk) is denoted by Ai, Ad(rk) by Adi, and so on.
Here we adopt the following state feedback controller:
where
Ki ∈ ℜ
m×n,
i ∈
V.
Remark 1. We choose linear state feedback control here because it is a quite classical and effective method to stabilize the system. If nonlinear feedback is applied, better control performances may be achieved although, the implementation may become a little more complex or difficult than that of linear state feedback. Furthermore, once the state feedback is successfully applied to the desired issue, based on which Luenburger-like state estimator which is of nonlinear type can be constructed to investigate the current issue further. To this regard, we made the choice of linear state feedback for its important role in further study.
Substituting
(3) in
(1), we obtain:
where
,
.
Definition 1. (FTB): Given 0≤
c1≤
β,
c2≥0,
Ri > 0,
N ∈
N0 and the time delay τ, ifsystem (4) is said to be FTB with respect to (
c1,c2,β,Ri,N).
Here we consider the following output:
where
Czi ∈ ℜ
l×n and
Dzwi ∈ ℜ
l×s are both mode-dependent matrices.
Definition 2. (H∞ FTB): With the FTB control performance defined in Definition 1 achieved, if the following index holds under zero initial conditions:system (4) is said to be H∞,
FTB for any nonzero w(
k)
, where γ > 0
is called the disturbance attenuation rate. Assumption 1. [
22]
: We assume the nonlinear functions in (1) are monotonically non-decreasing and globally Lipschitz, i.e.
, the following relation holds:where ∀
ε1, ε2 ∈ ℜ, ε
1 ≠ ε
2, l = 1,…
,L, hl>0. And in our work, the disturbance process is described by a Bernoulli distribution α
0(
k). According to
(4) and
(6), the disturbance enters the system states and the outputs respectively. Here we consider two main cases as follows, which is also shown in
Figure 1:
Case I:
No distribution of the disturbance occurs between two parts (system states and outputs), in another word, the influence degree of the disturbance for two parts are the same by 100%.
Case II:
The disturbance affects two parts by
100q% and 100(1−
q)% of the total influence degrees, respectively, where
q (0 ≤
q ≤ 1) is defined as the distribution ratio.
where Pr{
α0(
k) = 1} =
E{
α0(
k)} =
b.
Consider the Binomial distribution sequences as follows:
we define
,
v1 = 1,2,…,
v, where
v denotes the total trial numbers,
b1 denotes
E{
q}. Hence
E{
α1(
k)} =
vb1.
Remark 2. The Markovian process denoted by the Markov chain rk is independent of the Bernoulli distribution α0(k).
Remark 3. For the system under discussion, there are two kinds of noises (disturbances), i.e.,
the process noise which enters the system states and the measurement noise which enters the system outputs. Usually, these two kinds of noises are taken as mutually uncorrelated white noises when dealing with control problems such as state estimation. However, in practical engineering, colored noises may occur which makes it difficult for the controlled system to guarantee this assumption, especially for a discrete time system sampled from a continuous time system where the process noise is correlated to the measurement noise [
23].
Motivated by this kind of application or the like, in this paper we propose the idea of distributed disturbance subject to certain probabilistic distribution shown Figure 1 to make an alternative research. Taking the probabilistic distributed disturbance into account, we obtain the following augmented system:
3. Main Results
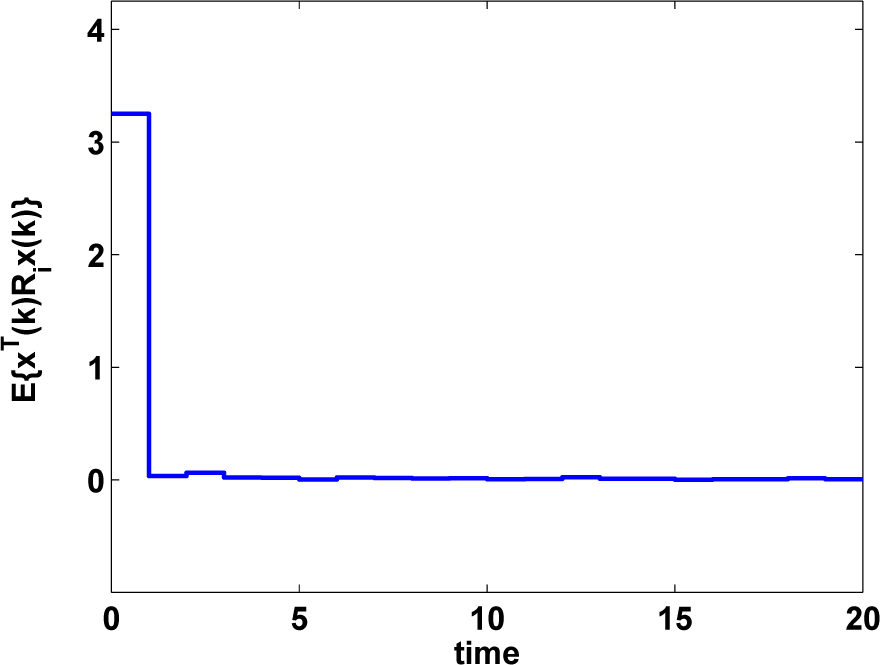
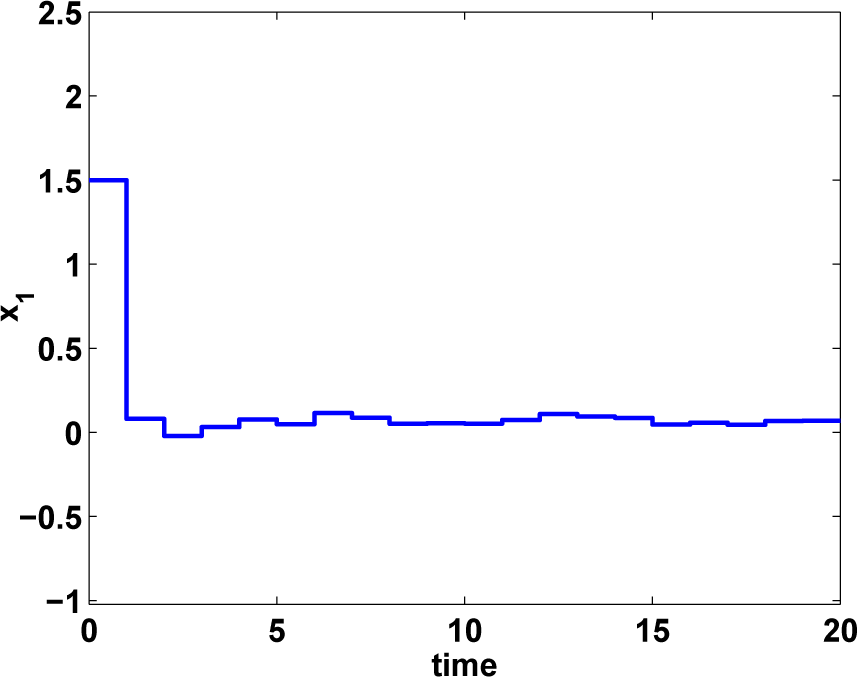
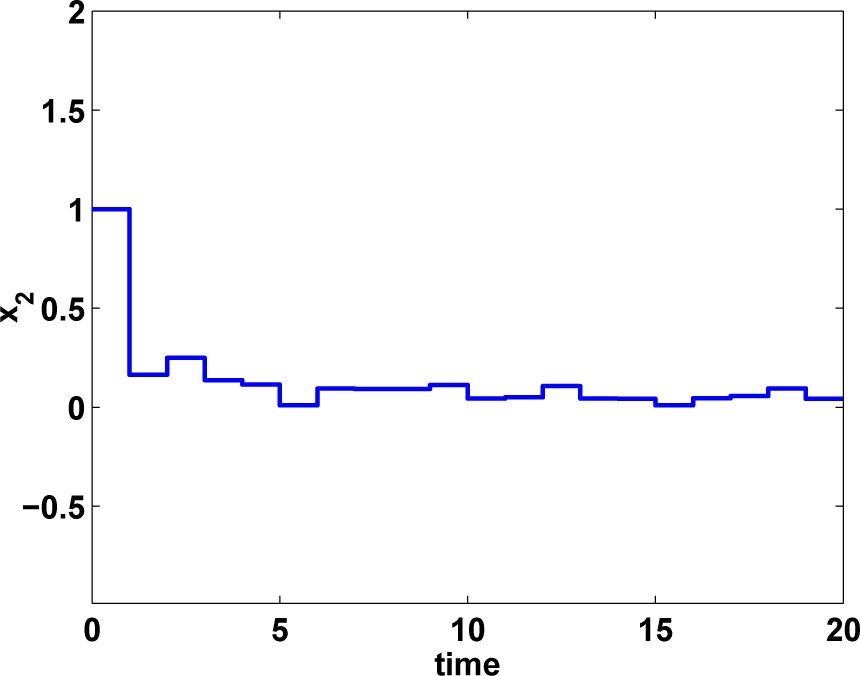
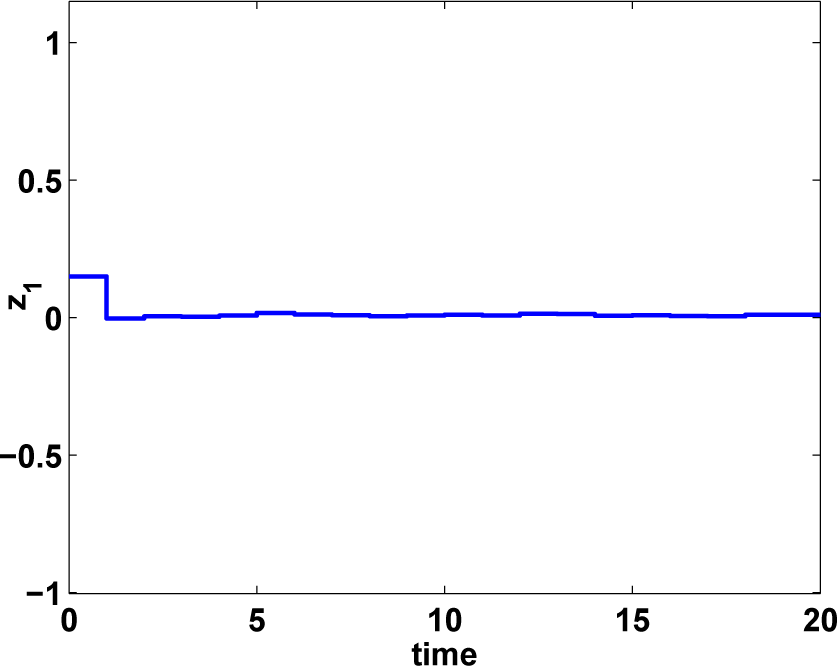
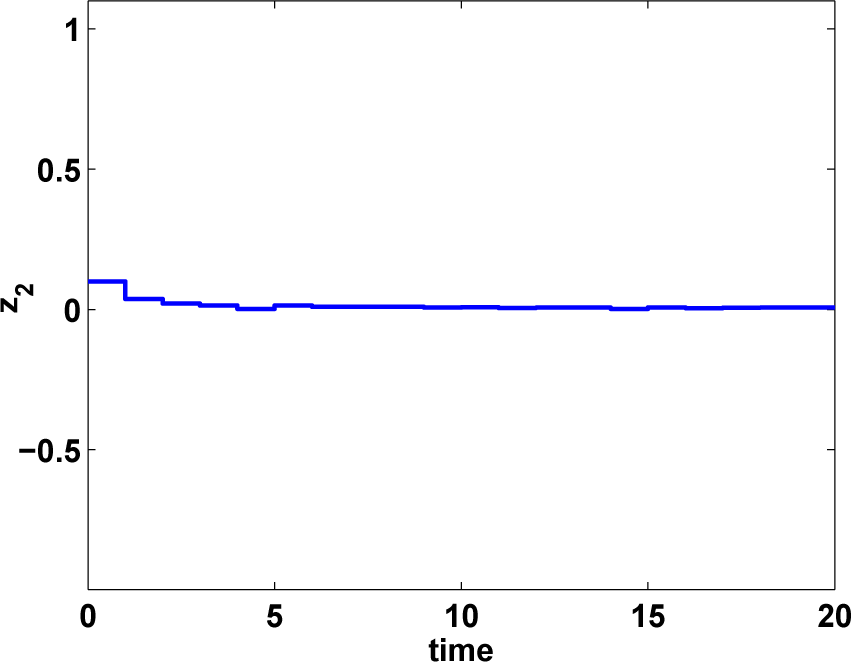
In this section, the conditions for the FTB performance and the H∞ FTB performance are derived in the first two theorems, respectively. To obtain the desired controller, Theorem 3 and Corollary 1 are displayed for time-delayed and non-delayed systems respectively.
Theorem 1. Given 0 ≤
c1 ≤
β,
c2 ≥ 0,
Ri > 0,
and N ∈
N0,
system (9) is said to be FTB with respect to (
c1,
c2,
β,
Ri,
N)
provided there exist σ
1−1 > 0, σ
2 > 0, σ
3−1 > 0,
α ≥1,
symmetric positive definite matrices Pi, Γ,
Qi,
a set of diagonal positive definite matrices Λ
i, and matrices Ki such that the following LMIs hold:where Proof. Take the following Lyapunov functional:
where
Pi > 0, Γ > 0.
Remark 4. Recently, the Differential/Difference LMIs (D/DLMIs) are applied to FTS of linear systems and deterministic hybrid systems [24,25], where necessary and sufficient conditions are derived. However, in this paper, due to the introduction of Markov jumps, Pi is a mode-dependent matrix which swifts between different values with the time instant going on. Since the number of modes is finite, Pi takes values from a finite set. If Difference Lyapunov functional is adopted, P will be derived by recursive algorithm rather than chosen from a finite set, which makes it hard to introduce the Markov jumps. Therefore in our opinions DLMIs cannot be applied to our current work directly. However, future work will concentrate on FTB issue of the nonlinear system without Markov jumps based on Difference Lyapunov functional such that less conservative criteria can be derived and output feedback control is also accessible. Construct the following function:
where
Qi>0,
α ≥ 1, and
d > 0.
Define
E{
V(
k+1)} =
E{
V(
k+1,
rk+1 =
j)|
rk =
i}, then
Since
using the following facts:
we have
According to
Assumption 1, the inequality
(8) can be rewritten as follows:
which is equivalent to
where
λil > 0,
l = 1,⋯,
L.
The above inequality can also be written in the matrix form as follows:
where Λ
i = {
λi1, ⋯,
λiL},
H = {
h1,⋯,
hL}.
Based on
(20) and
(23), we have
where Ψ = [
xT (
k)
xT(
k−1) ⋯
xT (
k−τ+1)
xT (
k−τ)
ϕT(ξ(
k ))
wT (
k)]
T.
Since
Gi < 0, we have
which implies that
Let
, we have
and let
, according to the preconditions of
Definition 1,
Based on
(28) and
(29), we derive the following inequality:
i.e.,
According to
(11), we have
By virtue of
(14), we obtain
According to
Definition 1, system
(9) is FTB with respect to {
c1,
c2,
β,
Ri, N}. Thus the proof is completed. □
Theorem 2. Given 0
≤ c1 ≤ ß,c2 ≥ 0,
Ri > 0,
N ∈
N0,
and d >0,
if there exist σ
1−1 > 0, σ
3−1 > 0, α ≥ 1,
symmetric positive definite matrices Pi, Γ,
a set of diagonal positive definite matrices Λ
i,
and matrices Ki such that the following LMIs hold:wherethen system (9) is said to be FTB with H∞ performances,
is called the disturbance attenuation rate. Proof. According to the Schur Complement [
26],
is equivalent to
In
Theorem 1, let
Qi =
I, then
Gi becomes the principle minor of the left side of
(40). Thus
Gi < 0 is derived according to
(40). Together with the conditions
(37)–
(39), it can be concluded that system
(9) is FTB based on
Theorem 1. On the other hand, consider the following function:
Consider the sector condition
(23), we derive
Since
, we have
i.e.,
which indicates that
Due to
E{
V(
k)} > 0 and V(0) = 0, we derive
i.e.,
Let
. According to
Definition 2, it concludes that system
(9) has
H∞ performances with the disturbance attenuation rate
. Thus the proof is completed. □
Theorem 3.
Given 0 ≤
c1 ≤ ß,
c2 ≥ 0,
Ri > 0
, N ∈
N0,
and d > 0
, if there exist σ
1 > 0
, σ3 > 0
, α ≥ 1,
symmetric positive definite matrices Xi,
Y,
a set of diagonal positive definite matrices Si,
and matrices Wi such that the following LMIs hold:wherethen system (9) is FTB with disturbance attenuation rate.
Furthermore, the feedback controller gains are determined by Ki = WiXi−1.
According to the Schur Complement [
26],
(53) is equivalent to
i.e.,
Pre-and-post multiply
on both sides of
(55), and let
we have
Mi < 0 in
(49).
Remark 5. If τ = 0
or Adi = Cqdi = 0
, system (9) becomes a non-delayed system denoted as follows In this case, H∞ FTB controller can still be designed by virtue of the following corollary.
Corollary 1. Given 0 ≤
c1 ≤
ß,
c2 ≥ 0,
Ri > 0,
N ∈ N0,
and d > 0,
if there exist σ
1 > 0
, α ≥ 1,
symmetric positive definite matrices Xi,
a set of diagonal positive definite matrices Si,
and matrices Wi such that the following LMIs hold:then system (57) is FTB with disturbance attenuation rate.
Furthermore, the feedback controller gains can still be determined by Ki = WiXi−1.