1. Introduction
With more than half of the global population living in cities and with an estimated annual increase of urban dwellers reaching nearly 60 million [
1], much recent research work has focused on urban-related aspects, including studying the wind environment where buildings are, or will be, placed. Common concerns of wind studies are pedestrian comfort [
2], air quality [
3,
4], safety [
5], energy use and natural ventilation [
6]. The approach used in each study depends on the length scale of the study area. In small-scale studies, such as those around buildings (distances up to 1–2 km) [
7], Computational Fluid Dynamics (CFD) modeling is commonly used to predict wind behavior.
Advantages of CFD modeling are that it allows treatment of a wide range of complicated geometries and it provides detailed information on airflow. Although CFD modeling may lead to reasonable predictions, results can be very different from field and laboratory experiments [
8]. Even so, predictions from the same mathematical model applied by different modelers may differ, or more than one model may exist that generates the same predictions [
9]. The application of CFD requires experienced users, and predictions are subject to challenges associated with precision, computational storage and execution time [
10]. Guidelines are available in the literature on the application of CFD in wind studies around and through urban canyons [
11,
12]. Recommendations on appropriate boundary conditions have also been provided [
13,
14], while others have proposed methodologies for evaluating environmental models [
15].
Uncertainties are inherent in wind modeling and they are associated with modeling assumptions as well as model application [
8]. A difficulty is that models used in CFD are derived from experiments repeated under controlled laboratory conditions or from real-world data collected under specific contexts. In most cases they are able to capture only an approximation of the true conditions [
16]. Consequently, models are not always applicable to a wide range of situations. In addition, wind studies around buildings involve open systems; a large number of reference variables influences climatic conditions and values of these variables are often unknown [
2,
17]. Furthermore, no information related to the accuracy of results is usually available.
Multiple-model approaches can be used to accommodate uncertainties involved in modeling and to account for many possible flow conditions with less risk of parametric-value compensation. In 1998, Raphael and Smith introduced a multiple-model approach for system identification of civil structures in order to account for uncertainties involved in modeling and measurement [
18,
19]. Mathematical models that describe system behavior are parameterized and populations of possible predictions are obtained. These model predictions are then compared with measurements of real systems and models whose predictions are incompatible with measured values are falsified. The remaining models comprise the candidate-model set. This task is known as system identification and among the approaches proposed to date, model falsification is the most robust when values of correlations are not known [
20].
Regardless of the approach used, good sensor placement is important for identifying candidate models. In system identification, measurement systems have been designed in order to place sensors at locations of high information value. Entropy, from information theory (also known as Shannon entropy or information entropy), has been used in earlier studies as a design criterion to identify sensor locations and number of sensors needed for identification; good locations were either positions of high entropy in values of model predictions [
21,
22] or positions that offered high entropy reduction [
23]. Although these early studies used model predictions to identify optimal sensor locations, they did not explicitly incorporate modeling error into the measurement-system design process. Systematic modeling errors have not been considered (except in previous research by the authors) and the effect of spatial distribution of modeling error on sensor placement has not been studied.
Goulet and Smith [
24] proposed a measurement-system-design methodology that includes error dependencies and their values. These error dependencies were described by correlation coefficients that were quantified using qualitative reasoning formulation (low, moderate, and high), given that little information was available to the authors. Comparing previous work [
21,
22], Goulet and Smith evaluated the usefulness of monitoring through the capability to reduce the number of candidate models and not through maximizing the entropy of model predictions. Papadimitriou and Lombaert have used an entropy-based sensor placement to stress the effect of spatial correlation of prediction errors [
25]. However, optimum locations were selected as positions of minimum entropy in probabilities of model parameter values. Such an approach is difficult to apply to complex, time-dependent systems where multiple models and varying parameter values exist, such as wind studies around buildings.
Earlier studies in system identification have demonstrated that information entropy can be successfully used as a design criterion to optimize measurement systems in order to improve the accuracy of model predictions [
22,
23]. The two sensor-placement strategies that have been identified are essentially sequential; sensors are placed one at a time at locations that provide either the higher reduction or higher value in information entropy. Subsequent sensor placement does not change the location of sensors that have already been placed. Sequential strategies are preferred to global search strategies such as genetic algorithms due to computational cost [
23]. Nevertheless, during sequential sensor placement, entropy is usually calculated at each location individually, disregarding the possibility of selecting locations with similar information content.
Field measurements are useful in wind studies in order to evaluate predictions and ensure that the modeling is sound; even when using modeling methods of high predictability, such as the large eddy simulation (LES) [
26]. However, field measurements have been rare since they are difficult to perform, expensive, but also result in limited quantities of data with low repeatability. The challenge is that flow properties vary considerably with space and time, and so the location of sensors, their type, and the duration of measurements significantly affect the value of such information [
27]. In addition, a limited number of feasible measurement locations remains a challenge [
28].
Until now, measurement systems in wind studies around buildings have been designed using educated guesses and common sense. Some research has studied optimal sensor configurations in built environments, either in terms of pollutant dispersion to protect against nuclear, biological, and chemical attacks (NBC) [
29] or with the aim to reconstruct a close approximation of the flow field [
30]. Recent work by Du
et al. [
31] proposed a methodology to identify optimal sensor locations for wind studies in an urban reservoir. In their study, an entropy-based sensor placement has been applied to wind predictions obtained from CFD simulations in order to identify optimum sensor locations. The objective was to use the readings from a limited number of sensors to predict the entire wind field over a reservoir surface. Although a limited number of two model parameters were selected to run CFD simulations, systematic modeling errors and the effect of modeling uncertainties on sensor placement have not been considered. Moreover, sensor placement has been performed iteratively and the possibility of selecting sensors having mutual information has not been considered. No rational and systematic methodology for sensor placement has been presented that includes modeling uncertainties and identifies configurations of sensors that could be used to improve the accuracy of wind predictions.
This paper proposes a hierarchical sensor placement strategy using joint entropy that explicitly incorporates spatial distribution of modeling errors and their values. The study also builds upon previous work in sensor placement where entropy was identified as a better design criterion than subset size [
32]. Another aim of this paper is to evaluate the effect of modeling errors on optimal sensor configurations. In Section 2 the sensor placement strategy is explained. The hierarchical algorithm and the entropy design-criterion are further summarized. Results of applying the framework to a full-scale real-world building are presented in Section 3. The final two sections discuss research findings as well as limitations of the framework.
2. Sensor Placement Strategy
Measurements are performed to collect quantitative information about physical variables, by comparing them with a known standard. The aim is to enhance knowledge and provide a better understanding of the underlying processes which otherwise could only be estimated. In this work, measurements are used to improve wind predictions around buildings and capture short-term wind variability. A sensor placement strategy is developed to identify optimal sensor configurations prior to measuring, with limited knowledge of wind behavior.
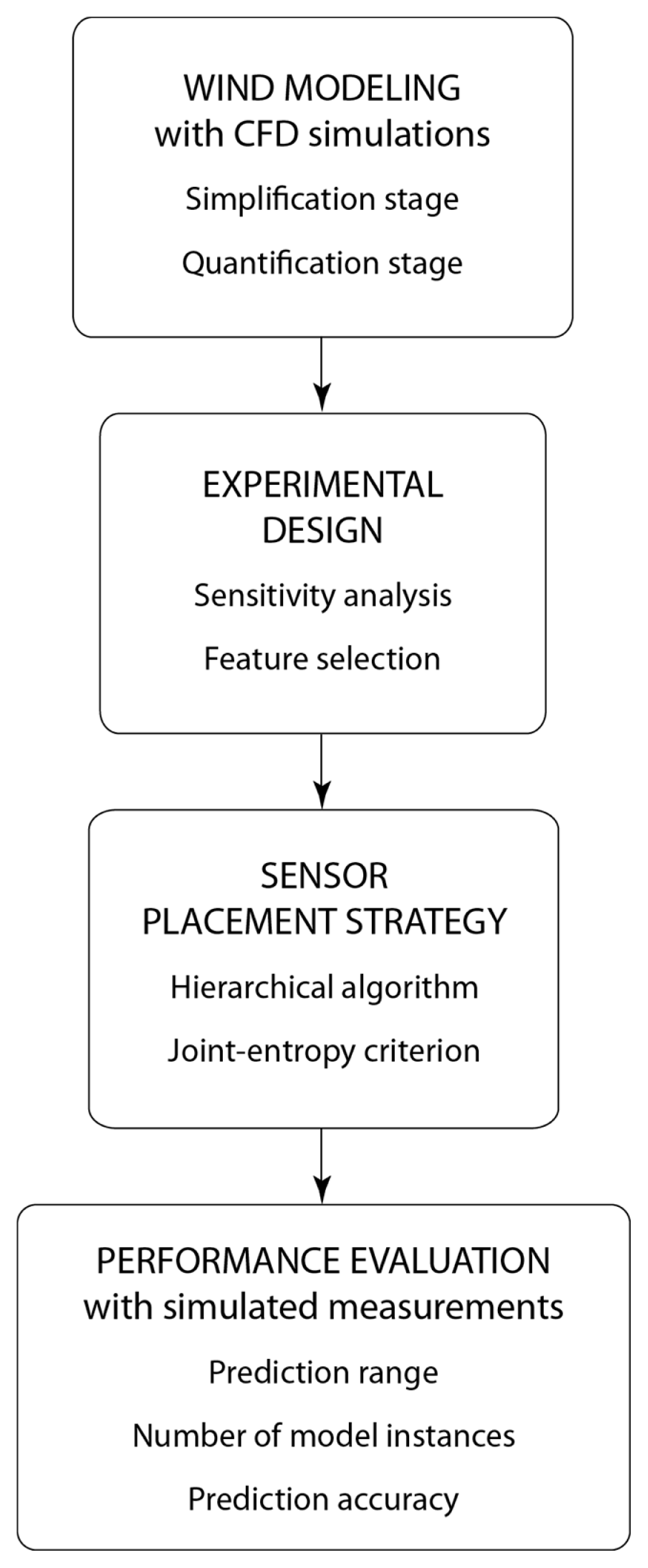
The research design is comprised of four stages as illustrated in
Figure 1. First, wind modeling is performed using CFD simulations to obtain possible wind predictions. Modeling focuses on two aspects in the simplification stage to include decisions related to geometrical simplifications and numerical methods, and the quantification stage, during which mathematical models, parameters, variables and constants that describe the system are identified and quantified. Due to the complexity of wind modeling, a significant degree of uncertainty is associated with mathematical models, parameters and boundary conditions.
During experimental design, sensitivity analysis is employed in order to evaluate the effect of variations in the values of model parameters on model predictions and feature selection to select a small number of parameters that have the highest impact on predictions. A multiple-model approach is adopted [
18] and values of model parameters are varied within plausible ranges to create populations of model instances. These instances comprise the initial model set, with which multiple, steady-state CFD simulations are executed to obtain a discrete population of predictions at possible measurement locations.
Sensor placement is performed using the simulation predictions and a hierarchical algorithm is used to place sensors at locations that satisfy the desired design criterion, in this case maximum information content that corresponds to maximum joint-entropy. The objective is to design a measurement system that supports model falsification approaches, such as [
20,
33], and improves predictions. Further details are given in the Sections 2.2 and 2.3.
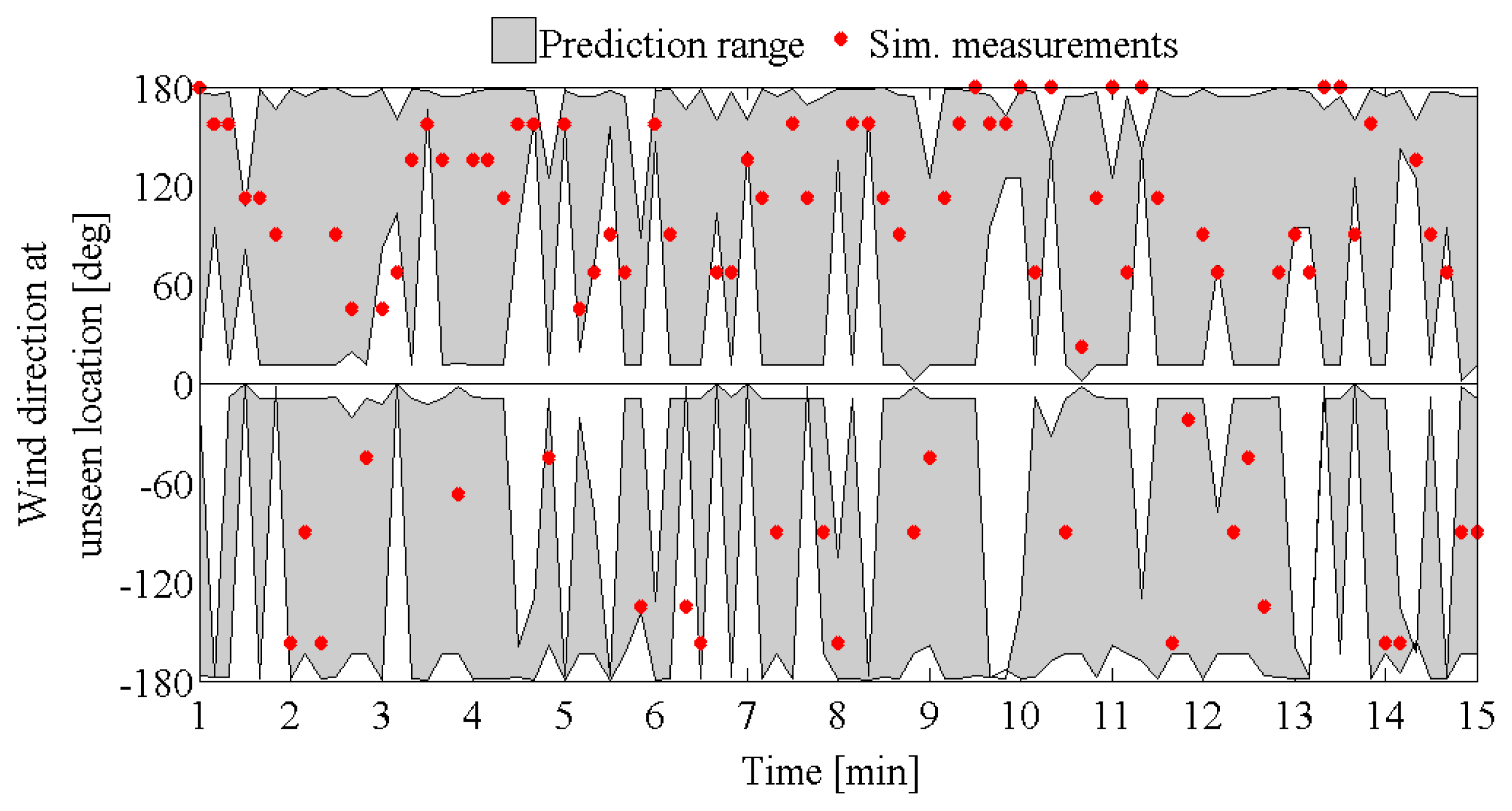
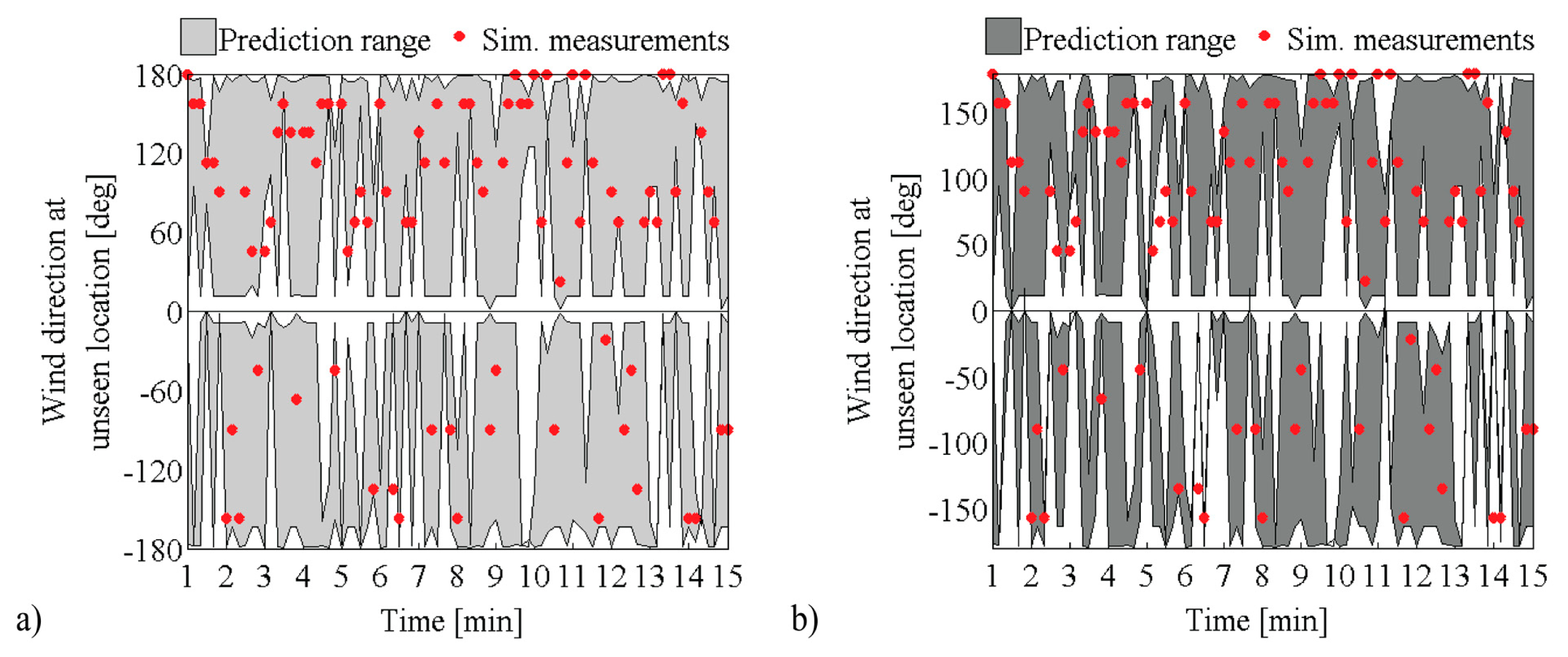
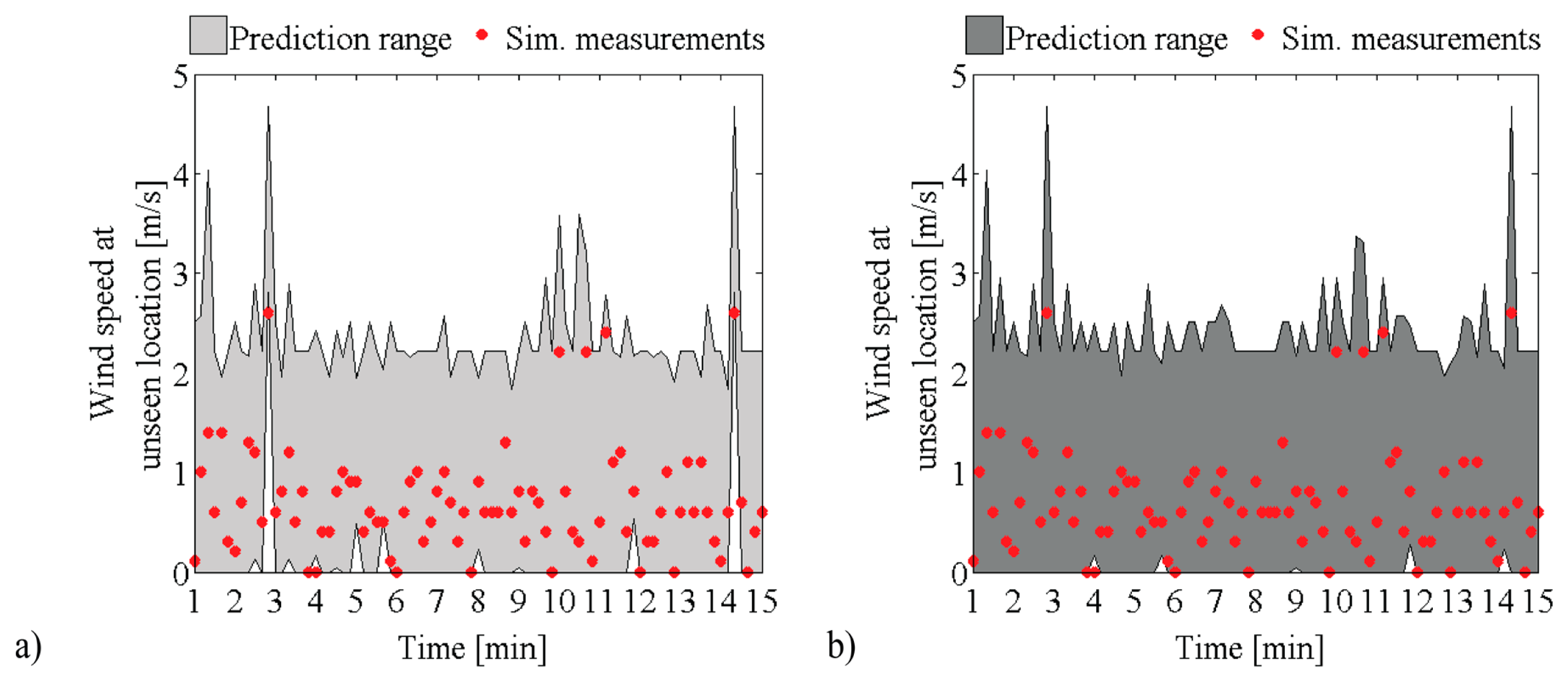
The performance of the sensor placement strategy is evaluated by demonstrating that optimal sensor configurations can improve wind predictions through the following three metrics: reducing the number of candidate models, minimizing the prediction range and increasing the accuracy of predictions. During performance evaluation, simulated measurements are created at optimum locations through combining predictions of the initial model set with modeling and measurement uncertainties. Historically, measured data from a full-scale study, available at other sensor locations, are used to create a more realistic distribution; it is assumed that the sample distribution at the same locations should follow the probability distribution of the measured data.
2.1. Errors in Wind-Speed and Wind-Direction
Measurements are essential for theory testing, yet in order to be useful they need to be accurate and precise. Collecting incorrect measurements results in misleading conclusions about the state of the system. The term accuracy is linked to how close the measurement is to the actual value. Precision is an indication of the consistency of a measurement. Obtaining precise measurements does not imply that they are accurate and accurate measurements are not necessarily precise. A good measurement system should perform well in terms of both these characteristics. In addition, for the purpose of this study, CFD simulations are used to obtain wind predictions and these predictions include modeling errors whose influence is taken into account.
In order to incorporate modeling and measurement uncertainties in the sensor placement strategy, a histogram of model predictions is built at potential sensor locations
j = 1, ...,
ns, where
ns is a predetermined number of possible locations. The width of the histogram intervals is computed such that the frequency count in each interval is the number of model predictions that lie within the error threshold if the measured value is at the midpoint of the interval. This is done by dividing the maximum range of prediction values, max{(
Ymax,j −
ymin,j):
j = 1, ...,
ns} of an output variable
y into intervals
i = 1, ...,
NI (
NI the maximum number of intervals at the
jth location) of width
W equal to the sum of measurement errors
emeasur and modeling errors
emod (
Figure 2). The intervals create subsets of model predictions that are then used to compute probabilities and entropy. Each subset represents model predictions that, given a potential measurement, will not be possible to separate further.
2.2. Hierarchical Sensor Placement
A hierarchical sensor placement strategy has been used to identify optimum sensor locations that increase the entropy in wind predictions. High entropy at a sensor location represents uniform distribution of model predictions among the intervals, which means that the sensor location has high potential to separate model predictions. Given a measurement at this location a large number of models will be falsified and a small number of candidate models will remain. Locations are selected iteratively during sensor placement in order to maximize the entropy of the sensor configuration. The advantage of employing a hierarchical strategy is reduced computational cost through the use of an efficient data structure. The proposed algorithm is described in pseudo-code in
Algorithm 1.
Algorithm 1.
Pseudo-code of the hierarchical algorithm.
Algorithm 1.
Pseudo-code of the hierarchical algorithm.
| 1: | Create a list locationList containing all possible locations. |
| 2: | Create a set sensorOptimum to store all possible sensors. The set is empty to start with. |
| 3: | Create a set modelSubsets to store subsets of models that cannot be separated using the current sensor configuration. To start with this set contains a single element, which is the initialModelSet. |
| 4: | Add the first sensor location that corresponds to maximum entropy to sensorOptimum. |
| 5: | Create a list of subsets of models that cannot be separated by the first sensor location and add these subsets to modelSubsets. Remove the initialModelSet from modelSubsets. |
| 6: | Repeat while locationList is not empty |
| { |
| 7: | Select a sensor location from locationList, let it be currentLocation. |
| 8: | Repeat for each set in modelSubsets |
| { |
| 9: | Divide and distribute models in the current set into intervals of the currentLocation. |
| } |
| 10: | Calculate the entropy of the distribution of the currentLocation. |
| } |
| 11: | Select the sensor location with maximum entropy. Add to sensorOptimum and remove from locationList. |
Model data is organized in a tree structure in which the initial model set (called initialModelSet in the algorithm description) is at the root, and branches contain subsets of model predictions (modelSubsets). Branches from a node in the tree represent division of the parent model set into smaller groups that can potentially be separated using measurements from the new sensor that is added to the configuration at each level in the tree. The number of model subsets that cannot be further separated with the sensor configuration at each stage (sensorOptimum) is stored for evaluating the performance of the configuration (more details are provided in Section 3.3).
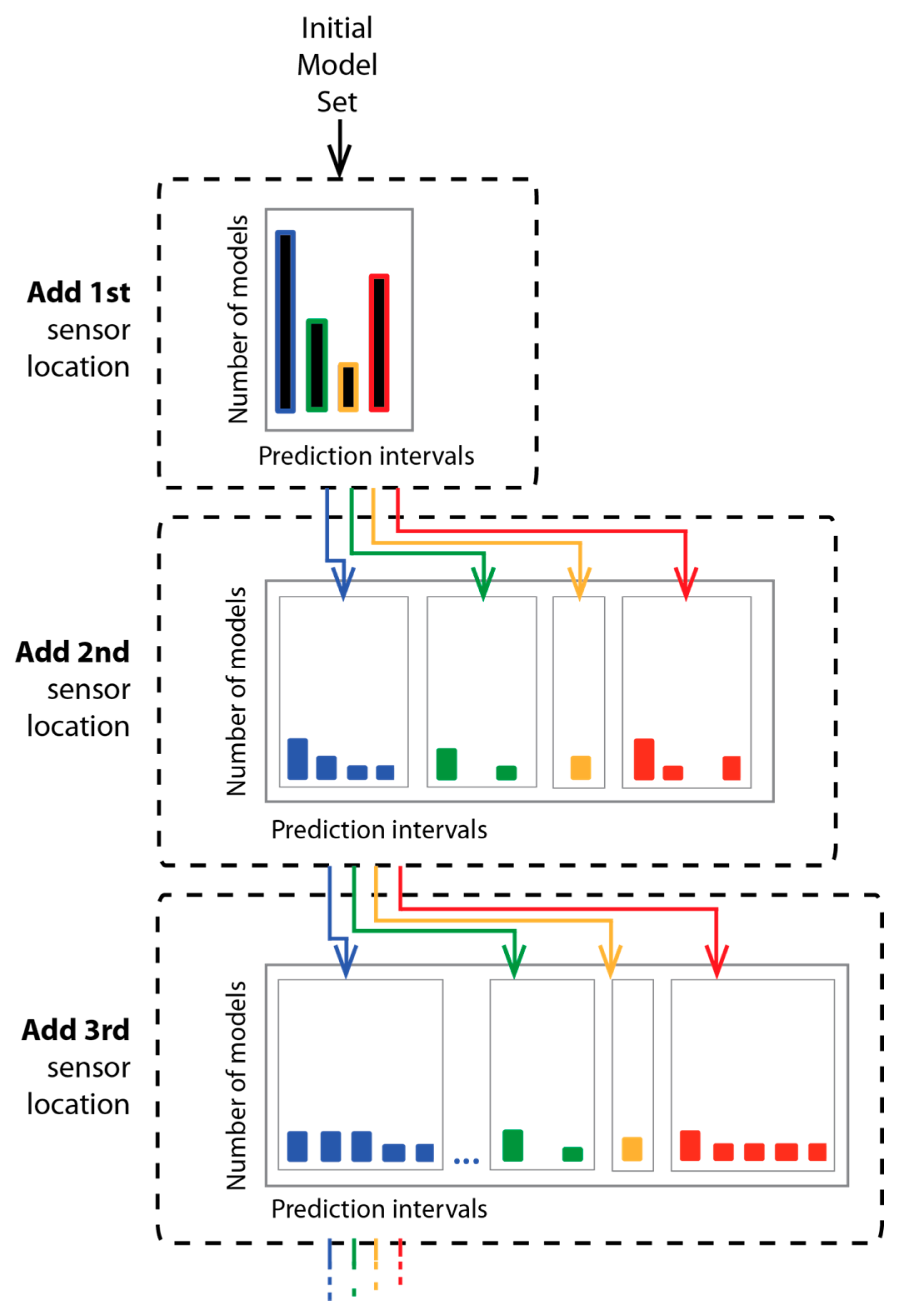
Figure 3 provides a schematic of the hierarchical sensor placement strategy proposed in this work. At the top of the figure is shown the intervals of model predictions at the first sensor location. Each interval contains a subset of models, which is shown in a different color. When the second sensor is added to the configuration, the subset in each interval is further subdivided. The rectangular box in the middle of
Figure 3 shows the intervals of model predictions of each subset at the second sensor location. This process is repeated to form a hierarchy of model subsets.
A tree data structure follows a hierarchical organization and takes advantage of an O(constant) computational complexity. At each stage of the sensor placement, a location is added to the configuration sensorOptimum that divides the existing subsets of model predictions into smaller subsets. The maximum number of divisions is restricted to the number of models within the prediction subsets.
2.3. Joint Entropy as a Design Criterion
The information obtained from measured data is clearly a major criterion for selecting sensor locations and this can be evaluated using entropy from information theory (also known as Shannon’s entropy or Information entropy). The importance of entropy is that it is a measure of uncertainty in parameter values, since it evaluates disorder in predictions. Here entropy is defined as:
where H(y)j is the entropy of a random variable y at a measurement location j, p(yi)j is the probability of the ith interval of a variable’s distribution with i = 1, ..., NI and NI the maximum number of intervals at the jth location. In order to compute the entropy, the number of models that lie within each interval mi is calculated and the probability of the interval is calculated as (mi/N).
Equation (1) is used to calculate the entropy of a variable at one sensor location. However, during sensor placement more than one location is selected. Adding sensors to the sensor configuration requires evaluating the common information between multiple sensor locations; it avoids selecting locations that are redundant. For example, the next sensor location having the highest entropy might contain substantially similar information as the previous sensor location. Therefore, selecting this sensor location does not improve the information obtained.
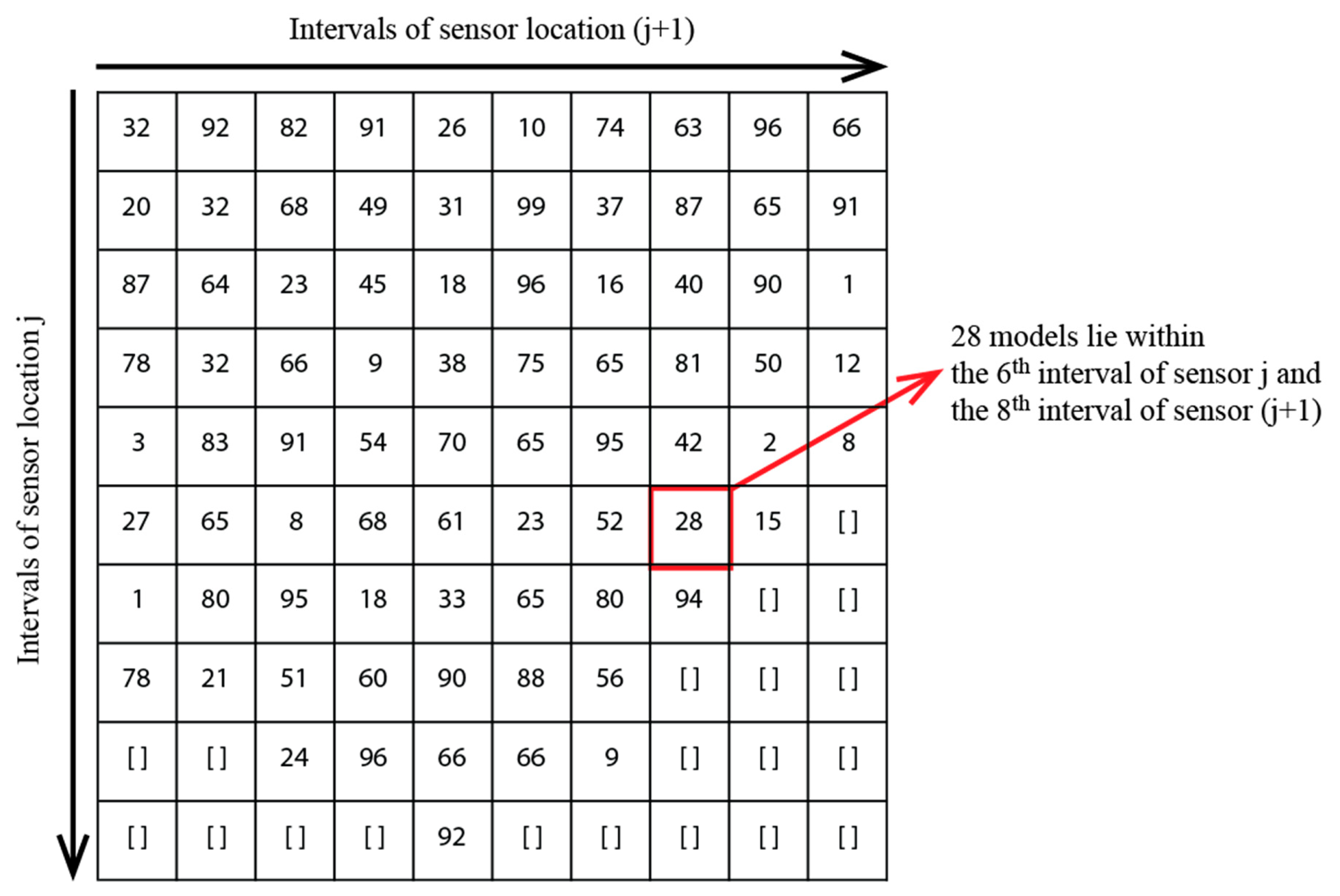
Joint entropy is a measure of uncertainty associated with multiple variables. It requires evaluating multiple sensor configurations while including the mutual information of data. In order to calculate joint entropy of two sensor locations
j and (
j + 1), the models that lie within each interval of location
j are further divided into sub-intervals using values of location (
j + 1) resulting in a rectangular grid (
Figure 4).
When this process is repeated for more sensors, a multi-dimensional grid corresponding to each combination of intervals is obtained. Then, the probability of each sub-interval is calculated by dividing the number of models in the sub-interval by the total number of models. The entropy between two sensor locations j and (j + 1), and the relation to mutual information, I(y)j,j+1 is defined as:
where i = 1, ..., Nk and Nk the maximum number of intervals at the location (j + 1).
From
Equations (2) and
(3) in order to calculate joint entropy all prediction subsets of the two sensor locations must be evaluated. In this work sensor placement is performed prior to measuring and no data is available, therefore all prediction subsets need to be evaluated. In forward sequential strategies, when the number of sensors increases, computation cost increases exponentially if a multi-dimensional regular grid is used to organize model subsets. This is because probabilities have to be summed up over every combination of intervals corresponding to each variable [
34]. In contrast, in a hierarchical strategy, when a new sensor is added to the configuration, the subsets of model predictions either remain the same or are further subdivided (
Figure 3) causing the probability to be further divided. The hierarchical strategy analyses how the initial models are distributed within subsets, which allows calculations of joint entropy of the sensor configurations, thereby avoiding exponential complexity.
3. Results
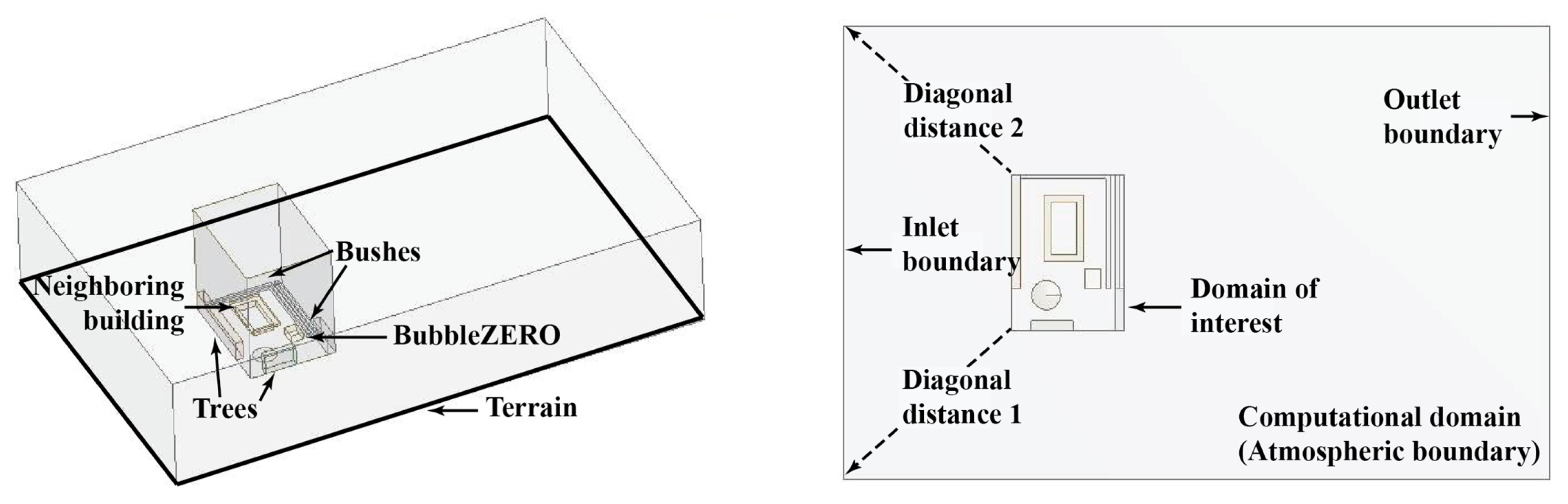
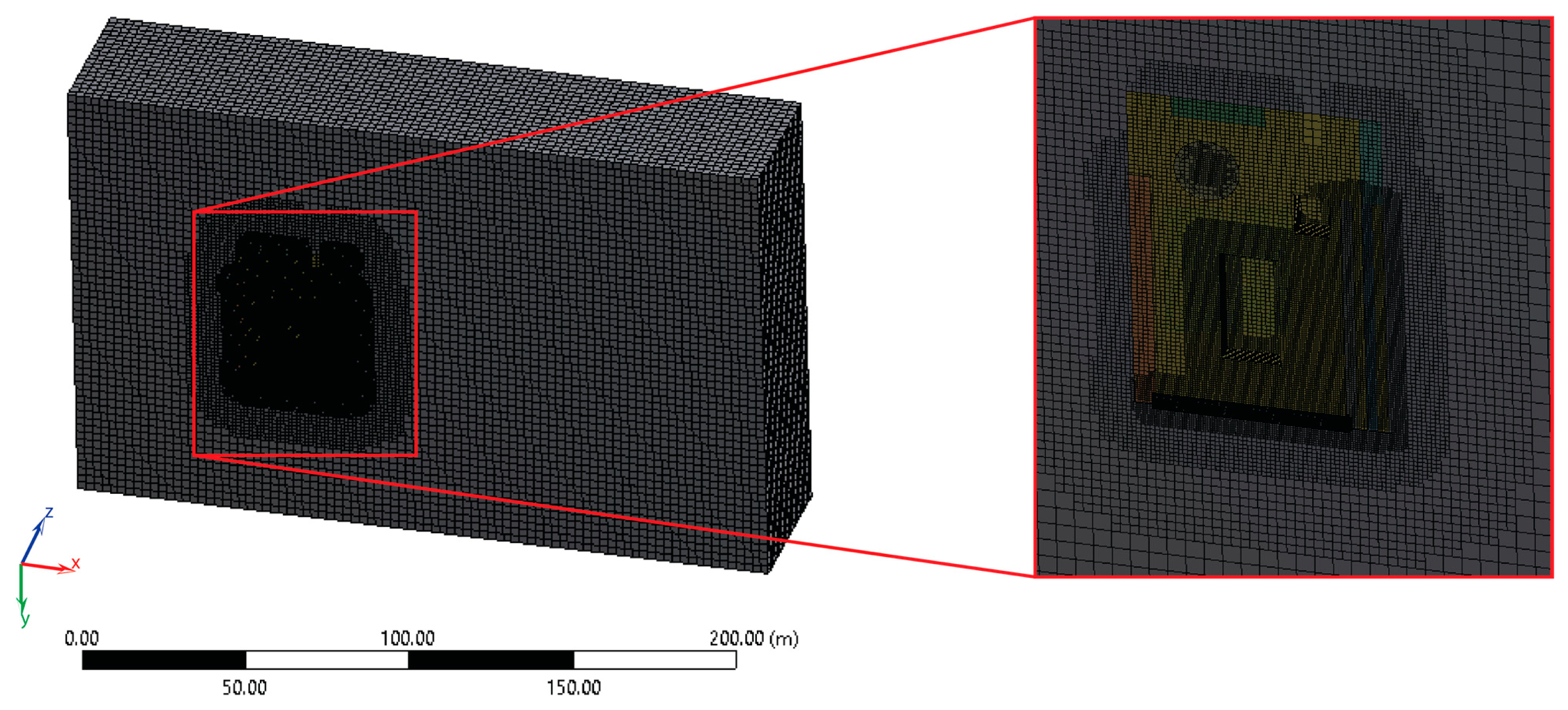
The sensor placement strategy was applied to lab-type building called BubbleZERO, which is an experimental facility of rectangular geometry, with dimensions 4.88 m × 6.06 m × 2.9 m, located at NUS Campus in Singapore. Wind modeling and CFD simulations around BubbleZERO were performed with ANSYS Workbench 14.5, a platform that offers FLUENT as a solver for the equations of flow and design exploration tools for sensitivity analysis and feature selection.
In the first stage of simulations, simplifications were made according to recommendations [
11,
12] in the geometrical representations of the BubbleZERO and the surrounding obstacles, as well as in the numerical methods that control the solver. The simulation volume, called computational domain, represented the atmospheric boundary domain with dimensions 220 m × 140 m × 40 m (
Figure 5). The entire domain was decomposed into finite elements, using the CutCell meshing method, within which an approximate solution was sought (
Figure 6). CutCell meshing is as a discretization method that generates a high percentage of hexahedral elements with minimum user input; it results in a quicker solver run time and better convergence compared to tetrahedral meshes. The SIMPLE algorithm was employed in order to achieve pressure-velocity coupling and a second-order discretization scheme in order to interpolate pressure values from the elements center to the faces. A single-precision solver was selected as sufficiently accurate for this study.
In the quantification stage, the behavior of the system was characterized by a set of mathematical models, parameters, variables and constants that describe flow motion. The mathematical models were selected in order to minimize computational cost and were: the steady RANS-equations, the realizable k-ɛ equations to represent turbulence and the standard wall-functions to treat near-wall turbulence. In total 15 parameters were selected related to the geometry, meshing as well as parameters for wall boundary conditions, such as terrain and surface roughness, for porous boundary conditions, such as the inertial resistance of vegetation and for atmospheric boundary conditions, such as wind speed, wind direction, turbulence kinetic energy (TKE) and turbulence eddy dissipation (TDE). Details of the parameters and their values are shown in
Table 1 (in Fluent the term boundary conditions is a general term used to describe bounds between fluid and solid regions; for instance the terrain roughness is a boundary-condition parameter of the wall boundary: terrain [
34]). Plausible ranges were specified for all parameter values based on engineering judgment and literature where available. For instance, the mesh growth rate, the rate at which the mesh grows away from the boundary, varied from 1.05 to 1.1 resulting in approximately 5.2 × 10
5 and 10.4 × 10
5 mesh elements.
where U(z) is the wind speed at height z, u* is the atmospheric-boundary-layer friction (or shear) velocity, z0 the surface roughness and κ ≅ 0.41 the von Kármán constant:
where k is the turbulence kinetic energy and Cμ a model constant:
where ɛ(z) is the turbulence eddy dissipation at height z.
In FLUENT, the surface roughness is represented by the roughness height, z0, which is modified using the equivalent sand-grain roughness, ks,ABL:
where Cs is the roughness constant, set to satisfy the constraint ks,ABL ≤ zp, and zp is the grid resolution (the distance of the centroid of the wall-adjacent cell to the wall).
Vegetation was modeled as porous media,
C, with inertial resistance set in the x- and y-direction as [
38]:
where
Cd is the drag coefficient, varying from 0.1 to 0.5, and
dSA is the local leaf-area density, with range 1 to 7 [
39].
Multiple, steady-state CFD simulations were run varying values of the identified parameters within the plausible ranges shown in
Table 1. In order to reduce computational complexity, sensitivity analysis was performed using ANSYS DesignXplorer: an Optimal Space-Filling design [
40] and CCD sampling [
41] were selected that reduced that number of simulations to 283. The simulations output variables were wind speed and wind direction and their output distributions were built as full second-order polynomial response-surface, which are expressed as a function of the input parameters. Predictions of wind speed and direction were obtained at 63 possible sensor locations, fixed uniformly and in close distance to the BubbleZERO (
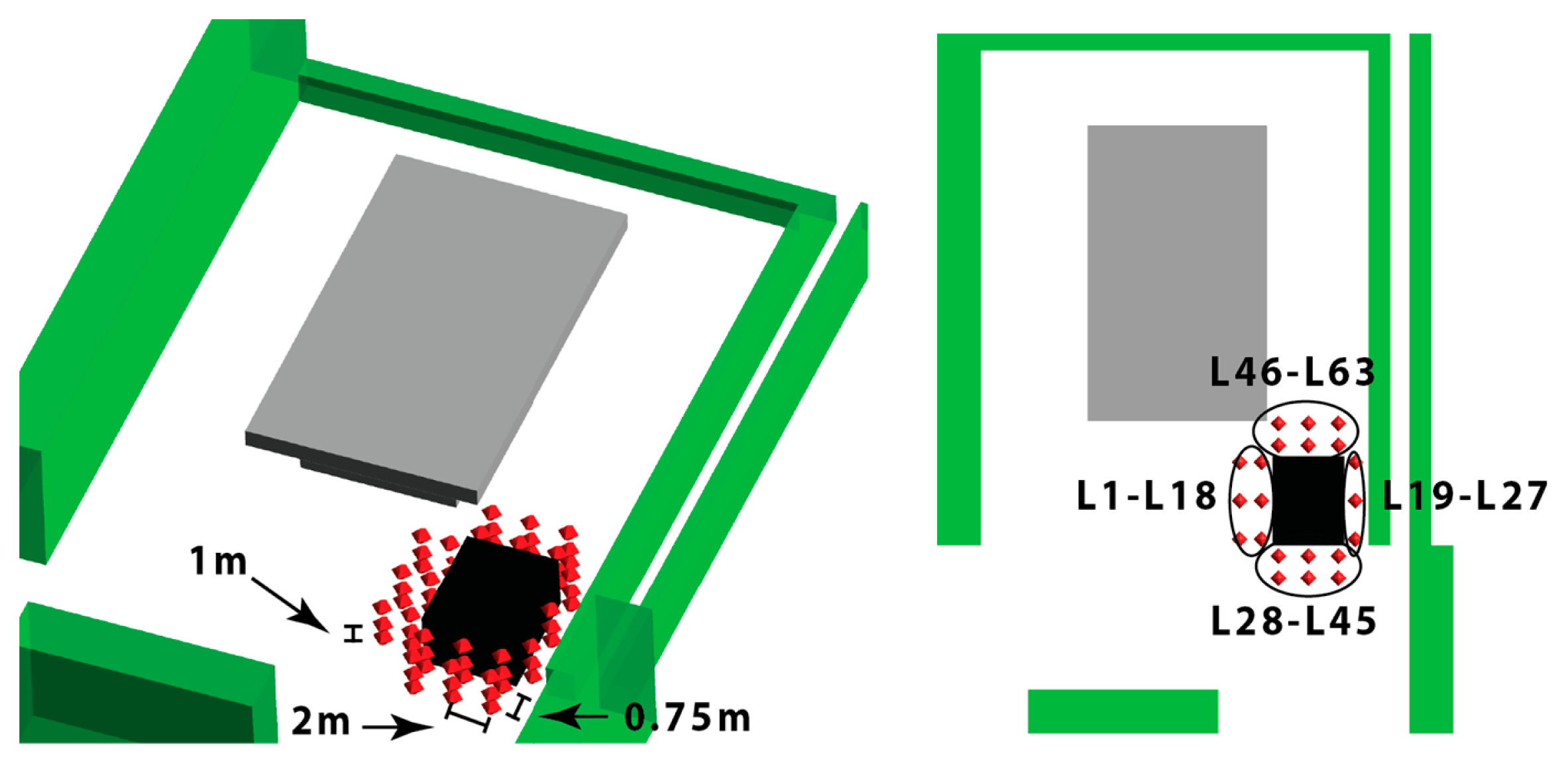
Figure 7). These locations were selected in order to be in proximity to the BubbleZERO. The dimensions of the BubbleZERO, the measurement equipment characteristics and the orography were considered during the selection of the possible locations.
Spearman’s rho correlation coefficient
ρj (
Equation (6)) was calculated between the 15 parameters and the wind predictions over all measurement locations. The wind speed, the wind direction and the turbulence kinetic energy at the inlet boundary were identified as the features with the highest impact on wind predictions (with average coefficients of 0.35, 0.35 and 0.8, respectively, for both output variables and over all locations):
where xk,j, yk,j are the ranks of the input parameters and output variables respectively at each location j ∈ {1, …, 63}, with k = 1, …, n the size of the sample and x̄j, ȳj the mean values.
A second set of multiple steady-state CFD simulations were performed varying values of these features within plausible ranges using a simple-grid sampling and selecting values uniformly within the ranges. A set of 1024 combinations of values was created that were used to run simulations and obtain a discrete population of wind predictions at the 63 sensor locations. This population of model instances of wind speed and wind direction formed the initial model set.
A hierarchical sensor placement strategy was employed using the initial model set in order to reveal optimal sensor configurations. Since model predictions were used in sensor placement, systematic modeling errors, as well as spatial correlations between errors, were considered. Recent research in our group has demonstrated that the range of modeling errors can vary from location to location between [−0.6, +0.4] and [−1, +0.8] m/s for wind speed and [−30, +30] and [−180, +180] deg for wind direction, depending on boundary conditions and sensor locations [
33]. Indeed, errors associated with wind direction can be the most that is possible—up to 180 degrees both ways—due to the RANS-based modeling used in this work, since time-averaged equations of flow motion are carried out. Although steady-state RANS is one of the most computational efficient approaches to approximate turbulent flows, thereby allowing multiple simulations to be run, it does not model small-scale local vortices that occur in reality due to local disturbances. The following systematic modeling errors with non-uniform spatial distribution were used for wind speed,
emod,speed, and wind direction,
emod,dir, following [
33]:
where uj(z) is the wind speed at height z at possible sensor locations j ∈ {1, …, 63}. Wind direction with
were not considered since modeling errors were high (around ±180 deg).
3.1. Effect of Modeling Error
The effect of modeling error on sensor placement is evaluated through comparing a sensor placement strategy that includes spatial variations in modeling errors against a strategy that assumes uniform values for errors at every location. Variations in error values are defined according to
Equations (7) and
(8), while uniform error-values are set constant and equal to the upper and lower bounds of the estimated ranges (Section 3). Measurement errors depend on the characteristics of the measurement equipment and for this case, error ranges are set to 0.1 m/s for wind speed and 22.5 deg for wind direction. At each stage of the sensor placement, a location was added to the optimum configuration and the joint entropy in wind predictions was calculated.
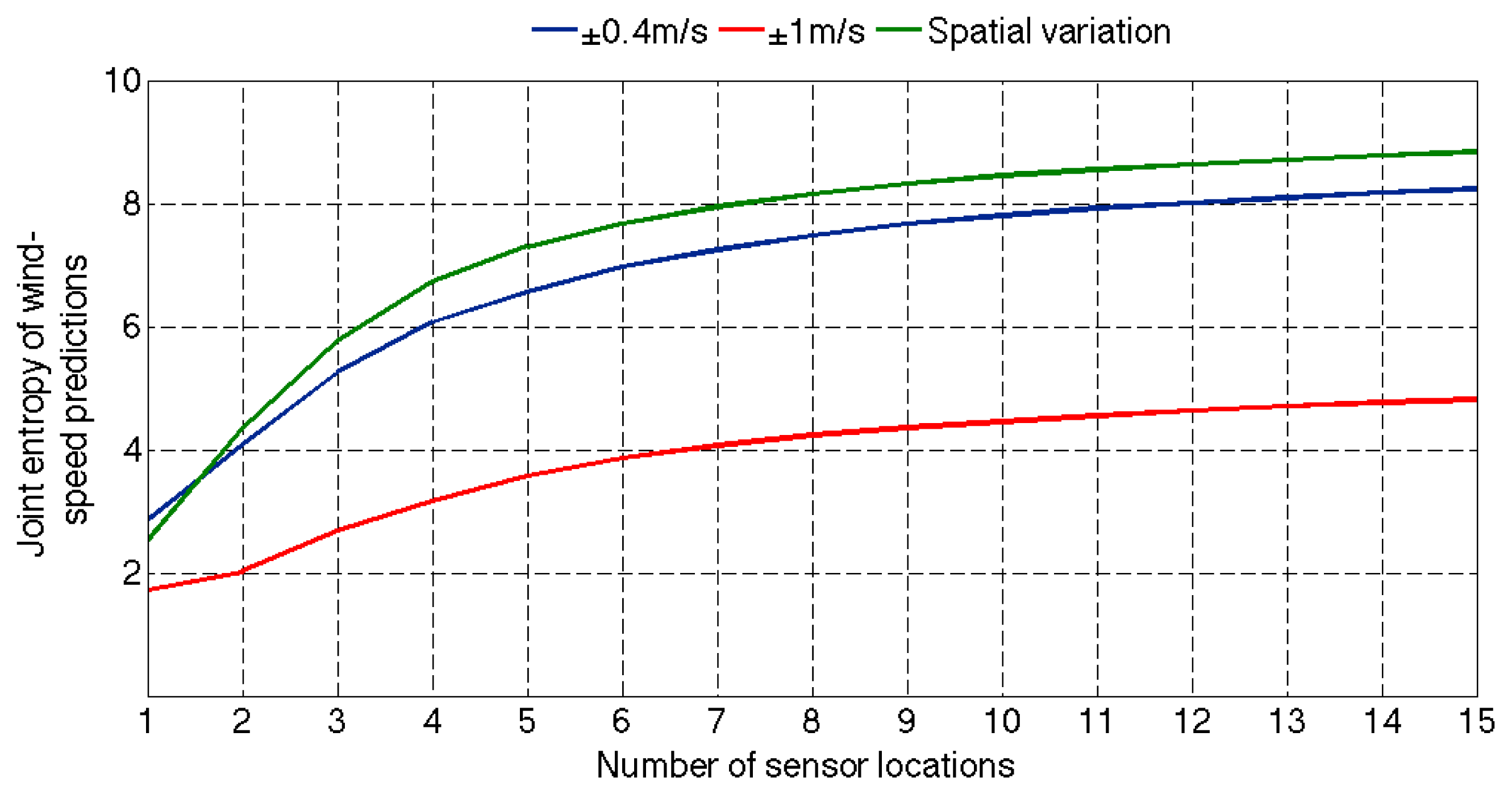
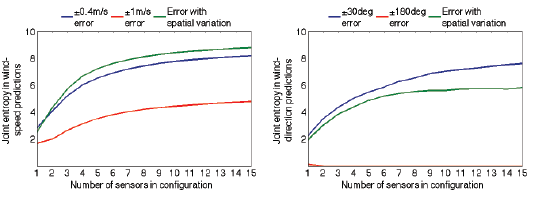
Figure 8 shows a comparison of the calculated joint entropy in wind-speed predictions of optimal sensor configurations, when either spatially uniform (±0.4 and ±1 m/s) or varying modeling errors (
Equation (7)) are considered. The increase in joint entropy is higher when the spatial variation in modeling errors is considered during sensor placement. In addition, entropy values are found to be higher when compared with using uniform and constant values of modeling errors, particularly when modeling errors are large.
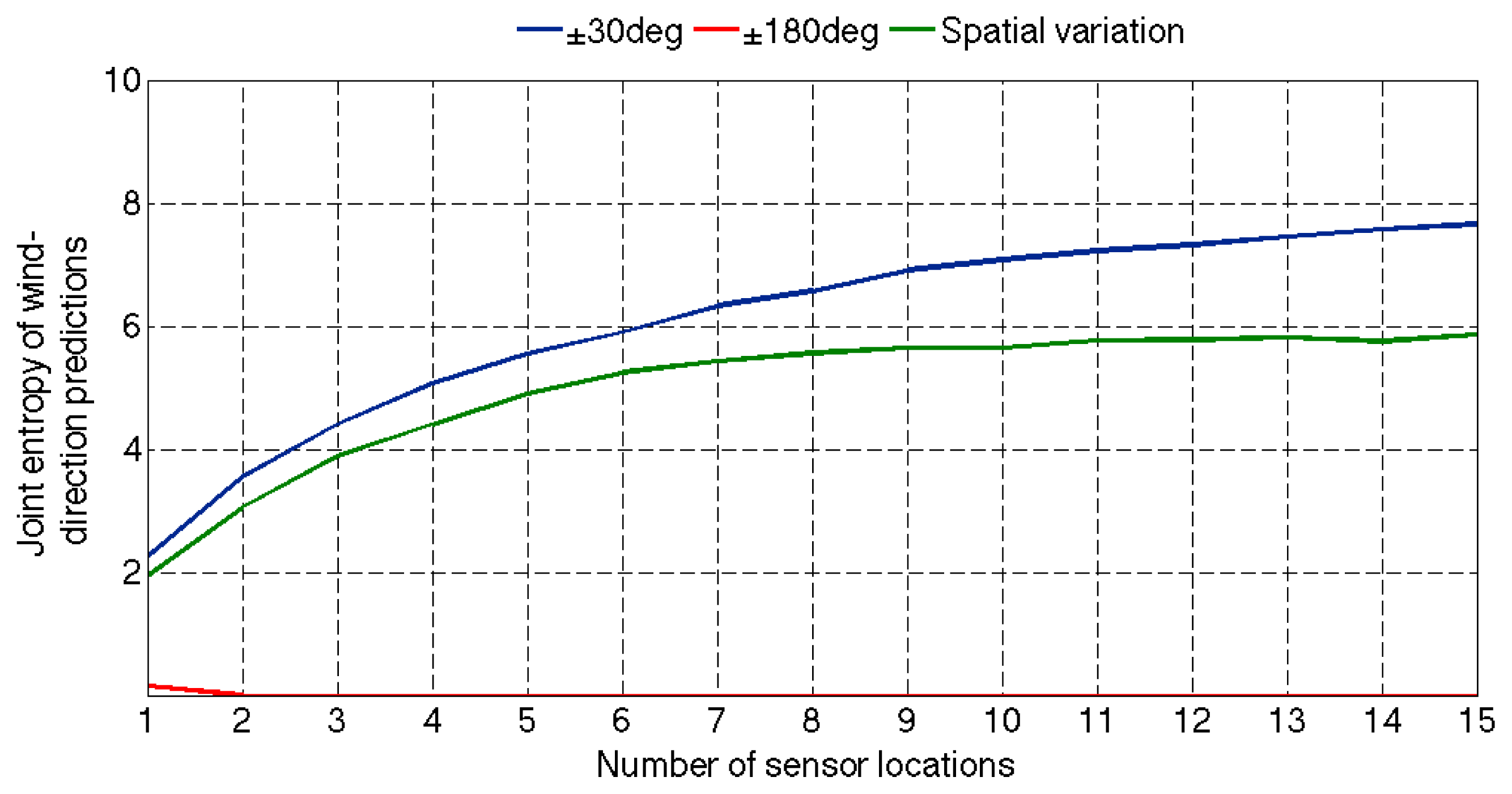
Figure 9 presents the joint entropy in wind-direction predictions of optimal sensor configurations, when either spatially uniform (±30 and ±180 deg) or varying modeling errors are considered (
Equation 8). Although using small and uniformly distributed errors (±30 deg) leads to a high increase in joint entropy, this increase stabilizes slower than using spatial variations in errors. Finally, assuming large and spatially uniform modeling errors (±180 deg), does not provide any optimum sensor location.
The results demonstrated that during sensor placement, the joint entropy in wind predictions is influenced by the spatial distribution of modeling errors that is assumed. In contrast with wind speed, using small and uniform errors identifies locations of that provide high entropy increase in wind direction. However the entropy increase stabilizes faster for both wind speed and wind direction when spatially variations in errors are included.
3.2. Optimum Sensor Configurations
Figure 10 provides a comparison of the calculated joint entropy in wind predictions using optimum configurations for wind speed and wind direction and including spatial variations in modeling errors. Overall, the entropy in wind speed is higher than that in wind direction, for the same number of sensor locations. For the purpose of this paper, an incremental change in joint entropy below half a unit is taken to be insignificant. This occurs after the 6th sensor is added to the configurations for wind-speed and wind-direction predictions.
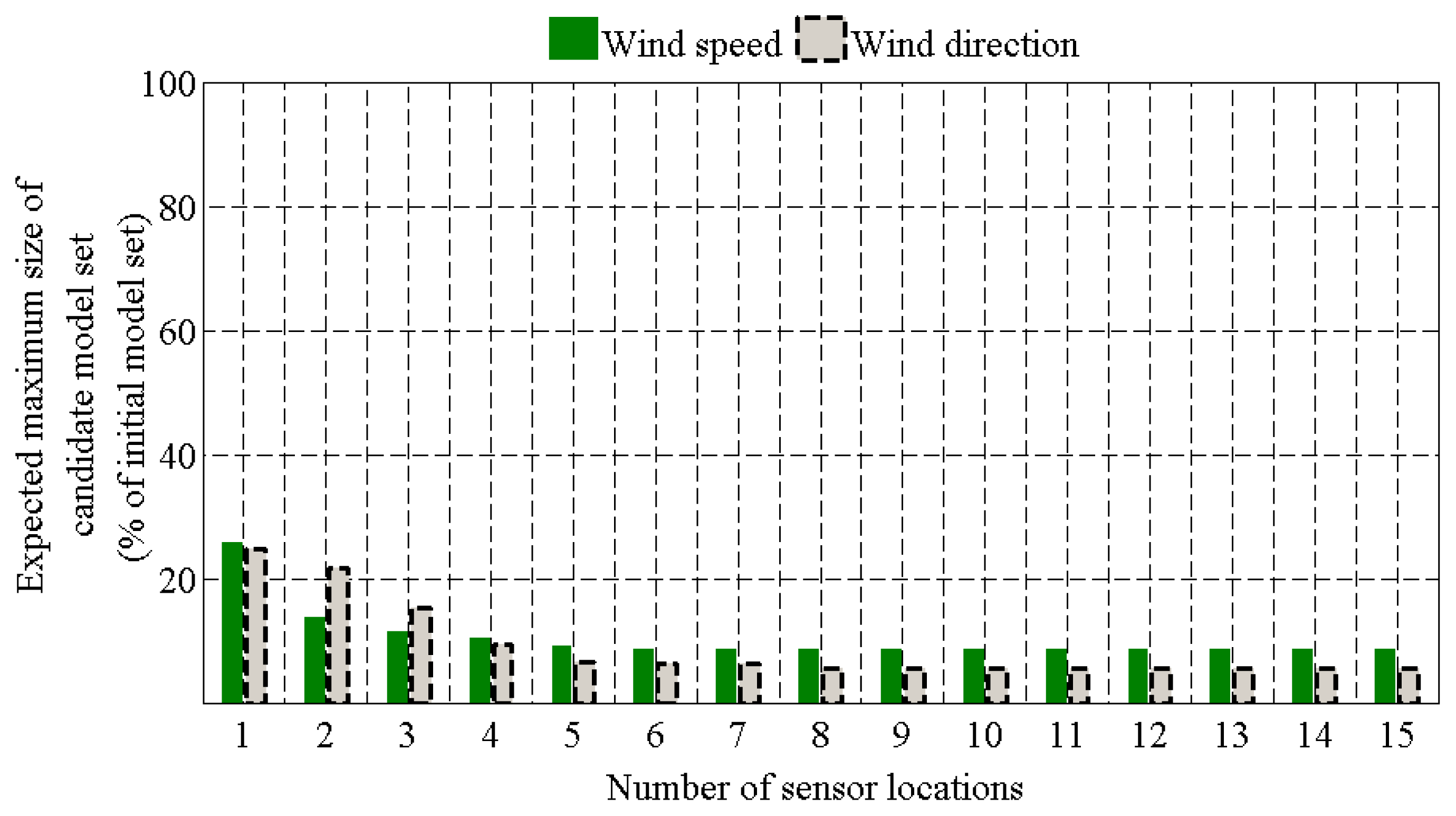
Figure 11 shows the expected maximum number of candidate models of wind speed and wind direction during sensor placement; spatial variations in modeling errors are included. Less than 1/5 of the model instances of wind speed and wind direction are retained using a sensor configuration of two sensors. Similarly to
Figure 10, the incremental reduction in the maximum number of candidate models stabilizes after the 4th sensor for both wind-speed and wind-direction predictions. The maximum number of candidate models of wind speed and of wind direction is retained to around 10% of the initial model set after the 4th sensor location was selected.
Figure 12 illustrates the optimum configurations of four sensors for wind-speed and wind-direction predictions in the simulation environment. The selected sensor locations for predicting wind speed are different from that for predicting wind direction: for wind speed locations are selected near all façades except the south, while for wind direction locations are selected near all façades except the east. One sensor location is commonly identified as optimal for predicting both wind speed and direction—location L16. Locations L39 and L37 have the same position, although L39 is at 2.7 m height and L37 at 0.6 m height (
Table 2).